1. Four scales, traditionally ascribed to St. Ambrose (A.D. 384), existed before the time of St. Gregory. These, known as the 'Authentic' modes, and since the 13th century named after the ancient Greek scales (from which they were supposed to be derived) are as follows: 1. Dorian, 2. Phrygian, 3. Lydian, 4. Mixo-lydian.

Each mode thus consists of 8 natural notes of the Diatonic scale—a perfect fifth, or diapente, below, joined to a perfect fourth, or diatessaron, above. The lowest note of the scale is called the 'Final' (corresponding to the Tonic of the modern scale) because though the melody may range through the entire octave it ends regularly on that note; and the fifth note above the final, that which forms the junction of the diapente and diatessaron, is called the 'Dominant,' except in the Phrygian mode, where C was substituted for B♮.[1]
The term Dominant in the ancient scales has not the same meaning that it has in modern tonality, but means the predominating sound in each mode, the note on which the recitation is made in each Psalm or Canticle tone.
One peculiarity of these ancient scales to modern ears is, that the place of the semitones varies in each; in the Dorian occurring between the 2nd and 3rd, 6th and 7th notes; in the Phrygian between the 1st and 2nd, 5th and 6th, and so on. The range of notes, from the lowest to the highest, in any ancient melody (seldom exceeding 8 or 9 notes) partly determines the mode to which it belongs. In some cases, melodies of small compass have their Tone determined by the Final of other portions of Plain Song preceding and following them. To the Dorian scale, for example, belong melodies extending from D (or C) upwards and having D as their Final.
The well-known tune, Luther's 'Ein feste Burg' (see p. 484a), ranging from F, its key-note or final, to the octave, may be mentioned in illustration of a modern tune in a quasi-Authentic mode.
2. To the 4 Authentic, St. Gregory added 4 'Plagal,' i.e. collateral or relative modes. Each is a 4th below its corresponding original, and is called by the same name, with the prefix hypo (ὑπο, below), as follows: 5. Hypo-dorian, 6. Hypo-phrygian, 7. Hypo-lydian, 8. Hypo-mixo-lydian[2]. Each scale here also consists of a perfect fifth and a perfect fourth; but the positions are reversed; the fourth is now below, and the fifth above.

In the Plagal scales the 'Final' is no longer the lowest note, but is the same as that in the corresponding Authentic scale. Thus the Final of the Hypo-dorian mode is not A but D, and a melody in that mode, though ranging from about A to A, ends regularly on D, as in the Dorian. As an exemplification of this, we may mention Handel's 'Hanover,' among modern tunes, which ranges from F to F, but has its Final on B♭. 'Should auld acquaintance be forgot' is also a specimen of a tune in a Plagal mode descending about a fourth below its final, and rising above it only six notes, closing upon the final of its tone. The semitones in each scale naturally vary as before. The Dominants of the new scales are in each case a third below those of the old ones, C being however substituted for B♮ in the Hypo-mixo-lydian, as it had been before in the Phrygian, on account of the irregularity of the relations between B♮ and the F above and below.
3. The system was afterwards further extended by the addition of two more Authentic scales having their Finals on A and C, and their Dominants on E and G, and called the Æolian (No. 9) and Ionian (No. 10)—
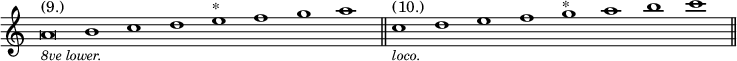
and two corresponding Plagal modes the Hypo-æolian (No. 11) and Hypo-ionian (No. 12):—
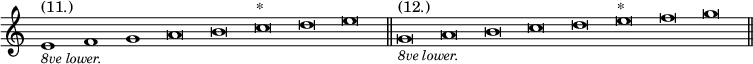
and the whole formed one great scheme, in which the Authentic modes were the 1st, 3rd 5th, 7th, 9th and 11th, and the Plagal ones the 2nd, 4th, 6th, 8th, 10th and 12th.
| No. | Mode. | Compass. | Final or Tonic. |
Domi- nant. |
| 1 | Dorian | D to D | D | A |
| 2 | Hypo-dorian | A to A | D | F |
| 3 | Phrygian | E to E | E | C |
| 4 | Hypo-phrygian | B to B | E | A |
| 5 | Lydian | F to F | F | C |
| 6 | Hypo-lydian | C to C | F | A |
| 7 | Mixo-lydian | G to G | G | D |
| 8 | Hypo-mixo-lydian | D to D | G | C |
| 9 | Æolian | A to A | A | E |
| 10 | Hypo-æolian | E to E | A | C |
| 11 | Ionian | C to C | C | G |
| 12 | Hypo-ionian | G to G | C | E |
4. Some inventors or innovators have however broken from the trammels of the perfect diapente and diatessaron law, and make the
