8th[1]—it must have been almost impossible for an Organist, playing with both hands, to avoid sounding concordant intervals simultaneously: and, when once the effects thus produced were imitated in singing, the first step towards the invention of Polyphony was already accomplished. This granted, nothing could be more natural than that the Instrument should lend its name to the new style of singing it had been the accidental means of suggesting; or that the Choristers who practised that method of vocalisation should be called Organizers, though we well know that they sang without any instrumental accompaniment whatever, and that they were held in high estimation for their readiness in extemporising such harmony as was then implied by the term Organum. A Necrologium of the 13th century, quoted by Du Cange, ordains, in one place, that 'the Clerks who organize the "Alleluia," in two, three, or four parts, shall receive six pence'; and in another, that 'the Clerks who assist in the Mass shall have two pence, and the four Organizers of the "Alleluia" two pence each.' This 'organization of the Alleluia' meant nothing more than the addition of one single Third, which was sung below the penultimate note of a Plain Chaunt Melody, in order to form a Cadence. When this Cadence was in two parts only, it was sung by two Tenors; when a third part was added, it was sung an Octave above the Canto fermo, by the Voice called 'Triplum' (whence our word Treble); the fourth part, a Quadruplum, was added in the Octave above the Organum, thus—
In Two Parts.

In Three Parts.
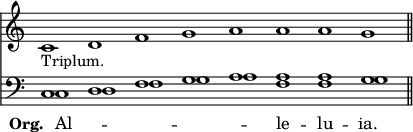
In Four Parts.

After a time the single Third gave place to a continuous Organum. The earliest writer who gives us any really intelligible account of the method of constructing such a Harmony is Hucbaldus, a Monk of S. Amand sur l'Elnon, in Flanders, who died at a very advanced age in the year 930, and whose attempts to improve the Notation of Plain Chaunt have already been described at page 469 of the present volume. It is noticeable that, though the multilinear Stave proposed by this learned Musician is mentioned as his own invention, he prefers no claim to be regarded as the originator of the new method of Singing, but speaks of it as a practice 'which they commonly call organization.' He understood it, however, perfectly; and gives very clear rules for its construction. From these we learn that, though it is perfectly lawful to sing a Plain Chaunt Melody either in Octaves or doubled Octaves, this method cannot fairly be said to constitute a true Organum, which should be sung either in Fourths or Fifths as shown in the following examples.
In Fourths.

In Fifths.

When four Voices are used, either the Fourths or the Fifths may be doubled.


These two methods, in which no mixture of Intervals is permitted, have been called by some modern historians Parallel-Organum, in contradistinction to another kind, in which the use of Seconds and Thirds is permitted, on condition that two Thirds are not allowed to succeed one another. Hucbald describes this also as a perfectly lawful method, provided the Seconds and Thirds are introduced only for the purpose of making the Fourths move more regularly.


To the modern student this stern prohibition of even two Consecutive Thirds, where any number of Consecutive Fifths or Octaves are freely permitted, is laughable enough; but our mediæval ancestors had some reason on their side. In the days of Hucbald, the Mathematics
- ↑ An Organ was presented to King Pepin by the Emperor Constantine VI. in 797.
