The images within the first sphere form a converging series, the sum of which is
This therefore is the quantity of electricity on the first or interior sphere. The images outside the second sphere form a diverging series, but the surface-integral of each with respect to the spherical surface is zero. The charge of electricity on the exterior spherical surface is therefore
If we substitute for these expressions their values in terms of , and , we find
charge on
charge on
If we suppose the radii of the spheres to become infinite, the case becomes that of a point placed between two parallel planes and . In this case these expressions become
charge on ,
charge on .
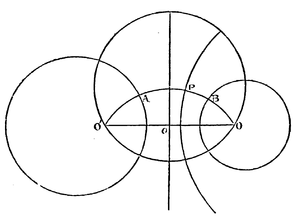
172.] In order to pass from this case to that of any two spheres not intersecting each other, we begin by finding the two common inverse points through which all circles pass that are orthogonal to both spheres. Then, inverting the system with respect to either of these points, the spheres become concentric, as in the first case.
The radius on which the successive images lie becomes an arc of a circle through and , and the ratio of to is















