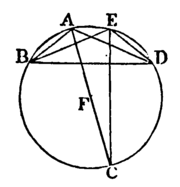
Next, let the segment BAED be not greater than a semicircle.
Draw AF to the centre, and produce it to meet the circumference at C, and join CE.
Then the segment BAEC is greater than a semicircle, and therefore the angles BAC, BEC in it, are equal, by the first case. For the same reason, because the segment CAED is greater than a semicircle, the angles CAD, CED are equal.
Therefore the whole angle BAD is equal to the whole angle BED. [Axiom 2.
Wherefore, the angles in the same segment &c. q.e.d.
PROPOSITION 22. THEOREM.
The opposite angles of any quadrilateral figure inscribed in a circle are together equal to two right angles.
Let ABCD be a quadrilateral figure inscribed in the circle ABCD: any two of its opposite angles shall be together equal to two right angles.
Join AC, BD.
Then, because the three angles of every triangle are together equal to two right angles, [I. 32.
the three angles of the triangle CAB, namely, CAB, ACB, ABC are together equal to two right angles.
But the angle CAB is equal to the angle CDB, because they are in the same segment CDAB; [III. 21.
and the angle ACB is equal to the angle ADB, because they are in the same segment ADCB;
therefore the two angles CAB, ACB are together equal to the whole angle ADC. [Axiom 2.
To each of these equals add the angle ABC;
