Then AG is equal to GC; [III. 3.
therefore the rectangle AE, EC, together with the square on EG, is equal to the square on AG. [II. 5.
To each of these equals add the square on GF;
then the rectangle AE, EC, together with the squares on EG, GF, is equal to the squares on AG, GF. [Axiom 2.
But the squares on EG, GF are equal to the square on EF;
and the squares on AG, GF are equal to the square on AF. [I. 47.
Therefore the rectangle AE, EC, together with the square on EF, is equal to the square on AF,
that is, to the square on FB.
But the square on FB is equal to the rectangle BE, ED, together with the square on EF. [II. 5.
Therefore the rectangle AE, EC, together with the square on EF, is equal to the rectangle BE, ED, together with the square on EF.
Take away the common square on EF;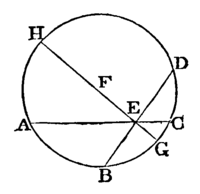
then the remaining rectangle AE, EG is equal to the remaining rectangle BE, ED. [Axiom 3.
Lastly, let neither of the straight lines AG, BD pass through the centre. Take the centre F, [III. 1.
and through E, the intersection of the straight lines AG, BD, draw the diameter GEFH.
Then, as has been shewn, the rectangle GE, EH is equal to the rectangle AE, EG, and also to the rectangle BE, ED; therefore the rectangle AE, EC is equal to the rectangle BE, ED. [Axiom 1.
Wherefore, if two straight lines &c. q.e.d.
