the angle B as the ſine of the angle AOQ + E + G to the radius; and an angle I to the angle N - AQQ E - G + H, as the length L is to the ſame length L diminiſhed by the co-ſine of the angle AQQ + E - G when that angle is leſs than a right angle, or increaſed there by when greater. And ſo we may proceed in infinitum. Laſtly, take the angle AOq equal to the angle AOQ + E + G + I + &c. and from its co-ſine Or and the ordinate pr, which is to its line ſine as the leſſer axis of the ellipſis to the greater, we ſhall have p the correct place of the body. When the angle N - AOQ + D happens to be negative, the ſign + of the angle E muſt be every where changed into -, and the ſign - into +. And the ſame thing is to be underſtood of the ſigns of the angles G and I, when the angles N - AOQ - E + F, and N - AOQ - E - G + H come out negative. But the infinite ſeries AOQ + B + G + I &c. converges ſo very faſt, that it will be ſcarcely ever needful to proceed beyond the ſecond term E. And the calculus is founded upon this theorem, that the area APS is as the difference between the arc AQ and the right line let fall from the focus S perpendicularly upon the radius OQ
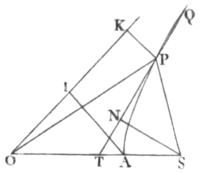
And by a calculus not unlike, the problem is ſolved in the hyperbola. Let its centre be O, (Pl. 14. Fig. 4.) its vertex A, its focus S, and aſymptote OK. And ſuppoſe the quantity of the area to be cut off is known, as being proportional to the time. Let that be A, and by conjecture ſuppoſe we know the poſition of a right line SP, that cuts off an area APS near the truth. Join OP, and from A and P to the aſymptote draw AI, PK parallel to the other aſymptote
