The Mathematical Principles of Natural Philosophy (1729)/Book 1/Section 9

Section IX.
Of the motion of bodies in moveable orbits; and of the motion of the apsides.
Proposition XLIII. Problem XXX.
It is required to make a body move, in a trajectory that revolves about the centre of force, in the same manner as another body in the same trajectory at rest.

In the orbit VPK (Pl. 18. Fig. 1.) given by position, let the body P revolve, proceeding from V towards K. From the centre C let there be continually drawn Cp, equal to CP, making the angle VCp proportional to the angle VCP; and the area which the line Cp describes, will be to the area VCP which the line CP describes at the same time, as the velocity of the describing line Cp, to the velocity of the describing line CP; that is, as the angle VCp to the angle VCP, therefore in a given ratio, and therefore proportional to the time. Since then the area described by the line Cp in an immovable plane is proportional to the time, it is manifest that a body, being acted upon by a just quantity of centripetal force, may revolve with the point p in the curve line which the same point p, by the method just now explained, may be made to describe in an immovable plane. Make the angle VCu equal to the angle PCp, and the line Cu equal to CV and the figure uCp equal to the figure VCP, and the body being always in the point p, will move in the perimeter of the revolving figure uCp, and will describe its (revolving) arc up in the same time that the other body P describes the similar and equal arc VP in the quiescent figure VPK. Find then by cor. 5. prop. 6. the centripetal force by which a body may be made to revolve in the curve line which the point p describes in an immovable plane, and the problem will be solved. Q. E. F.
Proposition XLIV. Theroem XIV.
The difference of the forces, by which two bodies may be made to move equally, one in a quiescent, the other in the same orbit revolving, is in a triplicate ratio of their common altitudes inversely.
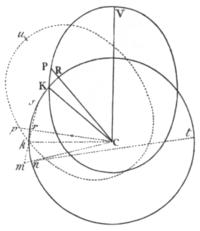
Let the parts of the quiescent orbit VP, PK, (Pl. 18. Fig. 2.) be similar and equal to the parts of the revolving orbit up, pk; and let the distance of the points P and K be supposed of the utmost smallness. Let fall a perpendicular kr from the point k to the right line pC, and produce it to m, so that mr may be to kr as the angle VCp to the angle VCP. Because the altitudes of the bodies, PC and pC, KC and kC, are always equal, it is manifest: that the increments or decrements of the lines PC and pC are always equal; and therefore if each of the several motions of the bodies in the places P and p be resolved into two, (by cor. 2. of the laws of motion) one of which is directed towards the center, or according to the lines PC, pC, and the other, transverse to the former, hath a direction perpendicular to the lines PC and pC; the motions towards the centre will be equal, and the transverse motion of the body p will be to the transverse motion of the body P, as the angular motion of the line pC to the angular motion of the line PC; that is, as the angle VCp to the angle VCP. Therefore at the same time that the body P, by both its motions, comes to the point K, the body p, having an equal motion towards the centre, will be equally moved from p towards C, and therefore that time being expired, it will be found somewhere in the line mkr, which, passing through the point k, is perpendicular to the line pC; and by its transverse motion, will acquire a distance from the line pC, that will be to the distance which the other body P acquires from the line PC, as the transverse motion of the body p, to the transverse motion of the other body P. Therefore since kr is equal to the distance which the body P acquires from the line PC, and mr is to kr as the angle VCp to the angle VCP, that is as the tranvers motion of the body p, to the transverse motion of the body P: it is manifest that the body p, at the expiration of that time, will be found in the place m. These things will be so, if the bodies p and P are equally moved in the directions of the lines pC and PC, and are therefore urged with equal forces in those directions. But if we take an angle pCn that is to the angle pCk as the angle VCp to the angle VCP, and nC be equal to kC in that case the body p at the expiration of the time will really be in n; and is therefore urged with a greater force than the body P, if the angle nCp is greater than the angle kCp, that is, if the orbit upk move either in consequantia, or in antecedentia with a celerity greater than the double of that with which the line CP moves in consequentia; and with a less force if the orbit moves flower in antecedentia. And the difference of the forces will be as the interval mn of the places through which the body would be carried by the action of that difference in that given space of time. About the centre C with the interval Cn or Ck suppose a circle described cutting the lines mr, mn produced in s and r, and the rectangle mn x mt will be equal to the rectangle mk x ms, and therefore mn will be equal to . But since the triangles pCk, pCn, in a given time, are of a given magnitude, kr and mr, and their difference mk, and their sum mr, are reciprocally as the altitude pC, and therefore the rectangle 'mk x rm is reciprocally as the square of the altitude pC. But moreover mr is directly as ms, that is, as the altitude pC. These are the first ratio's of the nascent lines; and hence , that is, the nascent lineola mn, and the difference of the forces proportional thereto, are reciprocally as the cube of the altitude pC. Q. E. D.
Cor. 1. Hence the difference of the forces in
the places P and p, or K and k, is to the force
with which a body may revolve with a circular
motion from R to K, in the same time that the
body P in an immovable orb describes the arc
PK, as the nascent line mn to the versed sine of
the nascent arc RK, that is as to ,
or as mk x ms to the square of rk; that is,
if we take given quantities F and G in the same
ratio to one another as the angle VCP bears to
the angle VCp, as GG - FF to FP. And there.
fore if from the centre C with any distance CP
or Cp, there be described a circular sector equal
to the whole area VPC, which the body revolving
in an immovable orbit, has by a radius
drawn to the centre described in any certain time;
the difference of the forces, with which the body
P revolves in an immovable orbit and the body
p in a moveable orbit, will be to the centripetal
force, with which another body by a radius drawn to
the centre can uniformly describe that sector in
the same time as the area VPC is described, as
CG - FF to FP. For that sector and the area
pCk are to one another as the times in which they
are described.
Cor. 2. If the orbit VPK be an ellipsis having its focus C, and its highest apsis V, and we suppose the ellipsis upk similar and equal to it, so that pC may be always equal to PC, and the angle VCp be to the angle VCP in the given ratio of G to F; and for the altitude PC or pC we put A, and a R for the latus rectum of the ellipsis; the force with which a body may be made to revolve in a moveable ellipsis will be as and vice versa. Let the force with which a body may revolve in an immovable ellipsis, be expressed by the quantity , and the force in V will be . But the force with which a body may revolve in a circle at the distance CV with the same velocity as a body revolving in an ellipsis has in V, is to the force with which a body revolving in an ellipsis is acted upon in the apsis V, as half the latus rectum of the ellipsis, to the semi-diameter CV of the circle, and therefore is as ; and the force which is to this as CG - FF to FF, is as (by cor. 1. of this prop.) is the difference of the forces in V with which the body P revolves in the immovable ellipsis VPK, and the body p in the moveable ellipsis upk, Therefore since by this prop. that difference at any other altitude A is to it self at the altitude CV as to , the same difference in every altitude A will be as . Therefore to the force , by which the body may revolve in an immovable ellipsis VPK, add the excess and the sum will be the whole force by which a body may revolve in the same time in the moveable ellipsis upk.
Cor. 3. In the same manner it will be found that if the immovable orbit VPK be an ellipsis having its centre in the centre of the forces C; and there be supposed a moveable ellipsis upkk similar, equal, and concentrical to it; and 2 R be the principal latus reclum of that ellipsis, and 2 T the latus transversum or greater axis; and the angle VCp be continually to the angle VCP as G to F; the forces with which bodies may revolve in the immovable and moveable ellipsis in equal times, will be as and resperctively.
Cor. 4. And universally, if the greatest altitude CV of the body be called T, and the radius of the curvature which the orbit VPK has in V, that is, the radius of a circle equally curve, be called R, and the centripetal force with which a body may revolve in any immovable trajectory VPK at the place K be called , and in other places P be indefinitely stiled X; and the altitude CP be called A, and G be taken to F in the given ratio of the angle VCp to the angle VCP: the centripetal force with which the same body will perform the same motions in the same time in the same trajectory mpk revolving with a circular motion, will be as the forces .
Cor. 5.. Therefore the motion of a body in an immovable orbit being given, its angular motion round the centre of the forces may be increased or diminished in a given ratio, and thence new immovable orbits may be found in which bodies may revolve with new centripetal forces.

Cor. 6. Therefore if there be erected (Pl. 18. Fig.
3.) the line VP of an indeterminate length, perpendicular
to the line CV given by position, and
CP be drawn, and Cp equal to it, making the angle
VCp having a given ratio to the angle VCP;
the force with which a body may revolve in the
curve line Vpk, which the point p is continually
describing, will be reciprocally as the cube of the
altitude Cp. For the body P, by its vis inertiæ
alone, no other force impelling it, will proceed
uniformly in the right line VP. Add then a force
tending to the centre C reciprocally as the cube of
the altitude CP or Cp, and (by what was just demonstrated)
the body will deflect from the rectilinear
motion into the curve line Vpk, But this curve
Vpk is the same with the curve VPQ found in cor.
3. prop. 41. in which, I said, bodies attracted with
such forces would ascend obliquely.
Proposition XLV. Problem XXXI.
To find the motion of the apsides in orbits approaching very near to circles.
This problem is solved arithmetically by reducing the orbit, which a body revolving in a moveable ellipsis (as in cor. 2. and 3 of the above prop.) describes in an immovable plane, to the figure of the orbit whose apsides are required; and then seeking the apsides of the orbit which that body describes in an immovable plane. But orbits acquire the same figure, if the centripetal forces with which they are described, compared between themselves, are made proportional at equal altitudes. Let the point V be the highest apsis, and write T for the greatest altitude CV, A for an other altitude CP or Cp, and X for the difference of the altitudes CV - CP, and the force with which a body moves in an ellipsis revolving about its focus C (as in cor. 2.) and which in cor. 2. was as , that is as , by substituting T - X for A will become . In like manner any other centripetal force is to be reduced to a fraction whose denominator is A and the numerators are to be made analogous by collating together the homologous terms. This will be made plainer by examples.
Exam 1.. Let us suppose the centripetal force to be uniform, and therefore as , or, writing T - X for A inthe numerator, as . Then collating together the correspondent terms of the numerators, that is, those that confist of given quantities. with those of given quantities, and those of quantities not given, with those of quantities not given, it will become RGG - EFF + TFF to as - FFX to or as - FF to - 3TT + 3TX - XX. Now since the orbit is supposed extreamly near to a circle, let it coincide with a circle, and because in that case R and T become equal, and X is infinitely diminished, the last ratio's will be, as RGG to so - FF to 3TT, or as GG to TT so FF to 3TT, and again as GG to FF so TT to 3TT, that is, as 1 to 3; and therefore G is to F, that is, the angle VCp to the angle VCP as 1 to, . Therefore since the body, in an immoveable ellipsis, in descending from the upper to the lower apsis, describes an angle, if I may so speak, of 180 deg. the other body in a moveable ellipsis, and therefore in the immovable orbit we are treating of, will, in its descent from the upper to the lower apsis, describe an angle VCp of deg. And this comes to pas by reason of the likeness of this orbit which a body acted upon by an uniform centripetal force describes, and of that orbit which a body performing its circuits in a revolving ellipsis will describe in a quiescent plane. By this collation of the terms, these orbits are made similar, not universally indeed, but then only when they approach very near to a circular fugure. A body therefore revolving with an uniform centripetal force in an orbit nearly circular, will always describe an angle of deg. or 103 deg. 55 m. 23 sec. at the centre; moving from the upper apsis to the lower apsis when it has once described that angle, and thence returning to the upper apsis when it has described that angle again; and so on in infinitum.
Exam. 2. Suppose the centripetal force to be as any power of the altitude A, as for example or ; where n - 3 and n signify any indices of powers whatever, whether integers or fractions, rational or surd, affirmative or negative. That numerator or being reduced to an indeterminate series by my method of converging series, will become &c. And conferring these terms with the terms of the other numerator RGG - RFF + TFF - FXX, it becomes as RGG - RFF + TFF to so - FF to &c. And taking the last ratio's where the orbits approach to circles, it becomes as RGG to so -FF to , or as GG to so FF to , and again GG to FF so to , that is, as 1 to n; and therefore G is to F, that is the angle VCp to the angle VCP as 1 to . Therefore since the angle VCP, described in the descent of the body from the upper apsis to the lower apsis in an ellipsis, is of 180 deg. the angle VCp, described in the descent of the body from the upper apsis to the lower apsis in an orbit nearly circular which a body describes with a centripetal force proportional to the power , will be equal to an angle of deg. and this angle being repeated the body will return from the lower to the upper apsis, and so on in infinitum. As if the centripetal force be as the distance of the body from the centre, that is, as A, or , n will be equal to 4 and, equal to 2; and therefore the angle between the upper and the lower apsis will be equal to deg. or 90 deg. Therefore the body having performed a fourth part of one revolution will arrive at the lower apsis, and having performed another fourth part, will arrive at the upper apsis, and so on by turns in infinitum. This appears also from prop. 10. For a body acted on by this centripetal force will revolve in an immovable ellipsis, whose centre is the centre of force. If the centripetal force is reciprocally as the distance, that is, directly as or as , n will be equal to 2, and therefore the angle between the upper and lower apsis will be of deg. or 127 deg. 16 min. 45 sec. and therefore a body revolving with such a force, will, by a perpetual repetition of this angle, move alternately from the upper to the lower, and from the lower to the upper apsis for ever. So also if the centripetal force be reciprocally as the biquadrate root of the eleventh power of the altitude, that is reciprocally as and therefore directly as or as , as will be equal to and deg. will be equal to 360 deg. and therefore the body parting from the upper apsis, and from thence perpetually descending will arrive at the lower apsis when it has compleated one entire revolution; and thence ascending perpetually, when it has compleated another entire revolution it will arrive again as the upper apsis; and so alternately for ever.
Exam. 3.. Taking m and n for any indices of the powers of the altitude, and b and c for any given numbers, suppose the centripetal force to be as or (by the method of converging series above-mentioned) as &c. and comparing the terms of the numerators, there will arise RGC - RFF + TFF to as -FF to &c. And taking the last ratio's that arise when the orbits come to a circular form, there will come forth GG to as FF to and again GG to FF as to . This proportion. by expressing the greatest altitude CV or T arithmetically by unity, becomes, GG to FF as b + c to mb + nc, and therefore as 1 to . Whence G becomes to F, that is the angle VCp to the angle VCP as 1 to . And therefore since the angle VCP between the upper and the lower apsis, in an immovable ellipsis, is of 180 deg. the angle VCp between the same apsides in an orbit which a body describes with a centripetal force. that is as will be equal to an angle of deg. And by the same reasoning if the centripetal force be as the angle between the apsides will be found equal to deg. After the same manner the problem is solved in more difficult cases. The quantity to which the centripetal force is proportional. must always be resolved into a converging series whose denominator is . Then the given part of the numerator arising from that operation is to be supposed in the same ratio to that part of it which is not given, as the given part of this numerator RGG - RFF + TFF - FFX is to that part of the same numerator which is not given. And taking away the superfluous quantities and writing unity for T, the proportion of G to F is obtainecx
Cor. 1. Hence I the centripetal force be as any power of the altitude. that power may be found from the motion of the apsides; and so contrary-wise. That is, if the whole angular motion, with which the body returns to the same apsis, be to the angular motion of one revolution. or 360 drg. as any number as m to another as n, and the altitude called A; the force will be as the power of the altitude A; the index of which power is . This appears by the second examples. Hence 'tis plain that the force in its recess from the centre cannot decrease in a greater than a triplicate ratio of the altitude. A body revolving with such a force and parting from the apsis, if it once begins to descend can never arrive at the lower apsis or least altitude, but will descend to the centre. describing the curve line treated of in cor. 3. prop. 41. But if it should, at its parting from the lower apsis begin to ascend never so little, it will ascend in infinitum and never come to the upper apsis; but will describe the curve line spoken of in the lame cot. and cor. 6. prop. 44. So that where the force in its recess from the centre descreases in a greater than a triplicate ratio of the altitude, the body at its parting from the apsis, will either descend to the centre or ascend in infinitum, according as it descends or ascends at the beginning of its motion. But if the force in its recess from the centre either decreases in a less than a triplicate ratio of the altitude, or increases in any ratio of the altitude whatsoever; the body will never descend to the centre, but will at some time arrive at the lower apsis; and on the contrary, if the body alternately ascending and descending from one apsis to another never comes to the centre, then either the force increases in the recess from the centre, or it decreases in a less than a triplicate ratio of the altitude; and the sooner the body returns from one apsis to another, the farther is the ratio of the forces from the triplicate ratio. As if the body should return to and from the upper apsis by an alternate descent and ascent in 8 revolutions, or in 4, or 2. or 1; that is if an should be to n as 8 or 4 or or 2 or 1, and therefore be , or , or , or , then the force will be as , or , or , or ; that is, it will be reciprocally as , or , or , or , If the body after each revolution returns to the same apsis, and the apsis remains unmoved, then m will be to n as 1 to 1, and therefore will be equal to or and therefore the decrease of the forces will be in a duplicate ratio of the altitude; as was demonstrateds above. If the body in three fourth parts or two thirds, or one third; or one fourth part of an entire revolution, return to the same apsis; m will be to n as or or or or to 1, and therefore is equal to or , or , or ; and therefore the force is either reciprocally as or or directly as or . Lastly, if the body in its progress from the upper apsis to the same upper apsis again, goes over one entire revolution and three deg. more, and therefore that apsis in each revolution of the body moves three deg. in consequentia; then m will be to n as 363 deg. to 360 deg. or as 121 to 120, and therefore will be equal to and therefore the centripetal force will be reciprocally as or reciprocally as very nearly. Therefore the centripetal force decreases in a ratio something greater than the duplicate; but approaching 59 times nearer to the duplicate than the triplicate.
Cor. 1. Hence also if a body, urged by a centripetal force which is reciprocally as the square of the altitude, revolves in an ellipsis whose focus is in the centre of the forces; and a new and foreign force should be added to or subducted from this centripetal force; the motion of the apsides arising from that foreign force may (by the third examples) be known; and so on the contrary. As if the force with which the body revolves in the ellipsis be as ; and the foreign force subducted as cA, and therefore the remaining force as ; then (by the third exam.) 6 will be equal to 1, m equal to 1, and n equal to 4; and therefore the angle of revolution between the apsides is equal to deg. Suppose that foreign force to be 357.45 parts less than the other force with which the body revolves in the ellipsis; that is c to be or T being equal to 1, and then will be 1 or 180.7623, that is, 180 deg. 45 min. 44 sec. Therefore the body parting from the upper apsis, will arrive at the lower apsis with an angular motion of 180 deg. 45 min. 44 sec. and this angular motion being repeated will return to the upper apsis; and therefore the upper apsis in each revolution will go forward 1 deg. 31 m. 28 sec. The apsis of the Moon is about twice as swift.
So much for the motion of bodies in orbits whose planes pass through the centre of force. It now remains to determine those motions in eccentrical planes. For those authors who treat of the motion of heavy bodies use to consider the ascent and descent of such bodies, not only in a perpendicular direction, but at all degrees obliquity upon any given planes; and for the same reason we are to consider in this place the motions of bodies tending to centres by means of any forces whatsoever. when those bodies move in eccentrical planes. These planes are supposed to be perfectly smooth and polished so as not to retard the motion of the bodies in the least. Moreover in thes demonstrations instead of the planes upon which those bodies roll or sslide, and which are therefore tangent plane; to the bodies, I shall use planes parallel to them, in which the centres of the bodies move, and by that motion describe orbits. And by the same method I afterwards determine the motions of bodies performed in curve superficies.





























































































