The Solar System/Chapter 4
IV
SATURN AND ITS SYSTEM
Saturn. Saturn marked to the ancients the outer boundary of the solar system. From its slow motion, they rightly conjectured it to be the farthest away of all the "wanderers," and wrongly to be sinister in intent. Our word "saturnine" expresses the feeling it inspired.
In the telescope, Saturn is undoubtedly the most immediately impressive object in the heavens. Few persons can be shown the planet for the first time without an exclamation. To see it sail into the field of view, its great ball diademed by an elliptic ring, and carrying with it a retinue of star-points set against the blue-black background of the sky, gives the most prosaic a sensation.
Saturn's self we shall leave till we come to speak of Jupiter (in the next chapter); and shall here consider the two systems of bodies dependent on it, its rings and its satellites.
The ring system.The Unique, so far as we know, is that appanage of Saturn which makes the planet so superb a sight,—the ring system. It baffled Galileo with his opera-glass, who first saw the planet triform, and then, to his surprise, marked the two smaller bodies disappear, as if Saturn had indeed eaten his offspring.
Crowning the planet's equator are several concentric flat rings of light. Three are usually distinguished, known as A, the outer ring ; B, the middle ring ; and C, the inner or dusky ring. The outer, A, has an extreme radius of about 85,700 miles. It is 12,000 miles across, and is separated from B by a dark space 3400 miles wide, known as Cassini's division. B, the broadest and brightest of the rings, is 17,000 miles in width, and is joined without perceptible interval by C, which is much fainter, resembling a crêpe veil stretched from the inner edge of B, 9500 miles toward the planet, from whose limb it is sundered by a gap of between 7000 and 8000 miles.
Two thirds way from the outer to the inner edge of A is another division or dark line, much narrower than Cassini's, and sometimes nearly invisible, known as Encke's division, though suspected before by Short.
Constitution of the rings.Edward Roche, in 1848, was the first to show that the rings were composed of discrete particles,—mere dust and ashes. He drew this sequence directly from his investigations on the minimum distance a small fluid satellite may safely approach a fluid primary; for within a certain distance the differential or tidal pull of the planet must disrupt the satellite. This distance is called Roche's limit.
For equal densities of planet and satellite, Roche's limit is 2.44 times the planet's radius ;
for unequal densities, as , where is the density of the primary; of the satellite.
Saturn's system offers the only instance where matter circulates within the limit, and Roche stated distinctly that the rings, therefore, must be mere meteoric stones.
Even Laplace had shown that the rings must be broken up for stability's sake into several narrow ones, each revolving at its own rate. Pierce proved that they could in no case be solid. Maxwell then demonstrated that they could not be so much as liquid, as disrupting waves would be set up, but must consist of a swarm of small bodies,—brickbats he likened them to,—each pursuing its own path. What the spectroscope in Keeler's ingenious hands made visible to the eye had thus been known to mechanics from the time of Laplace.
All in the same plane.These flights of small bodies are so exactly in one plane that they vanish when the rings are turned edgewise to the Earth. Their lustre shows them to be relatively densely packed, so that collisions among them must be not infrequent. In consequence of this, Maxwell predicted that they would eventually be forced both out or in, and in part fall upon the ball, in part be driven farther from the planet. Certainly such must ultimately happen; but the evidence is not conclusive that either process has yet been observed.
No air about them. The spectroscope shows that, unlike Saturn, they carry no air with them. This, from their minute size, was to be expected on the kinetic theory of gases and the clever deduction from it as to the atmosphere a body may retain, made by Johnstone Stoney.
Gaps in them.To attempt to account for their dimensions and divisions might at first seem hopeless. Why A is made up of an outer and an inner portion parted by Encke's streak; why B is sundered from A by Cassini's division; and why C is sharply contrasted with B at its inner edge, sound like difficult questions. But nothing in celestial mechanics is the outcome of chance, and this is no exception to the rule.
To begin with, Roche's limit falls just at the Roche's limit.outer edge of the system, supposing the density of the satellite to be of the primary's. Now the satellites of Saturn are certainly a little denser than the planet. From our present values of its mass and volume, Titan's density comes out .24. This, then, is what has limited the system externally.
For the rest of it, another force has proved fashioner.
Commenusrate periods.Our mathematics do not permit us to solve rigorously the problem of three bodies; that is, the motion of a first revolving round a second and perturbed by a third. We have to have recourse to approximations in series. We can thus determine to any degree of accuracy the result. Now the perturbative effect produced by a third body upon the major axis of a second revolving in its own plane may be expressed by a series developed in terms depending on powers of the eccentricity and cosines of multiple arcs of the mean motions. The typical form of one of these terms is
where is a function of and , the radii vectores.
From this, it appears that if and are nearly in the inverse ratio of the mean motions,
is nearly ,
If, then, the mean motions, and therefore the periods, of perturber and perturbed are commensurable, the disturbing effect upon the major axes of each will be great. The major axes will be altered until the periods cease to be commensurable, and it will be long before perturbation brings them back to commensurability again.
Greatest effect with the smallest ratio.Furthermore, the least value can have is
, while the period of the action of the term is ; whence the greatest term is when and are both as small as possible, since conjunctions will occur oftener in proportion as is small.
Effect Geometrically considered.Geometrically, the effect can be seen in the following way. Clearly, the disturbing pull is considered, greatest when the two bodies are in conjunction, and so long as the periods are incommensurable, conjunctions will occur in different parts of the orbit successively, and thus neutralize one another's effect upon the major axes. But if the periods of the two bodies be commensurable, conjunctions will occur in the same place over and over again, and the major axes will be altered there without compensatory alterations elsewhere;and this will go on until the major axes are so altered that commensurability of period, which depends on the major axis, ceases. Then the bodies will cease to affect each other forcibly. They will gradually meet each other elsewhere, finally oppositely to what they did at first, and the action first produced will be as gradually un-done; but it will be very long before the major axes attain their original value again; then they will pass rapidly through them once more in the reverse way.
If, then, the periods of the two bodies are commensurable, they will not appear to be so, since their major axes will stay commensurate but a brief time compared with the time they are out.
Gaps due to change of major axis.Now, if we have a swarm of bodies revolving at various distances round a central mass, and disturbed by a third, the third will seem, in consequence of this, to sweep out spaces where otherwise bodies would revolve in times commensurate with its own. Jupiter has done this very thing in the case of the asteroids, striping the zone with vacant belts. Calculation alone reveals this, as the asteroids are too few to disclose the fact to the eye. But in the rings of Saturn we can actually see the empty places. The gaps in the rings are shown in the following table and in the accompanying picture of the ring system :—

|
| Fig. X. Saturn's Rings. |
| Old Determination. |
New Determination. | |||
| Outer radius outer ring A | 84000 | 85700 | ||
| Encke's division | . | . | 80000 | 81010 |
| Inner radius outer ring A | 74000 | 75300 | ||
| Cassini's division | . | . | 73200 | 73620 |
| Outer radius ring B | . | . | 72400 | 71900 |
| Inner radius ring B | . | . | 56200 | 54700 |
| Outer radius ring C | . | . | 56200 | 54700 |
| Inner radius ring C | . | . | 46700 | 43900 |
| Planet radius... | . | . | 37500 | 37000 |
Gaps occasioned by Mimas.Let us note these gaps and edges and then calculate what perturbing effect the satellites would exert. The satellites which would have the greatest perturbative action on the rings is Mimas, his effect being more than three times that of Enceladus and more than twice that of Tethys.
The equations of motion are for x—
of which the first is the direct force of the central body, whose mass is taken as i, upon m; and the other terms are the perturbing force of m on m'.
Assuming the three to be in conjunction, this last becomes where . Supposing to be 74,000 miles from the centre of Saturn, and Mimas, Enceladus, and Tethys at 117,000, 150,000, and 186,000 miles respectively, and taking the masses as proportionate to their volumes, their radii being taken as 400, 400, and 600 miles, we find for their relative perturbative effects :—
| Mimas | . | . | . | . | . | . | . | 299 |
| Enceladus | . | . | . | . | . | . | . | 82 |
| Tethys | . | . | . | . | . | . | . | 110 |
The action of the others is smaller still. Now the major axis of a part of the ring which has a period commensurate with that of Mimas may be found from the formula —
Kepler's third law. Beginning, then, with the simplest, and therefore the most potent ratio, , we find 73,600 miles for the major axis of a particle whose period is that of Mimas. This distance falls almost exactly in the centre of Cassini's division.
Proceeding to the next simplest ratio, of Mimas's period, the corresponding distance comes out 56,170 miles. This is the distance from the centre of the planet to the inner edge of ring B.
Again, of the period of Mimas gives 46,370 miles. This is not far from the radius of the inner edge of the dark ring. So much for the action of Mimas.
By Enceladus.The major axis of one half the period of Enceladus falls without the system, but the major axis of one third the period occurs at 72,090 miles. This is not far from the inner edge of Cassini's division. But the striking coincidence with Enceladus is that the distance corresponding to of his period lies at 81,400 miles, or at Encke's division.
To Tehtys.For Tethys, the only commensurable ratio is . To Tethys.
This makes the distance fall at Cassini's division.
Thus Mimas, aided by Tethys, has been the divider of the rings into A, B, and C ; while Enceladus has subdivided A.
RELATIVE SIZE AND POSITION OF THE SATELLITES.
| No. | Name. | Diameter in Miles. |
Distance from Saturn in Miles. | |||||||
| I. | Mimas | . | . | . | 800 | . | . | . | . | 117,000 |
| II. | Enceladus | . | . | . | 800 | . | . | . | . | 150,000 |
| III. | Tethys | . | . | . | 1,200 | . | . | . | . | 186,000 |
| IV. | Dione | . | . | . | 1,100 | . | . | . | . | 238,000 |
| V. | Rhea | . | . | . | 1,500 | . | . | . | . | 332,000 |
| VI. | Titan | . | . | . | 3,500 | . | . | . | . | 771,000 |
| VII. | Hyperion | . | . | . | 500 | . | . | . | . | 934,000 |
| VIII. | lapetus | . | . | . | 2,000 | . | . | . | . | 2,225,000 |
Relative position of the masses of the satellites.It will be seen that the largest Titan - occupies a central position in the line. This might seem accidental until one recalls the fact that Jupiter, the largest of the planets, holds the same relative place in the solar system: for the planetary system tabulated in the same way is as follows :—
SOLAR SYSTEM.
| No. | Name. | Diameter in miles. |
Distance from Sun in Millions of Miles. | |||||||||
| I. | Mercury | . | . | . | 3,300 | . | . | . | . | . | 36 | |
| II. | Venus | . | . | . | 7,630 | . | . | . | . | . | 67 | |
| III. | Earth | . | . | . | 7,918 | . | . | . | . | . | 93 | |
| IV. | Mars | . | . | . | 4,220 | . | . | . | . | . | 141 | |
| V. | Asteroids | . | . | . | 10-500 | . | . | . | . | . | 250 | |
| VI. | Jupiter | . | . | . | 86,500 | . | . | . | . | . | 483 | |
| VII. | Saturn | . | . | . | 72,500 | . | . | . | . | . | 886 | |
| VIII. | Uranus | . | . | . | 31,900 | . | . | . | . | . | 1,782 | |
| IX. | Neptune | . | . | . | 34,800 | . | . | . | . | . | 2,792 | |
With the hint given by this, at least singular, coincidence, let us examine the other satellite systems. Two others available for comparison present themselves, that of Jupiter and that of Uranus. Jupiter's system is this :—
| No. | Name. | Diameter in Miles. |
Distance from Jupiter in miles. | |||||||
| V. | (Nameless) | . | . | . | 100 | . | . | . | . | 112,500 |
| I. | Io | . | . | . | 2,500 | . | . | . | . | 261,000 |
| II. | Europa | . | . | . | 2,100 | . | . | . | . | 415,000 |
| III. | Ganymede | . | . | . | 3,550 | . | . | . | . | 664,000 |
| IV. | Callisto | . | . | . | 2,960 | . | . | . | . | 1,167,000 |
Here, again, the largest body fills the centre of the field. With Uranus, we have:
| No. | Name. | Diameter in Miles. |
Distance from Uranus in Miles. | ||||||||
| I. | Ariel | . | . | . | 500 | . | . | . | . | . | 120,000 |
| II. | Umbriel | . | . | . | 400 | . | . | . | . | . | 167,000 |
| III. | Titania | . | . | . | 1,000 | . | . | . | . | . | 273,000 |
| IV. | Oberon | . | . | . | 800 | . | . | . | . | . | 365,000 |
The same relative agreement of position and mass !
Position of largest mass.Now consider the probability that this coincident arrangement should be due to chance. The greater mass might be found either at the beginning, in the middle, or at the end of the line. Take, as starting point, that it is found to occupy the middle of the line in the Saturnian system. The chance, if chance arranged it, that it should occupy the like position in the solar system is one out of three, or two to one that it did not. That it should also do so in the Jovian system is of , or eight to one against it. That furthermore the Uranian system should show the same is .
In other words, it is twenty-six to one that the largest satellite would not be found to occupy in all the same position. And it does. Twenty-six to one in betting is very much better than certainty odds.
Of second largest.This is not all. Consider the four systems more carefully. It will be seen that the second largest mass is in each of them found outside the first and in three out of the four next to it. In the fourth, it comes next but one. Now the chances against this being accident are much greater than for the first coincidence; while the chance that the two chances should occur together as they do is the product of both. You will see that we are getting outside any chance in the matter at all, and have come face to face with some cause working to this end.
Of second maximaBut we are by no means done with the analogies yet. If we construct a curve of positional sizes, we discover that it has two maxima, not one. A second lies inside the first. In the solar system, our Earth occupies this place; in the Jovian, lo; in the Saturnian, Tethys; in the Uranian, Ariel.
Plotted in curves, the profiles of the four systems show a striking family resemblance, as can be seen from the diagram; and from what we have noted of the probabilities in the case, we cannot doubt that this betokens a law of system development.
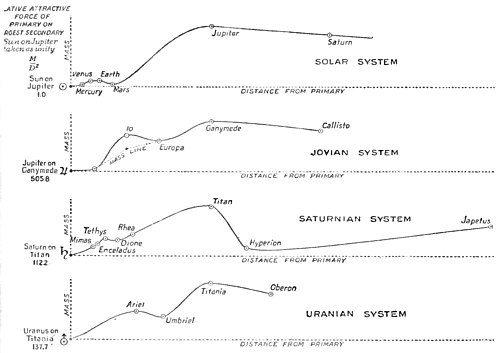
|
| POSITION OF MASSES IN SATELLITE SYSTEMS |
| FIG. XI. |
Inclinations of orbits to planet's equator with increase of distance of planet .A second point connected with the system is the relative inclinations of the orbits to the plane of the planet's equator. The inclinations to the distance from planet's equator of the rings and of the several satellites proceeding outward are as follows:
| Inclination of Orbit to | |||||||||||||
| Ecliptic | Planet's Equator | ||||||||||||
| ° | ' | " | ° | ' | " | ||||||||
| Planet's equator | . | . | . | 28 | 10 | 22 | |||||||
| Rings | . | . | . | . | . | . | . | 28 | 10 | 10 | 0 | 0 | 12 |
| Mimas | . | . | . | . | . | . | 28 | 10 | 10 | 0 | 0 | 12 | |
| Enceladus | . | . | . | . | . | 28 | 10 | 10 | 0 | 0 | 12 | ||
| Tethys | . | . | . | . | . | . | 28 | 10 | 10 | 0 | 0 | 12 | |
| Dione | . | . | . | . | . | . | . | 28 | 10 | 10 | 0 | 0 | 12 |
| Rhea | . | . | . | . | . | . | . | 28 | 10 | 10 | 0 | 0 | 12 |
| Titan | . | . | . | . | . | . | . | 27 | 38 | 49 | 0 | 31 | 33 |
| Hyperion | . | . | . | . | . | 28 | 4.8 | 1 | 5 | 43 | |||
| Ipateus | . | . | . | . | . | . | 18 | 28.3 | |||||
It thus appears that the inclinations of the planes of the orbits to the plane of the planet's equator increase as the distance from Saturn increases; furthermore, that the increase is regular. A smooth curve represents them all.
Now let us turn to the Jovian system.
Same in Jovian system.The inner satellite, or Benjamin of the family, moves apparently in the plane of its primary's equator. JOVIAN SYSTEM.
| Inclination of Orbit Plane to Planet's Equatorial Plane. | |||||||||||||
| I. | Io | . | . | . | . | . | . | . | . | . | 0° | 0' | 0" |
| II. | Europa | . | . | . | . | . | . | . | 0° | 1' | 6" | ||
| III. | Ganymede | . | . | . | . | . | . | 0° | 5' | 3" | |||
| IV. | Callisto | . | . | . | . | . | . | . | 0° | 24' | 35" | ||
Here, again, the inclinations increase as we go out, and the smooth curve representing them is,

|
| Fig. XII. |
when reduced in scale, almost the counterpart of the Saturnian.
Force occasioning this due to planet.Clearly some force has operated to compel the satellites to travel in the planet's equatorial plane, due to planet, and this force has emanated from the planet, since it grows less potent as one departs from him. What this force may be, we shall now proceed to ascertain.
Combination of rotations. In order to make the action in the case, complicated at best, as understandable as possible, I shall begin by considering what causes the precession of the equinoxes, or that slow rotation of the pole of the Earth round the pole of the ecliptic.
Effect of pull on stationary spheriod.Were the Earth a sphere, its axis would maintain an invariable position in the heavens, since any other body would act upon it as if all its matter were collected in its centre; but with a spheroid the case is different. We may consider the equatorial protuberance as a ring of matter fastened after the manner of a life-preserver around the Earth's waist. Now suppose the Earth tilted up from the line joining its centre and the centre of the attracting body. That body would tend to pull the nearer part of the ring down into its plane and the more distant portion of the same up into the same plane, and the result would be, if the Earth were not rotating, a swing round an axis at right angles to the line joining the centres of the two bodies, which would, after a few oscillations, bring the equatorial bulge to rest in the orbital plane of the outside body.
Upon rotating spheroid.Now suppose the Earth to be rotating at the time the pull is applied; then the simultaneous rotation and pull entirely alters the problem. From being a statical, it becomes a kinematical one, and the outcome is utterly different from what we might expect. Instead of bringing the plane of the equator into the plane of the ecliptic, it swings the pole of the equator round the pole of the ecliptic in a direction at right angles to the pull, and opposite to the rotation, but without changing the inclination of the two planes permanently at all. If the axis be in such position that the pull is perpendicular to the rotation, no change of inclination, even temporarily, occurs. If the axis be so circumstanced that the pull is at any other angle to it, then the change of axis being always perpendicular to the pull, one component of the change rotates the axis as before, the other alters its inclination.
Precession and nutation.Now if, as is the case with the attracting bodies of the solar system, the body which exerts the pull revolve about the other, either really or virtually, the axis will be presented to the force under varying angles. The axis will then alternately approach and recede from the pole of its small circle while going round it. But at the end of its orbital revolution it will come out again at the point on the celestial sphere from which it started. And this will happen whether the orbit be a circle or an ellipse. Even if the nodes of the ellipse or its line of apsides regress or progress, this will only postpone the reëntrance of the curve into itself to the time when the nodes or perihelia, or both, shall have completed their revolutions.
No Permanent change in the axis.No permanent change in the inclination of the axis to the orbit can ever result from the pull of a second body upon the first's equatorial bulge.
Since action and reaction are equal and opposite, the equatorial protuberance is equally impotent to make the satellite travel permanently in its plane.
Same analytically.This appears also analytically in the expressions for the effect produced in the line of nodes and the effect upon the inclination, the former having in addition to its periodic terms a term which increases with the time, while the latter has no such term.
It may be worth pointing out here an error which has crept into Young's excellent text-books, in which he states that "Laplace and Tisserand have shown that the equatorial protuberance of a planet, due to its axial rotation, compels a near satellite to move nearly in the equatorial plane." Neither Laplace nor Tisserand has ever shown this or ever could.
Laplace and Tisserand.
He made the mistake of post hoc ergo propter hoc. Tisserand is more guarded when he says: “Ainsi, l'inclinaison de l'orbite d'un satellite sur l'anneau demeure constante et toujours très petite si elle l'a été seulement à un moment donné.” This is so; but it is true, not because the force has an effect upon the inclination, but precisely because it has none. The spherical ellipse found by Tisserand, t. iv., ch. vi., to represent the change of inclination in the case of the satellites of Saturn, is the curve of the combined precessions due to each of the perturbing forces, the equatorial protuberance, the ring, the sun, and the other satellites.
Effect of tidal crest.Impotent on the inclination as the equatorial protuberance is, there is another protuberance which is not so impotent. For consider what effect the tide-raising force of an outside body would have upon the plastic matter of another rotating in a plane tilted to the orbital plane of the first. As we saw in Chapter II., the effect would be to raise two bosses or ansæ in the equatorial plane of the rotating planet, one preceding the position of the tide-raising body, the other diametrically opposite.
The action of these ansæ upon the attracting body would be analogous to, but in one vital respect different from, that of an equatorial protuberance. Like that, they would tend to alter the position of the axis of rotation at right angles to the pull upon them, but the pull being always backward the axis is constantly solicited forwards toward the attracting body. Consequently the axis of rotation, while rotating round the axis of the orbit, would generally seek the satellite. For the force here, when the axes are perpendicular, is at its maximum. The axis, therefore, continues to tend toward the orbital plane.
Same analytically.Analytically, in this case, unlike that of an equatorial bulge due to axial rotation, the expression for the change of inclination contains a term dependent on the time and increasing with it.
This term causes the inclination of the equatorial to the orbital plane to diminish until the axis of rotation lies in the plane of the orbit.
Inclination of satellite's orbital planes to planet's equator.The tidal force varies as , approx., and its work for any given time as , approx.
It should therefore be much more potent upon a near satellite than upon a far one, and we should expect the line expressing the action to prove a curve concave to the axis of x, when the bodies acted on are not too dissimilar in size. Such is precisely the opposite of the curve the diagrams present.
Nevertheless tidal action is probably the cause of the law of inclinations shown in the orbits of satellites to the equatorial plane of their primary. But it would seem to imply that the farther ones were given off first, and very much the first.
- ↑ See Laplace, Book IV., § 26. At the time, Hyperion was undiscovered and the “next to outer satellite” in consequence different.
![{\displaystyle \textstyle {\sqrt[{3}]{\frac {d}{d'}}}\times {2.44}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81034730da86da7fcaaa0027acc7c35328839027)


























