1911 Encyclopædia Britannica/Tide

by George Howard Darwin

TIDE (O. Eng. tid, cf. Ger. Zeit, time or season, connected with root of Sanskrit a-diti, endless), a term used generally for the daily rising and falling of the water of the sea, but more specifically defined below.

I.—General Account of Tides and Tidal Theories

§. 1. Definition of Tide.—When, as occasionally happens, a ship in the open sea meets a short succession of waves of unusual magnitude, we hear of tidal waves; and the large wave caused by an earthquake is commonly so described. But the use of the adjective “tidal” appears to us erroneous in this context, for the tide is a rising and falling of the water of the sea produced by the attraction of the sun and moon. A rise and fall of the sea. produced by a regular alternation of day and night breezes, by regular rainfall and evaporation, or by any influence which the moon may have on the weather cannot strictly be called a tide. Such alterations may be inextricably involved with the rise and fall of the true astronomical tide, but we shall here distinguish them as meteorological tides. It is well known that there are strongly marked diurnal and semi-diurnal inequalities of the barometer due to the sun’s heat, and they may be described as atmospheric meteorological tides?^[1] These movements both in the case of the sea and in that of the atmosphere are the result of the action of the sun, as a radiating body, on the earth. True astronomical tides in the atmosphere would be shown by a regular rise and fall in the barometer, but such tides are undoubtedly very minute, and we shall not discuss them in this article, merely referring the reader to the Atmospheric Tides. Mécanique céleste of Laplace, bks. i. and xiii. We shall in the present article extend the term “tide” to denote an elastic or viscous periodic deformation of a solid or viscous globe under the action of tide-generating forces.

§ 2. General Description of Tidal Phenomena.^[2]-If we live by the sea or on an estuary, we see that the water rises and falls nearly twice a day; speaking more exactly, the average interval from high-water to high-water is about 12^h 25^m, so that the average retardation from day to day is about 50^m. The times of high-water are then found to bear an intimate relation with the moon’s position. Thus at Ipswich high-water occurs when the moon is nearly south, at London Bridge when it is south-west, and at Bristol when it is east-south-east. For a very rough determination of the time of high-water it is sufficient to add the solar time of high-water on the days of new and full moon (called the “establishment of the port”) to the time of the moon’s passage over the meridian, either visibly above or invisibly below the horizon. The interval between the moon’s Variability of Interval after Moon’s Transit passage over the meridian and high-water varies sensibly with the moon’s age. From new moon to first quarter, and from full moon to third quarter (or rather from and to a day later than each of these phases), the interval diminishes from its average to a minimum, and then increases again to the average; and in the other two quarters it increases from the average to a maximum, and then diminishes again to the average.

The range of the rise and fall of water is also subject to great variability. On the days after new and full moon the range of tide is at its maximum, and on the day after the first and third quarter at its minimum. The maximum is called “spring tide” and the minimum “neap Spring and Neap. tide,” and the range of spring tide is usually nearly three times as great as that of neap tide. At many ports, however, especially non-European ones, two successive high-waters are of unequal heights, and the law of variability of the difference is somewhat complex; a statement of that law will be easier when we come to consider tidal theories. In considering any single oscillation of water level we find, especially in estuaries, that the interval from high to low-water is longer than that from low to high-water, and the difference between these two intervals is greater at springs than at neaps.

In a river the current continues to run up stream for some considerable time after high-water is attained and to run down similarly after low-water. Much confusion has been occasioned by the indiscriminate use of the term “tide” to denote a tidal current and a rise of water, and it has River Tides. often been incorrectly inferred that high-water must have been attained at the moment of cessation of the upward current. The distinction between “rising and falling” and “flowing and ebbing” must be maintained in rivers, whilst it is unnecessary at the seaboard. If we examine the progress of the tide-wave up a river we find that high-water occurs at the sea earlier than higher up. If, for instance, on a certain day it is high-water at Margate at noon, it is high-water at Gravesend at a quarter past Distinction of Rise and Fall from Flood and Ebb. two, and at London Bridge a few minutes before three. The interval from low to high-water diminishes also as we go up the river; and at some distance up certain rivers—as, for example, the Severn—the rising water spreads over the flat sands in a roaring surf and travels up the river almost like a wall of water. This kind of sudden rise is called a “bore”^[3] (q.v.). In other cases where the difference between the periods of rising and falling is considerable there are, in each high-water, two or three rises and falls. A double high-water exists at Southampton.

When an estuary contracts considerably, the range of tide becomes largely magnified as it narrows; for example, at the entrance of the Bristol Channel the range of spring tides is about 18 ft., and at Chepstow about 50 ft. This augmentation Augmentation of Height in Estuaries. of the height of the tide-wave is due to the concentration of the energy of motion of a large mass of a large mass of water into a narrow space. At oceanic ports the tidal phenomena are much less marked, the range of tide being usually only 2 or 3 ft., and the interval from high to low-water sensibly equal to that from low to high-water The changes from spring to neap tide and the relation of the time of high-water to the moon's transit are, however, the same both on the open coast and in rivers.

In long and narrow seas, such as the English Channel, the tide in mid-channel follows the same law as at a station near the mouth Landlocked Seas. of a river, rising and falling in equal times; the current runs in the direction analogous to up stream for three hours before and after high-water, and down stream for the same period before and after low-water. But near the sides of channels and near the mouths of bays the changes of the currents are very complex; and near the headlands separating two bays there is usually at certain times a very swift current, termed a “race.”

In inland seas, such as the Mediterranean, the tides are nearly insensible except at the ends of long inlets; Thus at Malta the tides are not noticed by the ordinary observer, whilst at Venice they are conspicuous.

The effect of a strong wind on the height of tide is generally supposed to be strongly marked, especially in estuaries. In the Wind. case of an exceptional gale, when the wind veered round appropriately, Airy states^[4] that the water has been known to depart from its predicted height at London by as much as 5 ft. The effect of wind will certainly be different at each port. The discrepancy of opinion on this subject appears to be great-so much so-that we hear of some Atmospheric Pressure. observers concluding that the effect of the wind is insensible. Variations in barometric pressure also cause departures from the predicted height of water, high barometer corresponding to decrease of height of water. Roughly speaking, an inch of the mercury column will correspond to about a foot of water, but the effect seems to vary much at different ports.^[5]

Mariners and hydrographers make use of certain technical terms which we shall now define and explain.

The “establishment of the port,” already referred to above, is the average interval which elapses between the moon's transit across Technical Terms used by Sailors. the meridian, at full moon and at change of moon, and the occurrence of high-water. Since at these times the moon crosses the meridian at twelve o'clock either of day or night; the “establishment” is the hour of the clock of high-water at full and change.

It has already been remarked that spring tide occurs at most places a day or a day and a half after full and change of moon. Now it is more important in the theory of the tides to know what occurs at spring tide than what occurs at full and change of moon. Thus the term “ the corrected establishment of the port ” is used to denote the interval in hours elapsing at spring tide between moon's transit and high-water. The difference between the ordinary and the corrected establishments is of small amount. At any other state of the moon, except full and change, the “interval” or “lunitidal interval” means the interval between the moon's upper or lower transit and high-water.

The average interval elapsing between full or change of moon and spring tide is called the “age of the tide"; as already remarked this interval is commonly about a day or a day and a half, but it may be twice as great in some places. The use of this term arises from the idea that spring tides are generated at some undefined place exactly at full or change of moon, and take an interval of time denoted the “age” to reach the place of observation. The term is not altogether satisfactory, since it implies a theory, but it must be referred to as in general use.

The average height at spring tide between high and low-water marks is called “the spring rise”; the similar height at neap tides is, however, called “the neap range.” “Neap rise” is used to mean the average height between high-water of neap tides and low-water of spring tides. Thus both at springs and neaps the term “rise” refers to the rise above the level of low-water at spring tide. French hydrographers call half the spring rise “the unit of height.”

The “diurnal inequality” of the tide denotes the fact that successive high-waters and successive low-waters are unequal to one another. In England the diurnal inequality scarcely exists.

The practice of the British admiralty is to refer their soundings and tide tables to “mean low-water mark of ordinary spring tides.” This datum is found by taking the mean of all the available observations of spring tides, excluding, however, from the mean any spring tides which may be considered abnormal. The admiralty datum is not, then, susceptible of exact scientific definition; but when it has once been fixed with reference to a bench-mark ashore it is expedient to adhere to it, by whatever process it was first fixed.^[6]

When new tidal stations are established in India the datum of reference has, since about 1885, been “Indian low-water mark,” which is defined as being below mean sea-level by the sum of the semi-ranges of the tides M₂, S₂, K₁, O (see §§ 24, 25 on Harmonic Analysis below).

In ordinary parlance sailors very commonly use the term “tide” when they mean what may be more accurately described as a tidal current.

§ 3. Tidal Observation: the Tide-gauge.—Tidal prediction is only possible when accurate observations have been made of the phenomena be predicted; and the like is true of verification after prediction. It was formerly thought sufficient to note the heights of the water at high and low-water, together with the times of those events, and the larger part of the observations which exist are still of this character, but complete investigation of the law of tidal oscillations demands that the height of the water should be measured at other times than at high and low-water.

With whatever degree of thoroughness it is proposed to observe the tides the procedure is much the same. The simplest sort of observation is to note the height of the water on a Tide-pole. graduated staff fixed in the sea, with such allowance as may be possible for wave motion. It is, however, far preferab1e to sink a tube into the sea into which the water penetrates through small holes; and the wave motion is thus annulled. In the calm water inside the tube there lies a float, to which is attached a cord passing over a pulley and counterpoised at the end. The motion of the counterpoise against a scale is observed. In either case the observations may be made every hour, or the times and heights of high and low-water may be noted.

In more careful observations than those referred to above the tidal record is automatic and continuous and is derived by means of an instrument called a tide-gauge.

This gauge should be placed in a place where we may obtain a fair representation of the oscillation of the surrounding sea. In such a site a well or tank is built on the, shore communicating Tide-gauge. by a channel with the sea at about 10 ft. below lowest low-water mark. In some cases an artificially constructed well may be dispensed with, where some lagoon or pool exists so near to the sea as to permit junction with the sea by means of a channel below low-water mark. At an rate we suppose that water is provided rising and falling with the tide, without much wave-motion: A cylindrical float, usually a hollow metallic box or a block of greenheart wood, hangs and floats in the well, and is of such density as just to sink without support. The float hangs under very light tension by a platinum wire, or by a metallic ribbon, or by a chain. The suspension wire is wrapped round a wheel, and imparts to it rotation proportional to the rise and fall of tide. By a simple gearing this wheel drives another, by which the range is reduced to any convenient extent. A fine wire wound on the final wheel of the train drags a pencil or pen up and down or to and fro proportionately to the tidal oscillations. The pencil is lightly pressed against a drum, which is driven by clockwork so as to make one revolution per day. The pen leaves its trace or tide-curve on paper wrapped round the drum. The paper is fixed to the drum with the edges of the paper at the XII o'clock line, and the record of a fortnight maybe taken without change of paper. An example of a tide-curve for Apollo Bunder, Bombay, from the 1st to the 15th of January 1884, is shown in fig. 1.

The curves are to be read from right to left, and when we reach the left-hand edge of the paper, we re-enter again at the same height on the right-hand edge. The numbers on the successive curves denote the days of the month.

We have chosen an example from a sub-tropical region because it illustrates the remarkable regularity of the tides in a region where the weather is equable. Further, if the reader will note the successive high-waters or low-waters which follow one another on any one day, he will see a strongly marked “diurnal inequality,” which would have been barely perceptible in a European tide-curve.

§4. Tide-Tables and the Degree of Accuracy in Tidal Prediction.

^[7] —The connexion between the tides and the movements of the Empirical Tide-tables. moon and sun is so obvious that tidal predictions were regularly made and published long before mathematicians had devoted their attention to them; and these predictions attained considerable success, although they were founded on empirical methods. During the 18th century, and even in the earlier part of the 19th, the art of prediction was regarded as a valuable family secret to be jealously guarded from the public. The best example of this kind of tide-table was afforded by Holden's tables for Liverpool, founded on twenty years of observation by a harbour-master named Hutchinson.^[8]

Fig. 1.—Tide-curve for Bombay from the beginning of the civil year 1884 to the midnight ending Jan. 14, 1884, or from 12^h Dec. 31, 1883, to 12^h Jan. 14, 1884, astronomical time.

About 1832 the researches of W. Whewell and of Sir John Lubbock (senior) pointed the way to improvement on the empirical tables prepared by secret methods, and since that time the preparation of tide-tables has become a branch of science.

A perfect tide-table would tell the height of the water at the place of observation at every moment of the day, but such a Prediction for each Day. table would be cumbrous; it is therefore usual to predict only the times and heights of high-water and of low-water. The best kind of tide-table contains definite forecasts for each day of a definite year, and we may describe it as a special table. Although the table is only made for one definite place, yet it is often possible to give fairly accurate predictions for neighbouring ports by the application of corrections both for time and height. Special tide-tables are published by all civilized countries for their most important harbours.

But there is another kind of table, which We may describe as a general one, where the heights and times are given by reference Prediction by Reference to Time of Moon's Transit to the time at which the moon crosses the meridian. Although such a table is only applicable to a definite place, yet it holds good for all time. In this case it is necessary to refer to the Nautical Almanac for the time of the moon's transit, and a simple calculation then gives the required result. In a general tide-table the heights and times are tabulated according to the hour of the clock at which the moon will cross the meridian at the place of observation, distinguishing between the visible and invisible transits. Certain simple corrections have also to be applied. A considerable degree of elaboration has to be given to the table, in order that it may give accurate results, and it would occupy some half-dozen to a dozen pages of a book, its extension varying according to the degree of accuracy aimed at. It might occupy about five minutes to extract prediction from the more elaborate form of such a table. There are many ports of considerable commercial importance where, nevertheless, it would hardly be worth while to incur the great and repeated expenditure involved in the publication of special tables. But this kind of elaborate general table has been used in few cases,^[9] and the information furnished to mariners usually consists either of a full prediction for every day of a future year, or of a meagre statement as to the average rise and interval, which must generally be almost useless.

The success of tidal predictions varies much according to the place of observation. In stormy regions the errors are Meteorological Disturbance of Prediction. often considerable, and the utmost that can be expected of a tide-table is that it shall be correct with a steady barometer and in calm weather. But such conditions are practically non-existent, and therefore errors are inevitable.

Notwithstanding these perturbations, tide-tables are usually of surprising accuracy even in northern latitudes; this may be seen from the following table showing the results of comparison Amount of Error at Portsmouth. between prediction and actuality at Portsmouth. The importance of the errors in height depends, of course, on the range of the tide; it is well, therefore, to note that the average ranges of the tide at springs and neaps are 13 ft. 9 in. and 7 ft. 9 in. respectively.

Prediction at such a place as Portsmouth is difficult, on account of the instability of the weather, but, on the other hand, the tides in themselves are remarkably simple in character. Let Amount of Error at Aden. us now turn to such a port as Aden, where the weather is very uniform, but the tides very complex on account of the large diurnal inequality, which frequently obliterates one of two successive high-waters. The short series of comprisons between actuality and prediction which we give below may be taken as a fair example of what would hold good when a long series is examined. The results refer to the intervals 10th of March to the 9th of April and the 12th of November to the 12th of December 1884. In these two periods there should have been 118 high waters, but the tide-gauge failed to register on one occasion, so that one comparison is lost. We thus have 117 cases to consider, but on one occasion the diurnal inequality obliterated a high-water, leaving 116 actual comparisons. The maximum range of the tide at Aden is 8 ft. 6 in., and this serves to give a standard of importance for the errors in height.

Table of Errors in the Prediction of High-Water at Portsmouth in the months of January, May and September 1897.

Time.		Heigth.
Magnitude of Error.	Number of Cases.	Magnitude of Error.	Number of Cases.
		Inches.
0m to  5m	69	0 to 6	89
6m to 10m	50	7 to 12	58
11m to 15m	25	13 to 18	24
16m to 20m	10	19 to 24	6
21m to 25m	11	—	—
26m to 30m	7	—	—
31m to 35m	4	—	—
52m	1	—	—
—	177	—	177

Table of Errors in the Prediction of High-Water at Aden in March-April and November-December 1884.

Time.		Heigth.
Magnitude of Error.	Number of Cases.	Magnitude of Error.	Number of Cases.
		Inches.
0m to  5m	35	0	15
5m to 10m	32	1	48
10m to 15m	19	2	28
15m to 20m	19	3	14
20m to 25m	5	4	11
26m to 28m	2	No high water.	1
33m to 36m	2	—	—
56m to 57m	2	—	—
No high water.	1	—	—
—	117	—	117

It would be natural to think that when a prediction is erroneous by as much as fifty-seven minutes it is a very bad one, but such a conclusion may be unjust. There was one case in which the high-water was completely obliterated by the diurnal inequality, but there were many others in which there was nearly complete obliteration, so that the water stood nearly stagnant for several hours. A measure of the degree of stagnation is afforded by the amount of rise from low to high-water. Now, on examining all the eleven cases where the error of time was equal to or over twenty minutes, we find five cases in which the range from low to high-water was less than 8 in., and these include the errors of fifty-six and of fifty-seven minutes. There is one case of a rise of 13 in. with an error of thirty-six minutes; one case of a rise of 17 in. with an error of twenty-two minutes; one of 19 in. rise with thirty-three minutes error. The remaining three cases have rises of 2 ft. 10 in., 3 ft. 9 in., 3 ft. 11 in., and errors of twenty-two, twenty-three, twenty minutes. Thus all the very large errors of time correspond with approximate stagnation, and are unimportant. It is fair to conclude, therefore, that the predictions as to time are very good. The predictions as to height are obviously good, for more than half were within 1 in., and only eleven had an error of as much as 4 in.

When it is considered that the incessant variability of the tidal forces, the complex outlines of the coast, the depth of the sea, the earth's rotation and the perturbations by meteorological influences are all involved, it should be admitted that the success of tidal prediction is remarkable. If further evidence were needed, we might appeal to tidal prediction as a convincing proof of the truth of the theory of gravitation.

§ 5. General Explanation of the Cause of Tides.—The moon attracts every particle of the earth and ocean, and by the law of gravitation the force acting on any particle is directed Tide-generating Forces. towards the moon's centre, and is jointly proportional to the masses of the particle and of the moon, and inversely proportional to the square of the distance between the particle and the moon's centre. If we imagine the earth and ocean subdivided into a number of small portions or particles of equal mass, then the average, both as to direction and intensity of the forces acting on these particles is equal to the force acting on that particle which is at the earth's centre. For there is symmetry about the line joining the centres of the two bodies, and, if we divide the earth into two portions by an ideal spherical surface passing through the earth's centre and having its centre at the moon, the portion remote from the moon is a little larger than the portion towards the moon, but the nearer portion is under the action of forces which are a little stronger than those acting on the farther portion, and the resultant of the weaker forces on the larger portion is exactly equal to the resultant of the stronger forces on the smaller. If every particle of the earth and ocean were being urged by equal and parallel forces there would be no cause for relative motion between the ocean and the earth. Hence it is the departure of the force acting on any particle from the average which constitutes the tide-generating force. Now it is obvious that on the side of the earth towards the moon the departure from the average is a small force directed towards the moon; and on the side of the earth away from the moon the departure is a small force directed away from the moon. Also these two departures are very nearly equal to one another, that on the near side being so little greater than that on the other that we may neglect the excess. All round the sides of the earth along a great circle perpendicular to the line joining the moon and earth the departure is a force directed inwards towards the earth's centre. Thus we see that the tidal forces tend to pull the water towards and away from the moon, and to depress the water at right angles to that direction.

Fig. 2.—Tide-generating Force.

Fig. 2.—Tide-generating Force.

In fig. 2 this explanation is illustrated graphically. The relative magnitudes of the tidal forces are given by the numbers on the figure. M is the direction of the moon, V the centre of the hemisphere of the earth at which the man in the moon would look, I the centre of the hemisphere which would be invisible to him, DD are the sides of the earth where the tidal force is directed towards the earth's centre. The outward forces at V and I are exactly double the inward forces at D and D.

If it were permissible to neglect the earth's rotation and to consider the system as at rest, we should find that the water was in equilibrium when elongated into a prolate ellipsoidal or oval form with its longest axis directed towards and away from the moon.

But it must not be assumed that this would be the case when there is motion. For, suppose that the ocean consisted of a canal round the equator, and that an earthquake Theory of Equatorial Canal on Earth. or any other cause were to generate a great wave in the canal, this wave would travel along it with a velocity dependent on the depth. If the canal were about 13 miles deep the velocity of the wave would be about 1000 miles an hour, and with depth about equal to the depth of our seas the velocity of the wave would be about half as great. We may conceive the moon's tide-generating force as making a wave in the canal and continually outstripping the wave it generates, for the moon travels along the equator at the rate of about 1000 miles an hour, and the sea is less than 13 miles deep. The resultant oscillation of the ocean must therefore be the summation of a series of partial waves generated at each instant by the moon and always falling behind her, and the aggregate wave, being the same at each instant, must travel 1000 m. an hour so as to keep up with the moon.

Now it is a general law of frictionless oscillation that, if a slowly varying periodic force acts on a system which would oscillate quickly if left to itself, the maximum excursion on one side of the equilibrium position occurs simultaneously with the maximum force in the direction of the excursion; but, if a quickly varying periodic force acts on a system which would oscillate slowly if left to itself, the maximum excursion on one side of the equilibrium position occurs simultaneously with the maximum force in the direction opposite to that of the excursion. An example of the first is a ball hanging by a short string, which we push slowly to and fro; the ball will never quit contact with the hand, and will agree with its excursions. If, however, the ball is hanging by a long string we can play at battledore and shuttlecock with it, and it always meets our blows. The latter is the analogue of the tides, for a free wave in our shallow canal Tides Inverted. goes slowly, whilst the moon's tide-generating action goes quickly. Hence when the system is left to settle into steady oscillation it is low-water under and opposite to the moon, whilst the forces are such as to tend to make high-water at those times.

If in this case we consider the moon as revolving round the earth, the water assumes nearly the shape of an oblate spheroid or orange-shaped body with the shortest axis pointed to the moon. The rotation of the earth in the actual case introduces a complexity which it is not easy to unravel by general reasoning. We can see, however, that if water moves from a lower to a higher latitude it arrives at the higher latitude with more velocity from west to east than is appropriate to its latitude, and it will move accordingly on the earth's surface. Following out this conception, we see that an oscillation of the water to and fro between south and north must be accompanied by an eddy. The solution of the difficult problem involved in working out this idea will be given below.

The conclusion at which we have arrived about the tides of an equatorial canal is probably more nearly true of the tides of a globe partially covered with land than if we were to suppose the ocean at each moment to assume the prolate figure of equilibrium. In fact, observation shows that it is more nearly low-water than high-water when the moon is on the meridian. If we consider how the oscillation of the water would appear to an observer carried round with the earth, we see that he will have low-water twice in the lunar day, somewhere about the time when the moon is on the meridian, either above or below the horizon, and high-water half-way between the low waters.

If the sun be now introduced we have another similar tide of about half the height, and this depends on solar time, giving Sun's Influence. low-water somewhere about noon and midnight. The superposition of the two, modified by friction and by the interference of land, gives the actually observed aggregate tide, and it is clear that about new and full moon we must have spring tides and at quarter moons neap tides, and that (the sum of the lunar and solar tide-generating forces being about three times their difference) the range of spring tide will be about three times that of neap tide.

So far we have supposed the luminaries to move on the equator; now let us consider the case where the moon is not on the equator. It is clear in this case that at any Diurnal Tides. place the moon's zenith distance at the upper transit is different from her nadir distance at the lower transit. But the tide-generating force is greater the smaller the zenith or nadir distance, and therefore the forces are different at successive transits. This was not the case when the moon was deemed to move on the equator. Thus there is a tendency for two successive lunar tides to be of unequal heights, and the resulting inequality of height is called a "diurnal tide." This tendency vanishes when the moon is on the equator; and as this occurs each fortnight the lunar diurnal tide is evanescent once a fortnight. Similarly in summer and winter the successive solar tides are generally of unequal height, whilst in spring and autumn this difference is inconspicuous.

One of the most remarkable conclusions of Laplace's theory of the tides, on a globe covered with ocean to a uniform depth, is that the diurnal tide is everywhere non-existent. Evanescent in Ocean of Uniform Depth. But this hypothesis differs much from the reality, and in fact at some ports, as for example Aden, the diurnal tide is so large that during two portions of each lunation there is only one great high-water and one great low-water in each twenty-four hours, whilst in other parts of the lunation the usual semi-diurnal tide is observed.

§ 6. Progress of the Tide-wave over the Ocean and in the British Seas.—Sufficient tidal data would give the state of the tide at every part of the world at the same instant of time, and if the tide wave is a progressive one, like such wave as we may observe travelling along a canal, we should be able to picture mentally the motion of the tide-wave over the ocean and the successive changes in the height of water at any one place. But we are not even sure that the wave is progressive, for in some oceans, such as perhaps the Atlantic, the motion may be only a see-saw about some line in mid-ocean—up on one side and down on the other; or it may more probably be partly a progressive wave and partly a see-saw or stationary oscillation. In contracted seas the wave is undoubtedly predominantly progressive in character, but too little is known to enable us to speak with any confidence as to wider seas.

Whewell and Airy, while acknowledging the uncertainty of their data, made the attempt to exhibit graphically the progress of the tide-wave over a large portion of the oceans of the world. In the first edition of this article (Ency. Brit., 9th ed.) we reproduced their chart. But, since doubts as to its correctness have gradually accumulated, we think it more prudent to refrain from reproducing it again.^[10]

As we have already indicated, the tide in British seas has mainly a progressive character, and the general march of the wave may be exhibited on a chart by what are called cotidal lines. If at the full and change of moon we draw lines on the sea through all the places which have high-water simultaneously, and if we mark such lines successively XII, I, II, &c., being the Greenwich time of high-water along each line, we shall have a succession of lines which show the progress of the wave from hour to hour.

For phases of the moon, other than full and change, the numbers may be taken to represent the interval in hours after the moon's transit, either visible or invisible, until the occurrence of high water. But for these other phases of the moon the interval varies by as much as one hour in excess or defect of the number written on any of the lines. Thus when the moon is about five days old, or five days past full, the numbers must all be reduced by about one hour so that I, II, III, &c., will then be replaced by XII, I, II, &c.; and when the moon is about ten days old, or ten days past full, the numbers must all be augmented by about one hour, and will read II, III, IV, &c. However, for a rough comprehension of the tides in these seas it is unnecessary to pay attention to this variation of the intervals.

Airy in his "Tides and Waves" gives such a chart for Great Britain and the North Sea, and he attempts to complete the cotidal lines conjecturally across the North Sea to Norway, Denmark and the German coast. In this case, as in the more ambitious attempt referred to above, further knowledge has led to further doubt. We therefore give in fig. 3 Berghaus's modification of Airy's Chart,^[11] abandoning the attempt to draw complete cotidal lines. In this chart we can watch, as it were, the tide-wave running in from the Atlantic, passing up the Bristol Channel and Irish Sea, travelling round the north of Scotland and southward along the east coasts of Scotland and England. Another branch comes up the Channel, and meets the wave from the north off the Dutch coast. The Straits of Dover are so narrow, however, that it may be doubted whether the tides on the English coasts would be profoundly modified if the Straits were completely closed.

It will be noticed that between Yarmouth and Holland the cotidal lines cross one another. Such an intersection of lines is in general impossible; it is indeed only possible if there is a region in which the water neither rises nor falls, because at such a place the cotidal line ceases to have a definite meaning. A set of observations by Captain Hewitt, R.N., made in 184O, appears to prove the existence of a region of this kind at the part of the chart referred to.

Fig. 3.—Cotidal Lines in British Seas.

(From Berghaus's Atlas.)

Fig. 3.—Cotidal Lines in British Seas.

§ 7. Historical Sketch.^[12]—The writings of various Chinese, Arabic and Icelandic authors show that some attention was paid by them to the tides, but the several theories advanced are fantastic. It is natural that the writings of the classical authors of antiquity should contain but few references to the tides, for the Greeks and Romans lived on the shores of an almost tideless sea. Nevertheless, Strabo quotes from Posidonius a clear account of the tides on the Atlantic coast of Spain, and connects the tides correctly with the motion of the moon. He also gives the law of the tide in the Indian Ocean as observed by Seleucus the Babylonian, and the passage shows that Seleucus had unravelled the law which governs the diurnal inequality of the tide in that sea.

We shall not give any details as to the medieval speculations on the tides, but pass on at once to Newton, who in 1687 laid the foundation for all that has since been added to the theory of the tides when he brought his grand generalization of universal gravitation to bear on the subject. Johann Kepler had indeed Kepler. at an early date recognized the tendency of the water of the ocean to move towards the centres of the sun and moon, but he was unable to submit his theory to calculation. Galileo expresses regret that so acute a man as Kepler should have produced a theory which appeared to him to reintroduce the occult qualities of the ancient philosophers. His own explanation referred the phenomenon to the rotation and orbital motion of the earth, and he considered that it afforded a principal proof of the Copernican system.

In the 19th corollary of the 66th proposition of bk. i. of the Principia, Sir Isaac Newton introduces the conception of a canal Newton. circling the earth, and he considers the influence of a satellite on the water in the canal. He remarks that the movement of each molecule of fluid must be accelerated in the conjunction and opposition of the satellite with the molecule, that is to say when the molecule, the earth's centre and the satellite are in a straight line, and retarded in the quadratures, that is to say when the line joining the molecule and the earth's centre is at right angles to the line joining the earth's centre and the satellite. Accordingly the fluid must undergo a tidal oscillation. It is, however, in propositions 26 and 27 of bk. iii. that he first determines the tidal force due to the sun and moon. The sea is here supposed to cover the whole earth and to assume at each instant a figure of equilibrium, and the tide-generating bodies are supposed to move in the equator. Considering only the action of the sun, he assumes that the figure is an ellipsoid of revolution with its major axis directed towards the sun, and he determines the ellipticity of such an ellipsoid. High solar tide then occurs at noon and midnight, and low-tide at sunrise and sunset. The action of the moon produces a similar ellipsoid, but of greater ellipticity. The superposition of these ellipsoids gives the principal variations of the tide. He then proceeds to consider the influence of latitude on the height of tide, and to discuss other peculiarities of the phenomenon. Observation shows, however, that spring tides occur a day and a half after full and change of moon, and Newton falsely attributed this to the fact that the oscillations would last for some time if the attractions of the two bodies were to cease.

The Newtonian hypothesis, although it fails in the form which he gave to it, may still be made to represent the tides if the lunar and solar ellipsoids have their major axes “Astres Fictifs” always directed toward a fictitious moon and sun, which are respectively at constant distances from the true bodies; these distances are such that the full and change of the fictitious moon as illuminated by the fictitious sun occur about a day or a day and a half later than the true full and change of moon. In fact, the actual tides may be supposed to be generated directly by the action of the real sun and moon, and the wave may be imagined to take a day and a half to arrive at the port of observation. This period has accordingly been called “the age of the tide.” In Age of Tide. what precedes the sun and moon have been supposed to move in the equator; but the theory of the two ellipsoids cannot be reconciled with the truth when they move, as in actuality, in orbits inclined to the equator. At equatorial ports the theory of the ellipsoids would at spring tides give morning and evening high waters of nearly equal height, whatever the declinations of the bodies. But at a port in any other latitude these high waters would be of very different heights, and at Brest, for example, when the declinations of the bodies are equal to the obliquity of the elliptic, the evening tide would be eight times as great as the morning tide. Now observation shows that at this port the two tides are nearly equal to one another, and that their greatest difference is not a thirtieth of their sum. Newton here also offered an erroneous explanation of the phenomenon.

In 1738 the Academy of Sciences of Paris offered, as a subject for a prize, the theory of the tides. The authors of four essays received prizes, viz. Daniel Bernoulli, Leonhard Euler, Colin Maclaurin and Antoine Cavalleri. The first D. Bernoulli and Others. three adopted not only the theory of gravitation, but also Newton's method of the superposition of the two ellipsoids. Bernoulli's essay contained an extended development of the conception of the two ellipsoids, and, under the name of the equilibrium theory, it is commonly associated with his name. Laplace gives an account and critique of the essays of Bernoulli and Euler in the Mécanique céleste. The essay of Maclaurin presented little that was new in tidal theory, but is notable as containing certain important theorems concerning the attraction of ellipsoids. In 1746 Jean-le-Rond D'Alembert wrote a paper in which he treated the tides of the atmosphere; but this work, like Maclaurin's, is chiefly remarkable for the importance of collateral points.

The theory of the tidal movements of an ocean was therefore, as Laplace remarks, almost untouched when in 1774 he first undertook the subject. In the Mécanique céleste he gives an interesting account of the manner in which he was led to attack the problem. We shall give below the investigation of the tides Laplace. of an ocean covering the whole earth; the theory is substantially Laplace's, although presented in a different form, and embodying an important extension of Laplace's work by S. S. Hough. This theory, although very wide, is far from representing the tides of our ports. Observation shows, in fact, that the irregular distribution of land and water and the various depths of the ocean in various places produce irregularities in the oscillations of the sea of such complexity that the rigorous solution of the problem is altogether beyond the power of analysis. Laplace, however, rested his discussion of tidal observation on this principle—The state of oscillation of a system of bodies in which the primitive conditions of movement have disappeared through friction is coperiodic with the forces acting on the system. Hence if the sea is acted on by forces which vary Principle of Forced Oscillations. periodically according to the law of simple oscillations (a simple time-harmonic), the oscillation of the sea will have exactly the same period, but the moment at which high-water will occur at any place and the amplitude of the oscillation can only be derived from observation. Now the tidal forces due to the moon and sun may be analysed into a number of constituent periodic parts of accurately determinable periods, and each of these will generate a corresponding oscillation of the sea of unknown amplitude and phase. These amplitudes and phases may be found from observation. But Laplace also used another principle, by which he was enabled to effect a synthesis of the various oscillations, so that he does not discuss a very large number of these constituent oscillations. As, however, it is impossible to give a full account of Laplace's methods without recourse to technical language, it must suffice to state here that this procedure enabled him to discuss the tides at any port by means of a combination of theory with observation. After the time of Laplace down to 1870, the most important workers in this field were Sir John Lubbock (senior), William Whewell Lubbock, Whewell and Airy. and Sir G. B. Airy. The work of Lubbock and Whewell (see § 33 below) is chiefly remarkable for the co-ordination and analysis of enormous masses of data at various ports, and the construction of trustworthy tide-tables and the attempt to construct cotidal maps. Airy contributed an important review of the whole tidal theory. He also studied profoundly the theory of waves in canals, and explained the effects of frictional resistance on the progress of tidal and other waves.

The comparison between tidal theory and tidal observations has been carried out in two ways which we may describe as the synthetic and the analytic methods. Nature is herself synthetic, since at any one time and place we only observe one single tide-wave. All the great investigators from Newton down to Airy have also been synthetic in their treatment, for they have sought to represent the oscillation of the sea by a single mathematical expression, as will appear more fully in chapter V. below. It is true that a presupposed analysis lay behind and afforded the basis of the synthesis. But when at length tide-gauges, giving continuous records, were set up in many places the amount of data to be co-ordinated was enormously increased, and it was found that the simple formulae previously in use had to be overloaded with a multitude of corrections, so that the simplicity became altogether Kelvin. fictitious. This state of matters at length led Lord Kelvin (then Sir William Thomson) to suggest, about 1870, the analytic method, in which the attempt at mathematical synthesis is frankly abandoned and the complex whole is represented as the sum of a large number of separate parts, each being a perfectly simple wave or harmonic oscillation. All the best modern tidal work is carried on by the analytic method, of which we give an account below in chapter IV.

Lord Kelvin's other contributions to tidal theory are also of profound importance; in particular we may mention that he established the correctness of Laplace's procedure in discussing the dynamical theory of the tides of an ocean covering the whole earth, which had been impugned by Airy and by William Ferrel. We shall have frequent occasion to refer to his name hereafter in the technical part of this article.

Amongst all the grand work which has been bestowed on the theory of this difficult subject, Newton, notwithstanding his errors, stands out first, and next to him we must rank Laplace. However original any future contribution to the science of the tides may be, it would seem as though it must perforce be based on the work of these two.

§ 8. The Tide-Predicting Instrument.—In the field of the practical application of theory Lord Kelvin also made another contribution of the greatest interest, when in 1872 he Tide-Predicting Instrument. suggested that the laborious task of constructing a tide-table might be effected mechanically. Edward Roberts bore a very important part in the first practical realization of such a machine, and a tide-predictor, now in regular use at the National Physical Laboratory for the Indian government was constructed by Légé. under his direction. We refer the reader to Sir William Thomson's (Lord Kelvin's) paper on “Tidal Instruments” in Inst. C. E., vol. lxv., and to the subsequent discussion, for a full account and for details of the share borne by the various persons concerned in the realization of the idea.

Fig. 4.—Tide-Predicting Instrument.

Fig. 4.—Tide-Predicting Instrument.

Fig. 4 illustrates diagrammatically the nature off the instrument. A cord passes over an under a succession of pulleys, every other pulley being fixed or rather balanced and the alternate ones being movable; the cord is fixed at one end and carries a pen or pencil at the other end. In the diagram there are two balanced pulleys and one movable one; a second unit would require one more movable pulley and one more balanced one. If, in our diagram the lowest or movable pulley were made to oscillate up and down (with a simple harmonic motion), the pencil would execute the same motion on half the linear scale. If the instrument possessed two units and the second movable pulley also rocked up and down, the pencil would add to its previous motion that of this second oscillation, again on half scale. So also if there were any number of additional units, each consisting of one movable and one balanced pulley, the pencil would add together all the separate simple oscillations, and would draw a curve upon a drum, which is supposed to be kept revolving uniformly at an appropriate rate.

The rocking motion is communicated to each movable pulley by means of a pin attached to a wheel C sliding in a slot attached to the pulley frame. All the wheels C and the drum are geared together so that, as the drum turns, all the movable pulleys rock up and down. The gearing is of such a nature that if one revolution 0 the drum represents a single day, the rocking motion of each movable pulley corresponds to one of the simple constituent oscillations or tides into which the aggregate tide-wave is analysed. The nature of the gearing is determined by theoretical considerations derived from the motions of the sun and moon and earth, but the throw of each crank, and the angle at which it has to be set at the start are derived from observation at the particular port for which the tide-curve is required. When the tide-predictor has been set appropriately, it will run off a complete tide-curve for a whole year; the curve is subsequently measured and the heights and times of high and low-water are tabulated and published for a year or two in advance.

The Indian instrument possesses about 20 units, so that the tide-curve is regarded as being the sum of 20 different simple tides; and tide-tables are published for 40 Indian and Oriental ports. A tide-predictor has been constructed for the French government under the supervision of Lord Kelvin and is in use at Paris; another has been made by the United States Coast Survey at Washington; in 1910 one was under construction for the Brazilian government. These instruments, although differing considerably in detail from the Indian predictor, are essentially the same in principle.

§ 9. Tidal Friction.—All solid bodies yield more or less to stress; if they are perfectly elastic they regain their shapes after the stresses are removed, if imperfectly elastic or viscous they yield to the stresses. We may thus feel certain that the earth yields to tide-generating force, either with perfect or imperfect elasticity. Chapter VIII. will contain some discussion of this subject, and it must suffice to say here that the measurement of the minute elastic tides of the solid earth has at length been achieved. The results recently obtained by Dr O. Hecker at Potsdam constitute a conspicuous advance on all the previous attempts.

The tides of an imperfectly elastic or viscous globe are obviously subject to frictional resistance, and the like is true of the tides of an actual ocean. In either case it is clear that the system must be losing energy, and this leads to results of so much general interest that we propose to give a short sketch of the subject, deferring to chapter VIII. a more rigorous investigation. It is unfortunately impossible to give even an outline of the principles involved without the use of some technical terms:

In fig. 5 the paper is supposed to be the plane of the orbit of a satellite M revolving in the direction of the arrow about the planet C, which rotates in the direction of the arrow about an General Explanation of Tidal Friction. axis perpendicular to the paper. The rotation of the planet is supposed to be more rapid than that of the satellite, so that the day is shorter than the month. Let us suppose that the planet is either entirely fluid, or has an ocean of such depth that it is high-water under or nearly under the satellite. When there is no friction, with the satellite at m, the planet is elongated into the ellipsoidal shape shown, cutting the mean sphere, which is dotted. The tidal protuberances

Fig. 5.

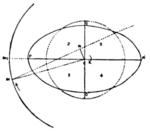
Fig. 5.

are drawn with much exaggeration and the satellite is shown as very close to the planet in order to illustrate the principle more clearly. Now, when there is friction in the fluid motion, the tide is retarded, and high-tide occurs after the satellite has passed the meridian. Then, if we keep the same figure to represent the tidal deformation, the satellite must be at M, instead of at m. If we number the four quadrants as shown, the satellite must be in quadrant I. The protuberance P is nearer to the satellite than P', and the deficiency Q is farther away than the deficiency Q'. Hence the resultant action of the planet on the satellite must be in some such direction as MN. The action of the satellite on the planet is equal and opposite, and the force in NM, not being through the planet's centre, must produce a retarding couple on the planet's rotation, the magnitude of which depends on the length of the arm CN. This tidal frictional couple varies as the height of the tide, and as the satellite's distance. The magnitude of the tidal protuberances varies inversely as the cube of the distance Planet's Rotation Retarded. of the satellite, and the difference between the attractions of the satellite on the nearer and farther protuberances also varies inversely as the cube of the distance. Accordingly the tidal frictional couple varies as the inverse sixth power of the satellite's distance. Let us now consider its effect on the satellite. If the force acting on M be resolved along and perpendicular to the direction CM, the perpendicular component tends to accelerate the satellite's velocity. It alone would carry the satellite farther from C than it would be dragged back by the central force towards C. The satellite would describe a spiral, the coils of which would be very nearly circular and very nearly coincident. If now we resolve the central component force along CM tangentially and perpendicular to the spiral, the tangential component tends to retard the velocity of the satellite, whereas the disturbing force, already considered, tends to accelerate it. With the gravitational Satellite's Velocity Retarded. law of force between the two bodies the retardation must prevail over the acceleration^[13] The action of tidal friction may appear somewhat paradoxical, but it is the exact converse of the acceleration of the linear and angular velocity and the diminution of distance of a satellite moving through a resisting medium. The latter result is generally more familiar than the action of tidal friction, and it may help the reader to realize the result in the present case. Tidal friction then diminishes planetary rotation, increases the satellite's distance and diminishes the orbital angular velocity. The comparative rate of diminution of the two angular velocities is generally very different. If the satellite be close to the planet the rate of increase of the satellite's periodic time or month is large compared with the rate of increase of the period of planetary rotation or day; but if the satellite is far off the converse is true. Hence, if the satellite starts very near the planet, with the month a little longer than the day, as the satellite recedes, the month soon increases so that it contains many days. The number of days in the month attains a maximum and then diminishes. Finally the two angular velocities subside to a second identity, the day and month being identical and both very long.

We have supposed that the ocean is of such depth that the tides are direct; if, however, they are inverted, with low-water under or nearly under the satellite, friction, instead of retarding, accelerates the tide; and it would be easy by drawing another figure to see that the whole of the above conclusions would hold equally true with inverted tides.

Attempts have been made to estimate the actual amount of the retardation of the earth's rotation, but without much success. It must be clear from the sketch just given that the effect of tidal friction is that the angular motion of the moon round the earth is retarded, but not to so great an extent as the earth's rotation. Thus a terrestrial observer, who regards the earth as a perfect timekeeper, would look on the real retardation of the moon's angular motion as being an acceleration. Now there is a true acceleration of the moon's angular motion which depends on a slow change in the eccentricity of the earth's orbit round the sun. After many thousands of years this acceleration will be reversed and it will become a retardation, but it will continue for a long time from now into the future; thus it is indistinguishable to us at present from a permanent acceleration. The amount of this true acceleration may be derived from the theories of the motions of the moon and of the earth when correctly developed. Laplace conceived that its observed amount was fully explained in this way, but John Couch Adams showed that Laplace had made a mistake and had only accounted for half of it. It thus appeared that there was an unexplained portion which might be only apparent and might be attributed to the effects of tidal friction.

The time and place of an eclipse of the sun depend on the motions of the moon and earth. Accordingly the records of ancient eclipses, which occurred centuries before the Christian era, afford exceedingly delicate tests of the motions of the moon and earth. At the time when Thomson and Tait's Natural Philosophy^[14] was first published it was thought that all the numerical data were known with sufficient precision to render it possible to give a numerical estimate of the retardation of the earth's rotation. But the various revisions of the lunar theory which have been made since that date throw the whole matter into doubt. It seems probable that there is some portion of the acceleration of the moon's motion which is unexplained by gravitation, and may therefore be attributed to tidal friction, but its amount is uncertain. We can only say that the amount is very small. It is, however, not impossible that this smallness may be due to counteracting influences which tend to augment the speed of the earth's rotation; such an augmentation would result from shrinkage of the earth's mass through cooling. However this matter may stand, it does not follow that, because the changes produced by tidal friction in a man's lifetime or in many generations of man are almost insensible, the same must be true when we deal with millions of years. It follows that it is desirable to trace the effects of tidal friction back to their beginnings.

We have seen above that this cause will explain the repulsion of a satellite from a position close to the planet to a more remote distance. Now when we apply these considerations to the moon and earth we find that the moon must once have been nearly in contact with the earth. This very remarkable initial configuration of the two bodies seems to point to the origin of the moon by detachment from the earth.

Further details concerning this speculation in cosmogony are given below in chapter VIII.^[15]

§ 10. Bibliography.—Many works on popular astronomy contain a few paragraphs on the tides, but the treatment is generally so meagre as to afford no adequate idea of the whole subject.

A complete list of works both general and technical bearing on the theory of the tides, from the time of Newton down to 1881, is contained in vol. ii. of the Bibliographie de l'astronomie by J. C. Houzeau and A. Lancaster (1882). This list does not contain papers on the tides of particular ports, and we are not aware of the existence of any catalogue of works on practical observation, reduction of observations, prediction and tidal instruments. The only general work on the tides, without mathematics, is George Darwin's Tides and Kindred Phenomena in the Solar Systems.^[16] This book treats of all the subjects considered in the present article (with references to original sources), and also others such as seiches (q.v.) and the bore (q.v.).

The most extensive monograph on the tides is A Manual of Tides by Mr Rollin A. Harris, published by the United States Coast Survey in a series of parts, of which pt. i. appeared in 1897, and pt. iv. B in 1904. This work contains an enormous mass of useful work, and gives not only complete technical developments both on the theoretical and practical sides but also has chapters of general interest. The present writer feels it his duty, however, to dissent from Mr Harris's courageous attempt to construct the cotidal lines of the various oceans.

This work contains the most complete account of the history of tidal theories of which we know. Laplace's admirable history of the subject down to his own time has been summarized in § 7. Dr Giovanni Magrini has an appendix to his translation of Darwin's book, entitled La Conoscenza della marea nell'antichità, founded on the researches of Dr Roberto Almagià. Dr Almagià himself gives the results of his researches more fully in a memoir, presented to the Accademia dei Lincei of Rome (5th series, vol. v. fascic. x., 1905, 137 pp).

Another monograph on tides, treating especially the mathematical developments, is Maurice Lévy's La Théorie des marées (Paris, 1898). Colonel Baird's Manual of Tidal Observation (1886) contains instructions for the installation of tide-gauges, and auxiliary tables for harmonic analysis. Airy's article on “Tides and Waves” in the Ency. Metrop., although superseded in many respects, still remains important. Harris's Manual contains a great collection of results of tidal observations made at ports all over time world.

The article "Die Bewegung der Hydrosphäre" in the Encyklopädie der mathematischen Wissenschaften (vi. 1, 1908) gives a technical account of the subject, with copious references. The same article is given in English in vol. iv. (1911) of G. H. Darwin's collected Scientific Papers; and vols. i. and ii. contain reprints of the several papers by the same author referred to in the present article.

Since the date of the 9th edition of the Ency. Brit. some technical discussion of the tides has appeared in textbooks, such as H. Lamb's Hydrodynamics.^[17] That work also reproduces in more modern form Airy's investigation of the effects of friction on the tides of rivers. We are thus able to abridge the present article, but we shall present the extension by Hough of Laplace's theory of the tides of an ocean-covered planet, which is still only to be found in the original memoirs.

II.—Tide-Generating Forces

§ 11. Investigations of Tide-Generating Potential and Forces.— We have already given a general explanation of the nature of tide-generating forces; we now proceed to a rigorous Tide-Generating Forces. investigation. If at planet is attended by a single satellite, the motion of any body relatively to the planet's surface is found by the process described as reducing the p1anet's centre to rest. The p1anet's centre will be at rest if every body in the system has impressed on it a velocity equal and opposite to that of the planet's centre; and this is accomplished by impressing on every body an acceleration equal and opposite to that of the planet's centre.

Let M, m be the masses of the planet and the satellite; r the radius vector of the satellite, measured from the planet's centre; ρ the radius vector, measured from same point, of the particle whose motion we wish to determine; and z the angle between r and ρ. The satellite moves in an elliptic orbit about the planet, and the acceleration relatively to the planet's centre of the satellite is (M+m)/r² towards the planet along the radius vector r. Now the centre of inertia of the planet and satellite remains fixed in space, and the centre of the planet describes an orbit round that centre of inertia similar to that described by the satellite round the planet but with linear dimensions reduced in the proportion of m to M+m. Hence the acceleration of the planet's centre is m/r² towards the centre of inertia of the two bodies. Thus, in order to reduce the planet's centre to rest, we apply to every particle of the system an acceleration m/r² parallel to r, and directed from satellite to planet.

Now take a set of rectangular axes fixed in the planet, and let M₁r, M₂r, M₃r be the co-ordinates of the satellite referred thereto; and let ξρ, ηρ, ζρ be the co-ordinates of the particle P whose radius vector is ρ. Then the component accelerations for reducing the planet's centre to rest are -mM₁/r², -mM₂/r², -mM₃/r²; and since these are the differential coefficients with respect to ρξ, ρη, ρζ of the function

$-{\frac {m\rho }{r^{2}}}(\mathrm {M} _{1}\xi +\mathrm {M} _{2}\eta +\mathrm {M} _{3}\zeta )$,

and since cos z = M₁ξ+M₂η+M₃ζ, it follows that the potential of the forces by which the planet's centre is to be reduced to rest is

$-{\frac {m\rho }{r^{2}}}\cos {z}$

Now let us, consider the, other forces acting on the particle. The planet is spheroidal, and therefore does not attract equally in all directions; but in this investigation we may make abstraction of the ellipticity of the planet and of the ellipticity of the ocean due to the planetary rotation. This, which we set aside, is considered in the theories of gravity and of the figures of planets. Outside its body, then, the planet contributes forces of which the potential is M/ρ. Next the direct attraction of the satellite contributes forces of which the potential is the mass of the satellite divided by the distance between the point P and the satellite; this is

${\frac {m}{\surd \{r^{2}+\rho ^{2}-2r\rho \cos {z}\}}}$.

To determine the forces from this potential we regard ρ and z as the variables for differentiation, and we may add to this potential any constant we please. As we are seeking to find the forces which urge P relatively to M, we add such a constant as will make the whole potential at the planet's centre zero, and thus we take as the potential of the forces due to the attraction of the satellite

${\frac {m}{\surd \{r^{2}+\rho ^{2}-2r\rho \cos {z}\}}}-{\frac {m}{r}}$.

It is obvious that in the case to be considered r is very large compared with ρ, and we may therefore expand this in powers of ρ/r. This expansion gives us

${\frac {m}{r}}\left\{{\frac {\rho }{r}}P_{1}+{\frac {\rho ^{2}}{r^{2}}}P_{2}+{\frac {\rho ^{3}}{r^{3}}}P_{3}+...\right\}$,

where P₁ = cos z, P₂ = 3/2 cos² z — 1/2, P₃ = 3/2 cos³ z - 3/2 cos z, &c. The reader familiar with spherical harmonic analysis of course recognizes the zonal harmonic functions; but the result for a few terms, which is all that is necessary, is easily obtainable by simple algebra.

Now, collecting together the various contributions to the potential, and noticing that ${\frac {m}{r}}\cdot {\frac {\rho }{r}}P_{1}={\tfrac {m\rho }{r^{2}}}\cos {z}$, and is therefore equal and opposite to the potential by which the planet's centre was reduced to rest, we have as the potential of the forces acting on a particle whose co-ordinates are ρξ, ρη, ρζ

${\frac {M}{p}}+{\frac {m\rho ^{2}}{r^{3}}}({\tfrac {3}{2}}\cos ^{2}{z}-{\tfrac {1}{2}})+{\frac {m\rho ^{3}}{r^{4}}}({\tfrac {5}{2}}\cos ^{3}{z}-{\tfrac {3}{2}}\cos {z})+...$(1)

The first term of (1) is the potential of gravity, and the terms of the series, of which two only are written, constitute the Potential. tide-generating potential. In all practical applications this series converges so rapidly that the first term is amply sufficient, and thus we shall generally denote

$V={\frac {3m}{2r^{8}}}\rho ^{2}(\cos ^{2}{z}-{\tfrac {1}{3}})$(2)

as the tide-generating potential.^[18]

At the surface of the earth ρ is equal to a the earth's radius.

§ 12. Form of Equilibrium.—Consider the shape assumed by an ocean of density σ, on a planet of mass M, density δ and radius a, when acted on by disturbing forces whose potential is a solid spherical harmonic of degree i, the planet not being in rotation.

If S_i denotes a surface spherical harmonic of order i, such a potential is given at the point whose radius vector is ρ by

$V={\frac {3ma^{2}}{2r^{3}}}\left({\frac {\rho }{a}}\right)^{i}S_{i}$.(3)

In the case considered in § II, i=2 and S_i becomes the second zonal harmonic cos² z - 1/3.

The theory of harmonic analysis tells us that the form of the ocean. when in equilibrium, must be given by the equation

$\rho =a+e_{i}S_{i}$.(4)

Our problem is to evaluate e_i. We know that the external potential of a layer of matter, of depth e_iS_i and density σ, has the value

${\frac {4\pi \delta a}{2i+1}}\left({\frac {a}{\rho }}\right)^{i+1}e_{i}S_{i}$.

Hence the whole potential externally to the planet and up to its surface is

${\frac {M}{\rho }}+{\frac {3ma^{2}}{2r^{3}}}\left({\frac {\rho }{a}}\right)^{i}S_{i}+{\frac {4\pi \delta a}{2i+1}}\left({\frac {a}{\rho }}\right)^{i+1}e_{i}S_{i}$.(5)

The first and most important term is the potential of the planet, the second that of the disturbing force, and the third that of the departure from sphericity.

Since the ocean must stand in a level surface, the expression (5) equated to a constant must be another form of (4). Hence, if we put ρ=a+e_iS_i, in the first term of (5) and ρ=a in the second and third terms, (5) must be constant; this can only be the case if the coefficient of S_i vanishes. Hence on effecting these substitutions and equating that coefficient to zero, we find

${-{\frac {M}{a^{2}}}e_{i}}+{\frac {3ma^{2}}{2r^{2}}}+{\frac {4\pi \sigma a}{2i+1}}e_{i}=o$.

But by the definitions of δ and a we have $M={\tfrac {4}{2}}\pi \sigma a^{3}=ga^{2}$, where g is gravity, and therefore

$e_{i}={\frac {\frac {3ma^{2}}{2gr^{3}}}{1-{\frac {3\sigma }{(2i+1)\delta }}}}$.(6)

In the particular case considered in § II we therefore have

$\rho =a{\biggl [}1+{\frac {3ma^{2}/2gr^{3}}{1-3\sigma /5\delta }}(\cos ^{2}{z}-{\tfrac {1}{2}}){\biggr ]}$(7)

as the equation to the equilibrium tide under the potential

$V={\frac {3m}{2r^{2}}}\rho ^{2}(\cos ^{2}{z}-{\begin{matrix}{\frac {1}{2}}\end{matrix}})$.

If σ were very small compared with δ the attraction of the water on itself would be very small compared with that of the planet on the water; hence we see in the general case that $1/\left(1-{\tfrac {3\sigma }{2i+1)\delta }}\right)$ is the factor by which the mutual gravitation of the ocean augments the deformation due to the external forces. This factor will occur frequently hereafter, and therefore for brevity we write

$b_{i}=1-{\frac {3\sigma }{2i+1}}\delta$(8)

and we may put (6) in the form

$e_{i}={\frac {3ma^{2}}{2gr^{3}b_{i}}}$(9)

Comparison with (5) then shows that

$V=gb_{i}\left({\frac {\rho }{a}}\right)^{i}\!e_{i}S_{i}$(10)

is the potential of the disturbing forces under which

$\rho =a+e_{i}S_{i}$(11)

is a figure of equilibrium.

We are thus provided with a convenient method of specifying any disturbing force by means of the figure of equilibrium which it is competent to maintain. In considering the dynamical theory of the tides on an ocean-covered planet, we shall specify the disturbing forces in the manner expressed by (10) and (11). This way of specifying a disturbing force is equally exact whether or not we choose to include the effects of the mutual attraction of the ocean. If the augmentation due to mutual attraction of the water is not included, b_i becomes equal to unity; there is no longer any necessity to use spherical harmonic analysis, and we see that if the equation to the surface of an ocean be

$\rho =a+S$,

where S is a function of latitude and longitude, it is in equilibrium under forces due to a potential whose value at the surface of the sphere (where $\rho =a$) is $gS$.

In treating the theory of tidal observation we shall specify the tide-generating forces in this way, and then by means of "the principle of forced vibrations," referred to in § 7 as used by Laplace for discussing the actual oscillations of the sea, we shall pass to the actual tides at the port of observation.

In this equilibrium theory it is assumed that the figure of the ocean is at each instant one of equilibrium under the action of gravity and of the tide-generating forces. Lord Kelvin has, however, Effect of Land in Equilibrium Theory. reasserted^[19] a point which was known to Bernoulli, but has since been overlooked, namely, that this law of rise and fall of water cannot, when portions of the globe are continents, be satisfied by a constant volume of water in the ocean. The necessary correction to the theory depends on the distribution of land and sea, but a numerical solution shows that it is practically of very small amount.

§ 13. Development of Tide-generating Potential in Terms of Hour-Angle and Declination.—We now proceed to develop the tide-generating, potential, and shall of course implicitly (§ 12) determine the equation to the equilibrium figure.

We have already seen that, if z be the moon's zenith distance at the point P on the earth's surface, whose co-ordinates referred to A, B, C, axes fixed in the earth, and aξ, aη, aζ,

$\cos ^{2}{z}=\xi M_{1}+\mu M_{2}+\zeta M_{3}$,

where M₁, M₂, M₃ are the moon's direction cosines referred to the same axes. Then, with this value of $\cos {z}$,

$\cos ^{2}{z}-{\tfrac {1}{2}}=2\xi \mu M_{1}M_{2}+2{\frac {\xi ^{2}-\mu ^{2}}{2}}{\frac {M_{1}^{2}-M_{2}^{2}}{2}}+2\mu \zeta M_{2}M_{3}+2\xi \zeta M_{1}M_{2}+{\tfrac {2}{3}}{\frac {\xi ^{2}+\mu ^{2}-|2\zeta ^{2}}{3}}{\frac {M_{1}^{2}+M_{2}^{2}+2M_{3}^{2}}{3}}$.(12)

The axis of C is taken as the polar axis, and AB is the equatorial plane, so that the functions of ξ, η, ζ are functions of the latitude and longitude of the point P, at which we wish to find the potential

The functions of M₁, M₂, M₃ depend on the moon's position and we shall have occasion to develop them in two different ways—first in terms of her hour-angle and declination, and secondly (§ 25) in terms of her longitude and the elements of the orbit.

Now let A be on the equator in the meridian of P, and B 90° east of A on the equator. Then, if M be the moon, the inclination of the plane MC to the plane CA is the moon's easterly local hour-angle. Let h₀=Greenwich westward hour-angle; l=the west longitude of the place of observation; λ=the latitude of the place; δ=moon's declination: then we have

$M_{1}=\cos {\delta }\cos {(h_{0}-l)}$, $M_{2}=-\cos {\delta }\sin {(h_{0}-l)}$, $M_{3}=\sin {\delta }$, $\xi =\cos {\epsilon }$, $\mu =0$, $\zeta =\sin {\epsilon }$.

Also the radius vector of the place of observation on the earth's surface is a. Whence we find

$V={\frac {3ma^{2}}{2r^{3}}}\left\{{\tfrac {1}{2}}\cos ^{2}{\lambda }\cos ^{2}{\delta }\cos {2(h_{0}-l)}+\sin {2\lambda }\sin {\delta }\cos {\delta }\cos {(h_{0}-l)}+{\tfrac {3}{2}}({\tfrac {1}{3}}-\sin ^{2}{\delta })({\tfrac {1}{3}}-\sin ^{2}{\lambda })\right\}$.(13)

The tide-generating forces are found by the rates of variation of V for latitude and longitude, and also for radius a, if we care to find the radial disturbing force.

The westward component of the tide-generating force at the earth's surface, where $\rho =a$, is $dV/a\cos {\lambda dl}$, and the northward component is $dV/ad\lambda$; the change of apparent level is the ratio of these to gravity g. On effecting the differentiations Potential Developed in Hour-angle and Declination. we find that the westward component is made up of two periodic terms, one going through its variations twice and the other once a day. The southward component has also two similar terms; but it has a third very small term, which does not oscillate about a zero value. This last term corresponds to forces which produce a constant heaping up of the water at the equator; or, in other words, the moon's attraction has the effect of causing a small permanent ellipticity of the earth's mean figure. This augmentation of ellipticity is of course very small, but it is necessary to mention it.

If we consider the motion of a pendulum-bob under the influence of these forces during any one day, we see that in consequence of the semi-diurnal changes of level it twice describes an ellipse with major axis east and west, and the formula when developed shows that the ratio of axes is equal to the sine of the latitude, and the linear dimensions proportional to $\cos ^{2}{\delta }$. It describes once a day an ellipse whose north and south axis is proportional to $\sin {2\delta }\cos {2\lambda }$ and whose east and west axis is proportional to $\sin {2\delta }\sin {\lambda }$. Obviously the latter is circular in latitude 30°. When the moon is on the equator, the maximum deflexion occurs when the moon's local hour-angle is 45°, and is then equal to

${\frac {3m}{2M}}\left({\frac {a}{r}}\right)^{3}\cos {\lambda }$.

This angle is equal to 0.0174" cos λ. Attempts actually to measure the deflexion of the vertical have at length proved successful (see Seismometer).

III.—Dynamical Theory of the Tides

§ 14. Recent Advances in the Dynamical Theory of the Tides.— The problem of the tidal oscillation of the sea is essentially dynamical. In two papers in the second volume of Liouville's Journal (1896) H. Poincaré has considered the mathematical principles involved in the problem, where the ocean is interrupted by land as in actuality. He has not sought to obtain numerical results applicable to any given configuration of land and sea, but he has aimed rather at pointing out methods by which it may some day be possible to obtain such solutions.

Even when the ocean is taken as covering the whole earth the problem presents formidable difficulties, and this is the only case in which it has been solved hitherto.^[20]

Laplace gives the solution in bks. i. and iv. of the Mécanique céleste; but his work is unnecessarily complicated. In the 9th edition of the Ency. Brit. we gave Laplace's theory without these complications, but the theory is now accessible in H. Lamb's Hydrodynamics and other works of the kind. It is therefore not reproduced here.

In 1897 and 1898 S. S. Hough undertook an important revision of Lap1ace's theory and succeeded not only in introducing the effects of the mutual gravitation of the ocean, but also in determining the nature and periods of the free oscillations of the sea.^[21] A dynamical problem of this character cannot be regarded as fully solved unless we are able not only to discuss the “ forced ” oscillations of the system but also the “free.” Hence we regard Mr Hough's work as the most important contribution to the dynamical theory of the tides since the time of Laplace. We shall accordingly present the theory briefly in the form due to Mr Hough.

The analysis is more complex than that of Laplace, where the mutual attraction of the ocean was neglected, but this was perhaps inevitable. Our first task is to form the equations of motion and continuity, which will be equally applicable to all forms of the theory.

§ 15. Equations of Motion.—Let $r,\theta ,\phi$ be the radius vector, colatitude and east longitude of a point with reference to an origin, a polar axis and a zero-meridian rotating with a uniform angular velocity $n$ from west to east. Then if $R,H,\Xi$ be the radial, colatitudinal and longitudinal accelerations of the point, we have

$R={\frac {d^{2}r}{dt^{2}}}-r\left({\frac {d\theta }{dt}}\right)^{2}-r\sin ^{2}\theta \left({\frac {d\phi }{dt}}+n\right)^{2}$

$\Xi ={\frac {I}{r}}{\frac {d}{dt}}\left(r^{2}{\frac {d\theta }{dt}}\right)-r\sin \theta \cos \theta \left({\frac {d\phi }{dt}}+n\right)^{2}$

$H={\frac {I}{r\sin \theta }}{\frac {d}{dt}}\left[r^{2}\sin ^{2}\theta \left({\frac {d\phi }{dt}}+n\right)\right].$

If the point were at rest with reference to the rotating meridian we should have

$R=-n^{2}r\sin \theta ,\;\Xi =-n^{2}r\sin \theta \cos \theta ,\;H=0.$

When these considerations are applied to the motion of an ocean relative to a rotating planet, it is clear that these accelerations, which still remain when the ocean is at rest, are annulled by the permanent oblateness of the ocean. As then they take no part in the oscillations of the ocean, and as we are not considering the figure of the planet, we may omit these terms from $R$ and $\Xi$. This being so we must replace $\left({\frac {d\phi }{dt}}+n\right)^{2}$ as it occurs in $R$ and $\Xi$ by $\left({\frac {d\phi }{dt}}\right)^{2}+2n{\frac {d\phi }{dt}}$.

Now suppose that the point whose accelerations are under consideration never moves far from its zero position, and that its displacements $\xi ,\eta \sin \theta$ in colatitude and longitude are very large compared with $\rho$ its radial displacement. Suppose, further, that the velocities of the point are so small that their squares and products are negligible compared with $n^{2}r^{2}$; then we have

${\frac {dr}{dt}}={\frac {d\rho }{dt}}$, a very small quantity;

$r\sin \theta {\frac {d\phi }{dt}}={\frac {d}{dt}}\left(\eta \sin \theta \right)$,

$r{\frac {d\theta }{dt}}={\frac {d\xi }{dt}}$.

Since the radial velocity always remains very small it is not necessary to concern ourselves further with the value of $R$, and we only require the two other components which have the approximate forms,

$\Xi ={\frac {d^{2}\xi }{dt^{2}}}-2n\sin \theta \cos \theta {\frac {d\eta }{dt}},$

$H=\sin \theta {\frac {d^{2}\eta }{dt^{2}}}+2n\cos \theta {\frac {d\xi }{dt}}$. ⁠ (14)

We have now to consider the forces by which an element of the ocean is urged in the direction of colatitude and longitude. These forces are those due to the external disturbing forces, to the pressure of the water, surrounding an element of the ocean, and to the attraction of the ocean itself.

If $e$ denotes the equilibrium height of the tide, it is function of colatitude and longitude, and may be expanded in a series of spherical surface harmonics $e_{i}$. Thus we may write the equation to the equilibrium tide in the form.

$r=a+e=a+\sum e_{i}$

Now it appears from (10) and (11) that the value of the potential, at the surface of the sphere where $\rho =a$, under which this is a figure of equilibrium, is

$V=\sum gb_{i}e_{i}$

We may use this as specifying the external disturbing force due to the known attractions of the moon and sun, so that $e_{i}$ may be regarded as known.

But in our dynamical problem the ocean is not a figure of equilibrium, and we may denote the elevation of the surface at any moment of time by ${\displaystyle }$. Then the equation to the surface may be written in the form

$r=a+b=a+\sum h_{i}$

where $h_{i}$ denotes a spherical harmonic just as $e_{i}$ did before.

The surface value of the potential of the forces which would maintain the ocean in equilibrium. in the shape it has at any moment is Egbabr. Hence it follows that in the actual case the forces due to fluid pressure and to the attraction of the ocean must be such as to balance the potential just determined. Therefore these forces are those due to a potential—Zgbqbf. If we add to this the potential of the external forces, we have a potential which will include all the forces, the expression for which is-gEb;(b;-eg). If further we perform the operations d/adθ and d/a sin θdΦ on this potential, we obtain the colatitudinal and longitudinal forces which are equal to the accelerations Ξ and H.

It follows, then, from (14) that the equations of motion are

$\left.{\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}-2n\sin \theta \cos \theta {\frac {d\eta }{dt}}&=-{\frac {g}{a}}\Sigma b_{i}{\frac {d}{d\theta }}(b_{i}-e_{i})\\\sin \theta {\frac {d^{2}\eta }{dt^{2}}}+2n\cos \theta {\frac {d\xi }{dt}}&=-{\frac {g}{a\sin \theta }}\Sigma b_{i}{\frac {d}{d_{\theta }}}(b_{i}-e)\end{aligned}}\right\}{\text{(15)}}$

Equations of Motion.

It remains to find the equation of continuity. This may be deduced geometrically from the consideration that the volume of an element of the fluid remains constant; but a shorter way is to derive it from the equation of continuity as it occurs in ordinary hydrodynamical investigations. If Φ be a velocity potential, the equation of continuity for incompressible fluid is

${\begin{aligned}\delta r{\frac {d}{dr}}(r^{2}{\frac {d\Phi }{dr}}\sin \theta \delta \theta \delta \phi )+\delta \theta {\frac {d}{d\theta }}(r\sin \theta {\frac {d\Phi }{rd\theta }}\delta r\delta \phi )\\+\delta \phi {\frac {d}{d\phi }}(r{\frac {I}{r\sin \theta }}{\frac {d\Phi }{d\phi }}\delta r\delta \theta )={\text{o.}}\end{aligned}}$

The element referred to in this equation is defined by r, θ, φ, r+δr, θ+δθ, φ+δφ. The colatitudinal and longitudinal velocities are the same for all the elementary prism defined by θ, φ, θ+δθ, φ+δφ, and the sea bottom. Then ${\frac {d\Phi }{rd\theta }}={\frac {d\xi }{dt}},{\frac {d\Phi }{r\sin \theta d\phi }}=\sin \theta {\frac {d\eta }{dt}}$; and, since the radial velocity is db/dt at the surface of the ocean, where r=a+γ, and is zero at the sea bottom, where r=a, we have ${\frac {d\Phi }{dr}}={\frac {r-a}{\gamma }}{\frac {db}{dt}}$. Hence, integrating with respect to r from r=a+γ to r=a, and again with respect to t from time t to the time when h, ξ, η all vanish, and treating γ and h as small compared with a, we have,

(16)

$ba\sin \theta +{\frac {d}{d\theta }}(\gamma \xi \sin \theta )+{\frac {d}{d\phi }}(\gamma \eta \sin \theta )={\text{0.}}$

This is the equation of continuity, and, together with (15), it forms the system which must be integrated in the general problem of the tides. The difficulties in the Equation of Continuity. way of a solution are so great that none has hitherto been found, except on the supposition that γ, the depth of the ocean, is only a function of latitude. In this-case (16) becomes

(17)

$ba+{\frac {I}{\sin \theta }}{\frac {d}{d\theta }}(\gamma \eta \sin \theta )+\gamma {\frac {d\eta }{d\phi }}={\text{o.}}$

§ 16. Adaptation to Forced Oscillations.—Since we may suppose that the free oscillations are annulled by friction, the solution required is that corresponding to forced oscillations. Now we have seen from (13) that e (which is proportional to V) has terms of three kinds, the first depending on twice the moon's (or sun's)' hour-angle, the second on the hour-angle, and the third independent thereof. The coefficients of the first and second vary slowly, and the whole of the third varies slowly. Hence e has a semi-diurnal, a diurnal and a long-period term. We shall see later that these terms may be expanded in a series of approximately semi-diurnal, diurnal and slowly varying terms, each of which is a strictly harmonic function of the time.

Thus according to the usual method of treating oscillating systems, we may make the following assumptions as to the form of the solution

$\left.{\begin{aligned}e&=\Sigma e_{i}=\Sigma e_{i}\cos(2nft+s\phi +\alpha )\\b&=b\Sigma _{i}=\Sigma h_{i}\cos(2nft+s\phi +\alpha )\\\xi &=\Sigma b_{i}x_{i}\cos(2nft+s\phi +\alpha )\\\eta &=\Sigma b_{i}y_{i}\sin(2nft+s\phi +\alpha )\end{aligned}}\right\}{\text{(18)}}$

where e_i, h_i, x_i, y_i are functions of colatitude only, and e_i, h_i are the associated functions of colatitude corresponding to the harmonic of order i and rank s.

For the semi-diurnal tides s=2 and f is approximately unity; for the diurnal tides s=1 and f is approximately 1/2; and for the tides of long period s=0 and f is a small fraction.

Substituting these values in (17) we have

(19)

$\Sigma \left[{\frac {I}{\sin \theta }}{\frac {d}{d\theta }}(\gamma b_{i}x_{i}\sin \theta )+s\gamma b_{i}y_{i}+h_{i}\alpha \right]={\text{o.}}$

Then if we write u_i for h_i-e_i, and put m=n²a/g, substitution from (18) in (15) leads at once to

$\left.{\begin{aligned}f^{2}\Sigma b_{i}x_{i}-f\sin \theta \cos \theta \Sigma b_{i}y_{i}&={\frac {I}{4m}}{\frac {d}{d\theta }}\Sigma b_{i}u_{i},\\f^{2}\sin \theta \Sigma b_{i}y_{i}+f\cos \theta \Sigma b_{i}x_{i}&=-{\frac {s}{4m\sin \theta }}\Sigma b_{i}u_{i}.\end{aligned}}\right\}\circ {\text{(20)}}$

Solving (20), we have

$\left.{\begin{aligned}&(\Sigma b_{i}x_{i})(f^{2}-\cos ^{2}\theta )={\frac {I}{4m}}\left[{\frac {d}{d\theta }}\Sigma b_{i}u_{i}+{\frac {s\cos \theta }{f\sin \theta }}\Sigma b_{i}u_{i}\right]\\&(\Sigma b_{i}y_{i})\sin ^{2}\theta (f^{2}-\cos ^{2}\theta )=-{\frac {I}{4m}}\left[{\frac {\cos \theta }{f}}{\frac {d}{d\theta }}\Sigma b_{i}u_{i}+{\frac {s}{\sin \theta }}\Sigma b_{i}u_{i}\right]\end{aligned}}\right\}{\text{(21)}}$

Then substituting from (21) in (19) we have

(22)

${\begin{aligned}{\frac {I}{\sin \theta }}&{\frac {d}{d\theta }}\left[{\frac {\gamma (\sin \theta {\frac {d}{d\theta }}\Sigma b_{i}u_{i}+{\frac {s}{f}}\cos \theta \Sigma b_{i}u_{i})}{f^{2}-\cos ^{2}\theta }}\right]\\&-{\frac {s\gamma \left[{\frac {\cos \theta }{f}}{\frac {d}{d\theta }}\Sigma b_{i}u_{i}+{\frac {s}{\sin \theta }}\Sigma b_{i}u_{i}\right]}{\sin \theta (f^{2}-\cos ^{2}\theta )}}+4ma\Sigma (u_{i}+e_{i})=o.\end{aligned}}$

This is almost the same as Laplace's equation for tidal oscillations in an ocean whose depth is only a function of latitude. If indeed we treat b_i as unity (thereby neglecting the mutual attraction of the water) and replace Σu_i and Σe_i by u and e, we obtain Laplace's equation.

When u_i is found from this equation, its value substituted in (21) will give x_i and y_i.

§ 17. Zonal Oscillations.—We might treat the general harmonic oscillations first, and proceed to the zonal oscillations by putting s=0. These waves are, however, comparatively simple, and it is well to begin with them. The zonal tides are those which Laplace describes as of the first species, and are now more usually called the tides of long period. As we shall only consider the case of an ocean of uniform depth, γ the depth of the sea is constant. Then since in this case s=0, our equation (22), to be satisfied by u_i; or h_i-e_i, becomes

${\frac {d}{d\theta }}\left[{\frac {\sin \theta {\frac {d}{d\theta }}\Sigma b_{i}u_{i}}{f^{2}-\cos ^{2}\theta }}\right]+{\frac {4ma}{\gamma }}\sin \theta \Sigma h_{i}=o.$

This may be written

(23)

${\frac {d}{d\theta }}\Sigma b_{i}u_{i}+{\frac {4ma}{\gamma }}{\frac {f^{2}-\cos ^{2}\theta }{\sin \theta }}\int ^{\theta }\Sigma h_{i}\sin \theta d\theta +A=o,$

where A is a constant.

Let us assume

h_i=C_iP_i,⁠ e_i=E_iP_i

where P_i denotes the ith zonal harmonic of cos θ. The coefficients C_i are unknown, but the E_i are known because the system oscillates under the action of known forces.

If the term involving the integral in this equation were expressed in terms of differentials of harmonics, we should be able to equate to zero the coefficient of each dP_i/dθ in the equation, and thus find the conditions for determining the C's.

The task then is to express P; sin θdθ in differentials of zonal harmonics.

It is well known that P_i satisfies the differential equation

(24)

${\frac {d}{d\theta }}\left(\sin \theta {\frac {dP_{i}}{d\theta }}\right)+i(i+I)P_{i}\sin \theta =o.$

Therefore $\int P_{i}\sin \theta d\theta =-{\frac {I}{i(i+I)}}\sin \theta {\frac {dP_{i}}{d\theta }}$, and

${\frac {f^{2}-\cos ^{2}\theta }{\sin \theta }}\int P_{i}\sin \theta d\theta =-{\frac {I}{i(i+I)}}(f^{2}-\cos ^{2}\theta ){\frac {dP_{i}}{d\theta }}=-{\frac {I}{i(i+I)}}(f^{2}-I){\frac {dP_{i}}{d\theta }}--{\frac {I}{i(i+I)}}\sin ^{2}\theta {\frac {dP_{i}}{d\theta }}$

Another well-known property of zonal harmonics is that

(25)

$\sin \theta {\frac {dP_{i}}{d\theta _{i}}}={\frac {i(i+I)}{2i+I}}(P_{i+I}-P_{i-I})$.

If we differentiate (25) and use (24) we have

(26)

${\frac {i(i+I)}{2i+I}}\left({\frac {dP_{i+I}}{d\theta }}-{\frac {dP_{i-I}}{d\theta }}\right)i(i+I)P_{i}\sin \theta =o.$

Multiplying (25) by sin θ, and using (26) twice over,

$\sin ^{2}\theta {\frac {dP_{i}}{d\theta }}={\frac {i(i+I)}{2i+I}}\left\{-{\frac {I}{2i+3}}\left({\frac {dP_{i+2}}{d\theta }}-{\frac {dP_{i}}{d\theta }}\right)+{\frac {I}{2i-I}}\left({\frac {dP_{i}}{d\theta }}-{\frac {dP_{i-2}}{d\theta }}\right)\right\}$

Therefore

${\begin{aligned}{\frac {f^{2}-\cos ^{2}\theta }{\sin \theta }}\int P_{i}\sin \theta d\theta ={\frac {I}{(2i-I)(2i+I)}}{\frac {dP_{i-2}}{d\theta }}\\-\left\{{\frac {f^{2}-I}{i(i+I)}}+{\frac {2}{(2i-I)(2i+3)}}\right\}{\frac {dP_{i}}{d\theta }}+{\frac {I}{(2i+I)(2i+3)}}{\frac {dP_{i+2}}{d\theta }}\end{aligned}}$

This expression, when multiplied by 4ma/γ and by C_i and summed, is the second term of our equation.

The first term is

$\Sigma b_{i}(C_{i}-E_{i}){\frac {dP_{i}}{d\theta }}$

In order that the equation may be satisfied, the coefficient of each dP_i/dθ must vanish identically. Accordingly we multiply the whole by γ/4ma and equate to zero the coefficient in question, and obtain

(27)

${\frac {b_{i}\gamma }{4ma}}(C_{i}-E_{i})+{\frac {C_{i-2}}{(2i-I)(2i-3)}}-\left\{{\frac {f^{2}-I}{i(i+I)}}+{\frac {2}{(2i-1)(2i+3)}}\right\}C_{i}+{\frac {C_{i+2}}{(2i+3)(2i+5)}}=o.$

This equation (27) is applicable for all values of i from 1 to infinity, provided that we take C₀, E_O, C_-1, E_-1 as being zero.

We shall only consider in detail the case of greatest interest, namely that of the most important of the tides generated by the attraction of the sun and moon. We know that in this case the equilibrium tide is expressed by a zonal harmonic of the second order; and therefore all the E_i, excepting E₂, are zero. Thus the equation (27) will not involve E_i in any case excepting when i=2.

If we write for brevity

$L_{i}={\frac {f^{2}-I}{i(i+I)}}+{\frac {2}{(2i-I)(2i+3)}}-{\frac {b_{i}\gamma }{4ma}}$

the equation (27) is

(28)

${\frac {C_{i+2}}{(2i+3)(2i+5)}}-L_{i}C_{i}+{\frac {C_{i-2}}{(2i-3)(2i-1)}}=o.$

Save that when i=2, the right-hand side is b₂γE₂/4ma, a known quantity ex hypothesi.

The equations naturally separate themselves into two groups in one of which all the suffixes are even and the other odd. Since our task is to evaluate all the C's in terms of E₂, it is obvious that all the C's with odd suffixes must be zero, and we are left to consider only the cases where i=2, 4, 6, &c.

We have, said that C₀ must be regarded as being zero; if however we take

$C_{0}=-3b_{2}\gamma E_{2}/4ma,$

so that C₀ is essentially a known quantity, the equation (28) has complete applicability for all even values of i from 2 upwards.

The equations are

${\begin{aligned}&{\frac {C_{0}}{1.3}}-L_{2}C_{2}+{\frac {C_{4}}{7.9}}=o\\&{\frac {C_{2}}{5.7}}-L_{4}C_{4}+{\frac {C_{6}}{11.13}}=o.\end{aligned}}$

It would seem at first sight as if these equations would suffice to determine all the C's in terms of C₂, and that C₂ would remain indeterminate; but we shall show that this is not the case.

For very large values of i the general equation of condition (28) tends to assume the form

${\frac {C_{i+2}+C_{i-2}}{C_{i}}}+{\frac {2^{3}\gamma }{ma}}=o.$

By writing successively i+2, i+4; i+6 for i in this equation, and taking the differences, we obtain an equation from which we see that, unless C_i/C_i+2 tends to became infinitely small, the equations are satisfied by C_i=C_i+1 in the limit for very large values of i.

Hence, if C_i does not tend to zero, the later portion of the series for h tends to assume the form C_i(P_i+P_i+2+P_i+4...). All the P's are equal to unity at the pole; hence the hypothesis that C, does not tend to zero leads to the conclusion that the tide is of infinite height at the pole. The expansion of the height of tide is essentially convergent, and therefore the hypothesis is negatived. Thus we are entitled to assume that C_i tends to zero for large values of i.

Now writing for brevity

a_i=1/(2i+1)(2i+3)²(2i+5),

we may put (28) into the form

${\frac {C_{i-2}/C_{i}}{(2i-3)(2i-1)}}=L_{i}-{\frac {\frac {\alpha _{i}}{C_{i}/C_{i+2}}}{(2i+1)(2i+3)}}$

By successive applications of this formula we may write the right hand side in the form of a continued fraction.

Let

$K_{i}={\frac {\alpha _{i}-2}{L_{i}-}}{\frac {\alpha _{i}}{L_{i+2}-}}{\frac {\alpha _{i}+2}{L_{i+4}-}}\dots$

Then we have

${\frac {C_{i-2}/C_{i}}{(2i-3)(2i-1)}}={\frac {\alpha _{i-2}}{K_{i}}}$,

or

$C_{i}/C_{i-2}=(2i-1)(2i+1)K_{i}$.

Thus

${\begin{aligned}C_{2}&=3.5K_{2}C_{0};\\C_{4}&=3.5.7.9K_{2}K_{4}C_{0};\\C_{6}&=3.5.7.9.11.13K_{2}K_{4}K_{6}C_{0},\end{aligned}}$&c.

If we assume that any of the higher C's, such as C₁₄ or C₁₆, is of negligible smallness, all the continued fractions K₂, K₄, K₆, &c., may be computed; and thus we find all the C's in terms of C₀, which is equal to -3b₂γE₂/4ma. The height of the tide is therefore given by

${\begin{aligned}h&=\Sigma h_{i}\cos(2nft+\alpha )\\&=-{\frac {3b_{2}\gamma }{4ma}}E_{2}\left\{3.5K_{2}P_{2}+3.5.7.9K_{2}K_{4}P_{4}+\dots \right\}\cos(2nft+\alpha )\end{aligned}}$.

It is however more instructive to express h as a multiple of the equilibrium tide e, which is as we know equal to E₂P₂ cos (2nft+a). Whence we find

$b=-{\frac {3b_{2}\gamma }{4ma}}{\frac {e}{P_{2}}}\left\{3.5K_{2}P_{2}+3.5.7.9K_{2}K_{4}P_{4}+3.5\dots 13K_{2}K_{4}K_{6}P_{6}\dots \right\}$.

The number f is a fraction such that its reciprocal is twice the number of sidereal days in the period of the tide. The greatest value of f is that appertaining to the lunar fortnightly tide (Mf in notation of harmonic analysis), and in this case f is in round numbers 1/28, or more exactly f² = .00133. The ratio of the density σ of sea-water to δ the mean density of the earth is .18093; which value gives us

$b_{2}=1-{\frac {3\sigma }{5\delta }}=\cdot 89144\cdot$

The quantity m is the ratio of equatorial certrifugal force to gravity, an is equal to 1/289. Finally, γ/a is the depth of the ocean expressed as a fraction of the earth's radius.

With these numerical values Mr Hough has applied the solution of determine the lunar fortnightly tide for oceans of various depths. Of his results we give two:—

First, when γ = 7260 ft. = 1210 fathoms, which makes γ/4ma = 1/5, he finds

$b={\frac {e}{P_{2}}}\left\{\cdot 2669P_{2}-\cdot 1678P_{4}+\cdot 0485P_{6}-\cdot 0081P_{8}+\cdot 0009P_{1}0-\cdot 0001P_{12}\dots \right\}$

If the equilibrium theory were true we should have

$b={\frac {e}{P_{2}}}\left\{P_{2}\right\}$;

thus we see how widely the dynamical solution differs from the equilibrium value.

Secondly, when γ=58080 ft.=9680 fathoms, and γ/4ma=1/5, he finds

$b={\frac {e}{P_{2}}}\left\{\cdot 7208P_{2}-\cdot 0973P_{4}+\cdot 0048P_{6}-\cdot 0001P_{8}\dots \right\}$.

From this we see that the equilibrium solution presents some sort of approximation to the dynamical one; and it is clear that the equilibrium solution would be fairly accurate for oceans which are still quite shallow when expressed as fractions of the earth's radius, although far deeper than the actual sea.

The tides of long period were not investigated by Laplace in this manner, for he was of opinion that a very small amount of friction would suffice to make the ocean assume its form of equilibrium. In the arguments which he adduced in support of this view the friction contemplated was such that the integral effect was proportional to the velocity of the water relatively to the bottom. It is probable that proportionality to the square of the velocity would have been nearer the truth, but the distinction is unimportant.

The most rapid of the oscillations of this class is the funar fortnightly tide, and the water of the ocean moves northward for a week and then southward for a week. In oscillating systems, where the resistances are proportional to the velocities, it is usual to specify the resistance by a “ modulus of decay, ” namely the time in which a velocity is reduced by friction to e^-t or 1/2.78 of its initial value. Now in order that the result contemplated by Laplace may be true, the friction must be such that the modulus of decay is short compared with the semi-period of oscillation. It seems certain that the friction of the ocean bed would not reduce a slow ocean current to one-third of its primitive value in a day or two, Hence we cannot accept Laplace's discussion as satisfactory, and the investigation which has just been given becomes necessary. (See § 34).

§ 18. Tesseral Oscillations.—The oscillations which we now have to consider are those in which the form of surface is expressible by the tesseral harmonics. The results will Transformation of Equation. be applicable to the diurnal and semi-diurnal tides— Laplace's second and third species.

If we write σ=s/f the equation (22) becomes

(29)

${\frac {d}{d\theta }}\left[{\frac {\left(\sin \theta {\frac {d}{d\theta }}+\sigma \cos \theta \right)\Sigma b_{i}u_{i}}{s^{2}-\sigma ^{2}\cos ^{2}\theta }}\right]-{\frac {\left(\sigma \cos \theta {\frac {d}{d\theta }}+s^{2}\operatorname {cosec} \theta \right)\Sigma b_{i}u_{i}}{s^{2}-\sigma ^{2}\cos ^{2}\theta }}+{\frac {4ma}{\gamma \sigma ^{2}}}\sin \theta \Sigma h_{i}=0$.

If we write D for the operation sin θd/dθ, the middle term may be arranged in the form

$-{\frac {\sigma \cot \theta (D+\sigma \cos \theta )(\Sigma b_{i}u_{i})}{s^{2}-\sigma ^{2}\cos ^{2}\theta }}-{\frac {\Sigma b_{i}u_{i}}{\sin \theta }}$.

Therefore on multiplying by sin θ the equation becomes

(30)

$(D-\sigma \cos \theta )\left[{\frac {(D+\sigma \cos \theta )(\Sigma b_{i}u_{i})}{s^{2}-\sigma ^{2}\cos ^{2}\theta }}\right]-(\Sigma b_{i}u_{i})+{\frac {4ma}{\gamma \sigma ^{2}}}\sin ^{2}\theta \Sigma h_{i}=0$.

We now introduce two auxiliary functions, such that

(31)

${\begin{aligned}\Sigma b_{i}(h_{i}-e_{i})&=\Sigma b_{i}u_{i}\\&=(D-\sigma \cos \theta )\Psi +(s^{2}-\sigma ^{2}\cos ^{2}\theta )\Phi \end{aligned}}$

It is easy to prove that

(32)

$\left.{\begin{aligned}&(D+\sigma \cos \theta )(D-\sigma \cos \theta )=D^{2}-s^{2}+\sigma \sin ^{2}\theta +(s^{2}-\sigma ^{2}\cos ^{2}\theta ),\\&(D-\sigma \cos \theta )(D+\sigma \cos \theta )=D^{2}-s^{2}-\sigma \sin ^{2}\theta +(s^{2}-\sigma ^{2}\cos ^{2}\theta ).\end{aligned}}\right\}$

Also

(33)

$(D+\sigma \cos \theta )(s^{2}-\sigma ^{2}\cos ^{2}\theta )\Phi =(s^{2}-\sigma ^{2}\cos ^{2}\theta )(D+\sigma \cos \theta )\Phi +2\sigma ^{2}\sin ^{2}\theta \cos \theta \Phi$.

Now perform D+σ cos θ on (31), and use the first of (32) and (33), and we have

(34)

$(D+\sigma \cos \theta )(\Sigma b_{i}u_{i})=(D^{2}-s^{2}+\sigma \sin ^{2}\theta +s^{2}-\sigma ^{2}\cos ^{2}\theta )\Psi .+(s^{2}-\sigma ^{2}\cos ^{2}\theta )(D+\sigma \cos \theta )\Phi +2\sigma ^{2}\sin ^{2}\theta \cos \theta \Phi .$

The functions Ψ and Φ are as yet indeterminate, and we may impose another condition on them. Let that condition be

(34)

$(D^{2}-s^{2}+\sigma \sin ^{2}\theta )\Psi =-2\sigma ^{2}\sin ^{2}\theta \cos \theta \Phi$.

Then (34) may be written,

${\frac {(D+\sigma \cos \theta )(\Sigma b_{i}u_{i})}{s^{2}-\sigma ^{2}\cos ^{2}\theta }}=\Psi +(D+\sigma \cos \theta )\Phi$.

Substituting from this in (30), and, using the second of (32), the function Ψ disappears and the equation reduces to

(36)

$(D^{2}-s^{2}-\sigma \sin ^{2}\theta )\Phi +{\frac {4ma}{\gamma \sigma ^{2}}}\sin ^{2}\theta \Sigma h_{i}=0$.

Since by (35)-$-\sigma ^{2}\cos ^{2}\theta \Phi ={\tfrac {1}{2}}{\frac {\cos \theta }{\sin ^{2}\theta }}(D^{2}-s^{2}+\sigma \sin ^{2}\theta )\Psi$, (31) may be written

(37)

$\Sigma b_{i}u_{i}=\left[D-\sigma \cos \theta +{\tfrac {1}{2}}{\frac {\cos \theta }{\sin ^{2}\theta }}(D^{2}-s^{2}+\sigma \sin ^{2}\theta )\right]\Psi +s^{2}\Phi$.

The equations (35), (36) and (37) define Ψ and Φ, and furnish the equation which must be satisfied.

If we denote cos Θ by μ the zonal harmonics are defined by

$P_{i}={\frac {1}{2^{i}i!}}\left({\frac {d}{d\mu }}\right)^{i}(\mu ^{2}-1)^{i}$.

The following are three well-known properties of zonal harmonics:

(38)

${\frac {d}{d\mu }}\left[(1-\mu ^{2}){\frac {dP_{i}}{d\mu }}\right]+i(i+1)P_{i}=0$,

(39)

$(i+1)P_{i+1}-(2i+1)\mu P_{i}+iP_{i-1}=0$,

(40)

${\frac {dP_{i+1}}{d\mu }}-{\frac {dP_{i-1}}{d\mu }}=(2i+1)P_{i}$.

If PQ s¢ are the two tesseral harmonics of order i and rank s, it is also known that

(41)

$P_{i}^{3}=(1-\mu ^{2})^{{\tfrac {1}{2}}3}{\frac {d^{3}P_{i}}{d\mu ^{3}}}$.

Let us now assume

$h_{i}=C_{i}^{3}P_{i}^{3},\quad e_{i}=E_{i}^{3}P_{i}^{3},\quad \Psi =\Sigma \alpha _{i}^{3}P_{i}^{3},\quad \Phi =\Sigma \beta _{i}^{3}P_{i}^{3}$.

These must now be substituted in our three equations (35), (36), (37), and the result must be expressed by series of the P: functions. It is clear then that we have to transform into P; functions the following functions of PQ, namely

${\frac {1}{\sin ^{2}\theta }}(D^{2}-s^{2}=\sigma \sin ^{2}\theta )P_{i}^{3},\cos \theta P_{i}^{3},\left[D-\sigma \cos \theta +{\tfrac {1}{2}}{\frac {\cos \theta }{\sin ^{2}\theta }}(D^{2}-s^{2}+\sigma \sin ^{2}\theta )\right]P_{i}^{3}$.

If we differentiate (38) s times, and express the result by means of the operator D, we find

(42)

$(D^{2}-s^{2})P_{i}^{2}+i(i+1)P_{i}^{2}\sin ^{2}\theta =0$.

Again, differentiating (39) s times and using (40), we find

(43)

$(i-s+1)P_{i+1}^{3}-(2i+1)\cos \theta P_{i}^{3}+(i+s)P_{i-1}^{3}=0$.

Lastly, differentiating (41) once and using (38), (40) and (43)

(44)

$DP_{i}^{3}={\frac {i(i-s+1)}{2i+1}}P_{i+1}^{3}-{\frac {(i+1)(i+s)}{2i+1}}P_{i-1}^{3}$.

By means of (42), (43) and (44) we have

${\frac {1}{\sin ^{2}\theta }}(D^{2}-s^{2}\pm \sigma \sin ^{2}\theta )P_{i}^{3}=[-i(i+1)\pm \sigma ]P_{i}^{3}$,

$\cos \theta P_{i}^{3}={\frac {i+s}{2i+1}}P_{i}^{3}+{\frac {i-s+1}{2i+1}}P_{i+1}^{3}$,

$\left[D-\sigma +{\tfrac {\cos \theta }{\sin ^{2}\theta }}(D^{2}-s^{2}+\sigma \sin ^{2}\theta )\right]P_{i}^{3}=-{\frac {(i-s+1)[\sigma +i(i-1)]}{2(2i+1)}}P_{i+1}^{3}$

$-{\frac {(i+s)[\sigma +(i+1)(i+2)]}{2(2i+1)}}P_{i-1}^{3}$

Therefore the equations (35), (36), (37) give

$\Sigma \left[\sigma _{i}^{3}\{-i(i+1)+\sigma \}P_{i}^{3}+2\sigma ^{2}\beta _{i}^{2}\left\{{\frac {i+s}{2i+1}}P_{i-1}^{3}+{\frac {i-s+1}{2i+1}}P_{i-1}^{3}\right\}\right]=0$,

$\Sigma \left[\beta _{i}^{3}\{-i(i+1)-\sigma \}P_{i}^{3}+{\frac {4ma}{\gamma \sigma ^{2}}}C_{i}^{3}P_{i}^{3}\right]=0$,

$\Sigma \left[b_{i}(C_{i}^{3}-E_{i}^{3})P_{i}^{3}+\alpha _{i}^{3}\left\{{\frac {(i-s+1)[\sigma +i(i-1)]}{2(2i+1)}}P_{i+1}^{3}+{\frac {(i+s)[\sigma +(i+1)(i+2)]}{2(2i+1)}}P_{i-1}^{3}\right\}-\beta _{i}^{3}s^{2}P_{i}^{3}\right]=0$.

Since these equations must be true identically, the coefficients

of P_i in each of them must vanish. Therefore

$\left.{\begin{aligned}\alpha _{i}^{3}\{\sigma -i(i+1)\}+2\sigma ^{2}\left\{\beta _{i+1}^{2}{\frac {i+s+1}{2i+3}}+\beta _{i-1}^{2}{\frac {i-s}{2i-1}}\right\}&=0,\\-\beta _{i}^{2}\{\sigma +i(i+1)\}+{\frac {4ma}{\gamma \sigma ^{2}}}C_{i}^{3}&=0,\\b_{i}(C_{i}^{3}-E_{i}^{3})+\alpha _{i-1}^{3}{\frac {(i-s)[\sigma +(i-1)(i-2)]}{2(2i-1)}}\\+\alpha _{i+1}^{3}{\frac {(i+s+1)[\sigma +(i+2)(i+3)]}{2(2i+3)}}-\beta _{i}^{3}s^{2}&=0.\end{aligned}}\right\}\qquad (45)$

If we eliminate the α's and β's from the third equation (45), by means of the first two, we find Solution for Tesseral Oscillations.

(46)

$\xi _{i-2}^{3}C_{i-2}^{3}-L_{i}^{3}C_{i}^{3}+\eta _{i+2}^{3}C_{i+2}^{3}={\frac {\gamma b_{i}}{4ma}}E_{i}^{3},$

where

${\begin{aligned}L_{i}^{3}={\frac {s^{2}}{\sigma ^{2}[\sigma +i(i+1)]}}&+{\frac {(i^{2}-s^{2})[\sigma +(i-1)(i-2)]}{(4i^{2}-1)[\sigma -(i-1)i][\sigma +i(i+1)]}}\\&+{\frac {[(i+1)^{2}-s^{2}][\sigma +(i+2)(i+3)]}{[4(i+1)^{2}-1][\sigma -(i+1)(i+2)][\sigma +i(i+1)]}}-{\frac {\gamma b_{i}}{4ma}},\\&\xi _{i-2}^{3}={\frac {-(i-s)(i-s-1)}{(2i-1)(2i-3)[\sigma -(i-1)i]}},\\&\eta _{i+2}^{3}={\frac {-(i+s+1)(i+s+2)}{(2i+3)(2i+5)[\sigma -(i+1)(i+2)]}}.\end{aligned}}$

In the case of the luni-solar semi-diurnal tide (called K₂ in the notation of harmonic analysis) we have i=2, s=2, σ=2. Hence it would appear that these formulae for L_i and ξ_i-2 fail by becoming indeterminate, but i and s are rigorously integers, whereas σ depends on the “ speed ” of the tide; accordingly in the case referred to we must regard terms involving (i-s) as vanishing in the limit when σ approaches to equality with i (i-1). For this particular case then we find

$L_{2}^{2}={\frac {3}{35}}-{\frac {\gamma b_{2}}{4ma}}\ {\text{and}}\ \xi _{0}^{3}=0$.

The equation (46) for the successive C's is available for all values of i provided that C_-1, E_-1, C₀, E₀ are regarded as being zero.

As in the case of the zonal oscillations, the equations with odd suffixes separate themselves from those with even suffixes, so that the two series may be treated independently of one another. Indeed, as we shall see immediately, the series with odd suffixes are satisfied by putting all the C's with odd suffixes zero for the case of such oscillations as may be generated by the attractions of the moon or sun.

For the semi-diurnal tides i=2, s==2, and f is approximately equal to unity. Hence the equilibrium tide is such that all the E_i, excepting E₂², are zero.

For the diurnal tides i=2, s=1, and f is approximately equal to 1/2. Hence all the E_i, excepting E 1/2, are zero. Since in neither case is there any E with an odd suffix, we need only consider those with even suffixes.

In both cases the first equation among the C's is A

$-L_{i}^{3}C_{2}^{3}+\eta _{4}^{3}C_{4}^{3}={\frac {\gamma b_{2}}{4ma}}E_{2}^{3}{\text{(s = 2 or 1).}}$

It follows that if we write

$\xi _{0}^{3}C_{0}^{3}=-{\frac {\gamma b_{2}}{4ma}}E_{2}^{3}{\text{(s = 2 or 1).}}$

the equation of condition amongst the C's would be of general applicability for all even values of i from 2 upwards.

The symbols ξ₀, η₂, do not occur in any of the equations, and therefore we may arbitrarily define them as denoting unity, although the general formulae for ξ and η would give them other values. Accordingly we shall take

$\xi _{0}^{3}C_{0}^{3}=C_{0}^{3}=-{\frac {\gamma b_{2}}{4ma}}E_{2}^{3}{\text{(s = 2 or 1).}}$

With this definition the equation

$\xi _{i-2}^{3}C_{i-2}^{3}L_{i}^{3}C_{i}^{3}+\eta _{i+2}^{3}C_{i+2}^{3}=0\ {\text{(s = 2 or 1).}}$

is applicable for i=2, 4, 6, &c.

It may be proved as in the case of the tides of long period that we may regard C_i/C_i+2 as tending to zero. Then our equation may be written in the form

$\xi _{i-2}^{3}{\frac {C_{i-2}^{3}}{C_{i}^{3}}}=L_{i}^{3}-{\frac {\xi _{i}^{3}\eta _{i+2}^{3}}{\xi _{i}^{3}C_{i}^{3}/C_{i+2}^{3}}}$,

and by successive applications the right-hand side may be expressed in the form of a continued fraction. Let us write

$H_{i}^{3}={\frac {\xi _{i-2}^{3}\eta _{i}^{3}}{L_{i}^{3}-}}{\frac {\xi _{i}^{3}\eta _{i+2}^{3}}{L_{i+2}^{3}-}}{\frac {\xi _{i+2}^{3}\eta _{i+4}^{3}}{L_{i+4}^{3}-}}\dots$

Hence our equation may be written

$\xi _{i-2}^{3}{\frac {C_{i-2}^{3}}{C_{i}^{3}}}={\frac {\xi _{i-2}^{3}\eta _{i}^{3}}{H_{i}^{3}}}$

Whence

$C_{i}^{3}={\frac {H_{i}^{3}}{\eta _{i}^{3}}}C_{i-2}^{3}$

It follows that

$C_{2}^{3}={\frac {H_{2}^{3}}{\eta _{2}^{3}}}C_{0}^{3},\quad C_{4}^{3}={\frac {H_{2}^{3}H_{4}^{3}}{\eta _{2}^{3}\eta _{4}^{3}}}C_{0}^{3},\quad C_{6}^{3}={\frac {H_{2}^{3}H_{4}^{3}H_{6}^{3}}{\eta _{2}^{3}\eta _{4}^{3}\eta _{6}^{3}}}C_{0}^{3},$ &c.

Then since we have defined

$\eta _{2}^{3}=1\ {\text{and}}\ C_{0}^{3}=-{\frac {\gamma b_{2}}{4ma}}E_{2}$,

all the C's are expressed in terms of known quantities. Hence the height of tide b is given by

${\begin{aligned}b&=\Sigma h_{i}\cos(2nft+s\phi +\alpha )\\&=-{\frac {\gamma b_{2}}{4ma}}E_{2}^{3}\cos(2nft+s\phi +\alpha )\left[H_{2}^{3}P_{2}^{3}+{\frac {H_{2}^{3}H_{4}^{3}}{\eta _{4}^{3}}}P_{4}^{3}+{\frac {H_{2}^{3}H_{4}^{3}H_{6}^{3}}{\eta _{4}^{3}\eta _{6}^{3}}}P_{6}^{3}\dots \right]\end{aligned}}$

But the equilibrium tide e is given by

$e=E_{2}^{3}P_{2}^{3}\cos(2nft+s\phi +\alpha )$.

Hence we may write our result in the following form, which shows the relationship between the true dynamical tide and equilibrium tide:—

$b=-{\frac {\gamma b_{2}}{4ma}}{\frac {e}{P_{2}^{3}}}\left\{H_{2}^{3}P_{2}^{3}+{\frac {H_{2}^{3}H_{4}^{3}}{\eta _{4}^{3}}}P_{4}^{3}+{\frac {H_{2}^{3}H_{4}^{3}H_{6}^{3}}{\eta _{4}^{3}\eta _{6}^{3}}}P_{6}^{3}+\dots \right\}$

From a formula equivalent to this Mr Hough finds for the lunar semi-diurnal tide (s=2), for a sea of 1210 fathoms $\left({\frac {\gamma }{4ma}}={\frac {1}{40}}\right)$,

$b={\frac {e}{P_{2}^{2}}}\left\{\cdot 10396P_{2}^{2}+\cdot 57998P_{4}^{2}-\cdot 19273P_{6}^{2}+\cdot 03054P_{8}^{2}\dots \right\}$.

This formula shows us that at the equator the tide is “inverted,” and has 2.4187 times as great a range as the equilibrium tide.

For this same ocean he finds that the solar semi-diurnal tide is “ direct ” at the equator, and has a range 7.9548 as great as the equilibrium tide.

Now the lunar equilibrium tide is 2.2 times as great as the solar equilibrium tide, and since 2.2 × 2.4187 is only 5.3, it follows that in such an ocean the solar tides would have a range half as great again as the lunar. Further, since the lunar tides are “inverted” and the solar “ direct,” spring tide would occur at quarter moon and neap tide at full and change.

We give one more example from amongst those computed by Mr Hough. In an ocean of 9680 fathoms (γ/4ma=1/5), he finds

$b={\frac {e}{P_{2}^{2}}}\left\{1\cdot 7646P_{2}^{2}-\cdot 06057P_{4}^{2}+\cdot 001447P_{6}^{2}\dots \right\}$.

At the equator the tides are “ direct ” and have a range of 1.9225 as great as the equilibrium tide. In this case the tides approximate in type to those of the equilibrium theory, although at the equator, at least, they have nearly twice the range.

We do not give any numerical results for the diurnal tides, for reasons which will appear from the following section.

§ 19. Diurnal Tide approximately evanescent.—The equilibrium diurnal tide is given by

e=E 1/2P 1/2 cos(2nft + Φ + a),

where f is approximately 1/2 and the associated function for i=2, s=1 is

P 1/2=3 sin θ cos θ.

Now the height of tide is given by

$b=\Sigma C_{i}^{3}P_{i}^{3}\cos(2nft+\phi +\alpha )$,

and the problem is to evaluate the constants C_i.

If possible suppose that b is also expressed by a single term like that which represents e, so that

b=3C 1/2 sin θ cos θ cos (2nft + Φ + a)

Then the differential equation (22) to be satisfied becomes

$\gamma (C{\tfrac {1}{2}}-E{\tfrac {1}{2}}\left\{{\frac {1}{\sin \theta }}{\frac {d}{d\theta }}\left({\frac {\sin \theta {\frac {du}{d\theta }}+{\frac {1}{f}}u\cos \theta }{f^{2}-\cos ^{2}\theta }}\right)-{\frac {{\frac {\cos \theta }{f}}{\frac {du}{d\theta }}+{\frac {u}{\sin \theta }}}{\sin \theta (f^{2}-\cos ^{2}\theta )}}\right\}+4maC{\tfrac {1}{2}}u=0$,

where u is written for brevity in place of sin θ cos θ.

Now when f is rigorously equal to 1/2 it may be proved by actual differentiation that the expression inside the brackets { } vanishes identically, and the equation reduces to C 1/2 = 0.

We thus find that in this case the differential equation is satisfied by zero oscillation of water-level. In other words we reach Laplace's remarkable conclusion that there is no diurnal rise and fall of the tides. There are, it is true, diurnal tidal currents, but they are so arranged that the water level remains unchanged.

In reality f is not rigorously 1/2 (except for the tide called K₂ and there will be a small diurnal tide. The lunar diurnal tide called O has been evaluated for various depths of ocean by Mr Hough and is found always to be small.

§ 20. Free Oscillations of the Ocean.—Mr Hough discusses the various types of free oscillations of the ocean. They are very complex, and consist of westward waves and eastward waves of very various periods. He finds, as was to be expected, that if for an ocean of given depth, a free wave very nearly coincides in period with the forced lunar or solar wave, the actual tide is largely augmented. Thus, for example, for an ocean of 29,000 ft. in depth the solar semi-diurnal tide would have a height at the equator 235 times as great as the equilibrium height, and would be inverted so that low water would agree with the high water of the equilibrium theory.

The general outcome of the discussion is that it is impossible to foresee the height of any forced tide-wave by mere general inspection. If this is so in the simple case of an ocean of uniform depth, how much more must it be true of oceans of various depths interrupted by continents?

§ 21. Stability of the Ocean.—Imagine a globe of density δ, surrounded by a spherical layer of water of density σ. Then, still maintaining the spherical figure, and with water still covering the nucleus, let the layer be displaced sideways. The force on any part of the water distant r' from the centre of the water and r from the centre of the nucleus is 4/3πσr' towards the centre of the fluid sphere and 4/3π(δ-σ)r towards the centre of the nucleus. If δ be greater than σ there is a force tending to carry the water from places where it is deeper to places where it is shallower; and therefore the equilibrium, thus arbitrarily disturbed, is stable. If, however, δ is less than σ (or the nucleus lighter than water) the force is such that it tends to carry the water from where it is shallower to where it is deeper and therefore the equilibrium of a layer of fluid distributed over a nucleus lighter than itself is unstable. As Lord Kelvin remarks,^[22] if the nucleus is lighter than the ocean, it will float in Stabilities of Various Orders. the ocean wit part of its surface dry. Suppose, again, that the fluid layer be disturbed, so that its equation is r=a(1+s_i), where s_i is a surface harmonic of degree i; then the potential due to this deformation is ${\frac {4\pi \sigma }{2i+1}}{\frac {\alpha ^{i+3}}{r^{i+1}}}s_{i}$, and the whole potential is

${\frac {4\pi \delta \alpha ^{3}}{3r}}+{\frac {4\pi \sigma }{2i+1}}{\frac {\alpha ^{i+3}}{r^{i+1}}}s_{i}$.

If, therefore, σ/(2i+1) is greater than 1/3δ, the potential of the forces due to deformation is greater than that due to the nucleus. But we have seen that a deformation tends to increase itself by mutual attraction, and therefore the forces are such as to increase the deformation. If, therefore, σ=1/3(2i+1)δ, all the deformations up to the ith are unstable, but the (i+1)th is stable.^[23] If, however, σ be less than δ, then all the deformations of any order are such that there are positive forces of restitution. For our present purpose it suffices that the equilibrium is stable when the fluid is lighter than the nucleus.

§ 22. Precession and Nutation.—Suppose we have a planet covered with a shallow ocean, and that the ocean is set into oscillation. Then, if there are no external disturbing forces, so that the oscillations are “ free,” not “ forced,” the resultant moment of momentum of the planet and ocean remains constant. And, since each particle of the ocean executes periodic oscillations about a mean position, it follows that the oscillation of the ocean imparts to the solid earth oscillations such that the resultant moment of momentum of the whole system remains constant. But the mass of the ocean being very small compared with that of the planet, the component angular velocities of the planet necessary to counterbalance the moment of momentum of the oscillations of the sea are very small compared with the component angular velocities of the sea, and therefore the disturbance of planetary rotation due to oceanic reaction is negligible. If now an external disturbing force, such as that of the moon, acts on the system, the resultant moment of momentum of sea and earth is unaffected by the interaction between them, and the processional and nutational couples are the same as if sea and earth were rigidly connected together. Therefore the additions to these couples on account of tidal oscillation are the couples due to the attraction of the moon on the excess or deficiency of water above or below mean sea-level. The tidal oscillations are very small in height compared with the equatorial protuberance of the earth, and the density of water is 4/11ths of that of surface rock; hence the additional couples are very small compared with the couples due to the moon's action on the solid equatorial protuberance. Therefore precession Corrections to Precession and Nutation Insensible. and nutation take place sensibly as though the sea were congealed in its mean position. If the ocean be regarded as frictionless, the principles of energy show us that these insensible additional couples must be periodic in time, and thus the corrections to nutation must consist of semi-diurnal, diurnal and fortnightly nutations of absolutely insensible magnitude. We shall have much to say below on the results of the introduction of friction into the conception of tidal oscillations as a branch of speculative astronomy.

§ 23. Some Phenomena of Tides in Rivers.—As a considerable part of our practical knowledge of tides is derived from observations in estuaries and rivers, we shall state the results of an investigation of waves which travel along a shallow canal, and we refer the reader to the article Waves for the mathematical investigations on which they are based.

It must be premised that when the profile of a wave does not present the simple harmonic form, it is convenient to analyse its shape into a series of partial waves superposed on a fundamental wave; and generally the principle of harmonic analysis is adopted in which the actual wave is regarded as the sum of a number of simple waves.

Suppose that the water is contained in a straight and shallow canal of uniform depth h, and that at one end the canal debouches on to the open sea. Suppose further that in the open sea there is a forced oscillation of water level, given by this formula

η=H sin nt

where η is the elevation of the water at time t above its mean level, 2π/n the period of the oscillation and H the amplitude of the oscillation.

Waves will clearly be transmitted along the canal, and the problem is to obtain a formula which shall represent the oscillations of level at any distance x measured from the mouth of the canal.

The mathematical investigation shows that, if g denotes gravity, the formula for the oscillation of water level at the point defined by x is

$\eta =H\sin n\left(t-{\frac {x}{\surd gh}}\right)+{\frac {3H^{2}n}{4h\surd gh}}x\sin 2n\left(t-{\frac {x}{\surd gh}}\right)$.

The second of these terms is proportional to x, and if the canal were infinitely long it would become infinite. The difficulty thus occasioned may be eluded by supposing the canal to debouch on a second sea in which a second appropriate oscillation is maintained. In actuality friction gradually annuls all motion, and no such difficulty arises.

The first term of the formula is called the fundamental tide, the second gives what is called the first over-tide; and further approximation would give second and third over-tides, &c. All the over-tides travel up the river at the same rate as the fundamental, but they have double, treble, quadruple frequencies or “speeds,” and the ratio of the amplitude of the first over-tide to the fundamental is

${\frac {3H}{4h}}{\frac {nx}{\surd gh}}$.

As a numerical example, let the range of tide at the river mouth be 20 ft., and the depth of the river 50 ft. The “ speed ” of the semi-diurnal tide, which is an angular velocity, is 28-98° per hour or 1/1.9 radians per hour; √gh=27 miles per hour; hence ${\frac {3H}{4h}}\quad {\frac {nx}{\surd gh}}={\frac {1}{342}}x$. Therefore 34 miles up the river the over-tide is 1/10th of the fundamental and has a range of 2 ft. If the river shallows very gradually, the formula wiil still hold, and we see that the height of the over-tide varies as (depth)-3/2.

Fig. 6^[24] read from left to right exhibits the progressive change of shape. The steepness of the advancing crest shows that a shorter

(From Airy's Tides and Waves.)

Fig. 6.—Tide Wave in Rivers.

time elapses between low to high water than inversely. The same investigation shows that the law of the ebb and flow of currents, mentioned in § 2, must hold good.

The second law of waves in rivers to which we draw attention relates to the effects produced by the simultaneous propagation into shallow water of two waves of different periods. It appears that the effect is not simply the summation of the two separate waves.

Suppose that at the mouth of the river the oscillation of the open sea is represented by

η=H_i sin n₁t+H₂ sin(n₂t+ε).

Then we find that at distance x from the river's mouth the wave is given by the formula

${\begin{aligned}\eta &=H_{1}\sin n_{1}\left(t-{\frac {x}{\surd gh}}\right)+H_{2}\sin \left[n_{2}\left(t-{\frac {x}{\surd gh}}\right)+\epsilon \right]\\&+{\frac {3H_{1}H_{2}}{4h}}{\frac {n_{1}+n_{2}}{\surd gh}}x\sin \left[(n_{1}+n_{2})\left(t-{\frac {x}{\surd gh}}\right)+\epsilon \right]\\&-{\frac {3H_{1}H_{2}}{4h}}{\frac {n_{1}-n_{2}}{\surd gh}}x\sin \left[(n_{1}+n_{2})\left(t-{\frac {x}{\surd gh}}\right)+\epsilon \right]\end{aligned}}$.

The first two terms give us the two waves just as if each existed by itself. The third and fourth terms give the results of their combination, and are called “compound” tides, the first being a summation tide and the second a difference tide.

As a numerical example, suppose at the mouth of a river 50 ft. deep that the solar semi-diurnal tide has a range 2H₁=4 ft., and the lunar semi-diurnal tide has a range 2H₂=12; then n₁+n₂ =59/57 radians per hour, and n₁-n₂=1/57 radians per hour, and as before √gh=27 miles per hour.

With these figures

${\frac {3H_{1}H_{2}}{4h}}{\frac {n_{1}+n_{2}}{\surd gh}}x={\frac {1}{170}}x$.

Thus 15 miles up the river the quater-diurnal tide (called MS in harmonic analysis) would have a range of 1/60 of an inch. Where the two interacting compound tides are nearly of the Same “speed” the summational compound tide is much the larger of the two. As before, when the river shallows gradually this formula will still hold true.

It is interesting to note the kind of effect produced by these compound tides. When the primary tides are in the same phase (as at spring tide)

$n_{1}t=n_{2}t+\epsilon$

and we may write the formula in the form

$\eta =(H_{1}+H_{2})\sin n_{1}{\Big (}t-{\frac {x}{\sqrt {gh}}}{\Big )}+{\frac {3H_{1}H_{2}}{4h}}{\frac {n_{1}+n_{2}}{\sqrt {gh}}}s\sin {\Big [}2n_{1}t-{\frac {(n_{1}+n_{2})x}{\sqrt {gh}}}{\Big ]}+{\frac {3H_{1}H_{2}}{4h}}{\frac {n_{1}-n_{2}}{\sqrt {gh}}}s\sin {\frac {n_{1}-n_{2}}{\sqrt {gh}}}$

Hence the front slope of the tide-wave is steeper at springs than at neaps, and the compound tide shows itself at springs in the form of an augmentation of the first over-tide; the converse holds at neaps. Also mean water-mark is affected to a slight extent as we go up the river by an inequality represented by the last term.

IV.—Harmonic Analysis

§ 24. Outline of the Method.—We have seen in § 13 that the potential of the tide-generating force of the moon consists of three terms, one being approximately semi-diurnal, one approximately diurnal, and one varying slowly. In consequence of the irregular motion cf the moon in right ascension and in declination and the variability of parallax, none of these three classes of terms is simply harmonic in time. The like is also true of the potential of the sun’s tide-generating force. In the method of harmonic analysis we conceive the tidal forces or potential due to each disturbing body to be developed in a series of terms each consisting of a constant (determined by the elements of the planet’s orbit and the obliquity of the ecliptic) multiplied by a simple harmonic function of the time. Thus in place of the three terms of the potential as developed in § 13 we have an indefinitely long series of terms for each of the three terms. The loss of simplicity in the expression for the forces is far more than counterbalanced by the gain of facility for the discussion of the oscillations of the water. This facility arises from the dynamical principle of forced oscillations, which we have explained in the historical sketch. Applying this principle, we see that each individual term of the harmonic development of the tide-generating forces corresponds to an oscillation of the sea of the same period, but the amplitude and phase of that oscillation must depend on a network of causes of almost inextricable complication. The analytic er harmonic method, then, represents the tide at any port by a series of simple harmonic terms whose periods are determined from theoretical considerations, but whose amplitudes and phases are found from observation. Fortunately the series representing the tidal forces converges with sufficient rapidity to permit us to consider only a moderate number of harmonic terms in the series.

Now it seems likely that the corrections which have been applied in the use of the older synthetic method might have been clothed) in a more satisfactory and succinct mathematical form had investigators first carried out the harmonic- development. In this article we shall therefore invert history and come back on the synthetic method from the analytic, and shall show how the formulae of correction stated in harmonic language may be made comparable with them in synthetic language. One explanation is expedient before proceeding with the harmonic development. There are certain terms in the tide-generating forces of the moon, depending on the longitude of the moon’s nodes, which complete their revolution in 18.6 years. Node Now it has been found practically convenient, in the application of the harmonic method, to follow the synthetic plan to the extent of classifying together terms whose periods differ only in consequence of the movement of the moon's node, and at the same time to conceive that there is a small variability in the intensity of the generating forces.

§ 25. Development of Equilibrium Theory of Tides in Terms of the Elements of the Orbits.—Within the limits at our disposal we cannot do more than indicate the processes to be followed in this development. We have already seen in (2) that the expression for the moon's tide-generating potential is

$V={\frac {3m}{2r^{3}}}\rho {^{2}}(\cos {^{2}}z-{\tfrac {1}{3}}),$

and in (12) that

cos² z − l= 2E11MiM2+2&;'2'1Lh%£+21ll'MzMa +2zrM.M. +§ £'+fl”-2s““ Mi'-l-M22-2M=',

2 3 3

where M₁, M₂, M₃ and ξ, η, ζ are respectively the direction cosines referred to axes fixed in the earth of the moon and of a place on the earth's surface at which the potential V is to be evaluated. At such a place the radius vector ρ is equal to a the earth's radius.

Let the axes fixed in the earth be taken as follows:the axis C the north polar axis; the axis A through the earth's centre and a point on the equator on the same meridian as the place of observation; the axis B at right angles to the other two and eastward of A. Then if A be the latitude of the place of observation £=cos >,17=0, § '=sin A.

With these values we have

cos² z-Q; =% cos')(M1'- M, ') +sin 27.M, l/I, -l-%(i-Sm' X) (Mr“-I-M22-2Ma')

In fig. 7 let ABC be the axes fixed in the earth; XYZ a second set of axes, XY being the plane of the moon's orbit; M the projection of the moon in her orbit; I = ZC, the obliquity of the lunar orbit to the equator; χ=AX=BCY; l=MX, the moon's longitude in her orbit measured from X, the descending node of the equator on the lunar orbit, hereafter called the “intersection.”

Fig. 7.

Fig. 7.

Then

M₁ =cos l cos X-l-sin I sin X cos I =cos' H cos (X-Z) +sin” %I cos (X--Z),

Mz= -cos Z sin X-l-sin I cos X cos I= -cos* %I sin (X-Z) -sin' $1 sin (7, -i-Z),

M3=sin l sin I =2 sin £1 cos H sin l.

When these expressions are substituted in M12+M22-2M;', it is clear that the first will cosines of 2(X-l), zx, 2(x+l); the second in X-i-21; and the third in cos 21, together with only on I .

Now let c be the moon's mean distance, e the eccentricity of her orbit, and let

M12-Mi, M1M;,

have terms in the

sines of X-21, X,

a term depending

2 2

x= EM.. Y = [L-?<' 7 ' TM.. Z = 5?-(' r “il iM., and 1 =%-

Then we have for the lunar tide-generating potential at nd” the place of observation generating

2

V=(%[; cos2 x. (X2-Y2) +sin 2).XZ P°f¢"1f#1+%(% -Sin' N) (X”-l-Yi-2Z') (47)

The only parts of this expression which are variable in time are the functions of X, Y, Z.

To complete the development the formulae of elliptic motion are introduced in these functions, and terms which appear numerically negligible are omitted. Finally, the three X-Y-Z functions are obtained as a series of simple time-harmonics, the arguments of the sines and cosines being linear functions of the earth's rotation, the moon's mean motion, and the longitude of the moon's perigee. The next step is to pass, according to the principle of forced oscillations, from the potential to the height of tide generated by the forces corresponding to that potential. The X-Y-Z functions being simple time-harmonics, the principle of forced oscillations allows us to conclude that the forces corresponding to V in (47) will generate oscillations in the ocean of the same periods and types as the terms in V, but of unknown amplitudes and phases. Now let X²−Y²−, XZ, (X²+Y² − 2Z²) be three functions having respectively similar forms to those of

X²−Y² 7 XZ and (X2-I-Y242Z2),

(1 -e2)f'*(I-e2)3' (I -e2)3

but differing from Elem in that the argument of each Haggm af of the simple time-harmonics has some angle subtracted Tide at any from it, and that the term is multiplied by a numerical pg, -1, factor. Then, if g be gravity and h the height of tide at the place of observation, we must have

h =i§ [; cog >. (36-122)-l-sin 2>o<z+ gg - sin2>)§ (2<2 +132-2z2)].(4s) 3

The factor -ra*/g may be more conveniently written§ i-V; a, where M is the earth's mass. It has been so chosen that, if the equilibrium theory of tides were fulfilled, with water covering the whole earth, the numerical factors in the X-Y-Z functions would be each unity and the alterations of phase would be zero. The terms in (3€'-Hg'-222) require special consideration. The function of the latitude being 1/2 − sin² λ, it follows that, when in the northern hemisphere it is high-water north of a certain critical latitude, it is low-water on the opposite side of that parallel; and the same is true of the southern hemisphere. It is best to adopt a uniform system for the whole earth, and to regard high-tide and high-water as consentaneous in the equatorial belt, and of opposite meanings outside the critical latitudes. We here conceive the function always to be written § -sin'}, so that outside the critical latitudes high-tide is low-water. We may in continuing the development write the 3€-ig-Z functions in the form appropriate to the equilibrium theory with water covering the whole earth, for the actual case it is only then necessary to multiply by the reducing factor, and to subtract the phase alteration K. As these are unknown constants for each place, they would only occur in the develo ment as symbols of quantities to be deduced from observation. iit will be understood, therefore, that in the followin schedules the “argument” is that part of the argument which is dirived from theory, the true complete argument being the “argument ” -wc, where K is derived from observation.

Up to this point we have sup osed the moon's longitude and the earth's position to be measured) from the “ intersection "; but in order to pass to the ordinary astronomical formulae we must measure the longitude and the earth's osition from tlre vernal equinox. Hence we determine the longitude; and right ascension of the ' inter# section " in terms of the longitude of the moon's node and the inclination of the lunar orbit, and introduce them into our formulae for the 36-Q1 functions. The expressions' for the functions corresponding to solar tides may be written down by symmetry, and in this case the intersection is actually the vernal equinox. The final result of the process sketched is to obtain a series of terms each of which is a function of the elements of the moon's or sun's orbit, and a function of the terrestrial latitude Exp""'””°" of the place of observation, multiplied by the cosine gzichedul” of an angle which increases uniformly with the time. W' We shall now write down the result in the form of a schedule; but we must first state the notation employed: e, e, = eccentricities of lunar and solar orbits; 'I, w =obliquities of equator to lunar orbit and ecliptic; p, p, f-'longitudes of lunar and solar perigees, 25, a1, =hourly increments of p, p, ; s, h=moon's and sun's mean longitudes; a, -q=hourly increments of 5, h; t=local mean solar time reduced to angle; 'y-1, =15° per hour;)= latitude of place of observation; E, v=longitude in lunar orbit, and R.A. of the intersection; N =longitude of moon's node; i- eed inclination of lunar orbit. The “ speed " of any tide Dzfined is defined as the rate of increase of its argument, and is expressible, therefore, as a linear function of -y, 17, a, U; for we may neglect ZIV, as being very small. The following schedules, then, give h the height, of tide. The arrangement is as follows. First, there is a universal coefficient gl ia, which multiplies every term of all the schedules. Secondly, there are general coefficients, one for each schedule, viz. cos') for the semi-diurnal terms, sin 2) for the diurnal, and éfi sin” A for the terms of long period. In each schedule the third column, headed “ coefficient, " gives the functions of I and e. In the fourth column is given the mean semi-range of the corresponding term in numbers, which is approximately the value of the coefficient in the first column when I =¢..»; but we pass over the explanation of the mode of computing the values. The fifth column contains ar uments, linearfunctionsof t, h, s, p, v, 2. In [A, i.] 2t+2(h-ig and in A, ii.] t+(h-v) are common to all the arguments. The arguments are grouped in a manner convenient for subsequent computation. Lastly, the sixth is a column of speeds, being the hourly increases of the arguments in the preceding column, estimated in degrees per hour. It has been found practically convenient to denote each of these partial tides by an initial letter, arbitrarily chosen. In the first column we give a descriptive name for the tide, and in the second the arbitrarily chosen initial. The schedule for the solar tides is drawn up in precisely the same manner, the only difference being that the coefficients are absolute constants. In order that the comparison of the importance of the solar tides with the lunar may be complete, the same universal coefficient L;-An; a is retained, and the special coefficient for each term is made to involve the factor Here -r, =§ ;-Q, m, being the I

sun's mass. With

M 1' I

=81~S» i='46°35=;%-To

write down any term, take the universal coefficient, the general coefficient for the class of tides, the special coefficient, and Mode of multiply by the cosine of the argument! The result, Reading taken with the positive sign, is a term in the equilibrium Schedules tide, with water covering the whole earth. The transi-Exp, amed tion to the actual case by the introduction of a factor and a delay of phase (to be derived from observation) has been already explained. The sum of all the terms is the complete expression for the height of tide h. It must be remarked that the schedule of tides is here largely abridged, and that the reader who desires fuller information must refer to the Brit. Assoc. Report for 1883, or vol. i. of G. H. Darwin's Scientijic Papers, or to Harris's Manual of Tides.

A.—Schedule of Lunar Tides.

Universal Coefficient

"la

3 a

2 M<c> a

ne

"T

i.-Semildiurnal Tides; Ge ral Coefficient =cos' X. A:gig speed in

D'§ ;n§ ;j"= gg coescim as gg, ;§ {*;';', § '§ ';f, ,2§ “, {f°§ if 2 § g Hour.

U

Q M2 . § (r-'F;e')cos' H ~45426 -2(r-§) 28'Q84104 2° Luni-solar

(lunar K2 1}(I +i§ e')§ sinzl -o3g29 3O'082I§ 72° portion)

L*§ '§§ , ,, } N l ~ Ee ws' 'll ~<»s1<»6 - zo- s- <5-1»> 2s~439m6° ii.-Diurnal Tides; General Coefficient =sin 2). gg; Speed in

iD°°'§§ l§§ "'e:E C°°'“°'@“f- § L¥§§ flwiif, iisigffiii I 5, 2§ 5 Hour.l

Linfilfi' i 0 <1 ~ gen Sin 1 C<>S'»l»I 18856 -=<s- s>++=f 13-¢43°3s6° Lu '- ola

(liiriar r K1 (l+§ e2)§ sin I cos I -r8rr5 -iff I5<>4lc686° L ”°“'° ) -=<:-:Hs-»> f

§§ f ;'dc M Q ge - i sin I cos' il -o;565r +int } 13-398660g° iii.-Lon Period Tides; General Coefficient é — Siflzx. K

-~ Speed in

»-J C

Dizcsgifve 3; CoeHicient. é§ éé; Argument. ggggf »< > Q our.

U

Change uf Of vztriablepart ' 1984.

Exit — (i»{¢§§ ¢2)§ (r-2. smfl) -z5z24l § I:;3;e long. per annum F': 'il;htly i Mf tx - MH sin' I 1 'O1821 z(.v- §) 1~oo8o330° B.—Schedule of Solar Tides.

M 3

Universal Coefficient =§ - T 5) u.

T; ' "<5;5§ Speed in

Delflcgxggw E Coefficient. Argument. "' > L23 Hour.

i.-Semi-diurnal Tides; General Coefficient = cos'>. Prxflfil. i S2 -::'(r- § e, ')} cos* 5-an -21 137 21 3o-ooooooo° L '~ r »

liglolzfi-3) K, ;4(r+3¢, ')} sin' w '01823 21-l-zh 30'O821372° portion

L“f$§ , ,C i T Qt Zn 005' tw '0¥243 21-(hen) 2a-os893r4° ii.-Diurnal Tides; General Coefficient = sin 2>. i°: T § § i' i P;f i(1 - ';e, “)1} sinw cosi »}w 4:8775 t-h-Hp: I4'QS803I4, ° n1~s ar

Lisolz; K1 z¢(I+§ ¢,2)§ - sin nu cos w ~o8407 f+h'§ '¥ I5-o410686 portion) T

iii.—Long Period Tides; General Coefficient =é-Q sln') S°;$;3“' g Ssa gh - § e,2)1} sin2 w -03643 2h 0'O821372° From the fourth columns we see that the coefficients in de# scending order of magnitude are M2, Ki (both combined); 52, O, K1 (lunar), N, P, K1 (solar) K2 (both combined), Seal f K, (lunar), Mf, Q, K. (so1ar), SSa~, ,, , § , § ', ,, The tides which we omit from the schedules are efgldes ce relatively unimportant, » but nevertheless commonly evaluated in accurate tidal work, are all lunar tides, viz. the following semi-diurnal tides: the smaller elliptic tide L, the larger and smaller evectional tides v, A, the variational t1de p. Also the, following diurnal tides, viz. the smaller elliptic tide Ml, a tide of speed y-l-o'-U called ]. Also amongst the tides of long period, the luni-solar fortnightly called MSf.

The tides depending on the fourth power of the moon's parallax The mean value of this coefficient is § (r -1-ge?) (1 -'gSil'1?'i)<I - g'sin%») = -25, and the variable part is approximately - (X +§ e2) sm 1 cos z smw cos w cos N= - -0328 eos N. arise from the potential V=m/r⁴ρ³(5/2cos³ z-3/2 cos z). They give rise to a small diurnal tide M₁, and to a small ter-diurnal tide M₃; but we shall not give the analytical development.

§ 26. Over-Tides. Compound Tides and Meteorological Tides.—We have in § 23 stated results derived from dynamical theory as to over-tides, which represent the change of profile Over-Tides. of the wave as it advances in shallow water. The only tides in which it has hitherto been thought necessary to represent this change of form belong to the principal lunar and principal solar series. Thus, besides the fundamental astronomical tides M₂ and S₂, the over-tides M₄, M₅, M₈ and S₄, S₅ are usually deduced by harmonic analysis.

Compound tides have been also referred to in § 23; they represent a result of the combination of two waves of different speeds travelling through shallow water. On combining the speeds Compound Tides. of the important tides, it will be found that there is in many cases a compound tide which has itself a speed identical with that of an astronomical or meteorological tide. We thus find that the tides O, K₁, P, M₂, Mf, Q, M₁, L are liable to perturbation in shallow water. We refer to the Brit. Assoc. Report for 1883 or to Harris's Manual for a schedule, with initials, of the compound tides which are usually evaluated.

All tides whose period is an exact multiple or submultiple of a mean solar day, or of a tropical year, are affected by meteorological conditions. Thus all the tides of the principal solar Meteorological Tides. astronomical series S, with speeds γ-η, 2(γ-η), 3(γ-η), &c., are subject to more or less meteorological perturbation. An annual inequality in the diurnal meteorological tide S₁ will also give rise to a tide γ-2η, and this will be fused with and indistinguishable from the astronomical P; it will also give rise to a tide with speed γ, which will be indistinguishable from the astronomical part of K₁. Similarly the astronomical tide K₂ may be perturbed by a semi-annual inequality in the semi-diurnal astronomical tide of speed 2(γ-η). Although the diurnal tide S₁, or γ-η and the semi-annual and annual tides of speeds 2η; and η are all quite insensible as arising from astronomical causes, yet they have been found of sufficient importance to be considered. The annual and semi-annual tides are of enormous importance in some rivers, representing in fact the yearly flooding in the rainy season. In the reduction of these tides the arguments of the S series are t, 2t, 3t, &c., and of the annual, semi-annual, ter-annual tides h, 2h, 3h. As far as can be foreseen, the magnitudes of these tides are constant from year to year.

§ 27. On the Form of Presentation of Results of Tidal Observations.— Supposing n to be the speed of any tide in degrees per mean solar hour, and t to be mean solar time elapsing since o^h of Immediate Result of Harmonic Analysis. the first day of (say) a year of continuous observation, then the immediate result of harmonic analysis is to obtain a height R and an angle ζ such that the height of this tide at the time t is given by

R cos (nt-ζ).

R is the semi-range of the tide (say) in British feet, and ζ is an angle such that ζ/n is the time elapsing after o^h of the first day until it is high water of this particular tide. It is obvious that ζ may have any value from 0° to 360°, and that the results of the analysis of successive years of observation will not be comparable with one another when presented in this form.

But let us suppose that the results of the analysis are presented in a number of terms of the form

fH cos (V+u-κ),

where V is a linear function of the moon's and sun's mean longitudes the mean longitude of the moon's and sun's perigees, and the local mean solar time at the place of observation, Final Form; Tidal Constants. reduced to angle at 15° per hour. V increases uniformly with the time, and its rate of increase per mean solar hour is the n of the first method, and is called the speed of the tide. It is supposed that u stands for a certain function of the longitude of the node of the lunar orbit at an epoch half a year later than o^h of the first day. Strictly speaking, u should be taken as the same function of the longitude of the moon's node, varying as the node moves; but, as the variation is but small in the course of a year, u may be treated as a constant and put equal to an average value for the year, which average value is a taken as the true value of u at exactly mid year. Together V+u constitute that function which has been tabulated as the “argument” in the schedules of § 25. Since V+u are togetther the whole argument according to the equilibrium theory of tides, with sea covering the whole earth, it follows that κ/n is the lagging of the tide which arises from kinetic action, friction of the water, imperfect elasticity of the earth, and the distribution of land It is supposed that H is the mean value in British feet of the semi-range of the particular tide in question; f is a numerical factor of augmentation or diminution, due to the variability of the obliquity of the lunar orbit. The value of f is the ratio of the “coefficient ” in the third column of the preceding schedules to the mean value of the same term. It is obvious, then, that, if the tidal observations are consistent from year to year, H and κ should come out the same from each year's reductions. It is only when the results are presented in such a form as this that it will be possible to judge whether the harmonic analysis is yielding satisfactory results. This mode of giving the tidal results is also essential for the use of a tide-predicting machine (see § 8).

We must now show how to determine H and κ from R and ζ. It is clear that H=R/f, and the determination of f from the schedules depends on the evaluation of the mean value of each of the terms in the schedules, into which we shall not enter. If V₀ be the value of V at 0^h of the first day when t is zero, then clearly

-ζ=V₀+u-κ

so that

κ=ζ+V₀+u

Thus the rule for the determination of κ is: Add to the value of ζ the value of the argument at 0^h of the first day.

The results of harmonic analysis are usually tabulated by giving H, κ under the initial letter of each tide; the results are thus comparable from year to year.^[25] For the purpose of using Tidal Constants. the tide-predicting machine the process of determining H and κ from R and ζ has simply to be reversed, with the difference that the instant of time to which to refer the argument is o^h of the first day of the new year, and we must take note of the different values of u and f for the new year. Tables ^[26] have been computed for f and u for all longitudes of the moon's node and for each kind of tide, and the mean longitudes of moon, sun, and lunar perigee may be extracted from any ephemeris. Thus when the mean semi-range H and the retardation κ of any tide are known its height may be computed for any instant. The sum of the heights for all the principal tides of course gives the actual height of water.

§ 28. Numerical Harmonic Analysis.—The tide-gauge furnishes us with a continuous graphical record of the height of the water above some known datum mark for every instant of Treatment of Tide Curves. time. The first operation performed on the tidal record is the measurement in feet and decimals of the height of water above the datum at every mean solar hour. The period chosen for analysis is about one year and the first measurement corresponds to noon.

If T be the period of any one of the diurnal tides, or the double period of any one of the semi-diurnal tides, it approximates more or less nearly to 24 solar hours, and, if we divide it into 24 equal parts, we may speak of each as a T-hour.

The process of harmonic analysis consists of finding the average height of water at each of the 24 T-hours of the T-day, but we shall not go into the way in which this may be done.^[27] It must suffice to say that it depends on the fact that in the long run any given T-hour will fall at all hours of any other special day.

The final outcome is that we obtain the height of water at each of the 24 T-hours of a T-day, freed from the influence of all the other tides. We may see that it is thus possible to isolate the T-tide. When this has been done let t denote T-time expressed in T-hours, and let n be 15°. Then we express the height h as given by the averaging process above indicated by the formula

h=A₀+A₁ cos nt+B₁ sin nt+A₂ cos 2nt+B₂ sin 2nt+ . . .,

where t is 0, 1, 2,. . . 23.

See the article Harmonic analysis for the numerical processes by which A₀ A_l, B_l, A₂, B₂, &c., may be evaluated. It is obvious that such a formula as A cos nt+B sin nt may easily be reduced to the form R cos (nt-ζ) An actual numerical example of harmonic analysis of tidal observations is given in the Admiralty Scientific Manual (1886) in the article “Tides, ” or G. H. Darwin's Scientific Papers, vol. i.

V.—Synthetic Method

§ 29. On the Method and Notation.—The general nature of the synthetic method has been already explained; we now propose to show how the expressions for the tide may be developed from the result as expressed in the harmonic notation If it should be desired to make a comparison of the results of tidal observation as expressed in the synthetic method with those of the harmonic method, or the converse, or to compute a tide-table from the harmonic constants by reference to the moon's transits and the declinations and parallaxes of sun and moon, analytical expressions founded on a procedure indicated in the following sections are necessary.

In chapter iv. the mean semi-range and angle of retardation of any one of the tides have been denoted by H and κ. We shall here, however, require to introduce several of the H's and κ's into the same expression, and they must therefore be distinguished from one another. This may in general be done conveniently by writing as a subscript letter the initial of the corresponding tide; for example H_m, κ_m will be taken to denote the H and κ of the lunar tide M₂. This notation does not suit the K₂ and K₁ tides, and we shall therefore write H”, κ” for the semi-diurnal K₂, and H', κ' for the diurnal K₁ tide. These two tides proceed according to sidereal time and arise from the sun and moon jointly, and a synthesis of the two parts of each is effected in the harmonic method, although that synthesis is not explained in chapter iv. It is now necessary to reverse this partial synthesis, in order to obtain a more complete one. We must therefore note that the ratio of the solar to the lunar part of the total K₂ tide is 0.46407; so that 0.683 H” is the lunar portion of the total K₂. There will be no occasion to separate the two portions of K₂, and we shall retain the synthesis which is effected in the harmonic method.

§ 3o. Semi-Diurnal Tides.—The process adopted is to replace the mean longitudes and elements of the orbit in each term of the harmonic development of the schedules Mean Longitude and Elements Replaced by Hour-angle, Declination and Parallax. of § 25 by hour-angles, declinations, and parallaxes.

At the time t (mean solar time of port reduced to angle) let α, δ, ψ be ☽︎'s R.A., declination, and hour-angle, and l ☽︎'s longitude measured from the “ intersection.” These and other symbols when written with a subscript accent are to apply to the sun. Then v being the R.A. of the intersection, we have from the right-angled spherical triangle of which the sides are l, δ, a-v the relations tan (a-v) = cos I tan l, sin 6 = sin I sin l. (49) Now s-ξ is the ☽︎'s mean longitude measured from the intersection and s-p is the mean anomaly; hence approximately l=s-E-l-2esin(s-p). (50)

From (49) and (50) we have approximately a = s + (v - E) + 26 sin (s - p)-tan' il sin 2(s - E). Now, h being the ☉'s mean longitude, t+h is the sidereal hour angle, and il/ = t -|- h - a.. Hence

t+h-s-(V-5) =, p+2e sin (s-p)-tan' il sin 2(s—5). -(51) Again, if we put

cos'A = I +5 sin* I (52)

we have approximately from (49) and (50) cos'5 - cos2A

T = cos 2 (5 - E)

whence sin 5 cos 6 d5 (53)

mfr a=Si“2<S“f>

Obviously A is such a declination that sin' A is the mean value of sin' 6 during a lunar month. Again, if P be the ratio of the 1>'s parallax to her mean parallax, the equation to the ellipse described gives EU, ” I) = C05 (5 " Pl

whence X:§ t-gig = Sin (5 . P) (54)

Now it appears in schedule A of § 25 that the arguments of all the lunar semi-diurnal tides are of the form 2(t+h-v) == 2(s-5) or r (s-p). It is clear, therefore, that the cosines of such angles may by the relations (51), (53), (54) be expressed in terms of hour-angles, declinations and parallaxes. Also by means of (52) we may introduce? in place of I in the coefficients of each term. An approximate formula for Δ is 16.51x +3-44 cos -o~19 cos 2 . etais will be found in the Brit. Assoc. Report for 1885.

We shall not follow the analytical processes in detail, but the formulae given show the possibility of replacing the symbols used in the method of harmonic analysis by others involving R.A., declination and parallax.

Before giving the results of the processes indicated it must be remarked that greater succinctness is obtained by the introduction of the symbol δ' to denote the ☽︎'s declination at a time Age of Declinational Parallactic and Corrections. earlier than that of observation by an interval which may be called the “ age of the declinational inequality, ” and is computed from the formula tan (κ”-κ_m)/2δ or 52.2^h tan (κ^h-κ_m). Similarly, it is convenient to introduce P' to denote the value of P at a time earlier than that of observation by the “ age of the parallactic inequality,” to be computed from tan (κ_m-κ_n)/(σ-ῶ) or 105.3^h tan (κ_m-κ_n). These two “ ages ” probably do not differ in general much from a third period, computed from (κ₂-κ_m/2(σ-η), which is called the “ age of the tide.”

The similar series of transformations when applied to the solar tides lead to simpler results, because A, is a constant, being I6-33°, and the " ages " may be treated as zero; besides the terms depending on df), /da and dP, /dt are negligible. Formulae for the semi-diurnal tide of great exactness are obtainable by means of these transformations, but they lack the simplicity of those obtained in the harmonic method. On the other hand they are in some respects even more exact, since all lunar inequalities are represented. We shall not give the complex formulae which represent the complete substitution of R.A., declination and parallax in the earlier formulae, but shall content ourselves with rougher results, which are still fairly accurate.

Let us write them

2 ', 2

M = P'1%(%§ ;H, ,, + o~683 H' cosf(u” - u, ,,), z I z If

2h = /<, ,, + o~683 -gzlsin (»<” - nm), (55) cos' 6

M, = P,3 HM

2/4, = K.-

Then we find that the height h₂ of the complete lunar and solar semi-diurnal tide is represented with a fair degree of approximation by r hi = M cos '2 (41 - /1) + M, COS 2(~P, - #,)- (56)

The first of these is the lunar tide, and it will be observed that the height M depends on the cube of the moon's parallax at a time earlier than that of observation by “ the age of the 5, ,, ,“, , s, s parallactic inequality, " and that it depends also on, dying one the moon's declination at a time earlier by “ the age [, ,, ,, ,-3, , d. of the declinational inequality." The phase of the one gala, - tide, represented by the angle 2;/., also has adeclinational Tide, inequality.

The second term is the solar tide, and it also has parallactic and declinational inequalities.

The formulae (55), (56) have been used in an example of the pompgitation of a tide-table given in the Admiralty Scientific Manual (1886).

§ 31. Synthesis of Lunar and Solar Semi-Diurnal Tides.—Let A be the excess of ☽︎'s over ☉'s R.A., so that 5 A =a—o., , V

~/1, = ~/f + A, (57)

and 5 h, =M cos 2(¢-it)-PM, cos 2(//+A-u,). A The synthesis is then completed by writing H cos2(u-¢)=M-1-M, cos2(A-;.¢, +p.),

H sin 2(/.t—¢)= M, sin 2(A—;i, -Hi), V

so that . h¢=H cos 2(¢-qi). ' . (58)

Then H is the height of the total semi-diurnal tide and ¢>/(-y-da/dl) or approximately 4:/(7-u) or 231; 41, when ¢> is given in Synthesis degrees, is the “ interval ” from the moon's transit to go gbfgln high water. Sing/5

The formulae for H and ¢> may be written Term; H =1oI/lM“+1Xk“+2l;[I;l, COS 2(A-H, -lrllll = . i (59)

tan 20' qi) M+M, cos 2 (A-p, -{-11)

Since A goes through its period in a lunation, it follows that H and ¢ have inequalities with a period of half a lunation. These are called the “ fortnightly inequalities in the F9"""3h”-Y height and interval. ""q"°"'-V

Spring tide obviously occurs when A=p, -/L Since the mean value of A is s-h (the difference of the mean longitudes), and since the mean values of /J and pn, are 'éKm, im, it follows that the mean value of the period elapsing after full moon and change of moon up to sprin tide is (K, -x, ,,)/2(a-11). The association of spring tide with full and change is obvious, and a fiction has been adopted by which it is held that spring tide is generated in those configurations of the moon and sun, but takes some time to reach the port of observation. Accordingly (K, -»<, ,,)/2 (o-11) has been called the “age of the tidel' The average age ° is about 36 hours as far as observations have yet been, e made. The age of the tide appears not in general to differ very much from the ages of the declinational and parallactic inequalities. In computing a tide-table it is found practically convenient not to use A, which is the difference of R.A.'s at the unknown time of high-water, but, to refer the tide to Ao, the difference of R.A.'s at the time of the moon's transit. It is clear that A0 is the apparent time of the moon's transit reduced to angle at 15° per hour. We have already remarked that 4>/(Y-da/dt) is the interval from transit to high-water, and hence at high-water

a/dt-da /dt* Y daI/dt ¢'; (60)

As an approximation we may attribute to all the quantities in the second term their mean values, and we then Reference to Moon's Transit. have

A = A0, Y*0

and A-~, +#=A., -», +£72/»=A»-», +n»».~ (61)

This approximate formula (61) may be used in computing from (59) the fortnightly inequality in the “ height ” and “ interval.”

In this investigation we have supposed that the declinational and parallactic corrections are applied to the lunar, and solar tides before their synthesis; but it is obvious that the process may be reversed, and that we may form a table of the fortnightly inequality based on mean values H_m and H₂ and afterwards apply corrections. This is the process usually adopted, but it is less exact. The labour of computing the fortnightly inequality, especially by graphical methods, is not great, and the plan here suggested seems preferable.

§ 32. Diurnal Tides.—These tides have not been usually treated with much completeness in the synthetic method. In the tide-tables of the British Admiralty we find that the tides at some ports are “affected by diurnal inequality"; such a statement may be interpreted as meaning that the tides are not to be predicted by the information given in the so-called tide-table. The diurnal tides are indeed complex, and do not lend themselves easily to a complete synthesis. In the harmonic notation the three important tides are K₁, O, P, and the lunar portion of K₁ is nearly equal to O in height, whilst the solar portion is nearly equal to P. A complete synthesis may be carried out on the lines adopted in treating the semi-diurnal tides, but the advantage of the plan is lost in consequence of large oscillations of the amplitude through the value zero, so that the tide is often represented by a negative quantity multiplied by a circular function. It is best, then, only to attempt a partial synthesis, and to admit the existence of two diurnal tides. One of these will be a tide consisting of K₁ and P united, and the other will be O.

We shall not give the requisite formulae, but refer the reader to the Brit. Assoc. Report for 1885. A numerical example is given in the Admiralty Manual for 1886.

§ 33. On the Reduction of Observations of High- and Low-Water.^[28]— A continuous register of the tide or observation at fixed intervals of time, such as each hour, is certainly the best; but for the adequate use of such a record some plan analogous to harmonic analysis is necessary. Observations of high- and low-water only have, at least until recently, been more usual. In the reduction the immediate object is to connect the times and heights of high- and low-water with the moon's transits by means of the establishment, age and fortnightly inequality in the interval and height. The reference of the tide to the establishment is not, however, scientifically desirable, and it is better to determine the mean establishment, which is the mean interval from the moon's transit to high-water at spring tide, and the age of the tide, which is the mean period from full moon and change of moon to spring tide.

For these purposes the observations may be conveniently treated graphically.^[29] An equally divided horizontal scale is taken to represent the twelve hours of the clock of civil time, Graphical Determination of Establishment, &c. regulated to the time of the port, or—more accurately— arranged always to show apparent time by being fast or slow by the equation of time; this time-scale represents the time-of-clock of the moon's transit, either upper or lower. The scale is perhaps most conveniently arranged in the order V, VI,...XII, I...III. Then each interval of time from transit to high-water is set off as an ordinate above the corresponding time-of-clock of the moon's transit. A sweeping curve is drawn nearly through the tops of the ordinates, so as to cut off minor irregularities. Next along the same ordinates are set off lengths corresponding to the height of water at each high-water. A second similar figure may be made for the interval and height at low-water. In the curve of high-water intervals the ordinate corresponding to XII. is the establishment, since it gives the time of high-water at full moon and change of moon. That ordinate of high-water intervals which is coincident with the greatest ordinate of high-water heights gives the mean establishment. Since the moon s transit falls about fifty minutes later on each day, in setting off a fortnight's observations there will be about five days for each four times-of-clock of the upper transit. Hence in these figures we may regard each division of the time-scale I to II, II to III, &c., as representing twenty-five hours instead of one hour. Then the distance from the greatest ordinate of high-water heights to XII is called the age of the tide. From these two figures the times and heights of high- and low-water may in general be predicted with fair approximation. We find the time-of-clock of the moon's upper or lower transit on the day, correct by the equation of time, read off the corresponding heights of high- and low-water from the figures, and the intervals being also read off are added to the time of the moon's transit and give the times of high- and low-water. At all ports there is, however, an irregularity of heights and intervals between successive tides, and in consequence of this the curves present more or less of a zigzag appearance. Where the zigzag is perceptible to the eye, the curves must be smoothed by drawing them so as to bisect the zigzags, because these diurnal inequalities will not present themselves similarly in the future. When, as in some equatorial ports, the diurnal tides are large, this method of tidal prediction fails in the simple form explained above. It may however be rendered applicable by greater elaboration.^[30]

This method of working out observations of high- and low-water was not the earliest. In the Mécanique Céleste, bks. i. and v., Laplace treats a large mass of tidal observations by dividing them into classes depending on the configurations of the tide-generating bodies. This he separates the two syzygial tides at full moon and change of moon and divides them into equinoctial and solstitial tides. He takes into consideration the tides of several days embracing these configurations. He goes through the tides at quadratures on the same general plan. The effects of declination and parallax and the diurnal inequalities are similarly Methods of Laplace, Lubbock, Whewell. treated. Lubbock (Phil. Trans., 1831, seq.) improved the method of Laplace by taking into account all the observed tides, and not merely those appertaining to certain configurations. He divided, the observations into a number of classes. First, the tides are separated into parcels, one for each month; then each parcel is sorted according to the hour of the moon's transit. Another classification is made according to declination; another according to parallax; and a last for the diurnal inequalities. This plan was followed in treating the tides of London, Brest, St Helena, Plymouth, Portsmouth and Sheerness. Whewell (Phil. Trans., 1834, seq.) did much to reduce Lubbock's results to a mathematical form, and made a highly important advance by the introduction of graphical methods by means of curves. The method explained above is due to him. Airy remarks of Whewell's papers that they appear to be “ the best specimens of reduction of new observations that we have ever seen.”

VI.—Tidal Deformation of the Solid Earth

§ 34. Elastic Tides.—The tide-generating potential varies as the square of the distance from the earth's centre, and the corresponding forces act at every point throughout its mass. No Elastic Tides. solid matter possesses the property of absolute rigidity, and we must therefore admit the probable existence of tidal elastic deformation of the solid earth. The problem of finding the state of strain of an elastic sphere under given stresses was first solved by G. Lamé;^[31] he made, however, but few physical deductions from his solution. An independent solution was found by Lord Kelvin,^[32] who drew some interesting conclusions concerning the earth.

His problem, in as far as it is now material, is as follows. Let a sphere of radius a and density w be made of elastic material whose bulk and rigidity moduli are k and n, and let it be subjected to forces due to a potential per unit volume, equal to τwr²(sin²λ)-1/3), where λ is latitude. Then it is required to find the strain of the sphere. We refer the reader to the original sources for the methods of solution applicable to spherical shells and to solid spheres. The investigation applies either to tidal or to rotational stresses. In the case of tides r=3/2m/c³, m and c being the moon's mass and distance, and in the case of rotation τ= -½ω², ω being the angular velocity about the polar axis. The equation to the surface is found to be

2 6' /

V r=a 1 +l-5% 1 + -r(s1n'1>-%) .

In most solids the bulk modulus is considerably larger than the rididity modulus, and in this discussion it is sufficient to neglect n compared with k. With this approximation, the ellipticity e of the surface becomes

e = QHT

19n

Now suppose the sphere to be endued with the power of gravitation, and write

I . = 1% = ZS,

r 5-wo" 9 5 a

where g is gravity at the surface of the globe. Then, if there were no elasticity, the ellipticity would be given by e=τ/g, and without, gravitation by e=τ/r. And it may he proved in several ways that, gravity and elasticity co-operating,

e=τ/r+g=r/g·1/1+r/g

If n be the rigidity of steel, and if the globe have the size and mean density of the earth, r/g=2, and with the rigidity of glass r/g=2/3. Hence the ellipticity of an earth of steel under tide-generating force would be 1/3 of that of a fluid earth, and the fraction for glass would be 3/5. If an ocean be superposed on the globe, the visible tide will be the excess of the fluid tide above the solid tide. Hence for steel the oceanic tides would be reduced to 2/3, and for glass to 3/5 of the tides on a rigid earth.

It is not possible in general to compute the tides of an ocean lying on an unyielding nucleus. But Laplace argued that friction would cause the tides of long period (§ 17) to conform to the equilibrium law, and thus be amenable to calculation. Acting on this belief, G. H. Darwin discussed the tides of long period as observed during 33 years at various ports, and found them to be 2/3 as great as on an unyielding globe, indicating an elasticity equal to that of steel.^[33] Subsequently W. Schweydar repeated the calculation from 194 years of observation with nearly the same result.^[34] But as Laplace's argument appears to be unsound (§ 17), the conclusion seems to become of doubtful validity. Yet subsequently Lord Rayleigh showed that the existence in the ocean of continental barriers would have the same effect as that attributed by Laplace to friction, and thus he re-established the soundness of the result.^[35]

A wholly independent estimate derived from what is called the variation of latitude also leads to the same conclusion, namely that the earth is about as stiff as steel.^[36]

The theory of the tides of an elastic planet gives, mutatis mutandis, that of the tides of a viscous spheroid. The reader who desires to know more of this subject and to obtain references to original memoirs may refer to G. H. Darwin's Tides.

VII.—Tidal Friction

§ 35. Investigation of the Secular Effects of Tidal Friction.—We have indicated in general terms in § 9 that the theory of tidal friction leads to an interesting speculation as to the origin of the moon. We shall therefore investigate the theory mathematically in the case where a planet is attended by a single satellite moving in a circular orbit, and rotates about an axis perpendicular to that orbit. In order, however, to abridge the investigation we shall only consider the case where the planetary rotation is more rapid than the satellite's orbital motion.

Suppose an attractive particle or satellite of mass m to be moving in a circular orbit, with an angular velocity ω, round a planet of mass M and suppose the planet to be rotating about an axis perpendicular to the plane of the orbit, with an angular velocity n; suppose, also, the mass of the planet to be partially or wholly imperfectly elastic or viscous, or that there are oceans on the surface of the planet; then the attraction of the satellite must produce a relative motion in the parts of the planet, and that motion must be subject to friction, or, in other words, there must be frictional tides of some sort or other. The system must accordingly Energy Diminished by Friction. be losing energy by friction, and its configuration must change in such a way that its whole energy diminishes. Such a system does not differ much from those of actual planets and satellites, and, therefore, the results deduced in this hypothetical case must agree pretty closely with the actual course of evolution, provided that time enough has been and will be given for such changes. Let C be the moment of inertia of the planet about its axis of rotation, r the distance of the satellite from the centre of the planet, h the resultant moment of momentum of the whole system, e the whole energy, both kinetic and potential, of the system. It is assumed that the figure of the planet and the distribution of its internal density are such that the attraction of the satellite causes no couple about any axis perpendicular to that of rotation. A special system of units of mass, length and time will now be adopted such that the analytical results may be reduced to their simplest forms. Let the unit of mass be Mm/(M+m). Let the unit of length γ be such a distance that the moment of inertia of the planet about its axis of rotation may be equal to the moment of inertia of the planet and satellite, treated as particles, about their centre of inertia, when distant γ apart from one another. This condition gives

m-1 = M1 5 .

M(M+m) +"'(M+m C

Let the unit of time r be the time in which the satellite revolves through 57.3° about the planet, when the satellite's radius vector is equal to γ, This system of units will be found to make the three following functions each equal to unity, viz. Special Units f/P':"' p.iMm(M+m)'i, μMm, and C, where μ is the attractional constant. The units are in fact derived from the consideration that these functions shall each be unity. In the case of the earth and moon, if we take the moon's mass as 1/82 of the earth's and the earth's moment of inertia as § Ma“ (as is very nearly the case), it may easily be shown that the unit of mass is 1/83 of the earth's mass, the unit of length 5.26 earth's radii or 33,506 kilometres (20,807 miles), and the unit of time 2 hrs. 41 mins. In these units the present angular velocity of the Moment of Momentum. earth's diurnal rotation is expressed by 0.7044, and the moon's present radius vector by 11.454. The two bodies being supposed to revolve in circles about their common centre of inertia with an angular velocity ω, the moment of momentum of orbital motion is

M '~+M(sif.1;.)”» =

Then, by the law of periodic times in a circular orbit, wzrs == u(M ;

whence wf'=;4i(M + m)ir5.

Thus the moment of momentum of orbital motion =uiMm(M 'l' m)'lfl,

and in the special units this is equal to r^1/2. The moment of momentum of the planet's rotation is Cn, and C=1 in the special units. Therefore h = n + fi. (62)

Since the moon's present radius vector is 11.454, it follows that the orbital momentum of the moon is 3.384. Adding to this the rotational momentum of the earth, which is 0.704, we obtain 4.088 for the total moment of momentum of the moon and earth. The ratio of the orbital to the rotational momentum is 4.80, so that the total moment of momentum of the system would, but for the obliquity of the ecliptic, be 5.80 times that of the earth's rotation. Again, the kinetic energy of orbital motion is mr ', (Mr 2 Mm, ,, , iMm

• M '”M+ml °' *im "M+ml °'z'iTJTf°' "iff, =

The kinetic energy of the planet's rotation is ½Cn². The potential energy of the system is -μMm/r. Adding the three energies together, and transforming into the special units, we have y ze = n” - 1/r. (63)

Now let⁠x=r^½,⁠y = n,⁠Y = 2e.
It will be noticed that x, the moment of momentum of orbital motion is equal to the square root of the satellite's distance from the planet. Then equations (62) and (63) become 7 h=2'+x (64)

Y=y'- I/x'= (h-x)'-1/x' (65)

(64) is the equation of conservation of moment of momentum, or, shortly, the equation of momentum; (65) is the equation of energy.

Now consider a system started with given positive moment of momentum h; and we have all sorts of ways in which it may be started. If the two rotations be of opposite Maximum and Minimum Energy. kinds, it is clear that we may start the system with any amount of energy, however great, but the true maxima and minima of energy compatible with the given moment of momentum are supplied by dY/dx=0,

or

x - h + 1/x³=0,

that is to say,

x⁴ - hx³ + 1 = 0.

(66)

We shall presently see that this quartic has either two real roots and two imaginary, or all imaginary roots. The quartic may be derived from quite a different consideration, No Relative Motion between Satellite and Planet when Energy Maximum or Minimum. viz. by finding the condition under which the satellite may move round the planet so that the planet shall always show the same face to the satellite-in fact, so that they move as parts of one rigid body. The condition is simply that the satellite's orbital angular velocity on ω=n, the planet's angular velocity of rotation, or y=1/x³, since n=y and r^3/2=ω^-1/3=x. By substituting this value of y in the equation of momentum (64), we get as before

x⁴—hx³+1=0.

At present we have only obtained one result, viz. that, if with given moment of momentum it is possible to set the satellite and planet moving as a rigid body, it is possible to do so in two ways, and one of these ways requires a maximum amount of energy and the other a minimum; from this it is clear that one must be a rapid rotation with the satellite near the planet and the other a slow one with the satellite remote from the planet. Of the three equations h=3'-HC, ' i "(65)

Y= (h-;7C)2- I/362, 4

xsy = Ir ' ' A

(67) is the equation of momentum, (68) that of energy, and (69) may be called the equation of rigidity, since it indicates that the two bodies move as though parts of one rigid body. To illustrate these equations geometrically, we may Equations of Momentum, Energy, and no Relative Motion. take as abscissa x, which is the moment of momentum of orbital motion, so that the axis of x may be called the axis of orbital momentum. Also, for equations (67) and (69) we may take as ordinate y, which is the moment of momentum of the planet's rotation, so that the axis of y may be called the axis of rotational momentum. For (68) we may take as ordinate Y, which is twice the energy of the system, so that the axis of Y may be called the axis of energy. Then, as it will be convenient to exhibit all three curves in the same figure, with a parallel axis of x, we must have the axis of energy identical with that of rotational momentum. It will not be necessary to consider the case where the resultant moment of momentum h is negative, because this would only be equivalent to reversing all the rotations; h is therefore to be taken as essentially positive. The line of momentum whose equation is (67) is a straight line inclined at 45° to either axis, having positive intercepts on both axes. The curve of rigidity whose equation is (69) is clearly of the same nature as a rectangular hyperbola, but it has a much more rapid rate of approach to the axis of orbital momentum than to that of rotational momentum. The intersections (if any) of the curve of rigidity with the line of momentum have abscissae which are the two roots of the quartic x⁴—hx³+1=0. The quartic has, therefore, two real roots or all imaginary roots. Then, since x=r^½, the intersection which is more remote from the origin indicates a configuration where the satellite is remote from the planet; the other gives the configuration where the satellite is closer to the planet. We have already learnt that these two correspond respectively to minimum and maximum energy. When x is very large the equation to the curve of energy is Y=(h-x)², which is the equation to a parabola with a vertical axis parallel to Y and distant h from the origin, so that the axis of the parabola passes through the intersection of the line of momentum with the axis of orbital momentum. When x is very small, the equation becomes Y = -1/x². Hence the axis of Y is asymptotic on both sides to the curve of energy. If the line of momentum intersects the curve of rigidity, the curve of energy has a maximum vertically underneath the point of intersection nearer the origin and a minimum underneath the point more remote. But if there are no intersections, it has no maximum or minimum.

Fig. 8 shows these curves when drawn to scale for the case of the earth and moon, that is to say, with h=4. The points a and b, which are the maximum and minimum of the curve of energy, are supposed to be on the same ordinates as A and B, the intersections of the curve of rigidity with the line of momentum. The intersection of the line of momentum with the axis of orbital momentum is

Fig. 8.

Fig. 8.

denoted by D, but in a figure of this size it necessarily remains indistinguishable from B. As the zero of energy is quite arbitrary the origin for the energy curve is displaced downwards, and this prevents the two curves from crossing one another in a confusing manner. On account of the limitation imposed we neglect the case where the quartic has no real roots. Every point of the line of momentum gives by its abscissa and ordinate the square root of the satellite's distance and the rotation of the planet, and the ordinate of the energy curve gives the energy corresponding to each distance of the satellite. Part of the figure has no physical meaning, for it is impossible for the satellite to move round the planet at a distance less than the sum of the radii of the planet and satellite. For example, the moon's diameter being about 2200 m. and the earth's about 8000, the moon's distance cannot be less than 5100 miles. Accordingly a strip is marked off and shaded on each side of the vertical axis within which the figure has no physical meaning. The point P indicates the present configuration of the earth and moon. The curve of rigidity x³y=1 is the same for all values of h, and by moving the line of momentum parallel to itself nearer to or further from the origin, we may represent Least Momentum for which so Relative Motion Possible. all possible moments of momentum of the whole system. The smallest amount of moment of momentum with which it is possible to set the system moving as a rigid body, with centrifugal force enough to balance the mutual attraction, is when the line of momentum touches the curve of rigidity. The condition for this is clearly that the equation x⁴-hx³+1=0 should have equal roots. If it has equal roots, each root must be 3/4h, and therefore

(3/4h)³-h(3/4h)³+1=0,

whence h⁴=4⁴/3³, or h=4/3^3/4 = 1.75. The actual value of h for the moon and earth is about 4; hence, if the moon-earth system were started with less than 7/16 of its actual moment of momentum, it would not be possible for the two bodies to Maximum Number of Days in Month. move so that the earth should always show the same face to the moon. Again, if we travel along the line of momentum, there must be some point for which yx³ is a maximum, and since yx³=n/ω there must be some point for which the number of planetary rotations is greatest during one revolution of the satellite; or, shortly, there must be some configuration for which there is a maximum number of days in the month. Now yx³ is equal to x³(h—x), and this is a maximum when x=3/4h and the maximum number of days in the month is (3/4h)³(h-3/4h) or 3³h⁴/4⁴; if h is equal to 4, as is nearly the case for the earth and moon, this becomes 27. Hence it follows that we now have very nearly the maximum number of days in the month. A more accurate investigation in a paper on the “Precession of a Viscous Spheroid” in Phil. Trans. (1879), pt. i., showed that, taking account of solar tidal friction and of the obliquity to the ecliptic, the maximum number of days is about 29, and that we have already passed through the phase of maximum.

We will now consider the physical meaning of the figure. It is assumed that the resultant moment of momentum of the whole system corresponds to a positive rotation. Now Discussion of Figure. imagine two points with the same abscissa, one on the momentum line and the other on the energy curve, and suppose the one on the energy curve to guide that on the momentum line. Since we are supposing frictional tides to be raised on the planet, the energy must degrade, and however the two points are set initially the point on the energy curve must always slide down a slope, carrying with it the other point. Looking at the figure, we see that there are four slopes in the energy curve, two running down to the planet and two down to the minimum. There are therefore four ways in which the system may degrade, according to the way it was started; but we shall only consider one, that corresponding to the portion ABba of the figure. For the part of the line of momentum AB the month is History of Satellite as Energy Degrades. longer than the day, and this is the case with all known satellites except the nearer one of Mars. Now, if a satellite be placed in the condition A-that is to say, moving rapidly round a planet which always shows the same face to the satellite- the condition is clearly dynamically unstable, for the least disturbance will determine whether the system shall degrade down the slopes ac or ab-that is to say, whether it falls into or recedes from the planet. If the equilibrium breaks down by the satellite receding, the recession will go on until the system has reached the state corresponding to B. It is clear that, if the intersection of the edge of the shaded strip with the line of momentum be identical with the point A, which indicates that the satellite is just touching the planet, then the two bodies are in effect parts of a single body in an unstable configuration. If, therefore, the moon was originally part of the earth, we should expect to find this identity. Now in fig. 9, drawn to scale to represent the earth and moon, there is so close an approach between the edge of the shaded band and the intersection of the line of momentum and curve of rigidity that it would be scarcely possible to distinguish them. Hence, there seems a probability that the two bodies once formed parts of a single one, which broke up in consequence of some kind of instability. This view is confirmed by the more detailed consideration of the case in the paper on the “Precession of a Viscous Spheroid,” already referred to, and subsequent papers, in the Phil. Trans.^[37]

§ 36. Effects of Tidal Friction on the Elements of the Moon's Orbit and on the Earth's Rotation.—It would be impossible within the limits of the present article to discuss completely the effects of tidal friction; we therefore confine ourselves to certain general considerations which throw light on the nature of those effects. We have in the preceding section supposed that the planet's axis is perpendicular to-the orbit of the satellite, and that the latter is circular; we shall now suppose the orbit to be oblique to the equator and eccentric. For the sake of brevity the planet will be called the earth, and the satellite the moon. The complete investigation was carried out on the hypothesis that the planet was a viscous spheroid, because this was the only theory of friction ally resisted tides which had been worked out. Although the results would be practically the same for any system of friction ally resisted tides, we shall speak below of the planet or earth as a viscous body. ^[38]

We shall show that if the tidal retardation be small the obliquity of the ecliptic increases, the earth's rotation is retarded, and the moon's distance and periodic time are increased. Obliquity of the Ecliptic Increases. Fig. 9 represents the earth as seen from above the south pole, so that S is the pole and the outer circle the equator. The earth's rotation is in the direction

Fig. 9.

Fig. 9.

of the curved arrow at S. The half of the inner circle which is drawn with a full line is a semi-small-circle of south latitude, and the dotted semicircle is a semi-small-circle in the same north latitude. Generally dotted lines indicate parts of the figure which are below the plane of the paper. If the moon were cut in two and one half retained at the place of the moon and the other half transported to a point diametrically opposite to the first half with reference to the earth, there would be no material change in the tide-generating forces. It is easy to verify this statement by reference to § 11. These two halves ma be described as moon and anti-moon, and such a substitution will facilitate the explanation. Let M and M' be the projections of the moon and anti-moon on to the terrestrial sphere. If the fluid in which the tides are raised were perfectly frictionless,^[39] or if the earth were a perfect fluid or perfectly elastic, the apices of the tidal spheroid would: be at M and M'. If however, there is internal friction, due to any sort of viscosity, the tides will lag, and we may suppose the tidal apices to be at T and T'. Now suppose the tidal protuberances to be replaced by two equal heavy particles at T and T', which are instantaneously rigidly connected with the earth. Then the attraction of the moon on T is greater than on T', and that of the anti-moon on T' is greater than on T. The resultant of these forces is clearly a pair of forces acting on the earth in the direction TM, T'M'. These forces cause a couple about the axis in the equator, which lies in the same meridian as the moon and anti-moon. The direction of the couple is shown by the curved arrows at L,L'. If the effects of this couple be compounded with the existing rotation of the earth according to the principle of the gyroscope, the south pole S will tend to approach M and the north pole to approach M'. Hence, supposing the moon to move in the ecliptic, the inclination of the earth's axis to the ecliptic diminishes, or the obliquity increases. Next the forces TM, T'M' clearly produce, as in the simpler case considered in § 9, a couple about the earth's polar axis, which tends to retard the diurnal rotation.

This general explanation remains a fair representation of the state of the case so long as the different harmonic constituents of the aggregate tide-wave do not suffer very different amounts of retardation; and this is the case so long as the viscosity is not great. The rigorous result for a viscous planet shows that in general the obliquity will increase, and it appears that, with small viscosity of the planet, if the period of the satellite be longer than two periods of rotation of the planet, the obliquity increases, and vice versâ. Hence, zero obliquity is only dynamically stable when the period of the satellite is less than two periods of the planet's rotation.

It is possible, by similar considerations, to obtain some insight into the effect which tidal friction must have on the plane of the Inclination of Plane of Orbit Generally Decreases. lunar orbit, but as the subject is somewhat complex we shall not proceed to a detailed examination of the question. It must suffice to say that in general the inclination of the lunar orbit must diminish. Now let us consider a satellite revolving about a planet in an elliptic orbit, with a periodic time which is long compared with the period of rotation of the planet; and suppose that frictional tides are raised in the planet. The major axis of the tidal spheroid always points in advance of the satellite, and exercises Eccentricity of Orbit Generally Increases. on it a force which tends to accelerate its linear velocity. When the satellite is in perigee the tides are higher, and this disturbing force is greater than when the satellite is in apogee. The disturbing force may therefore be represented as a constant force, always tending to accelerate the motion of the satellite, to which is added a periodic force accelerating in perigee and retarding in apogee. The constant force causes a secular increase of the satellite's mean distance and a retardation of its mean motion. The accelerating force in perigee causes the satellite to swing out farther than it would otherwise have done, so that when it comes round to apogee it is more remote from the planet. The retarding force in apogee acts exactly inversely, and diminishes the perigean distance. Thus, the apogean distance increases and the perigean distance diminishes, or in other words, the eccentricity of the orbit increases. Now consider another case, and suppose the satellite's periodic time to be identical with that of the planet's rotation. Then, when the satellite is in perigee, its angular motion is faster than that of the planet's rotation, and when in apogee it is slower; hence at apogee the tides lag, and at perigee they are accelerated. Now the lagging apogean tides give rise to an accelerating force on the satellite, and increase the perigean But it May Decrease. distance, whilst the accelerated perigean tides give rise to a retarding force, and decrease the apogean distance. Hence in this case the eccentricity of the orbit will diminish. It follows from these two results that there must be some intermediate periodic time of the satellite for which the eccentricity does not tend to vary.

But the preceding general explanation is in reality somewhat less satisfactory than it seems, because it does not make clear the existence of certain antagonistic influences, to which, however, we shall not refer. The full investigation for a viscous planet shows that in general the eccentricity of the orbit will increase. When the viscosity is small the law of variation of eccentricity is very simple: if eleven periods of the satellite occupy a longer time than eighteen rotations of the planet, the eccentricity increases, and vice versâ. Hence in the case of small viscosity a circular orbit is only dynamically stable if the eleven periods are shorter than the eighteen rotations.

VIII.—Cosmogonic Speculations Founded on Tidal Friction

§ 37. History of the Earth and Moon.—We shall not attempt to discuss the mathematical methods by which the complete history of a planet, attended by one or more satellites, is to be traced. The laws indicated in the preceding sections show that there is such a problem, and that it may be solved, and we refer to G. H. Darwin's papers for details (Phil. Trans., 1879-1881). It may be interesting, however, to give the various results of the investigation in the form of a sketch of the possible evolution of the earth and moon, followed by remarks on the other planetary systems and on the solar system as a whole.

We begin with a planet not very much more than 8000 m. in diameter, and probably partly solid, partly fluid, and partly gaseous. It is rotating about an axis inclined at about 11° or 12° to the normal to the ecliptic, with a period of from two to four hours, and is revolving about the sun with a period not much shorter than our present year. The rapidity of the planet's rotation causes so great a compression of its figure that it cannot continue to exist in an ellipsoidal form with stability; or else it is so nearly unstable that complete instability is induced by the solar tides. Conjectured Genesis of Moon from Earth. The planet then separates into two masses, the larger being the earth and the smaller the moon. It is not attempted to define the mode of separation, or to say whether the moon was initially a chain of meteorites. At any rate it must be assumed that the smaller mass became more or less conglomerated and finally fused into a spheroid, perhaps in consequence of impacts between its constituent meteorites, which were once part of the primeval planet. Up to this point the history is largely speculative, for the investigation of the conditions of instability in such a case surpasses the powers of the mathematician. We have now the earth and moon nearly in contact with one another, and rotating nearly as though Earth and Moon Subject to Investigation. they were parts of one rigid body. This is the system which was the subject of dynamical investigation. As the two masses are not rigid, the attraction of each distorts the other; and, if they do not move rigorously with the same periodic time, each raises a tide in the other. Also the sun raises tides in both. In consequence of the frictional resistance to these tidal motions, such a system is dynamically unstable. If the moon had moved orbitally a little faster than the earth rotated, she must have fallen back into the earth; thus the existence of the moon compels us to believe that the equilibrium broke down by the moon revolving orbitally a little slower than the earth rotates. In consequence of the tidal friction the periodic times both of the moon (or the month) and of the earth's rotation (or the day) increase; but the month increases in length at a much greater rate than the day. At some early stage in the history of the system the moon was conglomerated into a spheroidal form, and acquired a rotation about an axis nearly parallel to that of the earth.

The axial rotation of the moon is retarded by the attraction of the earth on the tides raised in the moon, and this retardation takes place at a far greater rate than the similar retardation The Moon. of the earth's rotation. As soon as the moon rotates round her axis with twice the angular velocity with which she revolves in her orbit, the position of her axis of rotation (parallel with the earth's axis) becomes dynamically unstable. The obliquity of the lunar equator to the plane of the orbit increases, attains a maximum, and then diminishes. Meanwhile the lunar axial rotation is being reduced towards identity with the orbital motion. Finally, her equator is nearly coincident with the plane of the orbit, and, the attraction of the earth on a tide, which degenerates into a permanent ellipticity of the lunar equator, causes her always to show the same face to the earth.

All this must have taken place early in the history of the earth, to which we now return. At first the month is identical with the day, and as both these increase in length the lunar orbit will retain its circular form until the month is equal to The Earth and Lunar Orbit. 1 7/11 days. From that time the orbit begins to be eccentric, and the eccentricity increases thereafter up to its orbit present magnitude. The plane of the lunar orbit is at first practically identical with the earth's equator, but as the moon recedes from the earth the sun's attraction begins to make itself felt. We shall not attempt to trace the complex changes by which the plane of the lunar orbit is affected. It must suffice to say that the present small inclination of the lunar orbit to the ecliptic accords with the theory.

As soon as the earth rotates with twice the angular velocity with which the moon revolves in her orbit, a new instability sets in. The month is then about twelve of our present hours, and the day about six such hours in length. The inclination of the equator to the ecliptic now begins to increase and continues to do so until finally it reached its present value of 23 1/2°. All these changes continue and no new phase now supervenes, and at length we have the system in its present configuration. The minimum time in which the changes from first to last can have taken place is 54,000,000 years.

There are other collateral results which must arise from a supposed primitive viscosity or plasticity of the earth's mass. For during this course of evolution the earth's mass must have Distortion of Plastic Planet. suffered a screwing motion, so that the polar regions have travelled a little from west to east relatively to the equator. This affords a possible, explanation of the north and south trend of our great continents. The whole of this argument reposes on the imperfect rigidity of solids and on the internal friction of semi-solids and fluids; these are verae causae. Thus changes of the kind here discussed must be going on, and must have gone on in the past. And for this The Theory Postulates Sufficient Lapse of Time. history of the earth and moon to be true throughout, it is only necessary to postulate sufficient lapse of time, and that there is not enough matter diffused through space materially to resist the motions of the moon and earth in perhaps 200,000,000 years. It seems hardly too much to say that, granting these two postulates, and the existence of a

^[40] primeval planet such as that above described, a system would necessarily be developed which would bear a strong resemblance to our own. A theory, reposing on verae causae which brings into quantitative correlation the lengths of the present day and month, the obliquity of the ecliptic, and the inclination and eccentricity of the lunar orbit should have claims to acceptance.

§ 38. The Influence of Tidal Friction on the Evolution of the Solar System and of the Planetary Sub-systems.^[41]—According to the nebular hypothesis of Kant and Laplace the planets and satellites are portions detached from contracting nebulous masses, and other theories have been advanced subsequently in explanation of the present configuration of the solar system. We shall here only examine what changes are called for by the present theory of tidal friction. It may be shown that the reaction of the tides raised in the sun by the planets must have had a very small influence in changing the dimensions of the planetary orbits round the sun, and it appears improbable that the planetary orbits have been sensibly enlarged by tidal friction since the origin of the several planets.

Similarly it appears unlikely that the satellites of Mars, Jupiter and Saturn originated very much nearer the present surfaces of the Planetary Sub-systems. planets that we now observe them. But, the data being insufficient, we cannot feel sure that the alteration in the dimensions of the orbits of these satellites has not been considerable. It remains, however, nearly certain that they cannot have first originated almost in contact with the present surfaces of the planets, in the same way as in the preceding sketch has been shown to be probable with regard to the moon and earth. Numerical data concerning the distribution of moment of momentum in the several planetary sub-systems exhibit so striking a difference between the terrestrial system and those of the other planets that we should from this alone have grounds for believing that the modes of evolution have been considerably different. The difference appears to lie in the genesis of the moon close to the present surface of the planet, and we shall see below that solar tidal friction may be assigned as a reason to explain how it has happened that the terrestrial planet had contracted to nearly its present dimensions before the genesis of a satellite, but that this was not the case with the exterior planets. The efficiency of solar tidal friction is very much greater in its action on the nearer planets than on the farther ones. The time, however, during which solar tidal friction has been operating on the external planets is probably much longer than the period of its efficiency for the interior ones, and a series of numbers proportional to the total amount of rotation destroyed in the several planets would present a far less rapid decrease as we recede from the sun than numbers simply expressive of the efficiency of tidal friction at the several planets. Nevertheless it must be admitted that the effect produced by solar tidal friction on Jupiter and Saturn has not been nearly so great as on the interior planets. And, as already stated, it is very improbable that so large an amount of momentum should have been destroyed as materially to affect the orbits of the planets round the sun.

We will now examine how the difference of distances from the sun may have affected the histories of the several planets. According to Distribution of Satellites Amongst the Planets. the nebula hypothesis, as a planetary nebula contracts, the increasing rapidity of the rotation causes it to become unstable, and an equatorial portion of matter detaches itself. The separation of that part of the mass which before the change had the greatest angular momentum permits the central portion to resume a planetary shape. The contraction and the increase of rotation proceed continually until another portion is detached, and so on. There thus recur at intervals epochs of instability, and something of the same kind must have occurred according to other rival theories. Now tidal friction must diminish the rate of increase of rotation due to contraction, and therefore if tidal friction and contraction are at work together the epochs of instability must recur more rarely than if contraction alone acted. If the tidal retardation is sufficiently great, the increase of rotation due to contraction will be so far counteracted as never to permit an epoch of instability to occur. Since the rate of retardation due to solar tidal friction decreases rapidly as we recede from the sun, these considerations accord with what we observe in the solar system. For Mercury and Venus have no satellites, and there is progressive increase in the number of satellites as we recede from the sun. Whether this be the true cause of the observed distribution of satellites amongst the planets or not, it is remarkable that the same cause also affords an explanation, as we shall now show, of that difference between the earth with the moon and the other planets with their satellites which has caused tidal friction to be the principal agent of change with the former, but not with the latter. In the case of the contracting terrestrial mass we may suppose that there was for a long time nearly a balance Case of Earth and Moon Different from others. between the retardation due to solar tidal friction and the acceleration due to contraction, and that it was not until the planetary mass had contracted to nearly its present dimensions that an epoch of instability could occur. It may also be noted that if there be two equal planetary masses which generate satellites, but under very different conditions as to the degree of condensation of the masses, the two satellites will be likely to differ in mass; we cannot, of course, tell which of the two planets would generate the larger satellite. Thus, if the genesis of the moon was deferred until a late epoch in the history of the terrestrial mass, the mass of the moon relatively to the earth would be likely to differ from the mass of other satellites relatively to their planets. If the contraction of the planetary mass be almost completed before the genesis of the satellite, tidal friction will thereafter be the great cause of change in the system; and thus the hypothesis that it is the sole cause of change will give an approximately accurate explanation of the motion of the planet and satellite at any subsequent time. We have already seen that the theory that tidal friction has been the ruling power in the evolution of the earth and moon co-ordinates the present motions of the two bodies and carries us back to an initial state when the moon first had a separate existence as a satellite; and the initial configuration of the two bodies is such that we are led to believe that the moon is a portion of the primitive earth detached by rapid rotation or by other causes.

Let us now turn to the other planetary sub-systems. The satellites of the larger planets revolve with short periodic times; for the smallness of their masses would have prevented tidal friction from being a very efficient cause of change in the dimensions of their orbits, and the largeness of the planet's masses would have caused them to proceed slowly in their evolution. The satellites of Mars present one of the most remarkable features in the solar system, for, whereas Mars rotates in 24h. 37m., Deimos has a period of 30h. 18m. and Phobos of only 7h. 39m. The minuteness of these satellites precludes us from supposing that they have had much influence on the rotation of the planet, or that the dimensions of their own orbits have been much changed.

The theory of tidal friction would explain the shortness of the periodic time of Phobos by the solar retardation of the planet's rotation, which would operate without directly affecting Satellites of Mars. the satellites' orbital motion. We may see that, given sufficient time, this must be the ultimate fate of all satellites. Numerical comparison shows that the efficiency of solar tidal friction in retarding the terrestrial and martian rotations is of about the same degree of importance, notwithstanding the much greater distance of the planet Mars. In the above discussion it will have been apparent that the earth and moon do actually differ from the other planets to such an extent as to permit tidal friction to have been the most important factor in their history.

By an examination of the probable effects of solar tidal friction on a contracting planetary mass, we have been led to assign a cause for the observed distribution of satellites in the solar Summary. system, and this again has itself afforded an explanation of how it happened that the moon so originated that the tidal friction of the lunar tides in the earth should have been able to exercise so large an influence. We have endeavoured not only to set forth the influence which tidal friction may have, and probably has had in the history of the system, if sufficient time be granted, but also to point out what effects it cannot have produced. These investigations afford no grounds for the rejection of theories more or less akin to the nebular hypothesis; but they introduce modifications of considerable importance. Tidal friction is a cause of change of which Laplace's theory took no account; and, although the activity of that cause may be regarded as mainly belonging to a later period than the events described in the nebular hypothesis, yet it seems that its influence has been of great, and in one instance of even paramount, importance in determining the present condition of the planets and their satellites. Throughout the whole of this discussion it has been supposed that sufficient time is at our disposal. Yet arguments have been adduced which Limitation of Time. seemed to show that this supposition is not justifiable, for Helmholtz, Lord Kelvin and others have attempted to prove that the history of the solar system must be comprised within a period considerably less than a hundred million years.^[42] But the discovery of radio-activity and the consequent remarkable advances in physics throw grave doubt on all such arguments, and we believe that it is still beyond our powers to assign definite numerical limits to the age of the solar system.

Dr T. J. J. See (Researches on the Evolution of Stellar Systems; vol. ii. (1910) Capture Theory) rejects the applicability of tidal friction to the cosmogony of the solar system, and argues that the satellites were primitively wandering bodies and were captured by the gravitational attraction of the planets. Such captures are considered by Dr See to be a necessary result of the presence in space of a resisting medium; but the present writer does not feel convinced by the arguments adduced.

(G. H. D.)

---

1. Lord Kelvin shows that the attraction of the sun on these tides must produce an excessively small acceleration of the earth’s rotation. See Société de physique (September 1881), or Proc. Roy. Soc. Edin. (1881–1882), p. 396.
2. Founded on G. B. Airy's “Tides and Waves,” in Ency. Metrop.
3. See a series of papers bearing on this kind of wave by Sir W. Thomson (Lord Kelvin) in Phil. Mag. (1886–1887).
4. Airy, “ Tides and Waves.”
5. Ibid. §§ 572-573.
6. See J. N. Shoolbred on datum levels, Brit. Assoc. Reports (1879).
7. References may be given to two papers by G. H. Darwin on this subject, viz. “Tidal Prediction,” Phil. Trans., A. (1891) pp. 159-229; and “An apparatus for facilitating the reduction of tidal observations.” Proc. Roy. Soc. (1892), vol. lii. For a general account without mathematics see Darwin's Tides, &c.; this section is founded on chs. xiii. and xiv. of that book. For mathematical methods see Maurice Lévy, Théorie des marées (Paris, 1898).
8. Whewell, History of Inductive Sciences, ii. 248; Darwin's Tides, &c., ch. iv.
9. Darwin, “Tidal Prediction,” quoted above. This kind of table has been applied with some success at Cairns in North Queensland, where there is a large diurnal inequality.
10. Portion of Airy's Chart (Encycl. Metrop., art. "Tides and Waves") is given in Darwin, Tides and Kindred Phenomena in the Solar System.
11. Berghaus's Physical Atlas (1891), pt. ii., "Hydrography."
12. The account from the time of Newton to that of Laplace is founded on Laplace's Mécanique céleste, bk. xiii. ch. i.
13. This way of presenting the action of tidal friction is due to Sir George G. Stokes.
14. See that work (ed. 1883), § 830; P. H. Cowell, M. N. R. Ast. Soc. (1905), lxv. 861.
15. For a discussion of the subject without mathematics, see G. H. Darwin's Tides.
16. London (1898) and with important changes (1901, 1911); (Boston, 1898); translations: German, by A. Pockels (Leipzig, 1902, 1911); Italian, by G. Magrini (Turin, 1905), with appendices by translator; Magyar, by Radó von Kövesligethy (Budapest, 1904), with appendices by translator.
17. The theory as presented in the Mécanique céleste is unnecessarily difficult, and was much criticized by Airy. Before, the publication of the 9th and 10th editions of the Ency. Brit. it was necessary for the student to read a number of controversial papers published all over the world in order to get at the matter.
18. The reader may refer to Thomson and Tait's Natural Philosophy (1883), pt. ii. §§ 798-821, for further considerations on this and analogous subjects, together with some interesting examples.
19. Thomson and Tait, Nat. Phil. § 807. G. H. Darwin and H. H. Tumer, Proc. Roy. Soc. (1886)
20. Lord Kelvin's (Sir W Thomson's) paper on the gravitational oscillations of rotating water, Phil. Mag. (October 1880), bears on this subject. It is the only attempt to obtain numerical results in respect to the effect of the earth's rotation on the oscillations of land-locked seas.
21. Phil. Trans., 189 A, pp. 201-258 and 191 A, pp. 139-185.
22. Thomson and Tait, Nat. Phil. § 816.
23. Compare an important paper by H. Poincaré, in Acta math. (1885), 7: 3. 4
24. From Airy's Tides and Waves, with omission of part which was erroneous.
25. See, for example, a collection of results by Baird and Darwin, Proc. Roy. Soc. (1885), No. 239, and a more extensive one in Harris's Manual.
26. Report on Harmonic Analysis to Brit. Assoc. (1883), and more extended table in Baird's Manual of Tidal Observation (London, 1887).
27. See Darwin's Tides for an account without mathematics.
28. Founded on Whewell's article “ Tides,” in Admiralty Manual (ed. 1841), and on Airy's “ Tides and Waves,” in Ency. Metrop.
29. For a numerical treatment, see Directions for Reducing Tidal Observations, by Commander Burdwood, R.N. (London, 1876).
30. G H. Darwin “ On Tidal Prediction,” Phil. Trans. (1891), vol. 189 A.
31. Théorie math. de l'élasticité (1866), p. 213.
32. Thomson and Tait, Nat. Phil. §§ 732-737 and 833-842, or Phil. Trans. (1863), pt. ii., p. 583. Compare, however, J. H. Jeans, Phil. Trans. (1903), 201 A, p. 157.
33. Thomson & Tait, Nat. Phil. § 843.
34. Beiträge zur Geophysik (1907) ix. 41.
35. Phil. Mag. (1903). v. 136.
36. Hough, Phil. Trans. (1897), 187 A, p. 319.
37. For further consideration of this subject see a series of papers by G. H. Darwin in Proceed. and Trans. of the Royal Society from 1878 to 1881, and app. G. (b) t. pt. ii. vol. i. of Thomson and Tait's Nat. Phil. (1883); or Scientific Papers, vol. ii.
38. These explanations, together with other remarks, are to be found in the abstracts of G. H. Darwin's memoirs in Proc. Roy. Soc., 1878 to 1881.
39. We here suppose the tides not to be inverted. If they are inverted the conclusion is precisely the same.
40. See criticism, by Nolan, Genesis of Moon (Melbourne, 1885); also Nature (Feb. 18, 1886).
41. A review of this and of cognate subjects is contained in G. H. Darwin's presidential address to the Brit. Assoc. in 1905.
42. Thomson and Tait's Nat. Phil., app. E; Nature (Jan. 27, 1887): Wolf, Théories cosmogoniques (1886).