1911 Encyclopædia Britannica/Capillary Action
CAPILLARY ACTION.[1] A tube, the bore of which is so small that it will only admit a hair (Lat. capilla), is called a capillary tube. When such a tube of glass, open at both ends, is placed vertically with its lower end immersed in water, the water is observed to rise in the tube, and to stand within the tube at a higher level than the water outside. The action between the capillary tube and the water has been called capillary action, and the name has been extended to many other phenomena which have been found to depend on properties of liquids and solids similar to those which cause water to rise in capillary tubes.
The forces which are concerned in these phenomena are those which act between neighbouring parts of the same substance, and which are called forces of cohesion, and those which act between portions of matter of different kinds, which are called forces of adhesion. These forces are quite insensible between two portions of matter separated by any distance which we can directly measure. It is only when the distance becomes exceedingly small that these forces become perceptible. G. H. Quincke (Pogg. Ann. cxxxvii. p. 402) made experiments to determine the greatest distance at which the effect of these forces is sensible, and he found for various substances distances about the twenty-thousandth part of a millimetre.
Historical.—According to J. C. Poggendorff (Pogg. Ann. ci. p. 551), Leonardo da Vinci must be considered as the discoverer of capillary phenomena, but the first accurate observations of the capillary action of tubes and glass plates were made by Francis Hawksbee (Physico-Mechanical Experiments, London, 1709, pp. 139-169; and Phil. Trans., 1711 and 1712), who ascribed the action to an attraction between the glass and the liquid. He observed that the effect was the same in thick tubes as in thin, and concluded that only those particles of the glass which are very near the surface have any influence on the phenomenon. Dr James Jurin (Phil. Trans., 1718, p. 739, and 1719, p. 1083) showed that the height at which the liquid is suspended depends on the section of the tube at the surface of the liquid, and is independent of the form of the lower part of the tube. He considered that the suspension of the liquid is due to “the attraction of the periphery or section of the surface of the tube to which the upper surface of the water is contiguous and coheres.” From this he showed that the rise of the liquid in tubes of the same substance is inversely proportional to their radii. Sir Isaac Newton devoted the 31st query in the last edition of his Opticks to molecular forces, and instanced several examples of the cohesion of liquids, such as the suspension of mercury in a barometer tube at more than double the height at which it usually stands. This arises from its adhesion to the tube, and the upper part of the mercury sustains a considerable tension, or negative pressure, without the separation of its parts. He considered the capillary phenomena to be of the same kind, but his explanation is not sufficiently explicit with respect to the nature and the limits of the action of the attractive force.
It is to be observed that, while these early speculators ascribe the phenomena to attraction, they do not distinctly assert that this attraction is sensible only at insensible distances, and that for all distances which we can directly measure the force is altogether insensible. The idea of such forces, however, had been distinctly formed by Newton, who gave the first example of the calculation of the effect of such forces in his theorem on the alteration of the path of a light-corpuscle when it enters or leaves a dense body.
Alexis Claude Clairault (Théorie de la figure de la terre, Paris, 1808, pp. 105, 128) appears to have been the first to show the necessity of taking account of the attraction between the parts of the fluid itself in order to explain the phenomena. He did not, however, recognize the fact that the distance at which the attraction is sensible is not only small but altogether insensible. J. A. von Segner (Comment. Soc. Reg. Götting. i. (1751) p. 301) introduced the very important idea of the surface-tension of liquids, which he ascribed to attractive forces, the sphere of whose action is so small “ut nullo adhuc sensu percipi potuerit.” In attempting to calculate the effect of this surface-tension in determining the form of a drop of the liquid, Segner took account of the curvature of a meridian section of the drop, but neglected the effect of the curvature in a plane at right angles to this section.
The idea of surface-tension introduced by Segner had a most important effect on the subsequent development of the theory. We may regard it as a physical fact established by experiment in the same way as the laws of the elasticity of solid bodies. We may investigate the forces which act between finite portions of a liquid in the same way as we investigate the forces which act between finite portions of a solid. The experiments on solids lead to certain laws of elasticity expressed in terms of coefficients, the values of which can be determined only by experiments on each particular substance. Various attempts have also been made to deduce these laws from particular hypotheses as to the action between the molecules of the elastic substance. We may therefore regard the theory of elasticity as consisting of two parts. The first part establishes the laws of the elasticity of a finite portion of the solid subjected to a homogeneous strain, and deduces from these laws the equations of the equilibrium and motion of a body subjected to any forces and displacements. The second part endeavours to deduce the facts of the elasticity of a finite portion of the substance from hypotheses as to the motion of its constituent molecules and the forces acting between them. In like manner we may by experiment ascertain the general fact that the surface of a liquid is in a state of tension similar to that of a membrane stretched equally in all directions, and prove that this tension depends only on the nature and temperature of the liquid and not on its form, and from this as a secondary physical principle we may deduce all the phenomena of capillary action. This is one step of the investigation. The next step is to deduce this surface-tension from a hypothesis as to the molecular constitution of the liquid and of the bodies that surround it. The scientific importance of this step is to be measured by the degree of insight which it affords or promises into the molecular constitution of real bodies by the suggestion of experiments by which we may discriminate between rival molecular theories.
In 1756 J. G. Leidenfrost (De aquae communis nonnullis qualitatibus tractatus, Duisburg) showed that a soap-bubble tends to contract, so that if the tube with which it was blown is left open the bubble will diminish in size and will expel through the tube the air which it contains. He attributed this force, however, not to any general property of the surfaces of liquids, but to the fatty part of the soap which he supposed to separate itself from the other constituents of the solution, and to form a thin skin on the outer face of the bubble.
In 1787 Gaspard Monge (Mémoires de l’Acad. des Sciences, 1787, p. 506) asserted that “by supposing the adherence of the particles of a fluid to have a sensible effect only at the surface itself and in the direction of the surface it would be easy to determine the curvature of the surfaces of fluids in the neighbourhood of the solid boundaries which contain them; that these surfaces would be linteariae of which the tension, constant in all directions, would be everywhere equal to the adherence of two particles, and the phenomena of capillary tubes would then present nothing which could not be determined by analysis.” He applied this principle of surface-tension to the explanation of the apparent attractions and repulsions between bodies floating on a liquid.
In 1802 John Leslie (Phil. Mag., 1802, vol. xiv. p. 193) gave the first correct explanation of the rise of a liquid in a tube by considering the effect of the attraction of the solid on the very thin stratum of the liquid in contact with it. He did not, like the earlier speculators, suppose this attraction to act in an upward direction so as to support the fluid directly. He showed that the attraction is everywhere normal to the surface of the solid. The direct effect of the attraction is to increase the pressure of the stratum of the fluid in contact with the solid, so as to make it greater than the pressure in the interior of the fluid. The result of this pressure if unopposed is to cause this stratum to spread itself over the surface of the solid as a drop of water is observed to do when placed on a clean horizontal glass plate, and this even when gravity opposes the action, as when the drop is placed on the under surface of the plate. Hence a glass tube plunged into water would become wet all over were it not that the ascending liquid film carries up a quantity of other liquid which coheres to it, so that when it has ascended to a certain height the weight of the column balances the force by which the film spreads itself over the glass. This explanation of the action of the solid is equivalent to that by which Gauss afterwards supplied the defect of the theory of Laplace, except that, not being expressed in terms of mathematical symbols, it does not indicate the mathematical relation between the attraction of individual particles and the final result. Leslie’s theory was afterwards treated according to Laplace’s mathematical methods by James Ivory in the article on capillary action, under “Fluids, Elevation of,” in the supplement to the fourth edition of the Encyclopaedia Britannica, published in 1819.
In 1804 Thomas Young (Essay on the “Cohesion of Fluids,” Phil. Trans., 1805, p. 65) founded the theory of capillary phenomena on the principle of surface-tension. He also observed the constancy of the angle of contact of a liquid surface with a solid, and showed how from these two principles to deduce the phenomena of capillary action. His essay contains the solution of a great number of cases, including most of those afterwards solved by Laplace, but his methods of demonstration, though always correct, and often extremely elegant, are sometimes rendered obscure by his scrupulous avoidance of mathematical symbols. Having applied the secondary principle of surface-tension to the various particular cases of capillary action, Young proceeded to deduce this surface-tension from ulterior principles. He supposed the particles to act on one another with two different kinds of forces, one of which, the attractive force of cohesion, extends to particles at a greater distance than those to which the repulsive force is confined. He further supposed that the attractive force is constant throughout the minute distance to which it extends, but that the repulsive force increases rapidly as the distance diminishes. He thus showed that at a curved part of the surface, a superficial particle would be urged towards the centre of curvature of the surface, and he gave reasons for concluding that this force is proportional to the sum of the curvatures of the surface in two normal planes at right angles to each other.
The subject was next taken up by Pierre Simon Laplace (Mécanique céleste, supplement to the tenth book, pub. in 1806). His results are in many respects identical with those of Young, but his methods of arriving at them are very different, being conducted entirely by mathematical calculations. The form into which he threw his investigation seems to have deterred many able physicists from the inquiry into the ulterior cause of capillary phenomena, and induced them to rest content with deriving them from the fact of surface-tension. But for those who wish to study the molecular constitution of bodies it is necessary to study the effect of forces which are sensible only at insensible distances; and Laplace has furnished us with an example of the method of this study which has never been surpassed. Laplace investigated the force acting on the fluid contained in an infinitely slender canal normal to the surface of the fluid arising from the attraction of the parts of the fluid outside the canal. He thus found for the pressure at a point in the interior of the fluid an expression of the form
where is a constant pressure, probably very large, which, however, does not influence capillary phenomena, and therefore cannot be determined from observation of such phenomena; is another constant on which all capillary phenomena depend; and and are the radii of curvature of any two normal sections of the surface at right angles to each other.
In the first part of our own investigation we shall adhere to the symbols used by Laplace, as we shall find that an accurate knowledge of the physical interpretation of these symbols is necessary for the further investigation of the subject. In the Supplement to the Theory of Capillary Action, Laplace deduced the equation of the surface of the fluid from the condition that the resultant force on a particle at the surface must be normal to the surface. His explanation, however, of the rise of a liquid in a tube is based on the assumption of the constancy of the angle of contact for the same solid and fluid, and of this he has nowhere given a satisfactory proof. In this supplement Laplace gave many important applications of the theory, and compared the results with the experiments of Louis Joseph Gay Lussac.
The next great step in the treatment of the subject was made by C. F. Gauss (Principia generalia Theoriae Figurae Fluidorum in statu Aequilibrii, Göttingen, 1830, or Werke, v. 29, Göttingen, 1867). The principle which he adopted is that of virtual velocities, a principle which under his hands was gradually transforming itself into what is now known as the principle of the conservation of energy. Instead of calculating the direction and magnitude of the resultant force on each particle arising from the action of neighbouring particles, he formed a single expression which is the aggregate of all the potentials arising from the mutual action between pairs of particles. This expression has been called the force-function. With its sign reversed it is now called the potential energy of the system. It consists of three parts, the first depending on the action of gravity, the second on the mutual action between the particles of the fluid, and the third on the action between the particles of the fluid and the particles of a solid or fluid in contact with it.
The condition of equilibrium is that this expression (which we may for the sake of distinctness call the potential energy) shall be a minimum. This condition when worked out gives not only the equation of the free surface in the form already established by Laplace, but the conditions of the angle of contact of this surface with the surface of a solid.
Gauss thus supplied the principal defect in the great work of Laplace. He also pointed out more distinctly the nature of the assumptions which we must make with respect to the law of action of the particles in order to be consistent with observed phenomena. He did not, however, enter into the explanation of particular phenomena, as this had been done already by Laplace, but he pointed out to physicists the advantages of the method of Segner and Gay Lussac, afterwards carried out by Quincke, of measuring the dimensions of large drops of mercury on a horizontal or slightly concave surface, and those of large bubbles of air in transparent liquids resting against the under side of a horizontal plate of a substance wetted by the liquid.
In 1831 Siméon Denis Poisson published his Nouvelle Théorie de l’action capillaire. He maintained that there is a rapid variation of density near the surface of a liquid, and he gave very strong reasons, which have been only strengthened by subsequent discoveries, for believing that this is the case. He proceeded to an investigation of the equilibrium of a fluid on the hypothesis of uniform density, and arrived at the conclusion that on this hypothesis none of the observed capillary phenomena would take place, and that, therefore, Laplace’s theory, in which the density is supposed uniform, is not only insufficient but erroneous. In particular he maintained that the constant pressure K, which occurs in Laplace’s theory, and which on that theory is very large, must be in point of fact very small, but the equation of equilibrium from which he concluded this is itself defective. Laplace assumed that the liquid has uniform density, and that the attraction of its molecules extends to a finite though insensible distance. On these assumptions his results are certainly right, and are confirmed by the independent method of Gauss, so that the objections raised against them by Poisson fall to the ground. But whether the assumption of uniform density be physically correct is a very different question, and Poisson rendered good service to science in showing how to carry on the investigation on the hypothesis that the density very near the surface is different from that in the interior of the fluid.
The result, however, of Poisson’s investigation is practically equivalent to that already obtained by Laplace. In both theories the equation of the liquid surface is the same, involving a constant H, which can be determined only by experiment. The only difference is in the manner in which this quantity H depends on the law of the molecular forces and the law of density near the surface of the fluid, and as these laws are unknown to us we cannot obtain any test to discriminate between the two theories.
We have now described the principal forms of the theory of capillary action during its earlier development. In more recent times the method of Gauss has been modified so as to take account of the variation of density near the surface, and its language has been translated in terms of the modern doctrine of the conservation of energy.[2]
J. A. F. Plateau (Statique expérimentale et théorique des liquides), who made elaborate study of the phenomena of surface-tension, adopted the following method of getting rid of the effects of gravity. He formed a mixture of alcohol and water of the same density as olive oil, and then introduced a quantity of oil into the mixture. It assumes the form of a sphere under the action of surface-tension alone. He then, by means of rings of iron-wire, disks and other contrivances, altered the form of certain parts of the surface of the oil. The free portions of the surface then assume new forms depending on the equilibrium of surface-tension. In this way he produced a great many of the forms of equilibrium of a liquid under the action of surface-tension alone, and compared them with the results of mathematical investigation. He also greatly facilitated the study of liquid films by showing how to form a liquid, the films of which will last for twelve or even for twenty-four hours. The debt which science owes to Plateau is not diminished by the fact that, while investigating these beautiful phenomena, he never himself saw them, having lost his sight in about 1840.
G. L. van der Mensbrugghe (Mém. de l’Acad. Roy. de Belgique, xxxvii., 1873) devised a great number of beautiful illustrations of the phenomena of surface-tension, and showed their connexion with the experiments of Charles Tomlinson on the figures formed by oils dropped on the clean surface of water.
Athanase Dupré in his 5th, 6th and 7th Memoirs on the Mechanical Theory of Heat (Ann. de Chimie et de Physique, 1866–1868) applied the principles of thermodynamics to capillary phenomena, and the experiments of his son Paul were exceedingly ingenious and well devised, tracing the influence of surface-tension in a great number of very different circumstances, and deducing from independent methods the numerical value of the surface-tension. The experimental evidence which Dupré obtained bearing on the molecular structure of liquids must be very valuable, even if our present opinions on this subject should turn out to be erroneous.
F. H. R. Lüdtge (Pogg. Ann. cxxxix. p. 620) experimented on liquid films, and showed how a film of a liquid of high surface-tension is replaced by a film of lower surface-tension. He also experimented on the effects of the thickness of the film, and came to the conclusion that the thinner a film is, the greater is its tension. This result, however, was tested by Van der Mensbrugghe, who found that the tension is the same for the same liquid whatever be the thickness, as long as the film does not burst. [The continued coexistence of various thicknesses, as evidenced by the colours in the same film, affords an instantaneous proof of this conclusion.] The phenomena of very thin liquid films deserve the most careful study, for it is in this way that we are most likely to obtain evidence by which we may test the theories of the molecular structure of liquids.
Sir W. Thomson (afterwards Lord Kelvin) investigated the effect of the curvature of the surface of a liquid on the thermal equilibrium between the liquid and the vapour in contact with it. He also calculated the effect of surface-tension on the propagation of waves on the surface of a liquid, and determined the minimum velocity of a wave, and the velocity of the wind when it is just sufficient to disturb the surface of still water.
Theory of Capillary Action
When two different fluids are placed in contact, they may either diffuse into each other or remain separate. In some cases diffusion takes place to a limited extent, after which the resulting mixtures do not mix with each other. The same substance may be able to exist in two different states at the same temperature and pressure, as when water and its saturated vapour are contained in the same vessel. The conditions under which the thermal and mechanical equilibrium of two fluids, two mixtures, or the same substance in two physical states in contact with each other, is possible belong to thermodynamics. All that we have to observe at present is that, in the cases in which the fluids do not mix of themselves, the potential energy of the system must be greater when the fluids are mixed than when they are separate.
It is found by experiment that it is only very close to the bounding surface of a liquid that the forces arising from the mutual action of its parts have any resultant effect on one of its particles. The experiments of Quincke and others seem to show that the extreme range of the forces which produce capillary action lies between a thousandth and a twenty-thousandth part of a millimetre.
We shall use the symbol to denote this extreme range, beyond which the action of these forces may be regarded as insensible. If denotes the potential energy of unit of mass of the substance, we may treat as sensibly constant except within a distance of the bounding surface of the fluid. In the interior of the fluid it has the uniform value . In like manner the density, , is sensibly equal to the constant quantity , which is its value in the interior of the liquid, except within a distance of the bounding surface. Hence if is the volume of a mass of liquid bounded by a surface whose area is , the integral
| (1) |
where the integration is to be extended throughout the volume , may be divided into two parts by considering separately the thin shell or skin extending from the outer surface to a depth , within which the density and other properties of the liquid vary with the depth, and the interior portion of the liquid within which its properties are constant.
Since is a line of insensible magnitude compared with the dimensions of the mass of liquid and the principal radii of curvature of its surface, the volume of the shell whose surface is and thickness will be , and that of the interior space will be .
If we suppose a normal less than to be drawn from the surface into the liquid, we may divide the shell into elementary shells whose thickness is , in each of which the density and other properties of the liquid will be constant.
The volume of one of these shells will be . Its mass will be . The mass of the whole shell will therefore be , and that of the interior part of the liquid . We thus find for the whole mass of the liquid
| (2) |
To find the potential energy we have to integrate
| (3) |
Substituting for in the process we have just gone through, we find
| (4) |
Multiplying equation (2) by , and subtracting it from (4),
| (5) |
In this expression and are both constant, so that the variation of the right-hand side of the equation is the same as that of the energy , and expresses that part of the energy which depends on the area of the bounding surface of the liquid. We may call this the surface energy.
The symbol expresses the energy of unit of mass of the liquid at a depth within the bounding surface. When the liquid is in contact with a rare medium, such as its own vapour or any other gas, is greater than , and the surface energy is positive. By the principle of the conservation of energy, any displacement of the liquid by which its energy is diminished will tend to take place of itself. Hence if the energy is the greater, the greater the area of the exposed surface, the liquid will tend to move in such a way as to diminish the area of the exposed surface, or, in other words, the exposed surface will tend to diminish if it can do so consistently with the other conditions. This tendency of the surface to contract itself is called the surface-tension of liquids.
Dupré has described an arrangement by which the surface-tension of a liquid film may be illustrated. A piece of sheet metal is cut out in the form AA (fig. 1). A very fine slip of metal is laid on it in the position BB, and the whole is dipped into a solution of soap, or M. Plateau’s glycerine mixture. When it is taken out the rectangle AACC if filled up by a liquid film. This film, however, tends to contract on itself, and the loose strip of metal BB will, if it is let go, be drawn up towards AA, provided it is sufficiently light and smooth.
Let be the surface energy per unit of area; then the energy of a surface of area will be . If, in the rectangle AACC, AA = , and AC = , its area is , and its energy . Hence if is the force by which the slip BB is pulled towards AA,
| (6) |
or the force arising from the surface-tension acting on a length a of the strip is Ta, so that T represents the surface-tension acting transversely on every unit of length of the periphery of the liquid surface. Hence if we write
| (7) |
we may define T either as the surface-energy per unit of area, or as the surface-tension per unit of contour, for the numerical values of these two quantities are equal.
If the liquid is bounded by a dense substance, whether liquid or solid, the value of χ may be different from its value when the liquid has a free surface. If the liquid is in contact with another liquid, let us distinguish quantities belonging to the two liquids by suffixes. We shall then have
| (8) |
| (9) |
Adding these expressions, and dividing the second member by S, we obtain for the tension of the surface of contact of the two liquids
| (10) |
If this quantity is positive, the surface of contact will tend to contract, and the liquids will remain distinct. If, however, it were negative, the displacement of the liquids which tends to enlarge the surface of contact would be aided by the molecular forces, so that the liquids, if not kept separate by gravity, would at length become thoroughly mixed. No instance, however, of a phenomenon of this kind has been discovered, for those liquids which mix of themselves do so by the process of diffusion, which is a molecular motion, and not by the spontaneous puckering and replication of the bounding surface as would be the case if T were negative.
It is probable, however, that there are many cases in which the integral belonging to the less dense fluid is negative. If the denser body be solid we can often demonstrate this; for the liquid tends to spread itself over the surface of the solid, so as to increase the area of the surface of contact, even although in so doing it is obliged to increase the free surface in opposition to the surface-tension. Thus water spreads itself out on a clean surface of glass. This shows that must be negative for water in contact with glass.
On the Tension of Liquid Films.—The method already given for the investigation of the surface-tension of a liquid, all whose dimensions are sensible, fails in the case of a liquid film such as a soap-bubble. In such a film it is possible that no part of the liquid may be so far from the surface as to have the potential and density corresponding to what we have called the interior of a liquid mass, and measurements of the tension of the film when drawn out to different degrees of thinness may possibly lead to an estimate of the range of the molecular forces, or at least of the depth within a liquid mass, at which its properties become sensibly uniform. We shall therefore indicate a method of investigating the tension of such films.
Let be the area of the film, its mass, and its energy; the mass, and the energy of unit of area; then
| (11) |
| (12) |
Let us now suppose that by some change in the form of the boundary of the film its area is changed from to . If its tension is the work required to effect this increase of surface will be , and the energy of the film will be increased by this amount. Hence
| (13) |
But since is constant,
| (14) |
Eliminating from equations (13) and (14), and dividing by , we find
| (15) |
In this expression denotes the mass of unit of area of the film, and the energy of unit of area.
If we take the axis of normal to either surface of the film, the radius of curvature of which we suppose to be very great compared with its thickness , and if is the density, and the energy of unit of mass at depth , then
| (16) |
and
| (17) |
Both and are functions of , the value of which remains the same when is substituted for . If the thickness of the film is greater than , there will be a stratum of thickness in the middle of the film, within which the values of and will be and . In the two strata on either side of this the law, according to which and depend on the depth, will be the same as in a liquid mass of large dimensions. Hence in this case
| (18) |
| (19) |
| (20) |
| (20) |
Hence the tension of a thick film is equal to the sum of the tensions of its two surfaces as already calculated (equation 7). On the hypothesis of uniform density we shall find that this is true for films whose thickness exceeds .
The symbol is defined as the energy of unit of mass of the substance. A knowledge of the absolute value of this energy is not required, since in every expression in which it occurs it is under the form , that is to say, the difference between the energy in two different states. The only cases, however, in which we have experimental values of this quantity are when the substance is either liquid and surrounded by similar liquid, or gaseous and surrounded by similar gas. It is impossible to make direct measurements of the properties of particles of the substance within the insensible distance ε of the bounding surface.
When a liquid is in thermal and dynamical equilibrium with its vapour, then if and are the values of and for the vapour, and and those for the liquid,
| (21) |
where is the dynamical equivalent of heat, is the latent heat of unit of mass of the vapour, and is the pressure. At points in the liquid very near its surface it is probable that is greater than , and at points in the gas very near the surface of the liquid it is probable that is less than , but this has not as yet been ascertained experimentally. We shall therefore endeavour to apply to this subject the methods used in Thermodynamics, and where these fail us we shall have recourse to the hypotheses of molecular physics.
We have next to determine the value of in terms of the action between one particle and another. Let us suppose that the force between two particles and at the distance is
| (22) |
being reckoned positive when the force is attractive. The actual force between the particles arises in part from their mutual gravitation, which is inversely as the square of the distance. This force is expressed by . It is easy to show that a force subject to this law would not account for capillary action. We shall, therefore, in what follows, consider only that part of the force which depends on , where is a function of which is insensible for all sensible values of , but which becomes sensible and even enormously great when is exceedingly small.
If we next introduce a new function of and write
| (23) |
then will represent—(1) The work done by the attractive force on the particle , while it is brought from an infinite distance from to the distance from ; or (2) The attraction of a particle on a narrow straight rod resolved in the direction of the length of the rod, one extremity of the rod being at a distance from , and the other at an infinite distance, the mass of unit of length of the rod being . The function is also insensible for sensible values of , but for insensible values of it may become sensible and even very great.
If we next write
| (24) |
then will represent—(1) The work done by the attractive force while a particle is brought from an infinite distance to a distance from an infinitely thin stratum of the substance whose mass per unit of area is ; (2) The attraction of a particle placed at a distance from the plane surface of an infinite solid whose density is .
Let us examine the case in which the particle is placed at a distance from a curved stratum of the substance, whose principal radii of curvature are and . Let (fig. 2) be the particle and a normal to the surface. Let the plane of the paper be a normal section of the surface of the stratum at the point , making an angle with the section whose radius of curvature is . Then if is the centre of curvature in the plane of the paper, and ,
| (25) |
Let ,
| (26) |
The element of the stratum at Q may be expressed by
or expressing in terms of by (26),
Multiplying this by and by , we obtain for the work done by the attraction of this element when is brought from an infinite distance to ,
Integrating with respect to from to , where a is a line very great compared with the extreme range of the molecular force, but very small compared with either of the radii of curvature, we obtain for the work
and since is an insensible quantity we may omit it. We may also write
since is very small compared with , and expressing in terms of by (25), we find
This then expresses the work done by the attractive forces when a particle is brought from an infinite distance to the point at a distance from a stratum whose surface-density is , and whose principal radii of curvature are and .
To find the work done when is brought to the point in the neighbourhood of a solid body, the density of which is a function of the depth below the surface, we have only to write instead of , and to integrate
where, in general, we must suppose a function of . This expression, when integrated, gives (1) the work done on a particle while it is brought from an infinite distance to the point , or (2) the attraction on a long slender column normal to the surface and terminating at , the mass of unit of length of the column being . In the form of the theory given by Laplace, the density of the liquid was supposed to be uniform. Hence if we write
the pressure of a column of the fluid itself terminating at the surface will be
and the work done by the attractive forces when a particle is brought to the surface of the fluid from an infinite distance will be
If we write
then will express the work done by the attractive forces, while a particle is brought from an infinite distance to a distance from the plane surface of a mass of the substance of density and infinitely thick. The function is insensible for all sensible values of . For insensible values it may become sensible, but it must remain finite even when , in which case .
If is the potential energy of unit of mass of the substance in vapour, then at a distance from the plane surface of the liquid
At the surface
At a distance within the surface
If the liquid forms a stratum of thickness c, then
The surface-density of this stratum is . The energy per unit of area is
Since the two sides of the stratum are similar the last two terms are equal, and
Differentiating with respect to , we find
Hence the surface-tension
Integrating the first term within brackets by parts, it becomes
Remembering that is a finite quantity, and that , we find
| (27) |
When is greater than this is equivalent to in the equation of Laplace. Hence the tension is the same for all films thicker than , the range of the molecular forces. For thinner films
Hence if is positive, the tension and the thickness will increase together. Now represents the attraction between a particle and the plane surface of an infinite mass of the liquid, when the distance of the particle outside the surface is . Now, the force between the particle and the liquid is certainly, on the whole, attractive; but if between any two small values of it should be repulsive, then for films whose thickness lies between these values the tension will increase as the thickness diminishes, but for all other cases the tension will diminish as the thickness diminishes.
We have given several examples in which the density is assumed to be uniform, because Poisson has asserted that capillary phenomena would not take place unless the density varied rapidly near the surface. In this assertion we think he was mathematically wrong, though in his own hypothesis that the density does actually vary, he was probably right. In fact, the quantity , which we may call with van der Waals the molecular pressure, is so great for most liquids (5000 atmospheres for water), that in the parts near the surface, where the molecular pressure varies rapidly, we may expect considerable variation of density, even when we take into account the smallness of the compressibility of liquids.
The pressure at any point of the liquid arises from two causes, the external pressure P to which the liquid is subjected, and the pressure arising from the mutual attraction of its molecules. If we suppose that the number of molecules within the range of the attraction of a given molecule is very large, the part of the pressure arising from attraction will be proportional to the square of the number of molecules in unit of volume, that is, to the square of the density. Hence we may write
where is a constant [equal to Laplace’s intrinsic pressure . But this equation is applicable only at points in the interior, where is not varying.]
[The intrinsic pressure and the surface-tension of a uniform mass are perhaps more easily found by the following process. The former can be found at once by calculating the mutual attraction of the parts of a large mass which lie on opposite sides of an imaginary plane interface. If the density be , the attraction between the whole of one side and a layer upon the other distant from the plane and of thickness is , reckoned per unit of area. The expression for the intrinsic pressure is thus simply
| (28) |
In Laplace’s investigation is supposed to be unity. We may call the value which (28) then assumes K0, so that as above
| (29) |
The expression for the superficial tension is most readily found with the aid of the idea of superficial energy, introduced into the subject by Gauss. Since the tension is constant, the work that must be done to extend the surface by one unit of area measures the tension, and the work required for the generation of any surface is the product of the tension and the area. From this consideration we may derive Laplace’s expression, as has been done by Dupre (Théorie mécanique de la chaleur, Paris, 1869), and Kelvin ("Capillary Attraction," Proc. Roy. Inst., January 1886. Reprinted, Popular Lectures and Addresses, 1889). For imagine a small cavity to be formed in the interior of the mass and to be gradually expanded in such a shape that the walls consist almost entirely of two parallel planes. The distance between the planes is supposed to be very small compared with their ultimate diameters, but at the same time large enough to exceed the range of the attractive forces. The work required to produce this crevasse is twice the product of the tension and the area of one of the faces. If we now suppose the crevasse produced by direct separation of its walls, the work necessary must be the same as before, the initial and final configurations being identical; and we recognize that the tension may be measured by half the work that must be done per unit of area against the mutual attraction in order to separate the two portions which lie upon opposite sides of an ideal plane to a distance from one another which is outside the range of the forces. It only remains to calculate this work.
If , represent the densities of the two infinite solids, their mutual attraction at distance z is per unit of area
| (30) |
or , if we write
| (31) |
The work required to produce the separation in question is thus
| (32) |
and for the tension of a liquid of density we have
| (33) |
The form of this expression may be modified by integration by parts. For
Since is finite, proportional to , the integrated term vanishes at both limits, and we have simply
| (34) |
and
| (35) |
In Laplace's notation the second member of (34), multiplied by , is represented by .
As Laplace has shown, the values for and may also be expressed in terms of the function , with which we started. Integrating by parts, we get
In all cases to which it is necessary to have regard the integrated terms vanish at both limits, and we may write
| (36) |
so that
| (37) |
A few examples of these formulae will promote an intelligent comprehension of the subject. One of the simplest suppositions open to us is that
| (38) |
From this we obtain
| (39) |
| (40) |
The range of the attractive force is mathematically infinite, but practically of the order , and we see that is of higher order in this small quantity than . That is in all cases of the fourth order and of the fifth order in the range of the forces is obvious from (37) without integration.
An apparently simple example would be to suppose . We get
| (41) |
The intrinsic pressure will thus be infinite whatever n may be. If be positive, the attraction of infinitely distant parts contributes to the result; while if be negative, the parts in immediate contiguity act with infinite power. For the transition case, discussed by William Sutherland (Phil. Mag. xxiv. p. 113, 1887), of , is also infinite. It seems therefore that nothing satisfactory can be arrived at under this head.
As a third example, we will take the law proposed by Young, viz.
| (42) |
and corresponding therewith,
| (43) |
| (44) |
Equations (37) now give
| (45) |
| (46) |
The numerical results differ from those of Young, who finds that "the contractile force is one-third of the whole cohesive force of a stratum of particles, equal in thickness to the interval to which the primitive equable cohesion extends," viz. ; whereas according to the above calculation . The discrepancy seems to depend upon Young having treated the attractive force as operative in one direction only. For further calculations on Laplace’s principles, see Rayleigh, Phil. Mag., Oct. Dec. 1890, or Scientific Papers, vol. iii. p. 397.]
On Surface-Tension
Definition.—The tension of a liquid surface across any line drawn on the surface is normal to the line, and is the same for all directions of the line, and is measured by the force across an element of the line divided by the length of that element.
Experimental Laws of Surface-Tension.—1. For any given liquid surface, as the surface which separates water from air, or oil from water, the surface-tension is the same at every point of the surface and in every direction. It is also practically independent of the curvature of the surface, although it appears from the mathematical theory that there is a slight increase of tension where the mean curvature of the surface is concave, and a slight diminution where it is convex. The amount of this increase and diminution is too small to be directly measured, though it has a certain theoretical importance in the explanation of the equilibrium of the superficial layer of the liquid where it is inclined to the horizon.
2. The surface-tension diminishes as the temperature rises, and when the temperature reaches that of the critical point at which the distinction between the liquid and its vapour ceases, it has been observed by Andrews that the capillary action also vanishes. The early writers on capillary action supposed that the diminution of capillary action was due simply to the change of density corresponding to the rise of temperature, and, therefore, assuming the surface-tension to vary as the square of the density, they deduced its variations from the observed dilatation of the liquid by heat. This assumption, however, does not appear to be verified by the experiments of Brunner and Wolff on the rise of water in tubes at different temperatures.
3. The tension of the surface separating two liquids which do not mix cannot be deduced by any known method from the tensions of the surfaces of the liquids when separately in contact with air.
When the surface is curved, the effect of the surface-tension is to make the pressure on the concave side exceed the pressure on the convex side by , where is the intensity of the surface-tension and , are the radii of curvature of any two sections normal to the surface and to each other.
If three fluids which do not mix are in contact with each other, the three surfaces of separation meet in a line, straight or curved. Let (fig. 3) be a point in this line, and let the plane of the paper be supposed to be normal to the line at the point . 
Fig. 3.The three angles between the tangent planes to the three surfaces of separation at the point are completely determined by the tensions of the three surfaces. For if in the triangle the side is taken so as to represent on a given scale the tension of the surface of contact of the fluids and , and if the other sides and are taken so as to represent on the same scale the tensions of the surfaces between and and between and respectively, then the condition of equilibrium at for the corresponding tensions , and is that the angle shall be the supplement of , of , and, therefore, of . Thus the angles at which the surfaces of separation meet are the same at all parts of the line of concourse of the three fluids. When three films of the same liquid meet, their tensions are equal, and, therefore, they make angles of 120° with each other. The froth of soap-suds or beaten-up eggs consists of a multitude of small films which meet each other at angles of 120°.
If four fluids, , , , , meet in a point , and if a tetrahedron is formed so that its edge represents the tension of the surface of contact of the liquids and , that of and , and so on; then if we place this tetrahedron so that the face is normal to the tangent at to the line of concourse of the fluids , and turn it so that the edge is normal to the tangent plane at to the surface of contact of the fluids and , then the other three faces of the tetrahedron will be normal to the tangents at to the other three lines of concourse of the liquids, and the other five edges of the tetrahedron will be normal to the tangent planes at to the other five surfaces of contact.
If six films of the same liquid meet in a point the corresponding tetrahedron is a regular tetrahedron, and each film, where it meets the others, has an angle whose cosine is . Hence if we take two nets of wire with hexagonal meshes, and place one on the other so that the point of concourse of three hexagons of one net coincides with the middle of a hexagon of the other, and if we then, after dipping them in Plateau’s liquid, place them horizontally, and gently raise the upper one, we shall develop a system of plane laminae arranged as the walls and floors of the cells are arranged in a honeycomb. We must not, however, raise the upper net too much, or the system of films will become unstable.
When a drop of one liquid, , is placed on the surface of another, , the phenomena which take place depend on the relative magnitude of the three surface-tensions corresponding to the surface between and air, between and air, and between and . If no one of these tensions is greater than the sum of the other two, the drop will assume the form of a lens, the angles which the upper and lower surfaces of the lens make with the free surface of and with each other being equal to the external angles of the triangle of forces. Such lenses are often seen formed by drops of fat floating on the surface of hot water, soup or gravy. But when the surface-tension of exceeds the sum of the tensions of the surfaces of contact of with air and with , it is impossible to construct the triangle of forces; so that equilibrium becomes impossible. The edge of the drop is drawn out by the surface-tension of with a force greater than the sum of the tensions of the two surfaces of the drop. The drop, therefore, spreads itself out, with great velocity, over the surface of till it covers an enormous area, and is reduced to such extreme tenuity that it is not probable that it retains the same properties of surface-tension which it has in a large mass. Thus a drop of train oil will spread itself over the surface of the sea till it shows the colours of thin plates. These rapidly descend in Newton’s scale and at last disappear, showing that the thickness of the film is less than the tenth part of the length of a wave of light. But even when thus attenuated, the film may be proved to be present, since the surface-tension of the liquid is considerably less than that of pure water. This may be shown by placing another drop of oil on the surface. This drop will not spread out like the first drop, but will take the form of a flat lens with a distinct circular edge, showing that the surface-tension of what is still apparently pure water is now less than the sum of the tensions of the surfaces separating oil from air and water.
The spreading of drops on the surface of a liquid has formed the subject of a very extensive series of experiments by Charles Tomlinson; van der Mensbrugghe has also written a very complete memoir on this subject (Sur la tension superficielle des liquides, Bruxelles, 1873).
When a solid body is in contact with two fluids, the surface of the solid cannot alter its form, but the angle at which the surface of contact of the two fluids meets the surface of the solid depends on the values of the three surface-tensions. If and are the two fluids and the solid then the 
Fig. 4.equilibrium of the tensions at the point depends only on that of thin components parallel to the surface, because the surface-tensions normal to the surface are balanced by the resistance of the solid. Hence if the angle (fig. 4) at which the surface of contact meets the solid is denoted by ,
Whence
As an experiment on the angle of contact only gives us the difference of the surface-tensions at the solid surface, we cannot determine their actual value. It is theoretically probable that they are often negative, and may be called surface-pressures.
The constancy of the angle of contact between the surface of a fluid and a solid was first pointed out by Dr Young, who states that the angle of contact between mercury and glass is about 140°. Quincke makes it 128° 52′.
If the tension of the surface between the solid and one of the fluids exceeds the sum of the other two tensions, the point of contact will not be in equilibrium, but will be dragged towards the side on which the tension is greatest. If the quantity of the first fluid is small it will stand in a drop on the surface of the solid without wetting it. If the quantity of the second fluid is small it will spread itself over the surface and wet the solid. The angle of contact of the first fluid is 180° and that of the second is zero.
If a drop of alcohol be made to touch one side of a drop of oil on a glass plate, the alcohol will appear to chase the oil over the plate, and if a drop of water and a drop of bisulphide of carbon be placed in contact in a horizontal capillary tube, the bisulphide of carbon will chase the water along the tube. In both cases the liquids move in the direction in which the surface-pressure at the solid is least.
[In order to express the dependence of the tension at the interface of two bodies in terms of the forces exercised by the bodies upon themselves and upon one another, we cannot do better than follow the method of Dupré. If denote the interfacial tension, the energy corresponding to unit of area of the interface is also , as we see by considering the introduction (through a fine tube) of one body into the interior of the other. A comparison with another method of generating the interface, similar to that previously employed when but one body was in question, will now allow us to evaluate .
The work required to cleave asunder the parts of the first fluid which lie on the two sides of an ideal plane passing through the interior, is per unit of area , and the free surface produced is two units in area. So for the second fluid the corresponding work is . This having been effected, let us now suppose that each of the units of area of free surface of fluid (1) is allowed to approach normally a unit area of (2) until contact is established. In this process work is gained which we may denote by for each pair. On the whole, then, the work expended in producing two units of interface is , and this, as we have seen, may be equated to . Hence
| (47) |
If the two bodies are similar,
and , as it should do.
Laplace does not treat systematically the question of interfacial tension, but he gives incidentally in terms of his quantity H a relation analogous to (47).
If , would be negative, so that the interface would of itself tend to increase. In this case the fluids must mix. Conversely, if two fluids mix, it would seem that must exceed the mean of and ; otherwise work would have to be expended to effect a close alternate stratification of the two bodies, such as we may suppose to constitute a first step in the process of mixture (Dupré, Théorie mécanique de la chaleur, p. 372; Kelvin, Popular Lectures, p. 53).
The value of has already been calculated (32). We may write
| (48) |
and in general the functions , or , must be regarded as capable of assuming different forms. Under these circumstances there is no limitation upon the values of the interfacial tensions for three fluids, which we may denote by , , . If the three fluids can remain in contact with one another, the sum of any two of the quantities must exceed the third, and by Neumann’s rule the directions of the interfaces at the common edge must be parallel to the sides of a triangle, taken proportional to , , . If the above-mentioned condition be not satisfied, the triangle is imaginary, and the three fluids cannot rest in contact, the two weaker tensions, even if acting in full concert, being incapable of balancing the strongest. For instance, if , the second fluid spreads itself indefinitely upon the interface of the first and third fluids.
The experimenters who have dealt with this question, C. G. M. Marangoni, van der Mensbrugghe, Quincke, have all arrived at results inconsistent with the reality of Neumann’s triangle. Thus Marangoni says (Pogg. Annalen, cxliii. p. 348, 1871):—“Die gemeinschaftliche Oberfläche zweier Flüssigkeiten hat eine geringere Oberflächenspannung als die Differenz der Oberflächenspannung der Flüssigkeiten selbst (mit Ausnahme des Quecksilbers).” Three pure bodies (of which one may be air) cannot accordingly remain in contact. If a drop of oil stands in lenticular form upon a surface of water, it is because the water-surface is already contaminated with a greasy film.
On the theoretical side the question is open until we introduce some limitation upon the generality of the functions. By far the simplest supposition open to us is that the functions are the same in all cases, the attractions differing merely by coefficients analogous to densities in the theory of gravitation. This hypothesis was suggested by Laplace, and may conveniently be named after him. It was also tacitly adopted by Young, in connexion with the still more special hypothesis which Young probably had in view, namely that the force in each case was constant within a limited range, the same in all cases, and vanished outside that range.
As an immediate consequence of this hypothesis we have from (28)
| (49) |
| (50) |
where , are the same for all bodies.
But the most interesting results are those which Young (Works, vol. i. p. 463) deduced relative to the interfacial tensions of three bodies. By (37), (48),
| (51) |
so that by (47), (50),
| (52) |
According to (52), the interfacial tension between any two bodies is proportional to the square of the difference of their densities. The densities , , being in descending order of magnitude, we may write
so that necessarily exceeds the sum of the other two interfacial tensions. We are thus led to the important conclusion that according to this hypothesis Neumann’s triangle is necessarily imaginary, that one of three fluids will always spread upon the interface of the other two.
Another point of importance may be easily illustrated by this theory, viz. the dependency of capillarity upon abruptness of transition. “The reason why the capillary force should disappear when the transition between two liquids is sufficiently gradual will now be evident. Suppose that the transition from to is made in two equal steps, the thickness of the intermediate layer of density being large compared to the range of the molecular forces, but small in comparison with the radius of curvature. At each step the difference of capillary pressure is only one-quarter of that due to the sudden transition from to , and thus altogether half the effect is lost by the interposition of the layer. If there were three equal steps, the effect would be reduced to one-third, and so on. When the number of steps is infinite, the capillary pressure disappears altogether.” (“Laplace’s Theory of Capillarity,” Rayleigh, Phil. Mag., 1883, p. 315.)
According to Laplace’s hypothesis the whole energy of any number of contiguous strata of liquids is least when they are arranged in order of density, so that this is the disposition favoured by the attractive forces. The problem is to make the sum of the interfacial tensions a minimum, each tension being proportional to the square of the difference of densities of the two contiguous liquids in question. If the order of stratification differ from that of densities, we can show that each step of approximation to this order lowers the sum of tensions. To this end consider the effect of the abolition of a stratum , contiguous to and . Before the change we have , and afterwards (. The second minus the first, or the increase in the sum of tensions, is thus
Hence, if be intermediate in magnitude between and , the sum of tensions is increased by the abolition of the stratum; but, if be not intermediate, the sum is decreased. We see, then, that the removal of a stratum from between neighbours where it is out of order and its introduction between neighbours where it will be in order is doubly favourable to the reduction of the sum of tensions; and since by a succession of such steps we may arrive at the order of magnitude throughout, we conclude that this is the disposition of minimum tensions and energy.
So far the results of Laplace’s hypothesis are in marked accordance with experiment; but if we follow it out further, discordances begin to manifest themselves. According to (52)
| (53) |
a relation not verified by experiment. What is more, (52) shows that according to the hypothesis is necessarily positive; so that, if the preceding argument be correct, no such thing as mixture of two liquids could ever take place.
There are two apparent exceptions to Marangoni’s rule which call for a word of explanation. According to the rule, water, which has the lower surface-tension, should spread upon the surface of mercury; whereas the universal experience of the laboratory is that drops of water standing upon mercury retain their compact form without the least tendency to spread. To Quincke belongs the credit of dissipating the apparent exception. He found that mercury specially prepared behaves quite differently from ordinary mercury, and that a drop of water deposited thereon spreads over the entire surface. The ordinary behaviour is evidently the result of a film of grease, which adheres with great obstinacy.
The process described by Quincke is somewhat elaborate; but there is little difficulty in repeating the experiment if the mistake be avoided of using a free surface already contaminated, as almost inevitably happens when the mercury is poured from an ordinary bottle. The mercury should be drawn from underneath, for which purpose an arrangement similar to a chemical wash bottle is suitable, and it may be poured into watch-glasses, previously dipped into strong sulphuric acid, rinsed in distilled water, and dried over a Bunsen flame. When the glasses are cool, they may be charged with mercury, of which the first part is rejected. Operating in this way there is no difficulty in obtaining surfaces upon which a drop of water spreads, although from causes that cannot always be traced, a certain proportion of failures is met with. As might be expected, the grease which produces these effects is largely volatile. In many cases a very moderate preliminary warming of the watch-glasses makes all the difference in the behaviour of the drop.
The behaviour of a drop of carbon bisulphide placed upon clean water is also, at first sight, an exception to Marangoni’s rule. So far from spreading over the surface, as according to its lower surface-tension it ought to do, it remains suspended in the form of a lens. Any dust that may be lying upon the surface is not driven away to the edge of the drop, as would happen in the case of oil. A simple modification of the experiment suffices, however, to clear up the difficulty. If after the deposition of the drop, a little lycopodium be scattered over the surface, it is seen that a circular space surrounding the drop, of about the size of a shilling, remains bare, and this, however often the dusting be repeated, so long as any of the carbon bisulphide remains. The interpretation can hardly be doubtful. The carbon bisulphide is really spreading all the while, but on account of its volatility is unable to reach any considerable distance. Immediately surrounding the drop there is a film moving outwards at a high speed, and this carries away almost instantaneously any dust that may fall upon it. The phenomenon above described requires that the water-surface be clean. If a very little grease be present, there is no outward flow and dust remains undisturbed in the immediate neighbourhood of the drop.]
On the Rise of a Liquid in a Tube.—Let a tube (fig. 6) whose internal radius is , made of a solid substance , be dipped into a liquid . Let us suppose that the angle of contact for this liquid with the solid is an acute angle. This implies that the tension of the free surface of the solid is greater than that of the surface of contact of the solid with the liquid . Now consider the tension of the free surface of the liquid . All round its edge there is a tension acting at an angle with the vertical. The circumference of the edge is , so that the resultant of this tension is a force acting vertically upwards on the liquid. Hence the liquid will rise in the tube till the weight of the vertical column between the free surface and the level of the liquid in the vessel balances the resultant of the surface-tension. The upper surface of this column is not level, so that the height of the column cannot be directly measured, but let us assume that is the mean height of the column, that is to say, the height of a column of equal weight, but with a flat top. Then if is the radius of the tube at the top of the column, the volume of the suspended column is , and its weight is , when is its density and the intensity of gravity. Equating this force with the resultant of the tension
or
Hence the mean height to which the fluid rises is inversely as the radius of the tube. For water in a clean glass tube the angle of contact is zero, and
For mercury in a glass tube the angle of contact is 128° 52′, the cosine of which is negative. Hence when a glass tube is dipped into a vessel of mercury, the mercury within the tube stands at a lower level than outside it.
Rise of a Liquid between Two Plates.—When two parallel plates are placed vertically in a liquid the liquid rises between them. If we now suppose fig. 6 to represent a vertical section perpendicular to the plates, we may calculate the rise of the liquid. Let be the breadth of the plates measured perpendicularly to the plane of the paper, then the length of the line which bounds the wet and the dry parts of the plates inside is for each surface, and on this the tension acts at an angle to the vertical. Hence the resultant of the surface-tension is . If the distance between the inner surfaces of the plates is a, and if the mean height of the film of fluid which rises between them is , the weight of fluid raised is . Equating the forces—
whence
This expression is the same as that for the rise of a liquid in a tube, except that instead of , the radius of the tube, we have a the distance of the plates.
Form of the Capillary Surface.—The form of the surface of a liquid acted on by gravity is easily determined if we assume that near the part considered the line of contact of the surface of the liquid with that of the solid bounding it is straight and horizontal, as it is when the solids which constrain the liquid are bounded by surfaces formed by horizontal and parallel generating lines. This will be the case, for instance, near a flat plate dipped into the liquid. If we suppose these generating lines to be normal to the plane of the paper, then all sections of the solids parallel to this plane will be equal and similar to each other, and the section of the surface of the liquid will be of the same form for all such sections.
Let us consider the portion of the liquid between two parallel sections distant one unit of length. Let , (fig. 7) be two points of the surface; , the inclination of the surface to the horizon at and ; , the heights of and above the level of the liquid at a distance from all solid bodies. The pressure at any point of the liquid which is above this level is negative unless another fluid as, for instance, the air, presses on the upper surface, but it is only the difference of pressures with which we have to do, because two equal pressures on opposite sides of the surface produce no effect.
We may, therefore, write for the pressure at a height
The forces acting on the portion of liquid are—first, the horizontal pressures, and ; second, the surface-tension acting at and in directions inclined and to the horizon. Resolving horizontally we find—
whence
or if we suppose fixed and variable, we may write
This equation gives a relation between the inclination of the curve to the horizon and the height above the level of the liquid.
Resolving vertically we find that the weight of the liquid raised above the level must be equal to , and this is therefore equal to the area multiplied by . The form of the capillary surface is identical with that of the “elastic curve,” or the curve formed by a uniform spring originally straight, when its ends are acted on by equal and opposite forces applied either to the ends themselves or to solid pieces attached to them. Drawings of the different forms of the curve may be found in Thomson and Tait’s Natural Philosophy, vol. i. p. 455.
We shall next consider the rise of a liquid between two plates of different materials for which the angles of contact are and , the distance between the plates being , a small quantity. Since the plates are very near one another we may use the following equation of the surface as an approximation:—
whence
whence we obtain
Let be the force which must be applied in a horizontal direction to either plate to keep it from approaching the other, then the forces acting on the first plate are in the negative direction, and in the positive direction. Hence
For the second plate
Hence
or, substituting the values of and ,
the remaining terms being negligible when is small. The force, therefore, with which the two plates are drawn together consists first of a positive part, or in other words an attraction, varying inversely as the square of the distance, and second, of a negative part of repulsion independent of the distance. Hence in all cases except that in which the angles and are supplementary to each other, the force is attractive when is small enough, but when and are of different signs, as when the liquid is raised by one plate, and depressed by the other, the first term may be so small that the repulsion indicated by the second term comes into play. The fact that a pair of plates which repel one another at a certain distance may attract one another at a smaller distance was deduced by Laplace from theory, and verified by the observations of the abbé Haüy.
A Drop between Two Plates.—If a small quantity of a liquid which wets glass be introduced between two glass plates slightly inclined to each other, it will run towards that part where the glass plates are nearest together. When the liquid is in equilibrium it forms a thin film, the outer edge of which is all of the same thickness. If is the distance between the plates at the edge of the film and the atmospheric pressure, the pressure of the liquid in the film is , and if is the area of the film between the plates and its circumference, the plates will be pressed together with a force
and this, whether the atmosphere exerts any pressure or not. The force thus produced by the introduction of a drop of water between two plates is enormous, and is often sufficient to press certain parts of the plates together so powerfully as to bruise them or break them. When two blocks of ice are placed loosely together so that the superfluous water which melts from them may drain away, the remaining water draws the blocks together with a force sufficient to cause the blocks to adhere by the process called Regelation.
[An effect of an opposite character may be observed when the fluid is mercury in place of water. When two pieces of flat glass are pressed together under mercury with moderate force they cohere, the mercury leaving the narrow crevasses, even although the alternative is a vacuum. The course of events is more easily followed if one of the pieces of glass constitutes the bottom, or a side, of the vessel containing the mercury.]
In many experiments bodies are floated on the surface of water in order that they may be free to move under the action of slight horizontal forces. Thus Sir Isaac Newton placed a magnet in a floating vessel and a piece of iron in another in order to observe their mutual action, and A. M. Ampère floated a voltaic battery with a coil of wire in its circuit in order to observe the effects of the earth’s magnetism on the electric circuit. When such floating bodies come near the edge of the vessel they are drawn up to it, and are apt to stick fast to it. There are two ways of avoiding this inconvenience. One is to grease the float round its water-line so that the water is depressed round it. This, however, often produces a worse disturbing effect, because a thin film of grease spreads over the water and increases its surface-viscosity. The other method is to fill the vessel with water till the level of the water stands a little higher than the rim of the vessel. The float will then be repelled from the edge of the vessel. Such floats, however, should always be made so that the section taken at the level of the water is as small as possible.
[The Size of Drops.—The relation between the diameter of a tube and the weight of the drop which it delivers appears to have been first investigated by Thomas Tate (Phil. Mag. vol. xxvii. p. 176, 1864), whose experiments led him to the conclusion that “other things being the same, the weight of a drop of liquid is proportional to the diameter of the tube in which it is formed.” Sufficient time must of course be allowed for the formation of the drops; otherwise no simple results can be expected. In Tate’s experiments the period was never less than 40 seconds.
The magnitude of a drop delivered from a tube, even when the formation up to the phase of instability is infinitely slow, cannot be calculated a priori. The weight is sometimes equated to the product of the capillary tension () and the circumference of the tube (), but with little justification. Even if the tension at the circumference of the tube acted vertically, and the whole of the liquid below this level passed into the drop, the calculation would still be vitiated by the assumption that the internal pressure at the level in question is atmospheric. It would be necessary to consider the curvatures of the fluid surface at the edge of attachment. If the surface could be treated as a cylindrical prolongation of the tube (radius ), the pressure would be , and the resulting force acting downwards upon the drop would amount to one-half () of the direct upward pull of the tension along the circumference. At this rate the drop would be but one-half of that above reckoned. But the truth is that a complete solution of the statical problem for all forms up to that at which instability sets in, would not suffice for the present purpose. The detachment of the drop is a dynamical effect, and it is influenced by collateral circumstances. For example, the bore of the tube is no longer a matter of indifference, even though the attachment of the drop occurs entirely at the outer edge. It appears that when the external diameter exceeds a certain value, the weight of a drop of water is sensibly different in the two extreme cases of a very small and of a very large bore.
But although a complete solution of the dynamical problem is impracticable, much interesting information may be obtained from the principle of dynamical similarity. The argument has already been applied by Dupré (Théorie mécanique de la chaleur, Paris, 1869, p. 328), but his presentation of it is rather obscure. We will assume that when, as in most cases, viscosity may be neglected, the mass () of a drop depends only upon the density (), the capillary tension (), the acceleration of gravity (), and the linear dimension of the tube (). In order to justify this assumption, the formation of the drop must be sufficiently slow, and certain restrictions must be imposed upon the shape of the tube. For example, in the case of water delivered from a glass tube, which is cut off square and held vertically, a will be the external radius; and it will be necessary to suppose that the ratio of the internal radius to a is constant, the cases of a ratio infinitely small, or infinitely near unity, being included. But if the fluid be mercury, the flat end of the tube remains unwetted, and the formation of the drop depends upon the internal diameter only.
The “dimensions” of the quantities on which depends are:—
of which , a mass, is to be expressed as a function. If we assume
we have, considering in turn length, time and mass,
so that
Accordingly
Since is undetermined, all that we can conclude is that is of the form
| (1) |
where denotes an arbitrary function.
Dynamical similarity requires that be constant; or, if be supposed to be so, that varies as . If this condition be satisfied, the mass (or weight) of the drop is proportional to and to .
If Tate’s law be true, that ceteris paribus varies as , it follows from (1) that is constant. For all fluids and for all similar tubes similarly wetted, the weight of a drop would then be proportional not only to the diameter of the tube, but also to the superficial tension, and it would be independent of the density.
Careful observations with special precautions to ensure the cleanliness of the water have shown that over a considerable range, the departure from Tate’s law is not great. The results give material for the determination of the function in (1).
| 2.58 | 4.13 |
| 1.16 | 3.97 |
| 0.708 | 3.80 |
| 0.441 | 3.73 |
| 0.277 | 3.78 |
| 0.220 | 3.90 |
| 0.169 | 4.06 |
In the preceding table, applicable to thin-walled tubes, the first column gives the values of , and the second column those of , all the quantities concerned being in C.G.S. measure, or other consistent system. From this the weight of a drop of any liquid of which the density and surface tension are known, can be calculated. For many purposes it may suffice to treat as a constant, say 3.8. The formula for the weight of a drop is then simply
| (2) |
in which 3.8 replaces the of the faulty theory alluded to earlier (see Rayleigh, Phil. Mag., Oct. 1899).]
Phenomena arising from the Variation of the Surface-tension.—Pure water has a higher surface-tension than that of any other substance liquid at ordinary temperatures except mercury. Hence any other liquid if mixed with water diminishes its surface-tension. For example, if a drop of alcohol be placed on the surface of water, the surface-tension will be diminished from 80, the value for pure water, to 25, the value for pure alcohol. The surface of the liquid will therefore no longer be in equilibrium, and a current will be formed at and near the surface from the alcohol to the surrounding water, and this current will go on as long as there is more alcohol at one part of the surface than at another. If the vessel is deep, these currents will be balanced by counter currents below them, but if the depth of the water is only two or three millimetres, the surface-current will sweep away the whole of the water, leaving a dry spot where the alcohol was dropped in. This phenomenon was first described and explained by James Thomson, who also explained a phenomenon, the converse of this, called the “tears of strong wine.”
If a wine-glass be half-filled with port wine the liquid rises a little up the side of the glass as other liquids do. The wine, however, contains alcohol and water, both of which evaporate, but the alcohol faster than the water, so that the superficial layer becomes more watery. In the middle of the vessel the superficial layer recovers its strength by diffusion from below, but the film adhering to the side of the glass becomes more watery, and therefore has a higher surface-tension than the surface of the stronger wine. It therefore creeps up the side of the glass dragging the strong wine after it, and this goes on till the quantity of fluid dragged up collects into a drop and runs down the side of the glass.
The motion of small pieces of camphor floating on water arises from the gradual solution of the camphor. If this takes place more rapidly on one side of the piece of camphor than on the other side, the surface-tension becomes weaker where there is most camphor in solution, and the lump, being pulled unequally by the surface-tensions, moves off in the direction of the strongest tension, namely, towards the side on which least camphor is dissolved.
If a drop of ether is held near the surface of water the vapour of ether condenses on the surface of the water, and surface-currents are formed flowing in every direction away from under the drop of ether.
If we place a small floating body in a shallow vessel of water and wet one side of it with alcohol or ether, it will move off with great velocity and skim about on the surface of the water, the part wet with alcohol being always the stern.
The surface-tension of mercury is greatly altered by slight changes in the state of the surface. The surface-tension of pure mercury is so great that it is very difficult to keep it clean, for every kind of oil or grease spreads over it at once.
But the most remarkable effects of change of surface-tension are those produced by what is called the electric polarization of the surface. The tension of the surface of contact of mercury and dilute sulphuric acid depends on the electromotive force acting between the mercury and the acid. If the electromotive force is from the acid to the mercury the surface-tension increases; if it is from the mercury to the acid, it diminishes. Faraday observed that a large drop of mercury, resting on the flat bottom of a vessel containing dilute acid, changes its form in a remarkable way when connected with one of the electrodes of a battery, the other electrode being placed in the acid. When the mercury is made positive it becomes dull and spreads itself out; when it is made negative it gathers itself together and becomes bright again. G. Lippmann, who has made a careful investigation of the subject, finds that exceedingly small variations of the electromotive force produce sensible changes in the surface-tension. The effect of one of a Daniell’s cell is to increase the tension from 30.4 to 40.6. He has constructed a capillary electrometer by which differences of electric potential less than 0.01 of that of a Daniell’s cell can be detected by the difference of the pressure required to force the mercury to a given point of a fine capillary tube. He has also constructed an apparatus in which this variation in the surface-tension is made to do work and drive a machine. He has also found that this action is reversible, for when the area of the surface of contact of the acid and mercury is made to increase, an electric current passes from the mercury to the acid, the amount of electricity which passes while the surface increases by one square centimetre being sufficient to decompose .000013 gramme of water.
[The movements of camphor scrapings referred to above afford a useful test of the condition of a water surface. If the contamination exceed a certain limit, the scrapings remain quite dead. In a striking form of the experiment, the water is contained, to the depth of perhaps one inch, in a large flat dish, and the operative part of the surface is limited by a flexible hoop of thin sheet brass lying in the dish and rising above the water-level. If the hoop enclose an area of (say) one-third of the maximum, and if the water be clean, camphor fragments floating on the interior enter with vigorous movements. A touch of the finger will then often reduce them to quiet; but if the hoop be expanded, the included grease is so far attenuated as to lose its effect. Another method of removing grease is to immerse and remove strips of paper by which the surface available for the contamination is in effect increased.
The thickness of the film of oil adequate to check the camphor movements can be determined with fair accuracy by depositing a weighed amount of oil (such as .8 mg.) upon the surface of water in a large bath. Calculated as if the density were the same as in a normal state, the thickness of the film is found to be about two millionths of a millimetre.
Small as is the above amount of oil, the camphor test is a comparatively coarse one. Conditions of a contaminated surface may easily be distinguished, upon all of which camphor fragments spin vigorously. Thus, a shallow tin vessel, such as the lid of a biscuit box, may be levelled and filled with tap-water through a rubber hose. Upon the surface of the water a little sulphur is dusted. An application of the finger for 20 or 30 seconds to the under surface of the vessel will then generate enough heat to lower appreciably the surface-tension, as is evidenced by the opening out of the dust and the formation of a bare spot perhaps 1½ in. in diameter. When, however, the surface is but very slightly greased, a spot can no longer be cleared by the warmth of the finger, or even of a spirit lamp, held underneath. And yet the greasing may be so slight that camphor fragments move with apparently unabated vigour.
The varying degrees of contamination to which a water surface is subject are the cause of many curious phenomena. Among these is the superficial viscosity of Plateau. In his experiments a long compass needle is mounted so as to swing in the surface of the liquid under investigation. The cases of ordinary clean water and alcohol are strongly contrasted, the motion of the needle upon the former being comparatively sluggish. Moreover, a different behaviour is observed when the surfaces are slightly dusted over. In the case of water the whole of the surface in front of the needle moves with it, while on the other hand the dust floating on alcohol is scarcely disturbed until the needle actually strikes it. Plateau attributed these differences to a special quality of the liquids, named by him “superficial viscosity.” It has been proved, however, that the question is one of contamination, and that a water surface may be prepared so as to behave in the same manner as alcohol.
Another consequence of the tendency of a moderate contamination to distribute itself uniformly is the calming effect of oil, investigated by B. Franklin. On pure water the propagation of waves would be attended by temporary extensions and contractions of the surface, but these, as was shown by O. Reynolds, are resisted when the surface is contaminated.
Indeed the possibility of the continued existence of films, such as constitute foam, depends upon the properties now under consideration. If, as is sometimes stated, the tension of a vertical film were absolutely the same throughout, the middle parts would of necessity fall with the acceleration of gravity. In reality, the tension adjusts itself automatically to the weight to be supported at the various levels.
Although throughout a certain range the surface-tension varies rapidly with the degree of contamination, it is remarkable that, as was first fully indicated by Miss Pockels, the earlier stages of contamination have little or no effect upon surface-tension. Lord Rayleigh has shown that the fall of surface-tension begins when the quantity of oil is about the half of that required to stop the camphor movements, and he suggests that this stage may correspond with a complete coating of the surface with a single layer of molecules.]
On the Forms of Liquid Films which are Figures of Revolution.— A soap bubble is simply a small quantity of soap-suds spread out so as to expose a large surface to the air. The bubble, in fact, has two surfaces, an outer and an inner Spherical soap-bubble. surface, both exposed to air. It has, therefore, a certain amount of surface-energy depending on the area of these two surfaces. Since in the case of thin films the outer and inner surfaces are approximately equal, we shall consider the area of the film as representing either of them, and shall use the symbol T to denote the energy of unit of area of the film, both surfaces being taken together. If T′ is the energy of a single surface of the liquid, T the energy of the film is 2T′. When by means of a tube we blow air into the inside of the bubble we increase its volume and therefore its surface, and at the same time we do work in forcing air into it, and thus increase the energy of the bubble.
That the bubble has energy may be shown by leaving the end of the tube open. The bubble will contract, forcing the air out, and the current of air blown through the tube may be made to deflect the flame of a candle. If the bubble is in the form of a sphere of radius this material surface will have an area
| (1) |
If be the energy corresponding to unit of area of the film the surface-energy of the whole bubble will be
| (2) |
The increment of this energy corresponding to an increase of the radius from to is therefore
| (3) |
Now this increase of energy was obtained by forcing in air at a pressure greater than the atmospheric pressure, and thus increasing the volume of the bubble.
Let be the atmospheric pressure and the pressure of the air within the bubble. The volume of the sphere is
| (4) |
and the increment of volume is
| (5) |
Now if we suppose a quantity of air already at the pressure , the work done in forcing it into the bubble . Hence the equation of work and energy is
| (6) |
or
| (7) |
or
| (8) |
This, therefore, is the excess of the pressure of the air within the bubble over that of the external air, and it is due to the action of the inner and outer surfaces of the bubble. We may conceive this pressure to arise from the tendency which the bubble has to contract, or in other words from the surface-tension of the bubble.
If to increase the area of the surface requires the expenditure of work, the surface must resist extension, and if the bubble in contracting can do work, the surface must tend to contract. The surface must therefore act like a sheet of india-rubber when extended both in length and breadth, that is, it must exert surface-tension. The tension of the sheet of india-rubber, however, depends on the extent to which it is stretched, and may be different in different directions, whereas the tension of the surface of a liquid remains the same however much the film is extended, and the tension at any point is the same in all directions.
The intensity of this surface-tension is measured by the stress which it exerts across a line of unit length. Let us measure it in the case of the spherical soap-bubble by considering the stress exerted by one hemisphere of the bubble on the other, across the circumference of a great circle. This stress is balanced by the pressure acting over the area of the same great circle: it is therefore equal to . To determine the intensity of the surface-tension we have to divide this quantity by the length of the line across which it acts, which is in this case the circumference of a great circle . Dividing by this length we obtain as the value of the intensity of the surface-tension, and it is plain from equation 8 that this is equal to . Hence the numerical value of the intensity of the surface-tension is equal to the numerical value of the surface-energy per unit of surface. We must remember that since the film has two surfaces the surface-tension of the film is double the tension of the surface of the liquid of which it is formed.
To determine the relation between the surface-tension and the pressure which balances it when the form of the surface is not spherical, let us consider the following case:—
Let fig. 9 represent a section through the axis of a soap-bubble in the form of a figure of revolution bounded by two circular disks and , and having the meridian section . Let Non-spherical soap bubble. be an imaginary section normal to the axis. Let the radius of this section by , and let , the tangent at , make an angle with the axis.
Let us consider the stresses which are exerted across this imaginary section by the lower part on the upper part. If the internal pressure exceeds the external pressure by , there is in the first place a force acting upwards arising from the pressure over the area of the section. In the next place, there is the surface-tension acting downwards, but at an angle with the vertical, across the circular section of the bubble itself, whose circumference is , and the downward force is therefore .
Now these forces are balanced by the external force which acts on the disk , which we may call . Hence equating the forces which act on the portion included between and
| (9) |
If we make , and suppose to vary, the shape of the bubble of course remaining the same, the values of and of a will change, but the other quantities will be constant. In studying these variations we may if we please take as our independent variable the length of the meridian section reckoned from . Differentiating equation 9 with respect to we obtain, after dividing by as a common factor,
| (10) |
Now
| (11) |
The radius of curvature of the meridian section is
| (12) |
The radius of curvature of a normal section of the surface at right angles to the meridian section is equal to the part of the normal cut off by the axis, which is
| (13) |
Hence dividing equation 10 by , we find
| (14) |
This equation, which gives the pressure in terms of the principal radii of curvature, though here proved only in the case of a surface of revolution, must be true of all surfaces. For the curvature of any surface at a given point may be completely defined in terms of the positions of its principal normal sections and their radii of curvature.
Before going further we may deduce from equation 9 the nature of all the figures of revolution which a liquid film can assume. Let us first determine the nature of a curve, such that if it is rolled on the axis its origin will trace out the meridian section of the bubble. Since at any instant the rolling curve is rotating about the point of contact with the axis, the line drawn from this point of contact to the tracing point must be normal to the direction of motion of the tracing point. Hence if N is the point of contact, NP must be normal to the traced curve. Also, since the axis is a tangent to the rolling curve, the ordinate is the perpendicular from the tracing point on the tangent. Hence the relation between the radius vector and the perpendicular on the tangent of the rolling curve must be identical with the relation between the normal and the ordinate of the traced curve. If we write for , then , and equation 9 becomes
This relation between and is identical with the relation between the perpendicular from the focus of a conic section on the tangent at a given point and the focal distance of that point, provided the transverse and conjugate axes of the conic are and respectively, where
Hence the meridian section of the film may be traced by the focus of such a conic, if the conic is made to roll on the axis.
On the different Forms of the Meridian Line.—1. When the conic is an ellipse the meridian line is in the form of a series of waves, and the film itself has a series of alternate swellings and contractions as represented in figs. 9 and 10. This form of the film is called the unduloid.
1a. When the ellipse becomes a circle, the meridian line becomes a straight line parallel to the axis, and the film passes into the form of a cylinder of revolution.
1b. As the ellipse degenerates into the straight line joining its foci, the contracted parts of the unduloid become narrower, till at last the figure becomes a series of spheres in contact.
In all these cases the internal pressure exceeds the external by where is the semi-transverse axis of the conic. The resultant of the internal pressure and the surface-tension is equivalent to a tension along the axis, and the numerical value of this tension is equal to the force due to the action of this pressure on a circle whose diameter is equal to the conjugate axis of the ellipse.
2. When the conic is a parabola the meridian line is a catenary (fig. 11); the internal pressure is equal to the external pressure, and the tension along the axis is equal to where is the distance of the vertex from the focus.
3. When the conic is a hyperbola the meridian line is in the form of a looped curve (fig. 12). The corresponding figure of the film is called the nodoid. The resultant of the internal pressure and the surface-tension is equivalent to a pressure along the axis equal to that due to a pressure acting on a circle whose diameter is the conjugate axis of the hyperbola.
When the conjugate axis of the hyperbola is made smaller and smaller, the nodoid approximates more and more to the series of spheres touching each other along the axis. When the conjugate axis of the hyperbola increases without limit, the loops of the nodoid are crowded on one another, and each becomes more nearly a ring of circular section, without, however, ever reaching this form. The only closed surface belonging to the series is the sphere.
These figures of revolution have been studied mathematically by C. W. B. Poisson,[3] Goldschmidt,[4] L. L. Lindelöf and F. M. N. Moigno,[5] C. E. Delaunay,[6] A. H. E. Lamarle,[7] A. Beer,[8] and V. M. A. Mannheim,[9] and have been produced experimentally by Plateau[10] in the two different ways already described.

Fig. 10.—Unduloid.Fig. 11.—Catenoid.Fig. 12.—Nodoid
The limiting conditions of the stability of these figures have been studied both mathematically and experimentally. We shall notice only two of them, the cylinder and the catenoid.
Stability of the Cylinder.—The cylinder is the limiting form of the unduloid when the rolling ellipse becomes a circle. When the ellipse differs infinitely little from a circle, the equation of the meridian line becomes approximately where is small. This is a simple harmonic wave-line, whose mean distance from the axis is a, whose wave-length is and whose amplitude is . The internal pressure corresponding to this unduloid is as before . Now consider a portion of a cylindric film of length terminated by two equal disks of radius and containing a certain volume of air. 
Fig. 13.Let one of these disks be made to approach the other by a small quantity . The film will swell out into the convex part of an unduloid, having its largest section midway between the disks, and we have to determine whether the internal pressure will be greater or less than before. If and (fig. 13) are the disks, and if the distance between the disks is equal to half the wave-length of the harmonic curve, the disks will be at the points where the curve is at its mean distance from the axis, and the pressure will therefore be as before. If , are the disks, so that the distance between them is less than , the curve must be produced beyond the disks before it is at its mean distance from the axis. Hence in this case the mean distance is less than , and the pressure will be greater than . If, on the other hand, the disks are at and , so that the distance between them is greater than , the curve will reach its mean distance from the axis before it reaches the disks. The mean distance will therefore be greater than , and the pressure will be less than . Hence if one of the disks be made to approach the other, the internal pressure will be increased if the distance between the disks is less than half the circumference of either, and the pressure will be diminished if the distance is greater than this quantity. In the same way we may show that if the distance between the disks is increased, the pressure will be diminished or increased according as the distance is less or more than half the circumference of either.
Now let us consider a cylindric film contained between two equal fixed disks. and , and let a third disk, , be placed midway between. Let be slightly displaced towards . If and are each less than half the circumference of a disk the pressure on will increase on the side of and diminish on the side of . The resultant force on will therefore tend to oppose the displacement and to bring back to its original position. The equilibrium of is therefore stable. It is easy to show that if had been placed in any other position than the middle, its equilibrium would have been stable. Hence the film is stable as regards longitudinal displacements. It is also stable as regards displacements transverse to the axis, for the film is in a state of tension, and any lateral displacement of its middle parts would produce a resultant force tending to restore the film to its original position. Hence if the length of the cylindric film is less than its circumference, it is in stable equilibrium. But if the length of the cylindric film is greater than its circumference, and if we suppose the disk to be placed midway between and , and to be moved towards , the pressure on the side next will diminish, and that on the side next will increase, so that the resultant force will tend to increase the displacement, and the equilibrium of the disk is therefore unstable. Hence the equilibrium of a cylindric film whose length is greater than its circumference is unstable. Such a film, if ever so little disturbed, will begin to contract at one secton and to expand at another, till its form ceases to resemble a cylinder, if it does not break up into two parts which become ultimately portions of spheres.
Instability of a Jet of Liquid.—When a liquid flows out of a vessel through a circular opening in the bottom of the vessel, the form of the stream is at first nearly cylindrical though its diameter gradually diminishes from the orifice downwards on account of the increasing velocity of the liquid. But the liquid after it leaves the vessel is subject to no forces except gravity, the pressure of the air, and its own surface-tension. Of these gravity has no effect on the form of the stream except in drawing asunder its parts in a vertical direction, because the lower parts are moving faster than the upper parts. The resistance of the air produces little disturbance until the velocity becomes very great. But the surface-tension, acting on a cylindric column of liquid whose length exceeds the limit of stability, begins to produce enlargements and contractions in the stream as soon as the liquid has left the orifice, and these inequalities in the figure of the column go on increasing till it is broken up into elongated fragments. These fragments as they are falling through the air continue to be acted on by surface-tension. They therefore shorten themselves, and after a series of oscillations in which they become alternately elongated and flattened, settle down into the form of spherical drops.
This process, which we have followed as it takes place on an individual portion of the falling liquid, goes through its several phases at different distances from the orifice, so that if we examine different portions of the stream as it descends, we shall find next the orifice the unbroken column, then a series of contractions and enlargements, then elongated drops, then flattened drops, and so on till the drops become spherical.
[The circumstances attending the resolution of a cylindrical jet into drops were admirably examined and described by F. Savart (“Mémoire sur la constitution des veines liquides lancées par des orifices circulaires en minces parois,” Ann. d. Chim. t. liii., 1833) and for the most part explained with great sagacity by Plateau. Let us conceive an infinitely long circular cylinder of liquid, at rest (a motion common to every part of the fluid is necessarily without influence upon the stability, and may therefore be left out of account for convenience of conception and expression), and inquire under what circumstances it is stable or unstable, for small displacements, symmetrical about the axis of figure.
Whatever the deformation of the originally straight boundary of the axial section may be, it can be resolved by Fourier’s theorem into deformations of the harmonic type. These component deformations are in general infinite in number, of very wave-length and of arbitrary phase; but in the first stages of the motion, with which alone we are at present concerned, each produces its effect independently of every other, and may be considered by itself. Suppose, therefore, that the equation of the boundary is
| (1) |
where is a small quantity, the axis of being that of symmetry. The wave-length of the disturbance may be called , and is connected with by the equation . The capillary tension endeavours to contract the surface of the fluid; so that the stability, or instability, of the cylindrical form of equilibrium depends upon whether the surface (enclosing a given volume) be greater or less respectively after the displacement than before. It has been proved by Plateau (vide supra) that the surface is greater than before displacement if , that is, if ; but less if , or . Accordingly, the equilibrium is stable if be less than the circumference; but unstable if be greater than the circumference of the cylinder. Disturbances of the former kind lead to vibrations of harmonic type, whose amplitudes always remain small; but disturbances, whose wave-length exceeds the circumference, result in a greater and greater departure from the cylindrical figure. The analytical expression for the motion in the latter case involves exponential terms, one of which (except in case of a particular relation between the initial displacements and velocities) increases rapidly, being equally multiplied in equal times. The coefficient () of the time in the exponential term () may be considered to measure the degree of dynamical instability; its reciprocal is the time in which the disturbance is multiplied in the ratio .
The degree of instability, as measured by , is not to be determined from statical considerations only; otherwise there would be no limit to the increasing efficiency of the longer wave-lengths. The joint operation of superficial tension and inertia in fixing the wave-length of maximum instability was first considered by Lord Rayleigh in a paper (Math. Soc. Proc., November 1878) on the “Instability of Jets.” It appears that the value of may be expressed in the form
| (2) |
where, as before, is the superficial tension, the density, and is given by the following table:—
| .05 | .1536 | .4 | .3382 |
| .1 | .2108 | .5 | .3432 |
| .2 | .2794 | .6 | .3344 |
| .3 | .3182 | .8 | .2701 |
| .9 | .2015 |
The greatest value of F thus corresponds, not to a zero value of , but approximately to , or to . Hence the maximum instability occurs when the wave-length of disturbance is about half as great again as that at which instability first commences.
Taking for water, in C.G.S. units, , , we get for the case of maximum instability
| (3) |
if be the diameter of the cylinder. Thus, if , ; or for a diameter of one centimetre the disturbance is multiplied 2.7 times in about one-ninth of a second. If the disturbance be multiplied 1000 fold in time, , , so that . For example, if the diameter be one millimetre, the disturbance is multiplied 1000 fold in about one-fortieth of a second. In view of these estimates the rapid disintegration of a fine jet of water will not cause surprise.
The relative importance of two harmonic disturbances depends upon their initial magnitudes, and upon the rate at which they grow. When the initial values are very small, the latter consideration is much the more important; for, if the disturbances be represented by , in which exceeds , their ratio is ; and this ratio decreases without limit with the time, whatever be the initial (finite) ratio . If the initial disturbances are small enough, that one is ultimately preponderant for which the measure of instability is greatest. The smaller the causes by which the original equilibrium is upset, the more will the cylindrical mass tend to divide itself regularly into portions whose length is equal to 4.5 times the diameter. But a disturbance of less favourable wave-length may gain the preponderance in case its magnitude be sufficient to produce disintegration in a less time than that required by the other disturbances present.
The application of these results to actual jets presents no great difficulty. The disturbances by which equilibrium is upset are impressed upon the fluid as it leaves the aperture, and the continuous portion of the jet represents the distance travelled during the time necessary to produce disintegration. Thus the length of the continuous portion necessarily depends upon the character of the disturbances in respect of amplitude and wave-length. It may be increased considerably, as F. Savart showed, by a suitable isolation of the reservoir from tremors, whether due to external sources or to the impact of the jet itself in the vessel placed to receive it. Nevertheless it does not appear to be possible to carry the prolongation very far. Whether the residuary disturbances are of external origin, or are due to friction, or to some peculiarity of the fluid motion within the reservoir, has not been satisfactorily determined. On this point Plateau’s explanations are not very clear, and he sometimes expresses himself as if the time of disintegration depended only upon the capillary tension, without reference to initial disturbances at all.
Two laws were formulated by Savart with respect to the length of the continuous portion of a jet, and have been to a certain extent explained by Plateau. For a given fluid and a given orifice the length is approximately proportional to the square root of the head. This follows at once from theory, if it can be assumed that the disturbances remain always of the same character, so that the time of disintegration is constant. When the head is given, Savart found the length to be proportional to the diameter of the orifice. From (3) it appears that the time in which a disturbance is multiplied in a given ratio varies, not as , but as . Again, when the fluid is changed, the time varies as . But it may be doubted whether the length of the continuous portion obeys any very simple laws, even when external disturbances are avoided as far as possible.
When the circumstances of the experiment are such that the reservoir is influenced by the shocks due to the impact of the jet, the disintegration usually establishes itself with complete regularity, and is attended by a musical note (Savart). The impact of the regular series of drops which is at any moment striking the sink (or vessel receiving the water), determines the rupture into similar drops of the portion of the jet at the same moment passing the orifice. The pitch of the note, though not absolutely definite, cannot differ much from that which corresponds to the division of the jet into wave-lengths of maximum instability; and, in fact, Savart found that the frequency was directly as the square root of the head, inversely as the diameter of the orifice, and independent of the nature of the fluid—laws which follow immediately from Plateau’s theory.
From the pitch of the note due to a jet of given diameter, and issuing under a given head, the wave-length of the nascent divisions can be at once deduced. Reasoning from some observations of Savart, Plateau finds in this way 4.38 as the ratio of the length of a division to the diameter of the jet. The diameter of the orifice was 3 millims., from which that of the jet is deduced by the introduction of the coefficient .8. Now that the length of a division has been estimated a priori, it is perhaps preferable to reverse Plateau’s calculation, and to exhibit the frequency of vibration in terms of the other data of the problem. Thus
| (4) |
But the most certain method of obtaining complete regularity of resolution is to bring the reservoir under the influence of an external vibrator, whose pitch is approximately the same as that proper to the jet. H. G. Magnus (Pogg. Ann. cvi., 1859) employed a Neef’s hammer, attached to the wooden frame which supported the reservoir. Perhaps an electrically maintained tuning-fork is still better. Magnus showed that the most important part of the effect is due to the forced vibration of that side of the vessel which contains the orifice, and that but little of it is propagated through the air. With respect to the limits of pitch, Savart found that the note might be a fifth above, and more than an octave below, that proper to the jet. According to theory, there would be no well-defined lower limit; on the other side, the external vibration cannot be efficient if it tends to produce divisions whose length is less than the circumference of the jet. This would give for the interval defining the upper limit : 4.508, which is very nearly a fifth. In the case of Plateau’s numbers (: 4.38) the discrepancy is a little greater.
The detached masses into which a jet is resolved do not at once assume and retain a spherical form, but execute a series of vibrations, being alternately compressed and elongated in the direction of the axis of symmetry. When the resolution is effected in a perfectly periodic manner, each drop is in the same phase of its vibration as it passes through a given point of space; and thence arises the remarkable appearance of alternate swellings and contractions described by Savart. The interval from one swelling to the next is the space described by the drop during one complete vibration, and is therefore (as Plateau shows) proportional ceteris paribus to the square root of the head.
The time of vibration is of course itself a function of the nature of the fluid and of the size of the drop. By the method of dimensions alone it may be seen that the time of infinitely small vibrations varies directly as the square root of the mass of the sphere and inversely as the square root of the capillary tension; and it may be proved that its expression is
| (5) |
being the volume of the vibrating mass.
In consequence of the rapidity of the motion some optical device is necessary to render apparent the phenomena attending the disintegration of a jet. Magnus employed a rotating mirror, and also a rotating disk from which a fine slit was cut out. The readiest method of obtaining instantaneous illumination is the electric spark, but with this Magnus was not successful. The electric spark had, however, been used successfully for this purpose some years before by H. Buff (Liebigs Ann. lxxviii. 1851), who observed the shadow of the jet on a white screen. Preferable to an opaque screen is a piece of ground glass, which allows the shadow to be examined from the farther side (Lord Rayleigh). Further, the jet may be very well observed directly, if the illumination is properly managed. For this purpose it is necessary to place it between the source of light and the eye. The best effect is obtained when the light of the spark is somewhat diffused by being passed (for example) through a piece of ground glass.
The spark may be obtained from the secondary of an induction coil, whose terminals are in connexion with the coatings of a Leyden jar. By adjustment of the contact breaker the series of sparks may be made to fit more or less perfectly with the formation of the drops. A still greater improvement may be effected by using an electrically maintained fork, which performs the double office of controlling the resolution of the jet and of interrupting the primary current of the induction coil. In this form the experiment is one of remarkable beauty. The jet, illuminated only in one phase of transformation, appears almost perfectly steady, and may be examined at leisure. In one experiment the jet issued horizontally from an orifice of about half a centimetre in diameter, and almost immediately assumed a rippled outline. The gradually increasing amplitude of the disturbance, the formation of the elongated ligament, and the subsequent transformation of the ligament into a spherule, could be examined with ease. In consequence of the transformation being in a more advanced stage at the forward than at the hinder end, the ligament remains for a moment connected with the mass behind, when it has freed itself from the mass in front, and thus the resulting spherule acquires a backwards relative velocity, which of necessity leads to a collision. Under ordinary circumstances the spherule rebounds, and may be thus reflected backwards and forwards several times between the adjacent masses. Magnus showed that the stream of spherules may be diverted into another path by the attraction of a powerfully electrified rod, held a little below the place of resolution.
Very interesting modifications of these phenomena are observed when a jet from an orifice in a thin plate (Tyndall has shown that a pinhole gas burner may also be used with advantage) is directed obliquely upwards. In this case drops which break away with different velocities are carried under the action of gravity into different paths; and thus under ordinary circumstances a jet is apparently resolved into a “sheaf,” or bundle of jets all lying in one vertical plane. Under the action of a vibrator of suitable periodic time the resolution is regularized, and then each drop, breaking away under like conditions, is projected with the same velocity, and therefore follows the same path. The apparent gathering together of the sheaf into a fine and well-defined stream is an effect of singular beauty.
In certain cases where the tremor to which the jet is subjected is compound, the single path is replaced by two, three or even more paths, which the drops follow in a regular cycle. The explanation has been given with remarkable insight by Plateau. If, for example, besides the principal disturbance, which determines the size of the drops, there be another of twice the period, it is clear that the alternate drops break away under different conditions and therefore with different velocities. Complete periodicity is only attained after the passage of a pair of drops; and thus the odd series of drops pursues one path, and the even series another.
Electricity, as has long been known, has an extraordinary influence upon the appearance of a fine jet of water ascending in a nearly perpendicular direction. In its normal state the jet resolves itself into drops, which even before passing the summit, and still more after passing it, are scattered through a considerable width. When a feebly electrified body (such as a stick of sealing-wax gently rubbed upon the coat sleeve) is brought into its neighbourhood, the jet undergoes a remarkable transformation and appears to become coherent; but under more powerful electrical action the scattering becomes even greater than at first. The second effect is readily attributed to the mutual repulsion of the electrified drops, but the action of feeble electricity in producing apparent coherence was long unexplained.
It was shown by W. von Beetz that the coherence is apparent only, and that the place where the jet breaks into drops is not perceptibly shifted by the electricity. By screening the various parts with metallic plates in connexion with earth, Beetz further proved that, contrary to the opinion of earlier observers, the seat of sensitiveness is not at the root of the jet where it leaves the orifice, but at the place of resolution into drops. An easy way of testing this conclusion is to excite the extreme tip of a glass rod, which is then held in succession to the root of the jet, and to the place of resolution. An effect is observed in the latter, and not in the former position.
The normal scattering of a nearly vertical jet is due to the rebound of the drops when they come into collision with one another. Such collisions are inevitable in consequence of the different velocities acquired by the drops under the action of the capillary force, as they break away irregularly from the continuous portion of the jet. Even when the resolution is regularized by the action of external vibrations of suitable frequency, as in the beautiful experiments of Savart and Plateau, the drops must still come into contact before they reach the summit of their parabolic path. In the case of a continuous jet, the equation of continuity shows that as the jet loses velocity in ascending, it must increase in section. When the stream consists of drops following one another in single file, no such increase of section is possible; and then the constancy of the total stream requires a gradual approximation of the drops, which in the case of a nearly vertical direction of motion cannot stop short of actual contact. Regular vibration has, however, the effect of postponing the collisions and consequent scattering of the drops, and in the case of a direction of motion less nearly vertical, may prevent them altogether.
Under moderate electrical influence there is no material change in the resolution into drops, nor in the subsequent motion of the drops up to the moment of collision. The difference begins here. Instead of rebounding after collision, as the unelectrified drops of clean water generally, or always, do, the electrified drops coalesce, and then the jet is no longer scattered about. When the electrical influence is more powerful, the repulsion between the drops is sufficient to prevent actual contact, and then, of course, there is no opportunity for amalgamation.
These experiments may be repeated with extreme ease, and with hardly any apparatus. The diameter of the jet may be about in., and it may issue from a glass nozzle. The pressure may be such as to give a fountain about 2 ft. high. The change in the sound due to the falling drops as they strike the bottom of the sink should be noticed, as well as that in the appearance of the jet.
The actual behaviour of the colliding drops becomes apparent under instantaneous illumination, e.g. by sparks from a Leyden jar. The jet should be situated between the sparks and the eye, and the observation is facilitated by a piece of ground glass held a little beyond the jet, so as to diffuse the light; or the shadow of the jet may be received on the ground glass, which is then held as close as possible on the side towards the observer.
In another form of the experiment, which, though perhaps less striking to the eye, lends itself better to investigation, the collision takes place between two still unresolved jets issuing horizontally from glass nozzles in communication with reservoirs containing water. One at least of the reservoirs must be insulated. In the absence of dust and greasy contamination, the obliquely colliding jets may rebound from one another without coalescence for a considerable time. In this condition there is complete electrical insulation between the jets, as may be proved by the inclusion in the circuit of a delicate galvanometer, and a low electromotive force. But if the difference of potential exceed a small amount (1 or 2 volts), the jets instantaneously coalesce. There is no reason to doubt that in the case of the fountain also, coalescence is due to differences of potential between colliding drops.
If the water be soapy, and especially if it contain a small proportion of milk, coalescence ensues without the help of electricity. In the case of the fountain the experiment may be made by leading tap-water through a Woulfe’s bottle in which a little milk has been placed. As the milk is cleared out, the scattering of the drops is gradually re-established.
In attempting to explain these curious phenomena, it is well to consider what occurs during a collision. As the liquid masses approach one another, the intervening air has to be squeezed out. In the earlier stages of approximation the obstacle thus arising may not be important; but when the thickness of the layer of air is reduced to the point at which the colours of thin plates are visible, the approximation must be sensibly resisted by the viscosity of the air which still remains to be got rid of. No change in the capillary conditions can arise until the interval is reduced to a small fraction of a wave-length of light; but such a reduction, unless extremely local, is strongly opposed by the remaining air. It is true that this opposition is temporary. The question is whether the air can everywhere be squeezed out during the short time over which the collision extends.
It would seem that the forces of electrical attraction act with peculiar advantage. If we suppose that upon the whole the air cannot be removed, so that the mean distance between the opposed surfaces remains constant, the electric attractions tend to produce an instability whereby the smaller intervals are diminished while the larger are increased. Extremely local contacts of the liquids, while opposed by capillary tension which tends to keep the surfaces flat, are thus favoured by the electrical forces, which moreover at the small distances in question act with exaggerated power.
A question arises as to the mode of action of milk or soap turbidity. The observation that it is possible for soap to be in excess may here have significance. It would seem that the surfaces, coming into collision within a fraction of a second of their birth, would still be subject to further contamination from the interior. A particle of soap rising accidentally to the surface would spread itself with rapidity. Now such an outward movement of the liquid is just what is required to hasten the removal of intervening air. It is obvious that the effect would fail if the contamination of the surface had proceeded too far previously to the collision.
This view is confirmed by experiments in which other gases are substituted for air as the environment of colliding jets. Oxygen and coal-gas were found to be without effect. On the other hand, the more soluble gases, carbon dioxide, nitrous oxide, sulphur dioxide, and steam, at once caused union.]
Stability of the Catenoid.—When the internal pressure is equal to the external, the film forms a surface of which the mean curvature at every point is zero. The only surface of revolution having this property is the catenoid formed by the revolution of a catenary about its directrix. This catenoid, however, is in stable equilibrium only when the portion considered is such that the tangents to the catenary at its extremities intersect before they reach the directrix.
To prove this, let us consider the catenary as the form of equilibrium of a chain suspended between two fixed points A and B. Suppose the chain hanging between A and B to be of very great length, then the tension at A or B will be very great. Let the chain be hauled in over a peg at A. At first the tension will diminish, but if the process be continued the tension will reach a minimum value and will afterwards increase to infinity as the chain between A and B approaches to the form of a straight line. Hence for every tension greater than the minimum tension there are two catenaries passing through A and B. Since the tension is measured by the height above the directrix these two catenaries have the same directrix. Every catenary lying between them has its directrix higher, and every catenary lying beyond them has its directrix lower than that of the two catenaries.
Now let us consider the surfaces of revolution formed by this system of catenaries revolving about the directrix of the two catenaries of equal tension. We know that the radius of curvature of a surface of revolution in the plane normal to the meridian plane is the portion of the normal intercepted by the axis of revolution.
The radius of curvature of a catenary is equal and opposite to the portion of the normal intercepted by the directrix of the catenary. Hence a catenoid whose directrix coincides with the axis of revolution has at every point its principal radii of curvature equal and opposite, so that the mean curvature of the surface is zero.
The catenaries which lie between the two whose direction coincides with the axis of revolution generate surfaces whose radius of curvature convex towards the axis in the meridian plane is less than the radius of concave curvature. The mean curvature of these surfaces is therefore convex towards the axis. The catenaries which lie beyond the two generate surfaces whose radius of curvature convex towards the axis in the meridian plane is greater than the radius of concave curvature. The mean curvature of these surfaces is, therefore, concave towards the axis.
Now if the pressure is equal on both sides of a liquid film, and if its mean curvature is zero, it will be in equilibrium. This is the case with the two catenoids. If the mean curvature is convex towards the axis the film will move from the axis. Hence if a film in the form of the catenoid which is nearest the axis is ever so slightly displaced from the axis it will move farther from the axis till it reaches the other catenoid.
If the mean curvature is concave towards the axis the film will tend to approach the axis. Hence if a film in the form of the catenoid which is nearest the axis be displaced towards the axis, it will tend to move farther towards the axis and will collapse. Hence the film in the form of the catenoid which is nearest the axis is in unstable equilibrium under the condition that it is exposed to equal pressures within and without. If, however, the circular ends of the catenoid are closed with solid disks, so that the volume of air contained between these disks and the film is determinate, the film will be in stable equilibrium however large a portion of the catenary it may consist of.
The criterion as to whether any given catenoid is stable or not may be obtained as follows:—
Let and (fig. 14) be two catenaries having the same directrix and intersecting in and . Draw and touching both catenaries, and will intersect at T, a point in the directrix; for since any catenary with its directrix is a similar figure to any other catenary with its directrix, 
Fig. 14.if the directrix of the one coincides with that of the other the centre of similitude must lie on the common directrix. Also, since the curves at and are equally inclined to the directrix, and are corresponding points and the line must pass through the centre of similitude. Similarly must pass through the centre of similitude. Hence , the point of intersection of and , must be the centre of similitude and must be on the common directrix. Hence the tangents at A and B to the upper catenary must intersect above the directrix, and the tangents at A and B to the lower catenary must intersect below the directrix. The condition of stability of a catenoid is therefore that the tangents at the extremities of its generating catenary must intersect before they reach the directrix.
Stability of a Plane Surface.—We shall next consider the limiting conditions of stability of the horizontal surface which separates a heavier fluid above from a lighter fluid below. Thus, in an experiment of F. Duprez (“Sur un cas particulier de l’équilibre des liquides,” Nouveaux Mém. del’ Acad. de Belgique, 1851 et 1853), a vessel containing olive oil is placed with its mouth downwards in a vessel containing a mixture of alcohol and water, the mixture being denser than the oil. The surface of separation is in this case horizontal and stable, so that the equilibrium is established of itself. Alcohol is then added very gradually to the mixture till it becomes lighter than the oil. The equilibrium of the fluids would now be unstable if it were not for the tension of the surface which separates them, and which, when the orifice of the vessel is not too large, continues to preserve the stability of the equilibrium.
When the equilibrium at last becomes unstable, the destruction of equilibrium takes place by the lighter fluid ascending in one part of the orifice and the heavier descending in the other. Hence the displacement of the surface to which we must direct our attention is one which does not alter the volume of the liquid in the vessel, and which therefore is upward in one part of the surface and downward in another. The simplest case is that of a rectangular orifice in a horizontal plane, the sides being and .
Let the surface of separation be originally in the plane of the orifice, and let the co-ordinates and be measured from one corner parallel to the sides and respectively, and let be measured upwards. Then if be the density of the upper liquid, and that of the lower liquid, and the original pressure at the surface of separation, then when the surface receives an upward displacement , the pressure above it will be , and that below it will be , so that the surface will be acted on by an upward pressure . Now if the displacement be everywhere very small, the curvature in the planes parallel to and will be and respectively, and if is the surface-tension the whole upward force will be
If this quantity is of the same sign as , the displacement will be increased, and the equilibrium will be unstable. If it is of the opposite sign from , the equilibrium will be stable. The limiting condition may be found by putting it equal to zero. One form of the solution of the equation, and that which is applicable to the case of a rectangular orifice, is
Substituting in the equation we find the condition
That the surface may coincide with the edge of the orifice, which is a rectangle, whose sides are a and b, we must have
when and are integral numbers. Also, if and are both unity, the displacement will be entirely positive, and the volume of the liquid will not be constant. That the volume may be constant, either or must be an even number. We have, therefore, to consider the conditions under which
cannot be made negative. Under these conditions the equilibrium is stable for all small displacements of the surface. The smallest admissible value of is , where is the longer side of the rectangle. Hence the condition of stability is that
is a positive quantity. When the breadth is less than the length may be unlimited.
When the orifice is circular of radius , the limiting value of is , where is the least root of the equation
The least root of this equation is
.
If is the height to which the liquid will rise in a capillary tube of unit radius, then the diameter of the largest orifice is
Duprez found from his experiments
[The above theory may be well illustrated by a lecture experiment. A thin-walled glass tube of internal diameter equal to 14 mm. is ground true at the lower end. The upper end is contracted and is fitted with a rubber tube under the control of a pinch-cock. Water is sucked up from a vessel of moderate size, the rubber is nipped, and by a quick motion the tube and vessel are separated, preferably by a downward movement of the latter. The inverted tube, with its suspended water, being held in a clamp, a beaker containing a few drops of ether is brought up from below until the free surface of the water is in contact with ether vapour. The lowering of tension, which follows the condensation of the vapour, is then strikingly shown by the sudden precipitation of the water.]
Effect of Surface-tension on the Velocity of Waves.—When a series of waves is propagated on the surface of a liquid, the surface-tension has the effect of increasing the pressure at the crests of the waves and diminishing it in the troughs. If the wave-length is λ, the equation of the surface is
The pressure due to the surface tension T is
This pressure must be added to the pressure due to gravity gy. Hence the waves will be propagated as if the intensity of gravity had been
instead of . Now it is shown in hydrodynamics that the velocity of propagation of waves in deep water is that acquired by a heavy body falling through half the radius of the circle whose circumference is the wave-length, or
| (1) |
This velocity is a minimum when
and the minimum value is
For waves whose length from crest to crest is greater than , the principal force concerned in the motion is that of gravitation. For waves whose length is less than the principal force concerned is that of surface-tension. Lord Kelvin proposed to distinguish the latter kind of waves by the name of ripples.
When a small body is partly immersed in a liquid originally at rest, and moves horizontally with constant velocity , waves are propagated through the liquid with various velocities according to their respective wave-lengths. In front of the body the relative velocity of the fluid and the body varies from where the fluid is at rest, to zero at the cutwater on the front surface of the body. The waves produced by the body will travel forwards faster than the body till they reach a distance from it at which the relative velocity of the body and the fluid is equal to the velocity of propagation corresponding to the wave-length. The waves then travel along with the body at a constant distance in front of it. Hence at a certain distance in front of the body there is a series of waves which are stationary with respect to the body. Of these, the waves of minimum velocity form a stationary wave nearest to the front of the body. Between the body and this first wave the surface is comparatively smooth. Then comes the stationary wave of minimum velocity, which is the most marked of the series. In front of this is a double series of stationary waves, the gravitation waves forming a series increasing in wave-length with their distance in front of the body, and the surface-tension waves or ripples diminishing in wave-length with their distance from the body, and both sets of waves rapidly diminishing in amplitude with their distance from the body.
If the current-function of the water referred to the body considered as origin is , then the equation of the form of the crest of a wave of velocity , the crest of which travels along with the body, is
where is an element of the length of the crest. To integrate this equation for a solid of given form is probably difficult, but it is easy to see that at some distance on either side of the body, where the liquid is sensibly at rest, the crest of the wave will approximate to an asymptote inclined to the path of the body at an angle whose sine is , where is the velocity of the wave and is that of the body.
The crests of the different kinds of waves will therefore appear to diverge as they get farther from the body, and the waves themselves will be less and less perceptible. But those whose wave-length is near to that of the wave of minimum velocity will diverge less than any of the others, so that the most marked feature at a distance from the body will be the two long lines of ripples of minimum velocity. If the angle between these is , the velocity of the body is , where for water is about 23 centimetres per second.
[Lord Kelvin’s formula (1) may be applied to find the surface-tension of a clean or contaminated liquid from observations upon the length of waves of known periodic time, travelling over the surface. If we have
| (2) |
denoting the depth of the liquid. In observations upon ripples the factor involving may usually be omitted, and thus in the case of water )
| (3) |
simply. The method has the advantage of independence of what may occur at places where the liquid is in contact with solid bodies.
The waves may be generated by electrically maintained tuning-forks from which dippers touch the surface; but special arrangements are needed for rendering them visible. The obstacles are (1) the smallness of the waves, and (2) the changes which occur at speeds too rapid for the eye to follow. The second obstacle is surmounted by the aid of the stroboscopic method of observation, the light being intermittent in the period of vibration, so that practically only one phase is seen. In order to render visible the small waves employed, and which we may regard as deviations of a plane surface from its true figure, the method by which Foucault tested reflectors is suitable. The following results have been obtained
| Clean | 74.0 |
| Greasy to the point where camphor motions nearly cease | 53.0 |
| Saturated with olive oil | 41.0 |
| Saturated with sodium oleate | 25.0 |
(Phil. Mag. November 1890) for the tensions of various water-surfaces at 18° C., reckoned in C.G.S. measure.
The tension for clean water thus found is considerably lower than that (81) adopted by Quincke, but it seems to be entitled to confidence, and at any rate the deficiency is not due to contamination of the surface.
A calculation analogous to that of Lord Kelvin may be applied to find the frequency of small transverse vibrations of a cylinder of liquid under the action of the capillary force. Taking the case where the motion is strictly in two dimensions, we may write as the polar equation of the surface at time
| (4) |
where is given by
| (5) |
If , the section remains circular, there is no force of restitution, and . The principal vibration, in which the section becomes elliptical, corresponds to .
Vibrations of this kind are observed whenever liquid issues from an elliptical or other non-circular hole, or even when it is poured from the lip of an ordinary jug; and they are superposed upon the general progressive motion. Since the phase of vibration depends upon the time elapsed, it is always the same at the same point in space, and thus the motion is steady in the hydrodynamical sense, and the boundary of the jet is a fixed surface. In so far as the vibrations may be regarded as isochronous, the distance between consecutive corresponding points of the recurrent figure, or, as it may be called, the wave-length of the figure, is directly proportional to the velocity of the jet, i.e. to the square root of the head. But as the head increases, so do the lateral velocities which go to form the transverse vibrations. A departure from the law of isochronism may then be expected to develop itself.
The transverse vibrations of non-circular jets allow us to solve a problem which at first sight would appear to be of great difficulty. According to Marangoni the diminished surface-tension of soapy water is due to the formation of a film. The formation cannot be instantaneous, and if we could measure the tension of a surface not more than of a second old, we might expect to find it undisturbed, or nearly so, from that proper to pure water. In order to carry out the experiment the jet is caused to issue from an elliptical orifice in a thin plate, about 2 mm. by 1 mm., under a head of 15 cm. A comparison under similar circumstances shows that there is hardly any difference in the wave-lengths of the patterns obtained with pure and with soapy water, from which we conclude that at this initial stage, the surface-tensions are the same. As early as 1869 Dupré had arrived at a similar conclusion from experiments upon the vertical rise of fine jets.
A formula, similar to (5), may be given for the frequencies of vibration of a spherical mass of liquid under capillary force. If, as before, the frequency be , and a the radius of the sphere, we have
| (6) |
denoting the order of the spherical harmonic by which the deviation from a spherical figure is expressed. To find the radius of the sphere of water which vibrates seconds, put , , , . Thus , or one inch very nearly.]
Tables of Surface-tension
In the following tables the units of length, mass and time are the centimetre, the gramme and the second, and the unit of force is that which if it acted on one gramme for one second would communicate to it a velocity of one centimetre per second:—
Table of Surface-Tension at 20° C. (Quincke).
| Liquid. | Specific Gravity. |
Tension of surface separating the liquid from |
Angle of contact with glass in presence of | ||||
| Air. | Water. | Mercury. | Air. | Water. | Mercury. | ||
| Water | 1 | 81 | · · | 418 | 25° 32′ | · · | 25° 6′ |
| Mercury | 13.5432 | 540 | 418 | · · | 51° 8′ | 26° 8′ | · · |
| Bisulfuride of Carbon | 1.2687 | 32.1 | 41.75 | 372.5 | 32° 16′ | 15° 8′ | · · |
| Chloroform | 1.4878 | 30.6 | 29.5 | 399 | · · | · · | · · |
| Alcohol | 0.7906 | 25.5 | · · | 399 | 25° 12′ | · · | · · |
| Olive Oil | 0.9136 | 36.9 | 20.56 | 335 | 21° 50′ | 17° | 47° 2′ |
| Turpentine | 0.8867 | 29.7 | 11.55 | 250.5 | 37° 44′ | 37° 44′ | 47° 2′ |
| Petroleum | 0.7977 | 31.7 | 27.8 | 284 | 36° 20′ | 42° 46′ | · · |
| Hydrochloric Acid | 1.1 | 70.1 | · · | 377 | · · | 42° 46′ | · · |
| Solution of Hyposulphite of Soda | 1.1248 | 77.5 | · · | 442.5 | 23° 20′ | · · | 10° 42′ |
Olive Oil and Alcohol, 12.2.
Olive oil and aqueous alcohol (sp. g. .9231, tension of free surface 25.5), 6.8, angle 87° 48′.
Quincke has determined the surface-tension of a great many substances near their point of fusion or solidification. His method was that of observing the form of a large drop standing on a plane surface. If K is the height of the flat surface of the drop, and k that of the point where its tangent plane is vertical, then
Quincke finds that for several series of substances the surface-tension is nearly proportional to the density, so that if we call the specific cohesion, we may state the general results of his experiments as follows:—
Surface-Tensions of Liquids at their Point of Solidification.
From Quincke.
| Substance. | Temperature of Solidification. |
Surface- Tension. |
| Platinum | 2000° C. | 1658 |
| Gold | 1200° | 983 |
| Zinc | 360° | 860 |
| Tin | 230° | 587 |
| Mercury | −40° | 577 |
| Lead | 330° | 448 |
| Silver | 1000° | 419 |
| Bismuth | 265° | 382 |
| Potassium | 58° | 364 |
| Sodium | 90° | 253 |
| Antimony | 432° | 244 |
| Borax | 1000° | 212 |
| Carbonate of Soda | 1000° | 206 |
| Chloride of Sodium | · · | 114 |
| Water | 0° | 86.2 |
| Selenium | 217° | 70.4 |
| Sulphur | 111° | 41.3 |
| Phosphorus | 43° | 41.1 |
| Wax | 68° | 33.4 |
The bromides and iodides have a specific cohesion about half that of mercury. The nitrates, chlorides, sugars and fats, as also the metals lead, bismuth and antimony, have a specific cohesion nearly equal to that of mercury. Water, the carbonates and sulphates, and probably phosphates, and the metals platinum, gold, silver, cadmium, tin and copper have a specific cohesion double that of mercury. Zinc, iron and palladium, three times that of mercury, and sodium, six times that of mercury.
Relation of Surface-tension to Temperature
It appears from the experiments of Brunner and of Wolf on the ascent of water in tubes that at the temperature centigrade
| (Brunner); | |
| , for a tube .02346 cm. diameter (Wolf); | |
| , for a tube .03098 cm. diameter (Wolf). |
Lord Kelvin has applied the principles of Thermodynamics to determine the thermal effects of increasing or diminishing the area of the free surface of a liquid, and has shown that in order to keep the temperature constant while the area of the surface increases by unity, an amount of heat must be supplied to the liquid which is dynamically equivalent to the product of the absolute temperature into the decrement of the surface-tension per degree of temperature. We may call this the latent heat of surface-extension.
It appears from the experiments of C. Brunner and C. J. E. Wolf that at ordinary temperatures the latent heat of extension of the surface of water is dynamically equivalent to about half the mechanical work done in producing the surface-extension.
References.—Further information on some of the matters discussed above will be found in Lord Rayleigh’s Collected Scientific Papers (1901). In its full extension the subject of capillarity is very wide. Reference may be made to A.W. Reinold and Sir A. W. Rücker (Phil. Trans. 1886, p. 627); Sir W. Ramsay and J. Shields (Zeitschr. physik. Chem. 1893, 12, p. 433); and on the theoretical side, see papers by Josiah Willard Gibbs; R. Eötvös (Wied. Ann., 1886, 27, p. 452); J.D. Van der Waals, G. Bakker and other writers of the Dutch school. (J. C. M.; R.)
Notes
[edit]- ↑ In this revision of James Clerk Maxwell’s classical article in the ninth edition of the Encyclopaedia Britannica, additions are marked by square brackets.
- ↑ See Enrico Betti, Teoria della Capillarità: Nuovo Cimento (1867); a memoir by M. Stahl, “Ueber einige Punckte in der Theorie der Capillarerscheinungen,” Pogg. Ann. cxxxix. p. 239 (1870); and J. D. Van der Waal’s Over de Continuiteit van den Gasen Vloeistoftoestand. A good account of the subject from a mathematical point of view will be found in James Challis’s “Report on the Theory of Capillary Attraction,” Brit. Ass. Report, iv. p. 235 (1834).
- ↑ Nouvelle théorie de l’action capillaire (1831).
- ↑ Determinatio superficiei minimae rotatione curvae data duo puncta jungentis circa datum axem ortae (Göttingen, 1831).
- ↑ Leçons de calcul des variations (Paris, 1861).
- ↑ “Sur la surface de révolution dont la courbure moyenne est constante,” Liouville’s Journal, vi.
- ↑ “Théorie géometrique des rayons et centres de courbure,” Bullet, de l’Acad. de Belgique, 1857.
- ↑ Tractatus de Theoria Mathematica Phaenomenorum in Liquidis actioni gravitatis detractis observatorum (Bonn, 1857).
- ↑ Journal de l’Institut, No. 1260.
- ↑ Statique expérimental et théorique des liquides, 1873.

















































































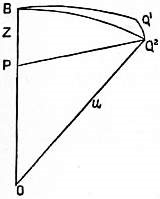

































































































































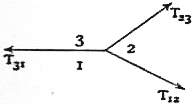





























































































































































































































![{\displaystyle v={\sqrt[{4}]{4{\frac {{\mbox{T}}g.}{\rho }}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01e08be4965a1ba8050970efbcc1c7a112bf417d)


























