Elements of the Differential and Integral Calculus/Chapter VIII part 2
1. It is desired to make an open-top box of greatest possible volume from a square piece of tin whose side is a, by cutting equal squares out of the corners and then folding up the tin to form the sides. What should be the length of a side of the squares cut out?

| Solution. Let | = side of small square = depth of box; | |
| then | = side of square forming bottom of box, | |
| and volume is | ; |
which is the function to be made a maximum by varying x. Applying rule,
First step. .
Second step. Solving gives critical values and .
It is evident from the figure that must give a minimum, for then all the tin would be cut away, leaving no material out of which to make a box. By the usual test, is found to give a maximum volume . Hence the side of the square to be cut out is one sixth of the side of the given square.
The drawing of the graph of the function in this and the following problems is left to the student.
2. Assuming that the strength of a beam with rectangular cross section varies directly as the breadth and as the square of the depth, what are the dimensions of the strongest beam that can be sawed out of a round log whose diameter is d?

Solution. If x = breadth and y = depth, then the beam will have maximum strength when the function is a maximum. From the figure, ; hence we should test the function
- .
First step. ,
Second step. . ∴ = critical value which gives a maximum.
Therefore, if the beam is cut so that
| depth | = of diameter of log, | and breadth | = of diameter of log, |
the beam will have maximum strength.

3. What is the width of the rectangle of maximum area that can be inscribed in a given segment OAA' of a parabola?
HINT. If OC = h, BC = h - x and PP' = 2y; therefore the area of rectangle PDD'P' is
- .
But since P lies on the parabola , the function to be tested is

4. Find the altitude of the cone of maximum volume that can be inscribed in a sphere of radius r.
HINT. Volume of cone = . But ; therefore the function to be tested is
- .

5. Find the altitude of the cylinder of maximum volume that can be inscribed in a given right cone.
HINT. Let AU = r and BC = h. Volume of cylinder = . But from similar triangles ABC and DBG
- r:x::h:h-y. ∴ .
Hence the function to be tested is
- .
6. Divide a into two parts such that their product is a maximum.
7. Divide 10 into two such parts that the sum of the double of one and square of the other may be a minimum.
8. Find the number that exceeds its square by the greatest possible quantity.
9. What number added to its reciprocal gives the least possible sum?
10. Assuming that the stiffness of a beam of rectangular cross section varies directly as the breadth and the cube of the depth, what must be the breadth of the stiffest beam that can be cut from a log 16 inches in diameter?
11. A water tank is to be constructed with a square base and open top, and is to hold 64 cubic yards. If the cost of the sides is $1 a square yard, and of the bottom $2 a square yard, what are the dimensions when the cost is a minimum? What is the minimum cost?
12. A rectangular tract of land is to be bought for the purpose of laying out a quarter-mile track with straightaway sides and semicircular ends. In addition a strip 35 yards wide along each straightaway is to be bought for grand stands, training quarters, etc. If the land costs $200 a.n acre, what will be the maximum cost of the land required? Ans. $856.
13. A torpedo boat is anchored 9 miles from the nearest point of a beach, and it is desired to send a messenger in the shortest possible time to a military camp situated 15 miles from that point along the shore. If he can walk 5 miles an hour but row only 4 miles an hour, required the place he must land.
14. A gas holder is a cylindrical vessel closed at the top and open at the bottom, where it sinks into the water. What should be its proportions for a given volume to require the least material (this would also give least weight)?
15. What should be the dimensions and weight of a gas holder of 8,000,000 cubic feet capacity, built in the most economical manner out of sheet iron of an inch thick and weighing lb. per sq. ft.?
16. A sheet of paper is to contain 18 sq. in. of printed matter. The margins at the top and bottom are to be 2 inches each and at the sides 1 inch each. Determine the dimensions of the sheet which will require the least amount of paper.
17. A paper-box manufacturer has in stock a quantity of strawboard 30 inches by 14 inches. Out of this material he wishes to make open-top boxes by cutting equal squares out of each corner and then folding up to form the sides. Find the side of the square that should be cut out in order to give the boxes maximum volume.

18. A roofer wishes to make an open gutter of maximum capacity whose bottom and sides are each 4 inches wide and whose sides have the same slope. What should be the width across the top?
19. Assuming that the energy expended in driving a steamboat through the water varies as the cube of her velocity, find her most economical rate per hour when steaming against a current running c miles per hour.
| HINT. Let | v | = most economical speed; |
| then | = energy expended each hour, a being a constant depending upon the particular conditions, | |
| and | v - c | = actual distance advanced per hour. |
Hence is the energy expended per mile of distance advanced, and it is therefore the function whose minimum is wanted.
20. Prove that a conical tent of a given capacity will require the least amount of canvas when the height is times the radius of the base. Show that when the canvas is laid out flat it will be a circle with a sector of 152° 9' cut out. A bell tent 10 ft. high should then have a base of diameter 14ft. and would require 272 sq. ft. of canvas.
21. A cylindrical steam boiler is to be constructed having a capacity of 1000 cu. ft. The material for the side costs $2 a square foot, and for the ends $3 a square foot. Find radius when the cost is the least.
22. In the corner of a field bounded by two perpendicular roads a spring is situated 6 rods from one road and 8 rods from the other. How should a straight road be run by this spring and across the corner so as to cut off as little of the field as possible?
What would be the length of the shortest road that could be run across?
23. Show that a square is the rectangle of maximum perimeter that can be inscribed in a given circle.
24. Two poles of height a and b feet are standing upright and are c feet apart. Find the point on the line joining their bases such that the sum of the squares of the distances from this point to the tops of the poles is a minimum.
When will the sum of these distances be a minimum?
25. A conical tank with open top is to be built to contain V cubic feet. Determine the shape if the material used is a minimum.
26. An isosceles triangle has a base 12 in. long and altitude 10 in. Find the rectangle of maximum area that can be inscribed in it, one side of the rectangle coinciding with the base of the triangle.
27. Divide the number 4 into two such parts that the sum of the cube of one part and three times the square of the other shall have a maximum value.
28. Divide the number a into two parts such that the product of one part by the fourth power of the other part shall be a maximum.
29. A can buoy in the form of a double cone is to be made from two equal circular iron plates of radius r. Find the radius of the base of the cone when the buoy has the greatest displacement (maximum volume).
30. Into a full conical wineglass of depth a and generating angle a there is carefully dropped a sphere of such size as to cause the greatest overflow. Show that the radius of the sphere is
31. A wall 27 ft. high is 8 ft. from a house. Find the length of the shortest ladder that will reach the house if one end rests on the ground outside of the wall.
32. A vessel is anchored 3 miles offshore, and opposite a point 5 miles further along the shore another vessel is anchored 9 miles from the shore. A boat from the first vessel is to land a passenger on the shore and then proceed to the other vessel.
What is the shortest course of the boat?
33. A steel girder 25 ft. long is moved on rollers along a passageway 12.8 ft. wide and into a corridor at right angles to the passageway. Neglecting the width of the girder, how wide must the corridor be?
34. A miner wishes to dig a tunnel from a point A to a point B 300 feet below and 500 feet to the east of A. Below the level of A it is bed rock and above A is soft earth. If the cost of tunneling through earth is $1 and through rock $3 per linear foot, find the minimum cost of a tunnel.
35. A carpenter has 108 sq. ft. of lumber with which to build a box with a square base and open top. Find the dimensions of the largest possible box he can make.
36. Find the right. triangle of maximum area that can be constructed on a line of length h as hypotenuse.
37. What is the isosceles triangle of maximum area that can be inscribed in a given circle?
38. Find the altitude of the maximum rectangle that can be inscribed in a right triangle with base b and altitude h.
39. Find the dimensions of the rectangle of maximum area that can be inscribed in the ellipse .
40. Find the altitude of the right cylinder of maximum volume that can be inscribed in a sphere of radius r.
41. Find the altitude of the right cylinder of maximum convex (curved) surface that can be inscribed in a given sphere.
42. What are the dimensions of the right hexagonal prism of minimum surface whose volume is 36 cubic feet?
43. Find the altitude of the right cone of minimum volume circumscribed about a given sphere.
44. A right cone of maximum volume is inscribed in a given right cone, the vertex of the inside cone being at the center of the base of the given cone. Show that the altitude of the inside cone is one third the altitude of the given cone.
45. Given a point on the axis of the parabola at a distance a from the vertex; find the abscissa of the point of the curve nearest to it.
46. What is the length of the shortest line that can be drawn tangent to the ellipse and meeting the coordinate axes?
47. A Norman window consists of a rectangle surmounted by a semicircle. Given the perimeter, required the height and breadth of the window when the quantity of light admitted is a maximum.
48. A tapestry 7 feet in height is hung on a wall so that its lower edge is 9 feet above an observer's eye. At what distance from the wall should he stand in order to obtain the most favorable view?
HINT. The vertical angle subtended by the tapestry in the eye of the observer must be at a maximum.

49. What are the most economical proportions of a tin can which. shall have a given capacity, making allowance for waste?
HINT. There is no waste in cutting out tin for the side of the can, but for top and bottom a hexagon of tin circumscribing the circular pieces required is used up.
NOTE 1. If no allowance is made for waste, then height = diameter.
NOTE 2. We know that the shape of a bee cell is hexagonal, giving a certain capacity for honey with the greatest possible economy of wax.
50. An open cylindrical trough is constructed by bending a given sheet of tin at breadth 2a. Find the radius of the cylinder of which the trough forms a part when the capacity of the trough is a maximum.

51. A weight W is to be raised by means of a lever with the force F at one end and the point of support at the other. If the weight is suspended from a point at a distance a from the point of support, and the weight of the beam is w pounds per linear foot, what should be the length of the lever in order that the force required to lift it shall be a minimum?
52. An electric arc light is to be placed directly over the center of a circular plot of grass 100 feet in diameter. Assuming that the intensity of light varies directly as the sine of the angle under which it strikes an illuminated surface, and inversely as the square of its distance from the surface, how high should the light he hung in order that the best possible light shall fall on a walk along the circumference of the plot?

53. The lower corner of a leaf, whose width is a, is folded over so as just to reach the inner edge of the page. (a) Find the width of the part folded over when the length of the crease is a minimum. (b) Find the width when the area folded over is a minimum.
54. A rectangular stockade is to be built which must have a certain area. If a stone wall already constructed is available for one of the sides, find the dimensions which would make the cost of construction the least.
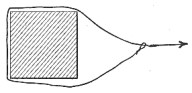
55. A cow is tethered by a perfectly smooth rope, a slip noose in the rope being thrown over a large square post. If the cow pulls the rope taut in the direction shown in the figure, at what angle will the rope leave the post?
56. When the resistance of air is taken into account, the inclination of a pendulum to the vertical may be given by the formula
- .
Show that the greatest elongations occur at equal intervals of time.
57. It is required to measure a certain unknown magnitude x with precision. Suppose that n equally careful observations of the magnitude are made, giving the results
- .
The errors of these observations are evidently
- .
some of which are positive and some negative.
It has been agreed that the most probable value of x is such that it renders the sum of the squares of the errors, namely
- .
a minimum. Show that this gives the arithmetical mean of the observations as the most probable value of x.

58. The bending moment at B of a beam of length l, uniformly loaded, is given by the formula
- .
where w = load per unit length. Show that the maximum bending moment is at the center of the beam.
59. If the total waste per mile in an electric conductor is
- , [c = constant]
where c = current in amperes, r = resistance in ohms per mile, and t = a constant depending on the interest on the investment and the depreciation of the plant, what is the relation between c, r, and t when the waste is a minimum?
60. A submarine telegraph cable consists of a core of copper wires with a covering made of nonconducting material. If x denote the ratio of the radius of the core to the thickness of the covering, it is known that the speed of signaling varies as
- .
Show that the greatest speed is attained when .
61. Assuming that the power given out by a voltaic cell is given by the formula
- .
when E = constant electromotive force, r = constant internal resistance, R = external resistance, prove that P is a maximum when r = R.
62. The force exerted by a circular electric current of radius a on a small magnet whose axis coincides with the axis of the circle varies as
- .
where x = distance of magnet from plane of circle. Prove that the force is a maximum when .
63. We have two sources of heat at A and B with intensities a and b respectively. The total intensity of heat at a distance of x from A is given by the formula
- .

Show that the temperature at P will be the lowest when
- .
that is, the distances BP and AP have the same ratio as the cube roots of the corresponding heat intensities. The distance of P from A is
- .
64. The range OX of a projectile in a vacuum is given by the formula
- .
where = initial velocity, g = acceleration due to gravity, = angle of projection with the horizontal. Find the angle of projection which gives the greatest range for a given initial velocity.
65. The total time of flight of the projectile in the last problem is given by the formula
- .
At what angle should it be projected in order to make the time of flight a maximum?
66. The time it takes a ball to roll down an inclined plane AB is given by the formula.
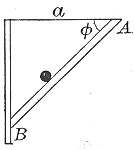
- .
Neglecting friction, etc., what must be the value of to make the quickest descent?
67. Examine the function for maximum and minimum values. Use the first method, p. 111.
| Solution. | . | |
| First step. | . | |
| Second step. | = 0, | |
| , which are critical values. | ||
| Third step. | . | |
| Fourth step. | Examine first for critical value x = 1 (C in figure). | |
- When .
- When .
Therefore, when x = 1 the function has a minimum value (= ordinate of C).
Examine now for the critical value (B in figure).
- When .
- When .
Therefore, when the function has a maximum value (= ordinate of B).
Examine lastly for the critical value x = -1</math> (A in figure).
- When .
- When .
Therefore, when x = - 1 the function has neither a maximum nor a minimum value.
68. Examine the function for maxima and minima.
| Solution. | . | |
Since x = c is a critical value for which , but for which is not infinite, let us test the function for maximum and minimum values when x = c.
- When .
- When .
Hence, when the function has a maximum value .
Examine the following functions for maximum and minimum values:
| 69. . | Ans. | , gives max. = ; |
| , gives min. = 0. | ||
| 70. . | , gives max. = .03456; | |
| , gives min. = 0; | ||
| , gives neither. | ||
| 71. . | Ans. | , gives max.; |
| , gives neither. | ||
| 72. . | , gives max.; | |
| , gives min.; | ||
| , gives neither. | ||
| 73. | , gives max.; | |
| x = -1 and 5, give min. | ||
| 74. . | , gives max.; | |
| x = 1 and , gives min.; | ||
| , gives neither. | ||
| 75. | , gives max.; | |
| x = 1 and , gives min.; | ||
| x = -1, gives neither. | ||
| 76. | x = -a and , give max.; | |
| x = | ||
| x = a, gives neither. | ||
| 77. . | x = a, gives min. = b. | |
| 78. . | No max. or min. | |
| 79. | x = 4, gives max. | |
| x = 16, gives min. | ||
| 80. | , gives min. | |
| 81. | , gives min. | |
| 82. | , gives min. = . | |
| , gives max. = . | ||
| , give neither. | ||
| 83. | , gives max. = . | |
| 84. . | , gives min.; | |
| , gives max. | ||
85. Examine for maxima and minima, Use the second method, p.113.

| Solution. | . | |
| First step. | . | |
| Second step, | ; |
hence the critical values are x = -1 and 3.
| Third step. | . | |
| Fourth step. | = -12. | |
| ∴ | = 10 = (ordinate of A) = maximum value. | |
| . | ∴ | (ordinate of B) = minimum value. |
86. Examine for maximum and minimum values.
Solution.
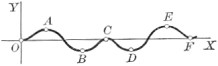
First step. f'(x) = .
Second step. ;
hence the critical values are
and .
| Third step. | . | ||
| Fourth step. | . | ∴ v = minimum value at O. | |
| . | ∴ = 0 = maximum value at C. | ||
| . | ∴ maximum value at A. | ||
| . | ∴ minimum value at B, etc. | ||
Examine the following functions for maximum and minimum values.
| 87. . | Ans. | x = -1, gives max. = 45; |
| x = 3, gives min. = - 51. | ||
| 88. . | x = 1, gives max. = -3; | |
| x = 6, gives min. = -128. | ||
| 89. . | x = 1, gives max. = ; | |
| x = 3, gives min. = 1. | ||
| 90. . | x = 2, gives max. = 38; | |
| x = 3, gives min. = 37. | ||
| 91. . | x = 1, gives max. = 4'; | |
| x = 5, gives min. = - 28. | ||
| 92. . | No max. or min. | |
| 93. . | x = 1, gives max. = 2; | |
| x = 3, gives min. = -26; | ||
| x = 0, gives neither. | ||
| 94. . | x = -4 and 3, give max.; | |
| x = -3 and 4, give min. | ||
| 95. . | 98. . |
| 96. . | 99. . |
| 97. . | 100. . |
| 101. . | Ans. | , give max. = ; |
| , give min. = ; | ||
| , give neither. | ||
| 102. | x = e, gives min. = e; | |
| x = 1, gives neither. | ||
| 103. . | , gives max. | |
| 104. . | , gives min. = . | |
| 105. . | , gives min. | |
| 106. . | x = e, gives max. | |
| 107. . | , gives max. = | |
| , gives min. = . | ||
| 108. . | , gives max.; | |
| , gives min. | ||
| 109. . | No max. or min. | |
| 110. . | , gives max. = ; | |
| , gives min. = ; | ||
| , gives neither. | ||
| 111. . | , gives max. | |
| 112. . | , gives max.; | |
| , gives min. | ||
| 113. . | , gives max. | |
| 114. . | , gives max. | |
| 115. . | , gives max.; | |
| , gives min. | ||




































![{\displaystyle {\frac {1}{\sqrt[{3}]{3\pi }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232ea88d9d8500d7d3c6ead484926031992a5b05)

































![{\displaystyle {\frac {d-x}{x}}={\frac {\sqrt[{3}]{b}}{\sqrt[{3}]{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa431bd5c53da465c29565cf55839555574d62f8)























































































































































