On the Second Postulate of the Theory of Relativity
XVIII. On the Second Postulate of the Theory of Relativity:
Experimental Demonstration of the Constancy of Velocity of the Light
reflected from a Moving Mirror.
By Q. Majorana,
Professor of Physics at the Polytechnic School of Turin [1].
THE Theory of Relativity is based upon two well-known fundamental postulates. The first affirms the impossibility of discovering the movement of a system without referring this system to other systems; that is to say, it denies the physical reality of absolute motion. The second postulate affirms that the velocity c of propagation of light in vacuo is a universal constant. Both these postulates are generalizations of facts or principles already admitted by physicists.
In fact, we may regard the first as the extension to optical or electrical phenomena of a classical principle of mechanics, an extension justified by the negative results of certain experiments (Michelson and Morley, Trouton and Noble) by which it was sought to discover the absolute motion of the earth, or the æthereal wind which must traverse all terrestrial objects. The second postulate is the generalization of a fundamental principle in the theory of æthereal or electromagnetic undulations.
But if these two principles, derived from quite different chapters of physics, have been fully accepted severally by modern physicists, their origin has been almost forgotten; an ingenious structure arose upon their union: the theory of relativity. This theory, while repudiating according to Einstein and others a theoretical conception which had given occasion for the formulation of the second postulate (the æther), serves well to explain the insuccess of the above-cited experiments.
Now our imagination, accustomed, as W. Ritz has said, to "substantialize" physical phenomena, if it easily grasps the essence of the first postulate, does not do so in the case of the second; and the more so since, as has already been said, some adherents to relativistic theories do not retain as necessary the existence of a medium of transmission (the æther) in order to explain the constancy of c. Moreover on the second postulate, or, more precisely, on a certain portion of this, depend the conclusions which appear artificial or extraordinary in the whole relativistic theory[2]. The second postulate must be understood in the sense that an observer who measures the velocity of light finds always the same value if both he and the source be at rest, relative or (if the possibility be admitted) absolute, or if the source or the observer, or both, have a uniform motion of translation. In short, the second postulate affirms the absolute independence of c of any contingency whatever of uniform motion of translation of the source or of the observer.
It is known that an hypothesis of a mechanical character (emissive or ballistic), according to which to the ordinary velocity of light must be added that of the source, can explain, like the theory of relativity, the failure of the above-quoted experiments. But this hypothesis is radically in contrast with the electromagnetic theory, and consequently is not much favoured[3]. But in any case laboratory experiments can be conceived which should decide between the above-mentioned hypothesis or mechanical theory and the relativistic one. It is indeed possible to see that some method, one moreover already in use, adopted for the verification of Doppler's principle may serve for the solution of the above-quoted problem.
In order to see this, let us consider a luminous source S which emits waves of length λ and of frequency n moving towards the observer fixed at O (fig. I). If we suppose
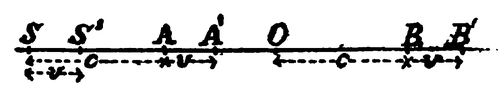
that the waves are transmitted through a stationary æther, the n waves emitted in a second by S will be distributed over the segment S'A = c — v. In the same time all the n waves distributed in the segment OB = c will have passed through O; we have therefore
, or .
If we put v/c = β and neglect terms of higher order than the first in β we have
n' = n(1 + β).
The new wave-length is obtained by the relations
λ' = λ(1 - β).
If now instead of the hypothesis of a stationary medium we adopt the ballistic or emissive hypothesis of which we have spoken above, we shall find that in one second the n waves emitted by S will be distributed over the segment S'A' = c. In the same time there will pass through O, n' waves which will be distributed over the segment OB' = c + v. We have, therefore,
, or n' = n(1 + β).
And since c = nλ and c + v = n'λ' we see that, in this case, λ' = λ.
As regards the frequency we arrive, therefore, at the same conclusions (with the exception of the terms in β²) whether we adopt the æthereal or the ballistic hypothesis; but for the wave-length we obtain different values from the two hypotheses, and these values differ by a term of the first order in β. If then the Doppler effect is measured, by observation of the wave-length, different results should lie obtained according as the one or the other hypothesis is adopted[4]. Now observations of the Doppler effect have already been made by measuring the displacement of the spectral lines, employing either prisms or diffraction-gratings. In the cage of prisms it may be observed that all the theories of dispersion hitherto admitted lead to the supposition that this phenomenon can only depend on the frequency of the incident luminous vibrations. Consequently the displacement of the spectral lines may be caused by the simple variation in frequency due to the Doppler effect, and this whether, for the light, the hypothesis of a stationary æther is adopted, or a ballistic or emissive theory. From this point of view, therefore, the question whether the velocity of propagation of the light emitted by a source does or does not change with the velocity of the latter remains unanswered.
But the Doppler effect has been established with diffraction-gratings as well as with prisms, and for astronomical as well as terrestrial sources[5]. Now the function of a grating, from the geometrical point of view, may be regarded as depending exclusively on the values of the incident wave-lengths; the positions of the successive spectral lines remain exactly determined by those values. But since, according to the ballistic or emissive hypothesis, the value of λ does not vary with the velocity of the source, we see that the grating should not give an appreciable result in the study of the Doppler effect, and this, as is known, is not in agreement with experience. We may then conclude from observations of the Doppler phenomenon in the stars and the limb of the sun with moving mirrors (Galitzin & Wilip), or again in the canal rays (Stark, Paschen), that the velocity of light is absolutely constant and independent of the movement of the source; this is equivalent to the rejection of the ballistic or emissive theory. This is Tolman's opinion[6], in contradiction to that of Stewart[7]. Indeed, it should be borne in mind that the ordinary grating theory[8] may not apply exactly in the case of a mechanical (ballistic or emissive) theory of light. In any case it should be remarked that astronomical observations of the Doppler effect are not always made with an à priori knowledge of the relative velocities of source and observer. In the case of the solar limb it is necessary, moreover, to be cautious in establishing a relation between the measure of displacement of the lines and the velocity of the limb established by observation of the solar spots; in fact, the light from the limb may be strongly refracted by the perispherical incandescent gases, and consequently the value of the Doppler effect may vary considerably[9]. So far as terrestrial observations are concerned, and those on the canal rays (Stark, Paschen), they give measures of the phenomenon of only small precision, and it is impossible to foresee by another method the exact velocity of the luminous particles; finally, observations made with moving mirrors bear no relation to those with moving sources, and these may produce different consequences[10].
From all this we may conclude that up to the present time we do not possess any quite certain evidence of the immutability of c with variable velocity of the source if, be it understood, we are not willing to admit as conclusive the simple electromagnetic theory or that of bodies in motion according to Lorentz or else Einstein's theory of relativity. This conclusion is confirmed by the study of the works of the chief supporters of the last theory, and, implicitly, of the second postulate. In these works we frequently find expressed the desire to discover further facts which will definitely confirm the said theory: this desire corresponds with the crisis of the latter years of the said theory.
But on the other hand, as Levi-Civita observes, after the latest researches of Einstein, which collect in an admirably comprehensive synthesis all the physical phenomena (gravitation included), it is difficult to avoid the impression that we are, as regards the theory of relativity, face to face with some definite acquisition. But, while taking account of this, it is not expedient to neglect any attempt at a definite confirmation, from an experimental point of view, of a theory which has subverted to so large an extent our simplest physical notions. This confirmation may follow from a precise study of the velocity of propagation of light emitted from a moving source, or, which is equivalent, of the wavelength of this light.
To realize this study we must devise an arrangement which will permit us to identify the structure of the luminous wave, freed from all external action, in its free propagation (or transmission) when the velocity of translation of the source can be varied at will. But, apart from the fact that we must inevitably experiment under the eventual action of our earth[11], two serious and almost insurmountable difficulties oppose themselves to the realization of such a programme. In the first place, it is not easy artificially to endow a luminous source with rapid movement[12], especially if this source (as is necessary in some interference methods) has to be very rigorously monochromatic; moreover, I shall publish an account in a forthcoming paper of a disposition of this nature with which I am about to experiment. Secondly, in order to be able to examine the structure of the light emitted by a moving source, with whatever disposition, the light itself has to be subjected to reflexion's, refractions, &c., sometimes fairly numerous; that is to say, the luminous ray must encounter ponderable matter after leaving the source. It does not follow, therefore, that even if c in a vacuum varies with the particular velocity of the source, this quantity does not return to the same fixed value after the said phenomena of reflexion, refraction, &c. It will be well, therefore, to endeavour to eliminate as far as possible, in an experiment of this nature, all causes tending to complicate the phenomenon, and in every case to consider its results carefully.
Meanwhile, to begin with a relatively simple experiment, we may undertake the study of the wave-length of a ray of light reflected by a moving mirror[13]. This may correspond with the experiment already realized, some years ago, by Belopolski, and afterwards repeated by Galitzin & Wilip; but if the first of these authors employed prisms for the observation of the Doppler effect (and consequently the question of the eventual variation of λ remained unsolved), the other two made use of a diffraction-grating, by which the controversy spoken of above arises. It would be better therefore to examine the ray reflected from a moving mirror by an interference method simpler than that on which the action of the diffraction depends, as has been said above.
Before expounding this method it is well to recall that many theoretical researches have been made on the influence of the motion of the mirror upon the reflected luminous wave, amongst them those of Abraham, Brown, Edser, Harnack, Larmor, Planck. These researches make of the problem either a simply geometrical investigation, or an application of the electromagnetic theory of light. But without discussing the result of these researches we may accept the conclusion of Harnack[14] respecting the frequency of the vibrations reflected by a mirror in uniform motion. Let v be the velocity of the latter, normal to its plane, reckoned as positive towards the source; c the velocity of the luminous ray in vacua which makes the angle of incidence θ with the mirror; n, n' the frequencies of the ray before and after reflexion, the source and observer being at rest. If we put β = v/c we shall have
which, neglecting the terms in β², reduces to
n' = n(1 + 2β cos θ).
This relation is the same as that of Ketteler[15], which was employed by Belopolski[16] in his investigation of the Doppler effect, and follows simply from the consideration that the image of the source moves with the velocity 2v in the direction of the normal to the mirror and, consequently, the component of this velocity in the direction of the reflected ray is 2v cos θ.
If now we suppose that the ray is, by suitable arrangements, reflected with the incidence θ, k times from several mirrors in motion with the velocity v, we shall have
n' = n(1 + 2kβ cos θ).
Therefore, according to the hypothesis of constant velocity of light, neglecting the terms in β² we shall have
λ' = λ(1 - 2kβ cos θ).
If, on the contrary, we suppose that the velocity of the reflected light is variable (and equal to the sum of c = 3.1010cm. and the component of the velocity of the image in the direction of the ray) we shall have
And since c' = n'λ' and c = nλ we have λ' = λ. It remains then to see by experiment whether or not we can observe, in addition to the Doppler effect, a variation in the value of λ; from this we can ascertain whether c remains constant or not on reflexion from a moving mirror. I have not proceeded to the observation of the Doppler effect in these researches since there is no doubt about its existence, already proved experimentally by the authors quoted; I have rather sought to find out whether and in what way λ varies when the velocity of the moving mirrors changes.
Belopolski's arrangement for the study of the Doppler effect was inconvenient on account of the excessive subtility of the luminous ray necessary to obtain multiple reflexions from the same mirrors; for this reason the author mentioned was unable to observe the displacement of the rays except by photography. I prefer to adopt the arrangement shown diagrammatically in fig. 2. A horizontal brass wheel R, 35 cm.
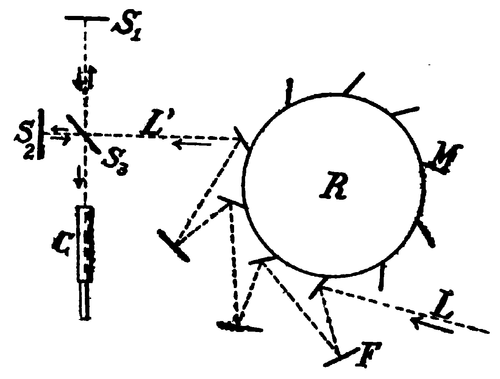
in diameter (6 mm. thick), which can be made to revolve with a maximum velocity of 80 turns per second, bears on its periphery ten mirrors similar to M, rectangular, plane, vertical, of glass silvered at the back. The velocity of the centres of the mirrors, corresponding to the greatest velocity of rotation, amounts therefore to more than 100 metres per second. The number of revolutions of the wheel was determined acoustically in each experiment. The mirrors, at equal intervals on the periphery of the wheel, are inclined to the radius from R passing through the centre of each of them at an angle α = 29°. They are fixed solidly to R by screw movements capable of permitting a rigorous adjustment. The support for the bearings of the axle of R carries also fixed mirrors F, vertical like M, of which the number in the figure is three; but this number may, at will, be reduced, or increased up to nine. The position of the F's and M's is such that a parallel beam of light L, after a certain number of reflexions from the F's and M's (seven in the figure), may be received at L' when R has determinate angular positions. Naturally the intensity of L' is much weaker than that of L, and this enfeeblement is much more marked if R is in rotation, because in this case the light arrives at L' only during certain very short instants (ten times per revolution). I have observed in practice, however, that the four moving and three fixed reflexions of the figure allow of experimenting with light sufficiently intense at L' even if R is in motion: that is to say, that direct observation (without photography) suffices to establish the luminous phenomenon of which we have spoken above.
To study the value of λ the light L' was examined with the well-known interferometer of Michelson, shown diagrammatically in the figure. It is known that if the distances S1S3 and S2S3 are exactly equal fringes are observed with the telescope C even if the light is not monochromatic; these fringes then have the coloration of Newton's rings. As soon as a difference of path occurs (even if only of a few microns) observation with white light is no longer possible. Monochromatic light must then be used, and the order of the interference fringes increases with this difference. Their visibility is greater, the simpler the luminous vibrations. From the researches of Michelson[17] it is known that from this point of view the line that gives the greatest visibility of the fringes with the greatest difference in path is the green one of mercury (λ = 546μμ). In this case numberless circular fringes are visible even for a difference of path l = 2(S1S3 - S2S3) = 40 cm. I have therefore employed as source L a mercury arc in vacuo the light of which is conveniently filtered by solutions of chromate of potassium and chloride of nickel to absorb the violet and yellow rays; in this manner I have been able to observe with the telescope C, with sufficient clearness, countless circular fringes, even for l = 32 cm. But for these researches I have limited the difference of path to l = 13 cm., or still less.
The disposition described above is particularly suitable for detecting very small differences in the value of the incident wave-length; in fact, the value of l being large a very great number of wave-lengths is comprised in this length (e.g., 200,000 if λ = 0.5μ, and l = 10 cm.), and correspondingly for the same variations very sensible displacements can be observed in the position of a fringe.
With the apparatus disposed as above, let us note with the micrometer wire of the telescope the position of a fringe, for instance the first central bright one, when R is in the position shown in the figure, or, still better, when it revolves with a negligible velocity (one turn per second). If, now, this velocity be increased to sixty turns per second a displacement of the fringe under observation is distinctly visible; if the mirrors are moving against the incident ray this displacement indicates a diminution of λ, and it changes sign when the direction of rotation of the wheel is reversed, and this indicates an increase of λ. In order to define the sense of the displacement, I will say that on examining the system of circular fringes with the telescope focussed for infinite distance the diameter of each of these increases when the mirrors move against the incident ray, and the fringes themselves crowd together as those of large diameter are very little displaced; at the same time some new fringes come out from the centre of the system. On the other hand, when the mirrors are moving in the sense of propagation of the incident light the diameter of each fringe diminishes; they become more widely separated, and some of them are as it were swallowed up by the centre.
Before stating the measure of the displacement observed we will see what it should amount to, making the hypothesis that the velocity of the light reflected from a mirror is the same as that of the incident light. Let g be the number of revolutions of R per second and d its diameter, reckoned between the centres of two opposite mirrors M, then πdg will be the instantaneous velocity of translation of the latter. Since the mirrors are inclined at an angle α to the radius of the wheel passing through each of them, the component of the given velocity in the direction normal to the plane of each mirror will be
v = πdg cos α.
and, by the hypothesis of the invariability of c,
If l is the difference of path of two interfering rays in Michelson's apparatus, the number of fringes which are seen to cross the micrometer thread of the telescope when λ becomes λ' (that is to say when the velocity of rotation varies between zero and g turns per second) is
.
If the observation is made by noting the position of the fringes when the wheel turns in one sense with the velocity g, and that corresponding to an equal and contrary velocity, the number of fringes crossing the micrometer thread will be 2f.
Now, in my apparatus d = 38 cm., α = 29°, θ = 27°, k = 4 (as in the figure); if λ is put equal to 0.546μ (green mercury line), l = 13 cm., c = 3·1010 cm., and g = 60 (turns of R per second in one sense and afterwards in the other), we may expect, according to the preceding formula, a fringe displacement 2f = 0.71.
Experiment gives, for the case mentioned, a displacement of between 0.7 and 0.8 fringes; and it is not possible, for reasons of visibility, to carry the precision of the observations further. But, as is seen, the agreement between the predicted result and observation is sufficient; this agreement is confirmed by observations made by choosing other convenient values of l and g, of which for brevity's sake I shall not speak here.
Experiment, therefore, authorizes the conclusion that reflexion of light by a moving metallic mirror does not alter the velocity of propagation of the light itself, in air, and consequently, with great probability, also in vacuo; at least, in the conditions of the experiment above described. This experimental result, as to which no doubt can be entertained, is contrary to the hypothesis of some physicists who, like Stewart[18], basing themselves upon the electromagnetic emission theory of Thomson, maintain the possibility that light, after reflexion, is propagated with the velocity c + v, where v is the component of the velocity of the image in the direction of the reflected ray.
To complete these researches I intend, as I have said above, to investigate further with the same interferential arrangements, the velocity of propagation of light from a source set in motion artificially; but of these, and of the general conclusions to be drawn from these investigations, I reserve mention for a future occasion.
- ↑ Communicated by the Author.
- ↑ Carmichael, Phys. Rev. xxxv. p. 168 (1912).
- ↑ In this connexion should be recalled the important critical work of W. Ritz (Œvres, p. 317) which perhaps has not been taken into sufficient consideration by physicists.
- ↑ These conclusions are identical with those already published by other authors; see, e. g., Tolman, Phy. Rev. xxi. p. 26 (1910).
- ↑ Galitzin & Wilip, Communications Acc. Russe, 1907, p. 213; Stark, Ann. d. Phys. xxviii. p. 974 (1909).
- ↑ Phys. Rev. xxxv. p. 136 (1912).
- ↑ Phys. Rev. xxxii. p. 418 (1911).
- ↑ La Rosa, Nuovo Cimento, iii. p. 356 (1912).
- ↑ Michelson, Astrophys. Journ. xiii. p. 192 (1901); Harnack, Ann. d. Phys. xhi. p. 558 (1915).
- ↑ See the theory proposed by Ritz, Œures, pp. 321, 371, 444.
- ↑ I cannot succeed in imagining an interplanetary experiment of the nature of that proposed (in jest) by Rose-Innes; see Phil. Mag. xxvii. p. 150 (1914).
- ↑ I understand by this a velocity higher than some hundreds of metres per second; this value may perhaps be attained, but it is difficult to conceive a practical disposition for a higher velocity. Naturally I leave out of account the employment of canal rays, which do not give simple and well-known velocities.
- ↑ While this article was in the press, M. Michelson has called my attention to his paper on the same subject, published in the 'Astrophysical Journal,' April 1913, the conclusions of which agree with those that I am stating.
- ↑ Ann. d. Phys. xxxix. p. 1053 (1912) and xlv. p. 547 (1915).
- ↑ Astronomische Undulationstheorie.
- ↑ Communications Acc. Russe, xiii. p. 451 (1900).
- ↑ Travaux et Mémoires, Bur. Int. de poids et mésures, xi. p. 146 (1895).
- ↑ Phys. Rev. xxxii. p. 418 (1911).
![]()
This work is in the public domain in the United States because it was published before January 1, 1929.
The longest-living author of this work died in 1957, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 66 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
![]()
Public domainPublic domainfalsefalse






