there, and his mother, Caroline Penn, belonged to an emigrated English family. He studied medicine in Berlin in 1839, and rose to be Teacher of Anatomy at the Berlin Academy in 1848. In the following year he became Professor of Physiology at Königsberg; in 1858, Professor of the same at Heidelberg, and Geheimrath. In 1871 he returned to the Berlin University as Professor of Natural Philosophy, and at Christmas, 1877, was elected Eector. His essay on the Conservation of Force ('Erhaltung der Kraft") appeared in 1847; his Physiological Optics ('Physiologische Optik') in 1856–66; and his Popular Scientific Lectures ('Pop. wissensch. Vorträge') at Brunswick, 1865–76. It is, however, with his 'Treatise on the Sensations of Tone as a physiological basis for the theory of Music,'[1] and with his valuable inventions and discoveries in relation to the art, that we are here concerned.
Professor Helmholtz has invented a double harmonium with 24 vibrators to the octave, by means of which the musician can modulate into all keys quite as easily as on a single manual tuned by equal temperament, and without the dissonant thirds and sixths which that mode of tuning introduces. The system may be easily applied to the organ and piano. It is extremely simple, as it does not add to the number of notes in the scale, and requires no new system of fingering to be learnt by the performer. This invention, originally suggested by the extremely unpleasant effect of the equally tempered harmonium, may not impossibly revolutionise modern musical practice, extending as it does to manual instruments that perfect intonation which has hitherto been attainable only by stringed instruments and the human voice. The following may be selected, amongst many others, to illustrate the nature of the discoveries of Helmholtz:—
1. Quality of Musical sounds determined by Harmonics. By means of a series of resonators, each of which on being applied to the ear reinforces any harmonic of equal pitch which may be present in a given note, Helmholtz has effected the most complete analysis of musical tone hitherto attained. The resonator is a hollow sphere of glass or metal, with two openings opposite to each other, one of which is funnel-shaped, for insertion into the ear. Let the note of the resonator be upper C, the air contained in it will vibrate very powerfully when that note is given by the voice or any musical instrument; and less powerfully when the note given is one of those lower notes which are harmonic sub-tones of C, or is, in other words, a note among the harmonics of which the upper C occurs.
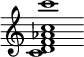 |
Resonator |
| Harmonic sub-tones. |
The chief results of Helmholtz's experiments with resonators have been given under the head Harmonics.
More curious is his determination of the nature of the vowel sounds of the human voice, in which Helmholtz has developed the discoveries of Wheatstone. The shape of the mouth-cavity is altered for the production of each particular vowel; and in each of the shapes which it assumes it may be considered as a musical instrument yielding a different note, and in the case of the compound vowels, yielding simultaneously two separate notes of different pitch, just as the neck and body of a glass bottle do. The natural resonance of the mouth-cavity, independently of the tension of the vocal chords, for different vowels, is as follows (the pronunciation of the vowels being not English but German):—
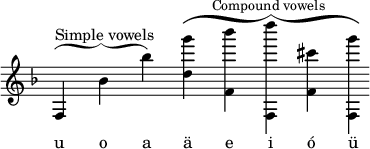
Thus, when the mouth-cavity is found to utter the sound u (oo), it is in effect a musical instrument, the natural pitch of which is lower f, and so on.
For the highly interesting experiments on vowel-pitch by means of the resonators, and the importance to singers and composers of the results deducible from them, the reader must be referred to Helmholtz's work (Ellis's translation, pp. 153–172).
2. Summational Tones. The fact that when two notes are sounded together they generate a third and deeper tone, whose vibrational number equals the difference of their several vibrational numbers, has been known to violinists ever since the time of Tartini. [See Tartini's Tones.] These tones Helmholtz calls differential tones, to distinguish them from another set of generated tones discovered by himself, the vibrational numbers of which equal the sum of the vibrational numbers of the generating tones, and which he hence calls summational tones. These tones are of course higher than the generating tones. Thus, if the chords in minims in the following figure be played forte on the violin, the double series of combinational tones above and below will be produced:—
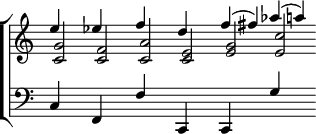 |
Summational tones. |
| Generating tones | |
| Differential or Tartini's tones. |
The summational tones are too weak to be distinguished by the unaided ear: while the differential tones are on some instruments intrusively audible. (In fact the violin player obtains perfect fifths on his strings by tuning until he hears the octave below the lower string.) The summational tones of the two last chords lie between F and F♯ and A♭ and A respectively.
- ↑ 'Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik.' Brunswick, 1863.
