of the Interval survives the operation, unchanged, and asserts itself, with equal force, in the Inversion. In whatever positionthey may be taken, Consonant Intervals remain always [1]consonant; Dissonant Intervals, dissonant; and Perfect Intervals, perfect. [See Interval.]
IV. A Chord is said to be Inverted, when ary note, other than its Root, is taken in the lowest part.
Thus, if the Root of a Common Chord be transposed from the lowest part, to one of the upper parts, and the Third placed in the Bass, the change will produce the Chord of the 6-3. If the Fifth be similarly treated, the result of the transference will be the Chord of the 6-4. Hence, the Chord of the 6-3 is called the First Inversion of the Common Chord; and the Chord of the 6-4, the Second.

If the same process be applied to the Chord of the Seventh, we shall, by successively taking the Third, Fifth, and Seventh, in the Bass, obtain its three Inversions, the 6-5-3, the 6-4-3, and the 6-4-2.

Chords, in their normal form, with the Root in the Bass, are called Fundamental Harmonies: those in which any other note occupies this position are called Derivative, or Inverted Chords. [See Harmony.]
V. A Pedal Point (Point d'orgue) is described as Inverted, when the sustained note, instead of being placed in the Bass, is transferred to an upper part, as in Mozart's Pianoforte Fantasia in C minor (op. 11 ):—
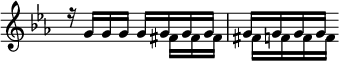
etc.
—or, to a middle one, as in the following passage from Deh vieni, non tardar, (Nozze di Figaro,) where the Inverted Pedal is sustained by the Second Violins:—

In these, and similar cases, the characteristic note (whether sustained, or reiterated), forms no part of the Harmony, which remains wholly unaffected, either by its presence, or removal. [See Harmony.]
[ W. S. R. ]
IONIAN MODE (Lat. Modus Ionicus, Modus Iastius). The Thirteenth—or, according to some writers, the Eleventh—of the Ecclesiastical Modes. [See Modes, the Ecclesiastical.]
The Final of the Ionian Mode is C. Its compass, in the Authentic form, extends upwards, from that note to its octave; and, as its semitones occur between the third and fourth, and the seventh and eighth degrees, its tonality corresponds exactly with that of the major diatonic scale as used in modern music—a circumstance which invests it with extraordinary interest, when considered in connexion with the history of musical science. Its Dominant is G—another point of coincidence with the modern scale. Its Mediant is E, and its Participant, D. Its Conceded Modulations are F, A, and B; and its Absolute Initials C, E, G, and frequently, in polyphonic music, D. Its chief characteristics, therefore, may be illustrated thus
Mode XIII (or XI).

The compass of the Plagal, or Hypo-ionian Mode, lies a fourth lower than that of the Authentic form, ranging from G to G. The Dominant of this Mode is E, its Mediant, A, and its Participant, G. Its Conceded Modulations are D, F, and the F below the initial G; and its Absolute Initials C, G, A, and, in polyphonic music, very frequently D.
Mode XIV (or XII).
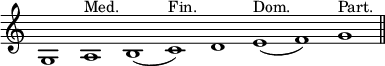
It will be seen, that the semitones here fall between the third and fourth, and sixth and seventh degrees—exactly the position they occupy in the Authentic Mixolydian Mode: and, as the compass of these Modes is also identical, the one is often mistaken for the other, though they are as clearly distinguished, by their respective Finals, as the modern keys of E♭, and F♯ minor.
Though not included in the system set forth by St. Gregory, the Ionian and Hypo-ionian Modes are certainly as old as the 8th or 9th century: for, when the question of the number of Modes to be retained in use was submitted to the Emperor Charlemagne, he at first said that eight seemed to be enough, but afterwards authorised the employment of twelve, thus extending his indulgence to all except the notoriously impure Locrian and Hypolocrian. Eight Modes have, indeed, been always considered enough for the chaunting of the Psalms: hence, we find no Psalm Tones in either the Ionian or Hypo-ionian Modes; though
- ↑ Although the Perfect Fourth—the Inversion of the Perfect Fifth—is classed, by Contrapuntists, among Discords, it only forms an apparent exception the general rule; since it is admitted to be a Consonance, when it appears between the upper parts of a Chord.
