The Mathematical Principles of Natural Philosophy (1729)/Book 1/Section 14

by Isaac Newton

Banner, section XIV

Section XIV.

Of the motion of very small bodies when agitated by centripetal forces tending to the several parts of any very great bofy.

---

Proposition XCIV. Theorem XLVIII.

If two similar mediums be separated from each other by a space terminated on both sides by parallel planes, and a body in its passge through that space be attracted or impelled perpendicular towards either of thos mediums, and not agitated or hindered by any other force; and the attraction be every where the same at equal diameter from either plane, taken towards the same hand of the plane; I say that the fine of incidence upon either plane will be to the due of emergence from the other plane, in a given ratio.

Plate 25, Figure 1

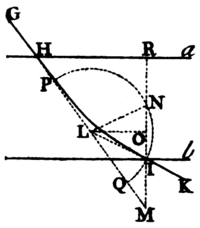
Case. 1. Let Aa and Bb (Pl. 25. Fig. 1.) be two parallel planes, and let the body light upon the first plane Aa in the direction of the line $\scriptstyle GH^{2}$ and in its whole passage through the intermediate space let it be attracted or impelled towards the medium of incidence, and by that action let it be made to describe a curve line HI, and let it emerge in the direction of the line IK. Let there be erected IM perpendicular to Bb the plane of emergence, and meeting the line of incidence GH prolonged in M and the plane of incidence Aa in R; and let the line of emergence KI be produced and meet HM in L. About the centre L, with the interval LI, let a circle be described cutting both HM in P and Q, and MI produced in N; and first, if the attraction or impulse be supposed uniform, the curve HI (by what Galileo has demonstrated) be a parabola, whose property is, that a rectangle under its given latus rectum and the line IM is equal to the square of HM; and moreover the line HM will be bisected in L. Whence if to MI there be let fall the perpendicular LO, MO, OR will be equal; and adding the equal lines ON, OI, the wholes MN, IR will be equal also. Therefore since IR is given MN is also given, and the rectangle NMI is to the rectangle under the latus rectum and IM, than is, to $\scriptstyle HM^{2}$ in a given ratio. But the rectangle NMI is equal to the rectangle PMQ that is, to the difference of the squares $\scriptstyle ML^{2}$, and $\scriptstyle PL^{2}$ or $\scriptstyle LI^{2}$; and $\scriptstyle HM^{2}$ hath a given ratio to its fourth part $\scriptstyle ML^{2}$ therefore the ratio of $\scriptstyle ML^{2}-LI^{2}$ to $\scriptstyle ML^{2}$ is given, and by conversion the ratio of LI to ML, and its subduplicate, the ratio of LI to ML. But in every triangle as LMI, the lines of the angles are proportional to the opposite sides. Therefore the ratio of the line of the angle of incidence LMR to the line of the angle of emergence LIR is given. Q. E. D.

Plate 25, Figure 2

Case 2. Let now the body pass successively through several spaces terminated with parallel planes, AabB, BbbC, &c. (Pl. 25. Fig. 2.) and let it be acted on by a force which is uniform in each of them separetly, but different in the different spaces; and by what was just demonstrated, the sine of the angle of incidence on the first plane Aa is to the line of emergence from the second plane Bb in a given ratio; and this line of incidence upon the second plane Bb will be to the line of emergence from the third plane Cc in a given ratio; and this sine to the sine of emergence from the fourth plane Dd in a given ration; and so on in infinitum and by equality, the sine of incidence on the first plane to the sine of emergence from the last plane in a given ratio. Let now the intervals of the planes be diminished, and their number be infinitely increased, so that the action of attraction or impulse, exerted according to any assigned law, may become continual, and the ratio of the line of incidence on the first plane to the sine of emergence from the last plane being all along given, will be given then also. Q. E. D.

Proposition XCV. Theorem XLIX.

The same things being supposed, I say that the velocity of the body before its incidence is to the veolocity after emergence as the sine of emergence to the sine of incidence.

Plate 25, Figure 3

Make AH and Id equal (PL. 25. Fig. 3.) and erect the perpendicualrs AG, dK meeting the lines of incidence and emergence GH, Ik in G and K. In GH take TH equal to IK, and to the plane Aa let fall a perpendicular Tv. And (by cor. 2. of the laws of motion) let the motion of the body be resolved into two, one perpendicular to the planes Aa, Bb, Cc, &c. and another parallel to them. The force of attraction or impulse, acting in directions perpendicular to those planes, does not at all alter the motion in parallel directions; and therefore the body proceeding with this motion will in equal times go through those equal parallel intervals that lie between the line AG and the point H, and between the point I and the line JK; that is. they will describe the lines GH, IK in equal times. Therefore the velocity before incidence is to the velocity after emergence as GK to IK or TH, that is as AH or Id to vH, that is (suppoling TH or IK radius) as the force of emergence to the sine of incidence. Q. E. D.

Proposition XCVI. Theorem L.

The same thing being supposed, and that the motion before incidence is swifter than afterwards; I say, that if the {{ls]]ine of incidence be inclined continually, the body will be at last reflected, and the angle of reflexion will be equal to the angle of incidence.

Plate 25, Figure 4

For conceive the body passing between the parallel planes Aa, Bb, Cc, &c. (Pl. 25. Fig. 4.) to describe parabolic arcs as above; and let those arcs be HP, PQ, QR, &c. And the obliquity of the line of incidence GH to the first plane Aa be such, that the sine of incidence may be to the radius of the circle whose sine it is, in the same ratio which the same sine of incidence hath to the sine of emergence from the plane Dd into the space DdeE; and because the sine of emergence is now become equal to radius, the angle of emergence will be a right one, and therefore the line of emergence will coincide with the plane Dd. Let the body come to this plane in the point R; and because the line of emergence coincides with that plane it is manifest that the body can proceed no farther towards the plane Ee. But neither can it proceed in the line of emergence Rd; because it is perpetually attracted or impelled towards the medium of incidence. It will return therefore between the planes Cc, Dd, describing an arc of a parabola QRq; whose principal vertex (by what Galileo has demonstrated) is in R, Cutting the plane Ce in the same angle at q, that it did before at Q; then going on in the parabolic arcs qp, ph, &c. similar and equal to the former arcs QP, PH &c. it will cut the rest of the planes in the same p, h &c. as it did before in P, H, &c. will emerge at last with the same obliquity at h, with which it first impinged on that plane at H. Conceive now the intervals of the planes Aa, Bb, Cc, Dd, Ee, &c. to be infinitely diminished, and the number infinitely increased, so that the action of attraction or impulse, exerted according to any assigned law, may become continual; and the angle of emergence remaining all along equal to the angle of incidence will be equal to the same also at last. Q. E. D.

Scholium.

These attractions bear a great ressemblance to the reflexions and refractions of light, made in a given ratio of the secants, as was discovered by Smelluis; and consequently in a given ratio of the sines, as was exhibited by Des Cartes. For it is now certain from the phænomena of Jupiter' Satellits confirmed by the observations of different Astronomers, that light is propagated in succession, and requires about seven or eight minutes to travel from the Sun to the Earth. Moreover the rays of light that are in our air (as lately was discovered by Grimaldus, by the admission of light into a dark room through a small hole, which I have also tried) in their passage near the angles of bodies whether transparent or opake (such as the circular and rectangular edges of gold, silver and brass coins, or of knives or broken pieces of stone or glass) are bent or inflected round those bodies as if they were attracted to them; and those rays which in their passage come nearest to the bodies are the most inflected, as if they were most attracted; which thing I my self have also carefully observed. And thole which pass at greater distances are less inflected; and those at still greater distances are a little inflected the contrary way and form three

Plate 25, Figure 6

fringes of colours. In Pl. 25. Fig. 6. represents the edge of a knife or any kind of wedge Asb, gowog, fnunf, emtme, dlsld, are rays rays inflected towards the knife in the arcs owo, nun, mtm, lal; which inflection is greater or less according to their distance from the knife. Now since this inflection of the rays is performed in the air without the knife, it follows that the which fall upon the knife are first inflected in the air before they touch the knife. And the case is the same of the rays falling upon glass. The refraction therefore is made, not in the point of incidence, but gradually, by a continual inflection of the rays; which is done partly in the air before they touch the glass, partly (if I mistake not) within the glass, after they have entred it

Plate 25, Figure 7

as is represented (Pl. 25. Fig. 7.) in the rays ckzc, buyb, ahxa, falling upon r, q, p and inflected between k and z, i and y, h and x. Therfore hecause of the analogy there is between the propagation of the rays of light, and the motion of bodies, I thought it not amiss to add the following propositions for optical uses; not at all considering the nature of the rays of light, or enquiring whether they are bodies or not; but only determining the trajectories of bodies which are extremely like the trarectories of the rays.

Proposition XCVII. Problem XLVII.

Supossing the sine of incidence upon any superficies to be in a given ratio to the sine of emergence; and that the inflection of the passs of those bodies near that superficies is performed in a very short space which may be confirmed as a point, it is required to determine such a superficies as may cause all the corpuscles issuing from any one given place to converge to another given place.

Plate 25, Figure 8

Let A (Pl. 25. Fig. 8.) be the place from whence the corpuscles diverge; B the place to which they should converge; CDE the curve line which by its revolution round the axis AB describes the superficies sought; D, E, any two points of that curve; and EF, EG perpendiculars let fall on the paths of the bodies AD, DB. Let the point D approach to and coalesce with the point E; and the ultimate ratio of the line DF by which AD is increased, to the line DG by which DB is diminished, will be the same as that of the sine of incidence to the sine of emergence. Therefore the ratio of the increment of the line AD to the decrement of the line D8 is given; and therefore if in the axis AB there be taken any where the point C through which the curve CDE must pass, and CM the increment of AC be taken in that given ratio to CN the decrement of BC, and from the centres A, B, with the intervals AM, BM there be described two circles cutting each other in D; that point D will touch the curve sought CDE, and by touching it any where at pleasure, will determine that curve. Q. E. I.

Cor. 1. By causing the point A or B to go off sometimes in infinitum, and sometimes to move towards other parts of the point C, will be obtained all those figures which Cartesuis has exhibited in his Optics and Geometry relating to refractions. The invention of which Cartesius having thought fit to conceal, is here laid open in this proposition.

Plate 25, Figure 9

Cor. 2. If a body lighting on any superficies CD (Pl. 25. Fig. 9.) in the direction of a right line AD, drawn according to any law, should emerge in the direction of another right line DK; and from the point C there be drawn curve lines CP, CQ always perpendicular to AD, DK; the increments of the lines PD, QD, and therefore the lines themselves PD, QD, generated by those increments, will be as the sines of incidence and emergence to each other, and é contra.

Proposition XCVIII. Problem XLVIII.

The same thing supposed, if round the axis AB (Pl. 25. Fig. 10) any attractive superficies be described as CD, regular or irregular, through which the bodies issuing from the given place A must pass; it is required to find a second attractive supercies EF, which may make those bodies converge to a given place B.

Let a line joining AB cut the first superficies in C and the second in E, the point D being taken any how at pleasure. And supposing the sine of incidence on the first superficies to s of emergence from the same, and the sine of emergence from the second superficies to the fine of incidence on the same, to as any given quantity M to another given quantity N; then produce AB to G, so that BG may be to CE as M - N to N; AD to H, so AH may be equal to AG; and DF to K so tha DK may be to DH as N to M. Join KB, and about the centre D with the interval DH describe a circle meeting KB produced in L, and raw BF parallel to DL; and the point F will couch the line EF, which being turned round the axis AB will describe the superficies sought. Q. E. F.

For conceive the lines CP, CQ to be every where perpendicular to AD, DF and the lines ER, ES to FB, FD respectively, and therefore QS to be always equal to CE; and (by cor. 2. prop. 97.) PD will be to QD as M to N, and therefore as DL to DK. or FB to FK; and by division as DL−FB or PH−PD−FB to FD or FQ−QD; and by composition as PH−FB to FQ, that is, (because PH and CG, QS and CE are equal) as CE+BG−FR to CE−FS. But (because BG is to CE, as M−N to N) it comes to pass also that CE+BG is to CE as M to N; and therefore, by division, FR is to FS as M to N; and therefore (by cor. 2. prop. 97.) the superficies EF compels a body, falling upon it in the direction DF to go on in the line FR to the place B. Q. E. D.

Scholium.

In the same manner one may go on to three or more superficies. But of all figures the sphærical is the most proper for optical uses. If the object glasses of telescopes were made of two glasses of a sphærical figure, containing water between them; it is not unlikely that the errors of the refractions made in the extreme parts of the superficies of the glasses, may be accurately enough corrected by the refractions of the water. Such object-glasses are to be preferred before elliptic and hyperbolic glasses, not only because they may be formed with more ease and accuracy, but because the pencils of rays situate without the axis of the glass would be more accurately refracted by them. But the different refrangibility of different rays is the real obstacle that hinders optics from being made perfect by sphærical or any other figures. Unless the errors thence arising can be corrected all the labour spent in correcting the others is quite thrown away.

The End of the First Volume.