The Mathematical Principles of Natural Philosophy (1729)/Book 1/Section 5

Section V.
How the orbits are to be found when neither focus is given.
Lemma XVII
If from any point P of a given conic section, to the four produced sides AB, CD, AC, DB of any trapezium ABDC inscribde in that section, as many right lines PQ, PR, PS, PT are drawn in given angles, each line to each side; the rectangle PQ x PR of those on the opposite sides AB, CD, will be to the rectangle PS x PT of those on the other two opposite sides AC, BD, in a given ratio.

Case 1. Let us suppose first that the lines drawn to one pair of opposite sides are parallel to either of the other sides; as PQ and PR (Pl. 8. Fig. 4) to the side AC, and PS and PT to the side AB. And farther, that one pair of the opposite sides, as AC and BD, are parallel betwixt themselves; then the right line which bis€cts those parallel sides will be one of the diameters of the conic section. and will likewise bisect RQ. Let O be the point in which RQ is bisected, and PO will be an ordinate to that diameter. Produce PO to K so that OK may be equal to PO, and OK will be an ordinate on the other side of that diameter. Since therefore the points A, B, P, and K are placed in the conic section, and PK cuts AB in a given angle, the rectangle PQK (by prop. 17. 19. 21. & 23. book 3. of Apolloniu's conics) will be to the rectangle AQB in a given ratio. But QK and PR are equal, as being the differences of the equal lines OK, OP, and OQ, OR; whence the rectangles PQK and PQ x PR are equal; and therefore the rectangle PQ x PR is to the rectangle AQB, that is, to the rectangle PS x PT in a given ratio. Q. E. D.

Case 2. Let us next suppose that the opposite sides AC and BD (Pl. 8. Fig.. 5.) of the trapezium, are not parallel. Draw Bd parallel to AC and meeting as well the right line ST in r, as the conic section in d. loin Cd cutting PQ in r, and draw DM parallel to PQ, cutting Cd in M and AB in N. Then (because of the similar triangles BTt, DBN) Bt or PQ is to Tt as DN to NB. And so Rr is to AQ or PS as DM to AN. Wherefore. by multiplying the antecedents by the antecedents and the consequents by the consequents, as the rectangle PQ x Rr is to the rectangle PS x Tt. so will the rectangle NDM be to the rectangle ANB, and (by case 1.) so is the rectangle PQ x Pr to the rectangle Ps x Pt, and by division, so is the rectangle PQ x PT to the rectangle PS x PT. Q. E. D.

Case 3. Let us suppose lastly the four lines PQ, PR, PS, PT (Pl. 8. Fig. 6.) not to be parallel to the sides AC, AB, but any way inclined to them. In their place draw Pq, Pr parallel to AC; and Ps, Pr parallel to AB; and because the angles of the triangles PQq, PRr, PSs, PTt are given, the ratio's of PQ to Pq, PR to to Pr, PS to Ps, PT to Pt will be also given; and therefore the compounded ratio's PQ X PR to Pq x Pr, and PS x PT to Ps x Pt are given. But from what we have demonstrated before, the ratio of Pq x Pr to Ps x Pt is given; and therefore also the ratio of PQ x PR to PS x PT. Q. E. D.
Lemma XVIII.
The same things supposed, it the rectangle PQ x PR of the lines drawn to the two opposite sdes of the trapezium is to the rectangle PS x PT of those drawn to the other two sides, in a given ratio; the point P, from whence those lines are drawn, will be placed in a conic section described about the trapezium. (PL 8. Fig. 7.)

Conceive a conic sction to he described passing through the points A, B, C, D, and any one of the infinite number of points P, as for example p; I say the point P will be always placed in this section. If you deny the thing, join AP cutting this conic section somewhere else if possible than in P, as in b. Therefore if from those points p and b, in the given angles to the sides of the trapezium, we draw the right lines pq, pr, ps, pt, and bk, bn, bf, bd, we shall have as bk x bn to bf x bd, so (by Lem. I7.) pq x pr to ps x pt; and so (hy supposition) PQ x PR to PS x PT. And because of the similar trapezia bkAf, PQAS, as bk to bf; so PQ to PS. Wherefore by dividing the terms of the preceding proportion by the correspondent terms of this, we shall have bm to bd as PR to PT. And therefore the equiangular trapezia Dubd, DRPT are similar, and consequently their diagonal Dk, DP do coincide. Wherefore b falls in the intersection of the right lines AP, DP, and consequently coincides with the point P. And therefore the point P where-ever it is taken falls to be in the assigned conic section. Q. E. D.
Cor. Hence if three right lines PQ, PR, PS, are
drawn from a common point P to as many other right
lines given in position AB, CD, AC, each to each,
in as many angles respectively given, and the rectangle
PQ x PR under any two of the lines drawn be to
the square of the third in a given ratio: The
point P, from which the right lines are drawn, will be
placed in a conic section that touches the lines AB,
CD in A and C; and the contrary. For the position
of the three right lines AB, CD, AC remain
the same, let the line BD approach to and coincide
with the line AC; then let the line PT come likewise
to coincide with the line PS; and the rectangle PS;
PT will become , and the right lines AB, CD,
which before did cut the curve in the points A and
B, C, and D, can no longer cut, but only touch, the
curve in those co-inciding points.
Scholium.
In this lemma, the name of conic section is to be understood in a large sense, comprehending as well the rectilinear section thro' the vertex of the cone, as the circular one parallel to the base. For if the point p happens to be in a right line, by which the points A and D or C and B are joined, the conic section will be changed into two right lines, one of which is that right line upon which the point p falls, and the other is a right line that joins other two of the four points. If the two opposite angles of the trapezium taken together are equal to two right angles, and if the four lines PQ, PR, PS, PT are drawn to the sides thereof at right angles, or any other equal angles, and the rectangle PQ x PR under two of the lines drawn PQ and PR, is equal to the rectangle PS x PT under the other two PS and PT the conic section will become a circle. And the same thing will happen, if the four lines are drawn in any angles, and the rectangle PQ x PR under one pair of the lines drawn, is to the rectangle PS x PT under the other pair, as the rectangle under the sines of the angles S, T in which the two last lines PS, PT are drawn, to the rectangle under the sines of the angles Q, R, in which the two first PQ, PR are drawn. In all other cases the locus of the point P will be one of the three figures, which pass commonly by the name of the conic sections. But in room of the trapezium ABCD, we may substitute a quadrilateral figure whose two opposite sides cross one another like diagonals. And one or two of the four points A, B, C, D may be supposed to be removed to an infinite distance, by which means the sides of the figure which converge to those points, will become parallel: And in this case the conic section will pass through the other points. and will go the same way as the parallels in infinitum.
Lemma XIX.

To find a point P (Pl. 8. Fig. 8.) from which if four right line: PQ, PR, PS, PT are drawn to as many other right lines AB, CD, AC, BD given by position, each to each, at given angles, the rectangle PQ x PR, under any two of the lines drawn, shall be to the rectangle PS x PT, under the other two, in a given ratio.
Suppose the lines AB, CD, to which the two right lines PQ, PR, containing one of the rectangles, are drawn to meet two other lines, given by position, in the points A, B, C, D. From one of those as A, draw any right line AH, in which you would find the point P. Let this cut the opposite lines BD, CD, in A and I; and, because all the angles of the figure are given, the ratio of PQ to PA, and PA to PS, and therefore of PQ to PS will be also given. Subducting this ratio from the given ratio of PQ x PR to PS x PT the ratio of PR to PT will be given; and adding the given ratio's of PI to PR, and PT to PH the ratio of PI to PH, and therefore the point P will be given. Q. E. I.
Cor. 1. Hence also a tangent may be drawn to any point D of the locus of all the points P. For the chord PD, where the points P and D meet, that is, where AH is drawn thro' the point D, becomes a tangent. In which case the ultimate ratio of the evanescent lines IP and PH will be found asabove. Therefore draw CF parallel to AD, meeting BD in F, and cut it in E in the same ultimate ratio, then DE will be the tangent; because CF and the evanescent IH are parallel, and similarly cut in E and P.

Cor. 2. Hence also the locus of all the points P may be determined. Through any of the points A, B, C, D, as A. (Pl. 9. Fig. 1.) draw AE touching the locus, and through any other point B parallel to the tangent, draw BF meeting the locus in F: And find the point F by this lemma. Bisect BF in G, and drawing the indefinite line AG, this will be the position of the diameter to which BG, and FG are ordinates. Let this AG meet the locus in H, and AH will be its diameter or latus transversum, to which the latus rectum will be as BG to AG x GH. If AG no where meets the locus, the line AH being infinite the locus will be a parabola; and its latus rectum corresponding to the diameter AG will be . But if it does meet it any where, the locus will be an hyperbola, when the points A and H are placed on the side the point G; and an ellipsis, If the point G falls between the points A and H; unless perhaps the angle AGB is a right angle, and at the lime time equal to the rectangle AGH, in which case the locus will be a circle.
And so we have given in this corollary a solution of
that famous problem of the ancients concerning four
lines, begun by Euclid, and carried on by Appolonius
and this not an analytical calculus, but a geometrical
composition, such as the ancients required.
Lemma XX.

If the two opposite angular points A and P (Pl. 9. Fig. 2.) of any parallelogram ASPQ touch any conic section in the points A and P; and the sides AQ, AS of one of those angles, indefinitely produced, meet the same conic section in B and C; and from the points of concourse B and C to any fifth point D of the conic section, two right lines BD, CD are drawn meeting the two other sides PS, PQ of the parallelogram, indefinitely produced, in T and R; the parts PR and PT, cut off from the sides, will always be one to the other in a given ratio. And vice versa, if those parts cut of are one to the other in a given ratio, the locus of the point D will be a conic section, passing through the the four points A, B, C, P.
Case 1. Join BP, CP, and from the point D draw the two right lines DG, DE, of which the first DG shall be parallel to AB, and meet PB, PQ, CA in H, I, G; and the other DE shall be parallel to AC, and meet PC, PS, AB, in F, K, E; and (by Lem. 17.) the rectangle DE x DF will be to the rectangle DG x DH, in a given ratio. But PQ in to DE (or IQ) as PB to HB, and consequently as PT to DH; and by permutation, PQ is to PT, as DE to DH. Likewise PR is to DF as RG to DC, and therefore as (IG or) PS to DG; and, by permutation, PR is to PS as DF to DG; and, by compounding those ratio's, the rectangle PQ x PR will be to tie rectangle PS x PT as the rectangle DE x DF is to the rectangle DG x DH, and consequently in a given ratio. But PQ and PS are given, and therefore the ratio of PR to PT is given. Q. E. D.
Case 2. But if PR and PT are supposed to be in a given ratio one to the other, then by going back again by a like reasoning, it will follow that the rectangle DE x DF is to the rectangle DG x DH in a given ratio; and so the point D (by lem. 18.) will lie in a conic section passing thro' the points A, B, C, P, as its locus. Q. E. D.
Cor 1. Hence if we draw BC cutting PQ in r, and in PT take Pt to Pr in the same ratio which PT has to PR: Then Pr will touch the conic section in the point B. For suppose the point D to coalesce with the point B, so that the chord BD vanishing, BT shall become a tangent, and CD and BT will coincide with CB and Br. Co tt. z. And vice verla, if B r is atangent, and the lines B D, C D meet in any point D of a conic section; P R will be to P Tas Pr to Pr. And on the contrary, if.PR is to PTasPr to Pr, (hm BD, and CD will meet in some point D of a conic section.
Cor. 2. One conic section cannot cut another conic section in more than four points. For, if it is possible, let two conic sections pass thro' the five points A, B, C, P, O; and let the right line BD cut them in the points D, d, and the right line Cd cut the right line PQ in q. Therefore PR is to PT as Pq to PT: Whence PR and Pq are equal one to the other, against the suppossition.
Lemma XXI.
if two moveable and indefinite right lines BM, CM drawn through given paints B, C, at poles, do by their point of course M descrihe a third right line MN given by position; and other two indefinite right lines BD, CD are drawn, making with the former two at those given points B, C, given angler, MBD, MCD: I say that those two right lines BD, CD will lines their point of concourse D descrihe a conic section passing through the points B, C. And vice versa, if the right lines BD, CD do by their point of concourse D describe a conic section passing through the given points B, C, A, and the angle DBM is always equal to the given angle ABC, as well as the angle DCM always equal to the given angle ACB: the point M will lie in a right line given by position, at its locus. Pl. 9. Fig. 3.

For in the right line MN let a point N be given, and when the moveable point M falls on the immoveable point N, let the moveable point D fall on an immoveable point P. Join CN, BN, CP BP, and from the point P draw the right lines PT, PR meeting BD, CD in T and R, and making the angle BPT equal to the given angle BNM and the angle CPR equal to the given angle CNM, Wherefore since (by supposition) the angles MBD, NBP are equal, as also the angles MCD, NCP; take away the angles NBD and NCD that are common, and there will remain the angles NBM and PBT, NCM and PCR equal; and therefore the triangless NCM, PBT are similar, as also the triangles NCM, PCR. Wherefore PT is to NM as PB to NB; and PR to NM, as PC to NC. But the points B, C, N, P are immovable: Wherefore PT and PR have a given ratio to NM, and consequently a given ratio between themselves; and therefore, (by lem. 20.) the point D wherein the moveable right lines BT and CR perpetually concur, will be placed in a conic section passing through the points B, C, P. Q. E. D.
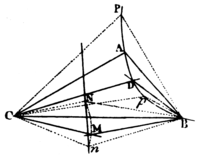
And vice versa, if the moveable point D (Pl. 9. Fig. 4.) lies in a conic section passing through the given points B, C, A; and the angle DBM is always equal to the given angle ABC, and the angle DCM always equal to the given angle ACB, and when the point D falls successively on any two immovable point p, P, of the conic section, the moveable point M falls successively on two immovable points n, N: through these points n, M draw the right line nM, this line nN will be the perpetual locus of that moveable point M. For if possible, let the point M be placed in any curve line. Therefore the point D will be placed in a conic section passing through the five points B, C, A, p, P, when the point M is perpetually placed in a curve line. But from what was demonstrated before, the point D will be also placed in a conic section, passing through the same five points B, C, A, p, P. when the point M is perpetually placed in a right line. Wherefore the two conic sections will both pass through the same given points, against corol. 3. lem. 20. It is therefore absurd to suppose that the point M is placed in a curve line. Q. E. D.
Proposition XXII. Problem XIV.
To describe a trajectory that shall pass through five given given points. Pl. 9 Fig. 5.

Let the five given points be A, B, C, P, D. From any one of them as A, to any other two as B, C, which may be called the poles, draw the right lines AB, AO, and parallel to those the lines TPS, PRQ through the fourth point P. Then from the two poles B, C, draw through the fifth point D two indefinite lines BDE, CRD, meeting with the last drawn lines TPS, PRQ (the former with the former, and the latter with the latter) in T and R. Then drawing
the right line tr parallel to TR, cutting off from the right lines PT, PR, any segments Pt, Pr, proportional to PT, PR; and if through their extremities
t, r, and the poles B, C, the right lines Bt, Cr are drawn, meeting in d, that point d will be placed in the trajectory required. For (by lem. 20.) that point d is placed in a conic section passing
through the four points A, B, C, P; and the lines Rr, Tt vanishing, the point d comes to coincide with the point D. Wherefore the conic section passes through the five points A, B, C, P, D. Q. E. D.
The same otherwise. Pl. 9. Fig. 6.
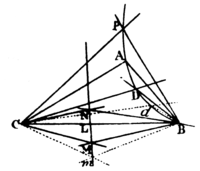
Of the given points join any three as A, B, C; and about two of them B, C, as poles, making the angles ABC, ACB of a given magnitude to revolve, apply the legs BA, CA, first to the point D, then to the point P, and mark the points M, N, in which the other legs BL, CL intersect each the other in both cases. Draw the indefinite right line MN and let those moveable angles revolve about their poles B, C, in such manner that the intersection, which is now supposed to be m, of the legs BL, CL, or BM, CM and always fall in that indefinite right line MN; and, the intersection which is now supposed to be d, of the legs BA, CA, or BD, CD, will describe the trajectory required PADdB. For, (by lem. 21.) the point d will be placed in a conic section passing through the points B, C; and when the point m comes to coincide with the points L, M, N, the point d will (by construction) come to coincide with the points A, D, P. Wherefore a conic section will be described that shall pass through the five points A, B, C, P, D. Q. E. F.
Cor. 1. Hence a right line may be readily drawn which shall be a tangent to the trajectory in any given point B. Let the point d come to coincide with the point B, and the right line Bd will become the tangent required.
Cor. 2. Hence also may be found the centres,
diameters, and latera recta of the trajectories, as
in cor. 2. lem. 19.
Scholium.
The former of these constructions (Fig. 5.) will become something more simple by joining BP, and in that line, produced if need be, taking Bp to BP as PR is to PT; and through p drawing the indefinite right line be parallel to SPT; and in that line pe taking always pe equal to Pr; and drawing the right lines Be, Cr to meet in d. For since Pr to Pt, PR to PT, pB to PB, pe to Pt, are all in the same ratio, pe and Pr will be always equal. After this manner the points of the trajectory are most readily found, unless you would rather describe the curve mechanically as in the second construction.
Proposition XXIII. Problem XV.
To describe a trajectory that shall pass through four given points, and touch a right line given by position. Pl. 10. Fig. 1.

Case 1. Suppose that HB is the given tangent,
B the point of contact, and C, D, P, the three other
given points. Join BC, and drawing PS parallel
to BH, and PQ parallel to BC, compleat the
parallelogram BSPQ. Draw BD cutting SP in
T and CD cutting PQ in R. Lastly, drawing any
line tr parallel to TR, cutting off from PQ, PS,
the segments Pr, Pt proportional to PR, PT respectively;
and drawing Cr, Bt, their point of concourse
will (by lem. 20.) always fall on the trajectory
to be described.
The same otherwise. Pl. 10. Fig. 2.

Let the angle CBH of a given magnitude revolve about the pole B, as also the rectilinear radius DC both ways produced. about the pole C. Mark the points M, N, on which the leg BC of the angle cuts that radius when BH the other leg thereof meets the same radius in the points P and D. Then drawing the indefinite line MN, let that radius CP or CD and the leg BC of the angle perpetually meet in this line; and the point of concourse of the other leg BH with the radius will delineate the trajectory required.
For if in the constructions of the preceding problem the point A comes to a coincidence with the point B the lines CA and CB will coincide, and the line AB, in its last situation, will become the tangent BH; and therefore the constructions there set down will become the same with the constructions here described. Wherefore the concourse of the leg BH with the radius will describe a conic section passing through the points C, D, P, and touching the line BH in the point B. Q. E. F.

Case 2. Suppose the four points B, C, D, P, (Pl. 10. Fig. 3.) given, being situated without the tangent HI join each two by the lines BD, CP, meeting in G, and cutting the tangent in H and I. Cut the tangent in A in such manner that HA may be to IA, as the rectangle under mean proportional between CG and GP, and a mean proportional between BH and HD, is to a rectangle under a mean proportional between GD and GB, and a mean pr0portional between PI and IC; and A will be the point of contact. For if HX, a parallel to the right line PI, cuts the trajectory in any points X and Y; the point A (by the properties of the conic sections) will come to be so placed, that will become to in a ratio that is compounded out of the ratio of the rectangle XHY to the rectangle BHD, or of the rectangle CGP to the rectangle DGB; and the ratio of the rectangle BHD to the rectangle PIC. But after the point of contact A is found, the trajectory will be described as in the firft case. Q. E. F. But the point A may be taken either between or without the points H and I; upon which account a twofold trajectory may be described.
Proposition XXIV. Problem XVI.
To describe a trajectory that shall pass through three given points, and touch two right lines given by position. Pl. 10. Fig. 4.

Suppose HI, KL to be the given tangents, and B, C, D, the given points. Through any two of those points as B, D, draw the in indefinite right line BD meeting the tangents in the points H, K. Then likewise through any other two of these points as C, D, draw the indefinite right line CD, meeting the tangents in the points I, L. Cut the lines drawn in R and S, so that HR may be to KR, as the mean proportional between BH and HD is to the mean proportional between BK and KD; and IS to LS, as the mean proportional between CI and ID is to the mean proportional between CL and LD, But you may cut, at pleasure, either within or between the points K and H, I and L, or without them; then draw RS cutting the tangents in A and P, and A and P will be the points of contact. For if A and P are supposed to be the points of contact situated any where else in the tangents, and through any of the points H, I, K, L, as I, situated in either tangent HI a right line IT is drawn, parallel to the other tangent KL, and meeting the curve in X and I and in that right line there be taken IZ equal to a mean proportional between IX and IT; the rectangle XIT or , will (by the properties of the conic sections) be to , as the rectangle CID is to the rectangle CLD, that is (by the construction) as is to , and therefore IZ is to LP; as SI to SL. Wherefore the points S, P, Z, are in one right line. Moreover, since the tangents meet in G, the rectangle XIY or will (by the properties of the conic sections) be to as is to , and consequently IZ will be to IA, as GP to GA. Wherefore the points P, Z, A, lie in one right line, and therefore the points S, P, and A are in one right line. And the same argument will prove that the points R, P, and A are in one right line. Wherefore the points of contact A and P lie in the right line RS. But after these points are found the trajectory may be described as in the first case of the preceding problem. Q. E. F.
In this proposition, and case 2. of the foregoing, the constructions are the same, whether the right line XY cut the trajectory in X and Y or not; neither do they depend upon that section. But the constructions being demonstrated where that right line does cut the trajectory, the constructions, where it does not, are also known; and therefore, for brevity's sake, I omit any farther demonstration of them.
Lemma XXII.
To transform figures into other figures of the same kind. Pl. 10. Fig. 5.

Suppose that any figure figure, HGI is to be transformed. Draw, at pleasure, two parallel lines AO, BL, cutting any third line AB given by pssition, in A and B, and from any point G of the figure, draw out any right line GD, parallel to OA, till it meet the right line AB. Then from any given point O in the line OA, draw to the point D the right line OD, meeting BL in d, and from the point of concourse raise the right line dg containing any given angle with the right line BL, and having such ratio to Od, as DG has to OD; and g will be the point in the new figure hgi, corresponding to the point G. And in like manner the several points of the first figure will give as many correspondent points of the new figure. If we therefore conceive the point G to be carried along by a continual motion through all the points of the first figure, the point g will be likewise carried along by a continual motion through all the points of the new figure, and describe the same. For distinction's sake, let us call DG the first ordinate, dg the new ordinate, AD the first abscissa, ad the new abscissa; O the pole, OD the abscinding radius, OA the first ordinate radius, and Oa (by which the parallelogram given OAB is compleated) the new ordinate radius.
I say, then, that if the point G is placed in a right line given by position, the point g will be also placed in a right line given by position. If the point G is placed in a conic section, the point will be likewise placed in a conic section. And here I understand the circle as one of the conic sections. But farther, if the point G is placed in a line of the third analytical order, the point g will also be placed in a line of the third order, and so on in curve lines of higher orders. The two lines in which the points G, g, are placed, will be always of the same analytical order. For as ad is to OA, so are ad to OD, dg to DG, and AB to AD; and therefore AD is equal to and DG equal to . Now if the point G is placed in a right line: and therefore, in any equation by which the relation between the abscissa AD and the ordinate DG is expressed, those in determined lines AD and DG rise no higher than to one dimension, by writing this equation in place of AD, and in place of DG, a new equation will be produced, in which the new abscissa ad and new ordinate dg rise only to one dimension; and which therefore must denote a right line, But if AD and DG (or either of them) had risen to two dimensions in the first equation, ad and dg would likewise have risen to two dimensions in the second equation. And so on in three or more dimensions. The indetermined lines ad, dg in the second equation, and AD, DG, in the first will always rise to the same number of dimensions; and therefore the lines in which the points G, g, are placed are of the same analytical order.
I say farther, that if any right line touches the curve line in the first figure, the same right line transferred the same way with the curve into the new figure, will touch that curve line in the new figure. and vice versa. For if any two points of the curve in the first figure are supposed to approach one the other till they come to coincide; the same points transferred will approach one the other till they come to coincide in the new figure; and therefore the lines with which those points are joined will come together tangents of the curves in both figures. I might have given demonstrations of these assertions in a more geometrical form; but I study to be brief.
Wherefore if one rectilinear figure is to be transformed into another we need only transfer the intersections of the right lines of which the first figure consists, and through the transferred intersections to draw right lines in the new figure. But if a curvilinear figure is to be transformed we must transfer the points, the tangents, and other right lines, by means of which the curve line is defined. This lemma is of use in the solution of the more difficult problems. For thereby we may transform the proposed figures if they are intricate into others that are more simple, Thus any right lines converging to a point are transformed into parallels; by taking for the first ordinate radius any right line that passes through the point of concourse of the converging lines, and that, beause their point of concourse is by this means made to go off in infinitum, and parallel lines are such tend to a point infinitely remote. And after the problem is solved in the new figure, if by the inverse operations we transform the new into the first figure we shall have the solution required.
This lemma is also of use in the solution of solid problems. For as often as two conic sections occur, by the intersection of which a problem may be solved; any one of them may be transformed, if it is an hyperbola or a parabola, into an ellipsis then this ellipsiss may be easily changed into a circle. So also a right line and a conic section, in the construction of plane problems, may be trasformed into a right line and a circle.
Proposition XXV. Problem XVII.
To desecribe a trajectory that shall pass through two given points, and touch three right lines given by position. Pl. 10, Fig. 6.
Through the concourse of any two of the tangents one with the other, and the concourse of the third
tangent with the right line which passes through
two given points, draw an indefinite right line; and,
taking this line for the first ordinate radius, transform
the figure by the preceding lemma into a new figure.
In this figure those two tangents will become
parallel to each other, and the third tangent will be
parallel to the right line that passes through the two
given points. Suppose hi, kl to be those two
parallel tangents. ik the third tangent, and bl a right
line parallel thereto, passing through thos points a, b, through which the conic section ought to pass in this
new figure; and compleating the parallelogram hikl,
let the right lines hi, ik, kl be so cut in c, d, e,
that be may be to the square root of the rectangle
ahb, ic to id, and ke to kd, as the sum of the
right lines hi and kl is to the sum of the three
lines. the first whereof is the right line ik, and the
other two are the square roots of the rectangles ahb
and alb; and c, d, e, will be the points of contact.
For by the properties of the conic sections
to the rectangle ahb, and to ,
and to and to the rectangle alb,
are all in the same ratio; and therefore hc to
the square root of ahb, ic to id, kc to kd,
and el to the square root of alb, are in the
subduplicate of that ratio; and by composition
in the given ratio of the sum of all the antecedents
hu + kl, to the sum of all the consequents
. Wherefore from that given ratio
we have the points of contact c, d, c, in the
new figure. By the inverted operations of the last,
lemma, let those points be transferred into the first
figure, and the trajectory will be there described by
prob. 14. Q. E. F. But according as the points
a, b, fall between the points h, l, or without them,
the points c, d, e, must be taken either between the
points b, i, k, l, or without them. If one of the
points h, l, falls between the points h, l, and the
other without
the points h, l, the problem is impossible.
Proposition XXVI. Problem XVIII.
To describe a trajectory that shall pass through a given point, and touch four right lines given by position. Pl. 11. Fig. 1

From the common intersections of any two of
the tangents to the common intersection of the other
two draw an indefinite right line; and taking
this line for the first ordinate radius transform the
figure (by lem. 22.) into a new figure, and the
two pairs of tangents each of which are concurred
in the first ordinate radius will now become
parallel. Let hi and kl, ik and hl, be those points
of parallels compleat, the parallelogram hikm. And
let p be the point in this new figure corresponding to
the given point in the first figure. Through O the
centre of the figure draw pq; and Oq being equal to
Op, q will be the other point through which the
conic section mull pass in this new figure. Let
this point be transferred by the inverse operation of
lem. 22. into the first figure. and there we shall
have the two points, through which the trajectory
is to be described. But through those points that
trajectory may be described by prob. 17. Q. E. F.
Lemma XXIIII.
If two right lines as AC, BD given by position, and terminating in given points A, B, are in a given ratio one to the other, and the right line CD, by which the indetermined points CD are joined, is cut in K in a given ratio; I say that the point K will be placed in a right line given by position. Pl. 11. Fig. 2.

For let the right lines AC, BD meet in E, and
in BE take BG to AE, as BD is to AC, and
let FD be always equal to the given line EG;
and by construction, EC will be to GD, that is,
to EF, as AC to BD, and therefore in a given
ratio; and therefore the triangle EFC will be given
in kind. Let CF be cut in L so as CL may
be to CF in the ratio of CK to CD; and because
that is a given ratio, the triangle EFL will
be given in kind, and therefore the point L will
be placed in the right line EL given by position.
Join LK and the triangles CLK, CFD will be
similar; and because FD is a given line, and LK
is to FD in a given ratio, LK will be also given.
To this let EH be taken equal, and ELKH will
be always a parallelogram. And therefore the point
K is always placed in the side HK (given by position)
of that parallelogram. Q. E. D.
Cor. Because the figure EFLC is given in kind the three right lines EF, EL and EC, that is GD, HK and EC will have given ratio's to each other.
Lemma XXIV.
If three right lines, two whereof are parallel, and given by position, touch any conic section; I say, that the semidiameter of the section which is parallel to those two is a mean proportional between the segments of those two, that are intercepted between the points of contact and the third tangent. Pl. 11. Fig. 3.

Let AF, GB be the two parallels touching the conic section ADB in A and B; EF the third right line touching the conic section in I, and meeting the two former tangents in F and G, and let CD he the semi-diameter of the figure parallel to those tangents; I say, that AE, CD, BG are continually proportional.
For if the conjugate diameters AB, DM meet the tangent FG in E and H, and cut one the other in C, and the parallelogram IKCL be compleated; from the nature of the conic sections, EC will be to CA as CA to CL, and so by division, EC - CA to CA - CL or EA to AL; and by composition, EA to EA + AL or EL, as EC to EC + CA or EB; and therefore (because of
EBG) AF is to LI as CH to BG. Likewise from the nature of the conic sections, LI (or CK) is to CD as CD to CH; and therefore ex æquo perturbate) AF is to CD, as CD to BG. Q. E. D.
Cor. 1. Hence if two tangents FG, PQ meet two parallel tangents AF, BG in F and G, P and Q and cut one the other in O; AF (ex æquo pertubate) will be to BQ as AP to BG, and by division, as FP to GQ and therefore as FP to OG.
Cor. 2. Whence also the two right lines PG, FQ drawn through the points P and G, F and Q, will meet in the right line ACB, passing through the centre of the figure and the points of contact A, B.
Lemma XXV.

If four sides of a parallelogram indefinitely produced touch any conic section, and are cut by a fifth tangent; I say, that taking thosse segments of any two conterminous side which is intercepted between the point of contact and the third side, is to the other segment. Pl. 11. Fig. 4.
Le the four sides ML, IK, KL, MI of the parallelogram MLIK touch the conic section in A, B, C, D; and let the fifth tangent FQ cut those sides in F, Q, H and E, and taking the segments ME, KQ of the sides MI, KI; or the segments KH, MF of the sides KL, ML; I say, that ME is to MI as BK to KQ; and KH to KL, as AM to MF. For, by cor. 1. of the preceding lemma, ME is to EL as (AM or) BK to BQ; and, by composition, ME is to MI as BK to KQ. Q. E. D. Also KH is to HL as (BK or) AM to AF and by division KH to KL, as AM to MF. Q. E. D.
Cor. 1. Hence if a parallelogram IKLM described about a given conic section is given, the rectangle KQ×ME, as also the rectangle KH×MF equal thereto, will be given. For, by reason of the similar triangles KQH, MFE, those rectangles are equal.
Cor. 2. And if a sixth tangent eq is drawn meeting the tangents KI, MI in q and e; the rectangle KQ×ME will be equal to the rectangle Kq×Me, and KQ will be to Me, as Kq to ME, and by division as Qq to Ee.
Cor. 3. Hence also if Eq, eQ are joined and bisected, and a right line is drawn through the points of bisection, this right line will pass through the centre of the conic section. For since Qq is to Ee, as KQ to Me; the same right line will pass through the middle of all the lines Eq, eQ, MK (by lem. 22.) and the middle point of the right line
MK is the centre of the section. Proposition XXVII. Problem XIX.
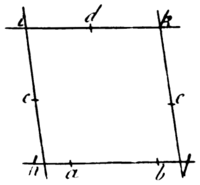
To describe a trajectory that may touch five right lines given by position. Pl. 11 . Fig. 5.

supposing ABG, BCF, GCD, FDE, EA to be the tangents given by position. Bisect in M and N, AF, BE the diagonals of the quadrilateral
figure ABFE contained under any four of them;
and (by cor. 3. lem. 25) the right line MN drawn through the points of bisection will pass through the centre of the trajectory. Again. bisect in P and Q the diagonals (if I may so call them) BD, GF of the quadrilateral figure BGDF contained under any other four tangents, and the right line PQ drawn through the points of bisection will pass through the centre of the trajectory. And therefore the centre will be given in the concourse of the bisecting lines. Suppose it to be O. Parallel to any tangent BC draw KL, at such distance that the centre O may be placed in the middle between the parallels; this KL will touch the trajectory to be described. Let this cut any other two tangents GCD, FDE, in L and K. Through the points C and K, F and L, where the tangents not parallel CL, FK meet the parallel tangents
CF, KL, draw CK, FL meeting in R; and the right line OR drawn and produced, will cut the parallel tangents CF, KL, in the points of contact. This appears from cor. 3. lem. 24. And by the same method the other points of contact may be found, and then the trajectory may be described
by prob. 14. Q. E. F.
Scholium.
Under the preceding propositions are comprehended those problems wherein either the centres or asymptotes of the trajectories are given. For when points and tangents and the centre are given, as many other points and as many other tangents are given at an equal distance on the other side of the centre. And an asymptote is to be considered as a tangent, and its infinitely remote extremity (if we may say so) is a point of contact. Conceive the point of contact of any tangent removed in infinitum, and the tangent will degenerate into an asymptote, and the constructions of the preceding problem will be changed into the constructions of those problems wherein the asymptote is given.

After the trajectory is described, we may find its axes and foci in this manner. In the construction and figure of lem. 21. (Pl. 12. Fig. 1.) let those legs BP, CP, of the moveable angles PBN, PCN, by the concourse of which the trajectory was described, be made parallel one to the other; and retaining that position, let them revolve about their poles in that figure. In the mean while let the other legs CN, BN of those angles, by their concourse K or k, describe the circle BKGC. Let O be the centre of this circle; and from this centre upon the ruler MN, wherein those legs CN, BN did concur while the trajectory was described, let fall the perpendicular OH meeting the circle in K and L. And when those other legs CK, BK meet in the point K that is nearest to the ruler, the first legs CP, BP will be parallel to the greater axis and perpendicular on the lesser; and the contrary will happen if those legs meet in the remotest point L. Whence if the centre of the trajectory is given, the axes will be given; and those being given, the foci will be readily found.
But the squares of the axes are one to the other as KH to LH, and thence it is easy to describe a trajectory given in kind through four given points. For if two of the given points are made the poles C, B, the third will give the moveable angles PCK, PBK; but those being given, the circle BGKC may be described. Then, because the trajectory is given in kind, the ratio of OH to OK, and therefore OH it self will be given. About the centre O, with the interval OH, describe another circle. and the right line that touches this circle and passes through the concourse of the legs CK, BK, when the first legs CP, BP, meet in the fourth given point, will be the ruler MN, by means of which the trajectory may be described. Whence also on the other hand a trapezium given in kind (excepting a few cases that are impossible) may be inscribed in a given conic section.
There are also other lemma's by the help of
which trajectories given in kind may be described
through given points, and touching given lines.
Of such a fort is this, that if a right line is drawn
through any point given by position. that may cut
a given conic section in two points, and the distance
of the intersections is bisected, the point of
bisection will touch another conic section of the
same kind with the former, and having its axes
parallel to the axes of the former. But I hasten
to things of greater use.
Lemma XXVI.
To place the three angles of a triangle both in kind and magnitude, in respect of as many right line given by position, provided they are not all parallel among themselves, in such manner that the several angles may touch the several lines. (Pl. 12. Fig. 2.)
Three indefinite right lines AB, AC, BC, are given by position, and it is required so to place the triangle DEF that its angle D may touch the line AB, its angle E the line AC, and its angle F the line BC. Upon DE, DF and EF, describe three segments of circles DRE, DGF, EMF, capable of angles equal to the angles BAC, ABC, AVB respectively. But those segments are to described towards such sides of the lines DE, DF, EF, that the letters DRED may turn round about in the same order with the letters BACB; and the letters DGFD in the same order with the letter ABCBA; and the letters EMFE in the same order with the letters ACBA; then completing those segments into entire circles, let the two former circles cut one the other in G, and suppose P and Q to be their centres. Then joining GP, PQ take Ga to AB, as GP is to PQ; and about the centre G, with the interval Ga describe a circle that may cut the first circle DGE in a. Join aD cutting the second circle DFG in b, as well as aE cutting the third circle EMF in c. Compleat the figure ABCdef similar and equal to the figure absDEF. I say the thing is done.
For drawing Fc meeting aD in n, and joining aG, bG, QG, QD, PD; by construction the angle EaD is equal to the angle CAB, and the angle acF equal to the angle ACB; and therefore the triangle anc equiangular to the triangle ABC. Wherefore the angle anc or FnD is equal to the angle ABC, and consequently to the angle FbD; and therefore the point n falls on the point b. Moreover the angle GPQ which is half the angle GPD at the centre is equal to the angle GaD at the circumference; and the angle GQP, which is half the angle GQD at the centre, is equal to the complement to two right angles of the angle GbD at the circumference, and therefore equal to the angle Gab. Upon which account the triangles GPQ, Gab, are similar, and Ga is to ab as GP to PQ; that is (by construction) as Ga to AB. Wherefore ab and AB are equal; and consequently the triangles abc, ABC, which we have now proved to be similar, are also equal. And therefore since the angles D, E, F, of the triangle DEF do respectively touch the sides ab, ac, be of the triangle abc, the figure ABCdef may be compleated similar and equal to the figure abcDEF, and by compleating it the problem will be solved. Q. E. F.
Cor. Hence a right line may be drawn whose parts given in length may be intercepted between three right lines given by position. Suppose the triangle DEF, by the access of its point D to the side EF, and by having the sides DE, DF placed in directum to be changed into a right line whose given part DF is to be interposed between the right lines AB, AC given position; then by applying the preceding construction to this case, the problem will be solved.
Proposition XXVIII. Problem XX.
To describe a trajectory given both in kind and magnitude, given parts of which shall be interposed berween three right lines given by position. (Pl. 12. Fig. 3.)
Suppose a trajectory is to be described that may be similar and equal to the curve line DEF, and may be cut by three rights lines AB, AC, BC, given by position, into parts DE and EF, similar and equal to the given parts of this curve line.
Draw the right lines DE, EF, DF; and place the angles D, E, F, of this triangle DEF, so as to touch those right lines given by position (by lem. 26). Then about the triangle describe the trajectory, similar and equal to curve DEF. Q. E. F.
Lemma XXVII.
To describe a trapezium given in kind, the angles whereof may be so placed in respect offout right lines given by position, that are neither all parallel among themselves nor converge to one common point, that the several lines.. Pl. 13. Fig. 1.
Let the four right lines ABC, AD, BD, CE, be given by position; the first cutting the second in A, the third in B, and the fourth in C; and suppose a trapezium fghi is to be described, that may be similarl to the trapezium FGHI; and whose angle L equal to the given angle F, may touch the right line ABC; and the other angles g, h, i, equal to the other given angles G, H, I, may touch the other lines AD, BD, CE, respectively. Join FH, and upon FG, FH, FI describe as many segments of circles FSG, FTH, FVI; the first of which FSG may be capable of an angle equal to the angle BAD; the second FTH capable of an angle equal to the angle CBD; and the third FVI of an angle equal to the angle ACE. But the segments are to be described towards those sides of the lines FG, FH, FI, that the circular order of the letters FSGF may be the same as of the letters BADB, and that the letters FTHF may turn about in the same order as the letters CDBC, and the letter FIVIF in the same order as the letters ACEA. Complete the segments into entire circles, and let P be the centre of the first circle FSG, Q the centre of the second FTH. Join and produce both ways the line PQ, and in it take QR in the same ratio to PQ as BC has to AB. But QR is to be taken towards that side of the point Q, that the order of the letters P, Q, R may be the same, as of the letters A, B, C; and about the centre R with interval RF describe a fourth circle FNc cutting third circle FVI in c. Join Fc cutting the first circle in a and the second in b. Draw aG, bH cI, and let the figure abcFGHI be made similar to the figure abcFGHI; and the trpezium fghi will be taht which was requited to be described.
For let the two first circles FSG, FTH cut one the other in K; join PK, QK, EK, aK, bK, cK, and and produce QP, to L. The angles FaK, FbK, FcK at the circumferences, are the halves of the angles LPK, LQK, LRK, the halves of those angles. Wherefore the figure PQRK is equiangular and similar to the figure abcK, and consequently ab is to bc as PQ to QR, that is, as AB to BC. But by construction, the angles fAg, fBh, fVi are equal to the angles FaG, FbH, FcI. And therefore the figure abcFGHI. Which done, a trapezium fghi will be constructed similar to the trapezium FGHI, and which by its angles, f, g, h, i will touch the right lines ABC, AD, BD, CE. Q. E. F.
Cor. Hence a right line may be drawn whose part intercepted in a given order, between four right lines given by position, shall have a given proportion among themselves. Let the angles FGH, GHI, be so far increased that the right lines FG, GH, HI, may lie in direction, and by constructing the problem in this case, a right line fghi will be drawn, whose parts fg, gh, hi, intercepted between the four right lines given by position, AB and AD, AD and BD, BD and CE, will be one to another as the lines FG, GH, HI, and will observe the same order among themselves. But the same thing may be more readily done in this manner.
Produce AB to K (Pl. 13. Fig. 2.) and BD to L, so as BK may be to B, as HI to GH; and DL to BD as GI to FG; and join KL meeting the right line CE in i. Produce iL to M, so as LM may be to iL as GH to HI; then draw MQ parallel to LB and meeting the right line AD in g, and join gi cutting AB, BD in f, h. I say the thing is done.
For let Mg cut the right line AB in Q and AD the right line KL in S, and draw, AP parallel to BD, and meeting iL in P, and gM to Lb (gi to bi, Mi to Li, GI to HI, AK to BK) and, AP to BL will be in the same ratio. Cut DL in R, so as DL to RL may be in that same ratio; and because gS to gM, AS to AP, and DS to DL are proportional; therefore (ex æquo) as gS to Lb, so will AS be to BL, and DS to RL; and mixtly BL - RL to Lh - BL, as AS - DS to gS - AS. That is, BR is to Bh, as AD is to Ag, and therefore as BD to gQ. And alternately BR is to BD, as Bh to gQ, or as fh to fg. But by construction the line BL was cut in D and R, in the same ratio as the line FI in G and H; and therefore BR it to BD as FH to FG. Wherefore fh is to fg as FH to FG. Since therefore, gi to hi likewise is as Mi to Li, that is, as GI to HI, it is manifest that the lines FL, fi, are similary cut in G and H, g and h. Q. E. F.
In the construction of this corollary, after the line LK is drawn cutting CE in i, we may produce iE to V, so as EV may be to Ei as FH to HI, and then draw Vf parallel to BD. It will come to the same, if about the centre i, with an interval IH, we describe a circle cutting BD in X, and produce iX to Y so as iY may be equal to IF, and then draw Yf parallel to BD.
Sir Christopher Wren, and Dr. Wallis have long ago given other solutions of this problem.
Proposition XXIX. Problem XXI.
To describe a trajectory given in kind, that may be cut by four right lines given by position, into parts given in order, kind and proportion.

Suppose a trajectory is to be described that may be similar to the curve line FGHI (Pl. 13 Fig. 4.) and whose parts. similar and proportional to the parts FG, GH, HI of the other, may be intercepted between the right lines AB and AD, AD and BD, BD and CE given by position, viz. the first between the first pair of those lines, the second between the second, and the third between the third. Draw the right lines FG, GH, HI, FI; and (by lem. 27.) describe a trapezium fghi that may be similar to the trapezium FGHI, and whose angles f, g, h, i, may touch the right lines given by position, AB, AD, BD, CE, severally according to their order. And then about this trapezium describe a trajectory, that trajectory will be similar to the curve line FGHI.
Scholium.
This problem may be likewise constructed in the following manner. Joining FG, GH, HI, FI, (Pl. 13. Fig. 4.), produce GF to V, and join FH, IG, and make the angles CAK, DAL equal to the angles FGH, VFH. Let AK, AL meet the right line BD in K and L, and thence draw KM, LM of which let KM make the angle AKM equal to the angle GHI, and be it self to AKM as HI is to GH; and let LN make the angle ALN equal to the angle FHI, and be it self to AL, as HI to FH But AK, KM, AL, LN are to be drawn towards those sides of the lines AD, AK, AL, that the letters CAKMC, ALKA, DALND may be carried round in the same order as the letters FGHIF; and draw MN meeting the right line CE in i. Make the angle iEP equal to the angle IGF and let PE be to Ei, as FG to GI; and through P draw PQf that may with the right line ADE contain an angle PQE equal to the angle FIG, and may meet the right line AB in f, and join fi. But PE and PQ are to be drawn towards those sides of the lines CE, PE, that the circular order of the letters PEiP and PEQP may be the same, asof the letters FGHIF, and if upon the line fi, in the same order of letters, and similar to the trapezium FGHI, a trapezium fghi is constructed, and a trajectory given in kind is circumscribed about it, the problem will be solved.
So far concerning the finding of the orbits. It remains that we determine the motions of bodies in the orbits so found.





















