Translation:The Principle of Relativity (Laue 1913)
III. The theory of relativity, kinematic part.
§ 6. The Lorentz transformation.
[edit]The[1] relativity principle claims: From the totality of natural phenomena, one can determine with increased approximation and increased exactitude, a reference system x, y, z, t in which the natural laws are valid in certain, mathematically simple forms. This reference system is, however, in no way uniquely defined by the phenomena. There is rather a three-times infinite manifold of equally valid systems, mutually moving with uniform velocity.
From this principle, we want to derive the transformation equations leading from one valid reference system to another. Therefore, we require the knowledge of an arbitrary natural law; which of them is chosen by us, must principally be irrelevant. If one arrives by a different choice at different results, then all laws wouldn't be invariable with respect to the same transformation, thus the relativity principle would be wrong. Evidently, such laws related to physical processes in empty space, are the most simple ones. Since in the other ones, the velocity of matter relative to the references system is included in its mathematical formulation, and must be co-transformed by a transformation; in vacuum, however, were we know nothing about moving things, this complication vanishes. We know of only two different actions propagating through vacuum, gravitation and electromagnetic processes. About the propagation of the first one we know nothing else than that its velocity is very great against astronomical velocities. That it is greater than the speed of light, although it is often claimed, finds no support in experience. Much better is our knowledge of the law of light propagation in vacuum, since it is proven by Michelson's experiment (with a precision which is hardly attained in other physical measurements) that it is equal in all directions with respect to all systems. We add the assumption, which goes beyond the experimental results but which is required by the relativity principle, that the speed of light has got in all systems the same value . The following consideration will be based on this law.
At first, we consider an example. From a material point at rest in a valid reference system at the origin of coordinates, a short light signal emanates at time into all directions. At time the points receiving this signal are all located upon a sphere, whose equation reads:
Two material points and (also resting in , and located at the same distance from on the same line with ), consequently are receiving the signal simultaneously, i.e. for the same value of .
The same process we relate now to another valid system moving relative to the first one with velocity in the direction . The material points thus have in the velocity parallel to . The origin of coordinates as well as time can evidently be defined by us, so that the light signal is emitted at time at origin (of primed coordinates) by the material point . After expiration of time , all points of the sphere
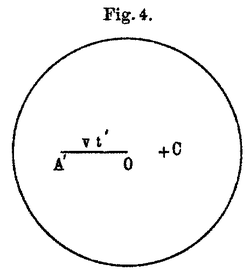
are reached by the signal. However, since has now moved away from to by the distance , there is no value for which the material points and (equally distant from ) are located on such a sphere; thus they won't be simultaneously reached by the signal, rather (as shown by Fig. 4) this happens earlier in than in , since approaches the light sphere, while runs away from it. Two events simultaneous in , are in general not simultaneous in . The identical transformation for time, which forms a part of the Galilean transformation, cannot be maintained at this place.
This forces us to subject the concept of time to a critical investigation. We measure the time at a place by clocks, however, we don't need to think of the usual mechanical instruments for which the periods of elastic oscillations serve as the measure of time, but we can read the time in terms of progression of any physical process, as long as we can control its causes so that no unknown or quantitatively uncontrollable reasons can act. Such completely equal clocks are located by us at different places of space, all in one and the same valid system . Thus the equality of the measure of time is guaranteed for all those places. However, to arrive at a unitedly defined time for the whole system , we must synchronize the clocks, i.e. the zero-points of their time indications must be brought into a suitable relation. This is given to us by the requirement, that in system the speed of light shall have the value , and namely is independent of the beam direction. If two clocks are mutually distant by , then the time indication of the first one (when a light signal is emanating from here) shall differ from that of the second one (when arriving here) by the amount . This definition doesn't lead to an inherent contradiction, when the clocks are (in pairs) combined on different ways. Namely, if the clocks in the arbitrarily chosen points and are synchronous with a clock at an arbitrary third point , and if we send at time a light signal from to , which is sent back without time loss to , and from there it is sent back to , then it's time of return is , since it has traversed the distance . It has reached point by the presupposition of synchronism of the clocks in and , when the clock in indicated the time , and has left point when the clock in indicated the time because of the synchronism of the clocks in and . When the signal started in and when it arrives in , the difference between the time indications of the clocks in and is , i.e. the clocks in and are mutually synchronous. – Events are simultaneous, when they occur at equal indications of clocks located at the places of the events.
That one achieves a specific time for any valid system, by which it differs from the other valid systems, is already shown by the previous example. Herein lies the boldness and the high philosophical meaning of Einstein's thought, that he removes the traditional prejudice of a time valid for all systems. As enormous this revolution (to which he forces our thinking) may be, there is not the slightest epistemological difficulty in it. Because time is (as space in Kant's way of expression) a pure form of our intuition; a scheme into which the events must be classified, so that they (contrary to subjective and highly accidental perceptions) gain objective meaning, and thus it is one of the conditions for the possibility of objective facts of experience. This classification can only be done on the basis of empirical knowledge of natural laws. Location and time of the observed change of a celestial body, for example, can only found out on the basis of optical laws. That two differently moving observers, when anyone considers himself as at rest, make this classification on the basis of the same natural laws in a different manner, doesn't contain a logical impossibility. However, both classifications have objective meaning, since from any of them (by means of the transformation formulas to be derived) one can unequivocally derive the valid classification for differently moving observers.
For example, one shall think of two astronomers on different, mutually moving celestial bodies, which are able to exchange thoughts with each other. They would find out, that they would have essentially different time indications of all astronomic events; and all of this (although they apply the same physical foundations as we will assume) because of the single reason that any of them considers himself as at rest. Consequently, the quarrel between them would result in the question, who of them is right with his assumption. According to the relativity principle, this is undecidable, both assumptions are completely equally valid. The time indications of both are just related to different systems. With this insight and with the aid of the transformation equation, the proof must be possible, that the meaning of both kinds of time specification is throughout the same, because they can be completely computed into each other.
To arrive at the transformation formulas, we ask after those linear relations between and which transform the wave equation
into itself; i.e. to which the identity applies:
| (25) |
where is a proportionality factor, which is different from zero and dependent (in a unknown way at first) on . Because equation (22) is the mathematical formulation of the law of light propagation[2]. We choose this substitutions as linear, because otherwise the coordinates and the origin of time (at least in one of both systems) would become preferred points, which cannot be displaced without essential changes. But we consider the equal validity of all spatial points and temporal moments as an empirically verified natural law, equally valid for both systems according to the relativity principle. Furthermore we define, that corresponding coordinate axes in both systems are parallel, namely the - and -axis by which the primed system is moving against the unprimed , shall be parallel to the velocity ; and that eventually the values shall correspond to the values . The most general equations which satisfy these conditions, read:
| (26) |
where and are functions of still to be determined. Namely, it is clear at first, that there is only one preferred direction, that of the -axis. Already because of this reason, and cannot occur in the equation for , since otherwise the direction would be preferred whose direction cosines behave as the coefficients of . Furthermore, plane must be identical with plane , plane with that of , and with that of . The proportionality factor between and as well as between and eventually must be the same because of the equal validity of all directions normal to .
However, additionally it can be shown, that it must be
Namely, from the start it must be clear, that can only be a function of , i.e. . Whether the motion of against happens in the positive or negative -direction, it is of course the same process for the - and -direction. On the other hand, the inversion of
must read:
since the motions of against and those of against only differ by the direction of . From that it follows, however, the value 1 for because of .
By substitution (26) a function arises now:
from which it follows:
If the equation (25) shall represent an identity, then in the course of summation of the last four equations and the multiplication with , the coefficients
must become equal to , while that of must vanish, i.e. it must be
| (27) |
For and we choose the positive sign, so that for the reference system becomes equal to , as it must be by the previous definition concerning the location of both cross-axes. Equations (26) then assume the form;
| (XI) |
Due to the equal validity of both systems it must be permitted, to permute the primed and unprimed magnitudes with each other in these equations, as long as one only reverses the signs of simultaneously, because system has (against ) the velocity parallel to the -axis. Thus one finds:
| (XIa) |
The calculation shows, that (XIa) is actually the inversion of (XI). The totality of equations (XI) or (XIa) we denote as a Lorentz transformation; the relativity principle claims, that all reference systems arising by such transformations from a valid reference system, are not only completely equally valid for the propagation of electromagnetic actions in vacuum, but also for all physical processes.
The first of equations (27) () shows by (25), that the expression is invariant with respect to a Lorentz transformation. One easily can convince himself, that instead of this, one can also use the invariance of expression as characteristic for a Lorentz transformation; namely, if one determines the coefficients in (26) for the latter requirement, then one finds the exact same values as above.
As well as the totality of all Galilean transformations, also the totality of all Lorentz transformations forms a group; if one applies (one after the other) two of them with arbitrarily directed relative velocities , then one obtains a result to be reached by a single transformation as well. Because, when both in the linear passage of a system to and in the linear passage of to , the expression
remains unchanged, then this is also the case in the (also linear) immediate passage from to .
We further notice, that it must be
| (28) |
otherwise the coefficients of (XI) would become imaginary or infinite.
§ 7. The kinematics of Einstein.
[edit]In order to discuss formulas (XI) and (XIa), we first investigate the rate of a clock at rest in the primed system (x'=const), as viewed from the unprimed system, by constantly comparing its hand position with the indication of the clock at rest in K at which it just passes by. According to (XIa), the time interval which will be read from it by a co-moving observer, corresponds (since is invariant) to the interval
which will be detected by an observer in system K by comparison of the times, that were given by two clocks (at rest in the start- and endpoint of the now completed distance) during the start and the arrival of the moving one. This can also be derived from (XI); because in time , the clock in system K travels the distance , from which it follows
| (29) |
The rate of a clock moving with velocity is thus slower in the ratio than for the same clock when at rest. This theorem is of course true, independent to which of the valid system we relate the expressions "at rest" or "in motion". We of course have to consider as a clock, every process whose progression can serve as a measure of time. In a moving hydrogen atom (canal rays), for example, the light-emanating proper oscillations will have a smaller frequency than in a stationary one.
Now we consider two equal clocks. Both are initially at rest in a valid reference system at the same location. The second one will be accelerated by us in a quasi-stationary way, i.e. so that its inner condition is always dependent only on the instant velocity, not on the acceleration. We let remain the clock for some time at uniform velocity, then we reverse it by quasi-stationary acceleration, and in this way we bring back the clock to its origin, where we — again quasi-stationary — bring it to rest. So in every moment of this process, the moving clock's rate is slower than the stationary clock, and thus it is retarded with respect to the latter. — This consequence of the theory of relativity, which was further explained in a very interesting manner namely by Langevin,[3] initially appears to be so paradox, that it even was subject to the objection,[4] that it disproves the principle of relativity; because it would be possible to consequently decide, which of the two clocks was at rest, and which one was in motion. Indeed we can decide, which one of the clocks was steadily at rest in one and the same reference system, and which one was in the meantime at rest in two or more such systems. However, among them there is of course a real physical difference. (see § 8.)
Quite similar relations occur with respect to measurements of the length of a moving rod. If it is at rest in and located parallel to the -axis, then its rest length is determined by the difference of the -coordinates of its endpoints, thus:
those can be determined by applying a measuring rod also at rest in . Its length related to is, however, equal to the difference of the -coordinates, which are to be attributed to its endpoints for equal values of t; therefore it follows from (XI):
| (30) |
The length of a body parallel to the direction of motion is considered greater (when viewed from the co-moving system) than in any other system. If we bring a rod under maintenance of its inner condition[5] (like in empty space and without heat supply) from a state of rest to velocity , then it contracts in the ratio ; namely if we call the system in which it was at rest at the beginning, and the other system in which it will be at rest after acceleration, then its length in the second state related to , will exactly have the value , as the length which it had in the first state of .

This theorem justifies the contraction hypothesis, employed by Fitzgerald[6] and Lorentz[7] (presented already before the theory of relativity) for the explanation of Michelson's experiment, and it is indeed necessarily required when one wants the give the theory of this experiment for an non-co-moving system. Namely, if in Fig. 1 (p. 14) the distance is contracted (in its motion parallel to it) to length , then the traversing time becomes by (13) and (14):
During the rotation of the apparatus, which is followed by the permutation of the roles of and , no replacement of the interference fringes takes place. That this time itself is still dependent on , lies in the fact that it is related to that system, in which the interferometer has the velocity . In the co-moving system , the traversing time would be according to (29), as it must be, since in the distances and are traversed with velocity .
The dimensions normal to motion were not altered by (XI). Consequently the angles, which were formed by a material line with the direction of velocity or another line, are in general different in and ; as well as the angles between two material planes or between a plane and a line. The volume of a body is to be transformed by the Lorentz transformation because of the same reason as the length parallel to the velocity. Since by that, in every system is equal to the volume in the co-moving system, if follows that the equation, which serves as the transformation formula for the volume of a body with velocity relative to and relative to , is:
| (31) |
Another consequence of contraction is, that the form of a body is differently seen in different systems. For example, a body that has (investigated in a co-moving system) a spherical form, is an oblated ellipsoid of revolution in all other systems.
In its first half (namely as far as it is spoken about the assessment of the lengths of different systems), the theorem on p. 43 is the consequence of different ways of application of the space- and time-scheme by differently moving observers. The two astronomers, about who we spoke on p. 38, despite of the same geometric foundations would be getting into quarrel, as soon as they apply them on real bodies. They just assess their shape in an essentially different way. But the main points of their quarrel would be located in the mutually contradicting assumptions concerning their state of rest. As soon as these assumptions would be recognized, it would be possible to transform both indications into each other by a Lorentz transformation. – In its second half, however, every theorem includes a statement about mechanics; the elastic forces that determine the shape of the body, must be influenced by motion so that they exactly cause this contraction.
As the last kinematic consequence, the transformation formula for the velocity of a material point shall be derived. If its coordinates in system are functions of time , then the velocity components are:
The corresponding definition applies to its velocity with respect to . From (XI) it follows, however:
thus
| (32) |
or, when one inversely expresses by :
| (33) |
If one mutually multiplies the equations in (32) and (33) related to the - or -components, then one finds:
| (34) |
Furthermore, a simple calculation shows, by squaring and adding the three equations (32) and is replaced by the scalar products :
| (35) |
From (31), (34) and (35) it follows:
| . | (36) |
Eventually, if we denote by the angle between velocity and the -axis, then it holds according to (33):
| (37) |
since
| (37a) |
These equations show, as to how the velocities and are composed when viewed from system ; they contain the famous Einstein addition theorem of velocity[8].
The most remarkable thing there, is that both velocities that have to be added, are not equally valid. For example, if is parallel to , parallel to , then by (33) under the assumption, that one adds to by setting instead of , instead of and , the resulting velocity obtains the components:
however, when in reverse is added to , where the indices 1 and 2 and furthermore the - and -direction permute their roles, then the velocity is given with components:

The absolute value is the same for both cases [see also the symmetric relation (37) in and ], however, the directions are different (Fig. 5). If we imagine a material right-angled triangle with velocity displaced parallel to the first side, and introduce a pencil along the second side with velocity , then its top follows on the drawing plane the line in unit time. However, if we replace the triangle parallel to the second side with velocity and the pencil along the first one with velocity , then its top follows the line [9].
By (28) . If we let grow starting from 0, then whatever the direction of may be, the denominator in (35) cannot vanish, as long as . The right-hand side therefore remains positive and finite, until it vanishes for .
To the value of corresponds, of course, the value , satisfying (35) as well. If is steadily increasing starting with this value, then also must be steadily changing, namely in a way, so that the left-hand side of (35), , as well as the right-hand side remain positive, until . For that, however, to a value of must necessarily correspond a value , however, to the value must correspond a value . Two added subluminal velocities thus again and again give a subliminal velocity. The addition of the velocity of light to a subluminal velocity gives the velocity of light. The latter plays in physics the role of an infinitely great velocity throughout, in so far as it can never be reached by an accumulation of subluminal velocities. There, also the determination represents no restriction of generality.
Not only the velocity of bodies, but also the physical actions of any kind, may they be propagating in vacuum or in matter, cannot exceed the velocity of light . If the action of an event occurring at time at point in system , would be propagating with velocity to point , then it would arrive there later in time by
By the last of equations (XI), the duration of this propagation, related to , would be:
Thus, by the choice of a sufficiently great value for subluminal velocity , one can achieve that becomes zero or even negative, i.e. there would be a valid system, in which the effect in would chronologically preceding the cause; however, this is impossible, since the natural law in question would remain unchanged in the passage from to in opposition to the relativity principle, when cause and effect would permute their roles with respect to time and causality.
This consequence from the relativity principle is only apparently refuted by the fact, that in dispersing bodies the refractive index is for some spectral areas, thus the "velocity of light" is . Because is namely the velocity, by which the phases of periodic waves propagate in the stationary state, i.e. when they are distributed over the whole space. As to the propagation of a suddenly occurring electromagnetic disturbance, it has no immediate meaning. The first precursor of such a disturbance, the head of the wave, is rather propagating, according to the theory of electrons, steadily with the velocity of light . [Sommerfeld[10]].
Also if one leads (in a valid system) a ruler above a resting second one which is nearly parallel, then the intersection of both can easily travel with superluminal velocity; since its velocity (like that of the first ruler) is divided by the angle between both, and can be increased above any limit by decreasing this angle. This contains no contradiction to the above; since the intersection is no material point, it also cannot be used to transfer actions along the resting ruler. It would be easy to install mechanisms upon it, which cause any physical event (like rings of bells) in the moment when the intersection passes them; and then one can claim in a certain sense, that the rings of bells are propagating with superluminal velocity. However, if one removes any number of these devices again, then the other ones will work as before – a clear sign that these rings of bells are not connected as cause and effect. Their common cause is rather in the motion of the second ruler.
However, it would be in contradiction to the previous theorems, when it would be possible to realize the following case: "At a point of the resting ruler, we again install one of the mentioned devises. At the beginning, also the second ruler is at rest; the intersection of both may coincide at that stage with point of the first one. However, afterwards an arbitrary event takes place in , by which the second ruler is practically momentarily brought into uniform motion. The intersection then traverses the resting ruler as the signal of the occurrence of the event in , and the event caused by it in becomes the effect of the cause happening in . The transfer from to happens with superluminal velocity."
Now, whey isn't it possible to realize the mentioned process between the quotes? Would the second ruler, as previously assumed, really be rigid and incapable of changes of shape, then it would indeed be executable. The transfer of the driving motion starting from would occur momentarily by the elastic forces. And by that we arrive at the reason of this contradiction. The assumption of a rigid body is incompatible with relativity theory. The ruler bulges (under all circumstances) at first in and then it doesn't remain straight; the conclusion to a superluminal velocity of the intersection, however, is essentially based on its straightness.
That any action through vacuum, thus also gravitation, must be propagated at the speed of light , when the relativity principle shall be correct, follows from the reasoning, that otherwise one obtains a substitution (by transfer of the consideration leading to equation (XI)), which would be different from (XI) by the value of , therefore it would define (together with (XI)) a preferred system again.
§ 8. Minkowski's geometric interpretation of the Lorentz transformation.
[edit]The principle of relativity, as it was announced in § 6 and mathematically formulated in the Lorentz-Transformation (XI), completely contains the foundations of relativity theory. Though the calculations partly become inelegant and complicated, because with respect to every vector, one has to transform the component parallel to velocity in a different way than the perpendicular ones. It is the great merit of the so early deceased mathematician of Göttingen, Hermann Minkowski, to have created a geometric interpretation that avoids this difficulty, and due to the elegance that it lends to the calculations of relativity theory, it forms a nearly indispensable tool for the reliable usage of it.[11]
In general, all coordinates are concerned by a Lorentz transformation. Only our special assumption concerning the location of the axis-cross in the systems and gave rise to the identical transformation in (XI) for the - and -coordinate. However, since also time must be altered, it can be easily seen that a geometric analogy can only consist in a four-dimensional manifold. That such one is inaccessible to our intuition, shall not frighten us; it is only about a symbolic illustration of certain analytical relations between four variables. We denote this manifold as "the world" and choose as "world coordinates" the space coordinates and the time coordinate
| (38) |
The -axes shall be mutually perpendicular; the -axis preliminarily shall also be perpendicular upon the three mentioned axes, i.e., and shall at first be ordinary rectangular coordinates in the -plane, and corresponding relations shall apply in the - and -plane. Then there are six coordinate planes (pairwise mutually perpendicular), and four (three-dimensional) coordinate spaces (mutually perpendicular). A point of this manifold we call a "world point"; it represents an event taking place at location at time .
The space coordinates are functions of time for any material point; thus it determines a curve in the world, a "world-line". At uniform velocity it is a straight line whose angle with respect to the -axis is equal to , thus it is smaller than , because ; in general it is an arbitrary curved line, whose inclination with respect to the -axis, however, never reaches the given amount.
In the special case of § 6, where the - and -axis are parallel to the translatory velocity, the transformation only takes place in the -plane, which we want to use as drawing plane (Fig. 6). Therein we draw hyperbolas of equal sides:
| (39) |
| (40) |
as well as their common pair of asymptotes:
| (41) |
From origin we draw the line in the direction of any point of that branch of the first hyperbola, for which is positive;

afterwards a second line into a point of branch of the second hyperbola; is thus determined, so that the asymptote becomes the angle bisector, i.e. that and become conjugate diameters for both hyperbolas (39) and (40). If U falls upon the -axis in the direction of , than coincides with . The Lorentz transformation (XI) consists in the fact, that instead of line and , one uses and as axes; and instead of the distances and , one uses and as distances.
Indeed: the lines and have the equations
The coordinates of and are therefore according to (39) and (40):
| (42) |
However, now in the primed system it should become:
The four constants available by a linear transformation from to , are definitely specified by that; the transformation equations thus must read:
| (43) |
according to (38), they go over into (XI) if one puts
| (44) |
The expression as well as therefore remain invariant with substitution (43). The equations of both hyperbolas and their pairs of asymptotes, read the same in the primed system as well as in the unprimed system. Angle in Fig. 6 is specified by equation
| (45) |
With respect to every world point of the -plane, for which , one evidently can draw a time-axis starting from , with direction when , and with direction when ; because there is alway a conjugate diameter to as the -axis. Conversely, every world point for which , can be made "simultaneous" to , by choosing the line with appropriate direction as the -axes, and its conjugate diameter as -axis.
To represent the general Lorentz transformation, at which the spatial axis-crosses and are arbitrarily oriented to the relative velocity , we have to design this construction in a four-dimensional way. Instead of hyperbolas, the two-sheet hyperbolic space occurs:
| (46) |
and the single-sheet hyperbolic space:
| (47) |
both will be asymptotically contacted by the conic space
| (48) |
The hyperbolas in Fig. 6 and their asymptotes are the intersections of those three-dimensional spaces with the -plane.
Now we choose, upon the positive sheet of the two-sheet hyperbolic space (46), an arbitrary point with coordinates , and draw in its direction the line from . Then we construct the conjugate diameter-space to this diameter:
| (49) |
which intersects the single-sheet hyperbolic space (47) into an ellipsoid. If falls into the vertex of the first hyperbolic space, than the conjugate diameter-space becomes the -space and the ellipsoid becomes a sphere
| (50) |
and all distances from in the direction of a point of this sphere have the same length 1; it is the measuring surface for distances in space . The general Lorentz transformation now consists in this, that instead of the line as -axis and the distance as unity, and instead of the -space with sphere (50) as measuring surface, we render the line (with as unity-distance) as the -axis, and its conjugate diameter-space with the mentioned ellipsoid as measuring surface we render as the corresponding -space. The latter condition expresses, that the equation of the ellipsoid should read
For confirmation, we first change the coordinate system by a rotation executed in -space; remains totally untouched here, while the sum is invariant; the same also holds for the expression . By rotation it can be achieved, that the intersection of -space becomes the plane (located through the and axis) to the -axis. By an analogous rotation of coordinate system , we move the -axis into the same plane. However, then we have the same relations as in Fig. 6: and became the (by construction) conjugate diameter of hyperbola , and since is invariant with respect to the special transformation illustrated there, then this also holds for the generalized construction now given, by which it proves to be a Lorentz transformation. Thus there exist as many valid systems as points in the positive sheet of hyperbolic space (46), i.e. three-times infinitely many, as already mentioned earlier. The mutual velocity of both systems is specified by the angle between the - and the -axis according to equation (45).
The conical space (48) separates the world into three parts:
1. . One can place a time-axis with direction after every world point of this area; it contains the world-points "beyond ", i.e. those arising later than in all valid systems.
2. . The world points of this area are arising earlier than in all systems, they are "on this side of ". One can draw a time-axis with direction with respect to them.
3. . Of the points of this "intermediary area", one can make three of them simultaneous with , because together with they specify an even space, forming a valid reference system with the conjugate diameter with respect to hyperbolic space (46). In this one, the three world points share the time with .
With respect to conical space (48) itself, we distinguish the "for-cone" for which , and the "after-cone" for which . The first one encloses those world points representing events, from which a possible effect propagating with the speed of light arrives at point at time . The after-cone on the other hand, represents the totality of events happening simultaneously with the arrival of a possible light-effect emanating from . We say, that the former ones "are sending light in the direction of ", and the latter ones "are receiving light from there".
Due to the invariance of expression , both hyperbolic spaces (46) and (47) as well as the conic space (48) have an absolute meaning; their equation is the same in all reference systems. Therefore, also this arrangement of

the world is independent from the reference system. Its physical meaning can be seen from the following consideration:
The world points and in Fig. 7 may represent two material points and at rest in ; the first at time when an arbitrary effect emanates from it; the latter at time when this effect reaches . Now, if the velocity (by which it propagates) could be greater than , then it would be
;
belongs to the intermediary area of , as it is also drawn in Fig. 7. Thus valid systems would always exist, in which as in system of the figure, i.e. would be earlier than ; thus the effect would arrive at before its cause would have taken place in . This geometric consideration thus again disproves the possibility of superluminal speeds (see p. 48 and 49). Thus all world points in a position to causally influence , are lying beyond or upon the after-cone, and all points from which can suffer such an influence, are on this side or upon the for-cone of . Points of the intermediary space, however, can never be in causal connection with .
For an infinitely small distance on the -axis or a curve-section parallel to it, it is given by the second of equations (43)
,
however, according to the first of these equations and due to ,
thus
| . | (51) |
The equation includes, like formula (29) with which it is identical, the theorem that a clock at rest in , when related to , is retarded. If we denote by dx, dy, dz the projections of the distance (as covered in time dt) upon the coordinate axes, and by q the velocity, then it is given
.
Furthermore, dx, dy, dz, du are the components of the worldline-element covered in time dt. By (51) the time increase is thus given
| (52) |
which is indicated by the clock while it traverses the element. We denote by the proper time of that worldline-element. For a finite section of a worldline, we find it by integration. The proper time of a worldline-section is an invariant of the Lorentz transformation. This already becomes clear due to its physical meaning, since the hand positions of the clock are the same for all reference systems at the start and the end of that section; this we can also recognize by the fact, that the expression in (52) is transformed the same way, as the invariant expression . However, it is to be noticed, that that equation (52) is initially derived only for uniformly moving clocks, i.e. derived for straight worldlines. In general, the acceleration will have an influence on the rate. Only when the acceleration is sufficiently small, i.e. the curvature of the worldlines is sufficiently weak, the proper time will directly have the given physical meaning. Where the limit for that is located, depends on the constitution of the clock. However, the proper time defined by (52), is always a mathematically useful concept.
Of all worldlines, which connect two given worldpoints 1 and 2, the straight connection has the longest proper time. Because, if we put the z-axis parallel to it — the choice of reference system is totally arbitrary due to the invariance of proper time —, then by (52) the proper time for this line is , though for another connecting line it is
.
Of the two clocks, of which we have spoken on pp. 42 and 43, one covers the straight worldline from 1 to 2, yet the other one covers a broken line. We confirm at this place, that the second one is retarded at the re-encounter; because its worldline corresponds to a shorter proper time. Simultaneously we also see the physical difference of both motions in the most illustrative way.
Let us come back to Fig. 7 once more. The endpoints of a rod (parallel to the -axis and at rest in ) are following straight (parallel to the -axis) world lines and . The ratio denotes its rest length . If a second rod is at rest in , then the world lines of its endpoints are two lines and parallel to the -axis, and its rest length which also may be equal to , is represented by the ratio . The length of the first rod in is, however, , because and are the -coordinates of its endpoints for the same value (0) of . Analogously, the length of the second rod in is . Now, according to (42):
furthermore according to Fig. 7 and (45):
Thus for the first rod
| (53) |
and for the second
| (54) |
Thus we confirm the theorem already found in §7, that a body when viewed from the co-moving system, appears to be longer than from any other system. Since it is chosen in Fig. 7 that , it thus can be seen that .
§ 9. The Lorentz transformation as an imaginary rotation
[edit]Analytically,[12] it is even more elegant to use the imaginary quantity
| (55) |
as time variable, where an imaginary point of the -manifold indeed corresponds to any real world-point. Thus it is
| (56) |
As we have seen in § 6, a Lorentz transformation is characterized by the invariance of this expression.
Let us first consider the simple case of the transformation expressed in (XI) and (43) again, by which only and are concerned. If we introduce into (43) instead of , then we find:
| (57) |
Now we can define an imaginary angle , so that
| (58) |
By (45), it is connected with angle of Fig. 6 and 7 by the relation
| (59) |
If one expresses by in (57), then one finds the equations:
| (60) |
and as their inversions:
| (61) |
If and were real quantities, this would mean that the coordinate system emerges from system by a clockwise rotation around the angle . But also here we can maintain the following mode of expression without doubts. The special Lorentz transformation (XI) is a rotation of the axis-cross in the -plane by the imaginary angle defined by (58).[13][14]
If one successively executes several such transformations in the -plane of rotational angles , then a single rotation around the angle
is resulting. The velocity of the th with respect to the th system, is according to (59):
that of the latter with respect to the first is accordingly:
The function
however, when its argument traverses the purely imaginary value from zero to , only increases from zero to value . Therefore it is under all circumstances and . The speed of light remains unreachable, as we have already seen in § 7.
If is confined to two terms, then it follows:
Einstein's addition theorem for velocities of same direction [see the first of relations (33)], thus directly emerges from the addition theorem of the tangent function.[9]
Already in § 8 (p. 55) we saw, that the most general Lorentz transformation can be derived from rotations of the spatial axis-cross in the systems and , as well as from the special transformation (43) being identical with (XI) and (57). All properties of the general one can already be recognized in the latter transformation; for example, the general one has always to be interpreted as an imaginary rotation in the plane determined by the - and -axis, to which only the inessential real rotations of the coordinate systems and are supplemented.
Analytically it is more elegant, however, to investigate in a quite general way those linear transformations of the world-coordinate system , which represent a Lorentz transformation, i.e., in which the expression (56) stays invariant. This task indeed corresponds to the question after the substitutions, which represent a rotation of the space-coordinate system . Because these are characterized by the invariance of . (see appendix under b.)
If shall follow from the linear substitution
| (62) |
then (as the calculation shows) the equations
| (63) |
must be satisfied, which are formed analogously to the condition of orthogonality (p. 255) throughout. Therefore only 6 of the 16 coefficients are arbitrary.[15] If we combine equations (61) for once with , and then with etc., one finds as there solutions with respect to the unprimed quantities:
| (64) |
so that by analogy of (63), it is also
| (65) |
We denote the determinant of the coefficient as :
| (66) |
their sub-determinants we denote as usually as . Resolving (62) into must give the form now:
etc.,
thus it must by according to (64)
| (67) |
If one substitutes these values into (66), if follows for the determinants of the sub-determinants:
According to a known theorem, however, we have when the number of the column is , thus in our case we have , therefore it must be
| ; | (68) |
because is excluded, since is a steady function of the coefficient, and with an identical transformation etc. it evidently has the value . By (67) it is then
| (69) |
We can combine transformations (62) and (64) into the scheme (being intelligible without further explanation):
| (XII) |
If the substitution (XII) shall represent a Lorentz transformation, the coefficients: 1. must satisfy the conditions of orthogonality (63) and (65); 2. those containing the index 4 once, must be purely imaginary, all others must be real; 3. its determinant and must be positive. We have added conditions 2., so that from the real values and an imaginary value of , real values for and imaginary values for are emerging again and again. Yet, must be positive since is always the cosine of the imaginary angle between the - and the -axis, thus [see (58)]:
One can see this most easily, when one derives the general transformation from the special substitution (57) in the way discussed above. This special transformation in which the - and -coordinate remains unchanged, can be found, when
| (70) |
and if one sets all other coefficients to zero. Thus their scheme looks as follows:
| (71) |
For the sub-determinants of second order , conditions apply corresponding to formulas (63) and (65). (The upper indices are always related to rows, the lower ones to the columns of .) As the coefficients themselves, these sub-determinants are real when the index 4 occurs not at all or twice, and purely imaginary when its appears once.
According to a known theorem, it is for an arbitrary determinant
By (67) and (68) it follows from that:
or more general if we denote as the sub-determinants supplementing :
| (72) |
Furthermore, a known theorem concerning the representability of a determinant as the sum of the production of sub-determinants, says:
By (68) and (72) we conclude from that:
| (73) |
We further imagine determinant as derived from , by replacing the terms of the second row by the corresponding ones of the third row; it is of course zero. Thus by the theorem now employed:
However, now it is
thus by (72):
| (74) |
Eventually we imagine determinant as formed in a way, where in not only the terms of the second row are replaced by the ones of the third row, but also those of the first are replaced by the corresponding ones of the fourth row. Then it is:
thus
| (75) |
Due to the equality of rows and columns in (73), (74), (75), one can permute the upper with the lower indices.
If one arranges the sub-determinants by this scheme:
then equations (73), (74), and (75) and their (not written) generalizations have the meaning: If one squares and adds the terms in the row or the column, then one obtains the value 1; if one multiplies the corresponding terms of two different rows or columns, then one finds the value zero at the addition.
The coefficients and the sub-determinants will be used in the following in the definition of the four- and six-vectors.
In the special transformation (57), the sub-determinants [see (70)] are:
| (76) |
all others are zero. The given scheme thus has the following shape:
| (77) |
In this way, one easily confirms the given rules.
- ↑ A. Einstein, Zur Elektrodynamik bewegter Körper. Ann. d. Phys. 17, 891, 1905; Jahr. der Radioaktivität u. Elektronik 4, 411, 1907
- ↑ The relation of with respect to both field strengths, is irrelevant up to a certain degree. By § 5, (22) is valid for any linear combination of their coordinates. Therefore it is not of interest here, whether has the same meaning in both reference systems. By § 14, any of such linear combinations goes over in another combination of the same kind when transformed.
- ↑ P. Langevin, Scientia 10, 31, 1911.
- ↑ M. Laue, Phys. Zeitschr. 13, 118, 1912
- ↑ In section VII we will call such accelerations adiabatic-isopiestic.
- ↑ O. Lodge, London Transact. (A) 184, 727, 1893
- ↑ H. A. Lorentz, v. Amsterdam, Ziggingsverlag, Acac. v. Wet. 1, 74, 1892.
- ↑ It may be alluded to the fact, that velocity is related to another system as . If both are to be related to the same system, the ordinary vector addition must of course apply to them. The velocity of light against a moving rod, related to a non-co-moving system, is for example still the vector sum of its velocity against the system and that of the rod; the explanation of Michelson's experiment, as it was given by us in § 2, thus remains valid (neglecting the modification forced by the Lorentz contraction) in relativity theory too.
- ↑ 9.0 9.1 A. Sommerfeld, Phys. Zeitschr. 10, 826, 1909.
- ↑ A. Sommerfeld, Phys. Zeitschr. 8, 841, 1907; Weberfestschrift, Leipzig 1912, p. 338.
- ↑ H. Minkowski, Raum und Zeit, Phys. Zeitschr. 10, 104, 1909. Also published as brochure. Leipzig. B. G. Teubner, 1909
- ↑ H. Minkowski, Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern, Göttinger Nachr. 1907, p. 1, and Mathematischen Ann. 68, 472, 1910, also separately published at B. G. Teubner, Leipzig 1911.
- ↑ The difference of the geometries in - and space is basically as follows: In the first we have to do with Euclidean geometry, yet it includes an imaginary coordinate; in the latter the coordinates are real, yet geometry becomes non-Euclidean [Klein]. To the imaginary Euclidean rotation around corresponds the real non-Euclidean rotation around
- ↑ F. Klein, Phys. Zeitschr. 12, 17, 1911. V. Variczak, Phys. Zeitschr. 11, 93, 287, 586, 1910.
- ↑ Of these six degrees of freedom, three are related to rotations of the spatial axis-cross , so that only three remain for the passage from a valid system to another one.
![]()
![]() This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
| Original: |
This work is in the public domain in the United States because it was published before January 1, 1929. The longest-living author of this work died in 1960, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 63 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
Public domainPublic domainfalsefalse |
|---|---|
| Translation: |
This work is released under the Creative Commons Attribution-ShareAlike 3.0 Unported license, which allows free use, distribution, and creation of derivatives, so long as the license is unchanged and clearly noted, and the original author is attributed.
Public domainPublic domainfalsefalse |






















































































































































































































































































































