What is the Fourth Dimension?
Limitations of Our Existence
AT the present time our actions are largely influenced by our theories. We have abandoned the simple and instinctive mode of life of the earlier civilizations for one regulated by the assumptions of our knowledge and supplemented by all the devices of intelligence. In such a state it is possible to conceive that a danger may arise, not only from a want of knowledge and practical skill, but even from the very presence and possession of them in any one department, if there is a lack of information in other departments. If, for instance, with our present knowledge of physical laws and mechanical skill, we were to build houses without regard to the conditions laid down by physiology, we should probably—to suit an apparent convenience—make them perfectly draught-tight, and the best-constructed mansions would be full of suffocating chambers. The knowledge of the construction of the body and the conditions of its health prevent it from suffering injury by the development of our powers over nature.
In no dissimilar way the mental balance is saved from the dangers attending an attention concentrated on the laws of mechanical science by a just consideration of the constitution of the knowing faculty, and the conditions of knowledge. Whatever pursuit we are engaged in, we are acting consciously or unconsciously upon some theory, some view of things. And when the limits of daily routine are continually narrowed by the ever-increasing complication of our civilization, it becomes doubly important that not one only but every kind of thought should be shared in.
There are two ways of passing beyond the domain of practical certainty, and of looking into the vast range of possibility. One is by asking, "What is knowledge? What constitutes experience?" If we adopt this course we are plunged into a sea of speculation. Were it not that the highest faculties of the mind find therein so ample a range, we should return to the solid ground of facts, with simply a feeling of relief at escaping from so great a confusion and contradictoriness.
The other path which leads us beyond the horizon of actual experience is that of questioning whatever seems arbitrary and irrationally limited in the domain of knowledge. Such a questioning has often been successfully applied in the search for new facts. For a long time four gases were considered incapable of being reduced to the liquid state. It is but lately that a physicist has succeeded in showing that there is no such arbitrary distinction among gases. Recently again the question has been raised, "Is there not a fourth state of matter?" Solid, liquid, and gaseous states are known. Mr. Crookes attempts to demonstrate the existence of a state differing from all of these. It is the object of these pages to show that, by supposing away certain limitations of the fundamental conditions of existence as we know it, a state of being can be conceived with powers far transcending our own. When this is made clear it will not be out of place to investigate what relations would subsist between our mode of existence and that which will be seen to be a possible one.
In the first place, what is the limitation that we must suppose away?
An observer standing in the corner of a room has three directions naturally marked out for him; one is upwards along the line of meeting of the two walls; another is forwards where the floor meets one of the walls; a third is sideways where the floor meets the other wall. He can proceed to any part of the floor of the room by moving first the right distance along one wall, and then by turning at right angles and walking parallel to the other wall. He walks in this case first of all in the direction of one of the straight lines that meet in the corner of the floor, afterwards in the direction of the other. By going more or less in one direction or the other, he can reach any point on the floor, and any movement, however circuitous, can be resolved into simple movements in these two directions.
But by moving in these two directions he is unable to raise himself in the room. If he wished to touch a point in the ceiling, he would have to move in the direction of the line in which the two walls meet. There are three directions then, each at right angles to both the other, and entirely independent of one another. By moving in these three directions or combinations of them, it is possible to arrive at any point in a room. And if we suppose the straight lines which meet in the corner of the room to be prolonged indefinitely, it would be possible by moving in the direction of those three lines, to arrive at any point in space. Thus in space there are three independent directions, and only three; every other direction is compounded of these three. The question that comes before us then is this. "Why should there be three and only three directions?" Space, as we know it, is subject to a limitation.
In order to obtain an adequate conception of what this limitation is, it is necessary to first imagine beings existing in a space more limited than that in which we move. Thus we may conceive a being who has been throughout all the range of his experience confined to a single straight line. Such a being would know what it was to move to and fro, but no more. The whole of space would be to him but the extension in both directions of the straight line to an infinite distance. It is evident that two such creatures could never pass one another. We can conceive their coming out of the straight line and entering it again, but they having moved always in one straight line, would have no conception of any other direction of motion by which such a result could be effected. The only shape which could exist in a one-dimensional existence of this kind would be a finite straight line. There would be no difference in the shapes of figures; all that could exist would simply be longer or shorter straight lines.
Again, to go a step higher in the domain of a conceivable existence. Suppose a being confined to a plane superficies, and throughout all the range of its experience never to have moved up or down, but simply to have kept to this one plane. Suppose, that is, some figure, such as a circle or rectangle, to be endowed with the power of perception; such a being if it moves in the plane superficies in which it is drawn, will move in a multitude of directions; but, however varied they may seem to be, these directions will all be compounded of two, at right angles to each other. By no movement so long as the plane superficies remains perfectly horizontal, will this being move in the direction we call up and down. And it is important to notice that the plane would be different to a creature confined to it, from what it is to us. We think of a plane habitually as having an upper and a lower side, because it is only by the contact of solids that we realize a plane. But a creature which had been confined to a plane during its whole existence would have no idea of there being two sides to the plane he lived in. In a plane there is simply length and breadth. If a creature in it be supposed to know of an up or down he must already have gone out of the plane.
Is it possible, then, that a creature so circumstanced would arrive at the notion of there being an up and down, a direction different from those to which he had been accustomed, and having nothing in common with them? Obviously nothing in the creature's circumstances would tell him of it. It could only be by a process of reasoning on his part that he could arrive at such a conception. If he were to imagine a being confined to a single straight line, he might realize that he himself could move in two directions, while the creature in a straight line could only move in one. Having made this reflection he might ask, "But why is the number of directions limited to two? Why should there not be three?"
A creature (if such existed), which moves in a plane would be much more fortunately circumstanced than one which can only move in a straight line. For, in a plane, there is a possibility of an infinite variety of shapes, and the being we have supposed could come into contact with an indefinite number of other beings. He would not be limited, as in the case of the creature in a straight line, to one only on each side of him.
It is obvious that it would be possible to play curious tricks with a being confined to a plane. If, for instance, we suppose such a being to be inside a square, the only way out that he could conceive would be through one of the sides of the square. If the sides were impenetrable, he would be a fast prisoner, and would have no way out.
What his case would be we may understand, if we reflect what a similar case would be in our own existence. The creature is shut in in all the directions he knows of. If a man is shut in in all the directions he knows of, he must be surrounded by four walls, a roof and a floor. A two-dimensional being inside a square would be exactly in the same predicament that a man would be, if he were in a room with no opening on any side. Now it would be possible to us to take up such a being from the inside of the square, and to set him down outside it. A being to whom this had happened would find himself outside the place he had been confined in, and he would not have passed through any of the boundaries by which he was shut in. The astonishment of such a being can only be imagined by comparing it to that which a man would feel, if he were suddenly to find himself outside a room in which he had been, without having passed through the window, doors, chimney or any opening in the walls, ceiling or floor.
Another curious thing that could be effected with a two-dimensional being, is the following. Conceive two beings at a great distance from one another on a plane surface. If the plane surface is bent so that they are brought close to one another, they would have no conception of their proximity, because to each the only possible movements would seem to be movements in the surface. The two beings might be conceived as so placed, by a proper bending of the plane, that they should be absolutely in juxtaposition, and yet to all the reasoning faculties of either of them a great distance could be proved to intervene. The bending might be carried so far as to make one being suddenly appear in the plane by the side of the other. If these beings were ignorant of the existence of a third dimension, this result would be as marvellous to them, as it would be for a human being who was at a great distance—it might be at the other side of the world—to suddenly appear and really be by our side, and during the whole time he not to have left the place in which he was.
Constructing a Four-Square
The foregoing examples make it clear that beings can be conceived as living in a more limited space than ours. Is there a similar limitation in the space we know?
At the very threshold of arithmetic an indication of such a limitation meets us.
If there is a straight line before us two inches long, its length is expressed by the number 2. Suppose a square to be described on the line, the number of square inches in this figure is expressed by the number 4, i.e., 2 × 2. This 2 × 2 is generally written 2^2, and named "2 squared."
Now, of course, the arithmetical process of multiplication is in no sense identical with that process by which a square is generated from the motion of a straight line, or a cube from the motion of a square. But it has been observed that the units resulting in each case, though different in kind, are the same in number.
If we touch two things twice over, the act of touching has been performed four times. Arithmetically, 2 × 2 = 4. If a square is generated by the motion of a line two inches in length, this square contains four square inches.
So it has come to pass that the second and third powers of numbers are called "square" and "cube."
We have now a straight line two inches long. On this a square has been constructed containing four square inches. If on the same line a cube be constructed, the number of cubic inches in the figure so made is 8, i.e., 2 × 2 × 2 or 2^3. Here, corresponding to the numbers 2, 2^2, 2^3, we have a series of figures. Each figure contains more units than the last, and in each the unit is of a different kind. In the first figure a straight line is the unit, viz., one linear inch; it is said to be of one dimension. In the second a square is the unit, viz., one square inch. The square is a figure of two dimensions. In the third case a cube is the unit, and the cube is of three dimensions. The straight line is said to be of one dimension because it can be measured only in one way. Its length can be taken, but it has no breadth or thickness. The square is said to be of two dimensions because it has both length and breadth. The cube is said to have three dimensions, because it can be measured in three ways.
The question naturally occurs, looking at these numbers 2, 2^2, 2^3, by what figure shall we represent 2^4, or 2 × 2 × 2 × 2. We know that in the figure there must be sixteen units, or twice as many units as in the cube. But the unit also itself must be different. And it must not differ from a cube simply in shape. It must differ from a cube as a cube differs from a square. No number of squares will make up a cube, because each square has no thickness. In the same way, no number of cubes must be able to make up this new unit. And here, instead of trying to find something already known, to which the idea of a figure corresponding to the fourth power can be affixed, let us simply reason out what the properties of such a figure must be. In this attempt we have to rely, not on a process of touching or vision, such as informs us of the properties of bodies in the space we know, but on a process of thought. Each fact concerning this unknown figure has to be reasoned out; and it is only after a number of steps have been gone through, that any consistent familiarity with its properties is obtained. Of all applications of the reason, this exploration is perhaps the one which requires, for the simplicity of the data involved, the greatest exercise of the abstract imagination, and on this account is well worth patient attention. The first steps are very simple. We must imagine a finite straight line to generate a square by moving on the plane of the paper, and this square in its turn to generate a cube by moving vertically upwards. Figure 1 represents a straight line; figure 2 represents a square formed by the motion of that straight line; figure 3 represents perspectively a cube formed by the motion of that square ABCD upwards. It would be well, instead of using figure 3, to place a cube on the paper. Its base would be ABCD, its upper surface EFGH.
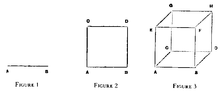
The straight line AB gives rise to the square ABCD by a movement at right angles to itself. If motion be confined to the straight line AB, a backward and forward motion is the only one possible. No sideway motion is admissible. And if we suppose a being to exist which could only move in the straight line AB, it would have no idea of any other movement than to and fro. The square ABCD is formed from the straight line by a movement in a direction entirely different from the direction which exists in AB. This motion is not expressible by means of any possible motion in AB. A being which existed in AB, and whose experience was limited to what could occur in AB, would not be able to understand the instructions we should give to make AB trace out the figure ABCD.
In the figure ABCD there is a possibility of moving in a variety of directions, so long as all these directions are confined to one plane. All directions in this plane can be considered as compounded of two, from A to B, and from A to C. Out of the infinite variety of such directions there is none which tends in a direction perpendicular to figure 2; there is none which tends upwards from the plane of the paper. Conceive a being to exist in the plane, and to move only in it. In all the movements which he went through there would be none by which he could conceive the alteration of figure 2 into what figure 3 represents in perspective. For 2 to become 3 it must be supposed to move perpendicularly to its own plane. The figure it traces out is the cube ABCDEFGH.
All the directions, manifold as they are, in which a creature existing in figure 3 could move, are compounded of three directions. From A to B, from A to C, from A to E, and there are no other directions known to it.
But if we suppose something similar to be done to figure 3, something of the same kind as was done to figure 1 to turn it into figure 2, or to figure 2 to turn it into figure 3, we must suppose the whole figure as it exists to be moved in some direction entirely different from any direction within it, and not made up of any combination of the directions in it. What is this? It is the fourth direction.
We are as unable to imagine it as a creature living in the plane figure 2 would be to imagine a direction such that moving in it the square 2 would become the cube 3. The third dimension to such a creature would be as unintelligible as the fourth is to us. And at this point we have to give up the aid that is to be got from any presentable object, and we have simply to investigate what the properties of the simplest figure in four dimensions are, by pursuing further the analogy which we know to exist between the process of formation of 2 from 1 and of 3 from 2, and finally of 4 from 3. For the sake of convenience, let us call the figure we are investigating—the simplest figure in four dimensions—a four-square.
First of all we must notice, that if a cube be formed from a square by the movement of the square in a new direction, each point of the interior of the square traces out part of the cube. It is not only the bounding lines that by their motion form the cube, but each portion of the interior of the square generates a portion of the cube. So if a cube were to move in the fourth dimension so as to generate a four-square, every point in the interior of the cube would start de novo, and trace out a portion of the new figure uninterfered with by the other points.
Or, to look at the matter in another light, a being in three dimensions, looking down on a square, sees each part of it extended before him, and can touch each part without having to pass through the surrounding parts, for he can go from above, while the surrounding parts surround the part he touches only in one plane.
So a being in four dimensions could look at and touch every point of a solid figure. No one part would hide another, for he would look at each part from a direction which is perfectly different from any in which it is possible to pass from one part of the body to another. To pass from one part of the body to another it is necessary to move in three directions, but a creature in four dimensions would look at the solid from a direction which is none of these three.
Let us obtain a few facts about the fourth figure, proceeding according to the analogy that exists between 1, 2, 3, and 4. In the figure 1 there are two points. In 2 there are four points—the four corners of the square. In 3 there are eight points. In the next figure, proceeding according to the same law, there would be sixteen points.
In the figure 1 there is one line. In the square there are four lines. In the cube there are twelve lines. How many lines would there be in the four-square? That is to say that there are three numbers—1, 4, and 12. What is the fourth, going on accordingly to the same law?
To answer this question let us trace out in more detail how the figures change into one another. The line, to become the square, moves; it occupies first of all its original position, and last of all its final position. It starts as AB, and ends as CD; thus the line appears twice, or it is doubled. The two other lines in the square, AC, BD, are formed by the motions of the points at the extremities of the moving line. Thus, in passing from the straight line to the square the lines double themselves, and each point traces out a line. If the same procedure holds good in the case of the change of the square into the cube, we ought in the cube to have double the number of lines as in the square—that is eight—and every point in the square ought to become a line. As there are four points in the square, we should have four lines in the cube from them, that is, adding to the previous eight, there Should be twelve lines in the cube. This is obviously the case. Hence we may with confidence, to deduce the number of lines in a four-square, apply this rule. Double the number of lines in the previous figure, and add as manv lines as there are points in the previous figure. Now in the cube there are twelve lines and eight points. Hence we get 2 × 12 + 8, or thirty-two lines in the four-square.
In the same way any other question about the four-square can be answered. We must throw aside our realizing power and answer in accordance with the analogy to be worked out from the three figures we know.
Thus, if we want to know how many plane surfaces the four-square has, we must commence with the line, which has none; the square has one; the cube has six. Here we get the three numbers, 0, 1, and 6. What is the fourth?
Consider how the planes of the cube arise. The square at the beginning of its motion determines one of the faces of the cube, at the end it is the opposite face, during the motion each of the lines of the square traces out one plane face of the cube. Thus we double the number of planes in the previous figure, and every line in the previous figure traces out a plane in the subsequent one.
Apply this rule to the formation of a square from a line. In the line there is no plane surface, and since twice nothing is nothing, we get, so far, no surface in the square; but in the straight line there is one line, namely itself, and this by its motion traces out the plane surface of the square. So in the square, as should be, the rule gives one surface.
Applying this rule to the case of the cube, we get, doubling the surfaces, 12; and adding a plane for each of the straight lines, of which there are 12, we have another 12, or 24 plane surfaces in all. Thus just as by handling or looking at it, it is possible to describe a figure in space, so by going through a process of calculation it is within our power to describe all the properties of a figure in four dimensions.
There is another characteristic so remarkable as to need a special statement. In the case of a finite straight line, the boundaries are points. If we deal with one dimension only, the figure 1, that of a segment of a straight line, is cut out of and separated from the rest of an imaginary infinitely long straight line by the two points at its extremities. In this simple case the two points correspond to the bounding surface of the cube. In the case of a two-dimensional figure an infinite plane represents the whole of space. The square is separated off by four straight lines, and it is impossible for an entry to be made into the interior of the square, except by passing through the straight lines. Now, in these cases, it is evident that the boundaries of the figure are of one dimension less than the figure itself. Points bound lines, lines bound plane figures, planes bound solid figures. Solids then must bound four dimensional figures. The four-square will be bounded in the following manner. First of all there is the cube which, by its motion in the fourth direction, generates the figure. This, in its initial position, forms the base of the four-square. In its final position it forms the opposite end. During the motion each of the faces of the cube give rise to another cube. The direction in which the cube moves is such that of all the six sides none is in the least inclined in that direction. It is at right angles to all of them. The base of the cube, the top of the cube, and the four sides of the cube, each and all of them form cubes. Thus the four-square is bounded by eight cubes. Summing up, the four-square would have 16 points, 32 lines, 24 surfaces, and it would be bounded by 8 cubes.
If a four-square were to rest in space it would seem to us like a cube.
To justify this conclusion we have but to think of how a cube would appear to a two-dimensional being. To come within the scope of his faculties at all, it must come into contact with the plane in which he moves. If it is brought into as close a contact with this plane as possible, it rests on it by one of its faces. This face is a square, and the most a two-dimensional being could get acquainted with of a cube would be a square.
Having thus seen how it is possible to describe the properties of the simplest shape in four dimensions, it is evident that the mental construction of more elaborate figures is simply a matter of time and patience.
In the study of the form and development of the chick in the egg, it is impossible to detect the features that are sought to be observed, except by the use of the microscope. The specimens are accordingly hardened by a peculiar treatment and cut into thin sections. The investigator going over each of these sections, noticing all their peculiarities, constructs in his mind the shape as it originally existed from the record afforded by an indefinite number of slices. So, to form an idea of a four-dimensional figure, a series of solid shapes bounded on every side differing gradually from one another, proceeding, it may be, to the most diverse forms, has to be mentally grasped and fused into a unitary conception.
If, for instance, a small sphere were to appear, this to be replaced by a larger one, and so on, and then, when the largest had appeared, smaller and smaller ones to make their appearance, what would be witnessed would be a series of sections of a four-dimensional sphere. Each section in space being a sphere.
Again, just as solid figures can be represented on paper by perspective, four-dimensional figures can be represented perspectively by solids. If there are two squares, one lying over the other, and the underneath one be pushed away, its sides remaining parallel with the one that was over it, then if each point of the one be joined to the corresponding point of the other, we have a fair representation on paper of a cube. Figure 3 may be considered to be such a representation if the square CDGH be considered to be the one that has been pushed away from lying originally under the square ABEF. Each of the planes which bound the cube is represented on the paper. The only thing that is wanting is the three-dimensional content of the cube. So if two cubes be placed with their sides parallel, but one somewhat diagonally with regard to the other, and all their corresponding points be supposed joined, there will be found a set of solid figures, each representing (though of course distortedly) the bounding cubes of the four-dimensional figure, and every plane and line in the four-dimensional figure will be found to be represented in a kind of solid perspective. What is wanting is of course the four-dimensional content.
Properties of Matter in the Fourth Dimension
Having now passed in review some of the properties of four-dimensional figures, it remains to ask what relations beings in four dimensions, if they did exist, would have with us.
And in the first place, a being in four dimensions would have to us exactly the appearance of a being in space. A being in a plane would only know solid objects as two-dimensional figures—the shapes namely in which they intersected his plane. So if there were four-dimensional objects, we should only know them as solids—the solids, namely, in which they intersect our space. Why, then, should not the four-dimensional beings be ourselves, and our successive states the passing of them through the three-dimensional space to which our consciousness is confined?
Let us consider the question in more detail. And for the sake of simplicity transfer the problem to the case of three and two dimensions instead of four and three.
Suppose a thread to be passed through a thin sheet of wax placed horizontally. It can be passed through in two ways. Either it can be pulled through, or it can be held at both ends, and moved downwards as a whole. Suppose a thread to be grasped at both ends, and the hands to be moved downwards perpendicularly to the sheet of wax. If the thread happens to be perpendicular to the sheet it simply passes through it, but if the thread be held, stretched slantingwise to the sheet, and the hands are moved perpendicularly downwards, the thread will, if it be strong enough, make a slit in the sheet.
If now the sheet of wax were to have the faculty of closing up behind the thread, what would appear in the sheet would be a moving hole.
Suppose that instead of a sheet and a thread, there were a straight line and a plane. If the straight line were placed slantingwise in reference to the plane and moved downwards, it would always cut the plane in a point, but that point of section would move on. If the plane were of such a nature as to close up behind the line, if it were of the nature of a fluid, what would be observed would be a moving point. If now there were a whole system of lines sloping in different directions, but all connected together, and held absolutely still by one framework, and if this framework with its system of lines were as a whole to pass slowly through the fluid plane at right angles to it, there would then be the appearance of a multitude of moving points in the plane, equal in number to the number of straight lines in the system. The lines in the framework will all be moving at the same rate—namely, at the rate of the framework in which they are fixed. But the points in the plane will have different velocities. They will move slower or faster, according as the lines which give rise to them are more or less inclined to the plane. A straight line perpendicular to the plane will, on passing through, give rise to a stationary point. A straight line that slopes very much inclined to the plane will give rise to a point moving with great swiftness. The motions and paths of the points would be determined by the arrangement of the lines in the system. It is obvious that if two straight lines were placed lying across one another like the letter X, and if this figure were to be stood upright and passed through the plane, what would appear would be at first two points. These two points would approach one another. When the part where the two strokes of the X meet came into the plane, the two points would become one. As the upper part of the figure passed through, the two points would recede from one another.
If the line be supposed to be affixed to all parts of the framework, and to loop over one another, and support one another (ABCD framework, X and Y two lines interlinked), it is obvious that they could assume all sorts of figures, and that the points on the plane would move in very complicated paths. Figure 4 represents a section of such a framework. Two lines XX and YY are shown, but there must be supposed to be a great number of others sloping backwards and forwards as well as sideways.

Let us now assume that instead of lines, very thin threads were attached to the framework: they on passing through the fluid plane would give rise to very small spots. Let us call the spots atoms, and I regard them as constituting a material system in the plane. There are four conditions which must be satisfied by these spots if they are to be admitted as forming a material system such as ours. For the ultimate properties of matter (if we eliminate attractive and repulsive forces, which may be caused by the motions of the smallest particles), are—1, Permanence; 2, Impenetrability; 3, Inertia; 4, Conservation of energy.
According to the first condition, or that of permanence, no one of these spots must suddenly cease to exist. That is, the thread which by sharing in the general motion of the system gives rise to the moving point, must not break off before the rest of them. If all the lines suddenly ended this would correspond to a ceasing of matter.
2. Impenetrability.—One spot must not pass through another. This condition is obviously satisfied. If the threads do not coincide at any point, the moving spots they give rise to cannot.
3. Inertia.—A spot must not cease to move or cease to remain at rest without coming into collision with another point. This condition gives the obvious condition with regard to the threads, that they, between the points where they come into contact with one another, must be straight. A thread which was curved would, passing through the plane, give rise to a point which altered in velocity spontaneously. This the particles of matter never do.
4. Conservation of energy.—The energy of a material system is never lost; it is only transferred from one form to another, however it may seem to cease. If we suppose each of the moving spots on the plane to be the unit of mass, the principle of the conservation of energy demands that when any two meet, the sum of the squares of their several velocities before meeting shall be the same as the sum of the squares of their velocities after meeting. Now we have seen that any statement about the velocities of the spots in the plane is really a statement about the inclinations of the threads to the plane. Thus the principle of the conservation of energy gives a condition which must be satisfied by the inclinations of the threads of the plane. Translating this statement, we get in mathematical language the assertion that the sum of the squares of the tangents of the angles the threads make with the normal to the plane remains constant.
Hence, all complexities and changes of a material system made up of similar atoms in a plane could result from the uniform motion as a whole of a system of threads.
We can imagine these threads as weaving together to form connected shapes, each complete in itself, and these shapes as they pass through the fluid plane give rise to a series of moving points. Yet, inasmuch as the threads are supposed to form consistent shapes, the motion of the points would not be wholly random, but numbers of them would present the semblance of moving figures. Suppose, for instance, a number of threads to be so grouped as to form a cylinder for some distance, but after a while to be pulled apart by other threads with which they interlink. While the cylinder was passing through the plane, we should have in the plane a number of points in a circle. When the part where the threads deviated came to the plane, the circle would break up by the points moving away. These moving figures in the plane are but the traces of the shapes of threads as those shapes pass on. These moving figures may be conceived to have a life and a consciousness of their own.
Or, if it be irrational to suppose them to have a consciousness when the shapes of which they are momentary traces have none, we may well suppose that the shapes of threads have consciousness, and that the moving figures share this consciousness, only that in their case it is limited to those parts of the shapes that simultaneously pass through the plane. In the plane, then, we may conceive bodies with all the properties of a material system, moving and changing, possessing consciousness. After a while it may well be that one of them becomes so disassociated that it appears no longer as a unit, and its consciousness as such may be lost. But the threads of existence of such a figure are not broken, nor is the shape which gave it origin altered in any way. It has simply passed on to a distance from the plane. Thus nothing which existed in the conscious life on the plane would cease. There would in such an existence be no cause and effect, but simply the gradual realization in a superficies of an already existent whole. There would be no progress, unless we were to suppose the threads as they pass to interweave themselves in more complex shapes.
Can a representation, such as the preceding, be applied to the case of the existence in space with which we have to do? Is it possible to suppose that the movements and changes of material objects are the intersections with a three-dimensional space of a four-dimensional existence? Can our consciousness be supposed to deal with a spatial profile of some higher actuality?
It is needless to say that all the considerations that have been brought forward in regard to the possibility of the production of a system satisfying the conditions of materiality by the passing of threads through a fluid plane, holds good with regard to a four-dimensional existence passing through a three-dimensional space. Each part of the ampler existence which passed through our space would seem perfectly limited to us. We should have no indication of the permanence of its existence. Were such a thought adopted, we should have to imagine some stupendous whole, wherein all that has ever come into being or will come co-exists, which passing slowly on, leaves in this flickering consciousness of ours, limited to a narrow space and a single moment, a tumultuous record of changes and vicissitudes that are but to us. Change and movement seem as if they were all that existed. But the appearance of them would be due merely to the momentary passing through our consciousness of ever existing realities.
In thinking of these matters it is hard to divest ourselves of the habit of visual or tangible illustration. If we think of a man as existing in four dimensions, it is hard to prevent ourselves from conceiving him prolonged in an already known dimension. The image we form resembles somewhat those solemn Egyptian statues which in front represent well enough some dignified sitting figure, but which are immersed to their ears in a smooth mass of stone which fits their contour exactly.
No material image will serve. Organized beings seem to us so complete that any addition to them would deface their beauty. Yet were we creatures confined to a plane, the outline of a Corinthian column would probably seem to be of a beauty unimprovable in its kind. We should be unable to conceive any addition to it, simply for the reason that any addition we could conceive would be of the nature of affixing an unsightly extension to some part of the contour. Yet, moving as we do in space of three dimensions, we see that the beauty of the stately column far surpasses that of any single outline. So all that we can do is to deny our faculty of judging of the ideal completeness of shapes in four dimensions.
Evidence of a Fourth Dimension
Let us now leave this supposition of framework and threads. Let us investigate the conception of a four-dimensional existence in a simpler and more natural manner in the same way that a two-dimensional being should think about us, not as infinite in the third dimension, but limited in three dimensions as he is in two. A being existing in four dimensions must then be thought to be as completely bounded in all four directions as we are in three. All that we can say in regard to the possibility of such beings is, that we have no experience of motion in four directions. The powers of such beings and their experience would be ampler, but there would be no fundamental difference in the laws of force and motion.
Such a being would be able to make but a part of himself visible to us, for a cube would be apprehended by a two-dimensional being as the square in which it stood. Thus a four-dimensional being would suddenly appear as a complete and finite body, and as suddenly disappear, leaving no trace of himself, in space, in the same way that anything lying on a flat surface, would, on being lifted, suddenly vanish out of the cognizance of beings, whose consciousness was confined to the plane. The object would not vanish by moving in any direction, but disappear instantly as a whole. There would be no barrier, no confinement of our devising that would not be perfectly open to him. He would come and go at pleasure; he would be able to perform feats of the most surprising kind. It would be possible by an infinite plane extending in all directions to divide our space into two portions absolutely separated from one another; but a four-dimensional being would slip round this plane with the greatest ease.
To see this clearly, let us first take the analogous case in three dimensions. Suppose a piece of paper to represent a plane. If it is infinitely extended in every direction, it will represent an infinite plane. It can be divided into two parts by an infinite straight line. A being confined to this plane could not get from one part of it to the other without passing through the line. But suppose another piece of paper laid on the first and extended infinitely, it will represent another infinite plane. If the being moves from the first plane by a motion in the third dimension, it will move into this new plane. And in it it finds no line. Let it move to such a position that when it goes back to the first plane it will be on the other side of the line. Then let it go back to the first plane. It has appeared now on the other side of the line which divides the infinite plane into two parts.
Take now the case of four dimensions. Instead of bringing before the mind a sheet of paper conceive a solid of three dimensions. If this solid were to become infinite it would fill up the whole of three-dimensional space. But it would not fill up the whole of four-dimensional space. It would be to four-dimensional space what an infinite plane is to three-dimensional space. There could be in four-dimensional space an infinite number of such solids, just as in three-dimensional space there could be an infinite number of infinite planes.
Thus, lying alongside our space, there can be conceived a space also infinite in all three directions. To pass from one to the other a movement has to be made in the fourth dimension, just as to pass from one infinite plane to another a motion has to be made in the third dimension.
Conceive, then, corresponding to the first sheet of paper mentioned above, a solid, and as the sheet of paper was supposed to be infinitely extended in two dimensions, suppose the solid to be infinitely extended in its three dimensions, so that it fills the whole of space as we know it.
Now divide this infinite solid in two parts by an infinite plane, as the infinite plane of paper was divided in two parts by an infinite line. A being cannot pass from one part of this infinite solid to another, on the other side of this infinite plane, without going through the infinite plane, so long as he keeps within the infinite solid.
But suppose beside this infinite solid a second infinite solid, lying next to it in the fourth dimension, as the second infinite plane of paper was next to the first infinite plane in the third dimension. Let now the being that wants to get on the other side of the dividing plane move off in the fourth dimension, and enter the second infinite solid. In this second solid there is no dividing plane. Let him now move, so that coming back to the first infinite solid he shall be on the other side of the infinite plane that divides it into two portions. If this is done, he will now be on the other side of the infinite plane, without having gone through it.
In a similar way a being, able to move in four dimensions, could get out of a closed box without going through the sides, for he could move off in the fourth dimension, and then move about, so that when he came back he would be outside the box.
Is there anything in the world as we know it, which would indicate the possibility of there being an existence in four dimensions? No definite answer can be returned to this question. But it may be of some interest to point out that there are certain facts which might be read by the light of the fourth-dimensional theory.
To make this clear, let us suppose that space is really four dimensional, and that the three-dimensional space we know is, in this ampler space, like a surface is in our space.
We should then be in this ampler space like beings confined to the surface of a plane would be in ours. Let us suppose that just as in our space there are centers of attraction whose influence radiates out in every direction, so in this ampler space there are centers of attraction whose influence radiates out in every direction. Is there anything to be observed in nature which would correspond to the effect of a center of attraction lying out of our space, and acting on all the matter in it? The effect of such a center of attraction would not be to produce motion in any known direction, because it does not lie off in any known direction.
Let us pass to the corresponding case in three and two dimensions, instead of four and three. Let us imagine a plane lying horizontally, and in it some creatures whose experience was confined to it. If now some water or other liquid were poured on to the plane, the creatures, becoming aware of its presence, would find that it had a tendency to spread out all over the plane. In fact it would not be to them as a liquid is to us—it would rather correspond to a gas. For a gas, as we know it, tends to expand in every direction, and gradually increase so as to fill the whole of space. It exercises a pressure on the walls of any vessel in which we confine it.
The liquid on the plane expands in all the dimensions which the two-dimensional creatures on the plane know, and at the same time becomes smaller in the third dimension, its absolute quantity remaining unchanged. In like manner we might suppose that gases (which by expansion become larger in the dimensions that we know) become smaller in the fourth dimension.
The cause in this case would have to be sought for in an attractive force, acting with regard to our space as the force of gravity acts with regard to a horizontal plane.
Can we suppose that there is a center of attraction somewhere off in the fourth dimension, and that the gases, which we know are simply more mobile liquids, expanding out in every direction under its influence. This view receives a certain amount of support from the fact proved experimentally that there is no absolute line of demarcation between a liquid and a gas. The one can be made to pass into the other with no moment intervening in which it can be said that now a change of state has taken place.
We might then suppose that the matter we know extending in three dimensions has also a small thickness in the fourth dimension; that solids are rigid in the fourth as in the other three dimensions; that liquids are too coherent to admit of their spreading out in space, and becoming thinner in the fourth dimension, under the influence of an attractive center lying outside of our space; but that gases, owing to the greater mobility of their particles, are subject to its action, and spread out in space under its influence, in the same manner that liquids, under the influence of gravity, spread out on a plane.
Then the density of a gas would be a measure of the relative thickness of it in the fourth dimension: and the diminution of the density would correspond to a diminution of the thickness in the fourth dimension. Could this supposition be tested in any way?
Suppose a being confined to a plane; if the plane is moved far off from the center of attraction lying outside it, he would find that liquids had less tendency to spread out than before.
Or suppose he moves to a distant part of the plane so that the line from his position to the center of attraction lies obliquely to the plane; he would find that in this position a liquid would show a tendency to spread out more in one direction than another.
Now our space considered as lying in four-dimensional space, as a plane does in three-dimensional space, may be shifted. And the expansive force of gases might be found to be different at different ages. Or, shifting as we do our position in space during the course of the earth's path round the sun, there might arise a sufficient difference in our position in space, with regard to the attractive center, to make the expansive force of gases different at different times of the year, or to cause them to manifest a greater expansive force in one direction than in another.
But although this supposition might be worked out at some length, it is hard to suppose that it could afford any definite test of the physical existence of a fourth dimension. No test has been discovered which is decisive. And, indeed, before searching for tests, a theoretical point of the utmost importance has to be settled. In discussing the geometrical properties of straight lines and planes, we suppose them to be respectively of one and two dimensions, and by so doing deny them any real existence. A plane and a line are mere abstractions. Every portion of matter is of three dimensions. If we consider beings on a plane not as mere idealities, we must suppose them to be of some thickness. If their experience is to be limited to a plane this thickness must be very small compared to their other dimensions. Transferring our reasoning to the case of four dimensions, we come to a curious result.
If a fourth dimension exists there are two possible alternatives.
One is, that there being four dimensions, we have a three-dimensional existence only. The other is that we really have a four-dimensional existence, but are not conscious of it. If we are in three dimensions only, while there are really four dimensions, then we must be relatively to those beings who exist in four dimensions, as lines and planes are in relation to us. That is, we must be mere abstractions. In this case we must exist only in the mind of the being that conceives us, and our experience must be merely the thoughts of his mind—a result which has apparently been arrived at, on independent grounds, by an idealist philosopher.
The other alternative is that we have a four-dimensional existence. In this case our proportions in it must be infinitely minute, or we should be conscious of them. If such be the case, it would probably be in the ultimate particles of matter, that we should discover the fourth dimension, for in the ultimate particles the sizes in the three dimensions are very minute, and the magnitudes in all four dimensions would be comparable.
The preceding two alternative suppositions are based on the hypothesis of the reality of four-dimensional existence, and must be conceived to hold good only on that hypothesis.
It is somewhat curious to notice that we can thus conceive of an existence relative to which that which we enjoy must exist as a mere abstraction.
Apart from the interest of speculations of this kind they have considerable value; for they enable us to express in intelligible terms things of which we can form no image. They supply us, as it were, with scaffolding, which the mind can make use of in building up its conceptions. And the additional gain to our power of representation is very great.
Many philosophical ideas and doctrines are almost unintelligible because there is no physical illustration which will serve to express them. In the imaginary physical existence which we have traced out, much that philosophers have written finds adequate representation. Much of Spinoza's Ethics, for example, could be symbolized from the preceding pages.
Thus we may discuss and draw perfectly legitimate conclusions with regard to unimaginable things.
It is, of course, evident that these speculations present no point of direct contact with fact. But this is no reason why they should be abandoned. The course of knowledge is like the flow of some mighty river, which, passing through the rich lowlands, gathers into itself the contributions from every valley. Such a river may well be joined by a mountain stream, which, passing with difficulty along the barren highlands, flings itself into the greater river down some precipitous descent, exhibiting at the moment of its union the spectacle of the utmost beauty of which the river system is capable. And such a stream is no inapt symbol of a line of mathematical thought, which, passing through difficult and abstract regions, sacrifices for the sake of its crystalline clearness the richness that comes to the more concrete studies. Such a course may end fruitlessly, for it may never join the main course of observation and experiment. But, if it gains its way to the great stream of knowledge, it affords at the moment of its union the spectacle of the greatest intellectual beauty, and adds somewhat of force and mysterious capability to the onward current.
![]()
This work was published before January 1, 1929, and is in the public domain worldwide because the author died at least 100 years ago.
Public domainPublic domainfalsefalse