1911 Encyclopædia Britannica/Dynamo
DYNAMO (a shortened form of “dynamo-electric machine,” from Gr. δύναμις, power), a machine for converting mechanical into electrical energy.
The dynamo ranks with the telegraph and telephone as one of the three striking applications of electrical and magnetic science to which the material progress that marked the second half of the 19th century was in no small measure due. Since the discovery of the principle of the dynamo by Faraday in 1831 the simple model which he first constructed has been gradually developed into the machines of 5000 horse-power or more which are now built to meet the needs of large cities for electric lighting and power, while at the same time the numbers of dynamos in use have increased almost beyond estimate. Yet such was the insight of Faraday into the fundamental nature of the dynamo that the theory of its action which he laid down has remained essentially unchanged. His experiments on the current which was 
Fig. 1.set up in a coil of wire during its movement across the poles of a magnet led naturally to the explanation of induced electromotive force as caused by the linking or unlinking of magnetic lines of flux with an electric circuit. For the more definite case of the dynamo, however, we may, with Faraday, make the transition from line-linkage to the equivalent conception of “line-cutting” as the source of E.M.F.—in other words, to the idea of electric conductors “cutting” or intersecting[1] the lines of flux in virtue of relative motion of the magnetic field and electric circuit. On the 28th of October 1831 Faraday mounted a copper disk so that it could be rotated edgewise between the poles of a permanent horse-shoe magnet. When so rotated, it cut the lines of flux which passed transversely through its lower half, and by means of two rubbing contacts, one on its periphery and the other on its spindle, the circuit was closed through a galvanometer, which indicated the passage of a continuous current so long as the disk was rotated (fig. 1). Thus by the invention of the first dynamo Faraday proved his idea that the E.M.F. induced through the interaction of a magnetic field and an electric circuit was due to the passage of a portion of the electric circuit across the lines of flux, or vice versa, and so could be maintained if the cutting of the lines were made continuous.[2] In comparison with Faraday’s results, the subsequent advance is to be regarded as a progressive perfecting of the mechanical and electro-magnetic design, partly from the theoretical and partly from the practical side, rather than as modifying or adding to the idea which was originally present in his mind, and of which he already saw the possibilities.
A dynamo, then, is a machine in which, by means of continuous relative motion, an electrical conductor or system of conductors forming part of a circuit is caused to cut the lines of a magnetic field or fields; the cutting of the magnetic flux induces an electromotive force in the conductors, and when the circuit is closed a current flows, whereby mechanical energy is converted into electrical energy.
Little practical use could be made of electrical energy so long as its only known sources were frictional machines and voltaic batteries. The cost of the materials for producing electrical currents on a large scale by chemical action was prohibitive, while the frictional machine only yielded very small currents at extremely high potentials. In the dynamo, on the other hand, electrical energy in a convenient form could be cheaply and easily obtained by mechanical means, and with its invention the application of electricity to a wide range of commercial purposes became economically possible. As a converter of energy from one form to another it is only surpassed in efficiency by another electrical appliance, namely, the transformer (see Transformers). In this there is merely conversion of electrical energy at a high potential into electrical energy at a low potential, or vice versa, but in the dynamo the mechanical energy which must be applied to maintain the relative movement of magnetic field and conductor is absorbed, and reappears in an electrical form. A true transformation takes place, and the proportion which the rate of delivery of electrical energy bears to the power absorbed, or in other words the efficiency, is the more remarkable. The useful return or “output” at the terminals of a large machine may amount to as much as 95% of the mechanical energy which forms the “input.” Since it needs some prime mover to drive it, the dynamo has not made any direct addition to our sources of energy, and does not therefore rank with the primary battery or oil-engine, or even the steam-engine, all of which draw their energy more immediately from nature. Yet by the aid of the dynamo the power to be derived from waterfalls can be economically and conveniently converted into an electrical form and brought to the neighbouring factory or distant town, to be there reconverted by motors into mechanical power. Over any but very short distances energy is most easily transmitted when it is in an electrical form, and turbine-driven dynamos are very largely and successfully employed for such transmission. Thus by conducing to the utilization of water-power which may previously have had but little value owing to its disadvantageous situation, the dynamo may almost be said to have added another to our available natural resources.
The two essential parts of the dynamo, as required by its definition, may be illustrated by the original disk machine of Faraday. They are (1) the iron magnet, between the poles of which a magnetic field exists, and (2) the electrical conductors, represented by the rotating copper disk. The sector of the disk cutting the lines of the field forms part of a closed electric circuit, and has an E.M.F. induced in it, by reason of which it is no longer simply a conductor, but has become “active.” In its more highly developed form the simple copper disk is elaborated into a system of many active wires or bars which form the “winding,” and which are so interconnected as to add up their several E.M.F.’s. Since these active wires are usually mounted on an iron structure, which may be likened to the keeper or “armature” of a magnet rotating between its poles, the term “armature” has been extended to cover not only the iron core, but also the wires on it, and when there is no iron core it is even applied to the copper conductors themselves. In the dynamo of Faraday the “armature” was the rotating portion, and such is the case with modern continuous-current dynamos; in alternators, however, the magnet, or a portion of it, is more commonly rotated while the armature is stationary. It is in fact immaterial to the action whether the one or the other is moved, or both, so long as their relative motion causes the armature conductors to cut the magnetic flux. 
Fig. 2.As to the ultimate reason why an E.M.F. should be thereby induced, physical science cannot as yet yield any surer knowledge than in the days of Faraday.[3] For the engineer, it suffices to know that the E.M.F. of the dynamo is due to the cutting of the magnetic flux by the active wires, and, further, is proportional to the rate at which the lines are cut.[4]
The equation of the electromotive force which is required in order to render this statement quantitative must contain three factors, namely, the density of the flux in the air-gap through which the armature conductors move, the active length of these wires, and the speed of their movement. For given values of the first and third factors and a single straight wire moved parallel to itself through a uniform field, the maximum rate of cutting is evidently obtained when the three directions of the lines of the conductor’s length and of the relative motion are respectively at right angles to each other, as shown by the three co-ordinate axes of fig. 2. The E.M.F. of the single wire is then
| E=BgLV × 10−8 volts | (1) |
where Bg is the density of the flux within the air-gap expressed in C.G.S. lines per square centimetre, L is the active length of the conductor within the field in centimetres, and V is the velocity of movement in centimetres per second. Further, the direction in which the E.M.F. has the above maximum value is along the length of the conductor, its “sense” being determined by the direction of the movement[5] in relation to the direction of the field.
The second fundamental equation of the dynamo brings to light its mechanical side, and rests on H. C. Oersted’s discovery of the interaction of a magnetic field and an electric current. If a straight electric conductor through which a current is passing be so placed in a magnetic field that its length is not parallel to the direction of the lines of flux, it is acted on by a force which will move it, if free, in a definite direction relatively to the magnet; or if the conductor is fixed and the magnet is free, the latter will itself move in the opposite direction. Now in the dynamo the active wires are placed so that their length is at right angles to the field; hence when they are rotated and an electric current begins to flow under the E.M.F. which they induce, a mutual force at once arises between the copper conductors and the magnet, and the direction of this force must by Lenz’s law be opposed to the direction of the movement. Thus as soon as the disk of fig. 1 is rotated and its circuit is closed, it experiences a mechanical pull or drag which must be overcome by the force applied to turn the disk. While the magnet must be firmly held so as to remain stationary, the armature must be of such mechanical construction that its wires can be forcibly driven through the magnetic field against the mutual pull. This law of electrodynamic action may be quantitatively stated in an equation of mechanical force, analogous to the equation (I.) of electromotive force, which states the law of electromagnetic induction. If a conductor of length L cm., carrying a current C amperes, is immersed in a field of uniform density Bg, and the length of the conductor is at right angles to the direction of the lines, it is acted on by a force
| F=BgLC × 10−1 dynes, | (2) |
and the direction of this force is at right angles to the conductor and to the field. The rate at which electrical energy is developed, when this force is overcome by moving the conductor as a dynamo through the field, is EC=BgLVC × 10−8 watts, whence the equality of the mechanical power absorbed and the electrical power developed (as required by the law of the conservation of energy) is easily established. The whole of this power is not, however, available at the terminals of the machine; if Ra be the resistance of the armature in ohms, the passage of the current Ca through the armature conductors causes a drop of pressure of CaRa volts, and a corresponding loss of energy in the armature at the rate of Ca2Ra watts. As the resistance of the external circuit Re is lowered, the current C=Ea / (Re + Ra) is increased. The increase of the current is, however, accompanied by a progressive increase in the loss of energy over the armature, and as this is expended in heating the armature conductors, their temperature may rise so much as to destroy the insulating materials with which they are covered. Hence the temperature which the machine may be permitted to attain in its working is of great importance in determining its output, the current which forms one factor therein being primarily limited by the heating which it produces in the armature winding. The lower the resistance of the armature, the less the rise of its temperature for a given current flowing through it; and the reason for the almost universal adoption of copper as the material for the armature conductors is now seen to lie in its high conductivity.[6]
Since the voltage of the dynamo is the second factor to which its output is proportional, the conditions which render the induced E.M.F. a maximum must evidently be reproduced as far as possible in practice, if the best use is to be made of a given mass of iron and copper. The first problem, therefore, in the construction of the dynamo is the disposition of the wires and field in such a manner that the three directions of field, length of active conductors, and movement are at right angles to one another, and so that the relative motion is continuous. Reciprocating motion, such as would be obtained by direct attachment of the conductors to the piston of a steam-engine, has been successfully employed only in the special case of an “oscillator,”[7] producing a small current very rapidly changing in direction. Rotary motion is therefore universally adopted, and with this two distinct cases arise. Either (A) the active length of the wire is parallel to the axis of rotation, or (B) it is at right angles to it.
 |
| Fig. 3. |
 |
| Fig. 4. |
(A) If a conductor is rotated in the gap between the poles of a horse-shoe magnet, and these poles have plane parallel faces opposing one another as in fig. 3, not only is the density of the flux in the interpolar gap small, but the direction of movement is not always at right angles to the direction of the lines, which for the most part pass straight across from one opposing face to the other. When the conductor is midway between the poles (i.e. either at its highest or lowest point), it is at this instant sliding along the lines and does not cut them, so that its E.M.F. is zero. Taking this position as the starting-point, as the conductor moves round, its rate of line-cutting increases to a maximum when it has moved through a right angle and is opposite to the centre of a pole-face (as in fig. 3), from which point onward the rate decreases to zero when it has moved through 180°. Each time the conductor crosses a line drawn symmetrically through the gap between the poles and at right angles to the axis of rotation, the E.M.F. along its length is reversed in direction, since the motion relatively to the direction of the field is reversed. If the ends of the active conductor are electrically connected to two collecting rings fixed upon, but insulated from, the shaft, two stationary brushes bb can be pressed on the rings so as to make a sliding contact. An external circuit can then be connected to the brushes, which will form the “terminals” of the machine, the periodically reversed or alternating E.M.F. induced in the active conductor will cause an alternating current to flow through conductor and external circuit, and the simplest form of “alternator” is obtained. If the field cut by the straight conductor is of uniform density, and all the lines pass straight across from one pole-face to the other (both of which assumptions are approximately correct), a curve connecting the instantaneous values of the E.M.F. as ordinates with time or degrees of angular movement as abscissae (as shown at the foot of fig. 3), will, if the speed of rotation be uniform, be a sine curve. If, however, the conductor is mounted on an iron cylinder (fig. 4),[8] a sufficient margin being allowed for mechanical clearance between it and the poles, not only will the reluctance of the magnetic circuit be reduced and the total flux and its density in the air-gap Bg be thereby increased, but the path of the lines will become nearly radial, except at the “fringe” near the edges of the pole-tips; hence the relative directions of the movement and of the lines will be continuously at right angles. The shape of the E.M.F. curve will then be as shown in fig. 4—flat-topped, with rounded corners rapidly sloping down to the zero line.
 |
| Fig. 5. |
 |
| Fig. 6. |
But a single wire cannot thus be made to give more than a few volts, and while dynamos for voltages from 5 to 10 are required for certain purposes, the voltages in common use range from 100 to 10,000. It is therefore necessary to connect a number of such wires in series, so as to form an “armature winding.” If several similar conductors are arranged along the length of the iron core parallel to the first (fig. 5), the E.M.F.’s generated in the conductors which at any moment are under the same pole are similarly directed, and are opposite to the directions of the E.M.F.’s in the conductors under the other pole (cf fig. 5 where the dotted and crossed ends of the wires indicate E.M.F.’s directed respectively towards and away from the observer). Two distinct methods of winding thence arise, the similarity of the E.M.F.’s under the same pole being taken advantage of in the first, and the opposite E.M.F.’s under N and S poles in the second.
1. The first, or ring-winding, was invented by Dr Antonio Pacinotti of Florence[9] in 1860, and was subsequently and independently reintroduced in 1870[10] by the Belgian electrician, Zénobe Théophile Gramme, whence it is also frequently called the “Gramme” winding. By this method the farther end of conductor 1 (fig. 5) is joined in series to the near end of conductor 2; this latter lies next to it on the surface of the core or immediately above it, so that both are simultaneously under the same pole-piece. For this series connexion to be possible, the armature core must be a hollow cylinder, supported from the shaft on an open non-magnetic spider or hub, between the arms of which there is room for the internal wire completing the loop (fig. 6). The end of one complete loop or turn embracing one side of the armature core thus forms the starting-point for another loop, and the process can be continued if required to form a coil of two or more turns. In the ring armature the iron core serves the double purpose of conducting the lines across from one pole to the other, and also of shielding from the magnetic flux the hollow interior through which the connecting wires pass. Any lines which leak across the central space are cut by the internal wires, and the direction of cutting is such that the E.M.F. caused thereby opposes the E.M.F. due to the active conductors proper on the external surface. If, however, the section of iron in the core be correctly proportioned, the number of lines which cross the interior will bear but a small ratio to those which pass entirely through the iron, and the counter E.M.F. of the internal wires will become very small; they may then be regarded simply as connectors for joining the external active wires in series.
 |
| Fig. 7. |
2. The second or drum method was used in the original “shuttle-wound” armatures invented by Dr Werner von Siemens in 1856, and is sometimes called the “Siemens” winding. The farther end of conductor 1 (fig. 5) is joined by a connecting wire to the farther end of another conductor 2′ situated nearly diametrically opposite on the other side of the core and under the opposite pole-piece. The near end of the complete loop or turn is then brought across the end of the core, and can be used as the starting-point for another loop beginning with conductor 2, which is situated by the side of the first conductor. The iron core may now be solid from the surface to the shaft, since no connecting wires are brought through the centre, and each loop embraces the entire armature core (fig. 7). By the formation of two loops in the ring armature and of the single loop in the drum armature, two active wires are placed in series; the curves of instantaneous E.M.F. are therefore similar in shape to that of the single wire (fig. 4), but with their ordinates raised throughout to double their former height, as shown at the foot of fig. 6.
Next, if the free ends of either the ring or drum loops, instead of being connected to two collecting rings, are attached to the two halves of a split-ring insulated from the shaft (as shown in fig. 7 in connexion with a drum armature), and the stationary brushes are so set relatively to the loops that they pass over from the one half of the split-ring to the other half at the moment when the loops are passing the centre of the interpolar gap, and so are giving little or no E.M.F., each brush will always remain either positive or negative. The current in the external circuit attached to the brushes will then have a constant direction, although the E.M.F. in the active wires still remains alternating; the curve of E.M.F. obtained at the brushes is thus (as in fig. 7) entirely above the zero line. The first dynamo of H. Pixii,[11] which immediately followed Faraday’s discovery, gave an alternating current, but in 1832[12] the alternator was converted into a machine giving a unidirected current by the substitution of a rudimentary “commutator” in place of mercury collecting cups.
(B) So far the length of the active wires has been parallel to the axis of rotation, but they may equally well be arranged perpendicularly thereto. The poles will then have plane faces and the active wires will be disposed with their length approximately radial to the axis of the shaft. In order to add their E.M.F.’s in series, two types of winding may be employed, which are precisely analogous in principle to the ring and drum windings under arrangement (A).
3. The discoidal or flat-ring armature is equivalent to a ring of which the radial depth greatly exceeds the length, with the poles presented to one side of the ring instead of embracing its cylindrical surface. A similar set of poles is also presented to the opposite side of the ring, like poles being opposite to one another, so that in effect each polar surface is divided into two halves, and the groups of lines from each side bifurcate and pass circumferentially through the armature core to issue into the adjacent poles of opposite sign.
4. In the disk machine, no iron core is necessary for the armature, the two opposite poles of unlike sign being brought close together, leaving but a short path for the lines in the air-gap through which the active wires are rotated.
 |
| Fig. 8. |
If the above elementary dynamos are compared with fig. 1, it will be found that they all possess a distinctive feature which is not present in the original disk machine of Faraday. In the four types of machine above described each active wire in each revolution first cuts the group of lines forming a field in one direction, and then cuts the same lines again in the opposite direction relatively to the sense of the lines, so that along the length of the wire the E.M.F. alternates in direction. But in the dynamo of fig. 1 the sector of the copper disk which is at any moment moving through the magnetic field and which forms the single active element is always cutting the lines in the same manner, so that the E.M.F. generated along its radial length is continuous and unchanged in direction. This radical distinction differentiates the two classes of heteropolar and homopolar dynamos, Faraday’s disk machine of fig. 1 being the type of the latter class. In it the active element may be arranged either parallel or at right angles to the axis of rotation; but in both cases, in order to increase the E.M.F. by placing two or more elements in series, it becomes necessary either (1) to employ some form of sliding contact by which the current may be collected from the end of one active element and passed round a connecting wire into the next element without again cutting the field in the reverse direction, or (2) to form on the armature a loop of which each side is alternately active and inactive. The first method limits the possibilities of the homopolar machine so greatly when large currents and high voltages are required that it is now only used in rare instances, as e.g. occasionally in dynamos driven by steam-turbines which have a very high speed of rotation. The second alternative may be carried into effect with any of the four methods of armature winding, but is practically confined to the drum and disk types. In its drum form the field is divided into two or more projecting poles, all of the same sign, with intervening neutral spaces of equal width, and the span of the loop in the direction of rotation is at least equal to the width of a polar projection, as in fig. 8, where two polar projections are shown. Each side of the loop then plays a dual part; it first cuts the lines of one polar projection and generates an E.M.F., and next becomes an inactive connecting wire, while the action is taken up by the opposite side of the loop which has previously served as a connector but now cuts the lines of the next polar projection. The E.M.F. is thus always in the same direction along the side which is at any moment active, but alternates round the loop as a whole, and the distinctive peculiarity of the homopolar machine, so soon as any form of “winding” is introduced into its armature, is lost. It results that the homopolar principle, which would prima facie appear specially suitable for the generation of a unidirectional E.M.F. and continuous current, can seldom be used for this purpose and is practically confined to alternators. It may therefore be said that in almost all dynamos, whether they supply an alternating or a continuous current in the external circuit, the E.M.F. and current in the armature are alternating.
Ring winding was largely employed in early continuous-current dynamos and also in the alternators of Gramme and H. Wilde, and later of Auguste de Méritens. Disk winding was also successfully introduced for alternators, as in the magneto-machines of Nollet (1849) and the alternators of Wilde (1866) and Siemens (1878), and its use was continued in the machines of W. M. Mordey and S. Z. Ferranti. But although the ring, discoidal-ring and disk methods of winding deserve mention from their historical importance, experience has shown that drum winding possesses a marked superiority for both electrical and manufacturing reasons; the three former methods have in fact been practically discarded in its favour, so that the drum method will hereafter alone be considered.
The drum coil, composed of several loops wound side by side, may therefore be regarded as the constituent active element out of which the armature winding of the modern dynamo is developed. Its application to the multipolar machine is easily followed from fig. 9, which illustrates the heteropolar type of dynamo. The span of the loops, which is nearly 180° or across the diameter of the two-pole machine, is reduced approximately to 90° in the four-pole or to 60° in the six-pole machine and so on, the curvature of the coil becoming gradually less as the number of poles is increased. The passage of a coil through two magnetic fields of opposite direction yields a complete wave of E.M.F., such as is shown in fig. 6, and the time in seconds taken to pass through such a complete cycle is the “period” of the alternating E.M.F. The number of complete periods through which the E.M.F. of the coil passes per second is called the “periodicity” or “frequency” of the machine. In the bipolar machine this is equal to the number of revolutions per second, and in the multipolar machine it is equal to the number of pairs of fields through which the coil passes in one second; hence in general the periodicity is pN / 60, where N = the number of revolutions per minute and p = the number of pairs of poles, and this holds true of the E.M.F. and current round the coil, even though the E.M.F. and current furnished to the external circuit may be rendered unidirectional or continuous. The only difference on this point is that in the continuous-current machine the poles are usually fewer than in the alternator, and the periodicity is correspondingly lower. Thus in the former case the number of poles ranges from 2 to 12 and the usual frequencies from 5 to 20; but with alternators the frequencies in commercial use range from 25 to 120, and in large machines driven by slow-speed engines the number of poles may even be as high as 96.
 | |
| I. Smooth. | II. Toothed. |
| Fig. 9. | |
 |
| Fig. 10. |
The drum coil may be applied either to the external surface of a rotating armature, the field-magnet being external and stationary (fig. 9), or to the internal surface of a stationary armature (fig. 10), the field-magnet being internal and rotating. While the former combination is universally adopted in the continuous-current dynamo, the latter is more usual in the modern alternator. In either case the iron armature core must be “laminated”; the passage of the lines of the field across its surface sets up E.M.F.’s which are in opposite directions under poles of opposite sign, so that if the core were a solid mass a current-sheet would flow along its surface opposite to a pole, and complete its circuit by passing through the deeper layers of metal or by returning in a sheet under a pole of opposite sign. Such “eddy-currents” can be practically avoided by dividing the metal core into laminations at right angles to the length of the active wires which are themselves arranged to secure the greatest rate of line-cutting and maximum E.M.F. The production of the eddy-current E.M.F. is not thereby prevented, but the paths of the eddy-currents are so broken up that the comparatively high resistance with which they meet reduces their amount very greatly. The laminae must be lightly insulated from one another, right up to their edges, so that the E.M.F.’s which still act across their thickness will not be added up along the length of the core, but will only produce extremely small currents circulating through the interior of the separate laminations. Each thin iron plate is either coated with an insulating varnish or has one of its sides covered with a sheet of very thin paper; the thickness of the laminae is usually about one-fortieth of an inch, and if this is not exceeded the rate at which energy is dissipated by eddy-currents in the core is so far reduced that it does not seriously impair the efficiency of the machine.
Lastly, the drum coils may be either attached to the surface of a smooth armature core (fig. 9, I.), or may be wound through holes formed close to the periphery of the core, or may be embedded in the slots between projecting iron teeth (figs. 9 [II.] and 10). Originally employed by Antonio Pacinotti in connexion with ring winding, the toothed armature was after some considerable use largely discarded in favour of the smooth core; it has, however, been reintroduced with a fuller understanding of the special precautions necessitated in its design, and it is now so commonly used that it may be said to have superseded the smooth-surface armature.
Not only does the toothed armature reduce the length of the air-gap to the minimum permitted by mechanical and magnetic considerations, and furnish better mechanical protection to the armature coils, but it also ensures the positive holding of the active wires against the mechanical drag which they experience as they pass through the magnetic field. Further, the active wires in the toothed armature are relieved of a large proportion of this mechanical drag, which is transferred to the iron teeth. The lines of the field, after passing through the air-gap proper, divide between the teeth and the slots in proportion to their relative permeances. Hence at any moment the active wires are situated in a weak field, and for a given armature current the force on them is only proportional to this weak field. This important result is connected with the fact that when the armature is giving current the distribution of the lines over the face of each tooth is distorted, so that they become denser on the “trailing” side than on the “leading” side;[13] the effect of the non-uniform distribution acting on all the teeth is to produce a magnetic drag on the armature core proportional to the current passing through the wires, so that the total resisting force remains the same as if the armature had a smooth core. The amount by which the stress on the active wires is reduced entirely depends upon the degree to which the teeth are saturated, but, since the relative permeability of iron even at a flux density of 20,000 lines per sq. cm. is to that of air approximately as 33 : 1, the embedded wires are very largely relieved of the driving stress. An additional gain is that solid bars of much greater width can be used in the toothed armature than on a smooth core without appreciable loss from eddy-currents within their mass.
A disadvantage of the slotted core is, however, that it usually necessitates the lamination of the pole-pieces. If the top of the slot is open, and its width of opening is considerably greater than the length of the air-gap from the iron of the pole-face to the surface of the teeth, the lines become unequally distributed not only at the surface of the teeth, but also at the face of the pole-pieces; and this massing of the lines into bands causes the density at the pole-face to be rhythmically varied as the teeth pass under it. No such variation can take place in a solid mass of metal without the production of eddy-currents within it; hence if the width of the slot-opening is equal to or exceeds twice the length of the single air-gap, lamination of the pole-pieces in the same plane as that of the armature core becomes advisable.
If the wires are threaded through holes or tunnels pierced close to the periphery of the core, the same advantages are gained as with open slots, and lamination of the pole-pieces is rendered unnecessary. But on the other hand, the process of winding becomes laborious and expensive, while the increase in the inductance of the coils owing to their being surrounded by a closed iron circuit is prejudicial to sparkless commutation in the continuous-current dynamo and to the regulation of the voltage of the alternator. A compromise is found in the half-closed slot, which is not uncommon in alternators, although the open slot is more usual in continuous-current dynamos.
 |
| Fig. 11. |
With the addition of more turns to the elementary drum loop or of several complete coils, new questions arise, and in connexion therewith the two great classes of machines, viz. alternators and continuous-current dynamos, which have above been treated side by side, diverge considerably, so that they are best considered separately. The electromotive-force equation of the alternator will be first deduced, and subsequently that of the continuous-current machine.
Corresponding to the number of pairs of poles in the multipolar alternator, it is evident that there may also be an equal number of coils as shown diagrammatically in fig. 11. The additional coils, being similarly situated in respect to other pairs of poles, will exactly reproduce the E.M.F. of the original coil in phase and magnitude, so that when they are connected in series the total E.M.F. will be proportional to the number of coils in series; or if they are connected in parallel, while not adding to the E.M.F., they will proportionately increase the current-carrying capacity of the combination. But within each coil the addition of more loops will not cause an equal increase in the total E.M.F., unless the phases of the component E.M.F.’s due to the several turns are identical, and on this account it becomes necessary to consider the effect of the width of the coil-side.
 |
| Fig. 12. |
If the additional loops are wound within the same slots as the original loop, the winding is “concentrated,” and each turn will then add the same E.M.F. But if the coil-side is divided between two or more slots, the phase of the E.M.F. yielded by the wires in one slot being different from that of the wires in another neighbouring slot, the sum of all the E.M.F.’s will be less than the E.M.F. of one component loop multiplied by the number of loops or turns in the coil. The percentage reduction in the E.M.F. will depend upon the number of the slots in a coil-side and their distance apart, i.e. on the virtual width of the coil-side expressed as a fraction of the “pole-pitch” or the distance measured along the pitch-line from the centre of one pole to the centre of a neighbouring pole of opposite sign (fig. 12). The winding is now to be regarded as “grouped,” since a small number of distinct phases corresponding to the groups within the two, three or four slots have to be compounded together. As the number of slots per coil-side is increased, an approach is gradually made to the case of “uniform distribution,” such as would obtain in a smooth-core armature in which the turns of the coil are wound closely side by side. Thus in the six-turn coil of fig. 12 A, which represents the development of a two-pole armature when the core is cut down to the shaft and opened out flat, there are in effect six phases compounded together, each of which differs but little from that of its next neighbour. With numerous wires lying still closer together a large number of phases are compounded until the distribution becomes practically uniform; the decrease in the E.M.F., as compared with that of a single turn multiplied by the number in series, is then immediately dependent upon the width of the coil-side relatively to the pole-pitch.
 |
| Fig. 13. |
If the width of the inner loop of fig. 12 A is less than that of the pole-face, its two sides will for some portion of each period be moving under the same pole, and “differential action” results, the net E.M.F. being only that due to the difference between the E.M.F.’s of the two sides. The loop of smallest width must therefore exceed the width of pole-face, if direct differential action is to be avoided. The same consideration also determines the width of the outer loop; if this be deducted from twice the pole-pitch, the difference should not be less than the width of the pole-face, so that, e.g., in a bipolar machine the outer loop may stand to the S. pole exactly as the inner loop stands to the N. pole (fig. 13). In other words, the width of the coil-side must not exceed the width of the interpolar gap between two fields. Evidently then if the ratio of the pole-width to the pole-pitch approaches unity, the width of the coil-side must be very small, and vice versa. A compromise between these conflicting considerations is found if the pole is made not much more than half the pole-pitch, and the width of the coil-side is similarly about half the pole-pitch and therefore equal in width to the pole (fig. 13). A single large coil, such as that of fig. 12 A, can, however, equally well be divided into two halves by taking the end-connexions of one half of the turns round the opposite side of the shaft (fig. 12 B), as indeed has already been done in fig. 13. Each sheaf or band of active wires corresponding to a pole is thereby unaffected, but the advantages are gained that the axial length of the end-connexions is halved, and that they have less inductance. Thus if in fig. 11 there are four turns per coil, fig. 14 is electrically equivalent to it (save that the coils are here shown divided into two parallel paths, each carrying half the total current). When the large coils are divided as above described, it results that there are as many coils as there are poles, the outer loop of the small coil having a width equal to the pole-pitch, and the inner a width equal to the pole-face.
 |
| Fig. 14. |
Such is the form which the “single-phase alternator” takes, but since only one-half of the armature core is now covered with winding, an entirely distinct but similar set of coils may be wound to form a second armature circuit between the coils of the first circuit. The phase of this second circuit will differ by 90° or a quarter of a period from that of the first, and it may either be used to feed an entirely separate external circuit possibly at a different pressure or, if it be composed of the same number of turns and therefore gives the same voltage, it may be interconnected with the first circuit to form a “quarter-phase alternator,” as will be more fully described later. By an extension of the same process, if the width of each side of a coil is reduced to one-sixth of the pole-pitch, three armature circuits can be wound on the same core, and a “three-phase alternator,” giving waves of E.M.F. differing in phase by 120°, is obtained.
The fundamental “electromotive-force equation” of the heteropolar alternator can now be given a more definite form. Let Za be the number of C. G. S. lines or the total flux, which issuing from any one pole flows through the armature core, to leave it by another pole of opposite sign. Since each active wire cuts these lines, first as they enter the armature core and then as they emerge from it to enter another pole, the total number of lines cut in one revolution by any one active wire is 2pZa. The time in seconds taken by one revolution is 60/N. The average E.M.F. induced in each active wire in one revolution being proportional to the number of lines cut divided by the time taken to cut them is therefore 2Za (pN / 60) × 10−8 volts. The active wires which are in series and form one distinct phase may be divided into as many bands as there are poles; let each such band contain t active wires, which as before explained may either form one side of a single large coil or the adjacent sides of two coils when the large coil is divided into two halves. Since the wires are joined up into loops, two bands are best considered together, which with either arrangement yield in effect a single coil of t turns. The average E.M.F.’s of all the wires in the two bands when added together will therefore be 4Za (pN / 60)t × 10−8. But unless each band is concentrated within a single slot, there must be some differential action as they cross the neutral line between the poles, so that the last expression is virtually the gross average E.M.F. of the loops on the assumption that the component E.M.F.’s always act in agreement round the coil and do not at times partially neutralize one another. The net average E.M.F. of the coil as a whole, or the arithmetical mean of all the instantaneous values of a half-wave of the actual E.M.F. curve, is therefore reduced to an extent depending upon the amount of differential action and so upon the width of the coil-side when this is not concentrated. Let k′=the coefficient by which the gross average E.M.F. must be multiplied to give the net average E.M.F.; then k′ may be called the “width-factor,” and will have some value less than unity when the wires of each band are spread over a number of slots. The net average E.M.F. of the two bands corresponding to a pair of poles is thus eav=4k′Za (pN / 60)t × 10−8.
The shape of the curve of instantaneous E.M.F. of the coil must further be taken into account. The “effective” value of an alternating E.M.F. is equal to the square root of the mean square of its instantaneous values, since this is the value of the equivalent unidirectional and unvarying E.M.F., which when applied to a given resistance develops energy at the same rate as the alternating E.M.F., when the effect of the latter is averaged over one or any whole number of periods. Let k″=the ratio of the square root of the mean square to the average E.M.F. of the coil, i.e.= Since it depends upon the shape of the E.M.F. curve, k″ is also known as the “form-factor”; thus if the length of gap between pole-face and armature core and the spacing of the wires were so graduated as to give a curve of E.M.F. varying after a sine law, the form-factor would have the particular value of π/2 √2=1·11, and to this condition practical alternators more or less conform. The effective E.M.F. of the two bands corresponding to a pair of poles is thus eeff=4k′k″Za (pN / 60)t × 10−8.
In any one phase there are p pairs of bands, and these may be divided into q parallel paths, where q is one or any whole number of which p is a multiple. The effective E.M.F. of a complete phase is therefore peeff/q. Lastly, if m=the number of phases into which the armature winding is divided, and τ=the total number of active wires on the armature counted all round its periphery, t=τ / 2pm, and the effective E.M.F. per phase is Ea=2k′k″Za (pNτ / 60mq) × 10−8.
The two factors k′ and k″ may be united into one coefficient, and the equation then takes its final form
| Ea=2KZa (pNτ / 60mq) × 10−8 volts | (1a) |
In the alternator q is most commonly 1, and there is only one circuit per phase; finally the value of K or the product of the width-factor and the form-factor usually falls between the limits of 1 and 1·25.
We have next to consider the effect of the addition of more armature loops in the case of dynamos which give a unidirectional E.M.F. in virtue of their split-ring collecting device, i.e. of the type shown in fig. 7 with drum armature or its equivalent ring form. As before, if the additional loops are wound in continuation of the first as one coil connected to a single split-ring, this coil must be more or less concentrated into a narrow band; since if the width becomes nearly equal to or exceeds the width of the interpolar gap, the two edges of the coil-side will just as in the alternator act differentially against one another during part of each revolution. The drum winding with a single coil thus gives an armature of the H- or “shuttle” form invented by Dr Werner von Siemens. Although the E.M.F. of such an arrangement may have a much higher maximum value than that of the curve of fig. 7 for a single loop, yet it still periodically varies during each revolution and so gives a pulsating current, which is for most practical uses unsuitable. But such pulsation might be largely reduced if, for example, a second coil were placed at right angles to the original coil and the two were connected in series; the crests of the wave of E.M.F. of the second coil will then coincide with the hollows of the first wave, and although the maximum of the resultant curve of E.M.F. may be no higher its fluctuations will be greatly decreased. A spacial displacement of the new coils along the pole-pitch, somewhat as in a polyphase machine, thus suggests itself, and the process may be carried still further by increasing the number of equally spaced coils, provided that they can be connected in series and yet can have their connexion with the external circuit reversed as they pass the neutral line between the poles.
 |
| Fig. 15. |
 |
| Fig. 16. |
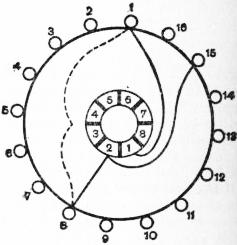
Given two coils at right angles and with their split-rings displaced through a corresponding angle of 90°, they may be connected in series by joining one brush to the opposite brush of the second coil, the external circuit being applied to the two remaining brushes.[14] The same arrangement may again be repeated with another pair of coils in parallel with the first, and we thus obtain fig. 15 with four split-rings, their connexions to the loops being marked by corresponding numerals; the four coils will give the same E.M.F. as the two, but they will be jointly capable of carrying twice the current, owing to their division into two parallel circuits. Now in place of the four split-rings may be employed the greatly simplified four-segment structure shown in fig. 16, which serves precisely the same purpose as the four split-rings but only requires two instead of eight brushes. The effect of joining brush 2 in fig. 15 across to brush 3, brush 4 to brush 5, 5 to 6, &c., has virtually been to connect the end of coil A with the beginning of coil B, and the end of coil B with the beginning of coil A′, and so on, until they form a continuous closed helix. Each sector of fig. 16 will therefore replace two halves of a pair of adjacent split-rings, if the end and beginning of a pair of adjacent coils are connected to it in a regular order of sequence. The four sectors are insulated from one another and from the shaft, and the whole structure is known as the “commutator,”[15] its function being not simply to collect the current but also to commute its direction in any coil as it passes the interpolar gap. The principle of the “closed-coil continuous-current armature” is thus reached, in which there are at least two parallel circuits from brush to brush, and from which a practically steady current can be obtained. Each coil is successively short-circuited, as a brush bridges over the insulation between the two sectors which terminate it; and the brushes must be so set that the period of short-circuit takes place when the coil is generating little or no E.M.F., i.e. when it is moving through the zone between the pole-tips. The effect of the four coils in reducing the percentage fluctuation of the E.M.F. is very marked, as shown at the foot of fig. 15 (where the upper curve is the resultant obtained by adding together the separate curves of coils A and B), and the levelling process may evidently be carried still further by the insertion of more coils and more corresponding sectors in the commutator, until the whole armature is covered with winding.
 |
| Fig. 17. |
 |
| Fig. 18. |
For example, figs. 17 and 18 show a ring and a drum armature, each with eight coils and eight commutator sectors; their resultant curve, on the assumption that a single active wire gives the flat-topped curve of fig. 4, will be the upper wavy line of E.M.F. obtained by adding together two of the resultant curves of fig. 15, with a relative displacement of 45°. The amount of fluctuation for a given number of commutator sectors depends upon the shape of the curve of E.M.F. yielded by the separate small sections of the armature winding; the greater the polar arc, the less the fluctuation. In practice, with a polar arc equal to about 0·75 of the pitch, any number of sectors over 32 per pair of poles yields an E.M.F. which is sensibly constant throughout one or any number of revolutions.
The fundamental electro-motive-force equation of the continuous-current heteropolar machine is easily obtained by analogy from that of the alternator. The gross average E.M.F. from the two sides of a drum loop without reference to its direction is as before 4Za (pN / 60) × 10−8 volts. But for two reasons its net average E.M.F. may be less; the span of the loop may be less than the pole-pitch, so that even when the brushes are so set that the position of short-circuit falls on the line where the field changes its direction, the two sides of the loop for some little time act against each other; or, secondly, even if the span of the loop be equal to the pole-pitch, the brushes may be so set that the reversal of the direction of its induced E.M.F. does not coincide with reversal of the current by the passage of the coil under the brushes. The net average E.M.F. of the loop is therefore proportional to the algebraic sum of the lines which it cuts in passing from one brush to another, and this is equal to the net amount of the flux which is included within the loop when situated in the position of short-circuit under a brush. The amount of this flux may be expressed as k′Za where k′ is some coefficient, less than unity if the span of the coil be less than the pole-pitch, and also varying with the position of the brushes. The net average E.M.F. of the loop is therefore
4k′Za (pN / 60) × 10−8.
In practice the number of sections of the armature winding is so large and their distribution round the armature periphery is so uniform, that the sum total of the instantaneous E.M.F.’s of the several sections which are in series becomes at any moment equal to the net average E.M.F. of one loop multiplied by the number which are in series. If the winding is divided into q parallel circuits, the number of loops in series is τ/2q, so that the total E.M.F. is Ea=2(k′ / q) Za (pN / 60)τ × 10−8 volts. Thus as compared with the alternator not only is there no division of the winding into separate phases, but the form-factor k′ disappears, since the effective and average E.M.F.’s are the same. Further whereas in the alternator q may=1, in the continuous-current closed-coil armature there can never be less than two circuits in parallel from brush to brush, and if more, their number must always be a multiple of two, so that q can never be less than two and must always be an even number. Lastly, the factor k′ is usually so closely equal to 1, that the simplified equation may in practice be adopted, viz.
| Ea=(2/q) (ZpN / 60) τ × 10−8 volts. | (1b) |
The fundamental equation of the electromotive force of the dynamo in its fully developed forms (1 a) (and 1 b) may be compared with its previous simple statement (I.). The three variable terms still find their equivalents, but are differently expressed, the density Bg being replaced by the total flux of one field Za, the length L of the single active wire by the total number of such wires τ, and the velocity of movement V by the number of revolutions per second. Even when the speed is fixed, an endless number of changes may be rung by altering the relative values of the remaining two factors; and in successful practice these may be varied between fairly wide limits without detriment to the working or economy of the machine. While it may be said that the equation of the E.M.F. was implicitly known from Faraday’s time onwards, the difficulty under which designers laboured in early days was the problem of choosing the correct relation of Za or τ for the required output; this, again, was due chiefly to the difficulty of predetermining the total flux before the machine was constructed. The general error lay in employing too weak a field and too many turns on the armature, and credit must here be given to the American inventors, E. Weston and T. A. Edison, for their early appreciation of the superiority in practical working of the drum armature, with comparatively few active wires rotating in a strong field.
Continuous-current Dynamos.—On passing to the separate consideration of alternators and continuous-current dynamos, the chief constructive features of the latter will first be taken in greater detail. As already stated in the continuous-current dynamo the armature is usually the rotating portion, and the The armature core.necessity of laminating its core has been generally described. The thin iron stampings employed to build up the core take the form of circular washers or “disks,” which in small machines are strung directly on the shaft; in larger multipolar machines, in which the required radial depth of iron is small relatively to the diameter, a central cast iron hub supports the disks. Since the driving force is transmitted through the shaft to the disks, they must in the former case be securely fixed by keys sunk into the shaft; when a central hub is employed (fig. 19) it is keyed to the shaft, and its projecting arms engage in notches stamped on the inner circumference of the disks, or the latter have dovetailed projections fitting into the arms. The disks are then tightly compressed and clamped between stout end-plates so as to form a nearly solid iron cylinder of axial length slightly exceeding the corresponding dimension of the poles. If the armature is more than 4 ft. in diameter, the disks become too large to be conveniently handled in one piece, and are therefore made in segments, which are built up so as to break joint alternately. Prior to assemblage, the external circumference of each disk is notched in a stamping machine with the required number of slots to receive the armature coils, and the longitudinal grooves thereby formed in the finished core only require to have their sharp edges smoothed off so that there may be no risk of injury to the insulation of the coils.
 |
| Fig. 19. |
With open slots either the armature coils may be encased with wrappings of oiled linen, varnished paper and thin flexible micanite sheeting in order to insulate them electrically from the iron slots in which they are afterwards embedded; or the slots may be themselves lined with moulded troughs of micanite, &c., Armature winding.for the reception of the armature coils, the latter method being necessary with half-closed slots. According to the nature of the coils armatures may be divided into the two classes of coil-wound and bar-wound. In the former class, round copper wire, double-cotton covered, is employed, and the coils are either wound by hand directly on to the armature core, or are shaped on formers prior to being inserted in the armature slots. Hand-winding is now only employed in very small bipolar machines, the process being expensive and accompanied by the disadvantage that if one section requires to be repaired, the whole armature usually has to be dismantled and re-wound. Former-wound coils are, on the other hand, economical in labour, perfectly symmetrical and interchangeable, and can be thoroughly insulated before they are placed in the slots. The shapers employed in the forming process are very various, but are usually arranged to give to the finished coil a lozenge shape, the two straight active sides which fit into the straight slots being joined by V-shaped ends; at each apex of the coil the wire is given a twist, so that the two sides fall into different levels, an upper and a lower, corresponding to the two layers which the coil-sides form on the finished armature. Rectangular wire of comparatively small section may be similarly treated, and if only one loop is required per section, wide and thin strip can be bent into a complete loop, so that the only soldered joints are those at the commutator end where the loops are interconnected. But finally with massive rectangular conductors, the transition must be made to bar-winding, in which each bar is a half-loop, insulated by being taped after it has been bent to the required shape; the separate bars are arranged on the armature in two layers, and their ends are soldered together subsequently to form loops. As a general rule, whether bars or former-wound coils are employed, the armature is barrel-wound, i.e. the end-connexions project outwards from the slots with but little change of level, so that they form a cylindrical mass supported on projections from the end-plates of the core (fig. 19); but, in certain cases, the end-connexions are bent downwards at right angles to the shaft, and they may then consist of separate strips of copper bent to a so-called butterfly or evolute shape.
After the coils or loops have been assembled in the slots on the armature core, and the commutator has been fixed in place on the shaft, the soldering of the ends of the coils proceeds, by which at once the union of the end of one coil with the beginning of the next, and also their connexion to the commutator sectors, is effected, and in this lies the essential part of armature winding.
 |
| Lap-loops Fig. 20. |
The development of the modern drum armature, with its numerous coils connected in orderly sequence into a symmetrical winding, as contrasted with the earlier Siemens armatures, was initiated by F. von Hefner Alteneck (1871), and the laws governing the interconnexion of the coils have now been elaborated into a definite system of Lap-winding.winding formulae. Whatever the number of wires or bars in each side of a coil, i.e. whether it consist of a single loop or of many turns, the final connexions of its free ends are not thereby affected, and it may be mentally replaced by a single loop with two active inducing sides. The coil-sides in their final position are thus to be regarded as separate primary elements, even in number, and distributed uniformly round the armature periphery or divided into small, equally spaced groups by being located within the slots of a toothed armature. Attention must then be directed simply to the span of the back connexion between the elements at the end of the armature further from the commutator, and to the span of the front connexion by which the last turn of a coil is finally connected to the first turn of the next in sequence, precisely as if each coil of many turns were reduced to a single loop. In order to avoid direct differential action, the span of the back connexion which fixes the width of the coil must exceed the width of the pole-face, and should not be far different from the pole-pitch; it is usually a little less than the pole-pitch. Taking any one element as No. 1 in fig. 20, where for simplicity a smooth-core bipolar armature is shown, the number of winding-spaces, each to be occupied by an element, which must be counted off in order to find the position of the next element in series, is called the “pitch” of the end-connexion, front or back, as the case may be. Thus the back pitch of the winding as marked by the dotted line in fig. 20 is 7, the second side of the first loop being the element numbered 1 + 7=8. In forming the front end-connexion which completes the loop and joins it to the next in succession, two possible cases present themselves. By the first, or “lap-winding,” the front end-connexion is brought backwards, and passing on its way to a junction with a commutator sector is led to a third element lying within the two sides of the first loop, i.e. the second loop starts with the element, No. 3, lying next but one to the starting-point of the first loop. The winding therefore returns backwards on itself to form each front end, but as a whole it works continually forwards round the armature, until it finally “re-enters,” after every element has been traversed. The development of the completed winding on a flat surface shows that it takes the form of a number of partially overlapping loops, whence its name originates. The firm-line portion of fig. 21 gives the development of an armature similar to that of fig. 18 when cut through at the point marked X and opened out; two of the overlapping loops are marked thereon in heavy lines. The multipolar lap-wound armature is obtained by simply repeating the bipolar winding p times, as indicated by the dotted additions of fig. 21 which convert it from a two-pole to a four-pole machine. The characteristic feature of the lap-wound armature is that there are as many parallel paths from brush to brush, and as many points at which the current must be collected, as there are poles. As the bipolar closed-coil continuous-current armature has been shown to consist in reality of two circuits in parallel, each giving the same E.M.F. and carrying half the total current, so the multipolar lap-wound drum consists of p pairs of parallel paths, each giving the same E.M.F. and carrying 1/2p of the total current. Thus in equation 1.b we have q=2p, and the special form which the E.M.F. equation of the lap-wound armature takes is Ea=Za (N / 60)τ × 10–8 volts. All the brushes which are of the same sign must be connected together in order to collect the total armature current. The several brush-sets of the multipolar lap-wound machine may again be reduced to two by “cross-connexion” of sectors situated 360°/p apart, but this is seldom done, since the commutator must then be lengthened p times in order to obtain the necessary brush contact-surface for the collection of the entire current.
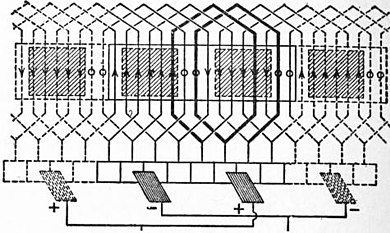 Fig. 21. |
 Wave-loops Fig. 22. |
 Fig. 23. |
But for many purposes, especially where the voltage is high and the current small, it is advantageous to add together the inductive effect of the several poles of the multipolar machine by throwing the E.M.F.’s of half the total number of elements Wave-winding. into series, the number of parallel circuits being conversely again reduced to two. This is effected by the second method of winding the closed-coil continuous current drum, which is known as “wave-winding.” The front pitch is now in the same direction round the armature as the back pitch (fig. 22), so that the beginning of the second loop, i.e. element No. 15, lies outside the first loop. After p loops have been formed and as many elements have been traversed as there are poles, the distance covered either falls short of or exceeds a complete tour of the armature by two winding-spaces, or the width of two elements. A second and third tour are then made, and so on, until finally the winding again closes upon itself. When the completed winding is developed as in fig. 23, it is seen to work continuously forwards round the armature in zigzag waves, one of which is marked in heavy lines, and the number of complete tours is equal to the average of the back and front pitches. Since the number of parallel circuits from brush to brush is q=2, the E.M.F. equation of the wave-wound drum is Ea=pZa (N / 60)τ × 10−8 volts. Only two sets of brushes are necessary, but in order to shorten the length of the commutator, other sets may also be added at the point of highest and lowest potential up to as many in number as there are poles. Thus the advantage of the wave-wound armature is that for a given voltage and number of poles the number of active wires is only 1/p of that in the lap-wound drum, each being of larger cross-section in order to carry p times as much current; hence the ratio of the room occupied by the insulation to the copper area is less, and the available space is better utilized. A further advantage is that the two circuits from brush to brush consist of elements influenced by all the poles, so that if for any reason, such as eccentricity of the armature within the bore of the pole-pieces, or want of uniformity in the magnetic qualities of the poles, the flux of each field is not equal to that of every other, the equality of the voltage produced by the two halves of the winding is not affected thereby.
In appearance the two classes of armatures, lap and wave, may be distinguished in the barrel type of winding by the slope of the upper layer of back end-connexions, and that of the front connexions at the commutator end being parallel to one another in the latter, and oppositely directed in the former.
 |
| Fig. 24. |
After completion of the winding, the end-connexions are firmly bound down by bands of steel or phosphor bronze binding wire, so as to resist the stress of centrifugal force. In the case of smooth-surface armatures, such bands are also placed at intervals along the length of the armature core, but in toothed armatures, although the coils are often in small machines secured in the slots by similar bands of a non-magnetic high-resistance wire, the use of hard-wood wedges driven into notches at the sides of the slots becomes preferable, and in very large machines indispensable. The external appearance of a typical armature with lap-winding is shown in fig. 24.
A sound mechanical construction of the commutator is of vital importance to the good working of the continuous-current dynamo. The narrow, wedge-shaped sectors of hard-drawn copper, with their insulating strips of thin mica, are built up into a cylinder, tightly clamped together, and turned in the lathe; The commutator.at each end a V-shaped groove is turned, and into these are fitted rings of micanite of corresponding section (fig. 19); the whole is then slipped over a cast iron sleeve, and at either end strong rings are forced into the V-shaped grooves under great pressure and fixed by a number of closely-pitched tightening bolts. In dynamos driven by steam-turbines in which the peripheral speed of the commutator is very high, rings of steel are frequently shrunk on the surface of the commutator at either end and at its centre. But in every case the copper must be entirely insulated from the supporting body of metal by the interposition of mica or micanite and the prevention of any movement of the sectors under frequent and long-continued heating and cooling calls for the greatest care in both the design and the manufacture.
On passing to the second fundamental part of the dynamo, namely, the field-magnet, its functions may be briefly recalled as follows:—It has to supply the magnetic flux; to provide for it an iron path as nearly closed as possible upon the armature, save for the air-gaps which must exist between the pole-system Forms of field-magnet.and the armature core, the one stationary and the other rotating; and, lastly, it has to give the lines such direction and intensity within the air-gaps that they may be cut by the armature wires to the best advantage. Roughly corresponding to the three functions above summarized are the three portions which are more or less differentiated in the complete structure. These are: (1) the magnet “cores” or “limbs,” carrying the exciting coils whereby the inert iron is converted into an electro-magnet; (2) the yoke, which joins the limbs together and conducts the flux between them; and (3) the pole-pieces, which face the armature and transmit the lines from the limbs through the air-gap to the armature core, or vice versa.
 |
| Fig. 25. |
Of the countless shapes which the field-magnet may take, it may be said, without much exaggeration, that almost all have been tried; yet those which have proved economical and successful, and hence have met with general adoption, may be classed under a comparatively small number of types. For bipolar machines the single horse-shoe (fig. 25), which is the lineal successor of the permanent magnet employed in the first magneto-electric machines, was formerly very largely used. It takes two principal forms, according as the pole-pieces and armature are above or beneath the magnet limbs and yoke. The “over-type” form is best suited to small belt-driven dynamos, while the “under-type” is admirably adapted to be directly driven by the steam-engine, the armature shaft being immediately coupled to the crank-shaft of the engine. In the latter case the magnet must be mounted on non-magnetic supports of gun-metal or zinc, so as to hold it at some distance away from the iron bedplate which carries both engine and dynamo; otherwise a large proportion of the flux which passes through the magnet limbs would leak through the bedplate across from pole to pole without passing through the armature core, and so would not be cut by the armature wires.
 |
| Fig. 26. |
Next may be placed the “Manchester” field (fig. 26)—the type of a divided magnetic circuit in which the flux forming one field or pole is divided between two magnets. An exciting coil is placed on each half of the double horse-shoe magnet, the pair being so wound that consequent poles are formed above and below the armature. Each magnet thus carries one-half of the total flux, the lines of the two halves uniting to form a common field where they issue forth into or leave the air-gaps. The pole-pieces may be lighter than in the single horse-shoe type, and the field is much more symmetrical, whence it is well suited to ring armatures of large diameter. Yet these advantages are greatly discounted by the excessive magnetic leakage, and by the increased weight of copper in the exciting coils. Even if the greater percentage which the leakage lines bear to the useful flux is neglected, and the cross sectional area of each magnet core is but half that of the equivalent single horse-shoe, the weight of wire in the double magnet for the same rise of temperature in the coils must be some 40% more than in the single horse-shoe, and the rate at which energy is expended in heating the coils will exceed that of the single horse-shoe in the same proportion.
Thirdly comes the two-pole ironclad type, so called from the exciting coil being more or less encased by the iron yoke; this latter is divided into two halves, which pass on either side of the armature. Unless the yoke be kept well away from the polar edges and armature, the leakage across the air into the yoke becomes considerable, especially if only one exciting coil is used, as in fig. 27 A; it is better, therefore, to divide the excitation between two coils, as in fig. 27 B, when the field also becomes symmetrical.
From this form is easily derived the multipolar type of fig. 28 or fig. 29, which is by far the most usual for any number of poles from four upwards; its leakage coefficient is but small, and it is economical in weight both of iron and copper.
 |
| Fig. 27. |
As regards the materials of which magnets are made, generally speaking there is little difference in the permeability of “wrought iron” or “mild steel forgings” and good “cast steel”; typical (B, H) curves connecting the magnetizing force required with different flux-densities for these materials are given under Electromagnetism. On the other hand there is a Materials of magnets.marked inferiority in the case of “cast iron,” which for a flux-density of B=8000 C.G.S. lines per sq. cm. requires practically the same number of ampere-turns per centimetre length as steel requires for B=16,000. Whatever the material, if the flux-density be pressed to a high value the ampere-turns are very largely increased owing to its approaching saturation, and this implies either a large amount of copper in the field coils or an undue expenditure of electrical energy in their excitation. Hence there is a limit imposed by practical considerations to the density at which the magnet should be worked, and this limit may be placed at about B=16,000 for wrought iron or steel, and at half this value for cast iron. For a given flux, therefore, the cast iron magnet must have twice the sectional area and be twice as heavy, although this disadvantage is partly compensated by its greater cheapness. If, however, cast iron be used for the portion of the magnetic circuit which is covered with the exciting coils, the further disadvantage must be added that the weight of copper on the field-magnet is much increased, so that it is usual to employ forgings or cast steel for the magnet cores on which the coils are wound. If weight is not a disadvantage, a cast iron yoke may be combined with the wrought iron or cast steel magnet cores. An absence of joints in the magnetic circuit is only desirable from the point of view of economy of expense in machining the component parts during manufacture; when the surfaces which abut against each other are drawn firmly together by screws, the want of homogeneity at the joint, which virtually amounts to the presence of a very thin film of air, produces little or no effect on the total reluctance by comparison with the very much longer air-gaps surrounding the armature. In order to reduce the eddy-currents in the pole-pieces, due to the use of toothed armatures with relatively wide slots, the poles themselves must be laminated, or must have fixed to them laminated pole-shoes, built up of thin strips of mild steel riveted together (as shown in fig. 29).
 |
| Fig. 28. |
However it be built up, the mechanical strength of the magnet system must be carefully considered. Any two surfaces between which there exists a field of density Bg experience a force tending to draw them together proportional to the square of the density, and having a value of Bg2 / (1·735 × 106) ℔ per sq. in. of surface, over which the density may be regarded as having the uniform value Bg. Hence, quite apart from the torque with which the stationary part of the dynamo tends to turn with the rotating part as soon as current is taken out of the armature, there exists a force tending to make the pole-pieces close on the armature as soon as the field is excited. Since both armature and magnet must be capable of resisting this force, they require to be rigidly held; although the one or the other must be capable of rotation, there should otherwise be no possibility of one part of the magnetic circuit shifting relatively to any other part. An important conclusion may be drawn from this circumstance. If the armature be placed exactly concentric within the bore of the poles, and the two or more magnetic fields be symmetrical about a line joining their centres, there is no tendency for the armature core to be drawn in one direction more than in another; but if there is any difference between the densities of the several fields, it will cause an unbalanced stress on the armature and its shaft, under which it will bend, and as this bending is continually reversed relatively to the fibres of the shaft, they will eventually become weakened and give way. Especially is this likely to take place in dynamos with short air-gaps, wherein any difference in the lengths of the air-gaps produces a much greater percentage difference in the flux-density than in dynamos with long air-gaps. In toothed armatures with short air-gaps the shaft must on this account be sufficiently strong to withstand the stress without appreciable bending.
Reference has already been made to the importance in dynamo design of the predetermination of the flux due to a given number of ampere-turns wound on the field-magnet, or, conversely, of the number of ampere-turns which must be furnished by the exciting coils in order that a certain flux corresponding to one field The magnetic circuit.may flow through the armature core from each pole. An equally important problem is the correct proportioning of the field-magnet, so that the useful flux Za may be obtained with the greatest economy in materials and exciting energy. The key to the two problems is to be found in the concept of a magnetic circuit as originated by H. A. Rowland and R. H. M. Bosanquet;[16] and the full solution of both may be especially connected with the name of Dr J. Hopkinson, from his practical application of the concept in his design of the Edison-Hopkinson machine, and in his paper on “Dynamo-Electric Machinery.”[17] The publication of this paper in 1886 begins the second era in the history of the dynamo; it at once raised its design from the level of empirical rules-of-thumb to a science, and is thus worthy to be ranked as the necessary supplement of the original discoveries of Faraday. The process of predetermining the necessary ampere-turns is described in a simple case under Electromagnetism. In its extension to the complete dynamo, it consists merely in the division of the magnetic circuit into such portions as have the same sectional area and permeability and carry approximately the same total flux; the difference of magnetic potential that must exist between the ends of each section of the magnet in order that the flux may pass through it is then calculated seriatim for the several portions into which the magnetic circuit is divided, and the separate items are summed up into one magnetomotive force that must be furnished by the exciting coils.

|
| Fig. 29. |
The chief sections of the magnetic circuit are (1) the air-gaps, (2) the armature core, and (3) the iron magnet.
The air-gap of a dynamo with smooth-core armature is partly filled with copper and partly with the cotton, mica, or other materials used to insulate the core and wires; all these substances are, however, sensibly non-magnetic, so that the whole interferric gap between the iron of the pole-pieces and the iron of the armature may be treated as an air-space, of which the permeability is constant for all values of the flux density, and in the C.G.S. system is unity. Hence if lg and Ag be the length and area of the single air-gap in cm. and sq. cm., the reluctance of the double air-gap is 2lg / Ag, and the difference of magnetic potential required to pass Za lines over this reluctance is Za·2lg / Ag=Bg·2lg; or, since one ampere-turn gives 1·257 C.G.S. units of magnetomotive force, the exciting power in ampere-turns required over the two air-gaps is Xg=Bg·2lg / 1·257=0·8Bg·2lg. In the determination of the area Ag small allowance must be made for the fringe of lines which extend beyond the actual polar face. In the toothed armature with open slots, the lines are no longer uniformly distributed over the air-gap area, but are graduated into alternate bands of dense and weak induction corresponding to the teeth and slots. Further, the lines curve round into the sides of the teeth, so that their average length of path in the air and the air-gap reluctance is not so easily calculated. Allowance must be made for this by taking an increased length of air-gap=mlg, where m is the ratio maximum density/mean density, of which the value is chiefly determined by the ratios of the width of tooth to width of slot and of the width of slot to the air-gap between pole-face and surface of the armature core.
The armature core must be divided into the teeth and the core proper below the teeth. Owing to the tapering section of the teeth, the density rises towards their root, and when this reaches a high value, such as 18,000 or more lines per sq. cm., the saturation of the iron again forces an increasing proportion of the lines outwards into the slot. A distinction must then be drawn between the “apparent” induction which would hold if all the lines were concentrated in the teeth, and the “real” induction. The area of the iron is obtained by multiplying the number of teeth under the pole-face by their width and by the net length of the iron core parallel to the axis of rotation. The latter is the gross length of the armature less the space lost through the insulating varnish or paper between the disks or through the presence of ventilating ducts, which are introduced at intervals along the length of the core. The former deduction averages about 7 to 10% of the gross length, while the latter, especially in large multipolar machines, is an even more important item. After calculating the density at different sections of the teeth, reference has now to be made to a (B, H) or flux-density curve, from which may be found the number of ampere-turns required per cm. length of path. This number may be expressed as a function of the density in the teeth, and ƒ(Bt) be its average value over the length of a tooth, the ampere-turns of excitation required over the teeth on either side of the core as the lines of one field enter or leave the armature is Xt=ƒ(Bt).2lt, where lt is the length of a single tooth in cm.
In the core proper below the teeth the length of path continually shortens as we pass from the middle of the pole towards the centre line of symmetry. On the other hand, as the lines gradually accumulate in the core, their density increases from zero midway under the poles until it reaches a maximum on the line of symmetry. The two effects partially counteract one another, and tend to equalize the difference of magnetic potential required over the paths of varying lengths; but since the reluctivity of the iron increases more rapidly than the density of the lines, we may approximately take for the length of path (la) the minimum peripheral distance between the edges of adjacent pole-faces, and then assume the maximum value of the density of the lines as holding throughout this entire path. In ring and drum machines the flux issuing from one pole divides into two halves in the armature core, so that the maximum density of lines in the armature is Ba=Za / 2ab, where a=the radial depth of the disks in centimetres and b=the net length of iron core. The total exciting power required between the pole-pieces is therefore, at no load, Xp=Xg + Xt + Xa, where Xa=ƒ(Ba).la; in order, however, to allow for the effect of the armature current, which increases with the load, a further term Xb, must be added.
 |
| Fig. 30. |
In the continuous-current dynamo it may be, and usually is, necessary to move the brushes forward from the interpolar line of symmetry through a small angle in the direction of rotation, in order to avoid sparking between the brushes and the commutator (vide infra). When the dynamo is giving current, the wires on either side of the diameter of commutation form a current-sheet flowing along the surface of the armature from end to end, and whatever the actual end-connexions of the wires, the wires may be imagined to be joined together into a system of loops such that the two sides of each loop are carrying current in opposite directions. Thus a number of armature ampere-turns are formed, and their effect on the entire system of magnet and armature must be taken into account. So long as the diameter of commutation coincides with the line of symmetry, the armature may be regarded as a cylindrical electromagnet producing a flux of lines, as shown in fig. 30. The direction of the self-induced flux in the air-gaps is the same as that of the lines of the external field in one quadrant on one side of DC, but opposed to it in the other quadrant on the same side of DC; hence in the resultant field due to the combined action of the field-magnet and armature ampere-turns, the flux is as much strengthened over the one half of each polar face as it is weakened over the other, and the total number of lines is unaffected, although their distribution is altered. The armature ampere-turns are then called cross-turns, since they produce a cross-field, which, when combined with the symmetrical field, causes the leading pole-corners ll to be weakened and the trailing pole-corners tt to be strengthened, the neutral line of zero field being thus twisted forwards in the direction of rotation. But when the brushes and diameter of commutation are shifted forward, as shown in fig. 31, it will be seen that a number of ampere-turns, forming a zone between the lines Dn and mC, are in effect wound immediately on the magnetic circuit proper, and this belt of ampere-turns is in direct opposition to the ampere-turns of the field, as shown by the dotted and crossed wires on the pole-pieces. The armature ampere-turns are then divisible into the two bands, the back-turns, included within twice the angle of lead λ, weakening the field, and the cross-turns, bounded by the lines Dm, nC, again producing distortion of the weakened symmetrical field. If, therefore, a certain flux is to be passed through the armature core in opposition to the demagnetizing turns, the difference of magnetic potential between the pole-faces must include not only Xa, Xt, and Xg, but also an item Xb, in order to balance the “back” ampere-turns of the armature. The amount by which the brushes must be shifted forward increases with the armature current, and in corresponding proportion the back ampere-turns are also 
Fig. 31.increased, their value being cτ2λ / 360°, where c=the current carried by each of the τ active wires. Thus the term Xb, takes into account the effect of the armature reaction on the total flux; it varies as the armature current and angle of lead required to avoid sparking are increased; and the reason for its introduction in the fourth place (Xp=Xg + Xt + Xa + Xb), is that it increases the magnetic difference of potential which must exist between the poles of the dynamo, and to which the greater part of the leakage is due. The leakage paths which are in parallel with the armature across the poles must now be estimated, and so a new value be derived for the flux at the commencement of the iron-magnet path. If P=their joint permeance, the leakage flux due to the difference of potential at the poles is zl=1·257Xp × P, and this must be added to the useful flux Za, or Zp=Za + Zl. There are also certain leakage paths in parallel with the magnet cores, and upon the permeance of these a varying number of ampere-turns is acting as we proceed along the magnet coils; the magnet flux therefore increases by the addition of leakage along the length of the limbs, and finally reaches a maximum near the yoke. Either, then, the density in the magnet Bm=Zm / Am will vary if the same sectional area be retained throughout, or the sectional area of the magnet must itself be progressively increased. In general, sufficient accuracy will be obtained by assuming a certain number of additional leakage lines zn as traversing the entire length of magnet limbs and yoke (= lm), so that the density in the magnet has the uniform value Bm=(Zp + zn) / Am. The leakage flux added on actually within the length of the magnet core or zn will be approximately equal to half the total M.M.F. of the coils multiplied by the permeance of the leakage paths around one coil. The corresponding value of H can then be obtained from the (B, H) curve of the material of which the magnet is composed, and the ampere-turns thus determined must be added to Xp, or X=Xp + Xm, where Xm=ƒ(Bm)lm. The final equation for the exciting power required on a magnetic circuit as a whole will therefore take the form
| X=AT=0·8Bg.2lg + ƒ(Bt) 2lt + ƒ(Ba) la + Xb + ƒ(Bm) lm. | (3) |
If the magnet cores are of wrought iron or cast steel, and the yoke is of cast iron, the last term must be divided into two portions corresponding to the different materials, i.e. into ƒ(Bm)lm + ƒ(By)ly. In the ordinary multipolar machine with as many magnet-coils as there are poles, each coil must furnish half the above number of ampere-turns.
Since no substance is impermeable to the passage of magnetic flux, the only form of magnetic circuit free from leakage is one uniformly wound with ampere-turns over its whole length. The reduction of the magnetic leakage to a minimum in any given type is therefore primarily a question of distributing the winding as far as possible Magnetic leakage.uniformly upon the circuit, and as the winding must be more or less concentrated into coils, it resolves itself into the necessity of introducing as long air-paths as possible between any surfaces which are at different magnetic potentials. No iron should be brought near the machine which does not form part of the magnetic circuit proper, and especially no iron should be brought near the poles, between which the difference of magnetic potential practically reaches its maximum value. In default of a machine of the same size or similar type on which to experiment, the probable direction of the leakage flux must be assumed from the drawing, and the air surrounding the machine must be mapped out into areas, between which the permeances are calculated as closely as possible by means of such approximate formulae as those devised by Professor G. Forbes.
In the earliest “magneto-electric” machines permanent steel magnets, either simple or compound, were employed, and for many years these were retained in certain alternators, some of which are still in use for arc lighting in lighthouses. But since the field they furnish is very weak, a great advance was made when they Excitation of field-magnet.were replaced by soft iron electromagnets, which could be made to yield a much more intense flux. As early as 1831 Faraday[18] experimented with electromagnets, and after 1850 they gradually superseded the permanent magnet. When the total ampere-turns required to excite the electromagnet have been determined, it remains to decide how the excitation shall be obtained; and, according to the method adopted, continuous-current machines may be divided into four well-defined classes.
 |
| Fig. 32. |
The simplest method, and that which was first used, is separate excitation from some other source of direct current, which may be either a primary or a secondary battery or another dynamo (fig. 32). But since the armature yields a continuous current, it was early suggested (by J. Brett in 1848 and F. Sinsteden in 1851) that this current might be utilized to increase the flux; combinations of permanent and electromagnets were therefore next employed, acting either on the main armature or on separate armatures, until in 1867 Dr Werner von Siemens and Sir C. Wheatstone almost simultaneously discovered that the dynamo could be made self-exciting through the residual magnetism retained in the soft iron cores of the electromagnet. The former proposed to take the whole of the current round the magnet coils which were in series with the armature and external circuit, while the latter proposed to utilize only a portion derived by a shunt from the main circuit; we thus arrive at the second and third classes, namely, series and shunt machines. The starting of the process of excitation in either case is the same; when the brushes are touching the commutator and the armature is rotated, the small amount of flux left in the magnet is cut by the wires, and a very small current begins to flow round the closed circuit; this increases the flux, which in turn further increases the E.M.F. and current, until, finally, the cumulative effect stops through the increasing saturation of the iron cores. Fig. 33, illustrating the series machine, shows the winding of the exciting coils to be composed of a few turns of thick wire. Since the current is undivided throughout the whole circuit, the resistance of both the armature and field-magnet winding must be low as compared with that of the external circuit, if the useful power available at the terminals of the machine is to form a large percentage of the total electrical power—in other words, if the efficiency is to be high. Fig. 34 shows the third method, in which the winding of the field-magnets is a shunt or fine-wire circuit of many turns applied to the terminals of the machine; in this ease the resistance of the shunt must be high as compared with that of the external circuit, in order that only a small proportion of the total energy may be absorbed in the field.
 | |
| Fig. 33. | Fig. 34. |
Since the whole of the armature current passes round the field-magnet of the series machine, any alteration in the resistance of the external circuit will affect the excitation and also the voltage. A curve connecting together corresponding values of external current and terminal voltage for a given speed of rotation is known as the external-characteristic of the machine; in its main features it has the same appearance as a curve of magnetic flux, but when the current exceeds a certain amount it begins to bend downwards and the voltage decreases. The reason for this will be found in the armature reaction at large loads, which gradually produces a more and more powerful demagnetizing effect, as the brushes are shifted forwards to avoid sparking; eventually the back ampere-turns overpower any addition to the field that would otherwise be due to the increased current flowing round the magnet. The “external characteristic” for a shunt machine has an entirely different shape. The field-magnet circuit being connected in parallel with the external circuit, the exciting current, if the applied voltage remains the same, is in no way affected by alterations in the resistance of the latter. As, however, an increase in the external current causes a greater loss of volts in the armature and a greater armature reaction, the terminal voltage, which is also the exciting voltage, is highest at no load and then diminishes. The fall is at first gradual, but after a certain critical value of the armature current is reached, the machine is rapidly demagnetized and loses its voltage entirely.
 |
| Fig. 35. |
The last method of excitation, namely, compound-winding (fig. 35), is a combination of the two preceding, and was first used by S. A. Varley and by C. F. Brush. If a machine is in the first instance shunt-wound, and a certain number of series-turns are added, the latter, since they carry the external current, can be made to counteract the effect which the increased external current would have in lowering the voltage of the simple shunt machine. The ampere-turns of the series winding must be such that they not only balance the increase of the demagnetizing back ampere-turns on the armature, but further increase the useful flux, and compensate for the loss of volts over their own resistance and that of the armature. The machine will then give for a constant speed a nearly constant voltage at its terminals, and the curve of the external characteristic becomes a straight line for all loads within its capacity. Since with most prime movers an increase of the load is accompanied by a drop in speed, this effect may also be counteracted; while, lastly, if the series-turns are still further increased, the voltage may be made to rise with an increasing load, and the machine is “over-compounded.”
At the initial moment when an armature coil is first short-circuited by the passage of the two sectors forming its ends under the contact surface of a brush, a certain amount of electromagnetic energy is stored up in its magnetic field as linked with the ampere-turns of the coil when carrying its full share of the total Commutation and sparking at the brushes.armature current. During the period of short-circuit this quantity of energy has to be dissipated as the current falls to zero, and has again to be re-stored as the current is reversed and raised to the same value, but in the opposite direction. The period of short-circuit as fixed by the widths of the brush and of the mica insulation between the sectors, and by the peripheral speed of the commutator is extremely brief, and only lasts on an average from 1200th to 11000th of a second. The problem of sparkless commutation is therefore primarily a question of our ability to dissipate and to re-store the required amount of energy with sufficient rapidity.
An important aid towards the solution of this problem is found in the effect of the varying contact-resistance between the brush and the surfaces of the leading and trailing sectors which it covers. As the commutator moves under the brush, the area of contact which the brush makes with the leading sector diminishes, and the resistance between the two rises; conversely, the area of contact between the brush and the trailing sector increases and the resistance falls. This action tends automatically to bring the current through each sector into strict proportionality to the amount of its surface which is covered by the brush, and so to keep the current-density and the loss of volts over the contacts uniform and constant. As soon as the current-density in the two portions of the brush becomes unequal, a greater amount of heat is developed at the commutator surface, and this in the first place affords an additional outlet for the dissipation of the stored energy of the coil, while after reversal of the current it is the accompaniment of a re-storage of the required energy. This energy, as well as that which is spent in heating the coil, can in fact, in default of other sources, be derived through the action of the unequal current-density from the electrical output of the rest of the armature winding, and so only indirectly from the prime mover.
In practice, when the normal contact-resistance of the brushes is low relatively to the resistance of the coil, as is the case with metal brushes of copper or brass gauze, but little benefit can be obtained from the action of the varying contact-resistance. It exerts no appreciable effect until close towards the end of the period of short-circuit, and then only with such a high-current-density at the trailing edge of the leaving sector that at the moment of parting the brush-tip is fused, or its metal volatilized, and sparking has in fact set in. With such brushes, then, it becomes necessary to call in the aid of a reversing E.M.F. impressed upon the coil by the magnetic field through which it is moving. If such a reversing field comes into action while the current is still unreversed, its E.M.F. is opposed to the direction of the current, and the coil is therefore driving the armature forward as in a motor; it thus affords a ready means of rapidly dissipating part of the initial energy in the form of mechanical work instead of as heat. After the current has been reversed, the converse process sets in, and the prime mover directly expends mechanical energy not only in heating the coil, but also in storing up electromagnetic energy with a rapidity dependent upon the strength of the reversing field. The required direction of external field can be obtained in the dynamo by shifting the brushes forward, so that the short-circuited coil enters into the fringe of lines issuing from the leading pole-tip, i.e. by giving the brushes an “angle of lead.” An objection to this process is that the main flux is thereby weakened owing to the belt of back ampere-turns which arises (v. supra). A still greater objection is that the amount of the angle of lead must be suited to the value of the load, the corrective power of copper brushes being very small if the reversing E.M.F. is not closely adjusted in proportion to the armature current.
On this account metal brushes have been almost entirely superseded by carbon moulded into hard blocks. With these, owing to their higher specific contact-resistance, a very considerable reversing effect can be obtained through the action of unequal current-density, and indeed in favourable cases complete sparklessness can be obtained throughout the entire range of load of the machine with a fixed position of the brushes. Yet if the work which they are called upon to perform exceeds certain limits, they tend to become overheated with consequent glowing or sparking at their tips, so that, wherever possible, it is advisable to reinforce their action by a certain amount of reversing field, the brushes being set so that its strength is roughly correct for, say, half load.
In the case of dynamos driven by steam-turbines, sparkless commutation is especially difficult to obtain owing to the high speed of rotation and the very short space of time in which the current has to be reversed. Special “reversing poles” then become necessary; these are wound with magnetizing coils in series with the main armature current, so that the strength of field which they yield is roughly proportional to the current which has to be reversed. These again may be combined with a “compensating winding” embedded in the pole-faces and carrying current in the opposite direction to the armature ampere-turns, so as to neutralize the cross effect of the latter and prevent distortion of the resultant field.
From the moment that a dynamo begins to run with excited field, heat is continuously generated by the passage of the current through the windings of the field-magnet coils and the armature, as well as by the action of hysteresis and eddy currents in the armature and pole-pieces. Whether the source of the heat be in the field-magnet or Heating effects.in the armature, the mass in which it originates will continue to rise in temperature until such a difference of temperature is established between itself and the surrounding air that the rate at which the heat is carried off by radiation, convection and conduction is equal to the rate at which it is being generated. Evidently, then, the temperature which any part of the machine attains after a prolonged run must depend on the extent and effectiveness of the cooling surface from which radiation takes place, upon the presence or absence of any currents of air set up by the rotation of itself or surrounding parts, and upon the presence of neighbouring masses of metal to carry away the heat by conduction. In the field-magnet coils the rate at which heat is being generated is easily determined, since it is equal to the square of the current passing through them multiplied by their resistance. Further, the magnet is usually stationary, and only indirectly affected by draughts of air due to the rotating armature. Hence for machines of a given type and of similar proportions, it is not difficult to decide upon some method of reckoning the cooling surface of the magnet coils Sc, such that the rise of temperature above that of the surrounding air may be predicted from an equation of the form t°=kW / Sc, where W=the rate in watts at which heat is generated in the coils, and k is some constant depending upon the exact method of reckoning their cooling surface. As a general rule the cooling surface of a field-coil is reckoned as equal to the exposed outer surface of its wire, the influence of the end flanges being neglected, or only taken into account in the case of very short bobbins wound with a considerable depth of wire. In the case of the rotating armature a similar formula must be constructed, but with the addition of a factor to allow for the increase in the effectiveness of any given cooling surface due to the rotation causing convection currents in the surrounding air. Only experiment can determine the exact effect of this, and even with a given type of armature it is dependent on the number of poles, each of which helps to break up the air-currents, and so to dissipate the heat. For example, in two-pole machines with drum bar-armatures, if the cooling surface be reckoned as equal to the cylindrical exterior plus the area of the two ends, the heating coefficient for a peripheral speed of 1500 ft. per minute is less than half of that for the same armature when at rest. A further difficulty still meets the designer in the correct predetermination of the total loss of watts in an armature before the machine has been tested. It is made up of three separate items, namely, the copper loss in the armature winding, the loss by hysteresis in the iron, and the loss by eddy currents, which again may be divided into those in the armature bars and end-connexions, and those in the core and its end-plates. The two latter items are both dependent upon the speed of the machine; but whereas the hysteresis loss is proportional to the speed for a given density of flux in the armature, the eddy current loss is proportional to the square of the speed, and owing to this difference, the one loss can be separated from the other by testing an armature at varying speeds. Thus for a given rise of temperature, the question of the amount of current which can be taken out of an armature at different speeds depends upon the proportion which the hysteresis and eddy watts bear to the copper loss, and the ratio in which the effectiveness of the cooling surface is altered by the alteration in speed. Experimental data, again, can alone decide upon the amount of eddy currents that may be expected in given armatures, and caution is required in applying the results of one machine to another in which any of the conditions, such as the number of poles, density in the teeth, proportions of slot depth to width, &c., are radically altered.
It remains to add, that the rise of temperature which may be permitted in any part of a dynamo after a prolonged run is very generally placed at about 70° Fahr. above the surrounding air. Such a limit in ordinary conditions of working leads to a final temperature of about 170° Fahr., beyond which the durability of the insulation of the wires is liable to be injuriously affected. Upon some such basis the output of a dynamo in continuous working is rated, although for short periods of, say, two hours the normal full-load current of a large machine may be exceeded by some 25% without unduly heating the armature.
For the electro-deposition of metals or the electrolytic treatment of ores a continuous current is a necessity; but, apart from such use, the purposes from which the continuous-current dynamo is well adapted are so numerous that they cover nearly the whole field of electrical engineering, with one important exception. Uses of continuous current dynamos.To meet these various uses, the pressures for which the machine is designed are of equally wide range; for the transmission of power over long distances they may be as high as 3000 volts, and for electrolytic work as low as five. Each electrolytic bath, with its leads, requires on an average only some four or five volts, so that even when several are worked in series the voltage of the dynamo seldom exceeds 60. On the other hand, the current is large and may amount to as much as from 1000 to 14,000 amperes, necessitating the use of two commutators, one at either end of the armature, in order to collect the current without excessive heating of the sectors and brushes. The field-magnets are invariably shunt-wound, in order to avoid reversal of the current through polarization at the electrodes of the bath. For incandescent lighting by glow lamps, the requirements of small isolated installations and of central stations for the distribution of electrical energy over large areas must be distinguished. For the lighting of a private house or small factory, the dynamo giving from 5 to 100 kilo-watts of output is commonly wound for a voltage of 100, and is driven by pulley and belt from a gas, oil or steam-engine; or, if approaching the higher limit above mentioned, it is often directly coupled to the crank-shaft of the steam-engine. If used in conjunction with an accumulator of secondary cells, it is shunt-wound, and must give the higher voltage necessary to charge the battery; otherwise it is compound-wound, in order to maintain the pressure on the lamps constant under all loads within its capacity. The compound-wound dynamo is likewise the most usual for the lighting of steamships, and is then directly coupled to its steam-engine; its output seldom exceeds 100 kilo-watts, at a voltage of 100 or 110. For larger installations a voltage of 250 is commonly used, while for central-station work, economy in the distributing mains dictates a higher voltage, especially in connexion with a three-wire system; the larger dynamos may then give 500 volts, and be connected directly across the two outer wires. A pair of smaller machines coupled together, and each capable of giving 250 volts, are often placed in series across the system, with their common junction connected to the middle wire; the one which at any time is on the side carrying the smaller current will act as a motor and drive the other as a dynamo, so as to balance the system. The directly-coupled steam dynamo may be said to have practically displaced the belt- or rope-driven sets which were formerly common in central stations. The generating units of the central station are arranged in progressive sizes, rising from, it may be, 250 or 500 horse-power up to 750 or 1000, or in large towns to as much as 5000 horse-power. If for lighting only, they are usually shunt-wound, the regulation of the voltage, to keep the pressure constant on the distributing system under the gradual changes of load, being effected by variable resistances in the shunt circuit of the field-magnets.
Generators used for supplying current to electric tramways are commonly wound for 500 volts at no load and are over-compounded, so that the voltage rises to 550 volts at the maximum load, and thus compensates for the loss of volts over the transmitting lines. For arc lighting it was formerly usual to employ a class of dynamo which, from the nature of its construction, was called an “open-coil” machine, and which gave a unidirectional but pulsating current. Of such machines the Brush and Thomson-Houston types were very widely used; their E.M.F. ranged from 2000 to 3000 volts for working a large number of arcs in series, and by means of special regulators their current was maintained constant over a wide range of voltage. But as their efficiency was low and they could not be applied to any other purpose, they have been largely superseded in central stations by closed-coil dynamos or alternators, which can also be used for incandescent lighting. In cases where the central station is situated at some distance from the district to which the electric energy is to be supplied, voltages from 1000 to 2000 are employed, and these are transformed down at certain distributing centres by continuous-current transformers (see Transformers and Electricity Supply). These latter machines are in reality motor-driven dynamos, and hence are also called motor-generators; the armatures of the motor and dynamo are often wound on the same core, with a commutator at either end, the one to receive the high-pressure motor current, and the other to collect the low-pressure current furnished by the dynamo.
In all large central stations it is necessary that the dynamos should be capable of being run in parallel, so that their outputs may be combined on the same “omnibus bars” and thence distributed to the network of feeders. With simple shunt-wound machines this is easily effected by coupling together terminals of like sign when the voltage of the two or more machines are closely equal. With compound-wound dynamos not only must the external terminals of like sign be coupled together, but the junctions of the brush leads with the series winding must be connected by an “equalizing” lead of low resistance; otherwise, should the E.M.F. of one machine for any reason fall below the voltage of the omnibus bars, there is a danger of its polarity being reversed by a back current from the others with which it is in parallel.
Owing to the necessary presence in the continuous-current dynamo of the commutator, with its attendant liability to sparking at the brushes, and further, owing to the difficulty of insulating the rotating armature wires, a pressure of 3000 volts has seldom been exceeded in any one continuous-current machine, and has been given above as the limiting voltage of the class. If therefore it is required to work with higher pressures in order to secure economy in the transmitting lines, two or more machines must be coupled in series by connecting together terminals which are of unlike sign.[19] The stress of the total voltage may still fall on the insulation of the winding from the body of the machine; hence for high-voltage transmission of power over very long distances, the continuous-current dynamo in certain points yields in convenience to the alternator. In this there is no commutator, the armature coils may be stationary and can be more thoroughly insulated, while further, if it be thought undesirable to design the machine for the full transmitting voltage, it is easy to wind the armature for a low pressure; this can be subsequently transformed up to a high pressure by means of the alternating-current transformer, which has stationary windings and so high an efficiency that but little loss arises from its use. With these remarks, the transition may be made to the fuller discussion of the alternator.
Alternators.
The frequency employed in alternating-current systems for distributing power and light varies between such wide limits as 25 and 133; yet in recent times the tendency has been towards standard frequencies of 25, 50 and 100 as a maximum. High frequencies involve more copper in the magnet coils, owing to the Frequency.greater number of poles, and a greater loss of power in their excitation, but the alternator as a whole is somewhat lighter, and the transformers are cheaper. On the other hand, high frequency may cause prejudicial effects, due to the inductance and capacity of the distributing lines; and in asynchronous motors used on polyphase systems the increased number of poles necessary to obtain reasonable speeds reduces their efficiency, and is otherwise disadvantageous, especially for small horse-powers. A frequency lower than 40 is, however, not permissible where arc lighting is to form any considerable portion of the work and is to be effected by the alternating current without rectification, since below this value the eye can detect the periodic alteration in the light as the carbons alternately cool and become heated. Thus for combined lighting and power 50 or 60 are the most usual frequencies; but if the system is designed solely or chiefly for the distribution of power, a still lower frequency is preferable. On this account 25 was selected by the engineers for the Niagara Falls power transmission, after careful consideration of the problem, and this frequency has since been widely adopted in similar cases.
The most usual type of heteropolar alternator has an internal rotating field-magnet system, and an external stationary armature, as in fig. 10. The coils of the armature, which must for high voltages be heavily insulated, are then not subjected to the additional stresses due to centrifugal force; and further, the collecting Alternator construction.rings which must be attached to the rotating portion need only transmit the exciting current at a low voltage.
 |
| Fig. 36. |
The homopolar machine possesses the advantages that only a single exciting coil is required, whatever the number of polar projections, and that both the armature and field-magnet coils may be stationary. From fig. 8 it will be seen that it is not essential that the exciting coil should revolve with the internal magnet, but it may be supported from the external stationary armature while still embracing the central part of the rotor. The E.M.F. is set up in the armature coils through the periodic variation of the flux through them as the iron projections sweep past, and these latter may be likened to a number of “keepers,” which complete the magnetic circuit. From the action of the rotating iron masses they may also be considered as the inducing elements or “inductors,” and the homopolar machine is thence also known as the “inductor alternator.” If the end of the rotor marked S in fig. 8 is split up into a number of S polar projections similar to the N poles, a second set of armature coils may be arranged opposite to them, and we obtain an inductor alternator with double armature. Or the polar projections at the two ends may be staggered, and a single armature winding be passed straight through the armature, as in fig. 36, which shows at the side the appearance of the revolving inductor with its crown of polar projections in one ring opposite to the gaps between the polar projections of the other ring. But in spite of its advantage of the single stationary exciting coil, the inductor alternator has such a high degree of leakage, and the effect of armature reaction is so detrimental in it, that the type has been gradually abandoned, and a return has been almost universally made to the heteropolar alternator with internal poles radiating outwards from a circular yoke-ring. The construction of a typical machine of this class is illustrated in fig. 37.
 |
| Fig. 37. |
Since the field-magnet coils rotate, they must be carefully designed to withstand centrifugal force, and are best composed of flat copper strip wound on edge with thin insulation between adjacent layers. The coil is secured by the edges of the pole-shoes which overhang the pole and tightly compress the coil against the yoke-ring; the only effect from centrifugal force is then to compress still further the flat turns of copper against the pole-shoes without deformation. The poles are either of cast steel of circular or oblong section, bolted to the rim of the yoke-ring, or are built up of thin laminations of sheet steel. When the peripheral speed is very high, the yoke-ring will be of cast steel or may itself be built up of sheet steel laminations, this material being reliable and easily tested to ensure its sound mechanical strength. If the armature slots are open, the pole-pieces will in any case be laminated to reduce the eddy currents set up by the variation of the flux-density.
Owing to the great number of poles[20] of the alternator when driven by a reciprocating steam-engine, the diameter of its rotor is usually larger and its length less than in the continuous-current dynamo of corresponding output. The support of the armature core when of large diameter is therefore a more difficult problem, since, apart from any magnetic strains to which it may be subjected, its own weight tends to deform it. The segmental core-disks are usually secured to the internal circumference of a circular cast iron frame; the latter has a box section of considerable radial depth to give stiffness to it, and the disks are tightly clamped between internal flanges, one being a fixed part of the frame and the other loose, with transverse bolts passing right through from side to side (fig. 37). In order to lessen the weight of the structure and its expense in material, the cast iron frame has in some cases been entirely dispensed with, and braced tie-rods have been used to render the effective iron of the armature core-disks self-supporting.
 |
| Fig. 38. |
Owing to the high speed of the turbo-alternator, its rotor calls for the utmost care in its design to withstand the effect of centrifugal force without any shifting of the exciting coils, and to secure a perfect balance.
The appearance of the armature of a typical three-phase alternator is illustrated in fig. 38, which shows a portion of the lower half after removal of the field-magnet.
With open slots the coils, after being wound on formers to the required shape, are thoroughly impregnated with insulating compound, dried, and after a further wrapping with several layers of insulating material, finally pressed into the slots together with a sheet of leatheroid or flexible micanite. The end-connexions of each group of coils of one phase project straight out from the slots or are bent upwards alternately with those of the other phases, so that they may clear one another (fig. 37). A wooden wedge driven into a groove at the top of each slot is often used to lock the coil in place. With slots nearly closed at the top, the coils are formed by hand by threading the wire through tubes of micanite or specially prepared paper lining the slots; or with single-turn loops, stout bars of copper of U-shape can be driven through the slots and closed by soldered connexions at the other end.
The first experimental determination of the shape of the E.M.F. curve of an alternator was made by J. Joubert in 1880. A revolving contact-maker charged a condenser with the E.M.F. produced by the armature at a particular instant during each period. The condenser was discharged through a ballistic galvanometer, and from Shape of E.M.F. curve.the measured throw the instantaneous E.M.F. could be deduced. The contact-maker was then shifted through a small angle, and the instantaneous E.M.F. at the new position corresponding to a different moment in the period was measured; this process was repeated until the E.M.F. curve for a complete period could be traced. Various modifications of the same principle have since been used, and a form of “oscillograph” (q.v.) has been perfected which is well adapted for the purpose of tracing the curves both of E.M.F. and of current. The machine on which Joubert carried out his experiments was a Siemens disk alternator having no iron in its armature, and it was found that the curve of E.M.F. was practically identical with a sine curve. The same law has also been found to hold true for a smooth-core ring or drum armature, but the presence of the iron core enables the armature current to produce greater distorting effect, so that the curves under load may vary considerably from their shape at no load. In toothed armatures, the broken surface of the core, and the still greater reaction from the armature current, may produce wide variations from the sine law, the general tendency being to give the E.M.F. curve a more peaked form. The great convenience of the assumption that the E.M.F. obeys the sine law has led to its being very commonly used as the basis for the mathematical analysis of alternator problems; but any deductions made from this premiss require to be applied with caution if they are likely to be modified by a different shape of the curve. Further, the same alternator will give widely different curves even of E.M.F., and still more so of current, according to the nature of the external circuit to which it is connected. As will be explained later, the phase of the current relatively to the E.M.F. depends not only on the inductance of the alternator itself, but also upon the inductance and capacity of the external circuit, so that the same current will produce different effects according to the amount by which it lags or leads. The question as to the relative advantages of differently shaped E.M.F. curves has led to much discussion, but can only be answered by reference to the nature of the work that the alternator has to do—i.e. whether it be arc lighting, motor driving, or incandescent lighting through transformers. The shape of the E.M.F. curve is, however, of great importance in one respect, since upon it depends the ratio of the maximum instantaneous E.M.F. to the effective value, and the insulation of the entire circuit, both external and internal, must be capable of withstanding the maximum E.M.F. While the maximum value of the sine curve is √2 or 1·414 times the effective value, the maximum value of a Λ curve is 1·732 times the effective value, so that for the same effective E.M.F. the armature wires must not only be more heavily insulated than in the continuous-current dynamo, but also the more peaked the curve the better must be the insulation.
Since an alternating current cannot be used for exciting the field-magnet, recourse must be had to some source of a direct current. This is usually obtained from a small auxiliary continuous-current dynamo, called an exciter, which may be an entirely separate machine, separately driven and used for exciting several alternators, or Excitation.may be driven from the alternator itself; in the latter case the armature of the exciter is often coupled directly to the rotating shaft of the alternator, while its field-magnet is attached to the bed-plate. Although separate excitation is the more usual method, the alternator can also be made self-exciting if a part or the whole of the alternating current is “rectified,” and thus converted into a direct current.
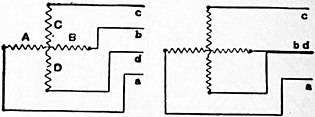 |
| Fig. 39. |
 |
| Fig. 40. |
The general idea of the polyphase alternator giving two or more E.M.F.’s of the same frequency, but displaced in phase, has been already described. The several phases may be entirely independent, and such was the case with the early polyphase machines of Gramme, who used four independent circuits, and also in the large Quarter-phase alternators.two-phase alternators designed by J. E. H. Gordon in 1883. If the phases are thus entirely separate, each requires two collector rings and two wires to its external circuit, i.e. four in all for two-phase and six for three-phase machines. The only advantage of the polyphase machine as thus used is that the whole of the surface of the armature core may be efficiently covered with winding, and the output of the alternator for a given size be thereby increased. It is, however, also possible so to interlink the several circuits of the armature that the necessary number of transmitting lines to the external circuits may be reduced, and also the weight of copper in them for a given loss in the transmission.[21] The condition which obviously must be fulfilled, for such interlinking of the phases to be possible, is that in the lines which are to meet at any common junction the algebraic sum of the instantaneous currents, reckoned as positive if away from such junction and as negative if towards it, must be zero. Thus if the phases be diagrammatically represented by the relative angular position of the coils in fig. 39, the current in the coils A and B differs in phase from the current in the coils C and D by a quarter of a period or 90°; hence if the two wires b and d be replaced by the single wire bd, this third wire will serve as a common path for the currents of the two phases either outwards or on their return. At any instant the value of the current in the third wire must be the vector sum of the two currents in the other wires, and if the shape of the curves of instantaneous E.M.F. and current are identical, and are assumed to be sinusoidal, the effective value of the current in the third wire will be the vector sum of the effective values of the currents in the other wires; in other words, if the system is balanced, the effective current in the third wire is √2, or 1·414 times the current in either of the two outer wires. Since the currents of the two phases do not reach their maximum values at the same time, the sectional area of the third wire need not be twice that of the others; in order to secure maximum efficiency by employing the same current density in all three wires, it need only be 40% greater than that of either of the outer wires. The effective voltage between the external leads may in the same way be calculated by a vector diagram, and with the above star connexion the voltage between the outer pair of wires a and c is √2, or 1·414 times the voltage between either of the outer wires and the common wire bd. Next, if the four coils are joined up into a continuous helix, just as in the winding of a continuous-current machine, four wires may be attached to equidistant points at the opposite ends of two diameters at right angles to each other (fig. 40). Such a method is known as the mesh connexion, and gives a perfectly symmetrical four-phase system of distribution. Four collecting rings are necessary if the armature rotates, and there is no saving in copper in the transmitting lines; but the importance of the arrangement lies in its use in connexion with rotary converters, in which it is necessary that the winding of the armature should form a closed circuit. If e=the effective voltage of one phase A, the voltage between any pair of adjacent lines in the diagram is e, and between m and o or n and p is e √2. The current in any line is the resultant of the currents in the two phases connected to it, and its effective value is c √2, where c is the current of one phase.
 |
| Fig. 41. |
When we pass to machines giving three phases differing by 120°, the same methods of star and mesh connexion find their analogies. If the current in coil A (fig. 41) is flowing away from the centre, and has its maximum value, the currents in coils B and C are flowing towards the centre, and are each of half the magnitude Three-phase alternators.of the current in A; the algebraic sum of the currents is therefore zero, and this will also be the case for all other instants. Hence the three coils can be united together at the centre, and three external wires are alone required. In this star or “Y” connexion, if e be the effective voltage of each phase, or the voltage between any one of the three collecting rings and the common connexion, the volts between any pair of transmitting lines will be E=e √3 (fig. 41); if the load be balanced, the effective current C in each of the three lines will be equal, and the total output in watts will be W=3Ce=3CE/√3=1·732 EC, or 1·732 times the product of the effective voltage between the lines and the current in any single line. Next, if the three coils are closed upon themselves in a mesh or delta fashion (fig. 42), the three transmitting wires may be connected to the junctions of the coils (by means of collecting rings if the armature rotates). The voltage E between any pair of wires is evidently that generated by one phase, and the current in a line wire is the resultant of that in two adjacent phases; or in a balanced system, if c be the current in each phase, the current in the line wire beyond a collecting ring is C=c√3, hence the watts are W=3cE=3CE/√3=1·732 EC, as before. Thus any three-phase winding may be changed over from the star to the delta connexion, and will then give 1·732 times as much current, but only 1/1·732 times the voltage, so that the output remains the same.
 |
| Fig. 42. |
The “armature reaction” of the alternator, when the term is used in its widest sense to cover all the effects of the alternating current in the armature as linked with a magnetic circuit or circuits, may be divided into three items which are different in their origin and consequences. In the first place the armature current produces Armature reaction in alternatorsa self-induced flux in local circuits independent of the main magnetic circuit, as e.g. linked with the ends of the coils as they project outwards from the armature core; such lines may be called “secondary leakage,” of which the characteristic feature is that its amount is independent of the position of the coils relatively to the poles. The alternations of this flux give rise to an inductive voltage lagging 90° behind the phase of the current, and this leakage or reactance voltage must be directly counterbalanced electrically by an equal component in the opposite sense in the voltage from the main field. The second and third elements are more immediately magnetic and are entirely dependent upon the position of the coils in relation to the poles and in relation to the phase of the current which they then carry. When the side of a drum coil is immediately under the centre of a pole, its ampere-turns are cross-magnetizing, i.e. produce a distortion of the main flux, displacing its maximum density to one or other edge of the pole. When the coil-side is midway between the poles and the axes of coil and pole coincide, the coil stands exactly opposite to the pole and embraces the same magnetic circuit as the field-magnet coils; its turns are therefore directly magnetizing, either weakening or strengthening the main flux according to the direction of the current. In intermediate positions the ampere-turns of the coil gradually pass from cross to direct and vice versa. When the instantaneous values of either the cross or direct magnetizing effect are integrated over a period and averaged, due account being taken of the number of slots per coil-side and of the different phases of the currents in the polyphase machine, expressions are obtained for the equivalent cross and direct ampere-turns of the armature as acting upon a pair of poles. For a given winding and current, the determining factor in either the one or the other is found to be the relative phase angle between the axis of a coil in its position when carrying the maximum current and the centre of a pole, the transverse reaction being proportional to the cosine of this angle, and the direct reaction to its sine. If the external circuit is inductive, the maximum value of the current lags behind the E.M.F. and so behind the centre of the pole; such a negative angle of lag causes the direct magnetizing turns to become back turns, directly weakening the main field and lowering the terminal voltage. Thus, just as in the continuous-current dynamo, for a given voltage under load the excitation between the pole-pieces Xp must not only supply the net excitation required over the air-gaps, armature core and teeth, but must also balance the back ampere-turns Xb of the armature.
Evidently therefore the characteristic curve connecting armature current and terminal volts will with a constant exciting current depend on the nature of the load, whether inductive or non-inductive, and upon the amount of inductance already possessed by the armature itself. With an inductive load it will fall more rapidly from its initial maximum value, or, conversely, if the initial voltage is to be maintained under an increasing load, the exciting current will have to be increased more than if the load were non-inductive. In practical working many disadvantages result from a rapid drop of the terminal E.M.F. under increasing load, so that between no load and full load the variation in terminal voltage with constant excitation should not exceed 15%. Thus the output of an alternator is limited either by its heating or by its armature reaction, just as is the output of a continuous-current dynamo; in the case of the alternator, however, the limit set by armature reaction is not due to any sparking at the brushes, but to the drop in terminal voltage as the current is increased, and the consequent difficulty in maintaining a constant potential on the external circuit.
The joint operation of several alternators so that their outputs may be delivered into the same external circuit is sharply distinguished from the corresponding problem in continuous-current dynamos by the necessary condition that they must be in synchronism, i.e. not only must they be so driven that their frequency is the same, but their The coupling of alternators.E.M.F.’s must be in phase or, as it is also expressed, the machines must be in step. Although in practice it is impossible to run two alternators in series unless they are rigidly coupled together—which virtually reduces them to one machine—two or more machines can be run in parallel, as was first described by H. Wilde in 1868 and subsequently redemonstrated by J. Hopkinson and W. G. Adams in 1884. Their E.M.F.’s should be as nearly as possible in synchronism, but, as contrasted with series connexion, parallel coupling gives them a certain power of recovery if they fall out of step, or are not in exact synchronism when thrown into parallel. In such circumstances a synchronizing current passes between the two machines, due to the difference in their instantaneous pressures; and as this current agrees in phase more nearly with the leading than with the lagging machine, the former machine does work as a generator on the latter as a motor. Hence the lagging machine is accelerated and the leading machine is retarded, until their frequencies and phase are again the same.
The chief use of the alternator has already been alluded to. Since it can be employed to produce very high pressures either directly or through the medium of transformers, it is specially adapted to the electrical transmission of energy over long distances.[22] In the early days of electric lighting, the alternate-current Uses of alternators.system was adopted for a great number of central stations; the machines, designed to give a pressure of 2000 volts, supplied transformers which were situated at considerable distances and spread over large areas, without an undue amount of copper in the transmitting lines. While there was later a tendency to return to the continuous current for central stations, owing to the introduction of better means for economizing the weight of copper in the mains, the alternating current again came into favour, as rendering it possible to place the central station in some convenient site far away from the district which it was to serve. The pioneer central station in this direction was the Deptford station of the London Electric Supply Corporation, which furnished current to the heart of London from a distance of 7 m. In this case, however, the alternators were single-phase and gave the high pressure of 10,000 volts immediately, while more recently the tendency has been to employ step-up transformers and a polyphase system. The advantage of the latter is that the current, after reaching the distant sub-stations, can be dealt with by rotary converters, through which it is transformed into a continuous current. The alternator is also used for welding, smelting in electric furnaces, and other metallurgical processes where heating effects are alone required; the large currents needed therein can be produced without the disadvantage of the commutator, and, if necessary, transformers can be interposed to lower the voltage and still further increase the current. The alternating system can thus meet very various needs, and its great recommendation may be said to lie in the flexibility with which it can supply electrical energy through transformers at any potential, or through rotary converters in continuous-current form.
Authorities.—For the further study of the dynamo, the following may be consulted, in addition to the references already given:—
General: S. P. Thompson, Dynamo-Electric Machinery—Continuous-Current Machines (1904), Alternating-Current Machinery (1905, London); G. Kapp, Dynamos, Alternators and Transformers (London, 1893); Id., Electric Transmission of Energy (London, 1894); Id., Dynamo Construction; Electrical and Mechanical (London, 1899); H. F. Parshall and H. M. Hobart, Electric Generators (London, 1900); C. C. Hawkins and F. Wallis, The Dynamo (London, 1903); E. Arnold, Konstruktionstafeln für den Dynamobau (Stuttgart, 1902); C. P. Steinmetz, Elements of Electrical Engineering (New York, 1901).
Continuous-Current Dynamos: J. Fischer-Hinnen, Continuous-Current Dynamos (London, 1899); E. Arnold, Die Gleichstrommaschine (Berlin, 1902); F. Niethammer, Berechnung und Konstruktion der Gleichstrommaschinen und Gleichstrommotoren (Stuttgart, 1904).
Alternators: D. C. Jackson and J. P. Jackson, Alternating Currents and Alternating Current Machinery (New York, 1903); J. A. Fleming, The Alternate Current Transformer (London, 1899); C. P. Steinmetz, Alternating Current Phenomena (New York, 1900); E. Arnold, Die Wechselstromtechnik (Berlin, 1904); S. P. Thompson, Polyphase Electric Currents (London, 1900); A. Stewart, Modern Polyphase Machinery (London, 1906); M. Oudin, Standard Polyphase Apparatus and Systems (New York, 1904). (C. C. H.)
- ↑ Experimental Researches in Electricity, series ii. § 6, pars. 256, 259-260, and series xxviii. § 34.
- ↑ Ibid. series i. § 4, pars. 84-90.
- ↑ “On the Physical Lines of Magnetic Force,” Phil. Mag., June 1852.
- ↑ Faraday, Exp. Res. series xxviii. § 34, pars. 3104, 3114-3115.
- ↑ Id., ib. series i. § 4, pars. 114-119.
- ↑ Id., ib. series ii. § 6, pars. 211, 213; series xxviii. § 34, par. 3152.
- ↑ Invented by Nikola Tesla (Elec. Eng. vol. xiii. p. 83. Cf. Brit. Pat. Spec. Nos. 2801 and 2812, 1894). Several early inventors, e.g. Salvatore dal Negro in 1832 (Phil. Mag. third series, vol. i. p. 45), adopted reciprocating or oscillatory motion, and this was again tried by Edison in 1878.
- ↑ The advantage to be obtained by making the poles closely embrace the armature core was first realized by Dr Werner von Siemens in his “shuttle-wound” armature (Brit. Pat. No. 2107, 1856).
- ↑ Nuovo Cimento (1865), 19, 378.
- ↑ Brit. Pat. No. 1668 (1870); Comptes rendus (1871), 73, 175.
- ↑ Ann. Chim. Phys. l. 322.
- ↑ Ibid. li. 76. Since in H. Pixii’s machine the armature was stationary, while both magnet and commutator rotated, four brushes were used, and the arrangement was not so simple as the split-ring described above, although the result was the same. J. Saxton’s machine (1833) and E. M. Clarke’s machine (1835, see Sturgeon’s Annals of Electricity, i. 145) were similar to one another in that a unidirected current was obtained by utilizing every alternate half-wave of E.M.F., but the former still employed mercury collecting cups, while the latter employed metal brushes. W. Sturgeon in 1835 followed Pixii in utilizing the entire wave of E.M.F., and abandoned the mercury cups in favour of metal brushes pressing on four semicircular disks (Scientific Researches, p. 252). The simple split-ring is described by Sir C. Wheatstone and Sir W. F. Cooke in their Patent No. 8345 (1840).
- ↑ By the “leading” side of the tooth or of an armature coil or sector is to be understood that side which first enters under a pole after passing through the interpolar gap, and the edge of the pole under which it enters is here termed the “leading” edge as opposed to the “trailing” edge or corner from under which a tooth or coil emerges into the gap between the poles; cf. fig. 30, where the leading and trailing pole-corners are marked ll and tt.
- ↑ Such was the arrangement of Wheatstone’s machine (Brit. Pat. No. 9022) of 1841, which was the first to give a more nearly “continuous” current, the number of sections and split-rings being five.
- ↑ Its development from the split-ring was due to Pacinotti and Gramme (Brit. Pat. No. 1668, 1870) in connexion with their ring armatures.
- ↑ And extended by G. Kapp, “On Modern Continuous-Current Dynamo-Electric Machines,” Proc. Inst. C.E. vol. lxxxiii. p. 136.
- ↑ Drs J. and E. Hopkinson, “Dynamo-Electric Machinery,” Phil. Trans., May 6, 1886; this was further expanded in a second paper on “Dynamo-Electric Machinery,” Proc. Roy. Soc., Feb. 15, 1892, and both are reprinted in Original Papers on Dynamo-Machinery and Allied Subjects.
- ↑ Exp. Res., series i. § 4, par. 111. In 1845 Wheatstone and Cooke patented the use of “voltaic” magnets in place of permanent magnets (No. 10,655).
- ↑ Between Moutiers and Lyons, a distance of 115 m., energy is transmitted on the Thury direct-current system at a maximum pressure of 60,000 volts. Four groups of machines in series are employed, each group consisting of four machines in series; the rated output of each component machine is 75 amperes at 3900 volts or 400 h.p. A water turbine drives two pairs of such machines through an insulating coupling, and the sub-base of each pair of machines is separately insulated from earth, the foundation being also of special insulating materials.
- ↑ For experiments on high-frequency currents, Nikola Tesla constructed an alternator having 384 poles and giving a frequency of about 10,000 (Journ. Inst. Elec. Eng. 1892, 21, p. 82). The opposite extreme is found in alternators directly coupled to the Parsons steam-turbine, in which, with a speed of 3000 revs. per min., only two poles are required to give a frequency of 50. By a combination of a Parsons steam-turbine running at 12,000 revs. per min. with an alternator of 140 poles a frequency of 14,000 has been obtained (Engineering, 25th of August 1899). For description of an experimental machine for 10,000 cycles per second when running at 3000 revs. per min., see Trans. Amer. Inst. Elect. Eng. vol. xxiii. p. 417.
- ↑ As in the historical transmission of energy from Lauffen to Frankfort (1891).
- ↑ In the pioneer three-phase transmission between Laufen and Frankfort (Electrician, vol. xxvi. p. 637, and xxvii. p. 548), the three-phase current was transformed up from about 55 to 8500 volts, the distance being 110 m. A large number of installations driven by water power are now at work, in which energy is transmitted on the alternating-current system over distances of about 100 m. at pressures ranging from 20,000 to 67,000 volts.
