1911 Encyclopædia Britannica/Magnetism
MAGNETISM. The present article is a digest, mainly from an experimental standpoint, of the leading facts and principles of magnetic science. It is divided into the following sections:
| 1. | General Phenomena. |
| 2. | Terminology and Elementary Principles. |
| 3. | Magnetic Measurements. |
| 4. | Magnetization in Strong Fields. |
| 5. | Magnetization in Weak Fields. |
| 6. | Changes of Dimensions attending Magnetization. |
| 7. | Effects of Mechanical Stress on Magnetization. |
| 8. | Effects of Temperature on Magnetism. |
| 9. | Magnetic Properties of Alloys and Compounds of Iron. |
| 10. | Miscellaneous Effects of Magnetization:— Electric Conductivity—Hall Effect—Electro-Thermal Relations—Thermo-electric Quality—Elasticity—Chemical and Voltaic Effects. |
| 11. | Feebly Susceptible Substances. |
| 12. | Molecular Theory of Magnetism. |
| 13. | Historical and Chronological Notes. |
Of these thirteen sections, the first contains a simple description of the more prominent phenomena, without mathematical symbols or numerical data. The second includes definitions of technical terms in common use, together with so much of the elementary theory as is necessary for understanding the experimental work described in subsequent portions of the article; a number of formulae and results are given for purposes of reference, but the mathematical reasoning by which they are obtained is not generally detailed, authorities being cited whenever the demonstrations are not likely to be found in ordinary textbooks. The subjects discussed in the remaining sections are sufficiently indicated by their respective headings. (See also Electromagnetism, Terrestrial Magnetism, Magneto-Optics and Units.)
1. General Phenomena
Pieces of a certain highly esteemed iron ore, which consists mainly of the oxide Fe3O4, are sometimes found to possess the power of attracting small fragments of iron or steel. Ore endowed with this curious property was well known to the ancient Greeks and Romans, who, because it occurred plentifully in the district of Magnesia near the Aegean coast, gave it the name of magnes, or the Magnesian stone. In English-speaking countries the ore is commonly known as magnetite, and pieces which exhibit attraction as magnets; the cause to which the attractive property is attributed is called magnetism, a name also applied to the important branch of science which has been evolved from the study of phenomena associated with the magnet.
If a magnet is dipped into a mass of iron filings and withdrawn, filings cling to certain parts of the stone in moss-like tufts, other parts remaining bare. There are generally two regions where the tufts are thickest, and the attraction therefore greatest, and between them is a zone in which no attraction is evidenced. The regions of greatest attraction have received the name of poles, and the line joining them is called the axis of the magnet; the space around a magnet in which magnetic effects are exhibited is called the field of magnetic force, or the magnetic field.
Up to the end of the 15th century only two magnetic phenomena of importance, besides that of attraction, had been observed. Upon one of these is based the principle of the mariner’s compass, which is said to have been known to the Chinese as early as 1100 B.C., though it was not introduced into Europe until more than 2000 years later; a magnet supported so that its axis is free to turn in a horizontal plane will come to rest with its poles pointing approximately north and south. The other phenomenon is mentioned by Greek and Roman writers of the 1st century: a piece of iron, when brought into contact with a magnet, or even held near one, itself becomes “inductively” magnetized, and acquires the power of lifting iron. If the iron is soft and fairly pure, it loses its attractive property when removed from the neighbourhood of the magnet; if it is hard, some of the induced magnetism is permanently retained, and the piece becomes an artificial magnet. Steel is much more retentive of magnetism than any ordinary iron, and some form of steel is now always used for making artificial magnets. Magnetism may be imparted to a bar of hardened steel by stroking it several times from end to end, always in the same direction, with one of the poles of a magnet. Until 1820 all the artificial magnets in practical use derived their virtue, directly or indirectly, from the natural magnets found in the earth: it is now recognized that the source of all magnetism, not excepting that of the magnetic ore itself, is electricity, and it is usual to have direct recourse to electricity for producing magnetization, without the intermediary of the magnetic ore. A wire carrying an electric current is surrounded by a magnetic field, and if the wire is bent into the form of an elongated coil or spiral, a field having certain very useful qualities is generated in the interior. A bar of soft iron introduced into the coil is at once magnetized, the magnetism, however, disappearing almost completely as soon as the current ceases to flow. Such a combination constitutes an electromagnet, a valuable device by means of which a magnet can be instantly made and unmade at will. With suitable arrangements of iron and coil and a sufficiently strong current, the intensity of the temporary magnetization may be very high, and electromagnets capable of lifting weights of several tons are in daily use in engineering works (see Electromagnetism). If the bar inserted into the coil is of hardened steel instead of iron, the magnetism will be less intense, but a larger proportion of it will be retained after the current has been cut off. Steel magnets of great strength and of any convenient form may be prepared either in this manner or by treatment with an electromagnet; hence the natural magnet, or lodestone as it is commonly called, is no longer of any interest except as a scientific curiosity.
Some of the principal phenomena of magnetism may be demonstrated with very little apparatus; much may be done with a small bar-magnet, a pocket compass and a few ounces of iron filings. Steel articles, such as knitting or sewing needles and pieces of flat spring, may be readily magnetized by stroking them with the bar-magnet; after having produced magnetism in any number of other bodies, the magnet will have lost nothing of its own virtue. The compass needle is a little steel magnet balanced upon a pivot; one end of the needle, which always bears a distinguishing mark, points approximately, but not in general exactly, to the north,[1] the vertical plane through the direction of the needle being termed the magnetic meridian. The bar-magnet, if suspended horizontally in a paper stirrup by a thread of unspun silk, will also come to rest in the magnetic meridian with its marked end pointing northwards. The north-seeking end of a magnet is in English-speaking countries called the north pole and the other end the south pole; in France the names are interchanged. If one pole of the bar-magnet is brought near the compass, it will attract the opposite pole of the compass-needle; and the magnetic action will not be sensibly affected by the interposition between the bar and the compass of any substance whatever except iron or other magnetizable metal. The poles of a piece of magnetized steel may be at once distinguished if the two ends are successively presented to the compass; that end which attracts the south pole of the compass needle (and is therefore north) may be marked for easy identification.
Similar magnetic poles are not merely indifferent to each other, but exhibit actual repulsion. This can be more easily shown if the compass is replaced by a magnetized knitting needle, supported horizontally by a thread. The north pole of the bar-magnet will repel the north pole of the suspended needle, and there will likewise be repulsion between the two south poles. Such experiments as these demonstrate the fundamental law that like poles repel each other; unlike poles attract. It follows that between two neighbouring magnets, the poles of which are regarded as centres of force, there must always be four forces in action. Denoting the two pairs of magnetic poles by N, S and N′, S′, there is attraction between N and S′, and between S and N′; repulsion between N and N′, and between S and S′. Hence it is not very easy to determine experimentally the law of magnetic force between poles. The difficulty was overcome by C. A. Coulomb, who by using very long and thin magnets, so arranged that the action of their distant poles was negligible, succeeded in establishing the law, which has since been confirmed by more accurate methods, that the force of attraction or repulsion exerted between two magnetic poles varies inversely as the square of the distance between them. Since the poles of different magnets differ in strength, it is important to agree upon a definite unit or standard of reference in terms of which the strength of a pole may be numerically specified. According to the recognized convention, the unit pole is that which acts upon an equal pole at unit distance with unit force: a north pole is reckoned as positive (+) and a south pole as negative (−). Other conditions remaining unchanged, the force between two poles is proportional to the product of their strengths; it is repulsive or attractive according as the signs of the poles are like or unlike.
If a wire of soft iron is substituted for the suspended magnetic
needle, either pole of the bar-magnet will attract either end of
the wire indifferently. The wire will in fact become temporarily
magnetized by induction, that end of it which is nearest to the
pole of the magnet acquiring opposite polarity, and behaving
as if it were the pole of a permanent magnet. Even a permanent
magnet is susceptible of induction, its polarity becoming thereby
strengthened, weakened, or possibly reversed. If one pole of a
strong magnet is presented to the like pole of a weaker one,
there will be repulsion so long as the two are separated by a
certain minimum distance. At shorter distances the magnetism
induced in the weaker magnet will be stronger than its permanent
magnetism, and there will be attraction; two magnets with
their like poles in actual contact will always cling together unless
the like poles are of exactly equal strength. Induction is an
effect of the field of force associated with a magnet. Magnetic
force has not merely the property of acting upon magnetic
poles, it has the additional property of producing a phenomenon
known as magnetic induction, or magnetic flux, a physical condition
which is of the nature of a flow continuously circulating
through the magnet and the space outside it. Inside the magnet
the course of the flow is from the south pole to the north pole;
thence it diverges through the surrounding space, and again
converging, re-enters the magnet at the south pole. When the
magnetic induction flows through a piece of iron or other magnetizable
substance placed near the magnet, a south pole is
developed where the flux enters and a north pole where it
leaves the substance. Outside the magnet the direction of the
magnetic induction is generally the same as that of the magnetic
force. A map indicating the direction of the force in different
parts of the field due to a magnet may be constructed in a
very simple manner. A sheet of cardboard is placed above the
magnet, and some iron filings are sifted thinly and evenly over
the surface: if the cardboard is gently tapped, the filings will
arrange themselves in a series of curves, as shown in fig. 1.

Fig. 1.
This experiment suggested to
Faraday the conception of
“lines of force,” of which the
curves formed by the filings
afford a rough indication;
Faraday’s lines are however
not confined to the plane of
the cardboard, but occur in
the whole of the space around
the magnet. A line of force
may be defined as an imaginary
line so drawn that its direction
at every point of its course
coincides with the direction of
the magnetic force at that
point. Through any point in the field one such line can be
drawn, but not more than one, for the force obviously cannot
have more than one direction; the lines therefore never
intersect. A line of force is regarded as proceeding from the
north pole towards the south pole of the magnet, its direction
being that in which an isolated north pole would be urged along
it. A south pole would be urged oppositely to the conventional
“direction” of the line; hence it follows that a very small
magnetic needle, if placed in the field, would tend to set itself
along or tangentially to the line of force passing through its
centre, as may be approximately verified if the compass be
placed among the filings on the cardboard. In the internal
field of a long coil of wire carrying an electric current, the lines
of force are, except near the ends, parallel to the axis of the
coil, and it is chiefly for this reason that the field due to a coil
is particularly well adapted for inductively magnetizing iron
and steel. The older operation of magnetizing a steel bar by
drawing a magnetic pole along it merely consists in exposing
successive portions of the bar to the action of the strong field
near the pole.
Faraday’s lines not only show the direction of the magnetic force, but also serve to indicate its magnitude or strength in different parts of the field. Where the lines are crowded together, as in the neighbourhood of the poles, the force is greater (or the field is stronger) than where they are more widely separated; hence the strength of a field at any point can be accurately specified by reference to the concentration of the lines. The lines presented to the eye by the scattered filings are too vague and ill-defined to give a satisfactory indication of the field-strength (see Faraday, Experimental Researches, § 3237) though they show its direction clearly enough. It is however easy to demonstrate by means of the compass that the force is much greater in some parts of the field than in others. Lay the compass upon the cardboard, and observe the rate at which its needle vibrates after being displaced from its position of equilibrium; this will vary greatly in different regions. When the compass is far from the magnet, the vibrations will be comparatively slow; when it is near a pole, they will be exceedingly rapid, the frequency of the vibrations varying as the square root of the magnetic force at the spot. In a refined form this method is often employed for measuring the intensity of a magnetic field at a given place, just as the intensity of gravity at different parts of the earth is deduced from observations of the rate at which a pendulum of known length vibrates.
It is to the non-uniformity of the field surrounding a magnet that the apparent attraction between a magnet and a magnetizable body such as iron is ultimately due. This was pointed out by W. Thomson (afterwards Lord Kelvin) in 1847, as the result of a mathematical investigation undertaken to explain Faraday’s experimental observations. If the inductively magnetized body lies in a part of the field which happens to be uniform there will be no resulting force tending to move the body, and it will not be “attracted.” If however there is a small variation of the force in the space occupied by the body, it can be shown that the body will be urged, not necessarily towards a magnetic pole, but towards places of stronger magnetic force. It will not in general move along a line of force, as would an isolated pole, but will follow the direction in which the magnetic force increases most rapidly, and in so doing it may cross the lines of force obliquely or even at right angles.
If a magnetized needle were supported so that it could move freely about its centre of gravity it would not generally settle with its axis in a horizontal position, but would come to rest with its north-seeking pole either higher or lower than its centre. For the practical observation of this phenomenon it is usual to employ a needle which can turn freely in the plane of the magnetic meridian upon a horizontal axis passing through the centre of gravity of the needle. The angle which the magnetic axis makes with the plane of the horizon is called the inclination or dip. Along an irregular line encircling the earth in the neighbourhood of the geographical equator the needle takes up a horizontal position, and the dip is zero. At places north of this line, which is called the magnetic equator, the north end of the needle points downwards, the inclination generally becoming greater with increased distance from the equator. Within a certain small area in the Arctic Circle (about 97° W. long., 70° N. lat.) the north pole of the needle points vertically downwards, the dip being 90°. South of the magnetic equator the south end of the needle is always inclined downwards, and there is a spot within the Antarctic Circle (148° E. long., 74° S. lat.) where the needle again stands vertically, but with its north end directed upwards. All these observations may be accounted for by the fact first recognized by W. Gilbert in 1600, that the earth itself is a great magnet, having its poles at the two places where the dipping needle is vertical. To be consistent with the terminology adopted in Britain, it is necessary to regard the pole which is geographically north as being the south pole of the terrestrial magnet, and that which is geographically south as the north pole; in practice however the names assigned to the terrestrial magnetic poles correspond with their geographical situations. Within a limited space, such as that contained in a room, the field due to the earth’s magnetism is sensibly uniform, the lines of force being parallel straight lines inclined to the horizon at the angle of dip, which at Greenwich in 1910 was about 67°. It is by the horizontal component of the earth’s total force that the compass-needle is directed.
The magnets hitherto considered have been assumed to have each two poles, the one north and the other south. It is possible that there may be more than two. If, for example, a knitting needle is stroked with the south pole of a magnet, the strokes being directed from the middle of the needle towards the two extremities alternately, the needle will acquire a north pole at each end and a south pole in the middle. By suitably modifying the manipulation a further number of consequent poles, as they are called, may be developed. It is also possible that a magnet may have no poles at all. Let a magnetic pole be drawn several times around a uniform steel ring, so that every part of the ring may be successively subjected to the magnetic force. If the operation has been skilfully performed the ring will have no poles and will not attract iron filings. Yet it will be magnetized; for if it is cut through and the cut ends are drawn apart, each end will be found to exhibit polarity. Again, a steel wire through which an electric current has been passed will be magnetized, but so long as it is free from stress it will give no evidence of magnetization; if, however, the wire is twisted, poles will be developed at the two ends, for reasons which will be explained later. A wire or rod in this condition is said to be circularly magnetized; it may be regarded as consisting of an indefinite number of elementary ring-magnets, having their axes coincident with the axis of the wire and their planes at right angles to it. But no magnet can have a single pole; if there is one, there must also be at least a second, of the opposite sign and of exactly equal strength. Let a magnetized knitting needle, having north and south poles at the two ends respectively, be broken in the middle; each half will be found to possess a north and a south pole, the appropriate supplementary poles appearing at the broken ends. One of the fragments may again be broken, and again two bipolar magnets will be produced; and the operation may be repeated, at least in imagination, till we arrive at molecular magnitudes and can go no farther. This experiment proves that the condition of magnetization is not confined to those parts where polar phenomena are exhibited, but exists throughout the whole body of the magnet; it also suggests the idea of molecular magnetism, upon which the accepted theory of magnetization is based. According to this theory the molecules of any magnetizable substance are little permanent magnets the axes of which are, under ordinary conditions, disposed in all possible directions indifferently. The process of magnetization consists in turning round the molecules by the application of magnetic force, so that their north poles may all point more or less approximately in the direction of the force; thus the body as a whole becomes a magnet which is merely the resultant of an immense number of molecular magnets.
In every magnet the strength of the south pole is exactly equal to that of the north pole, the action of the same magnetic force upon the two poles being equal and oppositely directed. This may be shown by means of the uniform field of force due to the earth’s magnetism. A magnet attached to a cork and floated upon water will set itself with its axis in the magnetic meridian, but it will be drawn neither northward nor southward; the forces acting upon the two poles have therefore no horizontal resultant. And again if a piece of steel is weighed in a delicate balance before and after magnetization, no change whatever in its weight can be detected; there is consequently no upward or downward resultant force due to magnetization; the contrary parallel forces acting upon the poles of the magnet are equal, constituting a couple, which may tend to turn the body, but not to propel it.
Iron and its alloys, including the various kinds of steel, though exhibiting magnetic phenomena in a pre-eminent degree, are not the only substances capable of magnetization. Nickel and cobalt are also strongly magnetic, and in 1903 the interesting discovery was made by F. Heusler that an alloy consisting of copper, aluminium and manganese (Heusler’s alloy), possesses magnetic qualities comparable with those of iron. Practically the metals iron, nickel and cobalt, and some of their alloys and compounds constitute a class by themselves and are called ferromagnetic substances. But it was discovered by Faraday in 1845 that all substances, including even gases, are either attracted or repelled by a sufficiently powerful magnetic pole. Those substances which are attracted, or rather which tend, like iron, to move from weaker to stronger parts of the magnetic field, are termed paramagnetic; those which are repelled, or tend to move from stronger to weaker parts of the field, are termed diamagnetic. Between the ferromagnetics and the paramagnetics there is an enormous gap. The maximum magnetic susceptibility of iron is half a million times greater than that of liquid oxygen, one of the strongest paramagnetic substances known. Bismuth, the strongest of the diamagnetics, has a negative susceptibility which is numerically 20 times less than that of liquid oxygen.
Many of the physical properties of a metal are affected by magnetization. The dimensions of a piece of iron, for example, its elasticity, its thermo-electric power and its electric conductivity are all changed under the influence of magnetism. On the other hand, the magnetic properties of a substance are affected by such causes as mechanical stress and changes of temperature. An account of some of these effects will be found in another section.[2]
2. Terminology and Elementary Principles
In what follows the C.G.S. electromagnetic system of units will be generally adopted, and, unless otherwise stated, magnetic substances will be assumed to be isotropic, or to have the same physical properties in all directions.
Vectors.—Physical quantities such as magnetic force, magnetic induction and magnetization, which have direction as well as magnitude, are termed vectors; they are compounded and resolved in the same manner as mechanical force, which is itself a vector. When the direction of any vector quantity denoted by a symbol is to be attended to, it is usual to employ for the symbol either a block letter, as H, I, B, or a German capital, as H, I, B.[3]
Magnetic Poles and Magnetic Axis.—A unit magnetic pole is that which acts on an equal pole at a distance of one centimetre with a force of one dyne. A pole which points north is reckoned positive, one which points south negative. The action between any two magnetic poles is mutual. If m1 and m2 are the strengths of two poles, d the distance between them expressed in centimetres, and f the force in dynes,
| f=m1m2 / d 2 | (1) |
The force is one of attraction or repulsion, according as the sign of the product m1m2 is negative or positive. The poles at the ends of an infinitely thin uniform magnet, or magnetic filament, would act as definite centres of force. An actual magnet may generally be regarded as a bundle of magnetic filaments, and those portions of the surface of the magnet where the filaments terminate, and so-called “free magnetism” appears, may be conveniently called poles or polar regions. A more precise definition is the following: When the magnet is placed in a uniform field, the parallel forces acting on the positive poles of the constituent filaments, whether the filaments terminate outside the magnet or inside, have a resultant, equal to the sum of the forces and parallel to their direction, acting at a certain point N. The point N, which is the centre of the parallel forces, is called the north or positive pole of the magnet. Similarly, the forces acting in the opposite direction on the negative poles of the filaments have a resultant at another point S, which is called the south or negative pole. The opposite and parallel forces acting on the poles are always equal, a fact which is sometimes expressed by the statement that the total magnetism of a magnet is zero. The line joining the two poles is called the axis of the magnet.
Magnetic Field.—Any space at every point of which there is a finite magnetic force is called a field of magnetic force, or a magnetic field. The strength or intensity of a magnetic field at any point is measured by the force in dynes which a unit pole will experience when placed at that point, the direction of the field being the direction in which a positive pole is urged. The field-strength at any point is also called the magnetic force at that point; it is denoted by H, or, when it is desired to draw attention to the fact that it is a vector quantity, by the block letter H, or the German character H. Magnetic force is sometimes, and perhaps more suitably, termed magnetic intensity; it corresponds to the intensity of gravity g in the theory of heavy bodies (see Maxwell, Electricity and Magnetism, § 12 and § 68, footnote). A line of force is a line drawn through a magnetic field in the direction of the force at each point through which it passes. A uniform magnetic field is one in which H has everywhere the same value and the same direction, the lines of force being, therefore, straight and parallel. A magnetic field is generally due either to a conductor carrying an electric current or to the poles of a magnet. The magnetic field due to a long straight wire in which a current of electricity is flowing is at every point at right angles to the plane passing through it and through the wire; its strength at any point distant r centimetres from the wire is
| H=2i/r, | (2) |
i being the current in C.G.S. units.[4] The lines of force are evidently circles concentric with the wire and at right angles to it; their direction is related to that of the current in the same manner as the rotation of a corkscrew is related to its thrust. The field at the centre of a circular conductor of radius r through which current is passing is
| H=2πi/r, | (3) |
the direction of the force being along the axis and related to the direction of the current as the thrust of a corkscrew to its rotation. The field strength in the interior of a long uniformly wound coil containing n turns of wire and having a length of l centimetres is (except near the ends)
| H=4πin / l. | (4) |
In the middle portion of the coil the strength of the field is very nearly uniform, but towards the end it diminishes, and at the ends is reduced to one-half. The direction of the force is parallel to the axis of the coil, and related to the direction of the current as the thrust of a corkscrew to its rotation. If the coil has the form of a ring of mean radius r, the length will be 2πr, and the field inside the coil may be expressed as
| H=2ni/r. | (5) |
The uniformity of the field is not in this case disturbed by the influence of ends, but its strength at any point varies inversely as the distance from the axis of the ring. When therefore sensible uniformity is desired, the radius of the ring should be large in relation to that of the convolutions, or the ring should have the form of a short cylinder with thin walls. The strongest magnetic fields employed for experimental purposes are obtained by the use of electromagnets. For many experiments the field due to the earth’s magnetism is sufficient; this is practically quite uniform throughout considerable spaces, but its total intensity is less than half a unit.
Magnetic Moment and Magnetization.—The moment, M, M or M, of a uniformly and longitudinally magnetized bar-magnet is the product of its length into the strength of one of its poles; it is the moment of the couple acting on the magnet when placed in a field of unit intensity with its axis perpendicular to the direction of the field. If l is the length of the magnet, M=ml. The action of a magnet at a distance which is great compared with the length of the magnet depends solely upon its moment; so also does the action which the magnet experiences when placed in a uniform field. The moment of a small magnet may be resolved like a force. The intensity of magnetization, or, more shortly, the magnetization of a uniformly magnetized body is defined as the magnetic moment per unit of volume, and is denoted by I, I, or I. Hence
I=M/v=ml/v=m/a,
v being the volume and a the sectional area. If the magnet is not uniform, the magnetization at any point is the ratio of the moment of an element of volume at that point to the volume itself, or I=m.ds/dv. where ds is the length of the element. The direction of the magnetization is that of the magnetic axis of the element; in isotropic substances it coincides with the direction of the magnetic force at the point. If the direction of the magnetization at the surface of a magnet makes an angle ε with the normal, the normal component of the magnetization, I cos ε, is called the surface density of the magnetism, and is generally denoted by σ.
Potential and Magnetic Force.—The magnetic potential at any point in a magnetic field is the work which would be done against the magnetic forces in bringing a unit pole to that point from the boundary of the field. The line through the given point along which the potential decreases most rapidly is the direction of the resultant magnetic force, and the rate of decrease of the potential in any direction is equal to the component of the force in that direction. If V denote the potential, F the resultant force, X, Y, Z, its components parallel to the co-ordinate axes and n the line along which the force is directed, then
| −δVδn=F,−δVδx=X,−δVδy=Y,−δVδz=Z. | (6) |
Surfaces for which the potential is constant are called equipotential surfaces. The resultant magnetic force at every point of such a surface is in the direction of the normal (n) to the surface; every line of force therefore cuts the equipotential surfaces at right angles. The potential due to a single pole of strength m at the distance r from the pole is
| V=m/r, | (7) |
the equipotential surfaces being spheres of which the pole is the centre and the lines of force radii. The potential due to a thin magnet at a point whose distance from the two poles respectively is r and r ′ is
| V=m(l/r=l/r ′). | (8) |
When V is constant, this equation represents an equipotential surface.
The equipotential surfaces are two series of ovoids surrounding the two poles respectively, and separated by a plane at zero potential passing perpendicularly through the middle of the axis. If r and r ′ make angles θ and θ′ with the axis, it is easily shown that the equation to a line of force is
| cos θ−cos′ θ=constant. | (9) |
At the point where a line of force intersects the perpendicular bisector of the axis r=r ′=r0, say, and cos θ − cos θ′ obviously=l/r0, l being

| |
| Fig. 2. | Fig. 3. |
the distance between the poles; l/r0 is therefore the value of the constant in (9) for the line in question. Fig. 2 shows the lines of force and the plane sections of the equipotential surfaces for a thin magnet with poles concentrated at its ends. The potential due to a small magnet of moment M, at a point whose distance from the centre of the magnet is r, is
| V=M cos θ/r2, | (10) |
where θ is the angle between r and the axis of the magnet. Denoting the force at P (see fig. 3) by F, and its components parallel to the co-ordinate axes by X and Y, we have
| X=δVδx=Mr 2(3 cos2θ−1), Y=δVδy=Mr 3(3 sin θ cos θ. |
(11) |
If Fr is the force along r and Ft that along t at right angles to r,
| Fr=X cosθ+Y sinθ=Mr 3 2 cos θ, | (12) |
| Ft=−X sinθ+Y cosθ=Mr 3 sin θ. | (13) |
For the resultant force at P,
| F=√(Fr2 + Ft2)=Mr 3 √(3 cos2 θ + 1). | (14) |
The direction of F is given by the following construction: Trisect OP at C, so that OC=OP/3; draw CD at right angles to OP, to cut the axis produced in D; then DP will be the direction of the force at P. For a point in the axis OX, θ=0; therefore cos θ=1, and the point D coincides with C; the magnitude of the force is, from (14),
| Fx=2M / r 3, | (15) |
its direction being along the axis OX. For a point in the line OY bisecting the magnet perpendicularly, θ=π/2 therefore cos θ=0, and the point D is at an infinite distance. The magnitude of the force is in this case
| Fy=M / r 3, | (16) |
and its direction is parallel to the axis of the magnet. Although the above useful formulae, (10) to (15), are true only for an infinitely small magnet, they may be practically applied whenever the distance r is considerable compared with the length of the magnet.
Couples and Forces between Magnets.—If a small magnet of moment M is placed in the sensibly uniform field H due to a distant magnet, the couple tending to turn the small magnet upon an axis at right angles to the magnet and to the force is
| MH sin θ, | (17) |
where θ is the angle between the axis of the magnet and the direction of the force. In fig. 4 S′N′ is a small magnet of moment M′, and SN a distant fixed magnet of moment M; the axes of SN and S′N′ make angles of θ and φ respectively with the line through their middle points. It can be deduced from (17), (12) and (13) that the couple on S′N′ due to SN, and tending to increase φ, is
| MM′ (sin θ cos φ − 2 sin φ cos θ) / r 3. | (18) |
This vanishes if sin θ cos φ=2 sin φ cos θ, i.e. if tan φ=12 tan θ, S′N′ being then along a line of force, a result which explains the construction given above for finding the direction of the force F in (14). If the axis of SN produced passes through the centre of S′N′, θ=0, and the couple becomes
| 2MM′ sin φ/r 3, | (19) |
tending to diminish φ; this is called the “end on” position. If the centre of S′N′ is on the perpendicular bisector of SN, θ=12π, and the couple will be
| MM′ cos φ/r 3, | (20) |
tending to increase φ; this is the “broadside on” position. These two positions are sometimes called the first and second (or A and B) principal positions of Gauss. The components X, Y, parallel and perpendicular to r, of the force between the two magnets SN and S′N′ are
| X=3MM′ (sin θ sin φ − 2 cos θ cos φ) / r 4, | (21) |
| Y=3MM′ (sin θ cos φ + sin φ cos θ) / r 4. | (22) |
It will be seen that, whereas the couple varies inversely as the cube of the distance, the force varies inversely as the fourth power.
Distributions of Magnetism.—A magnet may be regarded as consisting of an infinite number of elementary magnets, each having a pair of poles and a definite magnetic moment. If a series of such elements, all equally and longitudinally magnetized, were placed end to end with their unlike poles in contact, the external action of the filament thus formed would be reduced to that of the two extreme poles. The same would be the case if the magnetization of the filament varied inversely as the area of its cross-section a in different parts. Such a filament is called a simple magnetic solenoid, and the product aI is called the strength of the solenoid. A magnet which consists entirely of such solenoids, having their ends either upon the surface or closed upon themselves, is called a solenoidal magnet, and the magnetism is said to be distributed solenoidally; there is no free magnetism in its interior. If the constituent solenoids are parallel and of equal strength, the magnet is also uniformly magnetized. A thin sheet of magnetic matter magnetized normally to its surface in such a manner that the magnetization at any place is inversely proportional to the thickness h of the sheet at that place is called a magnetic shell; the constant product hI is the strength of the shell and is generally denoted by Φ or φ. The potential at any point due to a magnetic shell is the product of its strength into the solid angle ω subtended by its edge at the given point, or V=Φω. For a given strength, therefore, the potential depends solely upon the boundary of the shell, and the potential outside a closed shell is everywhere zero. A magnet which can be divided into simple magnetic shells, either closed or having their edges on the surface of the magnet, is called a lamellar magnet, and the magnetism is said to be distributed lamellarly. A magnet consisting of a series of plane shells of equal strength arranged at right angles to the direction of magnetization will be uniformly magnetized.
It can be shown that uniform magnetization is possible only when the form of the body is ellipsoidal. (Maxwell, Electricity and Magnetism, II., § 437). The cases of greatest practical importance are those of a sphere (which is an ellipsoid with three equal axes) and an ovoid or prolate ellipsoid of revolution. The potential due to a uniformly magnetized sphere of radius a for an external point at a distance r from the centre is
| V=43πa3I cos θ/r 2, | (23) |
θ being the inclination of r to the magnetic axis. Since 43πa3I is the moment of the sphere (=volume × magnetization), it appears from (10) that the magnetized sphere produces the same external effect as a very small magnet of equal moment placed at its centre and magnetized in the same direction; the resultant force therefore is the same as in (14). The force in the interior is uniform, opposite to the direction of magnetization, and equal to 43πI. When it is desired to have a uniform magnet with definitely situated poles, it it usual to employ one having the form of an ovoid, or elongated ellipsoid of revolution, instead of a rectangular or cylindrical bar. If the magnetization is parallel to the major axis, and the lengths of the major and minor axes are 2a and 2c, the poles are situated at a distance equal to 23a from the centre, and the magnet will behave externally like a simple solenoid of length 43a. The internal force F is opposite to the direction of the magnetization, and equal to NI, where N is a coefficient depending only on the ratio of the axes. The moment=43πac2I=−43πac2FN.
The distribution of magnetism and the position of the poles in magnets of other shapes, such as cylindrical or rectangular bars, cannot be specified by any general statement, though approximate determinations may be obtained experimentally in individual cases.[5] According to F. W. G. Kohlrausch[6] the distance between the poles of a cylindrical magnet the length of which is from 10 to 30 times the diameter, is sensibly equal to five-sixths of the length of the bar. This statement, however, is only approximately correct, the distance between the poles depending upon the intensity of the magnetization.[7] In general, the greater the ratio of length to section, the more nearly will the poles approach the end of the bar, and the more nearly uniform will be the magnetization. For most practical purpose a knowledge of the exact position of the poles is of no importance; the magnetic moment, and therefore the mean magnetization, can always be determined with accuracy.
Magnetic Induction or Magnetic Flux.—When magnetic force acts on any medium, whether magnetic, diamagnetic or neutral, it produces within it a phenomenon of the nature of a flux or flow called magnetic induction (Maxwell, loc. cit., § 428). Magnetic induction, like other fluxes such as electrical, thermal or fluid currents, is defined with reference to an area; it satisfies the same conditions of continuity as the electric current does, and in isotropic media it depends on the magnetic force just as the electric current depends on the electromotive force. The magnitude of the flux produced by a given magnetic force differs in different media. In a uniform magnetic field of unit intensity formed in empty space the induction or magnetic flux across an area of 1 square centimetre normal to the direction of the field is arbitrarily taken as the unit of induction. Hence if the induction per square centimetre at any point is denoted by B, then in empty space B is numerically equal to H; moreover in isotropic media both have the same direction, and for these reasons it is often said that in empty space (and practically in air and other non-magnetic substances) B and H are identical. Inside a magnetized body, B is the force that would be exerted on a unit pole if placed in a narrow crevasse cut in the body, the walls of the crevasse being perpendicular to the direction of the magnetization (Maxwell, §§ 399, 604); and its numerical value, being partly due to the free magnetism on the walls, is generally very different from that of H. In the case of a straight uniformly magnetized bar the direction of the magnetic force due to the poles of the magnet is from the north to the south pole outside the magnet, and from the south to the north inside. The magnetic flux per square centimetre at any point (B, B, or B) is briefly called the induction, or, especially by electrical engineers, the flux-density. The direction of magnetic induction may be indicated by lines of induction; a line of induction is always a closed curve, though it may possibly extend to and return from infinity. Lines of induction drawn through every point in the contour of a small surface form a re-entrant tube bounded by lines of induction; such a tube is called a tube of induction. The cross-section of a tube of induction may vary in different parts, but the total induction across any section is everywhere the same. A special meaning has been assigned to the term “lines of induction.” Suppose the whole space in which induction exists to be divided up into unit tubes, such that the surface integral of the induction over any cross-section of a tube is equal to unity, and along the axis of each tube let a line of induction be drawn. These axial lines constitute the system of lines of induction which are so often referred to in the specification of a field. Where the induction is high the lines will be crowded together; where it is weak they will be widely separated, the number per square centimetre crossing a normal surface at any point being always equal to the numerical value of B. The induction may therefore be specified as B lines per square centimetre. The direction of the induction is also of course indicated by the direction of the lines, which thus serve to map out space in a convenient manner. Lines of induction are frequently but inaccurately spoken of as lines of force.
When induction or magnetic flux takes place in a ferromagnetic metal, the metal becomes magnetized, but the magnetization at any point is proportional not to B, but to B−H. The factor of proportionality will be 1−4π, so that
| I=(B − H) / 4π, | (24) |
| or | B=H + 4πI. | (25) |
Unless the path of the induction is entirely inside the metal, free magnetic poles are developed at those parts of the metal where induction enters and leaves, the polarity being south at the entry and north at the exit of the flux. These free poles produce a magnetic field which is superposed upon that arising from other sources. The resultant magnetic field, therefore, is compounded of two fields, the one being due to the poles, and the other to the external causes which would be operative in the absence of the magnetized metal. The intensity (at any point) of the field due to the magnetization may be denoted by Hi, that of the external field by H0, and that of the resultant field by H. In certain cases, as, for instance, in an iron ring wrapped uniformly round with a coil of wire through which a current is passing, the induction is entirely within the metal; there are, consequently, no free poles, and the ring, though magnetized, constitutes a poleless magnet. Magnetization is usually regarded as the direct effect of the resultant magnetic force, which is therefore often termed the magnetizing force.
Permeability and Susceptibility.—The ratio B/H is called the permeability of the medium in which the induction is taking place, and is denoted by μ. The ratio I/H is called the susceptibility of the magnetized substance, and is denoted by κ. Hence
| B=μH and I=κH. | (26) |
| Also | μ=BH=H + 4πIH1 + 4πκ | (27) |
| and | κ=μ − 14π | (28) |
Since in empty space B has been assumed to be numerically equal to H, it follows that the permeability of a vacuum is equal to 1. The permeability of most material substances differs very slightly from unity, being a little greater than 1 in paramagnetic and a little less in diamagnetic substances. In the case of the ferromagnetic metals and some of their alloys and compounds, the permeability has generally a much higher value. Moreover, it is not constant, being an apparently arbitrary function of H or of B; in the same specimen its value may, under different conditions, vary from less than 2 to upwards of 5000. The magnetic susceptibility κ expresses the numerical relation of the magnetization to the magnetizing force. From the equation κ=(μ − 1)/4π, it follows that the magnetic susceptibility of a vacuum (where μ=1) is 0, that of a diamagnetic substance (where μ < 1) has a negative value, while the susceptibility of paramagnetic and ferromagnetic substances (for which μ > 1) is positive. No substance has yet been discovered having a negative susceptibility sufficiently great to render the permeability (=1 + 4πκ) negative.
Magnetic Circuit.—The circulation of magnetic induction or flux through magnetic and non-magnetic substances, such as iron and air, is in many respects analogous to that of an electric current through good and bad conductors. Just as the lines of flow of an electric current all pass in closed curves through the battery or other generator, so do all the lines of induction pass in closed curves through the magnet or magnetizing coil. The total magnetic induction or flux corresponds to the current of electricity (practically measured in amperes); the induction or flux density B to the density of the current (number of amperes to the square centimetre of section); the magnetic permeability to the specific electric conductivity; and the line integral of the magnetic force, sometimes called the magnetomotive force, to the electromotive force in the circuit. The principal points of difference are that (1) the magnetic permeability, unlike the electric conductivity, which is independent of the strength of the current, is not in general constant; (2) there is no perfect insulator for magnetic induction, which will pass more or less freely through all known substances. Nevertheless, many important problems relating to the distribution of magnetic induction may be solved by methods similar to those employed for the solution of analogous problems in electricity. For the elementary theory of the magnetic circuit see Electro-Magnetism.
Hysteresis, Coercive Force, Retentiveness.—It is found that when a piece of ferromagnetic metal, such as iron, is subjected to a magnetic field of changing intensity, the changes which take place in the induced magnetization of the iron exhibit a tendency to lag behind those which occur in the intensity of the field—a phenomenon to which J. A. Ewing (Phil. Trans. clxxvi. 524) has given the name of hysteresis (Gr. ὑστερέω, to lag behind). Thus it happens that there is no definite relation between the magnetization of a piece of metal which has been previously magnetized and the strength of the field in which it is placed. Much depends upon its antecedent magnetic condition, and indeed upon its whole magnetic history. A well-known example of hysteresis is presented by the case of permanent magnets. If a bar of hard steel is placed in a strong magnetic field, a certain intensity of magnetization is induced in the bar; but when the strength of the field is afterwards reduced to zero, the magnetization does not entirely disappear. That portion which is permanently retained, and which may amount to considerably more than one-half, is called the residual magnetization. The ratio of the residual magnetization to its previous maximum value measures the retentiveness, or retentivity, of the metal.[8] Steel, which is well suited for the construction of permanent magnets, is said to possess great “coercive force.” To this term, which had long been used in a loose and indefinite manner, J. Hopkinson supplied a precise meaning (Phil. Trans. clxxvi. 460). The coercive force, or coercivity, of a material is that reversed magnetic force which, while it is acting, just suffices to reduce the residual induction to nothing after the material has been temporarily submitted to any great magnetizing force. A metal which has great retentiveness may at the same time have small coercive force, and it is the latter quality which is of chief importance in permanent magnets.
Demagnetizing Force.—It has already been mentioned that when a ferromagnetic body is placed in a magnetic field, the resultant magnetic force H, at a point within the body, is compounded of the force H0, due to the external field, and of another force, Hi, arising from the induced magnetization of the body. Since Hi generally tends to oppose the external force, thus making H less than H0, it may be called the demagnetizing force. Except in the few special cases when a uniform external field produces uniform magnetization, the value of the demagnetizing force cannot be calculated, and an exact determination of the actual magnetic force within the body is therefore impossible. An important instance in which the calculation can be made is that of an elongated ellipsoid of revolution placed in a uniform field H0, with its axis of revolution parallel to the lines of force. The magnetization at any point inside the ellipsoid will then be
| I = | κH0 |
| 1 + κN |
where
| N = 4π | 1 | − 1 | 1 | log | 1 + e | − 1 , |
| e2 | 2e | 1 − e |
e being the eccentricity (see Maxwell’s Treatise, § 438). Since I = κH, we have
or
NI being the demagnetizing force Hi. N may be called, after H. du Bois (Magnetic Circuit, p. 33), the demagnetizing factor, and the ratio of the length of the ellipsoid 2c to its equatorial diameter 2a (= c/a), the dimensional ratio, denoted by the symbol m.
Since
| e = √( 1 − | a2 | ) = √( 1 − | 1 | ), |
| c2 | m2 |
the above expression for N may be written
| N = | 4π | m | log | m + √(m2 − 1) | − 1 | |
| m2 − 1 | 2√(m2 − 1) | m − √(m2 − 1) |
| = | 4π | { | m | log ( m+ √(m2 − 1) ) − 1 }, |
| m2 − 1 | √(m2 − 1) |
from which the value of N for a given dimensional ratio can be calculated. When the ellipsoid is so much elongated that 1 is negligible in relation to m2, the expression approximates to the simpler form
| N = | 4π | log 2m − 1 |
| m2 |
In the case of a sphere, e = O and N = 43π; therefore from (29)
| I = κH = | κH0 | = | 3κ | H0, |
| 1 + 43πκ | 3 + 4πκ |
Whence
| H = | 3 | H0 = | 3 | H0, |
| 3 + 4πκ | μ + 2 |
and
| B = μH = | 3μ | H0. |
| μ + 2 |
Equations (33) and (34) show that when, as is generally the case with ferromagnetic substances, the value of μ is considerable, the resultant magnetic force is only a small fraction of the external force, while the numerical value of the induction is approximately three times that of the external force, and nearly independent of the permeability. The demagnetizing force inside a cylindrical rod placed longitudinally in a uniform field H0 is not uniform, being greatest at the ends and least in the middle part. Denoting its mean value by Hi, and that of the demagnetizing factor by N, we have
Du Bois has shown that when the dimensional ratio m (= length/diameter) exceeds 100, Nm2 = constant = 45, and hence for long thin rods
From an analysis of a number of experiments made with rods of different dimensions H. du Bois has deduced the corresponding mean demagnetizing factors. These, together with values of m2N for cylindrical rods, and of N and m2N for ellipsoids of revolution, are given in the following useful table (loc. cit. p. 41):—
Demagnetizing Factors.
| m. | Cylinder. | Ellipsoid. | ||
| N. | m2N. | N. | m2N. | |
| 0 | 12.5664 | 0 | 12.5664 | 0 |
| 0.5 | — | — | 6.5864 | — |
| 1 | — | — | 4.1888 | — |
| 5 | — | — | 0.7015 | — |
| 10 | 0.2160 | 21.6 | 0.2549 | 25.5 |
| 15 | 0.1206 | 27.1 | 0.1350 | 30.5 |
| 20 | 0.0775 | 31.0 | 0.0848 | 34.0 |
| 25 | 0.0533 | 33.4 | 0.0579 | 36.2 |
| 30 | 0.0393 | 35.4 | 0.0432 | 38.8 |
| 40 | 0.0238 | 38.7 | 0.0266 | 42.5 |
| 50 | 0.0162 | 40.5 | 0.0181 | 45.3 |
| 60 | 0.0118 | 42.4 | 0.0132 | 47.5 |
| 70 | 0.0089 | 43.7 | 0.0101 | 49.5 |
| 80 | 0.0069 | 44.4 | 0.0080 | 51.2 |
| 90 | 0.0055 | 44.8 | 0.0065 | 52.5 |
| 100 | 0.0045 | 45.0 | 0.0054 | 54.0 |
| 150 | 0.0020 | 45.0 | 0.0026 | 58.3 |
| 200 | 0.0011 | 45.0 | 0.0016 | 64.0 |
| 300 | 0.00050 | 45.0 | 0.00075 | 67.5 |
| 400 | 0.00028 | 45.0 | 0.00045 | 72.0 |
| 500 | 0.00018 | 45.0 | 0.00030 | 75.0 |
| 1000 | 0.00005 | 45.0 | 0.00008 | 80.0 |
In the middle part of a rod which has a length of 400 or 500 diameters the effect of the ends is insensible; but for many experiments the condition of endlessness may be best secured by giving the metal the shape of a ring of uniform section, the magnetic field being produced by an electric current through a coil of wire evenly wound round the ring. In such cases Hi = 0 and H = H0.
The residual magnetization Ir retained by a bar of ferromagnetic metal after it has been removed from the influence of an external field produces a demagnetizing force NIr, which is greater the smaller the dimensional ratio. Hence the difficulty of imparting any considerable permanent magnetization to a short thick bar not possessed of great coercive force. The magnetization retained by a long thin rod, even when its coercive force is small, is sometimes little less than that which was produced by the direct action of the field.
Demagnetization by Reversals.—In the course of an experiment it is often desired to eliminate the effects of previous magnetization, and, as far as possible, wipe out the magnetic history of a specimen. In order to attain this result it was formerly the practice to raise the metal to a bright red heat, and allow it to cool while carefully guarded from magnetic influence. This operation, besides being very troublesome, was open to the objection that it was almost sure to produce a material but uncertain change in the physical constitution of the metal, so that, in fact, the results of experiments made before and after the treatment were not comparable. Ewing introduced the method (Phil. Trans. clxxvi. 539) of demagnetizing a specimen by subjecting it to a succession of magnetic forces which alternated in direction and gradually diminished in strength from a high value to zero. By means of a simple arrangement, which will be described farther on, this process can be carried out in a few seconds, and the metal can be brought as often as desired to a definite condition, which, if not quite identical with the virgin state, at least closely approximates to it.
Forces acting on a Small Body in the Magnetic Field.—If a small magnet of length ds and pole-strength m is brought into a magnetic field such that the values of the magnetic potential at the negative and positive poles respectively are V1 and V2, the work done upon the magnet, and therefore its potential energy, will be
which may be written
| W = mds | dV | = M | dV | = −MH0 = −vIH0, |
| ds | ds |
where M is the moment of the magnet, v the volume, I the magnetization, and H0 the magnetic force along ds. The small magnet may be a sphere rigidly magnetized in the direction of H0; if this is replaced by an isotropic sphere inductively magnetized by the field, then, for a displacement so small that the magnetization of the sphere may be regarded as unchanged, we shall have
| dW = −vI dH0 = −v | κ | H0 dH0; |
| 1 + 43πκ |
whence
| W = − | v | κ | H20. | |
| 2 | 1 + 43πκ |
The mechanical force acting on the sphere in the direction of displacement x is
| F = − | dW | = v | κ | dH20 | . | |
| dx | 1 + 43πκ | dx |
If H0 is constant, the force will be zero; if H0 is variable, the sphere will tend to move in the direction in which H0 varies most rapidly. The coefficient κ / (1 + 43πκ) is positive for ferromagnetic and paramagnetic substances, which will therefore tend to move from weaker to stronger parts of the field; for all known diamagnetic substances it is negative, and these will tend to move from stronger to weaker parts. For small bodies other than spheres the coefficient will be different, but its sign will always be negative for diamagnetic substances and positive for others;[9] hence the forces acting on any small body will be in the same directions as in the case of a sphere.[10]
Directing Couple acting on an Elongated Body.—In a non-uniform field every volume-element of the body tends to move towards regions of greater or less force according as the substance is paramagnetic or diamagnetic, and the behaviour of the whole mass will be determined chiefly by the tendency of its constituent elements. For this reason a thin bar suspended at its centre of gravity between a pair of magnetic poles will, if paramagnetic, set itself along the line joining the poles, where the field is strongest, and if diamagnetic, transversely to the line. These are the “axial” and “equatorial” positions of Faraday. It can be shown[11] that in a uniform field an elongated piece of any non-crystalline material is in stable equilibrium only when its length is parallel to the lines of force; for diamagnetic substances, however, the directing couple is exceedingly small, and it would hardly be possible to obtain a uniform field of sufficient strength to show the effect experimentally.
Relative Magnetization.—A substance of which the real susceptibility is κ will, when surrounded by a medium having the susceptibility κ′, behave towards a magnet as if its susceptibility were κa = (κ − κ′) / (1 + 4πκ′). Since 1 + 4πκ′ can never be negative, the apparent susceptibility κa will be positive or negative according as κ is greater or less than κ′. Thus, for example, a tube containing a weak solution of an iron salt will appear to be diamagnetic if it is immersed in a stronger solution of iron, though in air it is paramagnetic.[12]
Circular Magnetization.—An electric current i flowing uniformly through a cylindrical wire whose radius is a produces inside the wire a magnetic field of which the lines of force are concentric circles around the axis of the wire. At a point whose distance from the axis of the wire is r the tangential magnetic force is
it therefore varies directly as the distance from the axis, where it is zero.[13] If the wire consists of a ferromagnetic metal, it will become “circularly” magnetized by the field, the lines of magnetization being, like the lines of force, concentric circles. So long as the wire (supposed isotropic) is free from torsional stress, there will be no external evidence of magnetism.
Magnetic Shielding.—The action of a hollow magnetized shell on a point inside it is always opposed to that of the external magnetizing force,[14] the resultant interior field being therefore weaker than the field outside. Hence any apparatus, such as a galvanometer, may be partially shielded from extraneous magnetic action by enclosing it in an iron case. If a hollow sphere[15] of which the outer radius is R and the inner radius r is placed in a uniform field H0, the field inside will also be uniform and in the same direction as H0, and its value will be approximately
| Hi = | H0 | . |
| 1 + 29 (μ − 2) (1 − r 3/R3) |
For a cylinder placed with its axis at right angles to the lines of force,
| Hi = | H0 | . |
| 1 + 14 (μ − 2) (1 − r 2/R2) |
These expressions show that the thicker the screen and the greater
its permeability μ, the more effectual will be the shielding action.
Since μ can never be infinite, complete shielding is not possible.
Magneto-Crystallic Phenomenon.—In anisotropic bodies, such as crystals, the direction of the magnetization does not in general coincide with that of the magnetic force. There are, however, always three principal axes at right angles to one another along which the magnetization and the force have the same direction. If each of these axes successively is placed parallel to the lines of force in a uniform field H, we shall have
the three susceptibilities κ being in general unequal, though in some cases two of them may have the same value. For crystalline bodies the value of κ (+ or −) is nearly always small and constant, the magnetization being therefore independent of the form of the body and proportional to the force. Hence, whatever the position of the body, if the field be resolved into three components parallel to the principal axes of the crystal, the actual magnetization will be the resultant of the three magnetizations along the axes. The body (or each element of it) will tend to set itself with its axis of greatest susceptibility parallel to the lines of force, while, if the field is not uniform, each volume-element will also tend to move towards places of greater or smaller force (according as the substance is paramagnetic or diamagnetic), the tendency being a maximum when the axis of greatest susceptibility is parallel to the field, and a minimum when it is perpendicular to it. The phenomena may therefore be exceedingly complicated.[16]
3. Magnetic Measurements
Magnetic Moment.—The moment M of a magnet may be determined in many ways,[17] the most accurate being that of C. F. Gauss, which gives the value not only of M, but also that of H, the horizontal component of the earth’s force. The product MH is first determined by suspending the magnet horizontally, and causing it to vibrate in small arcs. If A is the moment of inertia of the magnet, and t the time of a complete vibration, MH = 4π2A / t2 (torsion being neglected). The ratio M/H is then found by one of the magnetometric methods which in their simplest forms are described below. Equation (44) shows that as a first approximation.
where l is half the length of the magnet, which is placed in the “broadside-on” position as regards a small suspended magnetic needle, d the distance between the centre of the magnet and the needle, and θ the angle through which the needle is deflected by the magnet. We get therefore
When a high degree of accuracy is required, the experiments and calculations are less simple, and various corrections are applied. The moment of a magnet may also be deduced from a measurement of the couple exerted on the magnet by a uniform field H. Thus if the magnet is suspended horizontally by a fine wire, which, when the magnetic axis points north and south, is free from torsion, and if θ is the angle through which the upper end of the wire must be twisted to make the magnet point east and west, then MH = Cθ, or M = Cθ/H, where C is the torsional couple for 1°. A bifilar suspension is sometimes used instead of a single wire. If P is the weight of the magnet, l the length of each of the two threads, 2a the distance between their upper points of attachment, and 2b that between the lower points, then, approximately, MH = P(ab/l) sin θ. It is often sufficient to find the ratio of the moment of one magnet to that of another. If two magnets having moments M, M′ are arranged at right angles to each other upon a horizontal support which is free to rotate, their resultant R will set itself in the magnetic meridian. Let θ be the angle which the standard magnet M makes with the meridian, then M′/R = sin θ, and M/R = cos θ, whence M′ = M tan θ.
 |
| Fig. 5. |
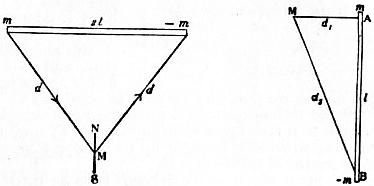
A convenient and rapid method of estimating a magnetic moment has been devised by H. Armagnat.[18] The magnet is laid on a table with its north pole pointing northwards, A compass having a very short needle is placed on the line which bisects the axis of the magnet at right angles, and is moved until a neutral point is found where the force due to the earth’s field H is balanced by that due to the magnet. If 2l is the distance between the poles m and −m, d the distance from either pole to a point P on the line AB (fig. 5), we have for the resultant force at P
When P is the neutral point, H is equal and opposite to R; therefore M = Hd 3, or the moment is numerically equal to the cube of the distance from the neutral point to a pole, multiplied by the horizontal intensity of the earth’s force. The distance between the poles may with sufficient accuracy for a rough determination be assumed to be equal to five-sixths of the length of the magnet.
Measurement of Magnetization and Induction.—The magnetic condition assumed by a piece of ferromagnetic metal in different circumstances is determinable by various modes of experiment which may be classed as magnetometric, ballistic, and traction methods. When either the magnetization I or the induction B corresponding to a given magnetizing force H is known, the other may be found by means of the formula B = 4πI + H.
Magnetometric Methods.—Intensity of magnetization is most directly measured by observing the action which a magnetized body, generally a long straight rod, exerts upon a small magnetic needle placed near it. The magnetic needle may be cemented horizontally across the back of a little plane or concave mirror, about 14 or 38 in. in diameter, which is suspended by a single fibre of unspun silk; this arrangement, when enclosed in a case with a glazed front to protect it from currents of air, constitutes a simple but efficient magnetometer. Deflections of the suspended needle are indicated by the movement of a narrow beam of light which the mirror reflects from a lamp and focusses upon a graduated cardboard scale placed at a distance of a few feet; the angular deflection of the beam of light is, of course, twice that of the needle. The suspended needle is, in the absence of disturbing causes, directed solely by the horizontal component of the earth’s field of magnetic force HE, and therefore sets itself approximately north and south. The magnetized body which is to be tested should be placed in such a position that the force HP due to its poles may, at the spot occupied by the suspended needle, act in a direction at right angles to that due to the earth—that is, east and west. The direction of the resultant field of force will then make, with that of HE, an angle θ, such that Hp / HE = tan θ, and the suspended needle will be deflected through the same angle. We have therefore
The angle θ is indicated by the position of the spot of light upon the scale, and the horizontal intensity of the earth’s field HE is known; thus we can at once determine the value of HP, from which the magnetization I of the body under test may be calculated.
In order to fulfil the requirement that the field which a magnetized rod produces at the magnetometer shall be at right angles to that of the earth, the rod may be conveniently placed in any one of three different positions with regard to the suspended needle.
 |
| Fig. 6. |
(1) The rod is set in a horizontal position level with the suspended needle, its axis being in a line which is perpendicular to the magnetic meridian, and which passes through the centre of suspension of the needle. This is called the “end-on” position, and is indicated in fig. 6. AB is the rod and C the middle point of its axis; NS is the magnetometer needle; AM bisects the undeflected needle NS at right angles. Let 2l = the length of the rod (or, more accurately, the distance between its poles), v = its volume, m and −m the strength of its poles, and let d = the distance CM. For most ordinary purposes the length of the needle may be assumed to be negligible in comparison with the distance between the needle and the rod. We then have approximately for the field at M due to the rod
| HP = | m | − | m | = m | 4dl | . |
| (d − l)2 | (d + l)2 | (d 2 − l 2)2 |
Therefore
| 2ml = M = | (d 2 − l 2)2 HP | = | (d 2 − l 2)2 HE tan θ | . |
| 2d | 2d |
And
| I = | M | = | (d 2 − l 2)2 HE | tan θ, |
| v | 2dv |
whence we can find the values of I which correspond to different angles of deflection.
(2) The rod may be placed horizontally east and west in such a position that the direction of the undeflected suspended needle bisects it at right angles. This is known as the “broadside-on” position, and is represented in fig. 7. Let the distance of each pole of the rod AB from the centre of the magnetometer needle = d. Then, since HP, the force at M due to m and −m, is the resultant of m/d 2 and −m/d 2, we have
| HP | = | 2l |
| m/d 2 | d |
or
| HP = | 2ml | , |
| d 3 |
the direction being parallel to AB.
And
| I = | d 3HP | = | d 3HE | tan θ. |
| v | v |
 | |
| Fig. 7. | Fig. 8. |
(3) In the third position the test rod is placed vertically with one of its poles at the level of the magnetometer needle, and in the line drawn perpendicularly to the undeflected needle from its centre of suspension. The arrangement is shown in fig. 8, where AB is the vertical rod and M indicates the position of the magnetometer needle, which is supposed to be perpendicular to the plane of the paper. Denoting the distance AM by d1, BM by d2, and AB by l, we have for the force at M due to the magnetism of the rod
| HP = | m | − horizontal component of | m |
| d12 | d22 |
| = m { | 1 | − | d1 | ). |
| d12 | d23 |
Therefore
| m = | HP | = | d12HE | tan θ, |
| (1 / d12) − (d1 / d23) | 1 − (d1 / d2)3 |
and
| I = | ld12 HE | tan θ. |
| v {1 − (d1 / d2)3 } |
This last method of arrangement is called by Ewing the “one-pole”
method, because the magnetometer deflection is mainly caused by
the upper pole of the rod (Magnetic Induction, p. 40). For experiments
with long thin rods or wires it has an advantage over the
other arrangements in that the position of the poles need not be
known with great accuracy, a small upward or downward displacement
having little effect upon the magnetometer deflection. On
the other hand, a vertically placed rod is subject to the inconvenience
that it is influenced by the earth’s magnetic field, which is not
the case when the rod is horizontal and at right angles to the magnetic
meridian. This extraneous influence may, however, be eliminated
by surrounding the rod with a coil of wire carrying a current
such as will produce in the interior a magnetic field equal and
opposite to the vertical component of the earth’s field.
If the cardboard scale upon which the beam of light is reflected by the magnetometer mirror is a flat one, the deflections as indicated by the movement of the spot of light are related to the actual deflections of the needle in the ratio of tan 2θ to θ. Since θ is always small, sufficiently accurate results may generally be obtained if we assume that tan 2θ = 2 tan θ. If the distance of the mirror from the scale is equal to n scale divisions, and if a deflection θ of the needle causes the reflected spot of light to move over s scale divisions, we shall have
We may therefore generally substitute s/2n for tan θ in the various expressions which have been given for I.
 |
| Fig. 9. |
Of the three methods which have been described, the first two are generally the most suitable for determining the moment or the magnetization of a permanent magnet, and the last for studying the changes which occur in the magnetization of a long rod or wire when subjected to various external magnetic forces, or, in other words, for determining the relation of I to H. A plan of the apparatus as arranged by Ewing for the latter purpose is shown diagrammatically in fig. 9. The cardboard scale SS is placed above a wooden screen, having in it a narrow vertical slit which permits a beam of light from the lamp L to reach the mirror of the magnetometer M, whence it is reflected upon the scale. A is the upper end of a glass tube, half a metre or so in length, which is clamped in a vertical position behind the magnetometer. The tube is wound over its whole length with two separate coils of insulated wire, the one being outside the other. The inner coil is supplied, through the intervening apparatus, with current from the battery of secondary cells B1; this produces the desired magnetic field inside the tube. The outer coil derives current, through an adjustable resistance R, from a constant cell B2; its object is to produce inside the tube a magnetic field equal and opposite to that due to the earth’s magnetism. C is a “compensating coil” consisting of a few turns of wire through which the magnetizing current passes; it serves to neutralize the effect produced upon the magnetometer by the magnetizing coil, and its distance from the magnetometer is so adjusted that when the circuit is closed, no ferromagnetic metal being inside the magnetizing coil, the magnetometer needle undergoes no deflection. K is a commutator for reversing the direction of the magnetizing current, and G a galvanometer for measuring it. The strength of the magnetizing current is regulated by adjusting the position of the sliding contact E upon the resistance DF. The current increases to a maximum as E approaches F, and diminishes to almost nothing when E is brought up to D; it can be completely interrupted by means of the switch H.
The specimen upon which an experiment is to be made generally consists of a wire having a “dimensional ratio” of at least 300 or 400; its length should be rather less than that of the magnetizing coil, in order that the field H0, to which it is subjected, may be approximately uniform from end to end. The wire is supported inside the glass tube A with its upper pole at the same height as the magnetometer needle. Various currents are then passed through the magnetizing coil, the galvanometer readings and the simultaneous magnetometer deflections being noted. From the former we deduce H0, and from the latter the corresponding value of I, using the formulae H0 = 4πin/l and
| I = | d12 HE | × s, |
| 2nπr 2 1 − d1d23 |
where s is the deflection in scale-divisions, n the distance in scale-divisions
between the scale and the mirror, and r the radius of the
wire.
 |
| Fig. 10. |
The curve, fig. 10, shows the result of a typical experiment made upon a piece of soft iron (Ewing, Phil. Trans. vol. clxxvi. Plate 59), the magnetizing field H0 being first gradually increased and then diminished to zero. When the length of the wire exceeds 400 diameters, or thereabouts, H0 may generally be considered as equivalent to H, the actual strength of the field as modified by the magnetization of the wire; but if greater accuracy is desired, the value of Hi (= NI) may be found by the help of du Bois’s table and subtracted from H0. For a dimensional ratio of 400, N =0.00028, and therefore H = H0 − 0.00028I. This correction may be indicated in the diagram by a straight line drawn from 0 through the point at which the line of I = 1000 intersects that of H = 0.28 (Rayleigh, Phil. Mag. xxii. 175), the true value of H for any point on the curve being that measured from the sloping line instead of from the vertical axis. The effect of the ends of the wire is, as Ewing remarks, to shear the diagram in the horizontal direction through the angle which the sloping line makes with the vertical.
Since the induction B is equal to H + 4πI, it is easy from the results of experiments such as that just described to deduce the relation between B and H; a curve indicating such relation is called a curve of induction. The general character of curves of magnetization and of induction will be discussed later. A notable feature in both classes of curves is that, owing to hysteresis, the ascending and descending limbs do not coincide, but follow very different courses. If it is desired to annihilate the hysteretic effects of previous magnetization and restore the metal to its original condition, it may be demagnetized by reversals. This is effected by slowly moving the sliding contact E (fig. 9) from F to D, while at the same time the commutator K is rapidly worked, a series of alternating currents of gradually diminishing strength being thus caused to pass through the magnetizing coil.
The magnetometric method, except when employed in connexion with ellipsoids, for which the demagnetizing factors are accurately known, is generally less satisfactory for the exact determination of induction or magnetization than the ballistic method. But for much important experimental work it is better adapted than any other, and is indeed sometimes the only method possible.[19]
Ballistic Methods.—The so-called “ballistic” method of measuring induction is based upon the fact that a change of the induction through a closed linear conductor sets up in the conductor an electromotive force which is proportional to the rate of change. If the conductor consists of a coil of wire the ends of which are connected with a suitable galvanometer, the integral electromotive force due to a sudden increase or decrease of the induction through the coil displaces in the circuit a quantity of electricity Q = δBns R, where δB is the increment or decrement of induction per square centimetre, s is the area of the coil, n the number of turns of wire, and R the resistance of the circuit. Under the influence of the transient current, the galvanometer needle undergoes a momentary deflection, or “throw,” which is proportional to Q, and therefore to δB, and thus, if we know the deflection produced by the discharge through the galvanometer of a given quantity of electricity, we have the means of determining the value of δB.
The galvanometer which is used for ballistic observations should have a somewhat heavy needle with a period of vibration of not less than five seconds, so that the transient current may have ceased before the swing has well begun; an instrument of the d’Arsonval form is recommended, not only because it is unaffected by outside magnetic influence, but also because the moving part can be instantly brought to rest by means of a short-circuit key, thus effecting a great saving of time when a series of observations is being made. In practice it is usual to standardize or “calibrate” the galvanometer by causing a known change of induction to take place within a standard coil connected with it, and noting the corresponding deflection on the galvanometer scale. Let s be the area of a single turn of the standard coil, n the number of its turns, and r the resistance of the circuit of which the coil forms part; and let S, N and R be the corresponding constants for a coil which is to be used in an experiment. Then if a known change of induction δBa inside the standard coil is found to cause a throw of d scale-divisions, any change of induction δB through the experimental coil will be numerically equal to the corresponding throw D multiplied by snRBa/SNrd. For a series of experiments made with the same coil this fraction is constant, and we may write δB = kD. Rowland and others have used an earth coil for calibrating the galvanometer, a known change of induction through the coil being produced by turning it over in the earth’s magnetic field, but for several reasons it is preferable to employ an electric current as the source of a known induction. A primary coil of length l, having n turns, is wound upon a cylinder made of non-conducting and non-magnetic material, and upon the middle of the primary a secondary or induction coil is closely fitted. When a current of strength i is suddenly interrupted in the primary, the increment of induction through the secondary is sensibly equal to 4πin/l units. All the data required for standardizing the galvanometer can in this way be determined with accuracy.
The ballistic method is largely employed for determining the relation of induction to magnetizing force in samples of the iron and steel used in the manufacture of electrical machinery, and especially for the observation of hysteresis effects. The sample may have the form of a closed ring, upon which are wound the induction coil and another coil for taking the magnetizing current; or it may consist of a long straight rod or wire which can be slipped into a magnetizing coil such as is used in magnetometric experiments, the induction coil being wound upon the middle of the wire. With these arrangements there is no demagnetizing force to be considered, for the ring has not any ends to produce one, and the force due to the ends of a rod 400 or 500 diameters in length is quite insensible at the middle portion; H therefore is equal to H0.
E. Grassot has devised a galvanometer, or “fluxmeter,” which greatly alleviates the tedious operation of taking ballistic readings.[20] The instrument is of the d’Arsonval type; its coil turns in a strong uniform field, and is suspended in such a manner that torsion is practically negligible, the swings of the coil being limited by damping influences, chiefly electromagnetic. The index therefore remains almost stationary at the limit of its deflection, and the deflection is approximately the same whether the change of induction occurs suddenly or gradually.
 |
| Fig. 11. Fig. 12. Fig. 13. |
Induction and Hysteresis Curves.—Some typical induction curves, copied from a paper by Ewing (Proc. Inst. C.E. vol. cxxvi.), are given in figs. 11, 12 and 13. Fig. 11 shows the relation of B to H in a specimen which has never before been magnetized. The experiment may be made in two different ways: (1) the magnetizing current is increased by a series of sudden steps, each of which produces a ballistic throw, the value of B after any one throw being proportional to the sum of that and all the previous throws; (2) the magnetizing current having been brought to any desired value, is suddenly reversed, and the observed throw taken as measuring twice the actual induction. Fig. 12 shows the nature of the course taken by the curve when the magnetizing current, after having been raised to the value corresponding to the point a, is diminished by steps until it is nothing, and then gradually increased in the reverse direction. The downward course of the curve is, owing to hysteresis, strikingly different from its upward course, and when the magnetizing force has been reduced to zero, there is still remaining an induction of 7500 units. If the operation is again reversed, the upward course will be nearly, but not exactly, of the form shown by the line d e a, fig. 13. After a few repetitions of the reversal, the process becomes strictly cyclic, the upward and downward curves always following with precision the paths indicated in the figure. In order to establish the cyclic condition, it is sufficient to apply alternately the greatest positive and negative forces employed in the test (greatest H = about ±5 C.G.S. units in the case illustrated in the figure), an operation which is performed by simply reversing the direction of the maximum magnetizing current a few times.
The closed figure a c d e a is variously called a hysteresis curve or diagram or loop. The area HdB enclosed by it represents the work done in carrying a cubic centimetre of the iron through the corresponding magnetic cycle; expressed in ergs this work is 14πHdB.[21] To quote an example given by J. A. Fleming, it requires about 18 foot-pounds of work to make a complete magnetic cycle in a cubic foot of wrought iron, strongly magnetized first one way and then the other, the work so expended taking the form of heat in the mass.
 |
| Fig. 14. |
Fig. 14 shows diagrammatically a convenient arrangement described by Ewing (see Proc. Inst. C.E. vol. cxxvi., and Phil. Trans., 1893A, p. 987) for carrying out ballistic tests by which either the simple B-H curve (fig. 11) or the hysteresis curve (figs. 12 and 13) can be determined. The sample under test is prepared in the form of a ring A, upon which are wound the induction and the magnetizing coils; the latter should be wound evenly over the whole ring, though for the sake of clearness only part of the winding is indicated in the diagram. The magnetizing current, which is derived from the storage battery B, is regulated by the adjustable resistance R and measured by the galvanometer G. The current passes through the rocking key K, which, when thrown over to the right, places a in contact with c and b with d, and when thrown over to the left, places a in contact with e and b with f. When the switch S is closed, K acts simply as a commutator or current-reverser, but if K is thrown over from right to left while S is opened, not only is the current reversed, but its strength is at the same time diminished by the interposition of the adjustable resistance R2. The induction coil wound upon the ring is connected to the ballistic galvanometer G2 in series with a large permanent resistance R3. In the same circuit is also included the induction coil E, which is used for standardizing the galvanometer; this secondary coil is represented in the diagram by three turns of wire wound over a much longer primary coil. The short-circuit key F is kept closed except when an observation is about to be made; its object is to arrest the swing of the d’Arsonval galvanometer G2. By means of the three-way switch C the battery current may be sent either into the primary of E, for the purpose of calibrating the galvanometer, or into the magnetizing coil of the ring under test. When it is desired to obtain a simple curve of induction, such as that in fig. 11, S is kept permanently closed, and corresponding values of H and B are determined by one of the two methods already described, the strength of the battery-current being varied by means of the adjustable resistance R. When a hysteresis curve is to be obtained, the procedure is as follows: The current is first adjusted by means of R to such a strength as will fit it to produce the greatest + and − values of the magnetizing force which it is intended to apply in the course of the cycle; then it is reversed several times, and when the range of the galvanometer throws has become constant, half the extent of an excursion indicates the induction corresponding to the extreme value of H, and gives the point a in the curve fig. 12. The reversing key K having been put over to the left side, the short-circuit key S is suddenly opened; this inserts the resistance R, which has been suitably adjusted beforehand, and thus reduces the current and therefore the magnetizing force to a known value. The galvanometer throw which results from the change of current measures the amount by which the induction is reduced, and thus a second point on the curve is found. In a similar manner, by giving different values to the resistance R, any desired number of points between a and c in the curve can be determined. To continue the process, the key K is turned over to the right-hand side, and then, while S is open, is turned back, thereby not only reversing the direction of the current, but diminishing its strength by an amount depending upon the previous adjustment of R2. In this way points can be found lying anywhere between c and d of fig. 12, and the determination of the downward limb of the curve is therefore completed. As the return curve, shown in fig. 13, is merely an inverted copy of the other, no separate determination of it is necessary.
 |
| Fig. 15. |
In fig. 15 (J. A. Fleming, Magnets and Electric Currents, p. 193) are shown three very different types of hysteresis curves, characteristic of the special qualities of the metals from which they were respectively obtained. The distinguishing feature of the first is the steepness of its outlines; this indicates that the induction increases rapidly in relation to the magnetic force, and hence the metal is well suited for the construction of dynamo magnets. The second has a very small area, showing that the work done in reversing the magnetization is small; the metal is therefore adapted for use in alternating current transformers. On the other hand, the form of the third curve, with its large intercepts on the axes of H and B, denotes that the specimen to which it relates possesses both retentiveness and coercive force in a high degree; such a metal would be chosen for making good permanent magnets.
Several arrangements have been devised for determining hysteresis more easily and expeditiously than is possible by the ballistic method. The best known is J. A. Ewing’s hysteresis-tester,[22] which is specially intended for testing the sheet iron used in transformers. The sample, arranged as a bundle of rectangular strips, is caused to rotate about a central horizontal axis between the poles of an upright C-shaped magnet, which is supported near its middle upon knife-edges in such a manner that it can oscillate about an axis in a line with that about which the specimen rotates; the lower side of the magnet is weighted, to give it some stability. When the specimen rotates, the magnet is deflected from its upright position by an amount which depends upon the work done in a single complete rotation, and therefore upon the hysteresis. The deflection is indicated by a pointer upon a graduated scale, the readings being interpreted by comparison with two standard specimens supplied with the instrument. G. F. Searle and T. G. Bedford[23] have introduced the method of measuring hysteresis by means of an electro-dynamometer used ballistically. The fixed and suspended coils of the dynamometer are respectively connected in series with the magnetizing solenoid and with a secondary wound upon the specimen. When the magnetizing current is twice reversed, so as to complete a cycle, the sum of the two deflections, multiplied by a factor depending upon the sectional area of the specimen and upon the constants of the apparatus, gives the hysteresis for a complete cycle in ergs per cubic centimetre. For specimens of large sectional area it is necessary to apply corrections in respect of the energy dissipated by eddy currents and in heating the secondary circuit. The method has been employed by the authors themselves in studying the effects of tension, torsion and circular magnetization, while R. L. Wills[24] has made successful use of it in a research on the effects of temperature, a matter of great industrial importance.
C. P. Steinmetz (Electrician, 1891, 26, p. 261; 1892, 28, pp. 384, 408, 425) has called attention to a simple relation which appears to exist between the amount of energy dissipated in carrying a piece of iron or steel through a magnetic cycle and the limiting value of the induction reached in the cycle. Denoting by W the work in ergs done upon a cubic centimetre of the metal (= 14π ∫ HdB or ∫ HdI), he finds W = ηB1.6 approximately, where η is a number, called the hysteretic constant, depending upon the metal, and B is the maximum induction. The value of the constant η ranges in different metals from about 0.001 to 0.04; in soft iron and steel it is said to be generally not far from 0.002. Steinmetz’s formula may be tested by taking a series of hysteresis curves between different limits of B, measuring their areas by a planimeter, and plotting the logarithms of these divided by 4π as ordinates against logarithms of the corresponding maximum values of B as abscissae. The curve thus constructed should be a straight line inclined to the horizontal axis at an angle θ, the tangent of which is 1.6. Ewing and H. G. Klaassen (Phil. Trans., 1893, 184, 1017) have in this manner examined how nearly and within what range a formula of the type W = ηBε may be taken to represent the facts. The results of an example which they quote in detail may be briefly summarized as follows:—
| Limits of B. | Hysteretic Constant. η | Index. ε (= tan θ) | Degrees. θ |
| 200 to 500 | . . . | 1.9 | 62.25 |
| 500 to 1,000 | . . . | 1.68 | 59.25 |
| 1,000 to 2,000 | . . . | 1.55 | 57.25 |
| 2,000 to 8,000 | 0.01 | 1.475 | 55.75 |
| 8,000 to 14,000 | 0.00134 | 1.70 | 59.50 |
It is remarked by the experimenters that the value of the index ε is by no means constant, but changes in correspondence with the successive well-marked stages in the process of magnetization. But though a formula of this type has no physical significance, and cannot be accepted as an equation to the actual curve of W and B, it is, nevertheless, the case that by making the index ε = 1.6, and assigning a suitable value to η, a formula may be obtained giving an approximation to the truth which is sufficiently close for the ordinary purposes of electrical engineers, especially when the limiting value of B is neither very great nor very small. Alexander Siemens (Journ. Inst. Eng., 1894, 23, 229) states that in the hundreds of comparisons of test pieces which have been made at the works of his firm, Steinmetz’s law has been found to be practically correct.[25] An interesting collection of W-B curves embodying the results of actual experiments by Ewing and Klaassen on different specimens of metal is given in fig. 16. It has been shown by Kennelly (Electrician, 1892, 28, 666) that Steinmetz’s formula gives approximately correct results in the case of nickel. Working with two different specimens, he found that the hysteresis loss in ergs per cubic centimetre (W) was fairly represented by 0.00125B1.6 and 0.00101B1.6 respectively, the maximum induction ranging from about 300 to 3000. The applicability of the law to cobalt has been investigated by Fleming (Phil. Mag., 1899, 48, 271), who used a ring of cast cobalt containing about 96% of the pure metal. The logarithmic curves which accompany his paper demonstrate that within wide ranges of maximum induction W = 0.01B1.6 = 0.527I1.62 very nearly. Fleming rightly regards it as not a little curious that for materials differing so much as this cast cobalt and soft annealed iron the hysteretic exponent should in both cases be so near to 1.6. After pointing out that, since the magnetization of the metal is the quantity really concerned, W is more appropriately expressed in terms of I, the magnetic moment per unit of volume, than of B, he suggests an experiment to determine whether the mechanical work required to effect the complete magnetic reversal of a crowd of small compass needles (representative of magnetic molecules) is proportional to the 1.6th power of the aggregate maximum magnetic moment before or after completion of the cycle.
 |
| Fig. 16. |
| a, Fine steel wire 0.257 mm. diam. |
The experiments of K. Honda and S. Shimizu[26] indicate that Steinmetz’s formula holds for nickel and annealed cobalt up to B = 3000, for cast cobalt and tungsten steel up to B = 8000, and for Swedish iron up to B = 18,000, the range being in all cases extended at the temperature of liquid air.
 |
| Fig. 17. |
The diagram, fig. 17, contains examples of ascending induction curves characteristic of wrought iron, cast iron, cobalt and nickel. These are to be regarded merely as typical specimens, for the details of a curve depend largely upon the physical condition and purity of the material; but they show at a glance how far the several metals differ from and resemble one another as regards their magnetic properties. Curves of magnetization (which express the relation of I to H) have a close resemblance to those of induction; and, indeed, since B = H + 4πI, and 4πI (except in extreme fields) greatly exceeds H in numerical value, we may generally, without serious error, put I = B/4π, and transform curves of induction into curves of magnetization by merely altering the scale to which the ordinates are referred. A scale for the approximate transformation for the curves in fig. 12 is given at the right-hand side of the diagram, the greatest error introduced by neglecting H/4π not exceeding 0.6%. A study of such curves as these reveals the fact that there are three distinct stages in the process of magnetization. During the first stage, when the magnetizing force is small, the magnetization (or the induction) increases rather slowly with increasing force; this is well shown by the nickel curve in the diagram, but the effect would be no less conspicuous in the iron curve if the abscissae were plotted to a larger scale. During the second stage small increments of magnetizing force are attended by relatively large increments of magnetization, as is indicated by the steep ascent of the curve. Then the curve bends over, forming what is often called a “knee,” and a third stage is entered upon, during which a considerable increase of magnetizing force has little further effect upon the magnetization. When in this condition the metal is popularly said to be “saturated.” Under increasing magnetizing forces, greatly exceeding those comprised within the limits of the diagram, the magnetization does practically reach a limit, the maximum value being attained with a magnetizing force of less than 2000 for wrought iron and nickel, and less than 4000 for cast iron and cobalt. The induction, however, continues to increase indefinitely, though very slowly. These observations have an important bearing upon the molecular theory of magnetism, which will be referred to later.
The magnetic quality of a sample of iron depends very largely upon the purity and physical condition of the metal. The presence of ordinary impurities usually tends to diminish the permeability, though, as will appear later, the addition of small quantities of certain other substances is sometimes advantageous. A very pure form of iron, which from the method of its manufacture is called “steel,” is now extensively used for the construction of dynamo magnets; this metal sometimes contains not more than 0.3% of foreign substances, including carbon, and is magnetically superior to the best commercial wrought iron. The results of some comparative tests published by Ewing (Proc. Inst. C.E., 1896) are given in the accompanying table. Those in the second column are quoted from a paper by F. Lydall and A. W. Pocklington (Proc. Roy. Soc., 1892, 52, 228) and relate to an exceptional specimen containing nearly 99.9% of the pure metal.
| Magnetic Force. |
Magnetic Induction. | |||
|---|---|---|---|---|
| Pure Iron. |
Low Moor Iron. |
Steel Forging. |
Steel Casting. | |
| 5 | 12,700 | 10,900 | 12,300 | 9,600 |
| 10 | 14,980 | 13,120 | 14,920 | 13,050 |
| 15 | 15,800 | 14,010 | 15,800 | 14,600 |
| 20 | 16,300 | 14,580 | 16,280 | 15,310 |
| 30 | 16,950 | 15,280 | 16,810 | 16,000 |
| 40 | 17,350 | 15,760 | 17,190 | 16,510 |
| 50 | .. | 16,060 | 17,500 | 16,900 |
| 60 | .. | 16,340 | 17,750 | 17,180 |
| 70 | .. | 16,580 | 17,970 | 17,400 |
| 80 | .. | 16,800 | 18,180 | 17,620 |
| 90 | .. | 17,000 | 18,390 | 17,830 |
| 100 | .. | 17,200 | 18,600 | 18,030 |
To secure the highest possible permeability it is essential that the iron should be softened by careful annealing. When it is mechanically hardened by hammering, rolling or wire-drawing its permeability may be greatly diminished, especially under a moderate magnetizing force. An experiment by Ewing showed that by the operation of stretching an annealed iron wire beyond the limits of elasticity the permeability under a magnetizing force of about 3 units was reduced by as much as 75%. Ewing has also studied the effect of vibration in conferring upon iron an apparent or spurious permeability of high value; this effort also is most conspicuous when the magnetizing force is weak. The permeability of a soft iron wire, which was tapped while subjected to a very small magnetizing force, rose to the enormous value of about 80,000 (Magnetic Induction, § 85). It follows that in testing iron for magnetic quality the greatest care must be exercised to guard the specimen against any accidental vibration.
Low hysteresis is the chief requisite for iron which is to be used for transformer cores, and it does not necessarily accompany high permeability. In response to the demand, manufacturers have succeeded in producing transformer plate in which the loss of energy due to hysteresis is exceedingly small. Tests of a sample supplied by Messrs. Sankey were found by Ewing to give the following results, which, however, are regarded as being unusually favourable. In a valuable collection of magnetic data (Proc. Inst. C.E., cxxvi.) H. F. Parshall quotes tests of six samples of iron, described as of good quality, which showed an average hysteresis loss of 3070 ergs per c.cm. per cycle at an induction of 8000, being 1.6 times the loss shown by Ewing’s specimen at the same induction.
| Limits of Induction. |
Ergs per c.cm. per cycle. |
Watts per ℔. Frequency, 100. |
|---|---|---|
| 2000 | 220 | 0.129 |
| 3000 | 410 | 0.242 |
| 4000 | 640 | 0.376 |
| 5000 | 910 | 0.535 |
| 6000 | 1200 | 0.710 |
| 7000 | 1520 | 0.890 |
| 8000 | 1900 | 1.120 |
| 9000 | 2310 | 1.360 |
The standard induction in reference to determinations of hysteresis is generally taken as 2500, while the loss is expressed in watts per ℔ at a frequency of 100 double reversals, or cycles, per second. In many experiments, however, different inductions and frequencies are employed, and the hysteresis-loss is often expressed as ergs per cubic centimetre per cycle and sometimes as horse-power per ton. In order to save arithmetical labour it is convenient to be provided with conversion factors for reducing variously expressed results to the standard form. The rate at which energy is lost being proportional to the frequency, it is obvious that the loss at frequency 100 may be deduced from that at any other frequency n by simply multiplying by 100/n. Taking the density of iron to be 7.7, the factor for reducing the loss in ergs per c.cm. to watts per ℔ with a frequency of 100 is 0.000589 (Ewing). Since 1 horse-power = 746 watts, and 1 ton = 2240 ℔, the factor for reducing horse-power per ton to watts per ℔ is 746/2240, or just 1/3. The loss for any induction B within the range for which Steinmetz’s law holds may be converted into that for the standard induction 2500 by dividing it by B1.6/25001.6. The values of this ratio for different values of B, as given by Fleming (Phil. Mag., 1897), are contained in the second column of the annexed table. The third column shows the relative amount of hysteresis deduced by Ewing as a general mean from actual tests of many samples (Journ. Inst. Elec. Eng., 1895). Incidentally, these two columns furnish an undesigned test of the accuracy of Steinmetz’s law: the greatest difference is little more than 1%.
| Induction B. |
B1.625001.6 | Observed relative Hysteresis. |
|---|---|---|
| 2000 | 0.700 | 0.702 |
| 2500 | 1.000 | 1.000 |
| 3000 | 1.338 | 1.340 |
| 4000 | 2.118 | 2.128 |
| 5000 | 3.031 | 3.000 |
| 6000 | 4.058 | 4.022 |
| 7000 | 5.193 | 5.129 |
| 8000 | 6.430 | 6.384 |
Curves of Permeability and Susceptibility.—The relations of μ (= B/H) to B, and of κ (= I/H) to I may be instructively exhibited by means of curves, a method first employed by H. A. Rowland.[27] The dotted curve for μ and B in fig. 18 is copied from Rowland’s paper. The actual experiment to which it relates was carried only as the point marked X, corresponding to a magnetizing force of 65, and an induction of nearly 17,000. Rowland, believing that the curve would continue to fall in a straight line meeting the horizontal axis, inferred that the induction corresponding to the point B—about 17,500—was the highest that could be produced by any magnetizing force, however great. It has, however, been shown that, if the magnetizing force is carried far enough, the curve always becomes convex to the axis instead of meeting it. The full line shows the result of an experiment in which the magnetizing force was carried up to 585,[28] but though the force was thus increased ninefold, the induction only reached 19,800, and the ultimate value of the permeability was still as much as 33.9.
 |
| Fig. 18. |
Ballistic Method with Yoke.—J. Hopkinson (Phil. Trans.,
1885, 176, 455) introduced a modification of the usual ballistic
arrangement which presents the following advantages; (1)
very considerable magnetizing forces can be applied with ordinary
means; (2) the samples to be tested, having the form of
cylindrical bars, are more easily prepared than rings or wires;
(3) the actual induction at any time can be measured, and not
only changes of induction.
Fig. 19.
On the
other hand, a very
high degree of accuracy
is not claimed
for the results. Fig.
19 shows the apparatus
by which the
ends of the bar are
prevented from
exerting any material demagnetizing force, while the permeance
of the magnetic circuit is at the same time increased. A A,
called the “yoke,” is a block of annealed wrought iron
about 18 in. long, 612 in. wide and 2 in. thick, through
which is cut a rectangular opening to receive the two
magnetizing coils B B. The test bar C C, which slides
through holes bored in the yoke, is divided near the
middle into two parts, the ends which come into contact
being faced true and square. Between the magnetizing coils
is a small induction coil D, which is connected with a ballistic
galvanometer. The induction coil is carried upon the end of
one portion of the test bar, and when this portion is suddenly
drawn back the coil slips off and is pulled out of the field by
an india-rubber spring. This causes a ballistic throw proportional
to the induction through the bar at the moment when the
two portions were separated. With such an arrangement it is
possible to submit the sample to any series of magnetic forces,
and to measure its magnetic state at the end. The uncertainty
with which the results are affected depends chiefly upon the imperfect
contact between the bar and the yoke and also between
the ends of the divided bar. It is probable that Hopkinson did
not attach sufficient importance to the demagnetizing action of
the cut (cf. Ewing, Phil. Mag., Sept. 1888, p. 274), and that the
values which he assigned to H are consequently somewhat too
high. He applied his method with good effect, however, in
testing a large number of commercial specimens of iron and steel,
the magnetic constants of which are given in a table accompanying
his paper. When it is not required to determine the residual
magnetization there is no necessity to divide the sample bar,
and ballistic tests may be made in the ordinary way—by steps
or by reversals—the source of error due to the transverse cut
thus being avoided. Ewing (Magnetic Induction, § 194) has devised
an arrangement in which two similar test bars are placed
side by side; each bar is surrounded by a magnetizing coil, the
two coils being connected to give opposite directions of magnetization,
and each pair of ends is connected by a short massive
block of soft iron having holes bored through it to fit the bars,
which are clamped in position by set-screws. Induction coils
are wound on the middle parts of both bars, and are connected
in series. With this arrangement it is possible to find the actual
value of the magnetizing force, corrected for the effects of joints
and other sources of error. Two sets of observations are taken,
one when the blocks are fixed at the ends of the bars, and another
when they are nearer together, the clear length of the bars
between them and of the magnetizing coils being reduced to
one-half. If H1 and H2 be the values of 4πin/l and 4πi′n2 / l2 for the
same induction B, it can be shown that the true magnetizing
force is H = H1 − (H2 − H1). The method, though tedious
in operation, is very accurate, and is largely employed for
determining the magnetic quality of bars intended to serve as
standards.
Traction Methods.—The induction of the magnetization may be measured by observing the force required to draw apart the two portions of a divided rod or ring when held together by their mutual attraction. If a transverse cut is made through a bar whose magnetization is I and the two ends are placed in contact, it can be shown that this force is 2πI2 dynes per unit of area (Mascart and Joubert, Electricity and Magnetism, § 322); and if the magnetization of the bar is due to an external field H produced by a magnetizing coil or otherwise, there is an additional force equal to HI. Thus the whole force, when the two portions of the bar are surrounded by a loosely-fitting magnetizing coil, is
expressed as dynes per square centimetre. If each portion of the bar has an independent magnetizing coil wound tightly upon it, we have further to take into account the force due to the mutual action of the two magnetizing coils, which assists the forces already considered. This is equal to H28π per unit of sectional area. In the case supposed therefore the total force per square centimetre is
| F | = 2πI2 + HI + H28π |
| = (4πI + H)38π | |
| = B28π |
The equation F = B2/8π is often said to express “Maxwell’s law of magnetic traction” (Maxwell, Electricity and Magnetism, §§ 642–646). It is, of course, true for permanent magnets, where H = 0, since then F = 2πI2; but if the magnetization is due to electric currents, the formula is only applicable in the special case when the mutual action of the two magnets upon one another is supplemented by the electromagnetic attraction between separate magnetizing coils rigidly attached to them.[29]
The traction method was first employed by S. Bidwell (Proc. Roy. Soc., 1886, 40, 486), who in 1886 published an account of some experiments in which the relation of magnetization to magnetic field was deduced from observations of the force in grammes weight which just sufficed to tear asunder the two halves of a divided ring electromagnet when known currents were passing through the coils. He made use of the expression
where W is the weight in grammes per square centimetre of sectional area, and g is the intensity of gravity which was taken as 981. The term for the attraction between the coils was omitted as negligibly small (see Phil. Mag., 1890, 29, 440). The values assigned to H were calculated from H = 2ni/r, and ranged from 3.9 to 585, but inasmuch as no account was taken of any demagnetizing action which might be due to the two transverse cuts, it is probable that they are somewhat too high. The results, nevertheless, agree very well with those for annealed wrought iron obtained by other methods. Below is given a selection from Bidwell’s tables, showing corresponding values of magnetizing force, weight supported, magnetization, induction, susceptibility and permeability:—
| H. | W. | I. | B. | κ. | μ. |
|---|---|---|---|---|---|
| 3.9 | 2,210 | 587 | 7,390 | 151.0 | 1889.1 |
| 5.7 | 3,460 | 735 | 9,240 | 128.9 | 1621.3 |
| 10.3 | 5,400 | 918 | 11,550 | 89.1 | 1121.4 |
| 22.2 | 8,440 | 1147 | 14,450 | 51.7 | 650.9 |
| 40 | 9,680 | 1226 | 15,460 | 30.7 | 386.4 |
| 115 | 12,170 | 1370 | 17,330 | 11.9 | 150.7 |
| 208 | 13,810 | 1452 | 18,470 | 7.0 | 88.8 |
| 362 | 14,740 | 1489 | 19,080 | 4.1 | 52.7 |
| 465 | 15,275 | 1508 | 19,420 | 3.2 | 41.8 |
| 585 | 15,905 | 1530 | 19,820 | 2.6 | 33.9 |
A few months later R. H. M. Bosanquet (Phil. Mag., 1886,
22, 535) experimented on the relation of tractive force to
magnetic induction. Instead of a divided ring he
employed a divided straight bar, each half of which
was provided with a magnetizing coil. The joint
Fig. 20.
was surrounded by an induction coil connected
with a ballistic galvanometer, an arrangement
which enabled him to make an independent
measurement of the induction at the moment
when the two portions of the bar were separated.
He showed that there was, on the whole, a fair
agreement between the values determined ballistically
and those given by the formula B = √8πF.
The greatest weight supported in the experiments
was 14,600 grammes per square cm., and the corresponding
induction 18,500 units. Taylor Jones
subsequently found a good agreement between the
theoretical and the observed values of the tractive
force in fields ranging up to very high intensities
(Phil. Mag., 1895, 39, 254, and 1896, 41, 153).
Permeameters.—Several instruments in which the traction method is applied have been devised for the rapid measurement of induction or of magnetization in commercial samples of iron and steel. The earliest of these is S. P. Thompson’s permeameter (Journ. Sci. Arts, 1890, 38, 885), which consists of a rectangular block of iron shaped like Hopkinson’s yoke, and slotted out in the same way to receive a magnetizing coil (fig. 20); the block is bored through at the upper end only, and its inner face opposite the hole is made quite flat and smooth. The sample has the form of a thin rod, one end of which is faced true; it is slipped into the magnetizing coil from above, and when the current is turned on its smooth end adheres tightly to the surface of the yoke. The force required to detach it is measured by a registering spring balance, which is clamped to the upper end of the rod, and thence the induction or the magnetization is deduced by applying the formula
where P is the pull in grammes weight, S the sectional area of
the rod in square cm., and g = 981. If the pull is measured in
pounds and the area in square inches, the formula may be written
B = 1317 × √P/S + H. The instrument exhibited by Thompson
would, without undue heating, take a current of 30 amperes, which
was sufficient to produce a magnetizing force of 1000 units. A
testing apparatus of a similar type devised by Gisbert Kapp (Journ.
Inst. Elec. Eng. xxiii. 199) differs only in a few details from
Thompson’s permeameter. Ewing has described an arrangement
in which the test bar has a soft-iron pole piece clamped to each
of its ends; the pole pieces are joined by a long well-fitting block
of iron, which is placed upon them (like the “keeper” of a
magnet), and the induction is measured by the force required to
detach the block. In all such measurements a correction should
be made in respect of the demagnetizing force due to the joint,
and unless the fit is very accurate the demagnetizing action will
be variable. In the magnetic balance of du Bois (Magnetic Circuit,
p. 346) the uncertainty arising from the presence of a joint is
avoided, the force measured being that exerted between two pieces of
iron separated from each other by a narrow air-gap of known width.
The instrument is represented diagrammatically in fig. 21. The
test-piece A, surrounded by a magnetizing coil, is clamped between
two soft-iron blocks B, B′. Y Y′ is a soft iron yoke, which rocks
upon knife-edges K and constitutes the beam of the balance. The
yoke has two projecting pieces C, C′ at unequal distances from the
knife-edges, and separated from the blocks B, B′ by narrow air-gaps.
The play of the beam is limited by a stop S and a screw R, the latter
being so adjusted that when the end Y of the beam is held down the
two air-gaps are of equal
width. W is a weight
capable of sliding from end
Fig. 21.
to end of the yoke along
a graduated scale. When
there is no magnetization,
the yoke is in equilibrium;
but as soon as the current
is turned on the block C is
drawn downwards as far as
the screw R will allow, for,
though the attractive forces F between B and C and between
B′ and C′ are equal, the former has a greater moment. The
weight W is moved along the scale until the yoke just tilts over
upon the stop S; the distance of W from its zero position is then, as
can easily be shown, proportional to F, and therefore to B2, and
approximately to I2. The scale is graduated in such a manner that
by multiplying the reading by a simple factor (generally 10 or 2) the
absolute value of the magnetization is obtained. The actual
magnetizing force H is of course less than that due to the coil; the
corrections required are effected automatically by the use of a set of
demagnetization lines drawn on a sheet of celluloid which is supplied
with the instrument. The celluloid sheet is laid upon the squared
paper, and in plotting a curve horizontal distances are reckoned
from the proper demagnetization line instead of from the vertical
axis. An improved but somewhat more complex form of the instrument
is described in Ann. d. Phys., 1900, 2, 317.
In Ewing’s magnetic balance (Journ. Inst. Elec. Eng. 1898, 27, 526), the value of the magnetic induction corresponding to a single stated magnetizing force is directly read off on a divided scale. The specimen, which has the form of a turned rod, 4 in. long and 14 in. in diameter, is laid across the poles of a horseshoe electromagnet, excited by a current of such strength as to produce in the rod a magnetizing force H = 20. One pole has a V-shaped notch for the rod to rest in; the surface of the other is slightly rounded, forming a portion of a cylinder, the axis of which is perpendicular to the direction of the length of the rod. The rod touches this pole at a single point, and is pulled away from it by the action of a lever, the long arm of which is graduated and carries a sliding weight. The position of the weight at the moment when contact is broken indicates the induction in the rod. The standard force H = 20 was selected as being sufficiently low to distinguish between good and bad specimens, and at the same time sufficiently high to make the order of merit the same as it would be under stronger forces.
Permeability Bridges.—Several pieces of apparatus have been invented for comparing the magnetic quality of a sample with that of a standard iron rod by a zero method, such as is employed in the comparison of electrical resistances by the Wheatstone bridge. An excellent instrument of the class is Ewing’s permeability bridge. The standard rod and the test specimen, which must be of the same dimensions, are placed side by side within two magnetizing coils, and each pair of adjacent ends is joined by a short rectangular block or “yoke” of soft iron. An iron bar shaped like an inverted L projects upwards from each of the yokes, the horizontal portions of the bars being parallel to the rods, and nearly meeting at a height of about 8 in. above them (thus Г ⅂). A compass needle placed in the gap serves to detect any flow of induction that may exist between the bent bars. For simplicity of calculation, the clear length of each rod between the yokes is made 12.56 (= 4π) centimetres, while the coil surrounding the standard bar contains 100 turns; hence the magnetizing force due to a current of n amperes will be 10n C.G.S. units. The effective number of turns in the coil surrounding the test rod can be varied by means of three dial switches (for hundreds, tens and units), which also introduce compensating resistances as the number of effective turns in the coil is reduced, thus keeping the total resistance of the circuit constant. The two coils are connected in series, the same current passing through both. Suppose the switches to be adjusted so that the effective number of turns in the variable coil is 100; the magnetizing forces in the two coils will then be equal, and if the test rod is of the same quality as the standard, the flow of induction will be confined entirely to the iron circuit, the two yokes will be at the same magnetic potential, and the compass needle will not be affected. If, however, the permeability of the test rod differs from that of the standard, the number of lines of induction flowing in opposite directions through the two rods will differ, and the excess will flow from one yoke to the other, partly through the air, and partly along the path provided by the bent bars, deflecting the compass needle. But a balance may still be obtained by altering the effective number of turns in the test coil, and thus increasing or decreasing the magnetizing force acting on the test rod, till the induction in the two rods is the same, a condition which is fulfilled when reversal of the current has no effect on the compass needle. Let m be the number of turns in use, and H1 and H2 the magnetizing forces which produce the same induction B in the test and the standard rods respectively; then H1 = H2 × m/100. The value of B which corresponds to H2m/100 can be found from the (B, H) curve for the standard, which is assumed to have been determined; and this same value corresponds to the force H in the case of the test bar. Thus any desired number of corresponding values of H and B can be easily and quickly found.
Measurement of Field Strength. Exploring Coil.—Since in air B = H, the ballistic method of measuring induction described above is also available for determining the strength of a magnetic field, and is more often employed than any other. A small coil of fine wire, connected in series with a ballistic galvanometer, is placed in the field, with its windings perpendicular to the lines of force, and then suddenly reversed or withdrawn from the field, the integral electromotive force being twice as great in the first case as in the second. The strength of the field is proportional to the swing of the galvanometer-needle, and, when the galvanometer is calibrated, can be expressed in C.G.S. units. Convenient arrangements have been introduced whereby the coil is reversed or withdrawn from the field by the action of a spring.
Bismuth Resistance.—The fact, which will be referred to later, that the electrical resistance of bismuth is very greatly affected by a magnetic field has been applied in the construction of apparatus for measuring field intensity. A little instrument, supplied by Hartmann and Braun, contains a short length of fine bismuth wire wound into a flat double spiral, half an inch or thereabouts in diameter, and attached to a long ebonite handle. Unfortunately the effects of magnetization upon the specific resistance of bismuth vary enormously with changes of temperature; it is therefore necessary to take two readings of the resistance, one when the spiral is in the magnetic field, the other when it is outside.
Electric Circuit.—If a coil of insulated wire is suspended so that it is in stable equilibrium when its plane is parallel to the direction of a magnetic field, the transmission of a known electric current through the coil will cause it to be deflected through an angle which is a function of the field intensity.
One of the neatest applications of this principle is that described by Edser and Stansfield (Phil. Mag., 1893, 34, 186), and used by them to test the stray fields of dynamos. An oblong coil about an inch in length is suspended from each end by thin strips of rolled German silver wire, one of which is connected with a spiral spring for regulating the tension, the other being attached to a torsion-head. Inside the torsion-head is a commutator for automatically reversing the current, so that readings may be taken on each side of zero, and the arrangement is such that when the torsion-head is exactly at zero the current is interrupted. To take a reading the torsion-head is turned until an aluminium pointer attached to the coil is brought to the zero position on a small scale; the strength of the field is then proportional to the angular torsion. The small current required is supplied to the coil from a single dry cell. The advantages of portability, very considerable range (from H = 1 upwards), and fair accuracy are claimed for the instrument.
Polarized Light.—The intensity of a field may be measured by the rotation of the plane of polarization of light passing in the direction of the magnetic force through a transparent substance. If the field is uniform, H = θ/ωd, where θ is the rotation, d the thickness of the substance arranged as a plate at right angles to the direction of the field, and ω Verdet’s constant for the substance.
For the practical measurement of field intensity du Bois has used plates of the densest Jena flint glass. These are preferably made slightly wedge-shape, to avoid the inconvenience resulting from multiple internal reflections, and they must necessarily be rather thin, so that double refractions due to internal strain may not exert a disturbing influence. Since Verdet’s constant is somewhat uncertain for different batches of glass even of the same quality, each plate should be standardized in a field of known intensity. As the source of monochromatic light a bright sodium burner is used, and the rotation, which is exactly proportional to H, is measured by an accurate polarimeter. Such a plate about 1 mm. in thickness is said to be adapted for measuring fields of the order of 1000 units. A part of one surface of the plate may be silvered, so that the polarized ray, after having once traversed the glass, is reflected back again; the rotation is thus doubled, and moreover, the arrangement is, for certain experiments, more convenient than the other.
4. Magnetization in Strong Fields
 |
| Fig. 22. |
Fields due to Coils.—The most generally convenient arrangement for producing such magnetic fields as are required for experimental purposes is undoubtedly a coil of wire through which an electric current can be caused to flow. The field due to a coil can be made as nearly uniform as we please throughout a considerable space; its intensity, when the constants of the coil are known, can be calculated with ease and certainty and may be varied at will through wide ranges, while the apparatus required is of the simplest character and can be readily constructed to suit special purposes. But when exceptionally strong fields are desired, the use of a coil is limited by the heating effect of the magnetizing current, the quantity of heat generated per unit of time in a coil of given dimensions increasing as the square of the magnetic field produced in its interior. In experiments on magnetic strains carried out by H. Nagaoka and K. Honda (Phil. Mag., 1900, 49, 329) the intensity of the highest field reached in the interior of a coil was 2200 units; this is probably the strongest field produced by a coil which has hitherto been employed in experimental work. In 1890 some experiments in which a coil was used were made by du Bois (Phil. Mag., 1890, 29, 253, 293) on the magnetization of iron, nickel, and cobalt under forces ranging from about 100 to 1250 units. Since the demagnetizing factor was 0.052, the strongest field due to the coil was about 1340; but though arrangements were provided for cooling the apparatus by means of ice, great difficulty was experienced owing to heating. Du Bois’s results, which, as given in his papers, show the relation of H to the magnetic moment per unit of mass, have been reduced by Ewing to the usual form, and are indicated in fig. 22, the earlier portions of the curves being sketched in from other data.
Fields due to Electromagnets.—The problem of determining the magnetization of iron and other metals in the strong fields formed between the poles of an electromagnet was first attacked by J. A. Ewing and W. Low. An account of their preliminary experiments by what they call the isthmus method was published in 1887 (Proc. Roy. Soc. 42, 200), and in the following year they described a more complete and perfect series (Phil. Trans., 1889, 180, 221).
 |
| Fig. 23. |
The sample to be inserted between the magnet poles was prepared in the form of a bobbin resembling an ordinary cotton reel, with a short narrow neck (constituting the “isthmus”) and conical ends. Upon the central neck was wound a coil consisting of one or two layers of very fine wire, which was connected with a ballistic galvanometer for measuring the induction in the iron; outside this coil, and separated from it by a small and accurately determined distance, a second coil was wound, serving to measure the induction in the iron, together with that in a small space surrounding it. The difference of the ballastic throws taken with the two coils measured the intensity of the field in the space around the iron, and it also enabled a correction to be made for the non-ferrous space between the iron neck and the centre of the thickness of the inner coil. The pole pieces of the electromagnet (see fig. 23) were furnished with a pair of truncated cones b b, of soft iron forming an extension of the conical ends of the bobbin c. The most suitable form for the pole faces is investigated in the paper, and the conclusion arrived at is that to produce the greatest concentration of force upon the central neck, the cones should have a common vertex in the middle of the neck with a semi-vertical angle of 54° 44′, while the condition for a uniform field is satisfied when the cones have a semi-vertical angle of 39° 14′; in the latter case the magnetic force in the air just outside is sensibly equal to that within the neck. A pair of cones having a semi-vertical angle of 45° were considered to combine high concentrative power with a sufficient approximation to uniformity of field. In most of the experiments the measurements were made by suddenly withdrawing the bobbin from its place between the pole pieces. Two groups of observations were recorded, one giving the induction in the inner coil and the other that in the outer coil. The value of the residual induction which persisted when the bobbin was drawn out was added to that of the induction measured, and thus the total induction in the iron was determined. The highest induction reached in these experiments was 45,350 units, more than twice the value of any previously recorded. The corresponding intensity of the outside field was 24,500, but, owing to the wide angle of the cones used (about 2 × 63°), this was probably greater than the value of the magnetic force within the metal. The following table shows some results of other experiments in which H was believed to have sensibly the same value inside as outside the metal. Values of I are derived from (B − H)/4π and of μ from B/H.
| Metal. | H | B | I | μ |
| Swedish Iron | 1,490 | 22,650 | 1680 | 15.20 |
| 6,070 | 27,130 | 1680 | 4.47 | |
| 8,600 | 30,270 | 1720 | 3.52 | |
| 19,450 | 40,820 | 1700 | 2.10 | |
| 19,880 | 41,140 | 1700 | 2.07 | |
| Cast Iron | 4,560 | 20,070 | 1230 | 4.40 |
| 13,460 | 28,710 | 1210 | 2.13 | |
| 16,200 | 30,920 | 1170 | 1.91 | |
| 16,900 | 31,760 | 1180 | 1.88 | |
| Tool Steel | 6,210 | 25,480 | 1530 | 4.10 |
| 9,970 | 29,650 | 1570 | 2.97 | |
| 12,170 | 31,620 | 1550 | 2.60 | |
| 14,660 | 34,550 | 1580 | 2.36 | |
| 15,530 | 35,820 | 1610 | 2.31 | |
| Hard Nickel | 2,220 | 7,100 | 390 | 3.20 |
| 4,440 | 9,210 | 380 | 2.09 | |
| 7,940 | 12,970 | 400 | 1.63 | |
| 14,660 | 19,640 | 400 | 1.34 | |
| 16,000 | 21,070 | 400 | 1.32 | |
| Cobalt | 1,350 | 16,000 | 1260 | 12.73 |
| 4,040 | 18,870 | 1280 | 4.98 | |
| 8,930 | 23,890 | 1290 | 2.82 | |
| 14,990 | 30,210 | 1310 | 2.10 |
These results are of extreme interest, for they show that under sufficiently strong magnetizing forces the intensity of magnetization I reaches a maximum value, as required by W. E. Weber’s theory of molecular magnetism. There appears to be no definite limit to the value to which the induction B may be raised, but the magnetization I attains a true saturation value under magnetizing forces which are in most cases comparatively moderate. Thus the magnetization which the sample of Swedish iron received in a field of 1490 was not increased (beyond the limits of experimental error) when the intensity of the field was multiplied more than thirteen-fold, though the induction was nearly doubled. When the saturation value of I has been reached, the relation of magnetic induction to magnetic force may be expressed by
The annexed table gives the saturation values of I for the particular metals examined by Ewing and Low:—
| Saturation Value of I | |
| Wrought iron | 1,700 |
| Cast iron | 1,240 |
| Nickel (0.75% iron) | 515 |
| Nickel (0.56% iron) | 400 |
| Cobalt (1.66% iron) | 1,300 |
It is shown in the paper that the greatest possible force which the isthmus method can apply at a point in the axis of the bobbin is
Is being the saturation value of the magnet poles, a the radius of the neck on which the cones converge, and b the radius of the bases of the cones.
Some experiments made by H. du Bois (Phil. Mag., 1890, 29, 293) with an electromagnet specially designed for the production of strong fields, confirm Ewing’s results for iron, nickel and cobalt. The method employed did not admit of the production of such high magnetizing forces, but was of special interest in that both B and I were measured optically—B by means of the rotation of a polarized ray inside a glass plate, as before described, and I by the rotation of a polarized ray reflected from the polished surface of the magnetized metal (see “Kerr’s constant,” Magneto-Optics). H(= B − 4πI) was calculated from corresponding values of I and B. Taylor Jones (Wied. Ann., 1896, 57, 258, and Phil. Mag., 1896, 41, 153), working with du Bois’s electromagnet and using a modification of the isthmus method, succeeded in pushing the induction B up to 74,200 with H = 51,600, the corresponding value of I being 1798, and of μ only 1.44. The diameter of the isthmus was 0.241 mm., and the electromagnet was excited by a current of 40 amperes.
Tractive Force of a Magnet.—Closely connected with the results just discussed is the question what is the greatest tractive force that can be exerted by a magnet. In the year 1852 J. P. Joule (Phil. Mag., 1852, 3, 32) expressed the opinion that no “force of current could give an attraction equal to 200 ℔ per sq. in.,” or 14,000 grms. per square centimetre, and a similar view prevailed among high authorities more than twenty years later. For the greatest possible “lifting power” of permanent magnets this estimate is probably not very far from the truth, but it is now clearly understood that the force which can be exerted by an electromagnet, or by a pair of electromagnets with opposite poles in contact, is only limited by the greatest value to which it is practically possible to raise the magnetizing force H. This is at once evident when the tractive force due to magnetization is expressed as 2πI2 + HI. For fields of moderate intensity the first term of the expression is the more important, but when the value of H exceeds 12,000 or thereabouts, the second preponderates, and with the highest values that have been actually obtained, HI is several times greater than 2πI2. If H could be increased without limit, so also could the tractive force. The following table shows the greatest “lifting powers” experimentally reached at the dates mentioned:—
| Observer. | Kilos per sq. cm. | ℔ per sq. in. | Date. |
| Joule | 12.3 | 175 | 1852 |
| Bidwell | 15.9 | 226 | 1886 |
| Wilde | 26.8 | 381 | 1891 |
| T. Jones | 114.9 | 1634 | 1896 |
5. Magnetization in Very Weak Fields
Some interesting observations have been made of the effects produced by very small magnetic forces. It was first pointed out by C. Baur (Wied. Ann., 1880, 11, 399) that in weak fields the relation of the magnetization I to the magnetizing force H is approximately expressed by an equation of the form
whence it appears that within the limits of Baur’s experiments the magnetization curve is a parabola, and the susceptibility curve an inclined straight line, κ being therefore a known function of H. If these equations could be assumed to hold when H is indefinitely small, it would follow that κ has a finite initial value, from which there would be no appreciable deviation in fields so weak that bH was negligibly small in comparison with a. Such an assumption could not, however, without dangerous extrapolation, be founded upon the results of Baur’s experiments, which did not go far enough to justify it. In some experiments carried out in 1887, Lord Rayleigh (Phil. Mag., 1887, 23, 225) approached very much more nearly than Baur to the zero of magnetic force. Using an unannealed Swedish iron wire, he found that when H was gradually diminished from 0.04 to 0.00004 C.G.S. unit, the ratio of magnetization to magnetizing force remained sensibly constant at 6.4, which may therefore with great probability be assumed to represent the initial value of κ for the specimen in question. Experiments with annealed iron gave less satisfactory results, on account of the slowness with which the metal settled down into a new magnetic state, thus causing a “drift” of the magnetometer needle, which sometimes persisted for several seconds. Apart from this complication, it appeared that I was proportional to H when the value of H was less than 0.02.
The observations of Baur and Rayleigh have been confirmed and discussed by (amongst others) W. Schmidt (Wied. Ann., 1895, 54, 655), who found the limiting values of κ to be 7.5 to 9.5 for iron, and 11.2 to 13.5 for steel, remaining constant up to H = .06; by P. Culmann (Elekt. Zeit., 1893, 14, 345; Wied. Ann., 1895, 56, 602); and by L. Holborn (Berl. Ber., 1897, p. 95, and Wied. Ann., 1897, 61, 281). The latter gives values of the constants a and b for different samples of iron and steel, some of which are shown in the following table:—
| κ = a + bH | ||
| Metal. | a | b |
| English tungsten steel | 8.90 | 0.264 |
| Tungsten steel, hardened | 2.23 | 0.032 |
| Silver steel | 8.66 | 0.384 |
| Tool steel | 8.30 | 0.400 |
| Refined steel | 11.28 | 1.92 |
| Cast iron | 3.16 | 0.236 |
| Soft iron | 16.6 | 18.6 |
| Hard drawn iron | 5.88 | 1.76 |
For most samples of steel the straight-line law was found to hold approximately up to H = 3; in the case of iron and of soft steel the approximation was less close.
The behaviour of nickel in weak fields has been observed by Ewing (Phil. Trans., 1888, 179A, 325), who found that the initial value of κ was 1.7, and that it remained sensibly constant until H had reached a value of about five units. While therefore the initial susceptibility of nickel is less than that of iron and steel, the range of magnetic force within which it is approximately constant is about one hundred times greater. Ewing has also made a careful study (Proc. Roy. Soc., 1889, 46, 269) of “magnetic viscosity” under small forces—the cause of the magnetometer “drift” referred to by Rayleigh. On the application of a small magnetizing force to a bar of soft annealed iron, a certain intensity of magnetization is instantly produced; this, however, does not remain constant, but slowly increases for some seconds or even minutes, and may ultimately attain a value nearly twice as great as that observed immediately after the force was applied.[30] When the magnetizing current is broken, the magnetization at once undergoes considerable diminution, then gradually falls to zero, and a similar sudden change followed by a slow one is observed when a feeble current is reversed. Ewing draws attention to a curious consequence of this time-lag. By the alternate application and withdrawal of a small magnetizing force a cyclic condition may be established in an iron rod. If now the alternations are performed so rapidly that time is not allowed for more than the first sudden change in the magnetization, there will be no hysteresis loss, the magnetization exactly following the magnetizing force. Further, if the alternations take place so slowly that the full maximum and minimum values of the magnetization are reached in the intervals between the reversals, there will again be no dissipation of energy. But at any intermediate frequency the ascending and descending curves of magnetization will enclose a space, and energy will be dissipated. It is remarkable that the phenomena of magnetic viscosity are much more evident in a thick rod than in a thin wire, or even in a large bundle of thin wires. In hardened iron and steel the effect can scarcely be detected, and in weak fields these metals exhibit no magnetic hysteresis of any kind.
6. Changes of Dimensions Attending Magnetization
It is well known that the form of a piece of ferromagnetic
metal is in general slightly changed by magnetization. The
phenomenon was first noticed by J. P. Joule, who in 1842 and
1847 described some experiments which he had made upon
bars of iron and steel. His observations, were for the most
part confirmed by a number of subsequent workers, notably
by A. M. Mayer; but with the single exception of the discovery
by W. F. Barrett in 1882 that a nickel bar contracts when
magnetized, nothing of importance was added by Joule’s results
for nearly forty years. Later researches have however thrown
much new light upon a class of phenomena which cannot fail
to have an important bearing upon the complete theory of
molecular magnetism.[31] According to Joule’s observations,
the length of a bar of iron or soft steel was increased by magnetization,
the elongation being proportional up to a certain
point to the square of the intensity of magnetization; but
when the “saturation point” was approached the elongation
was less than this law would require, and a stage was finally
reached at which further increase of the magnetizing force
produced little or no effect upon the length. From data
contained in Joule’s paper it may be calculated that the strongest
external field H0 produced by his coil was about 126 C.G.S.
units, but since the dimensional ratio of his bars was comparatively
Fig. 24.
small, the actual magnetizing force H must have
been materially below that value. In 1885 it was shown
by Bidwell, in the first of a series of papers on the subject,
that if the magnetizing force is pushed beyond the point at
which Joule discontinued his experiments, the extension of
the bar does not remain unchanged, but becomes gradually
less and less, until the bar, after first returning to its original
length, ultimately becomes actually shorter than when in the
unmagnetized condition. The elongation is generally found
to reach a maximum under a magnetizing force of 50 to 120
units, and to vanish under a force of 200 to 400, retraction
occurring when still higher forces are applied. In order to
meet the objection that the phenomenon might be due to
electromagnetic action between the coil and the rod, Bidwell
made some experiments with iron rings, and found that the
length of their diameters varied under magnetization in precisely
the same manner as the length of a straight rod. Experiments
were afterwards made with rods of iron, nickel, and
cobalt, the external field
being carried up to the
high value of 1500 units.
The results are indicated
in Fig. 24. It appears
that the contraction
which followed the initial
extension of the iron
reached a limit in fields
of 1000 or 1100. Nickel
exhibited retraction
from the very beginning (as observed by Barrett), its greatest
change of length considerably exceeding that undergone by
iron; in a field of 800 the original length was diminished by
as much as 1/40,000 part, but stronger forces failed to
produce any further effect. The curve for cobalt is a very
remarkable one. Little or no change of length was observed
until the strength of the field H0 reached about 50; then
the rod began to contract, and after passing a minimum at
H0 = 400, recovered its original length at H0 = 750; beyond
this point there was extension, the amount of which was still
increasing fast when the experiment was stopped at H0 = 1400.
Similar results were obtained with three different samples
of the metal. Roughly speaking, therefore, cobalt behaves
oppositely to iron.
Joule and others experimented with hardened steel, but failed to find a key to the results they obtained, which are rather complex, and have been thought to be inconsistent. The truth appears to be that a hardened steel rod generally behaves like one of iron or soft steel in first undergoing extension under increasing magnetizing force, and recovering its original length when the force has reached a certain critical value, beyond which there is contraction. But this “critical value” of the force is found to depend in an unexpected manner upon the hardness of the steel; the critical value diminishes as the hardness becomes greater up to a certain point, corresponding to a yellow temper, after which it increases and with the hardest steel becomes very high. For steel which has been made red-hot, suddenly cooled, and then let down to a yellow temper, the critical value of the magnetizing force is smaller than for steel which is either softer or harder; it is indeed so small that the metal contracts like nickel even under weak magnetizing forces, without undergoing any preliminary extension that can be detected.
Joule also made experiments upon iron wires under tension,
and drew the erroneous inference (which has been often quoted
as if it were a demonstrated fact) that under a certain critical
tension (differing for different specimens of iron but independent
of the magnetizing
force) magnetization
Fig. 25.
would produce no
effect whatever upon
the dimensions of the
wire. What actually
happens when an iron
wire is loaded with
various weights is
clearly shown in Fig.
25. Increased tension
merely has the effect
of diminishing the maximum elongation and hastening the
contraction; with the two greatest loads used in the experiment
there was indeed no preliminary extension at all.[32] The effects
of tension upon the behaviour of a nickel wire are of a less
simple character. In weak fields the magnetic contraction is
always diminished by pulling stress; in strong fields the contraction
increases under a small load and diminishes under a
heavy one. Cobalt, curiously enough, was found to be quite
unaffected by tensile stress.
Certain experiments by C. G. Knott on magnetic twist, which will be referred to later, led him to form the conclusion that in an iron wire carrying an electric current the magnetic elongation would be increased. This forecast was shown by Bidwell to be well founded. The effect produced by a current is exactly opposite to that of tension, raising the elongation curve instead of depressing it. In the case of a wire 0.75 mm. in diameter the maximum elongation was nearly doubled when a current of two amperes was passing through the iron, while the “critical value” of the field was increased from 130 to 200. Yet notwithstanding this enormous effect in iron, the action of a current upon nickel and cobalt turned out to be almost inappreciable.
Some experiments were next undertaken with the view of ascertaining how far magnetic changes of length in iron were dependent upon the hardness of the metal, and the unexpected result was arrived at that softening produces the same effect as tensile stress; it depresses the elongation curve, diminishing the maximum extension, and reducing the “critical value” of the magnetizing force. A thoroughly well annealed ring of soft iron indeed showed no extension at all, beginning to contract, like nickel, under the smallest magnetizing forces. The experiments were not sufficiently numerous to indicate whether, as is possible, there is a critical degree of hardness for which the height of the elongation curve is a maximum.
Finally, experiments were made to ascertain the effect of magnetization upon the dimensions of iron rings in directions perpendicular to the magnetization, and upon the volume of the rings.[33] It was found that the curve showing the relation of transverse changes of dimensions to magnetizing force was similar in general character to the familiar elongation curves, but the signs were reversed; the curve was inverted, indicating at first retraction, which, after passing a maximum and vanishing in a critical field, was succeeded by elongation. The curve showing the circumferential (or longitudinal) changes was also plotted, and from the two curves thus obtained it was easy, on the assumption that the metal was isotropic in directions at right angles to the magnetization, to calculate changes of volume; for if circumferential elongation be denoted by l1, and transverse elongation by l2, then the cubical dilatation (+ or −) = l1 + 2l2 approximately. If l1 were exactly equal to -2l2 for all values of the magnetizing force, it is clear that the volume of the ring would be unaffected by magnetization. In the case of the ring in question, the circumferential changes were in weak fields less than twice as great as the transverse ones, while in strong fields they were more than twice as great; under increasing magnetic force therefore the volume of the ring was first diminished, then it regained its original value (for H = 90), and ultimately increased. It was also shown that annealing, which has such a large effect upon circumferential (or longitudinal) changes, has almost none upon transverse ones. Hence the changes of volume undergone by a given sample of wrought iron under increasing magnetization must depend largely upon the state of the metal as regards hardness; there may be always contraction, or always expansion, or first one and then the other.
Most of the experiments described above have been repeated and the results confirmed by other workers, some of whom have added fresh observations. The complicated hysteresis effects which attend magnetic elongation and retraction have been studied by H. Nagaoka, who also, in conjunction with K. Honda, measured the changes of length of various metals shaped in the form of ovoids instead of cylindrical rods, and determined the magnetization curves for the same specimens; a higher degree of accuracy was thus attained, and satisfactory data were provided for testing theories. Among other things, it was found that the behaviour of cast cobalt was entirely changed by annealing; the sinuous curve shown in Fig. 24 was converted into an almost perfectly straight line passing through the origin, and lying below the horizontal axis; while the permeability of the metal was greatly diminished by the operation. They also tested several varieties of nickel-steel in the form of both ovoids and wires. With a sample containing 25% of nickel no appreciable change was detected; others containing larger percentages, and tested in fields up to 2000, all exhibited elongation, which tended to an asymptotic value as the field was increased. The influence of temperature varying between wide limits has formed the subject of a research by K. Honda and S. Shimizu. For soft iron, tungsten-steel and nickel little difference appeared to result from lowering the temperature down to −186° C. (the temperature of liquid air); at sufficiently high temperatures, 600° to 1000° or more, it was remarked that the changes of length in iron, steel and cobalt tended in every case to become proportional to the magnetic force, the curves being nearly straight lines entirely above the axis. The retraction of nickel was diminished by rising temperature, and at 400° had almost vanished. The influence of high temperature on cobalt was very remarkable, completely altering the character of the change of length: the curves for annealed cobalt show that at 450° this metal behaves just like iron at ordinary temperatures, lengthening in fields up to about 300 and contracting in stronger ones. The same physicists have made some additional experiments upon the effect of tension on magnetic change of length. Bidwell’s results for iron and nickel were confirmed, and it was further shown that the elongation of nickel-steel was very greatly diminished by tension; when magnetized under very heavy loads, the wire was indeed found to undergo slight contraction. Honda subjected tubes of iron, steel and nickel to the simultaneous action of circular and longitudinal fields, and observed the changes of length when one of the fields was varied while the other remained constant at different successive values from zero upwards. The experimental results agreed in sign though not in magnitude with those calculated from the changes produced by simple longitudinal magnetization, discrepancies being partly accounted for by the fact that the metals employed were not actually isotropic. Heusler’s alloy has been tested for change of length by L. Austin, who found continuous elongation with increasing fields, the curves obtained bearing some resemblance to curves of magnetization.
As regards the effect of magnetization upon volume there are some discrepancies. Nagaoka and Honda, who employed a fluid dilatometer, found that the volume of several specimens of iron, steel and nickel was always slightly increased, no diminution being indicated in low fields; cobalt, on the other hand, was diminished in volume, and the amount of the change, though still very small, was greater than that shown by the other metals. Various nickel-steels all expanded under magnetization, the increase being generally considerable and proportional to the field; in the case of an alloy containing 29% of nickel the change was nearly 40 times greater than in soft iron. C. G. Knott, who made an exhaustive series of experiments upon various metals in the form of tubes, concluded that in iron there was always a slight increase of volume, and in nickel and cobalt a slight decrease. It is uncertain how far these various results are dependent upon the physical condition of the metals.
Attempts have been made to explain magnetic deformation by various theories of magnetic stress,[34] notably that elaborated by G. R. Kirchhoff (Wied. Ann., 1885, 24, 52, and 1885, 25, 601), but so far with imperfect success. E. Taylor Jones showed in 1897 that only a small proportion of the contraction exhibited by a nickel wire when magnetized could be accounted for on Kirchhoff’s theory from the observed effects of pulling stress upon magnetization; and in a more extended series of observations Nagaoka and Honda found wide quantitative divergences between the results of experiment and calculation, though in nearly all cases there was agreement as to quality. They consider, however, that Kirchhoff’s theory, which assumes change of magnetization to be simply proportional to strain, is still in its infancy, the present stage of its evolution being perhaps comparable with that reached by the theory of magnetization at the time when the ratio I/H was supposed to be constant. In the light of future researches further development may reasonably be expected.
It has been suggested[35] that an iron rod under magnetization may be in the same condition as if under a mechanically applied longitudinal stress tending to shorten the iron. If a long magnetized rod is divided transversely and the cut ends placed nearly in contact, the magnetic force inside the narrow air gap will be B = H + 4πI. The force acting on the magnetism of one of the faces, and urging this face towards the other, will be less than B by 2πI, the part of the total force due to the first face itself; hence the force per unit of area with which the faces would press against each other if in contact is
The width of the gap may be diminished until it is no greater than the distance between two neighbouring molecules, when it will cease to be distinguishable, but, assuming the molecular theory of magnetism to be true, the above statement will still hold good for the intermolecular gap. The same pressure P will be exerted across any imaginary section of a magnetized rod, the stress being sustained by the intermolecular springs, whatever their physical nature may be, to which the elasticity of the metal is due. The whole of the rod will therefore be subject to a compressive longitudinal stress P, the associated contraction R, expressed as a fraction of the original length, being
where M is Young’s modulus. This was found to be insufficient to account for the whole of the retraction exhibited by iron in strong fields, but it was pointed out by L. T. More[36] that R ought to be regarded as a “correction” to be applied to the results of experiments on magnetic change of length, the magnetic stress being no less an extraneous effect than a stress applied mechanically. Those who support this view generally speak of the stress as “Maxwell’s stress,” and assume its value to be B2/8π. The stress in question seems, however, to be quite unconnected with the “stress in the medium” contemplated by Maxwell, and its value is not exactly B2/8π except in the particular case of a permanent ring magnet, when H = O. Further, Maxwell’s stress is a tension along the lines of force, and is equal to B2/8π only when B = H, and there is no magnetization.[37] Some writers have indeed contended that the stress in magnetized iron is not compressive, but tensile, even when, as in the case of a ring-magnet, there are no free ends. The point at issue has an important bearing upon the possible correlation of magnetic phenomena, but, though it has given rise to much discussion, no accepted conclusion has yet been reached.[38]
7. Effects of Mechanical Stress upon Magnetization
The effects of traction, compression and torsion in relation to magnetism have formed the subject of much patient investigation, especially at the hands of J. A. Ewing, C. G. Knott and the indefatigable physicists of Tokyo University. The results of their experiments embrace a multiplicity of details of which it is impossible to give an adequate summary. Only a few of the most important can be mentioned here; the reader who wishes for fuller information should consult the original papers.[39]
It was first discovered by E. Villari in 1868 that the magnetic susceptibility of an iron wire was increased by stretching when the magnetization was below a certain value, but diminished when that value was exceeded; this phenomenon has been termed by Lord Kelvin, who discovered it independently, the “Villari reversal,” the value of the magnetization for which stretching by a given load produces no effect being known as the “Villari critical point” for that load. The Villari critical point for a given sample of iron is reached with a smaller magnetizing force when the stretching load is great than when it is small; the reversal also occurs with smaller loads and with weaker fields when the iron is soft than when it is hard. The following table shows the values of I and H corresponding to the Villari critical point in some of Ewing’s experiments:—
| Soft Iron. | Hard Iron. | ||||
| Kilos per sq. mm. | I. | H. | Kilos per sq. mm. | I. | H. |
| 2.15 | 1220 | 7.3 | 27.6 | 1180 | 34 |
| 4.3 | 1040 | 4.3 | 32.2 | 1150 | 32 |
| 8.6 | 840 | 3.4 | 37.3 | 1110 | 29 |
| 12.9 | 690 | 3.05 | 42.5 | 1020 | 25 |
The effects of pulling stress may be observed either when the wire is stretched by a constant load while the magnetizing force is varied, or when the magnetizing force is kept constant while the load is varied. In the latter case the first application of stress is always attended by an increase—often a very great one—of the magnetization, whether the field is weak or strong, but after a load has been put on and taken off several times the changes of magnetization become cyclic. From experiments of both classes it appears that for a given field there is a certain value of the load for which the magnetization is a maximum, the maximum occurring at a smaller load the stronger the field. In very strong fields the maximum may even disappear altogether, the effect of the smallest stress being to diminish the magnetization; on the other hand, with very weak fields the maximum may not have been reached with the greatest load that the wire can support without permanent deformation. When the load on a hardened wire is gradually increased, the maximum value of I is found to correspond with a greater stress than when the load is gradually diminished, this being an effect of hysteresis. Analogous changes are observed in the residual magnetization which remains after the wire has been subjected to fields of different strength. The effects of longitudinal pressure are opposite to those of traction; when the cyclic condition has been reached, pressure reduces the magnetization of iron in weak fields and increases it in strong fields (Ewing, Magnetic Induction, 1900, 223).
The influence of traction in diminishing the susceptibility of nickel was first noticed by Kelvin (W. Thomson), and was subsequently investigated by Ewing and Cowan. The latter found the effect to be enormous, not only upon the induced magnetization, but in a still greater degree upon the residual. Even under so “moderate” a load as 33 kilogrammes per square mm., the induced magnetization of a hard-drawn nickel wire in a field of 60 fell from 386 to 72 units, while the residual was reduced from about 280 to 10. Ewing has also examined the effects produced by longitudinal compression upon the susceptibility and retentiveness of nickel, and found, as was to be expected, that both were greatly increased by pressure. The maximum susceptibility of one of his bars rose from 5.6 to 29 under a stress of 19.8 kilos per square mm. There were reasons for believing that no Villari reversal would be found in nickel. Ewing and Cowan looked carefully for it, especially in weak fields, but failed to discover anything of the kind.[40] Some experiments by A. Heydweiller,[41] which appeared to indicate a reversal in weak fields (corresponding to I = 5, or thereabouts), have been shown by Honda and Shimizu to be vitiated by the fact that his specimen was not initially in a magnetically neutral state; they found that when the applied field had the same direction as that of the permanent magnetization, Heydweiller’s fallacious results were easily obtained; but if the field were applied in the direction opposite to that of the permanent magnetization, or if, as should rightly be the case, there were no permanent magnetization at all, then there was no indication of any Villari reversal. Thus a very important question, which has given rise to some controversy, appears to be now definitely settled.
The effects of longitudinal pressure upon the magnetization of cast cobalt have been examined by C. Chree,[42] and also by J. A. Ewing.[43] Chree’s experiments were undertaken at the suggestion of J. J. Thomson, who, from the results of Bidwell’s observations on the magnetic deformation of cobalt, was led to expect that that metal would exhibit a reversal opposite in character to the effect observed in iron. The anticipated reversal was duly found by Chree, the critical point corresponding, under the moderate stress employed, to a field of about 120 units. Ewing’s independent experiments showed that the magnetization curve for a cobalt rod under a load of 16.2 kilogrammes per square mm. crossed the curve for the same rod when not loaded at H = 53. Both observers noticed analogous effects in the residual magnetization. The effect of tension was subsequently studied by Nagaoka and Honda, who in 1902 confirmed, mutatis mutandis, the results obtained by Chree and Ewing for cast cobalt, while for annealed cobalt it turned out that tension always caused diminution of magnetization, the diminution increasing with increasing fields. They also investigated the magnetic behaviour of various nickel-steels under tension, and found that there was always increase of magnetization. Thus it has been proved that in annealed cobalt and in nickel-steel there is no Villari reversal.
It has been pointed out by J. J. Thomson (Applications of Dynamics to Physics and Chemistry, 47) that on dynamical principles there must be a reciprocal relation between the changes of dimensions produced by magnetization and the changes of magnetization attending mechanical strain. Since, for example, stretching diminishes the magnetization of nickel, it follows from theory that the length of a nickel rod should be diminished by magnetization and conversely. So, too, the Villari reversals in iron and cobalt might have been predicted—as indeed that in cobalt actually was—from a knowledge of the changes of length which those metals exhibit when magnetized.
The complete reciprocity of the effects of magnetization upon length and of stretching upon magnetization is shown by the following parallel statements:—
| Iron. | |
| Magnetization produces increase of length in weak fields, decrease in strong fields. |
Tension produces increase of magnetization in weak fields, decrease in strong fields. |
| Cast Cobalt. | |
| Magnetization produces decrease of length in weak fields, increase in strong fields. |
Tension produces decrease of magnetization in weak fields, increase in strong fields. |
| Nickel and Annealed Cobalt. | |
| Magnetization produces decrease of length in all fields. | Tension produces decrease of magnetization in all fields. |
| Nickel-Steel. | |
| Magnetization produces increase of length in all fields. | Tension produces increase of magnetization in all fields. |
Nagaoka and Honda (Phil. Mag., 1898, 46, 261) have investigated the effects of hydrostatic pressure upon magnetization, using the same pieces of iron and nickel as were employed in their experiments upon magnetic change of volume. In the iron cylinder and ovoid, which expanded when magnetized, compression caused a diminution of magnetization; in the nickel rod, which contracted when magnetized, pressure was attended by an increase of magnetization. The amount of the change was in both cases exceedingly small, that in iron being less than 0.1 C.G.S. unit with a pressure of 250 atmospheres and H = 54. It would hardly be safe to generalize from these observations; the effects may possibly be dependent upon the physical condition of the metals. In the same paper Nagaoka and Honda describe an important experiment on the effect of transverse stress. An iron tube, having its ends closed by brass caps, was placed inside a compressing vessel into which water was forced until the pressure upon the outer surface of the tube reached 250 atmospheres. The experiment was the reverse of one made by Kelvin with a gun-barrel subjected to internal hydrostatic pressure (Phil. Trans., 1878, 152, 64), and the results were also the reverse. Under increasing magnetizing force the magnetization first increased, reached a maximum, and then diminished until its value ultimately became less than when the iron was in the unstrained condition. Experiments on the effect of external hydrostatic pressure upon the magnetization of iron rings have also been made by F. Frisbie,[44] who found that for the magnetizing forces used by Nagaoka and Honda pressure produced a small increase of magnetization, a result which appears to be in accord with theory.
The relations of torsion to magnetization were first carefully studied by G. Wiedemann, whose researches are described in his Elektricität, iii. 671. The most interesting of his discoveries, now generally known as the “Wiedemann effect,” is the following: If we magnetize longitudinally a straight wire which is fixed at one end and free at the other, and then pass an electric current through the wire (or first pass the current and then magnetize), the free end of the wire will twist in a certain direction depending upon circumstances: if the wire is of iron, and is magnetized (with a moderate force) so that its free end has north polarity, while the current through it passes from the fixed to the free end, then the free end as seen from the fixed end will twist in the direction of the hands of a watch; if either the magnetization or the current is reversed, the direction of the twist will be reversed. To this mechanical phenomenon there is a magnetic reciprocal. If we twist the free end of a ferromagnetic wire while a current is passing through it, the wire becomes longitudinally magnetized, the direction of the magnetization depending upon circumstances: if the wire is of iron and is twisted so that its free end as seen from the fixed end turns in the direction of the hands of a watch, while the current passes from the fixed to the free end, then the direction of the resulting magnetization will be such as to make the free end a north pole. The twist effect exhibited by iron under moderate longitudinal magnetization has been called by Knott a positive Wiedemann effect; if the twist were reversed, the other conditions remaining the same, the sign of the Wiedemann effect would be negative. An explanation of the twist has been given by Maxwell (Electricity and Magnetism, § 448). The wire is subject to two superposed magnetizations, the one longitudinal, the other circular, due to the current traversing the wire; the resultant magnetization is consequently in the direction of a screw or spiral round the wire, which will be right-handed or left-handed according as the relation between the two magnetizations is right-handed or left-handed; the magnetic expansion or contraction of the metal along the spiral lines of magnetization produces the Wiedemann twist. Iron (moderately magnetized) expands along the lines of magnetization, and therefore for a right-handed spiral exhibits a right-handed twist. This explanation was not accepted by Wiedemann,[45] who thought that the effect was accounted for by molecular friction. Now nickel contracts instead of lengthening when it is magnetized, and an experiment by Knott showed, as he expected, that caeteris paribus a nickel wire twists in a sense opposite to that in which iron twists. The Wiedemann effect being positive for iron is negative for nickel. Further, although iron lengthens in fields of moderate strength, it contracts in strong ones; and if the wire is stretched, contraction occurs with smaller magnetizing forces than if it is unstretched. Bidwell[46] accordingly found upon trial that the Wiedemann twist of an iron wire vanished when the magnetizing force reached a certain high value, and was reversed when that value was exceeded; he also found that the vanishing point was reached with lower values of the magnetizing force when the wire was stretched by a weight. These observations have been verified and extended by Knott, whose researches have brought to light a large number of additional facts, all of which are in perfect harmony with Maxwell’s explanation of the twist.
Maxwell has also given an explanation of the converse effect,
namely, the production of longitudinal magnetization by twisting
a wire when circularly magnetized by a current passing through
it. When the wire is free from twist, the magnetization at any
point P is in the tangential direction PB (see fig. 26).
Fig. 26.
Suppose the wire to be fixed at the top and twisted
at the bottom in the direction of the arrow-head T;
then the element of the wire at P will be stretched
in the direction Pe and compressed in the direction
Pr. But tension and compression produce opposite
changes in the magnetic susceptibility; if the metal
is iron and its magnetization is below the Villari
critical point, its susceptibility will be greater along
Pe than along Pr; the direction of the magnetization
therefore tends to approach Pe and to recede
from Pr, changing, in consequence of the twist,
from PB to some such direction as PB′, which has a vertical
component downwards; hence the lower and upper ends will
respectively acquire north and south polarity, which will disappear
when the wire is untwisted. This effect has never been
actually reversed in iron, probably, as suggested by Ewing,
because the strongest practicable circular fields fail to raise the
components of the magnetization along Pe and Pr up to the
Villari critical value. Nagaoka and Honda have approached
very closely to a reversal, and consider that it would occur if
a sufficiently strong current could be applied without undue
heating.
One other effect of torsion remains to be noticed. If a longitudinally magnetized wire is twisted, circular magnetization is developed; this is evidenced by the transient electromotive force induced in the iron, generating a current which will deflect a galvanometer connected with the two ends of the wire. The explanation given of the last described phenomenon will with the necessary modification apply also to this; it is a consequence of the aeolotropy produced by the twist. There are then three remarkable effects of torsion:
- A. A wire magnetized longitudinally and circularly becomes twisted.
- B. Twisting a circularly magnetized wire produces longitudinal magnetization.
- C. Twisting a longitudinally magnetized wire produces circular magnetization.
And it has been shown earlier that—
- D. Magnetization produces change of length.
- E. Longitudinal stress produces change of magnetization.
Each of these five effects may occur in two opposite senses. Thus in A the twist may be right-handed or left-handed; in B the polarity of a given end may become north or south; in C the circular magnetization may be clockwise or counter-clockwise; in D the length may be increased or diminished; in E the magnetization may become stronger or weaker. And, other conditions remaining unchanged, the “sense” of any effect depends upon the nature of the metal under test, and (sometimes) upon the intensity of its magnetization. Let each of the effects A, B, C, D and E be called positive when it is such as is exhibited by moderately magnetized iron, and negative when its sense is opposite. Then the results of a large number of investigations may be briefly summarized as follows:
| (W) = weakly magnetized. | (S) = strongly magnetized. | ||
| Metal. | Effects. | Sign. | |
| Iron (W) | A, B, C, | D, E | + |
| Unannealed Cobalt (S) | A, | D, E | + |
| Nickel-Steel (W) | A, | D, E | + |
| Nickel | A, B, C, | D, E | − |
| Annealed Cobalt | D, E | − | |
| Iron (S) | A, C, | D, E | − |
| Unannealed Cobalt | A, | D, E | − |
Several gaps remain to be filled, but the results so far recorded can leave no doubt that the five effects, varied as they may at first sight appear, are intimately connected with one another. For each of the metals tabulated in the first column all the effects hitherto observed have the same sign; there is no single instance in which some are positive and others negative. Until the mysteries of molecular constitution have been more fully explored, perhaps D may be most properly regarded as the fundamental phenomenon from which the others follow. Nagaoka and Honda have succeeded in showing that the observed relations between twist and magnetization are in qualitative agreement with an extension of Kirchhoff’s theory of magnetostriction.
The effects of magnetization upon the torsion of a previously twisted wire, which were first noticed by Wiedemann, have been further studied by F. J. Smith[47] and by G. Moreau.[48] Nagaoka[49] has described the remarkable influence of combined torsion and tension upon the magnetic susceptibility of nickel, and has made the extraordinary observation that, under certain conditions of stress, the magnetization of a nickel wire may have a direction opposite to that of the magnetizing force.
8. Effects of Temperature upon Magnetism
High Temperature.—It has long been known that iron, when raised to a certain “critical temperature” corresponding to dull red heat, loses its susceptibility and becomes magnetically indifferent, or, more accurately, is transformed from a ferromagnetic into a paramagnetic body. Recent researches have shown that other important changes in its properties occur at the same critical temperature. Abrupt alterations take place in its density, specific heat, thermo-electric quality, electrical conductivity, temperature-coefficient of electrical resistance, and in some at least of its mechanical properties. Ordinary magnetizable iron is in many respects an essentially different substance from the non-magnetizable metal into which it is transformed when its temperature is raised above a certain point (see Brit. Assoc. Report, 1890, 145). The first exact experiments demonstrating the changes which occur in the permeability of iron, steel and nickel when heated up to high temperatures were those of J. Hopkinson (Phil. Trans., 1889, 180, 443; Proc. Roy. Soc., 1888, 44, 317). The metal to be tested was prepared in the form of a ring, upon which were wound primary and secondary coils of copper wire insulated with asbestos. The primary coil carried the magnetizing current; the secondary, which was wound inside the other, could be connected either with a ballistic galvanometer for determining the induction, or with a Wheatstone’s bridge for measuring the resistance, whence the temperature was calculated. The ring thus prepared was placed in a cast-iron box and heated in a gas furnace. The following are the chief results of Hopkinson’s experiments: For small magnetizing forces the magnetization of iron steadily increases with rise of temperature till the critical temperature is approached, when the rate of increase becomes very high, the permeability in some cases attaining a value of about 11,000; the magnetization then with remarkable suddenness almost entirely disappears, the permeability falling to about 1.14. For strong magnetizing forces (which in these experiments did not exceed H = 48.9) the permeability remains almost constant at its initial value (about 400), until the temperature is within nearly 100° of the critical point; then the permeability diminishes more and more rapidly until the critical point is reached and the magnetization vanishes. Steel behaves in a similar manner, but the maximum permeability is not so high as in iron, and the fall, when the critical point is approached, is less abrupt. The critical temperature for various samples of iron and steel ranges from 690° C. to 870° C.; it is the temperature at which Barrett’s “recalescence” occurs. The critical temperature for the specimen of nickel examined (which contained nearly 5% of impurities) was 310° C. F. Lydall and A. W. Pocklington found that the critical temperature of nearly pure iron was 874° C. (Proc. Roy. Soc., 1893, 52, 228).
An exhaustive research into the effects of heating on the magnetic properties of iron has been carried out by D. K. Morris (Proc. Phys. Soc., 1897, 15, 134; and Phil. Mag., 1897, 44, 213), the results being embodied in a paper containing twelve pages of tables and upwards of 120 curves. As in Hopkinson’s experiments, ring magnets were employed; these were wound with primary and secondary coils of insulated platinum wire, which would bear a much higher temperature than copper without oxidation or fusion. A third platinum coil, wound non-inductively between the primary and the secondary, served to carry the current by which the ring was heated; a current of 4.6 amperes, with 16 volts across the terminals, was found sufficient to maintain the ring at a temperature of 1150° C. In the ring itself was embedded a platinum-thermometer wire, from the resistance of which the temperature was determined. The whole was wrapped in several coverings of asbestos and placed in a glass vessel from which the air was partially exhausted, additional precautions being taken to guard against oxidation of the iron.
 |
| Fig. 27. |
Some preliminary experiments showed the striking difference in the effects of annealing at a red heat (840° C.) and at a low white heat (1150° C). After one of the rings had been annealed at 840°, its maximum permeability at ordinary temperatures was 4000 for H = 1.84; when it had been subsequently annealed at 1150°, the maximum permeability rose to 4680 for H = 1.48, while the hysteresis loss for B= ±4000 was under 500 ergs per c.cm. As regards the effects of temperature, Morris’s results are in general agreement with those of Hopkinson, though no doubt they indicate details with greater clearness and accuracy. Specimens of curves showing the relation of induction to magnetic field at various temperatures, and of permeability to temperature with fields of different intensities, are given in figs. 27 and 28. The most striking feature presented by these is the enormous value, 12,660, which, with H = 0.153, is attained by the permeability at 765° C., followed by a drop so precipitous that when the temperature is only 15° higher, the value of the permeability has become quite insignificant. The critical temperatures for three different specimens of iron were 795°, 780°, and 770° respectively. Above these temperatures the little permeability that remained was found to be independent of the magnetizing force, but it appeared to vary a little with the temperature, one specimen showing a permeability of 100 at 820°, 2.3 at 950°, and 17 at 1050°. These last observations are, however, regarded as uncertain. The effects of temperature upon hysteresis were also carefully studied, and many hysteresis loops were plotted. The results of a typical experiment are given in the annexed table, which shows how greatly the hysteresis loss is diminished as the critical temperature is approached. The coercive force at 764°.5 is stated to have been little more than 0.1 C.G.S. unit; above the critical temperature no evidence of hysteresis could be obtained.
 |
| Fig. 28. |
| Hysteresis Loss in Ergs per c.cm. Max. H. = ±6.83. | |||
| Temp. C.° | Ergs. | Temp. C.° | Ergs. |
| 764.5 | 120 | 457 | 2025 |
| 748 | 328 | 352 | 2565 |
| 730 | 426 | 249 | 3130 |
| 695 | 797 | 137.5 | 3500 |
| 634 | 1010 | 24 | 3660 |
| 554 | 1345 | ||
A paper by H. Nagaoka and S. Kusakabe[50] generally confirms Morris’s results for iron, and gives some additional observations for steel, nickel and cobalt. The magnetometric method was employed, and the metals, in the form of ovoids, were heated by a specially designed burner, fed with gas and air under pressure, which directed 90 fine jets of flame upon the asbestos covering the ovoid. The temperature was determined by a platinum-rhodium and platinum thermo-junction in contact with the metal. Experiments were made at several constant temperatures with varying magnetic fields, and also at constant fields with rising and falling temperatures. For ordinary steel the critical temperature, at which magnetization practically disappeared, was found to be about 830°, and the curious fact was revealed that, on cooling, magnetization did not begin to reappear until the temperature had fallen 40° below the critical value. This retardation was still more pronounced in the case of tungsten-steel, which lost its magnetism at 910° and remained non-magnetic till it was cooled to 570°, a difference of 240°. For nearly pure nickel the corresponding temperature-difference was about 100°. This phenomenon is of the same nature as that first discovered by J. Hopkinson for nickel-steel. The paper contains tables and curves showing details of the magnetic changes, sometimes very complex, at different temperatures and with different fields. The behaviour of cobalt is particularly noticeable; its permeability increased with rising temperature up to a maximum at 500°, when it was about twice as great as at ordinary temperatures, while at 1600°, corresponding to white heat, there was still some magnetization remaining.
Further contributions to the subject have been made by K. Honda and S. Shimizu,[51] who experimented at temperatures ranging from −186° to 1200°. As regards the higher temperatures, the chief point of interest is the observation that the curve of magnetization for annealed cobalt shows a small depression at about 450°, the temperature at which they had found the sign of the length-change to be reversed for all fields. In the case of all the metals tested a small but measurable trace of magnetization remained after the so-called critical temperature had been exceeded; this decreased very slightly up to the highest temperature reached (1200°) without undergoing any such variation as had been suspected by Morris. When the curve after its steep descent has almost reached the axis, it bends aside sharply and becomes a nearly horizontal straight line; the authors suggest that the critical temperature should be defined as that corresponding to the point of maximum curvature. As thus defined the critical temperatures for iron, nickel and cobalt were found to be 780°, 360° and 1090° respectively, but these values are not quite independent of the magnetizing force.
Experiments on the effect of high temperatures have also been made by M. P. Ledeboer,[52] H. Tomlinson,[53] P. Curie,[54] and W. Kunz,[55] R. L. Wills,[56] J. R. Ashworth[57] and E. P. Harrison.[58]
Low Temperature.—J. A. Fleming and J. Dewar (Proc. Roy. Soc., 1896, 60, 81) were the first to experiment on the permeability and hysteresis of iron at low temperatures down to that of liquid air (−186° C.). Induction curves of an annealed soft-iron ring were taken first at a temperature of 15° C., and afterwards when the ring was immersed in liquid air, the magnetizing force ranging from about 0.8 to 22. After this operation had been repeated a few times the iron was found to have acquired a stable condition, and the curves corresponding to the two temperatures became perfectly definite. They showed that the permeability of this sample of iron was considerably diminished at the lower temperature. The maximum permeability (for H = 2) was 3400 at 15° and only 2700 at −186°, a reduction of more than 20%; but the percentage reduction became less as the magnetizing force departed from the value corresponding to maximum permeability. Observations were also made of the changes of permeability which took place as the temperature of the sample slowly rose from −186° to 15°, the magnetizing force being kept constant throughout an experiment. The values of the permeability corresponding to the highest and lowest temperatures are given in the following table. Most of the permeability-temperature curves were more or less convex towards the axis of temperature, and in all the experiments, except those with annealed iron and steel wire, the permeability was greatest at the lowest temperature.[59] The hysteresis of the soft annealed iron turned out to be sensibly the same for equal values of the induction at −186° as at 15°, the loss in ergs per c.cm. per cycle being approximately represented by 0.002 B1.56 when the maximum limits of B were ±9000. Experiments with the sample of unannealed iron failed to give satisfactory results, owing to the fact that no constant magnetic condition could be obtained.
| Sample of Iron. | H. | μ at 15°. | μ at −186°. |
| Annealed Swedish | 1.77 | 2835 | 2332 |
| Unannealed ” | 1.78 | 917 | 1272 |
| ” ” | 9.79 | 1210 | 1293 |
| Hardened ” | 2.66 | 56 | 132 |
| ” ” | 4.92 | 106.5 | 502 |
| ” ” | 11.16 | 447.5 | 823 |
| ” ” | 127.7 | 109 | 124 |
| Steel wire | 7.50 | 86 | 64.5 |
| ” | 20.39 | 361 | 144 |
Honda and Shimizu have made similar experiments at the temperature of liquid air, employing a much wider range of magnetizing forces (up to about 700 C.G.S.) and testing a greater variety of metals. They found that the permeability of Swedish iron, tungsten-steel and nickel, when the metals were cooled to −186°, was diminished in weak fields but increased in strong ones, the field in which the effect of cooling changed its sign being 115 for iron and steel and 580 for nickel. The permeability of cobalt, both annealed and unannealed, was always diminished at the low temperature. The hysteresis-loss in Swedish iron was decreased for inductions below about 9000 and increased for higher inductions; in tungsten-steel, nickel and cobalt the hysteresis-loss was always increased by cooling. The range of ±B within which Steinmetz’s formula is applicable becomes notably increased at low temperature. It may be remarked that, whereas Fleming and Dewar employed the ballistic method, their specimens having the form of rings, Honda and Shimizu worked magnetometrically with metals shaped as ovoids.
Permanent Magnets.—Fleming and Dewar (loc. cit. p. 57) also investigated the changes which occurred in permanently magnetized metals when cooled to the temperature of liquid air. The metals, which were prepared in the form of small rods, were magnetized between the poles of an electromagnet and tested with a magnetometer at temperatures of −186° and 15°. The first immersion into liquid air generally produced a permanent decrease of magnetic moment, and there was sometimes a further decrease when the metal was warmed up again; but after a few alternations of temperature the changes of moment became definite and cyclic. When the permanent magnetic condition had been thus established, it was found that in the case of all the metals, except the two alloys containing large percentages of nickel, the magnetic moment was temporarily increased by cooling to −186°. The following table shows the principal results. It is suggested that a permanent magnet might conveniently be “aged” (or brought into a constant condition) by dipping it several times into liquid air.
| Metal. | Percentage Gain or Loss of Moment at −186° C. | |
| First Effect. | Cyclic Effect. | |
| Carbon steel, hard | −6 | +12 |
| Carbon steel, medium | Decrease | +22 |
| Carbon steel, annealed | −33 | +33 |
| Chromium steels (four samples) | Increase | +12 |
| Aluminium steels (three samples) | −2 | +10 |
| Nickel steels, up to 7.65% | Small | +10 |
| Nickel steels, up to 9.64% | −50 | −25 |
| Nickel steels, up to 29% | −20 | −10 |
| Pure nickel | Decrease | +3 |
| Silicon steel, 2.67% | ” | +4 |
| Iron, soft | None | +2.5 |
| Iron, hard | Decrease | +10 |
| Tungsten steel, 15% | ” | +6 |
| Tungsten steel, 7.5% | ” | +10 |
| Tungsten steel, 1% | ” | +12 |
Other experiments relating to the effect of temperature upon permanent magnets have been carried out by J. R. Ashworth,[60] who showed that the temperature coefficient of permanent magnets might be reduced to zero (for moderate ranges of temperature) by suitable adjustment of temper and dimension ratio; also by R. Pictet,[61] A. Durward[62] and J. Trowbridge.[63]
Alloys of Nickel and Iron.—A most remarkable effect of temperature was discovered by Hopkinson (Proc. Roy. Soc., 1890, 47, 23; 1891, 48, 1) in 1889. An alloy containing about 3 parts of iron and 1 of nickel—both strongly magnetic metals—is under ordinary conditions practically non-magnetizable (μ = 1.4 for any value of H). If, however, this non-magnetic substance is cooled to a temperature a few degrees below freezing-point, it becomes as strongly magnetic as average cast-iron (μ = 62 for H = 40), and retains its magnetic properties indefinitely at ordinary temperatures. But if the alloy is heated up to 580° C. it loses its susceptibility—rather suddenly when H is weak, more gradually when H is strong—and remains non-magnetizable till it is once more cooled down below the freezing-point. This material can therefore exist in either of two perfectly stable conditions, in one of which it is magnetizable, while in the other it is not. When magnetizable it is a hard steel, having a specific electrical resistance of 0.000052; when non-magnetizable it is an extremely soft, mild steel, and its specific resistance is 0.000072. Alloys containing different proportions of nickel were found to exhibit the phenomenon, but the two critical temperatures were less widely separated. The following approximate figures for small magnetizing forces are deduced from Hopkinson’s curves:—
| Percentage of Nickel. | Susceptibility lost at temp. C. | Susceptibility gained at temp. C. |
| 0.97 | 890 | — |
| 4.7 | 820 | 660 |
| 4.7 | 780 | 600 |
| 24.5 | 680 | −10 |
| 30.0 | 140 | 125 |
| 33.0 | 207 | 193 |
| 73.0 | 202 | 202 |
Honda and Shimizu (loc. cit.) have determined the two critical temperatures for eleven nickel-steel ovoids, containing from 24.04 to 70.32% of nickel, under a magnetizing force of 400, and illustrated by an interesting series of curves, the gradual transformation of the magnetic properties as the percentage of nickel was decreased. They found that the hysteresis-loss, which at ordinary temperatures is very small, was increased in liquid air, the increase for the alloys containing less than 30% of nickel being enormous. Steinmetz’s formula applies only for very weak inductions when the alloys are at the ordinary temperature, but at the temperature of liquid air it becomes applicable through a wide range of inductions. According to C. E. Guillaume[64] the temperature at which the magnetic susceptibility of nickel-steel is recovered is lowered by the presence of chromium; a certain alloy containing chromium was not rendered magnetic even by immersion in liquid air. Experiments on the subject have also been made by E. Dumont[65] and F. Osmond.[66]
9. Alloys and Compounds or Iron
In 1885 Hopkinson (Phil. Trans., 1885, 176, 455) employed his yoke method to test the magnetic properties of thirty-five samples of iron and steel, among which were steels containing substantial proportions of manganese, silicon, chromium and tungsten. The results, together with the chemical analysis of each sample, are given in a table contained in this paper, some of them being also represented graphically. The most striking phenomenon which they bring into prominence is the effect of any considerable quantity of manganese in annihilating the magnetic property of iron. A sample of Hadfield’s manufacture, containing 12.36% of manganese, differed hardly at all from a non-magnetic substance, its permeability being only 1.27. According to Hopkinson’s calculation, this sample behaved as if 91% of the iron contained in it had completely lost its magnetic property.[67]Another point to which attention is directed is the exceptionally great effect which hardening has upon the magnetic properties of chrome steel; one specimen had a coercive force of 9 when annealed, and of no less than 38 when oil-hardened. The effect of the addition of tungsten in increasing the coercive force is very clearly shown; in two specimens containing respectively 3.44 and 2.35% of tungsten the coercive force was 64.5 and 70.7. These high values render hardened tungsten-steel particularly suitable for the manufacture of permanent magnets. Hopkinson (Proc. Roy. Soc., 1890, 48, 1) also noticed some peculiarities of an unexpected nature in the magnetic properties of the nickel-steel alloys already referred to. The permeability of the alloys containing from 1 to 4.7% of nickel, though less than that of good soft iron for magnetizing forces up to about 20 or 30, was greater for higher forces, the induction reached in a field of 240 being nearly 21,700. The induction for considerable forces was found to be greater in a steel containing 73% of nickel than in one with only 33%, though the permeability of pure nickel is much less than that of iron.
The magnetic qualities of various alloys of iron have been submitted to a very complete examination by W. F. Barrett, W. Brown and R. A. Hadfield (Trans. Roy. Dub. Soc., 1900, 7, 67; Journ. Inst. Elec. Eng., 1902, 31, 674).[68] More than fifty different specimens were tested, most of which contained a known proportion of manganese, nickel, tungsten, aluminium, chromium, copper or silicon: in some samples two of the substances named were present. Of the very numerous results published, a few of the most characteristic are collected in the following table. The first column contains the symbols of the various elements which were added to the iron, and the second the percentage proportion in which each element was present; the sample containing 0.03% of carbon was a specimen of the best commercial iron, the values obtained for it being given for comparison. All the metals were annealed.
A few among several interesting points should be specially noticed. The addition of 15.2% of manganese produced an enormous effect upon the magnetism of iron, while the presence of only 2.25% was comparatively unimportant. When nickel was added to the iron in increasing quantities the coercive force increased until the proportion of nickel reached 20%; then it diminished, and when the proportion of nickel was 32% the coercive force had fallen to the exceedingly low value of 0.5. In the case of iron containing 7.5% of tungsten (W), the residual induction had a remarkably high value; the coercive force, however, was not very great. The addition of silicon in small quantities considerably diminished permeability and increased coercive force; but when the proportion amounted to 2.5% the maximum permeability (μ = 5100 for H = 2) was greater than that of the nearly pure iron used for comparison, while the coercive force was only 0.9.[69] A small percentage of aluminium produced still higher permeability (μ = 6000 for H = 2), the induction in fields up to 60 being greater than in any other known substance, and the hysteresis-loss for moderate limits of B far less than in the purest commercial iron. Certain non-magnetizable alloys of nickel, chromium-nickel and chromium-manganese were rendered magnetizable by annealing.
| Element. | Per cent. | B for H = 45. |
B residual. |
μ for H = 8. |
Coercive Force. |
|---|---|---|---|---|---|
| C | 0.03 | 16800 | 9770 | 1625 | 1.66 |
| Cu | 2.5 | 14300 | 10410 | .. | 5.4 |
| Mn | 2.25 | 14720 | 10460 | 1080 | 6.0 |
| Mn | 15.2 | 0 | .. | .. | .. |
| Ni | 3.82 | 16190 | 9320 | 1375 | 2.76 |
| Ni | 19.64 | 7770 | 4770 | 90 | 20.0 |
| Ni | 31.4 | 4460 | 1720 | 357 | 0.5 |
| W | 7.5 | 15230 | 13280 | 500 | 9.02 |
| Al | 2.25 | 16900 | 10500 | 1700 | 1.0 |
| Cr | 3.25 | .. | .. | .. | 12.25 |
| Si | 2.5 | 16420 | 4080 | 1680 | 0.9 |
| Si | 5.5 | 15980 | 3430 | 1630 | 0.85 |
Later papers[70] give the results of a more minute examination of those specimens which were remarkable for very low and very high permeabilities, and were therefore likely to be of commercial importance. The following table gives the exact composition of some alloys which were found to be non-magnetizable, or nearly so, in a field of 320.
| An. = Annealed. Un. = Unannealed. | ||
| State. | Percentage Composition. | I, for H = 320. |
| Un. | Fe, 85.77; C, 1.23; Mn, 13. | 0 |
| An. | Fe, 84.64; C, 0.15; Mn, 15.2 | 0 |
| An. | Fe, 80.16; C, 0.8; Mn, 5.04; Ni, 14.55. | 3 |
| Un. | Ditto | 0 |
| Un. | Fe, 75.36; C, 0.6; Mn, 5.04; Ni, 19. | 3 |
| An. | Fe, 86.61; C, 1.08; Mn, 10.2; W, 2.11. | 5 |
A very small difference in the constitution often produces a remarkable effect upon the magnetic quality, and it unfortunately happens that those alloys which are hardest magnetically are generally also hardest mechanically and extremely difficult to work; they might however be used rolled or as castings. The specimens distinguished by unusually high permeability were constituted as follows:—
- Silicon-iron.—Fe, 97.3; C, 0.2; Si, 2.5.
- Aluminium-iron.—Fe, 97.33; C, 0.18; Al, 2.25.
The silicon-iron had, in fields up to about 10, a greater permeability than a sample of the best Swedish charcoal-iron, and its hysteresis-loss for max. B = 9000, at a frequency of 100 per second, was only 0.254 watt per pound, as compared with 0.382 for the Swedish iron. The aluminium-iron attained its greatest permeability in a field of 0.5, about that of the earth’s force, when its value was 9000, this being more than twice the maximum permeability of the Swedish iron. Its hysteresis-loss for B = 9000 was 0.236 per pound. It was, however, found that the behaviour of this alloy was in part due to a layer of pure iron (“ferrite”) averaging 0.1 mm. in thickness, which occurred on the outside of the specimen, and the exceptional magnetic quality which has been claimed for aluminium-iron cannot yet be regarded as established.
A number of iron alloys have been examined by Mme. Curie (Bull. Soc. d’Encouragement, 1898, pp. 36-76), chiefly with the object of determining their suitability for the construction of permanent magnets. Her tests appear to show that molybdenum is even more effective than tungsten in augmenting the coercive force, the highest values observed being 70 to 74 for tungsten-steel, and 80 to 85 for steel containing 3.5 to 4% of molybdenum. For additional information regarding the composition and qualities of permanent magnet steels reference may be made to the publications cited below.[71] Useful instructions have been furnished by Carl Barus (Terrestrial Magnetism, 1897, 2, 11) for the preparation of magnets calculated to withstand the effects of time, percussion and ordinary temperature variations. The metal, having first been uniformly tempered glass-hard, should be annealed in steam at 100° C. for twenty or thirty hours; it should then be magnetized to saturation, and finally “aged” by a second immersion in steam for about five hours.
Magnetic Alloys of Non-Magnetic Metals.—The interesting discovery was made by F. Heusler[72] in 1903 that certain alloys of the non-magnetic metal manganese with other non-magnetic substances were strongly magnetizable, their susceptibility being in some cases equal to that of cast iron. The metals used in different combinations included tin, aluminium, arsenic, antimony, bismuth and boron; each of these, when united in certain proportions with manganese, together with a larger quantity of copper (which appears to serve merely as a menstruum), constituted a magnetizable alloy. So far, the best results have been attained with aluminium, and the permeability was greatest when the percentages of manganese and aluminium were approximately proportional to the atomic weights of the two metals. Thus in an alloy containing 26.5% of manganese and 14.6% of aluminium, the rest being copper, the induction for H = 20 was 4500, and for H = 150, 5550. When the proportion of aluminium to manganese was made a little greater or smaller, the permeability was diminished. Next to aluminium, tin was found to be the most effective of the metals enumerated above. In all such magnetizable alloys the presence of manganese appears to be essential, and there can be little doubt that the magnetic quality of the mixtures is derived solely from this component. Manganese, though belonging (with chromium) to the iron group of metals, is commonly classed as a paramagnetic, its susceptibility being very small in comparison with that of the recognized ferromagnetics; but it is remarkable that its atomic susceptibility in solutions of its salts is even greater than that of iron. Now iron, nickel and cobalt all lose their magnetic quality when heated above certain critical temperatures which vary greatly for the three metals, and it was suspected by Faraday[73] as early as 1845 that manganese might really be a ferromagnetic metal having a critical temperature much below the ordinary temperature of the air. He therefore cooled a piece of the metal to −105° C., the lowest temperature then attainable, but failed to produce any change in its magnetic quality. The critical temperature (if there is one) was not reached in Faraday’s experiment; possibly even the temperature of −250° C., which by the use of liquid hydrogen has now become accessible, might still be too high.[74] But it has been shown that the critical temperatures of iron and nickel may be changed by the addition of certain other substances. Generally they are lowered, sometimes, however, they are raised[75]; and C. E. Guillaume[76] explains the ferromagnetism of Heusler’s alloy by supposing that the naturally low critical temperature of the manganese contained in it is greatly raised by the admixture of another appropriate metal, such as aluminium or tin; thus the alloy as a whole becomes magnetizable at the ordinary temperature. If this view is correct, it may also be possible to prepare magnetic alloys of chromium, the only other paramagnetic metals of the iron group.
J. A. Fleming and R. A. Hadfield[77] have made very careful experiments on an alloy containing 22.42% of manganese, 11.65% of aluminium and 60.49% of copper. The magnetization curve was found to be of the same general form as that of a paramagnetic metal, and gave indications that with a sufficient force magnetic saturation would probably be attained. There was considerable hysteresis, the energy-loss per cycle being fairly represented by W = 0.0005495B2.238. The hysteretic exponent is therefore much higher than in the case of iron, nickel and cobalt, for which its value is approximately 1.6.
10. Miscellaneous Effects of Magnetization
Electrical Conductivity.—The specific resistance of many electric conductors is known to be temporarily changed by the action of a magnetic field, but except in the case of bismuth the effect is very small.
A. Gray and E. Taylor Jones (Proc. Roy. Soc., 1900, 67, 208) found that the resistance of a soft iron wire was increased by about 1700 in a field of 320 C.G.S. units. The effect appeared to be closely connected with the intensity of magnetization, being approximately proportional to I. G. Barlow (Proc. Roy. Soc., 1903, 71, 30), experimenting with wires of iron, steel and nickel, showed that in weak fields the change of resistance was proportional to a function aI2 + bI4 + cI6, where a, b and c are constants for each specimen. W. E. Williams (Phil. Mag., 1902, 4, 430) found that for nickel the curves showing changes of resistance in relation to magnetizing force were strikingly similar in form to those showing changes of length. H. Tomlinson (Phil. Trans., 1883, Part I., 153) discovered in 1881 that the resistance of a bismuth rod was slightly increased when the rod was subjected to longitudinal magnetic force, and a year or two later A. Righi (Atti R. A. Lincei, 1883–1884, 19, 545) showed that a more considerable alteration was produced when the magnetic force was applied transversely to the bismuth conductor; he also noticed that the effect was largely dependent upon temperature (see also P. Lenard, Wied. Ann., 1890, 39, 619). Among the most important experiments on the influence of magnetic force at different temperatures are those of J. B. Henderson and of Dewar and Fleming. Henderson (Phil. Mag., 1894, 38, 488) used a little spiral of the pure electrolytic bismuth wire prepared by Hartmann and Braun; this was placed between the pole-pieces of an electromagnet and subjected to fields of various strengths up to nearly 39,000 units. At constant temperature the resistance increased with the field; the changes in the resistance of the spiral when the temperature was 18° C. are indicated in the annexed table, from which it will be seen that in the strongest transverse field reached the resistance was increased more than threefold. Other experiments showed the relation of resistance to temperature (from 0° to about 90°) in different constant fields. It appears that as the temperature rises the resistance decreases to a minimum and then increases, the minimum point occurring at a higher temperature the stronger the field. For H = 11,500 the temperature of minimum resistance was about 50°; for much lower or higher values of H the actual minimum did not occur within the range of temperature dealt with. Dewar and Fleming (Proc. Roy. Soc., 1897, 60, 425) worked with a similar specimen of bismuth, and their results for a constant temperature of 19° agree well with those of Henderson. They also experimented with constant temperatures of −79°, −185° and −203°, and found that at these low temperatures the effect of magnetization was enormously increased. The following table gives some of their results, the specific resistance of the bismuth being expressed in C.G.S. units.
| H. | R. | H. | R. |
| 0 | 1.000 | 27450 | 2.540 |
| 6310 | 1.253 | 32730 | 2.846 |
| 12500 | 1.630 | 38900 | 3.334 |
| 20450 | 2.160 |
| Field Strength. | Temp. 19°C. | Temp. −185°C. | ||
| Spec. Res. | Comp. Res. | Spec. Res. | Comp. Res. | |
| 0 | 116200 | 1.000 | 41000 | 1.00 |
| 1375 | 118200 | 1.017 | 103300 | 2.52 |
| 2750 | 123000 | 1.059 | 191500 | 4.67 |
| 8800 | 149200 | 1.284 | 738000 | 18.0 |
| 14150 | 186200 | 1.602 | 1730000 | 42.2 |
| 21800 | 257000 | 2.212 | 6190000 | 151 |
At the temperature of liquid air (−185°) the application of a field of 21,800 multiplied the resistance of the bismuth no less than 150 times. Fig. 29 shows the variations of resistance in relation to temperature for fields of different constant values. It will be seen that for H = 2450 and H = 5500 the minimum resistance occurs at temperatures of about −80° and −7° respectively.
Hall Effect.—If an electric current is passed along a strip of thin metal, and the two points at opposite ends of an equipotential line are connected with a galvanometer, its needle will of course not be deflected. But the application of a magnetic field at right angles to the plane of the metal causes the equipotential lines to rotate through a small angle, and the points at which the galvanometer is connected being no longer at the same potential, a current is indicated by the galvanometer.[78]
 |
| Fig. 29. |
The tranverse electromotive force is equal to KCH/D, where C is the current, H the strength of the field, D the thickness of the metal, and K a constant which has been termed the rotatory power or rotational coefficient. (See Hopkinson, Phil. Mag., 1880, 10, 430). The following values of K for different metals are given by E. H. Hall, the positive sign indicating that the electromotive force is in the same direction as the mechanical force acting upon the conductor. A. von Ettinghausen and W. Nernst (Wien. Ber., 1886, 94, 560) have found that the rotational coefficient of tellurium is more than fifty times greater than that of bismuth, its sign being positive. Several experimenters have endeavoured to find a Hall effect in liquids, but such results as have been hitherto obtained are by no means free from doubt. E. A. Marx (Ann. d. Phys., 1900, 2, 798) observed a well-defined Hall effect in incandescent gases. A large effect, proportional to the field, has been found by H. A. Wilson (Cam. Phil. Soc. Proc., 1902, 11, pp. 249, 391) in oxygen, hydrogen and air at low pressures, and by C. D. Child (Phys. Rev., 1904, 18, 370) in the electric arc.
| Metal. | K × 1015 | Metal. | K × 1015 |
| Antimony | +114000 | Copper | −520 |
| Steel | +12060 | Gold | −660 |
| Iron | +7850 | Nickel | −14740 |
| Cobalt | +2460 | Bismuth[79] | −8580000 |
| Zinc | +820 |
Electro-Thermal Relations.—The Hall electromotive force is only one of several so-called “galvano-magnetic effects” which are observed when a magnetic field acts normally upon a thin plate of metal traversed by an electric current. It is remarkable that if a flow of heat be substituted for a current of electricity a closely allied group of “thermo-magnetic effects” is presented. The two classes of phenomena have been collated by M. G. Lloyd (Am. Journ. Sci., 1901, 12, 57), as follows:—
| Galvano-Magnetic Effects. | Thermo-Magnetic Effects. |
| 1. A transverse difference of electric potential (Hall effect). | i. A transverse difference of electric potential (Nernst effect). |
| 2. A transverse difference of temperature (Ettinghausen effect). | ii. A transverse difference of temperature (Leduc effect). |
| 3. Longitudinal change of electric conductivity. | iii. Longitudinal change of thermal conductivity. |
| 4. Longitudinal difference of temperature. | iv. Longitudinal difference of electric potential.[80] |
 |
If in the annexed diagram ABCD represents the metallic plate through which the current of electricity or heat flows in the direction AB, then effects (1), (2), (i.) and (ii.) are exhibited at C and D, effects (4) and (iv.) at A and B, and effects (3) and (iii.) along AB. The transverse effects are reversed in direction when either the magnetic field or the primary current (electric or thermal) is reversed, but the longitudinal effects are independent of the direction of the field. It has been shown by G. Moreau (C. R., 1900, 130, pp. 122, 412, 562) that if K is the coefficient of the Hall effect (1) and K′ the analogous coefficient of the Nernst effect (i.) (which is constant for small values of H), then K′ = Kσ/ρ, σ being the coefficient of the Thomson effect for the metal and ρ its specific resistance. He considers that Hall’s is the fundamental phenomenon, and that the Nernst effect is essentially identical with it, the primary electromotive force in the case of the latter being that of the Thomson effect in the unequally heated metal, while in the Hall experiment it is derived from an external source.
Attempts have been made to explain these various effects by the electron theory.[81]
Thermo-electric Quality.—The earliest observations of the effect of magnetization upon thermo-electric power were those of W. Thomson (Lord Kelvin), who in 1856 announced that magnetization rendered iron and steel positive to the unmagnetized metals.[82] It has been found by Chassagny,[83] L. Houllevigue[84] and others that when the magnetizing force is increased, this effect passes a maximum, while J. A. Ewing[85] has shown that it is diminished and may even be reversed by tensile stress. Nickel was believed by Thomson to behave oppositely to iron, becoming negative when magnetized; but though his conclusion was accepted for nearly fifty years, it has recently been shown to be an erroneous one, based, no doubt, upon the result of an experiment with an impure specimen. Nickel when magnetized is always positive to the unmagnetized metal. So also is cobalt, as was found by H. Tomlinson.[86] The curves given by Houllevigue for the relation of thermo-electric force to magnetic field are of the same general form as those showing the relation of change of length to field. E. Rhoads[87] obtained a cyclic curve for iron which indicated thermo-electric hysteresis of the kind exhibited by Nagaoka’s curves for magnetic strain. He also experimented with nickel and again found a resemblance to the strain curve. The subject was further investigated by S. Bidwell,[88] who, adopting special precautions against sources of error by which former work was probably affected, measured the changes of thermo-electric force for iron, steel, nickel and cobalt produced by magnetic fields up to 1500 units. In the case of iron and nickel it was found that, when correction was made for mechanical stress due to magnetization, magnetic change of thermo-electric force was, within the limits of experimental error, proportional to magnetic change of length. Further, it was shown that the thermo-electric curves were modified both by tensile stress and by annealing in the same manner as were the change-of-length curves, the modification being sometimes of a complex nature. Thus a close connexion between the two sets of phenomena seems to be established. In the case of cobalt no such relation could be traced; it appeared that the thermo-electric power of the unmagnetized with respect to the magnetized cobalt was proportional to the square of the magnetic induction or of the magnetization. Of nickel six different specimens were tested, all of which became, like iron, thermo-electrically positive to the unmagnetized metals.
As to what effect, if any, is produced upon the thermo-electric quality of bismuth by a magnetic field there is still some doubt. E. van Aubel[89] believes that in pure bismuth the thermo-electric force is increased by the field; impurities may neutralize this effect, and in sufficient quantities reverse it.
Elasticity.—The results of experiments as to the effect of magnetization were for long discordant and inconclusive, sufficient care not having been taken to avoid sources of error, while the effects of hysteresis were altogether disregarded. The subject, which is of importance in connexion with theories of magnetostriction, has been investigated by K. Honda and T. Terada in a research remarkable for its completeness and the ingenuity of the experimental methods employed.[90] The results are too numerous to discuss in detail; some of those to which special attention is directed are the following: In Swedish iron and tungsten-steel the change of elastic constants (Young’s modulus and rigidity) is generally positive, but its amount is less than 0.5%; changes of Young’s modulus and of rigidity are almost identical. In nickel the maximum change of the elastic constants is remarkably large, amounting to about 15% for Young’s modulus and 7% for rigidity; with increasing fields the elastic constants first decrease and then increase. In nickel-steels containing about 50 and 70% of nickel the maximum increase of the constants is as much as 7 or 8%. In a 29% nickel-steel, magnetization increases the constants by a small amount. Changes of elasticity are in all cases dependent, not only upon the field, but also upon the tension applied; and, owing to hysteresis, the results are not in general the same when the magnetization follows as when it precedes the application of stress; the latter is held to be the right order.
Chemical and Voltaic Effects.—If two iron plates, one of which is magnetized, are immersed in an electrolyte, a current will generally be indicated by a galvanometer connected with the plates.
As to whether the magnetized plate becomes positive or negative to the other, different experimenters are not in agreement. It has, however, been shown by Dragomir Hurmuzescu (Rap. du Congrès Int. de Phys., Paris, 1900, p. 561) that the true effect of magnetization is liable to be disguised by secondary or parasitic phenomena, arising chiefly from polarization of the electrodes and from local variations in the concentration and magnetic condition of the electrolyte; these may be avoided by working with weak solutions, exposing only a small surface in a non-polar region of the metal, and substituting a capillary electrometer for the galvanometer generally used. When such precautions are adopted it is found that the “electromotive force of magnetization” is, for a given specimen, perfectly definite both in direction and in magnitude; it is independent of the nature of the corrosive solution, and is a function of the field-strength alone, the curves showing the relation of electromotive force to field-intensity bearing a rough resemblance to the familiar I-H curves. The value of the E.M.F. when H = 2000 is of the order of 1/100 volt for iron, 1/1000 volt for nickel and 1/10,000 for bismuth. When the two electrodes are ferromagnetic, the direction of the current through the liquid is from the unmagnetized to the magnetized electrode, the latter being least attacked; with diamagnetic electrodes the reverse is the case. Hurmuzescu shows that these results are in accord with theory. Applying the principle of the conservation of internal energy, he demonstrates that for iron in a field of 1000 units and upwards the E.M.F. of magnetization is
| E = | l | · | I2 |
| δ | 2κ |
approximately, l being the electrochemical equivalent and δ the density of the metal. Owing to the difficulty of determining the magnetization I and the susceptibility κ with accuracy, it has not yet been possible to submit this formula to a quantitative test, but it is said to afford an indication of the results given by actual experiment. It has been discovered by E. L. Nichols and W. S. Franklin (Am. Journ. Sci., 1887, 34, 419; 1888, 35, 290) that the transition from the “passive” to the active state of iron immersed in strong nitric acid is facilitated by magnetization, the temperature of transition being lowered. This is attributed to the action of local currents set up between unequally magnetized portions of the iron. Similar results have been obtained by T. Andrews (Proc. Roy. Soc., 1890, 48, 116).
11. Feebly Susceptible Substances
Water.—The following are recent determinations of the magnetic susceptibility of water:—
| Observer. | κ × 106. | Publication. |
| G. Quincke | −0.797 at 18° C. | Wied. Ann., 1885, 24, 387. |
| H. du Bois | −0.837 (1 − 0.0025t − 15°) | Wied. Ann., 1888, 35, 137. |
| P. Curie | −0.790 at 4° C. | C. R., 1893, 116, 136. |
| J. Townsend | −0.77 | Phil. Trans., 1896, 187, 544. |
| J. A. Fleming and J. Dewar | −0.74 | Proc. Roy. Soc., 1898, 63, 311. |
| G. Jäger and S. Meyer 707. | −0.689 (1 − 0.0016t) | Wied. Ann., 1899, 67, |
| J. Koenigsberger | −0.781 at 22° C. | Ann. d. Phys., 1901, 6, 506. |
| H. D. Stearns | −0.733 at 22° C. | Phys. Rev., 1903, 16, 1. |
| A. P. Wills | −0.720 at 18° C. | Phys. Rev., 1905, 20, 188. |
Wills found that the susceptibility was constant in fields ranging from 4200 to 15,000.
Oxygen and Air.—The best modern determinations of the value of κ for gaseous oxygen agree very fairly well with that given by Faraday in 1853 (Exp. Res. III, 502). Assuming that for water κ = −0.8 × 10−6, his value of κ for oxygen at 15° C. reduces to 0.15 × 10−6. Important experiments on the susceptibility of oxygen at different pressures and temperatures were carried out by P. Curie (C.R. 1892, 115, 805; 1893, 116, 136). Journ. de Phys., 1895, 4, 204. He found that the susceptibility for unit of mass, K, was independent of both pressure and magnetizing force, but varied inversely as the absolute temperature, θ, so that 106K = 33700/θ. Since the mass of 1 cub. cm. of oxygen at 0° C. and 760 mm. pressure is 0.00141 grm., the mass at any absolute temperature θ is by Charles’s law 0.00141 × 273θ = 0.3849/θ grm.; hence the susceptibility per unit of volume at 760 mm. will be
κ = 10−6 × 0.3849 × 33700 / θ2
At 15° C. θ = 273 + 15 = 288, and therefore κ = 0.156 × 10−6, nearly the same as the value found by Faraday. At 0° C., κ = 0.174 × 10−6. For air Curie calculated that the susceptibility per unit mass was 106K = 7830/θ; or, taking the mass of 1 c.c. of air at 0° C. and 760 mm. as 0.001291 grm., κ = 10−6 × 2760/θ2 for air at standard atmospheric pressure. It is pointed out that this formula may be used as a temperature correction in magnetic determinations carried out in air.
Fleming and Dewar determined the susceptibility of liquid oxygen (Proc. Roy. Soc., 1896, 60, 283; 1898, 63, 311) by two different methods. In the first experiments it was calculated from observations of the mutual induction of two conducting circuits in air and in the liquid; the results for oxygen at −182° C. were
In the second series, to which greater importance is attached, measurements were made of the force exerted in a divergent field upon small balls of copper, silver and other substances, first when the balls were in air and afterwards when they were immersed in liquid oxygen. If V is the volume of a ball, H the strength of the field at its centre, and κ′ its apparent susceptibility, the force in the direction x is f = κ′VH × dH/dx; and if κ′a and κ′0 are the apparent susceptibilities of the same ball in air and in liquid oxygen, κ′a − κ′0 is equal to the difference between the susceptibilities of the two media. The susceptibility of air being known—practically it was negligible in these experiments—that of liquid oxygen can at once be found. The mean of 36 experiments with 7 balls gave
A small but decided tendency to a decrease of susceptibility in very strong fields was observed. It appears, therefore, that liquid oxygen is by far the most strongly paramagnetic liquid known, its susceptibility being more than four times greater than that of a saturated solution of ferric chloride. On the other hand, its susceptibility is about fifty times less than that of Hadfield’s 12% manganese steel, which is commonly spoken of as non-magnetizable.
Bismuth.—Bismuth is of special interest, as being the most strongly diamagnetic substance known, the mean value of the best determinations of its susceptibility being about −14 × 10−6 (see G. Meslin, C. R., 1905, 140, 449). The magnetic properties of the metal at different temperatures and in fields up to 1350 units have been studied by P. Curie (loc. cit.), who found that its “specific susceptibility” (Κ) was independent of the strength of the field, but decreased with rise of temperature up to the melting-point, 273°C. His results appear to show the relation
Assuming the density of Bi to be 9.8, and neglecting corrections for heat dilatation, his value for the susceptibility at 20°C. is equivalent to κ = −13.23 × 10−6. As the temperature was raised up to 273°, κ gradually fell to −9.38 × 10−6, rising suddenly when fusion occurred to −0.37 × 10−6, at which value it remained constant when the fluid metal was further heated. Fleming and Dewar give for the susceptibility the values −13.7 × 10−6 at 15°C. and −15.9 × 10−6 at −182°, the latter being approximately equivalent to Κ × 106 = −1.62. Putting t° = −182 in the equation given above for Curie’s results, we get Κ × 106 = −1.66, a value sufficiently near that obtained by Fleming and Dewar to suggest the probability that the diamagnetic susceptibility varies inversely as the temperature between −182° and the melting-point.
Other Diamagnetics.—The following table gives Curie’s determinations (Journ. de Phys., 1895, 4, 204) of the specific susceptibility Κ of other diamagnetic substances at different temperatures. It should be noted that Κ = κ/density.
| Substance | Temp. °C. | −Κ × 106. |
| Water | 15–189 | 0.790 |
| Rock salt | 16–455 | 0.580 |
| Potassium chloride | 18–465 | 0.550 |
| Potassium sulphate | 17–460 | 0.430 |
| Potassium nitrate (fusion 350°) | 18–420 | 0.330 |
| Quartz | 18–430 | 0.441 |
| Sulphur, solid or fused | 18–225 | 0.510 |
| Selenium, solid or fused | 20–200 | 0.320 |
| Selenium, fused | 240–415 | 0.307 |
| Tellurium | 20–305 | 0.311 |
| Bromine | 20 | 0.410 |
| Iodine, solid or fused | 18–164 | 0.385 |
| Phosphorus, solid or fused | 19–71 | 0.920 |
| Phosphorus, amorphous | 20–275 | 0.730 |
| Antimony, electrolytic | 20 | 0.680 |
| Antimony | 540 | 0.470 |
| Bismuth, solid | 20 | 1.350 |
| Bismuth, solid | 273 | 0.957 |
| Bismuth, fused | 273–405 | 0.038 |
For all diamagnetic substances, except antimony and bismuth, the value of Κ was found to be independent of the temperature.
Paramagnetic Substances.—Experiments by J. S. Townsend (Phil. Trans., 1896, 187, 533) show that the susceptibility of solutions of salts of iron is independent of the magnetizing force, and depends only on the quantity of iron contained in unit volume of the liquid. If W is the weight of iron present per c.c. at about 10°C., then for ferric salts
and for ferrous salts
the quantity −0.77 arising from the diamagnetism of the water of solution. Annexed are values of 106κ for the different salts examined, w being the weight of the salt per c.c. of the solution.
| Salt. | 106κ + 0.77 | Salt. | 106κ + 0.77 |
| Fe2Cl6 | 91.6w | FeCl2 | 90.8w |
| Fe2(SO4)3 | 74.5w | FeSO4 | 74.9w |
| Fe2(NO3)6 | 61.5w |
Susceptibility was found to diminish greatly with rise of temperature. According to G. Jäger and S. Meyer (Wien. Akad. Sitz., 1897, 106, II. a, p. 623, and 1898, 107, II. a, p. 5) the atomic susceptibilities k of the metals nickel, chromium, iron, cobalt and manganese in solutions of their salts are as follows:—
| Metal. | k × 106 | Metal. | k × 106. |
| Ni | 4.95 = 2.5 × 2 | Co | 10.0 = 2.5 × 4 |
| Cr | 6.25 = 2.5 × 2.5 | Fe(2) | 12.5 = 2.5 × 5 |
| Fe(1) | 7.5 = 2.5 × 3 | Mn | 15.0 = 2.5 × 6 |
Fe(1) is iron contained in FeCl2 and Fe(2) iron contained in Fe2(NO3)6.
Curie has shown, for many paramagnetic bodies, that the specific susceptibility K is inversely proportional to the absolute temperature θ. Du Bois believes this to be an important general law, applicable to the case of every paramagnetic substance, and suggests that the product Kθ should be known as “Curie’s constant” for the substance.
Elementary Bodies and Atomic Susceptibility.—Among a large number of substances the susceptibilities of which have been determined by J. Koenigsberger (Wied. Ann., 1898, 66, 698) are the following elements:—
| Element. | κ × 106. | Element. | κ × 106. |
| Copper | −0.82 | Tellurium | − 2.10 |
| Silver | −1.51 | Graphite | + 2 |
| Gold | −3.07 | Aluminium | + 1.80 |
| Zinc | −0.96 | Platinum | +22 |
| Tin | +0.46 | Palladium | +50 to 60 |
| Lead | −1.10 | Tungsten | +14 |
| Thallium | −4.61 | Magnesium | + 4 |
| Sulphur | −0.86 | Sodium | + 2.2 |
| Selenium (red) | −0.50 | Potassium | + 3.6 |
In a table accompanying Koenigsberger’s paper the elements are arranged upon the periodic system and the atomic susceptibility (product of specific susceptibility into atomic weight) is given for each. It appears that the elements at about the middle of each row are the most strongly paramagnetic; towards the ends of a row the susceptibility decreases, and ultimately becomes negative. Thus a relation between susceptibility and atomic weight is clearly indicated. Tables similarly arranged, but much more complete, have been published by S. Meyer (Wied. Ann., 1899, 68, 325 and 1899, 69, 236), whose researches have filled up many previously existing gaps. The values assigned to the atomic susceptibilities of most of the known elements are appended. According to the notation adopted by Meyer the atomic susceptibility k = κ × atomic-weight / (density × 1000).
Meyer thinks that the susceptibilities of the metals praseodymium, neodymium, ytterbium, samarium, gadolinium, and erbium, when obtained in a pure form, will be found to equal or even exceed those of the well-known ferromagnetic metals. Many of their compounds are very strongly magnetic; erbium, for example, in Er2O3 being four times as strong as iron in the familiar magnetite or lodestone, Fe2O3. The susceptibilities of some hundreds of inorganic compounds have also been determined by the same investigator (loc. cit.). Among other researches relating to atomic and molecular magnetism are those of O. Liebknecht and A. P. Wills (Ann. d. Phys., 1900, 1, 178), H. du Bois and O. Liebknecht (ibid. p. 189), and Meyer (ibid. p. 668). An excellent summary regarding the magnetic properties of matter, with many tables and references, has been compiled by du Bois (Report to the Congrès Int. de Phys., Paris, 1900, ii. 460).
| Element | 106k | Element | 106k | Element | 106k | ||
| Be | +0.72 | Cu | −0.006 | Cs | − 0.03* | ||
| B | +0.05 | Zn | −0.010 | Ba | − 0.02* | ||
| C | −0.05 | Ga | − | La | +13.0 | ||
| N | ? | Ge | − | Ce | +34.0 | ||
| O | + | As | ? | Pr | + | Strong | |
| F | −0.01* | Se | −0.025 | Nd | + | ||
| · · · · · · · · · · | Br | −0.033 | Sa | + | |||
| Na | −0.005* | · · · · · · · · · · | Gd | + | |||
| Mg | +0.014 | Rb | −0.02* | · · · · · · · · · · | |||
| Al | + | Sr | −0.02* | Er | +41.8(?) | ||
| Si | +0.002 | Y | +3.2(?) | · · · · · · · · · · | |||
| P | −0.007 | Zr | −0.014 | Yb | + (?) | ||
| S | −0.011 | Nb | +0.49(?) | Ta | + 1.02(?) | ||
| Cl | −0.02* | Mo | +0.024 | W | + 0.1 | ||
| · · · · · · · · · · | Ru | + | Os | + 0.074 | |||
| K | −0.001* | Rh | + | Ir | + | ||
| Ca | −0.003* | Pd | +0.55 | Pt | + 0.227 | ||
| Sc | ? | Ag | −0.016 | Au | − 0.031 | ||
| Ti | +0.09 | Cd | −0.015 | Hg | − 0.030 | ||
| V | +0.17 | In | +0.01* | Tl | − 0.93 | ||
| Cr | + | Strong | Sn | +0.004* | Pb | − 0.025 | |
| Mn | + | Sb | −0.069 | Bi | − 0.023 | ||
| Fe | + | Te | −0.039 | · · · · · · · · · · | |||
| Co | + | I | −0.040 | Th | +16.0(?) | ||
| Ni | + | · · · · · · · · · · | U | + 0.21 | |||
* Calculated.
12. Molecular Theory of Magnetism
According to W. E. Weber’s theory, the molecules of a ferromagnetic metal are small permanent magnets, the axes of which under ordinary conditions are turned indifferently in every direction, so that no magnetic polarity is exhibited by the metal as a whole; a magnetic force acting upon the metal tends to turn the axes of the little magnets in one direction, and thus the entire piece acquires the properties of a magnet. If, however, the molecules could turn with perfect freedom, it is clear that the smallest magnetizing force would be sufficient to develop the highest possible degree of magnetization, which is of course not the case. Weber therefore supposed each molecule to be acted on by a force tending to preserve it in its original direction, the position actually assumed by the axis being in the direction of the resultant of this hypothetical force and the applied magnetizing force. Maxwell (Electricity and Magnetism, § 444), recognizing that the theory in this form gave no account of residual magnetization, made the further assumption that if the deflection of the axis of the molecule exceeded a certain angle, the axis would not return to its original position when the deflecting force was removed, but would retain a permanent set. Although the amended theory as worked out by Maxwell is in rough agreement with certain leading phenomena of magnetization, it fails to account for many others, and is in some cases at variance with observed facts.
J. A. Ewing (Proc. Roy. Soc., 1890, 48, 342) has demonstrated that it is quite unnecessary to assume either the directive force of Weber, the permanent set of Maxwell, or any kind of frictional resistance, the forces by which the molecular magnets are constrained being simply those due to their own mutual attractions and repulsions. The effect of these is beautifully illustrated by a model consisting of a number of little compass needles pivoted on sharp points and grouped near to one another upon a board, which is placed inside a large magnetizing coil. When no current is passing through the coil and the magnetic field is of zero strength, the needles arrange themselves in positions of stable equilibrium under their mutual forces, pointing in many different directions, so that there is no resultant magnetic moment. This represents the condition of the molecules in unmagnetized iron. If now a gradually increasing magnetizing force is applied, the needles at first undergo a stable deflection, giving to the group a small resultant moment which increases uniformly with the force; and if the current is interrupted while the force is still weak, the needles merely return to their initial positions. This illustrates the first stage in the process of magnetization, when the moment is proportional to the field and there is no hysteresis or residual magnetism (see ante). A somewhat stronger field will deflect many of the needles beyond the limits of stability, causing them to turn round and form new stable combinations, in which the direction assumed by most of them approximates to that of the field. The rearrangement is completed within a comparatively small range of magnetizing force, a rapid increase of the resultant moment being thus brought about. When the field is removed, many of the newly formed combinations are but slightly disturbed, and the group may consequently retain a considerable resultant moment. This corresponds to the second stage of magnetization, in which the susceptibility is large and permanent magnetization is set up. A still stronger magnetizing force has little effect except in causing the direction of the needles to approach still more nearly to that of the field; if the force were infinite, every member of the group would have exactly the same direction and the greatest possible resultant moment would be reached; this illustrates “magnetic saturation”—the condition approached in the third stage of magnetization. When the strong magnetizing field is gradually diminished to zero and then reversed, the needles pass from one stable position of rest to another through a condition of instability; and if the field is once more reversed, so that the cycle is completed, the needles again pass through a condition of instability before a position of stable equilibrium is regained. Now the unstable movements of the needles are of a mechanically irreversible character; the energy expended in dissociating the members of a combination and placing them in unstable positions assumes the kinetic form when the needles turn over, and is ultimately frittered down into heat. Hence in performing a cycle there is a waste of energy corresponding to what has been termed hysteresis-loss.
Supposing Ewing’s hypothesis to be correct, it is clear that if the magnetization of a piece of iron were reversed by a strong rotating field instead of by a field alternating through zero, the loss of energy by hysteresis should be little or nothing, for the molecules would rotate with the field and no unstable movements would be possible.[91] Some experiments by F. G. Baily (Phil. Trans., 1896, 187, 715) show that this is actually the case. With small magnetizing forces the hysteresis was indeed somewhat larger than that obtained in an alternating field, probably on account of the molecular changes being forced to take place in one direction only; but at an induction of about 16,000 units in soft iron and 15,000 in hard steel the hysteresis reached a maximum and afterwards rapidly diminished. In one case the hysteresis loss per cubic centimetre per cycle was 16,100 ergs for B = 15,900, and only 1200 ergs for B = 20,200, the highest induction obtained in the experiment; possibly it would have vanished before B had reached 21,000.[92] These experiments prove that actual friction must be almost entirely absent, and, as Baily remarks, the agreement of the results with the previously suggested deduction affords a strong verification of Ewing’s form of the molecular theory. Ewing has himself also shown how satisfactorily this theory accords with many other obscure and complicated phenomena, such as those presented by coercive force, differences of magnetic quality, and the effects of vibration, temperature and stress; while as regards simplicity and freedom from arbitrary assumptions it leaves little to be desired.
The fact being established that magnetism is essentially a molecular phenomenon, the next step is to inquire what is the constitution of a magnetic molecule, and why it is that some molecules are ferromagnetic, others paramagnetic, and others again diamagnetic. The best known of the explanations that have been proposed depend upon the magnetic action of an electric current. It can be shown that if a current i circulates in a small plane circuit of area S, the magnetic action of the circuit for distant points is equivalent to that of a short magnet whose axis is perpendicular to the plane of the circuit and whose moment is iS, the direction of the magnetization being related to that of the circulating current as the thrust of a right-handed screw to its rotation. Ferromagnetism was explained by Ampère on the hypothesis that the magnetization of the molecule is due to an electric current constantly circulating within it. The theory now most in favour is merely a development of Ampère’s hypothesis, and applies not only to ferromagnetics, but to paramagnetics as well. To account for diamagnetism, Weber supposed that there exist within the molecules of diamagnetic substances certain channels around which an electric current can circulate without any resistance. The creation of an external magnetic field H will, in accordance with Lenz’s law, induce in the molecule an electric current so directed that the magnetization of the equivalent magnet is opposed to the direction of the field. The strength of the induced current is −HS cos θ/L, where θ is the inclination of the axis of the circuit to the direction of the field, and L the coefficient of self-induction; the resolved part of the magnetic moment in the direction of the field is equal to −HS2 cos2 θ/L, and if there are n molecules in a unit of volume, their axes being distributed indifferently in all directions, the magnetization of the substance will be −13nHS2/L, and its susceptibility -13S2/L (Maxwell, Electricity and Magnetism, § 838). The susceptibility is therefore constant and independent of the field, while its negative sign indicates that the substance is diamagnetic. There being no resistance, the induced current will continue to circulate round the molecule until the field is withdrawn, when it will be stopped by the action of an electromotive force tending to induce an exactly equal current in the opposite direction. The principle of Weber’s theory, with the modification necessitated by lately acquired knowledge, is the basis of the best modern explanation of diamagnetic phenomena.
There are strong reasons for believing that magnetism is a phenomenon involving rotation, and as early as 1876 Rowland, carrying out an experiment which had been proposed by Maxwell, showed that a revolving electric charge produced the same magnetic effects as a current. Since that date it has more than once been suggested that the molecular currents producing magnetism might be due to the revolution of one or more of the charged atoms or “ions” constituting the molecule. None of the detailed hypotheses which were based on this idea stood the test of criticism, but towards the end of the 19th century the researches of J. J. Thomson and others once more brought the conception of moving electric charges into prominence. Thomson has demonstrated the existence under many different conditions of particles more minute than anything previously known to science. The mass of each is about 1/1700th part of that of a hydrogen atom, and with each is indissolubly associated a charge of negative electricity equal to about 3.1 × 10−10 C.G.S. electrostatic unit. These particles, which were termed by their discoverer corpuscles, are more commonly spoken of as electrons,[93] the particle thus being identified with the charge which it carries. An electrically neutral atom is believed to be constituted in part, or perhaps entirely, of a definite number of electrons in rapid motion within a “sphere of uniform positive electrification” not yet explained. One or more of the electrons may be detached from the system by a finite force, the number so detachable depending on the valency of the atom; if the atom loses an electron, it becomes positively electrified; if it receives additional electrons, it is negatively electrified. The process of electric conduction in metals consists in the movement of detached electrons, and many other phenomena, both electrical and thermal, can be more or less completely explained by their agency. It has been supposed that certain electrons revolve like satellites in orbits around the atoms with which they are associated, a view which receives strong support from the phenomena of the Zeeman effect, and on this assumption a theory has been worked out by P. Langevin,[94] which accounts for many of the observed facts of magnetism. As a consequence of the structure of the molecule, which is an aggregation of atoms, the planes of the orbits around the latter may be oriented in various positions, and the direction of revolution may be right-handed or left-handed with respect to the direction of any applied magnetic field. For those orbits whose projection upon a plane perpendicular to the field is right-handed, the period of revolution will be accelerated by the field (since the electron current is negative), and the magnetic moment consequently increased; for those which are left-handed, the period will be retarded and the moment diminished. The effect of the field upon the speed of the revolving electrons, and therefore upon the moments of the equivalent magnets, is necessarily a very small one. If S is the area of the orbit described in time τ by an electron of charge e, the moment of the equivalent magnet is M = eSτ; and the change in the value of M due to an external field H is shown to be ΔM = −He2S/4πm, m being the mass of the electron. Whence
| ΔM | = − | Hτ e | . |
| M | 4π m |
According to the best determinations the value of e/m does not exceed 1.8 × 107, and τ is of the order of 10−15 second, the period of luminous vibrations; hence ΔM/M must always be less than 10−9H, and therefore the strongest fields yet reached experimentally, which fall considerably short of 105, could not change the magnetic moment M by as much as a ten-thousandth part. If the structure of the molecule is so perfectly symmetrical that, in the absence of any external field, the resultant magnetic moment of the circulating electrons is zero, then the application of a field, by accelerating the right-handed (negative) revolutions, and retarding those which are left-handed, will induce in the substance a resultant magnetization opposite in direction to the field itself; a body composed of such symmetrical molecules is therefore diamagnetic. If however the structure of the molecule is such that the electrons revolving around its atoms do not exactly cancel one another’s effects, the molecule constitutes a little magnet, which under the influence of an external field will tend to set itself with its axis parallel to the field. Ordinarily a substance composed of asymmetrical molecules is paramagnetic, but if the elementary magnets are so conditioned by their strength and concentration that mutual action between them is possible, then the substance is ferromagnetic. In all cases however it is the diamagnetic condition that is initially set up—even iron is diamagnetic—though the diamagnetism may be completely masked by the superposed paramagnetic or ferromagnetic condition. Diamagnetism, in short, is an atomic phenomenon; paramagnetism and ferromagnetism are molecular phenomena. Hence may be deduced an explanation of the fact that, while the susceptibility of all known diamagnetics (except bismuth and antimony) is independent of the temperature, that of paramagnetics varies inversely as the absolute temperature, in accordance with the law of Curie.
13. Historical and Chronological Notes
The most conspicuous property of the lodestone, its attraction for iron, appears to have been familiar to the Greeks at least as early as 800 B.C., and is mentioned by Homer, Plato, Aristotle, Theophrastus and others. A passage in De rerum natura (vi. 910–915) by the Roman poet, Lucretius (96-55 B.C.), in which it is stated that the stone can support a chain of little rings, each adhering to the one above it, indicates that in his time the phenomenon of magnetization by induction had also been observed. The property of orientation, in virtue of which a freely suspended magnet points approximately to the geographical north and south, is not referred to by any European writer before the 12th century, though it is said to have been known to the Chinese at a much earlier period. The application of this property to the construction of the mariner’s compass is obvious, and it is in connexion with navigation that the first references to it occur (see Compass). The needles of the primitive compasses, being made of iron, would require frequent re-magnetization, and a “stone” for the purpose of “touching the needle” was therefore generally included in the navigator’s outfit. With the constant practice of this operation it is hardly possible that the repulsion acting between like poles should have entirely escaped recognition; but though it appears to have been noticed that the lodestone sometimes repelled iron instead of attracting it, no clear statement of the fundamental law that unlike poles attract while like poles repel was recorded before the publication in 1581 of the New Attractive by Robert Norman, a pioneer in accurate magnetic work. The same book contains an account of Norman’s discovery and correct measurement of the dip (1576). The downward tendency of the north pole of a magnet pivoted in the usual way had been observed by G. Hartmann of Nüremberg in 1544, but his observation was not published till much later.
The foundations of the modern science of magnetism were laid by William Gilbert (q.v.). His De magnete magneticisque corporibus et de magno magnete tellure physiologia nova (1600), contains many references to the expositions of earlier writers from Plato down to those of the author’s own age. These show that the very few facts known with certainty were freely supplemented by a number of ill-founded conjectures, and sometimes even by “figments and falsehoods, which in the earliest times, no less than nowadays, used to be put forth by raw smatterers and copyists to be swallowed of men.”[95] Thus it was taught that “if a lodestone be anointed with garlic, or if a diamond be near, it does not attract iron,” and that “if pickled in the salt of a sucking fish, there is power to pick up gold which has fallen into the deepest wells.” There were said to be “various kinds of magnets, some of which attract gold, others silver, brass, lead; even some which attract flesh, water, fishes;” and stories were told about “mountains in the north of such great powers of attraction that ships are built with wooden pegs, lest the iron nails should be drawn from the timber.” Certain occult powers were also attributed to the stone. It was “of use to thieves by its fume and sheen, being a stone born, as it were, to aid theft,” and even opening bars and locks; it was effective as a love potion, and possessed “the power to reconcile husbands to their wives, and to recall brides to their husbands.” And much more of the same kind, which, as Gilbert says, had come down “even to [his] own day through the writings of a host of men, who, to fill out their volumes to a proper bulk, write and copy out pages upon pages on this, that and the other subject, of which they know almost nothing for certain of their own experience.” Gilbert himself absolutely disregarded authority, and accepted nothing at second-hand. His title to be honoured as the “Father of Magnetic Philosophy” is based even more largely upon the scientific method which he was the first to inculcate and practise than upon the importance of his actual discoveries. Careful experiment and observation, not the inner consciousness, are, he insists, the only foundations of true science. Nothing has been set down in his book “which hath not been explored and many times performed and repeated” by himself. “It is very easy for men of acute intellect, apart from experiment and practice, to slip and err.” The greatest of Gilbert’s discoveries was that the globe of the earth was magnetic and a magnet; the evidence by which he supported this view was derived chiefly from ingenious experiments made with a spherical lodestone or terrella, as he termed it, and from his original observation that an iron bar could be magnetized by the earth’s force. He also carried out some new experiments on the effects of heat, and of screening by magnetic substances, and investigated the influence of shape upon the magnetization of iron. But the bulk of his work consisted in imparting scientific definiteness to what was already vaguely known, and in demolishing the errors of his predecessors.
No material advance upon the knowledge recorded in Gilbert’s book was made until the establishment by Coulomb in 1785 of the law of magnetic action. The difficulties attending the experimental investigation of the forces acting between magnetic poles have already been referred to, and indeed a rigorously exact determination of the mutual action could only be made under conditions which are in practice unattainable. Coulomb,[96] however, by using long and thin steel rods, symmetrically magnetized, and so arranged that disturbing influences became negligibly small, was enabled to deduce from his experiments with reasonable certainty the law that the force of attraction or repulsion between two poles varies inversely as the square of the distance between them. Several previous attempts had been made to discover the law of force, with various results, some of which correctly indicated the inverse square; in particular the German astronomer, J. Tobias Mayer (Gött. Anzeiger, 1760), and the Alsatian mathematician, J. Heinrich Lambert (Hist. de l’Acad. Roy. Berlin, 1766, p. 22), may fairly be credited with having anticipated the law which was afterwards more satisfactorily established by Coulomb. The accuracy of this law was in 1832 confirmed by Gauss,[97] who employed an indirect but more perfect method than that of Coulomb, and also, as Maxwell remarks, by all observers in magnetic observatories, who are every day making measurements of magnetic quantities, and who obtain results which would be inconsistent with each other if the law of force had been erroneously assumed.
Coulomb’s researches provided data for the development of a mathematical theory of magnetism, which was indeed initiated by himself, but was first treated in a complete form by Poisson in a series of memoirs published in 1821 and later.[98] Poisson assumed the existence of two dissimilar magnetic fluids, any element of which acted upon any other distant element in accordance with Coulomb’s law of the inverse square, like repelling and unlike attracting one another. A magnetizable substance was supposed to consist of an indefinite number of spherical particles, each containing equivalent quantities of the two fluids, which could move freely within a particle, but could never pass from one particle to another. When the fluids inside a particle were mixed together, the particle was neutral; when they were more or less completely separated, the particle became magnetized to an intensity depending upon the magnetic force applied; the whole body therefore consisted of a number of little spheres having north and south poles, each of which exerted an elementary action at a distance. On this hypothesis Poisson investigated the forces due to bodies magnetized in any manner, and also originated the mathematical theory of magnetic induction. The general confirmation by experiment of Poisson’s theoretical results created a tendency to regard his hypothetical magnetic fluids as having a real existence; but it was pointed out by W. Thomson (afterwards Lord Kelvin) in 1849 that while no physical evidence could be adduced in support of the hypothesis, certain discoveries, especially in electromagnetism, rendered it extremely improbable (Reprint, p. 344). Regarding it as important that all reasoning with reference to magnetism should be conducted without any uncertain assumptions, he worked out a mathematical theory upon the sole foundation of a few well-known facts and principles. The results were substantially the same as those given by Poisson’s theory, so far as the latter went, the principal additions including a fuller investigation of magnetic distribution, and the theory of magnetic induction in aeolotropic or crystalline substances. The mathematical theory which was constructed by Poisson, and extended and freed from doubtful hypotheses by Kelvin, has been elaborated by other investigators, notably F. E. Neumann, G. R. Kirchhoff, and Maxwell. The valuable work of Gauss on magnetic theory and measurements, especially in relation to terrestrial magnetism, was published in his Intensitas vis magneticae terrestris, 1833, and in memoirs communicated to the Resultate aus den Beobachtungen des magnetischen Vereins, 1838 and 1839, which, with others, are contained in vol. 5 of the collected Werke. Weber’s molecular theory, which has already been referred to, appeared in 1852.[99]
An event of the first importance was the discovery made in 1819 by H. C. Oersted [100] that a magnet placed near a wire carrying an electric current tended to set itself at right angles to the wire, a phenomenon which indicated that the current was surrounded by a magnetic field. This discovery constituted the foundation of electromagnetism, and its publication in 1820 was immediately followed by A. M. Ampère’s experimental and theoretical investigation of the mutual action of electric currents,[101] and of the equivalence of a closed circuit to a polar magnet, the latter suggesting his celebrated hypothesis that molecular currents were the cause of magnetism. In the same year D. F. Arago[102] succeeded in magnetizing a piece of iron by the electric current, and in 1825 W. Sturgeon[103] publicly exhibited an apparatus “acting on the principle of powerful magnetism and feeble galvanism” which is believed to have constituted the first actual electromagnet. Michael Faraday’s researches were begun in 1831 and continued for more than twenty years. Among the most splendid of his achievements was the discovery of the phenomena and laws of magneto-electric induction, the subject of two papers communicated to the Royal Society in 1831 and 1832. Another was the magnetic rotation of the plane of polarization of light, which was effected in 1845, and for the first time established a relation between light and magnetism. This was followed at the close of the same year by the discovery of the magnetic condition of all matter, a discovery which initiated a prolonged and fruitful study of paramagnetic and diamagnetic phenomena, including magnecrystallic action and “magnetic conducting power,” now known as permeability. Throughout his researches Faraday paid special regard to the medium as the true seat of magnetic action, being to a large extent guided by his pregnant conception of “lines of force,” or of induction, which he considered to be “closed curves passing in one part of the course through the magnet to which they belong, and in the other part through space,” always tending to shorten themselves, and repelling one another when they were side by side (Exp. Res. §§ 3266–8, 3271). In 1873 James Clerk Maxwell published his classical Treatise on Electricity and Magnetism, in which Faraday’s ideas were translated into a mathematical form. Maxwell explained electric and magnetic forces, not by the action at a distance assumed by the earlier mathematicians, but by stresses in a medium filling all space, and possessing qualities like those attributed to the old luminiferous ether. In particular, he found that the calculated velocity with which it transmitted electromagnetic disturbances was equal to the observed velocity of light; hence he was led to believe, not only that his medium and the ether were one and the same, but, further, that light itself was an electromagnetic phenomenon. Since the experimental confirmation of Maxwell’s views by H. R. Hertz in 1888 (Weid. Ann., 1888, 34, 155, 551, 609; and later vols.) they have commanded universal assent, and his methods are adopted in all modern work on electricity and magnetism.
The practice of measuring magnetic induction and permeability with scientific accuracy was introduced in 1873 by H. A. Rowland,[104] whose careful experiments led to general recognition of the fact previously ignored by nearly all investigators, that magnetic susceptibility and permeability are by no means constants (at least in the case of the ferromagnetic metals) but functions of the magnetizing force. New light was thrown upon many important details of magnetic science by J. A. Ewing’s Experimental Researches of 1885; throughout the whole of his work special attention was directed to that curious lagging action to which the author applied the now familiar term “hysteresis.”[105] His well-known modification[106] of Weber’s molecular theory, published in 1890, presented for the first time a simple and sufficient explanation of hysteresis and many other complexities of magnetic quality. The amazing discoveries made by J. J. Thomson in 1897 and 1898[107] resulted in the establishment of the electron theory, which has already effected developments of an almost revolutionary character in more than one branch of science. The application of the theory by P. Langevin to the case of molecular magnetism has been noticed above, and there can be little doubt that in the near future it will contribute to the solution of other problems which are still obscure.
See W. Gilbert, De magnete (London, 1600; trans. by P. F. Mottelay, New York, 1893, and for the Gilbert Club, London, 1900); M. Faraday, Experimental Researches in Electricity, 3 vols. (London, 1839, 1844 and 1855); W. Thomson (Lord Kelvin), Reprint of Papers on Electrostatics and Magnetism (London, 1884, containing papers on magnetic theory originally published between 1844 and 1855, with additions); J. C. Maxwell, Treatise on Electricity and Magnetism (3rd ed., Oxford, 1892); E. Mascart and J. Joubert, Leçons sur l’électricité et le magnétisme (2nd ed., Paris, 1896–1897; trans., not free from errors, by E. Atkinson, London, 1883); J. A. Ewing, Magnetic Induction in Iron and other Metals (3rd ed., London, 1900); J. J. Thomson, Recent Researches in Electricity and Magnetism (Oxford, 1893); Elements of Mathematical Theory of Electricity and Magnetism (3rd ed., Cambridge, 1904); H. du Bois, The Magnetic Circuit (trans. by E. Atkinson, London, 1896); A. Gray, Treatise on Magnetism and Electricity, vol. i. (London, 1898); J. A. Fleming, Magnets and Electric Currents (London, 1898); C. Maurain, Le magnétisme du fer (Paris, 1899; a lucid summary of the principal facts and laws, with special regard to their practical application); Rapports présentés au Congrès international de physique, vol. ii. (Paris, 1900); G. C. Foster and A. W. Porter, Treatise on Electricity and Magnetism (London, 1903); A. Winkelmann, Handbuch der Physik, vol. v. part i. (2nd ed., Leipzig, 1905; the most exhaustive compendium of magnetic science yet published, containing references to all important works and papers on every branch of the subject). (S. Bi.)
- ↑ In London in 1910 the needle pointed about 16° W. of the geographical north. (See Terrestrial Magnetism.)
- ↑ For the relations between magnetism and light see Magneto-Optics.
- ↑ Clerk Maxwell employed German capitals to denote vector quantities. J. A. Fleming first recommended the use of blockletters as being more convenient both to printers and readers.
- ↑ The C.G.S. unit of current=10 amperes.
- ↑ The principal theoretical investigations are summarized in Mascart and Joubert’s Electricity and Magnetism, i. 391–398 and ii. 646–657. The case of a long iron bar has been experimentally studied with great care by C. G. Lamb, Proc. Phys. Soc., 1899, 16, 509.
- ↑ Wied. Ann., 1884, 22, 411.
- ↑ See C. G. Lamb, loc. cit. p. 518.
- ↑ Hopkinson specified the retentiveness by the numerical value of the “residual induction” (= 4πI).
- ↑ For all except ferromagnetic substances the coefficient is sensibly equal to κ.
- ↑ See W. Thomson’s Reprint, §§ 615, 634–651.
- ↑ Ibid. §§ 646, 684.
- ↑ Faraday, Exp. Res. xxi.
- ↑ J. J. Thomson, Electricity and Magnetism, § 205.
- ↑ Maxwell, Electricity and Magnetism, § 431.
- ↑ H. du Bois, Electrician, 1898, 40, 317.
- ↑ M. Faraday, Exp. Res. xxii., xxiii.; W. Thomson, Reprint, § 604; J. C. Maxwell, Treatise, § 435; E. Mascart and J. Joubert, Electricity and Magnetism, §§ 384, 396, 1226; A. Winkelmann, Physik, v. 287.
- ↑ See A. Winkelmann, Physik, v. 69-94; Mascart and Joubert. Electricity and Magnetism, ii. 617.
- ↑ Sci. Abs. A, 1906, 9, 225.
- ↑ See C. G. Lamb, Proc. Phys. Soc., 1899, 16, 517.
- ↑ Soc. Franc. Phys. Séances, 1904, 1, 27.
- ↑ E. G. Warburg, Wied. Ann. 1881, 13, 141; Ewing, Phil. Trans., 1885, 176, 549; Hopkinson, Phil. Trans. 1885, 176, 466. For a simple proof, see Ewing, Magnetic Induction (1900), p. 99. Hopkinson pointed out that the greatest dissipation of energy which can be caused by a to-and-fro reversal is approximately represented by Coercive force × maximum induction /π.
- ↑ Magnetic Induction, 1900, 378.
- ↑ Phil. Trans., 1902, 198, 33.
- ↑ Phil. Mag., 1903, 5, 117.
- ↑ Some experiments by F. G. Baily showed that hysteresis ceased to increase when B was carried beyond 23,000. This value of B corresponds to I = 1640, the saturation point for soft iron.—Brit. Assoc. Rep., 1895, p. 636.
- ↑ Tokyo Phys.-Math. Soc., 1904, 2, No. 14.
- ↑ Phil. Mag., 1873, 46, 140.
- ↑ S. Bidwell, Proc. Roy. Soc., 1886, 40, 495.
- ↑ Since in most practicable experiments H3 is negligible in comparison with B2, the force may be taken as B2/8π without sensible error.
- ↑ The same phenomenon is exhibited in a less marked degree when soft iron is magnetized in stronger fields (Ewing, Phil. Trans., 1885, 176, 569).
- ↑ Principal publications: J. P. Joule, Scientific Papers, pp. 46, 235; A. M. Meyer, Phil. Mag., 1873, 46, 177; W. F. Barrett, Nature, 1882, 26, 585; S. Bidwell, Phil. Trans., 1888, 179A, 205; Proc. Roy. Soc., 1886, 40, 109 and 257; 1888, 43, 406; 1890, 47, 469; 1892, 51, 495; 1894, 55, 228; 1894, 56, 94; 1904, 74, 60; Nature, 1899, 60, 222; M. Cantone, Mem. d. Acc d. Lincei, 1889, 6, 487; Rend. d. Acc. d. Lincei, 1890, 6, 252; A. Berget, C.R., 1892, 115, 722; S. J. Lochner, Phil. Mag., 1893, 36, 498; H. Nagaoka, Phil. Mag., 1894, 37, 131; Wied. Ann., 1894, 53, 487; C. G. Knott, Proc. Roy. Soc. Ed., 1891, 18, 315; Phil. Mag., 1894, 37, 141; Trans. Roy. Soc. Ed., 1896, 38, 527; 1898, 39, 457; C. G. Knott and A. Shand, Proc. Roy. Soc. Ed., 1892, 19, 85 and 249; 1894, 20, 295; L. T. More, Phil. Mag., 1895, 40, 345; G. Klingenberg, Rostock Univ. Thesis, Berlin, 1897; E. T. Jones, Phil. Trans., 1897, 189A, 189; B. B. Brackett, Phys. Rev., 1897, 5, 257; H. Nagaoka and K. Honda, Phil. Mag., 1898, 46, 261; 1900, 49, 329; Journ. Coll. Sci. Tokyo, 1900, 13, 57; 1903, 19, art. 11; J. S. Stevens, Phys. Rev., 1898, 7, 19; E. Rhoads, Phys. Rev., 1898, 7, 5; Phil. Mag., 1901, 2, 463; G. A. Shakespear, Phil. Mag., 1899, 17, 539; K. Honda, Journ. Coll. Sci. Tokyo, 1900, 13, 77; L. W. Austin, Phys. Rev., 1900, 10, 180; Deutsch. Phys. Gesell. Verh., 1904, 6, 4, 211; K. Honda and S. Shimizu, Phil. Mag., 1902, 4, 338; 1905, 10, 548.
- ↑ The loads were successively applied in decreasing order of magnitude. They are indicated in fig. 25 as kilos per sq. cm.
- ↑ Joule believed that the volume was unchanged.
- ↑ For a discussion of theories of magnetic stress, with copious references, see Nagaoka, Rap. du Congrès International de Physique (Paris, 1900), ii. 545. Also Nagaoka and Jones, Phil. Mag., 1896, 41, 454.
- ↑ S. Bidwell, Phil. Trans., 1888, 179a, 321.
- ↑ Phil. Mag., 1895, 40, 345.
- ↑ J. C. Maxwell, Treatise, § 643.
- ↑ See correspondence in Nature, 1896, 53, pp. 269, 316, 365, 462, 533; 1906, 74, pp. 317, 539; B. B. Brackett, loc. cit., quotes the opinion of H. A. Rowland in support of compressive stress.
- ↑ J. A. Ewing, Phil. Trans., 1885, 176, 580; 1888, 179, 333; Magnetic Induction, 1900, ch. ix.; J. A. Ewing and G. C. Cowan, Phil. Trans., 1888, 179a, 325; C. G. Knott, Trans. Roy. Soc. Ed., 1882–1883, 32, 193; 1889, 35, 377; 1891, 36, 485; Proc. Roy. Soc. Ed., 1899, 586; H. Nagaoka, Phil. Mag., 1889, 27, 117; 1890, 29, 123; H. Nagaoka and K. Honda, Journ. Coll. Sci. Tokyo, 1900, 13, 263; 1902, 16, art. 8; Phil. Mag., 1898, 46, 261; 1902, 4, 45; K. Honda and S. Shimizu, Ann. d. Phys., 1904, 14, 791; Tokyo Physico-Math. Soc. Rep., 1904, 2, No. 13; K. Honda and T. Terada, Journ. Coll. Sci. Tokyo, 1906, 21, art. 4.
- ↑ H. Tomlinson found a critical point in the “temporary magnetization” of nickel (Proc. Phys. Soc., 1890, 10, 367, 445), but this does not correspond to a Villari reversal. Its nature is made clear by Ewing and Cowan’s curves (Phil. Trans., 1888, 179, plates 15, 16).
- ↑ Wied. Ann., 1894, 52, 462; Electrician, 1894, 34, 143.
- ↑ Phil. Trans., 1890, 131, 329.
- ↑ Magnetic Induction, 1900, 222.
- ↑ Phys. Rev., 1904, 18, 432.
- ↑ Phil. Mag., 1886, 22, 50.
- ↑ Ibid. 251.
- ↑ Phil. Mag., 1891, 32, 383.
- ↑ C.R., 1896, 122, 1192; 1898, 126, 463.
- ↑ Phil. Mag., 1889, 27, 117.
- ↑ Journ. Coll. Sci. Tokyo, 1904, 19, art. 9.
- ↑ Phil. Mag., 1905, 10, 548; Tokyo Phys.-Math. Soc. Rep., 1904, 2, No. 14; Journ. Coll. Sci. Tokyo, 1905, 20, art. 6.
- ↑ C.R., 1888, 106, 129.
- ↑ Proc. Phys. Soc., 1888, 9, 181.
- ↑ C.R., 1892, 115, 805; 1894, 118, 796 and 859.
- ↑ Elekt. Zeits., 1894, 15, 194.
- ↑ Phil. Mag., 1900, 50, 1.
- ↑ Phil. Trans., 1903, 201, 1.
- ↑ Phil. Mag., 1904, 8, 179.
- ↑ A. M. Thiessen (Phys., 1899, 8, 65) and G. Claude (C. R., 1899, 129, 409) found that for considerable inductions (B = 15,000) the permeability and hysteresis-loss remained nearly constant down to −186°; for weak inductions both notably diminished with temperature.
- ↑ Proc. Roy. Soc., 1898, 62, 210.
- ↑ C.R., 1895, 120, 263.
- ↑ Amer. Journ. Sci., 1898, 5, 245.
- ↑ Phys. Rev., 1901, 14, 181.
- ↑ C.R., 1897, 124, 176 and 1515; 1897, 125, 235; 1898, 126, 738.
- ↑ Ibid., 1898, 126, 741.
- ↑ Ibid., 1899, 128, 304 and 1395.
- ↑ See also J. Hopkinson, Journ. Inst. Elect. Eng., 1890, 19, 20, and J. A. Ewing, Phil. Trans., 1889, 180, 239.
- ↑ Many of the figures which, through an error, were inaccurately stated in the first paper are corrected in the second.
- ↑ The marked effect of silicon in increasing the permeability of cast iron has also been noticed by F. C. Caldwell, Elect. World, 1898, 32, 619.
- ↑ Trans. Roy. Dub. Soc., 1902–4, 8, 1 and 123.
- ↑ J. Trowbridge and S. Sheldon, Phil. Mag., 1890, 29, 136; W. H. Preece, Journ. Inst. Elec. Eng., 1890, 19, 62; Electrician, 1890, 25, 546; I. Klemençiç, Wien. Ber., 1896, 105, IIa, 635; B. O. Peirce, Am. Journ. Sci., 1896, 2, 347; A. Abt, Wied. Ann., 1898, 66, 116; F. Osmond, C. R., 1899, 128, 1513.
- ↑ Deutsch. phys. Gesell. Verh., 1903, 5, 220 and 224.
- ↑ Exp. Res., iii. 440.
- ↑ No record can be found of experiments with manganese at the temperature of liquid air or hydrogen; probably, however, negative results would not be published.
- ↑ The critical temperature of iron, for instance, is raised more than 100° by the addition of a little carbon and tungsten.
- ↑ Bull. Soc. Int. des Électriciens, 1906, 6, 301.
- ↑ Proc. Roy. Soc., 1905, 76A, 271.
- ↑ E. H. Hall, Phil. Mag., 1880, 9, 225; 1880, 10, 301; 1881, 12, 157; 1883, 15, 341; 1885, 19, 419.
- ↑ The large Hall effect in bismuth was discovered by Righi, Journ. de Phys., 1884, 3, 127.
- ↑ References.—(2) A. von Ettinghausen, Wied. Ann., 1887, 31, 737.—(4) H. W. Nernst, ibid., 784.—(i.) and (iv.); A. von Ettinghausen and H. W. Nernst, Wied. Ann., 1886, 29, 343.—(ii.) and (iii.); A. Righi, Rend. Acc. Linc., 1887, 3 II, 6 and I, 481; and A. Leduc, Journ. de Phys., 1887, 6, 78. Additional authorities are quoted by Lloyd, loc. cit.
- ↑ P. Drude, Ann. d. Phys., 1900, 1, 566; 1900, 3, 369; 1902, 7, 687. See also E. van Everdingen, Arch. Néerlandaises, 1901, 4, 371; G. Barlow, Ann. d. Phys., 1903, 12, 897; H. Zahn, ibid. 1904, 14, 886; 1905, 16, 148.
- ↑ Phil. Trans., 1856, p. 722. According to the nomenclature adopted by the best modern authorities, a metal A is said to be thermo-electrically positive to another metal B when the thermo-current passes from A to B through the cold junction, and from B to A through the hot (see Thermo-Electricity).
- ↑ C.R., 1893, 116, 997.
- ↑ Journ. de Phys., 1896, 5, 53.
- ↑ Phil. Trans., 1887, 177, 373.
- ↑ Proc. Roy. Soc., 1885, 39, 513.
- ↑ Phys. Rev., 1902, 15, 321. The sign of the thermo-electric effect for nickel, as given by Rhoads, is incorrect.
- ↑ Proc. Roy. Soc., 1904, 73, 413.
- ↑ C.R., 1903, 136, 1131.
- ↑ Journ. Coll. Sci. Tokyo, 1906, 21, art. 4. The paper contains 40 tables and 85 figures.
- ↑ This deduction from Ewing’s theory appears to have been first suggested by J. Swinburne. See Industries, 1890, 289.
- ↑ R. Beattie (Phil. Mag., 1901, 1, 642) has found similar effects in nickel and cobalt.
- ↑ The charge associated with a corpuscle is the same as that carried by a hydrogen atom. G. J. Stoney in 1881 (Phil. Mag., 1881, 11, 387) pointed out that this latter constituted the indivisible “atom of electricity” or natural unit charge. Later he proposed (Trans. Roy. Dub. Soc., 1891, 4, 583) that such unit charge should be called an “electron.” The application of this term to Thomson’s corpuscle implies, rightly or wrongly, that notwithstanding its apparent mass, the corpuscle is in fact nothing more than an atom of electricity. The question whether a corpuscle actually has a material gravitating nucleus is undecided, but there are strong reasons for believing that its mass is entirely due to the electric charge.
- ↑ Jour. de Phys., 1905, 4, 678; translated in Electrician, 1905, 56, 108 and 141.
- ↑ The quotations are from the translation published by the Gilbert Club, London, 1900.
- ↑ C. A. Coulomb, Mem. Acad. Roy. Paris, 1785, p. 578.
- ↑ Intensitas vis magneticae, § 21, C. F. Gauss’s Werke, 5, 79. See also J. J. Thomson, Electricity and Magnetism, § 132.
- ↑ S. D. Poisson, Mém. de l’Institut, 1821 and 1822, 5, 247, 488; 1823, 6, 441; 1838, 16, 479.
- ↑ For outlines of the mathematical theory of magnetism and references see H. du Bois, Magnetic Circuit, chs. iii. and iv.
- ↑ Gilbert’s Ann. d. phys., 1820, 6, 295.
- ↑ Ann. de chim. et de phys., 1820, 15, 59, 170; Recueil d’observations électrodynamiques, 1822; Théories des phénomènes électrodynamiques, 1826.
- ↑ Ann. de chim. et de phys., 1820, 15, 93.
- ↑ Trans. Soc. Arts, 1825, 43, 38.
- ↑ Phil. Mag., 1873, 46, 140; 1874, 48, 321.
- ↑ Phil. Trans., 1885, 176, 523; Magnetic Induction, 1900.
- ↑ Proc. Roy. Soc., 1890, 48, 342.
- ↑ Phil. Mag., 1897, 44, 293; 1898, 46, 528.










