1911 Encyclopædia Britannica/Mechanics
MECHANICS. The subject of mechanics may be divided into two parts: (1) theoretical or abstract mechanics, and (2) applied mechanics.
1. Theoretical Mechanics
Historically theoretical mechanics began with the study of practical contrivances such as the lever, and the name mechanics (Gr. τὰ μηχανικά), which might more properly be restricted to the theory of mechanisms, and which was indeed used in this narrower sense by Newton, has clung to it, although the subject has long attained a far wider scope. In recent times it has been proposed to adopt the term dynamics (from Gr. δύναμις force,) as including the whole science of the action of force on bodies, whether at rest or in motion. The subject is usually expounded under the two divisions of statics and kinetics, the former dealing with the conditions of rest or equilibrium and the latter with the phenomena of motion as affected by force. To this latter division the old name of dynamics (in a restricted sense) is still often applied. The mere geometrical description and analysis of various types of motion, apart from the consideration of the forces concerned, belongs to kinematics. This is sometimes discussed as a separate theory, but for our present purposes it is more convenient to introduce kinematical motions as they are required. We follow also the traditional practice of dealing first with statics and then with kinetics. This is, in the main, the historical order of development, and for purposes of exposition it has many advantages. The laws of equilibrium are, it is true, necessarily included as a particular case under those of motion; but there is no real inconvenience in formulating as the basis of statics a few provisional postulates which are afterwards seen to be comprehended in a more general scheme.
The whole subject rests ultimately on the Newtonian laws of motion and on some natural extensions of them. As these laws are discussed under a separate heading (Motion, Laws of), it is here only necessary to indicate the standpoint from which the present article is written. It is a purely empirical one. Guided by experience, we are able to frame rules which enable us to say with more or less accuracy what will be the consequences, or what were the antecedents, of a given state of things. These rules are sometimes dignified by the name of “laws of nature,” but they have relation to our present state of knowledge and to the degree of skill with which we have succeeded in giving more or less compact expression to it. They are therefore liable to be modified from time to time, or to be superseded by more convenient or more comprehensive modes of statement. Again, we do not aim at anything so hopeless, or indeed so useless, as a complete description of any phenomenon. Some features are naturally more important or more interesting to us than others; by their relative simplicity and evident constancy they have the first hold on our attention, whilst those which are apparently accidental and vary from one occasion to another arc ignored, or postponed for later examination. It follows that for the purposes of such description as is possible some process of abstraction is inevitable if our statements are to be simple and definite. Thus in studying the flight of a stone through the air we replace the body in imagination by a mathematical point endowed with a mass-coefficient. The size and shape, the complicated spinning motion which it is seen to execute, the internal strains and vibrations which doubtless take place, are all sacrificed in the mental picture in order that attention may be concentrated on those features of the phenomenon which are in the first place most interesting to us. At a later stage in our subject the conception of the ideal rigid body is introduced; this enables us to fill in some details which were previously wanting, but others are still omitted. Again, the conception of a force as concentrated in a mathematical line is as unreal as that of a mass concentrated in a point, but it is a convenient fiction for our purpose, owing to the simplicity which it lends to our statements.
The laws which are to be imposed on these ideal representations are in the first instance largely at our choice. Any scheme of abstract dynamics constructed in this way, provided it be self-consistent, is mathematically legitimate; but from the physical point of view we require that it should help us to picture the sequence of phenomena as they actually occur. Its success or failure in this respect can only be judged a posteriori by comparison of the results to which it leads with the facts. It is to be noticed, moreover, that all available tests apply only to the scheme as a whole; owing to the complexity of phenomena we cannot submit any one of its postulates to verification apart from the rest.
It is from this point of view that the question of relativity of motion, which is often felt to be a stumbling-block on the very threshold of the subject, is to be judged. By “motion” we mean of necessity motion relative to some frame of reference which is conventionally spoken of as “fixed.” In the earlier stages of our subject this may be any rigid, or apparently rigid, structure fixed relatively to the earth. If we meet with phenomena which do not fit easily into this view, we have the alternatives either to modify our assumed laws of motion, or to call to our aid adventitious forces, or to examine whether the discrepancy can be reconciled by the simpler expedient of a new basis of reference. It is hardly necessary to say that the latter procedure has hitherto been found to be adequate. As a first step we adopt a system of rectangular axes whose origin is fixed in the earth, but whose directions are fixed by relation to the stars; in the planetary theory the origin is transferred to the sun, and afterwards to the mass-centre of the solar system; and so on. At each step there is a gain in accuracy and comprehensiveness; and the conviction is cherished that some system of rectangular axes exists with respect to which the Newtonian scheme holds with all imaginable accuracy.
A similar account might be given of the conception of time as a measurable quantity, but the remarks which it is necessary to make under this head will find a place later.
The following synopsis shows the scheme on which the treatment is based:—
| Part 1.—Statics. | |
| 1. | Statics of a particle. |
| 2. | Statics of a system of particles. |
| 3. | Plane kinematics of a rigid body. |
| 4. | Plane statics. |
| 5. | Graphical statics. |
| 6. | Theory of frames. |
| 7. | Three-dimensional kinematics of a rigid body. |
| 8. | Three-dimensional statics. |
| 9. | Work. |
| 10. | Statics of inextensible chains. |
| 11. | Theory of mass-systems. |
| Part 2.—Kinetics. | |
| 12. | Rectilinear motion. |
| 13. | General motion of a particle. |
| 14. | Central forces. Hodograph. |
| 15. | Kinetics of a system of discrete particles. |
| 16. | Kinetics of a rigid body. Fundamental principles. |
| 17. | Two-dimensional problems. |
| 18. | Equations of motion in three dimensions. |
| 19. | Free motion of a solid. |
| 20. | Motion of a solid of revolution. |
| 21. | Moving axes of reference. |
| 22. | Equations of motion in generalized co-ordinates. |
| 23. | Stability of equilibrium. Theory of vibrations. |
§ 1. Statics of a Particle.—By a particle is meant a body whose position can for the purpose in hand be sufficiently specified by a mathematical point. It need not be “infinitely small,” or even small compared with ordinary standards; thus in astronomy such vast bodies as the sun, the earth, and the other planets can for many purposes be treated merely as points endowed with mass.
A force is conceived as an effort having a certain direction and a certain magnitude. It is therefore adequately represented, for mathematical purposes, by a straight line AB drawn in the direction in question, of length proportional (on any convenient scale) to the magnitude of the force. In other words, a force is mathematically of the nature of a “vector” (see Vector Analysis, Quaternions). In most questions of pure statics we are concerned only with the ratios of the various forces which enter into the problem, so that it is indifferent what unit of force is adopted. For many purposes a gravitational system of measurement is most natural; thus we speak of a force of so many pounds or so many kilogrammes. The “absolute” system of measurement will be referred to below in Part II., Kinetics. It is to be remembered that all “force” is of the nature of a push or a pull, and that according to the accepted terminology of modern mechanics such phrases as “force of inertia,” “accelerating force,” “moving force,” once classical, are proscribed. This rigorous limitation of the meaning of the word is of comparatively recent origin, and it is perhaps to be regretted that some more technical term has not been devised, but the convention must now be regarded as established.
 |
| Fig. 1. |
The fundamental postulate of this part of our subject is that the two forces acting on a particle may be compounded by the “parallelogram rule.” Thus, if the two forces P,Q be represented by the lines OA, OB, they can be replaced by a single force R represented by the diagonal OC of the parallelogram determined by OA, OB. This is of course a physical assumption whose propriety is justified solely by experience. We shall see later that it is implied in Newton’s statement of his Second Law of motion. In modern language, forces are compounded by “vector-addition”; thus, if we draw in succession vectors HK→, KL→ to represent P, Q, the force R is represented by the vector HL→ which is the “geometric sum” of HK→, KL→.
By successive applications of the above rule any number of forces acting on a particle may be replaced by a single force which is the vector-sum of the given forces: this single force is called the resultant. Thus if AB→, BC→, CD→ ..., HK→ be vectors representing the given forces, the resultant will be given by AK→. It will be understood that the figure ABCD ... K need not be confined to one plane.
 |
| Fig. 2. |
If, in particular, the point K coincides with A, so that the resultant vanishes, the given system of forces is said to be in equilibrium—i.e. the particle could remain permanently at rest under its action. This is the proposition known as the polygon of forces. In the particular case of three forces it reduces to the triangle of forces, viz. “If three forces acting on a particle are represented as to magnitude and direction by the sides of a triangle taken in order, they are in equilibrium.”
A sort of converse proposition is frequently useful, viz. if three forces acting on a particle be in equilibrium, and any triangle be constructed whose sides are respectively parallel to the forces, the magnitudes of the forces will be to one another as the corresponding sides of the triangle. This follows from the fact that all such triangles are necessarily similar.
 |
| Fig. 3. |
As a simple example of the geometrical method of treating statical problems we may consider the equilibrium of a particle on a “rough” inclined plane. The usual empirical law of sliding friction is that the mutual action between two plane surfaces in contact, or between a particle and a curve or surface, cannot make with the normal an angle exceeding a certain limit λ called the angle of friction. If the conditions of equilibrium require an obliquity greater than this, sliding will take place. The precise value of λ will vary with the nature and condition of the surfaces in contact. In the case of a body simply resting on an inclined plane, the reaction must of course be vertical, for equilibrium, and the slope α of the plane must therefore not exceed λ. For this reason λ is also known as the angle of repose. If α > λ, a force P must be applied in order to maintain equilibrium; let θ be the inclination of P to the plane, as shown in the left-hand diagram. The relations between this force P, the gravity W of the body, and the reaction S of the plane are then determined by a triangle of forces HKL. Since the inclination of S to the normal cannot exceed λ on either side, the value of P must lie between two limits which are represented by L1H, L2H, in the right-hand diagram. Denoting these limits by P1, P2, we have
P2/W = L2H/HK = sin (α + λ)/cos (θ − λ).
It appears, moreover, that if θ be varied P will be least when L1H is at right angles to KL1, in which case P1 = W sin (α − λ), corresponding to θ = −λ.
 |
| Fig. 4. |
Just as two or more forces can be combined into a single resultant, so a single force may be resolved into components acting in assigned directions. Thus a force can be uniquely resolved into two components acting in two assigned directions in the same plane with it by an inversion of the parallelogram construction of fig. 1. If, as is usually most convenient, the two assigned directions are at right angles, the two components of a force P will be P cos θ, P sin θ, where θ is the inclination of P to the direction of the former component. This leads to formulae for the analytical reduction of a system of coplanar forces acting on a particle. Adopting rectangular axes Ox, Oy, in the plane of the forces, and distinguishing the various forces of the system by suffixes, we can replace the system by two forces X, Y, in the direction of co-ordinate axes; viz.—
Y = P1 sin θ1 + P2 sin θ2 + . . . = Σ (P sin θ).
These two forces X, Y, may be combined into a single resultant
R making an angle φ with Ox, provided
whence
For equilibrium we must have R = 0, which requires X = 0, Y = 0; in words, the sum of the components of the system must be zero for each of two perpendicular directions in the plane.
 |
| Fig. 5. |
A similar procedure applies to a three-dimensional system. Thus if, O being the origin, OH→ represent any force P of the system, the planes drawn through H parallel to the co-ordinate planes will enclose with the latter a parallelepiped, and it is evident that OH→ is the geometric sum of OA→, AN→, NH→, or OA→, OB→, OC→, in the figure. Hence P is equivalent to three forces Pl, Pm, Pn acting along Ox, Oy, Oz, respectively, where l, m, n, are the “direction-ratios” of OH→. The whole system can be reduced in this way to three forces
X = Σ (Pl), Y = Σ (Pm), Z = Σ (Pn),
acting along the co-ordinate axes. These can again be combined into a single resultant R acting in the direction (λ, μ, ν), provided
If the axes are rectangular, the direction-ratios become direction-cosines, so that λ2 + μ2 + ν2 = 1, whence
The conditions of equilibrium are X = 0, Y = 0, Z = 0.
§ 2. Statics of a System of Particles.—We assume that the mutual forces between the pairs of particles, whatever their nature, are subject to the “Law of Action and Reaction” (Newton’s Third Law); i.e. the force exerted by a particle A on a particle B, and the force exerted by B on A, are equal and opposite in the line AB. The problem of determining the possible configurations of equilibrium of a system of particles subject to extraneous forces which are known functions of the positions of the particles, and to internal forces which are known functions of the distances of the pairs of particles between which they act, is in general determinate. For if n be the number of particles, the 3n conditions of equilibrium (three for each particle) are equal in number to the 3n Cartesian (or other) co-ordinates of the particles, which are to be found. If the system be subject to frictionless constraints, e.g. if some of the particles be constrained to lie on smooth surfaces, or if pairs of particles be connected by inextensible strings, then for each geometrical relation thus introduced we have an unknown reaction (e.g. the pressure of the smooth surface, or the tension of the string), so that the problem is still determinate.
 |
| Fig. 6. |
 |
| Fig. 7. |
 |
| Fig. 8. |
The case of the funicular polygon will be of use to us later. A number of particles attached at various points of a string are acted on by given extraneous forces P1, P2, P3 . . . respectively. The relation between the three forces acting on any particle, viz. the extraneous force and the tensions in the two adjacent portions of the string can be exhibited by means of a triangle of forces; and if the successive triangles be drawn to the same scale they can be fitted together so as to constitute a single force-diagram, as shown in fig. 6. This diagram consists of a polygon whose successive sides represent the given forces P1, P2, P3 . . ., and of a series of lines connecting the vertices with a point O. These latter lines measure the tensions in the successive portions of string. As a special, but very important case, the forces P1, P2, P3 . . . may be parallel, e.g. they may be the weights of the several particles. The polygon of forces is then made up of segments of a vertical line. We note that the tensions have now the same horizontal projection (represented by the dotted line in fig. 7). It is further of interest to note that if the weights be all equal, and at equal horizontal intervals, the vertices of the funicular will lie on a parabola whose axis is vertical. To prove this statement, let A, B, C, D . . . be successive vertices, and let H, K . . . be the middle points of AC, BD . . .; then BH, CK . . . will be vertical by the hypothesis, and since the geometric sum of BA→, BC→ is represented by 2BH→, the tension in BA: tension in BC: weight at B
The tensions in the successive portions of the string are therefore proportional to the respective lengths, and the lines BH, CK . . . are all equal. Hence AD, BC are parallel and are bisected by the same vertical line; and a parabola with vertical axis can therefore be described through A, B, C, D. The same holds for the four points B, C, D, E and so on; but since a parabola is uniquely determined by the direction of its axis and by three points on the curve, the successive parabolas ABCD, BCDE, CDEF . . . must be coincident.
§ 3. Plane Kinematics of a Rigid Body.—The ideal rigid body is one in which the distance between any two points is invariable. For the present we confine ourselves to the consideration of displacements in two dimensions, so that the body is adequately represented by a thin lamina or plate.
 |
| Fig. 9. |
The position of a lamina movable in its own plane is determinate when we know the positions of any two points A, B of it. Since the four co-ordinates (Cartesian or other) of these two points are connected by the relation which expresses the invariability of the length AB, it is plain that virtually three independent elements are required and suffice to specify the position of the lamina. For instance, the lamina may in general be fixed by connecting any three points of it by rigid links to three fixed points in its plane. The three independent elements may be chosen in a variety of ways (e.g. they may be the lengths of the three links in the above example). They may be called (in a generalized sense) the co-ordinates of the lamina. The lamina when perfectly free to move in its own plane is said to have three degrees of freedom.
 |
| Fig. 10. |
 |
| Fig. 11. |
By a theorem due to M. Chasles any displacement whatever of the lamina in its own plane is equivalent to a rotation about some finite or infinitely distant point J. For suppose that in consequence of the displacement a point of the lamina is brought from A to B, whilst the point of the lamina which was originally at B is brought to C. Since AB, BC, are two different positions of the same line in the lamina they are equal, and it is evident that the rotation could have been effected by a rotation about J, the centre of the circle ABC, through an angle AJB. As a special case the three points A, B, C may be in a straight line; J is then at infinity and the displacement is equivalent to a pure translation, since every point of the lamina is now displaced parallel to AB through a space equal to AB.
Next, consider any continuous motion of the lamina. The latter may be brought from any one of its positions to a neighbouring one by a rotation about the proper centre. The limiting position J of this centre, when the two positions are taken infinitely close to one another, is called the instantaneous centre. If P, P′ be consecutive positions of the same point, and δθ the corresponding angle of rotation, then ultimately PP′ is at right angles to JP and equal to JP·δθ. The instantaneous centre will have a certain locus in space, and a certain locus in the lamina. These two loci are called pole-curves or centrodes, and are sometimes distinguished as the space-centrode and the body-centrode, respectively. In the continuous motion in question the latter curve rolls without slipping on the former (M. Chasles). Consider in fact any series of successive positions 1, 2, 3... of the lamina (fig. 11); and let J12, J23, J34... be the positions in space of the centres of the rotations by which the lamina can be brought from the first position to the second, from the second to the third, and so on. Further, in the position 1, let J12, J′23, J′34 . . . be the points of the lamina which have become the successive centres of rotation. The given series of positions will be assumed in succession if we imagine the lamina to rotate first about J12 until J′23 comes into coincidence with J23, then about J23 until J′34 comes into coincidence with J34, and so on. This is equivalent to imagining the polygon J12 J′23 J′34 . . ., supposed fixed in the lamina, to roll on the polygon J12 J23 J34 . . ., which is supposed fixed in space. By imagining the successive positions to be taken infinitely close to one another we derive the theorem stated. The particular case where both centrodes are circles is specially important in mechanism.
 |
| Fig. 12. |
 |
| Fig. 13. |
The theory may be illustrated by the case of “three-bar motion.” Let ABCD be any quadrilateral formed of jointed links. If, AB being held fixed, the quadrilateral be slightly deformed, it is obvious that the instantaneous centre J will be at the intersection of the straight lines AD, BC, since the displacements of the points D, C are necessarily at right angles to AD, BC, respectively. Hence these displacements are proportional to JD, JC, and therefore to DD′ CC′, where C′D′ is any line drawn parallel to CD, meeting BC, AD in C′, D′, respectively. The determination of the centrodes in three-bar motion is in general complicated, but in one case, that of the “crossed parallelogram” (fig. 13), they assume simple forms. We then have AB = DC and AD = BC, and from the symmetries of the figure it is plain that
Hence the locus of J relative to AB, and the locus relative to CD are equal ellipses of which A, B and C, D are respectively the foci. It may be noticed that the lamina in fig. 9 is not, strictly speaking, fixed, but admits of infinitesimal displacement, whenever the directions of the three links are concurrent (or parallel).
The matter may of course be treated analytically, but we shall only require the formula for infinitely small displacements. If the origin of rectangular axes fixed in the lamina be shifted through a space whose projections on the original directions of the axes are λ, μ, and if the axes are simultaneously turned through an angle ε, the co-ordinates of a point of the lamina, relative to the original axes, are changed from x, y to λ + x cos ε − y sin ε, μ + x sin ε + y cos ε, or λ + x − yε, μ + xε + y, ultimately. Hence the component displacements are ultimately
If we equate these to zero we get the co-ordinates of the instantaneous centre.
§ 4. Plane Statics.—The statics of a rigid body rests on the following two assumptions:—
(i) A force may be supposed to be applied indifferently at any point in its line of action. In other words, a force is of the nature of a “bound” or “localized” vector; it is regarded as resident in a certain line, but has no special reference to any particular point of the line.
(ii) Two forces in intersecting lines may be replaced by a force which is their geometric sum, acting through the intersection. The theory of parallel forces is included as a limiting case. For if O, A, B be any three points, and m, n any scalar quantities, we have in vectors
provided
Hence if forces P, Q act in OA, OB, the resultant R will pass through C, provided
also
and
These formulae give a means of constructing the resultant by means of any transversal AB cutting the lines of action. If we now imagine the point O to recede to infinity, the forces P, Q and the resultant R are parallel, and we have
 |
| Fig. 14. |
When P, Q have opposite signs the point C divides AB externally on the side of the greater force. The investigation fails when P + Q = 0, since it leads to an infinitely small resultant acting in an infinitely distant line. A combination of two equal, parallel, but oppositely directed forces cannot in fact be replaced by anything simpler, and must therefore be recognized as an independent entity in statics. It was called by L. Poinsot, who first systematically investigated its properties, a couple.
We now restrict ourselves for the present to the systems of forces in one plane. By successive applications of (ii) any such coplanar system can in general be reduced to a single resultant acting in a definite line. As exceptional cases the system may reduce to a couple, or it may be in equilibrium.
 |
| Fig. 15. |
 |
| Fig. 16. |
The moment of a force about a point O is the product of the force into the perpendicular drawn to its line of action from O, this perpendicular being reckoned positive or negative according as O lies on one side or other of the line of action. If we mark off a segment AB along the line of action so as to represent the force completely, the moment is represented as to magnitude by twice the area of the triangle OAB, and the usual convention as to sign is that the area is to be reckoned positive or negative according as the letters O, A, B, occur in “counter-clockwise” or “clockwise” order.
The sum of the moments of two forces about any point O is equal to the moment of their resultant (P. Varignon, 1687). Let AB, AC (fig. 16) represent the two forces, AD their resultant; we have to prove that the sum of the triangles OAB, OAC is equal to the triangle OAD, regard being had to signs. Since the side OA is common, we have to prove that the sum of the perpendiculars from B and C on OA is equal to the perpendicular from D on OA, these perpendiculars being reckoned positive or negative according as they lie to the right or left of AO. Regarded as a statement concerning the orthogonal projections of the vectors AB→ and AC→ (or BD), and of their sum AD→, on a line perpendicular to AO, this is obvious.
It is now evident that in the process of reduction of a coplanar system no change is made at any stage either in the sum of the projections of the forces on any line or in the sum of their moments about any point. It follows that the single resultant to which the system in general reduces is uniquely determinate, i.e. it acts in a definite line and has a definite magnitude and sense. Again it is necessary and sufficient for equilibrium that the sum of the projections of the forces on each of two perpendicular directions should vanish, and (moreover) that the sum of the moments about some one point should be zero. The fact that three independent conditions must hold for equilibrium is important. The conditions may of course be expressed in different (but equivalent) forms; e.g. the sum of the moments of the forces about each of the three points which are not collinear must be zero.
 |
| Fig. 17. |
The particular case of three forces is of interest. If they are not all parallel they must be concurrent, and their vector-sum must be zero. Thus three forces acting perpendicular to the sides of a triangle at the middle points will be in equilibrium provided they are proportional to the respective sides, and act all inwards or all outwards. This result is easily extended to the case of a polygon of any number of sides; it has an important application in hydrostatics.
Again, suppose we have a bar AB resting with its ends on two smooth inclined planes which face each other. Let G be the centre of gravity (§ 11), and let AG = a, GB = b. Let α, β be the inclinations of the planes, and θ the angle which the bar makes with the vertical. The position of equilibrium is determined by the consideration that the reactions at A and B, which are by hypothesis normal to the planes, must meet at a point J on the vertical through G. Hence
whence
| cot θ = | a cot α − b cot β | . |
| a + b |
If the bar is uniform we have a = b, and
The problem of a rod suspended by strings attached to two points of it is virtually identical, the tensions of the strings taking the place of the reactions of the planes.
 |
| Fig. 18. |
Just as a system of forces is in general equivalent to a single force, so a given force can conversely be replaced by combinations of other forces, in various ways. For instance, a given force (and consequently a system of forces) can be replaced in one and only one way by three forces acting in three assigned straight lines, provided these lines be not concurrent or parallel. Thus if the three lines form a triangle ABC, and if the given force F meet BC in H, then F can be resolved into two components acting in HA, BC, respectively. And the force in HA can be resolved into two components acting in BC, CA, respectively. A simple graphical construction is indicated in fig. 19, where the dotted lines are parallel. As an example, any system of forces acting on the lamina in fig. 9 is balanced by three determinate tensions (or thrusts) in the three links, provided the directions of the latter are not concurrent.
 |
| Fig. 19. |
If P, Q, R, be any three forces acting along BC, CA, AB, respectively, the line of action of the resultant is determined by the consideration that the sum of the moments about any point on it must vanish. Hence in “trilinear” co-ordinates, with ABC as fundamental triangle, its equation is Pα + Qβ + Rγ = 0. If P : Q : R = a : b : c, where a, b, c are the lengths of the sides, this becomes the “line at infinity,” and the forces reduce to a couple.
 |
| Fig. 20. |
The sum of the moments of the two forces of a couple is the same about any point in the plane. Thus in the figure the sum of the moments about O is P·OA − P·OB or P·AB, which is independent of the position of O. This sum is called the moment of the couple; it must of course have the proper sign attributed to it. It easily follows that any two couples of the same moment are equivalent, and that any number of couples can be replaced by a single couple whose moment is the sum of their moments. Since a couple is for our purposes sufficiently represented by its moment, it has been proposed to substitute the name torque (or twisting effort), as free from the suggestion of any special pair of forces.
A system of forces represented completely by the sides of a plane polygon taken in order is equivalent to a couple whose moment is represented by twice the area of the polygon; this is proved by taking moments about any point. If the polygon intersects itself, care must be taken to attribute to the different parts of the area their proper signs.
 |
| Fig. 21. |
Again, any coplanar system of forces can be replaced by a single force R acting at any assigned point O, together with a couple G. The force R is the geometric sum of the given forces, and the moment (G) of the couple is equal to the sum of the moments of the given forces about O. The value of G will in general vary with the position of O, and will vanish when O lies on the line of action of the single resultant.
 |
| Fig. 22. |
The formal analytical reduction of a system of coplanar forces is as follows. Let (x1, y1), (x2, y2), . . . be the rectangular co-ordinates of any points A1, A2, . . . on the lines of action of the respective forces. The force at A1 may be replaced by its components X1, Y1, parallel to the co-ordinate axes; that at A2 by its components X2, Y2, and so on. Introducing at O two equal and opposite forces ±X1 in Ox, we see that X1 at A1 may be replaced by an equal and parallel force at O together with a couple −y1X1. Similarly the force Y1 at A1 may be replaced by a force Y1 at O together with a couple x1Y1. The forces X1, Y1, at O can thus be transferred to O provided we introduce a couple x1Y1 − y1X1. Treating the remaining forces in the same way we get a force X1 + X2 + . . . or Σ(X) along Ox, a force Y1 + Y2 + . . . or Σ(Y) along Oy, and a couple (x1Y1 − y1X1) + (x2Y2 − y2X2) + . . . or Σ(xY − yX). The three conditions of equilibrium are therefore
If O′ be a point whose co-ordinates are (ξ, η), the moment of the couple when the forces are transferred to O′ as a new origin will be Σ{(x − ξ) Y − (y − η) X}. This vanishes, i.e. the system reduces to a single resultant through O′, provided
If ξ, η be regarded as current co-ordinates, this is the equation of the line of action of the single resultant to which the system is in general reducible.
If the forces are all parallel, making say an angle θ with Ox, we may write X1 = P1 cos θ, Y1 = P1 sin θ, X2 = P2 cos θ, Y2 = P2 sin θ, . . . . The equation (9) then becomes
If the forces P1, P2, . . . be turned in the same sense through the same angle about the respective points A1, A2, . . . so as to remain parallel, the value of θ is alone altered, and the resultant Σ(P) passes always through the point
| x̄ = | Σ(x P) | , ȳ = | Σ(y P) | , |
| Σ(P) | Σ(P) |
which is determined solely by the configuration of the points
A1, A2, . . . and by the ratios P1 : P2 : . . . of the forces acting at
them respectively. This point is called the centre of the given
system of parallel forces; it is finite and determinate unless
Σ(P) = 0. A geometrical proof of this theorem, which is not
restricted to a two-dimensional system, is given later (§ 11). It
contains the theory of the centre of gravity as ordinarily understood.
For if we have an assemblage of particles whose mutual
distances are small compared with the dimensions of the earth, the
forces of gravity on them constitute a system of sensibly parallel
forces, sensibly proportional to the respective masses. If now
the assemblage be brought into any other position relative to the
earth, without alteration of the mutual distances, this is equivalent
to a rotation of the directions of the forces relatively to the
assemblage, the ratios of the forces remaining unaltered. Hence
there is a certain point, fixed relatively to the assemblage,
through which the resultant of gravitational action always
passes; this resultant is moreover equal to the sum of the forces
on the several particles.
 |
| Fig. 23. |
The theorem that any coplanar system of forces can be reduced to a force acting through any assigned point, together with a couple, has an important illustration in the theory of the distribution of shearing stress and bending moment in a horizontal beam, or other structure, subject to vertical extraneous forces. If we consider any vertical section P, the forces exerted across the section by the portion of the structure on one side on the portion on the other may be reduced to a vertical force F at P and a couple M. The force measures the shearing stress, and the couple the bending moment at P; we will reckon these quantities positive when the senses are as indicated in the figure.
If the remaining forces acting on the portion of the structure on either side of P are known, then resolving vertically we find F, and taking moments about P we find M. Again if PQ be any segment of the beam which is free from load, Q lying to the right of P, we find
hence F is constant between the loads, whilst M decreases as we travel to the right, with a constant gradient −F. If PQ be a short segment containing an isolated load W, we have
 |
| Fig. 24. |
hence F is discontinuous at a concentrated load, diminishing by an amount equal to the load as we pass the loaded point to the right, whilst M is continuous. Accordingly the graph of F for any system of isolated loads will consist of a series of horizontal lines, whilst that of M will be a continuous polygon.
To pass to the case of continuous loads, let x be measured horizontally along the beam to the right. The load on an element δx of the beam may be represented by wδx, where w is in general a function of x. The equations (12) are now replaced by
whence
The latter relation shows that the bending moment varies as the area cut off by the ordinate in the graph of F. In the case of uniform load we have
 |
| Fig. 25. |
where the arbitrary constants A,B are to be determined by the conditions of the special problem, e.g. the conditions at the ends of the beam. The graph of F is a straight line; that of M is a parabola with vertical axis. In all cases the graphs due to different distributions of load may be superposed. The figure shows the case of a uniform heavy beam supported at its ends.
§ 5. Graphical Statics.—A graphical method of reducing a plane system of forces was introduced by C. Culmann (1864). It involves the construction of two figures, a force-diagram and a funicular polygon. The force-diagram is constructed by placing end to end a series of vectors representing the given forces in magnitude and direction, and joining the vertices of the polygon thus formed to an arbitrary pole O. The funicular or link polygon has its vertices on the lines of action of the given forces, and its sides respectively parallel to the lines drawn from O in the force-diagram; in particular, the two sides meeting in any vertex are respectively parallel to the lines drawn from O to the ends of that side of the force-polygon which represents the corresponding force. The relations will be understood from the annexed diagram, where corresponding lines in the force-diagram (to the right) and the funicular (to the left) are numbered similarly.
 |
| Fig. 26. |
The sides of the force-polygon may in the first instance be arranged in any order; the force-diagram can then be completed in a doubly infinite number of ways, owing to the arbitrary position of O; and for each force-diagram a simply infinite number of funiculars can be drawn. The two diagrams being supposed constructed, it is seen that each of the given systems of forces can be replaced by two components acting in the sides of the funicular which meet at the corresponding vertex, and that the magnitudes of these components will be given by the corresponding triangle of forces in the force-diagram; thus the force 1 in the figure is equivalent to two forces represented by O1 and 12. When this process of replacement is complete, each terminated side of the funicular is the seat of two forces which neutralize one another, and there remain only two uncompensated forces, viz., those resident in the first and last sides of the funicular. If these sides intersect, the resultant acts through the intersection, and its magnitude and direction are given by the line joining the first and last sides of the force-polygon (see fig. 26, where the resultant of the four given forces is denoted by R). As a special case it may happen that the force-polygon is closed, i.e. its first and last points coincide; the first and last sides of the funicular will then be parallel (unless they coincide), and the two uncompensated forces form a couple. If, however, the first and last sides of the funicular coincide, the two outstanding forces neutralize one another, and we have equilibrium. Hence the necessary and sufficient conditions of equilibrium are that the force-polygon and the funicular should both be closed. This is illustrated by fig. 26 if we imagine the force R, reversed, to be included in the system of given forces.
It is evident that a system of jointed bars having the shape of the funicular polygon would be in equilibrium under the action of the given forces, supposed applied to the joints; moreover any bar in which the stress is of the nature of a tension (as distinguished from a thrust) might be replaced by a string. This is the origin of the names “link-polygon” and “funicular” (cf. § 2).
If funiculars be drawn for two positions O, O′ of the pole in the force-diagram, their corresponding sides will intersect on a straight line parallel to OO′. This is essentially a theorem of projective geometry, but the following statical proof is interesting. Let AB (fig. 27) be any side of the force-polygon, and construct the corresponding portions of the two diagrams, first with O and then with O′ as pole. The force corresponding to AB may be replaced by the two components marked x, y; and a force corresponding to BA may be represented by the two components marked x′, y′. Hence the forces x, y, x′, y′ are in equilibrium. Now x, x′ have a resultant through H, represented in magnitude and direction by OO′, whilst y, y′ have a resultant through K represented in magnitude and direction by O′O. Hence HK must be parallel to OO′. This theorem enables us, when one funicular has been drawn, to construct any other without further reference to the force-diagram.
 |
| Fig. 27. |
The complete figures obtained by drawing first the force-diagrams of a system of forces in equilibrium with two distinct poles O, O′, and secondly the corresponding funiculars, have various interesting relations. In the first place, each of these figures may be conceived as an orthogonal projection of a closed plane-faced polyhedron. As regards the former figure this is evident at once; viz. the polyhedron consists of two pyramids with vertices represented by O, O′, and a common base whose perimeter is represented by the force-polygon (only one of these is shown in fig. 28). As regards the funicular diagram, let LM be the line on which the pairs of corresponding sides of the two polygons meet, and through it draw any two planes ω, ω′. Through the vertices A, B, C, . . . and A′, B′, C′, . . . of the two funiculars draw normals to the plane of the diagram, to meet ω and ω′ respectively. The points thus obtained are evidently the vertices of a polyhedron with plane faces.
 |
| Fig. 28. |
 |
| Fig. 29. |
To every line in either of the original figures corresponds of course a parallel line in the other; moreover, it is seen that concurrent lines in either figure correspond to lines forming a closed polygon in the other. Two plane figures so related are called reciprocal, since the properties of the first figure in relation to the second are the same as those of the second with respect to the first. A still simpler instance of reciprocal figures is supplied by the case of concurrent forces in equilibrium (fig. 29). The theory of these reciprocal figures was first studied by J. Clerk Maxwell, who showed amongst other things that a reciprocal can always be drawn to any figure which is the orthogonal projection of a plane-faced polyhedron. If in fact we take the pole of each face of such a polyhedron with respect to a paraboloid of revolution, these poles will be the vertices of a second polyhedron whose edges are the “conjugate lines” of those of the former. If we project both polyhedra orthogonally on a plane perpendicular to the axis of the paraboloid, we obtain two figures which are reciprocal, except that corresponding lines are orthogonal instead of parallel. Another proof will be indicated later (§ 8) in connexion with the properties of the linear complex. It is convenient to have a notation which shall put in evidence the reciprocal character. For this purpose we may designate the points in one figure by letters A, B, C, . . . and the corresponding polygons in the other figure by the same letters; a line joining two points A, B in one figure will then correspond to the side common to the two polygons A, B in the other. This notation was employed by R. H. Bow in connexion with the theory of frames (§ 6, and see also Applied Mechanics below) where reciprocal diagrams are frequently of use (cf. Diagram).
When the given forces are all parallel, the force-polygon consists of a series of segments of a straight line. This case has important practical applications; for instance we may use the method to find the pressures on the supports of a beam loaded in any given manner. Thus if AB, BC, CD represent the given loads, in the force-diagram, we construct the sides corresponding to OA, OB, OC, OD in the funicular; we then draw the closing line of the funicular polygon, and a parallel OE to it in the force diagram. The segments DE, EA then represent the upward pressures of the two supports on the beam, which pressures together with the given loads constitute a system of forces in equilibrium. The pressures of the beam on the supports are of course represented by ED, AE. The two diagrams are portions of reciprocal figures, so that Bow’s notation is applicable.
 |
| Fig. 30. |
 |
| Fig. 31. |
A graphical method can also be applied to find the moment of a force, or of a system of forces, about any assigned point P. Let F be a force represented by AB in the force-diagram. Draw a parallel through P to meet the sides of the funicular which correspond to OA, OB in the points H, K. If R be the intersection of these sides, the triangles OAB, RHK are similar, and if the perpendiculars OM, RN be drawn we have
which is the moment of F about P. If the given forces are all parallel (say vertical) OM is the same for all, and the moments of the several forces about P are represented on a certain scale by the lengths intercepted by the successive pairs of sides on the vertical through P. Moreover, the moments are compounded by adding (geometrically) the corresponding lengths HK. Hence if a system of vertical forces be in equilibrium, so that the funicular polygon is closed, the length which this polygon intercepts on the vertical through any point P gives the sum of the moments about P of all the forces on one side of this vertical. For instance, in the case of a beam in equilibrium under any given loads and the reactions at the supports, we get a graphical representation of the distribution of bending moment over the beam. The construction in fig. 30 can easily be adjusted so that the closing line shall be horizontal; and the figure then becomes identical with the bending-moment diagram of § 4. If we wish to study the effects of a movable load, or system of loads, in different positions on the beam, it is only necessary to shift the lines of action of the pressures of the supports relatively to the funicular, keeping them at the same, distance apart; the only change is then in the position of the closing line of the funicular. It may be remarked that since this line joins homologous points of two “similar” rows it will envelope a parabola.
The “centre” (§ 4) of a system of parallel forces of given magnitudes, acting at given points, is easily determined graphically. We have only to construct the line of action of the resultant for each of two arbitrary directions of the forces; the intersection of the two lines gives the point required. The construction is neatest if the two arbitrary directions are taken at right angles to one another.
§ 6. Theory of Frames.—A frame is a structure made up of pieces, or members, each of which has two joints connecting it with other members. In a two-dimensional frame, each joint may be conceived as consisting of a small cylindrical pin fitting accurately and smoothly into holes drilled through the members which it connects. This supposition is a somewhat ideal one, and is often only roughly approximated to in practice. We shall suppose, in the first instance, that extraneous forces act on the frame at the joints only, i.e. on the pins.
On this assumption, the reactions on any member at its two joints must be equal and opposite. This combination of equal and opposite forces is called the stress in the member; it may be a tension or a thrust. For diagrammatic purposes each member is sufficiently represented by a straight line terminating at the two joints; these lines will be referred to as the bars of the frame.
 |
| Fig. 32. |
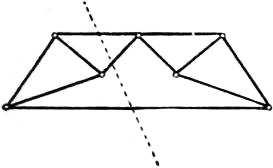
In structural applications a frame must be stiff, or rigid, i.e. it must be incapable of deformation without alteration of length in at least one of its bars. It is said to be just rigid if it ceases to be rigid when any one of its bars is removed. A frame which has more bars than are essential for rigidity may be called over-rigid; such a frame is in general self-stressed, i.e. it is in a state of stress independently of the action of extraneous forces. A plane frame of n joints which is just rigid (as regards deformation in its own plane) has 2n − 3 bars, for if one bar be held fixed the 2(n − 2) co-ordinates of the remaining n − 2 joints must just be determined by the lengths of the remaining bars. The total number of bars is therefore 2(n − 2) + 1. When a plane frame which is just rigid is subject to a given system of equilibrating extraneous forces (in its own plane) acting on the joints, the stresses in the bars are in general uniquely determinate. For the conditions of equilibrium of the forces on each pin furnish 2n equations, viz. two for each point, which are linear in respect of the stresses and the extraneous forces. This system of equations must involve the three conditions of equilibrium of the extraneous forces which are already identically satisfied, by hypothesis; there remain therefore 2n − 3 independent relations to determine the 2n − 3 unknown stresses. A frame of n joints and 2n − 3 bars may of course fail to be rigid owing to some parts being over-stiff whilst others are deformable; in such a case it will be found that the statical equations, apart from the three identical relations imposed by the equilibrium of the extraneous forces, are not all independent but are equivalent to less than 2n − 3 relations. Another exceptional case, known as the critical case, will be noticed later (§ 9).
A plane frame which can be built up from a single bar by successive steps, at each of which a new joint is introduced by two new bars meeting there, is called a simple frame; it is obviously just rigid. The stresses produced by extraneous forces in a simple frame can be found by considering the equilibrium of the various joints in a proper succession; and if the graphical method be employed the various polygons of force can be combined into a single force-diagram. This procedure was introduced by W. J. M. Rankine and J. Clerk Maxwell (1864). It may be noticed that if we take an arbitrary pole in the force-diagram, and draw a corresponding funicular in the skeleton diagram which represents the frame together with the lines of action of the extraneous forces, we obtain two complete reciprocal figures, in Maxwell’s sense. It is accordingly convenient to use Bow’s notation (§ 5), and to distinguish the several compartments of the frame-diagram by letters. See fig. 33, where the successive triangles in the diagram of forces may be constructed in the order XYZ, ZXA, AZB. The class of “simple” frames includes many of the frameworks used in the construction of roofs, lattice girders and suspension bridges; a number of examples will be found in the article Bridges. By examining the senses in which the respective forces act at each joint we can ascertain which members are in tension and which are in thrust; in fig. 33 this is indicated by the directions of the arrowheads.
 |
| Fig. 33. |
 |
| Fig. 34. |
When a frame, though just rigid, is not “simple” in the above sense, the preceding method must be replaced, or supplemented, by one or other of various artifices. In some cases the method of sections is sufficient for the purpose. If an ideal section be drawn across the frame, the extraneous forces on either side must be in equilibrium with the forces in the bars cut across; and if the section can be drawn so as to cut only three bars, the forces in these can be found, since the problem reduces to that of resolving a given force into three components acting in three given lines (§ 4). The “critical case” where the directions of the three bars are concurrent is of course excluded. Another method, always available, will be explained under “Work” (§ 9).
When extraneous forces act on the bars themselves the stress in each bar no longer consists of a simple longitudinal tension or thrust. To find the reactions at the joints we may proceed as follows. Each extraneous force W acting on a bar may be replaced (in an infinite number of ways) by two components P, Q in lines through the centres of the pins at the extremities. In practice the forces W are usually vertical, and the components P, Q are then conveniently taken to be vertical also. We first alter the problem by transferring the forces P, Q to the pins. The stresses in the bars, in the problem as thus modified, may be supposed found by the preceding methods; it remains to infer from the results thus obtained the reactions in the original form of the problem. To find the pressure exerted by a bar AB on the pin A we compound with the force in AB given by the diagram a force equal to P. Conversely, to find the pressure of the pin A on the bar AB we must compound with the force given by the diagram a force equal and opposite to P. This question arises in practice in the theory of “three-jointed” structures; for the purpose in hand such a structure is sufficiently represented by two bars AB, BC. The right-hand figure represents a portion of the force-diagram; in particular ZX→ represents the pressure of AB on B in the modified problem where the loads W1 and W2 on the two bars are replaced by loads P1, Q1, and P2, Q2 respectively, acting on the pins. Compounding with this XV→, which represents Q1, we get the actual pressure ZV→ exerted by AB on B. The directions and magnitudes of the reactions at A and C are then easily ascertained. On account of its practical importance several other graphical solutions of this problem have been devised.
 |
| Fig. 35. |
§ 7. Three-dimensional Kinematics of a Rigid Body.—The position of a rigid body is determined when we know the positions of three points A, B, C of it which are not collinear, for the position of any other point P is then determined by the three distances PA, PB, PC. The nine co-ordinates (Cartesian or other) of A, B, C are subject to the three relations which express the invariability of the distances BC, CA, AB, and are therefore equivalent to six independent quantities. Hence a rigid body not constrained in any way is said to have six degrees of freedom. Conversely, any six geometrical relations restrict the body in general to one or other of a series of definite positions, none of which can be departed from without violating the conditions in question. For instance, the position of a theodolite is fixed by the fact that its rounded feet rest in contact with six given plane surfaces. Again, a rigid three-dimensional frame can be rigidly fixed relatively to the earth by means of six links.
 | |
| Fig. 36. | Fig. 37. |
The six independent quantities, or “co-ordinates,” which serve to specify the position of a rigid body in space may of course be chosen in an endless variety of ways. We may, for instance, employ the three Cartesian co-ordinates of a particular point O of the body, and three angular co-ordinates which express the orientation of the body with respect to O. Thus in fig. 36, if OA, OB, OC be three mutually perpendicular lines in the solid, we may denote by θ the angle which OC makes with a fixed direction OZ, by ψ the azimuth of the plane ZOC measured from some fixed plane through OZ, and by φ the inclination of the plane COA to the plane ZOC. In fig. 36 these various lines and planes are represented by their intersections with a unit sphere having O as centre. This very useful, although unsymmetrical, system of angular co-ordinates was introduced by L. Euler. It is exemplified in “Cardan’s suspension,” as used in connexion with a compass-bowl or a gyroscope. Thus in the gyroscope the “flywheel” (represented by the globe in fig. 37) can turn about a diameter OC of a ring which is itself free to turn about a diametral axis OX at right angles to the former; this axis is carried by a second ring which is free to turn about a fixed diameter OZ, which is at right angles to OX.
We proceed to sketch the theory of the finite displacements of a
rigid body. It was shown by Euler (1776) that any displacement
in which one point O of the body is fixed is equivalent to a pure
rotation about some axis through O. Imagine two spheres of
equal radius with O as their common centre, one fixed in the body
and moving with it, the other fixed in space. In any displacement
about O as a fixed point, the former sphere slides over the
Fig. 10.
latter, as in a “ball-and-socket” joint. Suppose that as the
result of the displacement a point of the moving sphere is brought
from A to B, whilst the point which
was at B is brought to C (cf. fig. 10).
Let J be the pole of the circle ABC
(usually a “small circle” of the fixed
sphere), and join JA, JB, JC, AB, BC
by great-circle arcs. The spherical
isosceles triangles AJB, BJC are congruent,
and we see that AB can be
brought into the position BC by a
rotation about the axis OJ through an
angle AJB.
 |
| Fig. 38. |
 |
| Fig. 39. |
It is convenient to distinguish the two senses in which rotation may take place about an axis OA by opposite signs. We shall reckon a rotation as positive when it is related to the direction from O to A as the direction of rotation is related to that of translation in a right-handed screw. Thus a negative rotation about OA may be regarded as a positive rotation about OA′, the prolongation of AO. Now suppose that a body receives first a positive rotation α about OA, and secondly a positive rotation β about OB; and let A, B be the intersections of these axes with a sphere described about O as centre. If we construct the spherical triangles ABC, ABC′ (fig. 38), having in each case the angles at A and B equal to 12α and 12β respectively, it is evident that the first rotation will bring a point from C to C′ and that the second will bring it back to C; the result is therefore equivalent to a rotation about OC. We note also that if the given rotations had been effected in the inverse order, the axis of the resultant rotation would have been OC′, so that finite rotations do not obey the “commutative law.” To find the angle of the equivalent rotation, in the actual case, suppose that the second rotation (about OB) brings a point from A to A′. The spherical triangles ABC, A′BC (fig. 39) are “symmetrically equal,” and the angle of the resultant rotation, viz. ACA′, is 2π − 2C. This is equivalent to a negative rotation 2C about OC, whence the theorem that the effect of three successive positive rotations 2A, 2B, 2C about OA, OB, OC, respectively, is to leave the body in its original position, provided the circuit ABC is left-handed as seen from O. This theorem is due to O. Rodrigues (1840). The composition of finite rotations about parallel axes is a particular case of the preceding; the radius of the sphere is now infinite, and the triangles are plane.
In any continuous motion of a solid about a fixed point O, the limiting position of the axis of the rotation by which the body can be brought from any one of its positions to a consecutive one is called the instantaneous axis. This axis traces out a certain cone in the body, and a certain cone in space, and the continuous motion in question may be represented as consisting in a rolling of the former cone on the latter. The proof is similar to that of the corresponding theorem of plane kinematics (§ 3).
It follows from Euler’s theorem that the most general displacement of a rigid body may be effected by a pure translation which brings any one point of it to its final position O, followed by a pure rotation about some axis through O. Those planes in the body which are perpendicular to this axis obviously remain parallel to their original positions. Hence, if σ, σ′ denote the initial and final positions of any figure in one of these planes, the displacement could evidently have been effected by (1) a translation perpendicular to the planes in question, bringing σ into some position σ″ in the plane of σ′, and (2) a rotation about a normal to the planes, bringing σ″ into coincidence with σ (§ 3). In other words, the most general displacement is equivalent to a translation parallel to a certain axis combined with a rotation about that axis; i.e. it may be described as a twist about a certain screw. In particular cases, of course, the translation, or the rotation, may vanish.
The preceding theorem, which is due to Michel Chasles (1830), may be proved in various other interesting ways. Thus if a point of the body be displaced from A to B, whilst the point which was at B is displaced to C, and that which was at C to D, the four points A, B, C, D lie on a helix whose axis is the common perpendicular to the bisectors of the angles ABC, BCD. This is the axis of the required screw; the amount of the translation is measured by the projection of AB or BC or CD on the axis; and the angle of rotation is given by the inclination of the aforesaid bisectors. This construction was given by M. W. Crofton. Again, H. Wiener and W. Burnside have employed the half-turn (i.e. a rotation through two right angles) as the fundamental operation. This has the advantage that it is completely specified by the axis of the rotation, the sense being immaterial. Successive half-turns about parallel axes a, b are equivalent to a translation measured by double the distance between these axes in the direction from a to b. Successive half-turns about intersecting axes a, b are equivalent to a rotation about the common perpendicular to a, b at their intersection, of amount equal to twice the acute angle between them, in the direction from a to b. Successive half-turns about two skew axes a, b are equivalent to a twist about a screw whose axis is the common perpendicular to a, b, the translation being double the shortest distance, and the angle of rotation being twice the acute angle between a, b, in the direction from a to b. It is easily shown that any displacement whatever is equivalent to two half-turns and therefore to a screw.
 |
| Fig. 16. |
In mechanics we are specially concerned with the theory of infinitesimal displacements. This is included in the preceding, but it is simpler in that the various operations are commutative. An infinitely small rotation about any axis is conveniently represented geometrically by a length AB measures along the axis and proportional to the angle of rotation, with the convention that the direction from A to B shall be related to the rotation as is the direction of translation to that of rotation in a right-handed screw. The consequent displacement of any point P will then be at right angles to the plane PAB, its amount will be represented by double the area of the triangle PAB, and its sense will depend on the cyclical order of the letters P, A, B. If AB, AC represent infinitesimal rotations about intersecting axes, the consequent displacement of any point O in the plane BAC will be at right angles to this plane, and will be represented by twice the sum of the areas OAB, OAC, taken with proper signs. It follows by analogy with the theory of moments (§ 4) that the resultant rotation will be represented by AD, the vector-sum of AB, AC (see fig. 16). It is easily inferred as a limiting case, or proved directly, that two infinitesimal rotations α, β about parallel axes are equivalent to a rotation α + β about a parallel axis in the same plane with the two former, and dividing a common perpendicular AB in a point C so that AC/CB = β/α. If the rotations are equal and opposite, so that α + β = 0, the point C is at infinity, and the effect is a translation perpendicular to the plane of the two given axes, of amount α·AB. It thus appears that an infinitesimal rotation is of the nature of a “localized vector,” and is subject in all respects to the same mathematical laws as a force, conceived as acting on a rigid body. Moreover, that an infinitesimal translation is analogous to a couple and follows the same laws. These results are due to Poinsot.
The analytical treatment of small displacements is as follows. We first suppose that one point O of the body is fixed, and take this as the origin of a “right-handed” system of rectangular co-ordinates; i.e. the positive directions of the axes are assumed to be so arranged that a positive rotation of 90° about Ox would bring Oy into the position of Oz, and so on. The displacement will consist of an infinitesimal rotation ε about some axis through O, whose direction-cosines are, say, l, m, n. From the equivalence of a small rotation to a localized vector it follows that the rotation ε will be equivalent to rotations ξ, η, ζ about Ox, Oy, Oz, respectively, provided
and we note that
Thus in the case of fig. 36 it may be required to connect the infinitesimal rotations ξ, η, ζ about OA, OB, OC with the variations of the angular co-ordinates θ, ψ, φ. The displacement of the point C of the body is made up of δθ tangential to the meridian ZC and sin θ δψ perpendicular to the plane of this meridian. Hence, resolving along the tangents to the arcs BC, CA, respectively, we have
 |
| Fig. 40. |
Again, consider the point of the solid which was initially at A′ in the figure. This is displaced relatively to A′ through a space δψ perpendicular to the plane of the meridian, whilst A′ itself is displaced through a space cos θ δψ in the same direction. Hence
To find the component displacements of a point P of the body, whose co-ordinates are x, y, z, we draw PL normal to the plane yOz, and LH, LK perpendicular to Oy, Oz, respectively. The displacement of P parallel to Ox is the same as that of L, which is made up of ηz and −ζy. In this way we obtain the formulae
The most general case is derived from this by adding the component displacements λ, μ, ν (say) of the point which was at O; thus
δx = λ + ηz − ζy, |
The displacement is thus expressed in terms of the six independent
quantities ξ, η, ζ, λ, μ, ν. The points whose displacements
are in the direction of the resultant axis of rotation are
determined by δx : δy : δz = ξ : η : ζ, or
These are the equations of a straight line, and the displacement is in fact equivalent to a twist about a screw having this line as axis. The translation parallel to this axis is
The linear magnitude which measures the ratio of translation to rotation in a screw is called the pitch. In the present case the pitch is
Since ξ2 + η2 + ζ2, or ε2, is necessarily an absolute invariant for all transformations of the (rectangular) co-ordinate axes, we infer that λξ + μη + νζ is also an absolute invariant. When the latter invariant, but not the former, vanishes, the displacement is equivalent to a pure rotation.
If the small displacements of a rigid body be subject to one constraint, e.g. if a point of the body be restricted to lie on a given surface, the mathematical expression of this fact leads to a homogeneous linear equation between the infinitesimals ξ, η, ζ, λ, μ, ν, say
The quantities ξ, η, ζ, λ, μ, ν are no longer independent, and the body has now only five degrees of freedom. Every additional constraint introduces an additional equation of the type (10) and reduces the number of degrees of freedom by one. In Sir R. S. Ball’s Theory of Screws an analysis is made of the possible displacements of a body which has respectively two, three, four, five degrees of freedom. We will briefly notice the case of two degrees, which involves an interesting generalization of the method (already explained) of compounding rotations about intersecting axes. We assume that the body receives arbitrary twists about two given screws, and it is required to determine the character of the resultant displacement. We examine first the case where the axes of the two screws are at right angles and intersect. We take these as axes of x and y; then if ξ, η be the component rotations about them, we have
where h, k, are the pitches of the two given screws. The equations (7) of the axis of the resultant screw then reduce to
Hence, whatever the ratio ξ : η, the axis of the resultant screw lies on the conoidal surface
where c = 12(k − h). The co-ordinates of any point on (13) may be written
hence if we imagine a curve of sines to be traced on a circular cylinder so that the circumference just includes two complete undulations, a straight line cutting the axis of the cylinder at right angles and meeting this curve will generate the surface. This is called a cylindroid. Again, the pitch of the resultant screw is
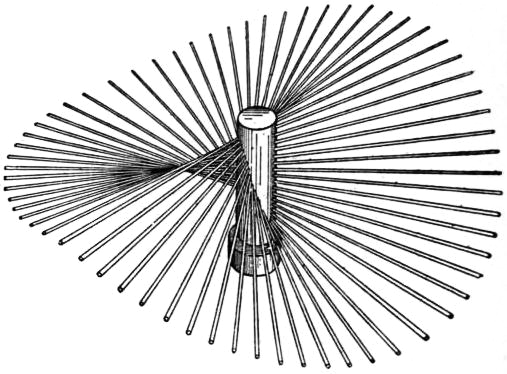 |
| From Sir Robert S. Ball’s Theory of Screws. |
| Fig. 41. |
The distribution of pitch among the various screws has therefore a simple relation to the pitch-conic
viz. the pitch of any screw varies inversely as the square of that diameter of the conic which is parallel to its axis. It is to be noticed that the parameter c of the cylindroid is unaltered if the two pitches h, k be increased by equal amounts; the only change is that all the pitches are increased by the same amount. It remains to show that a system of screws of the above type can be constructed so as to contain any two given screws whatever. In the first place, a cylindroid can be constructed so as to have its axis coincident with the common perpendicular to the axes of the two given screws and to satisfy three other conditions, for the position of the centre, the parameter, and the orientation about the axis are still at our disposal. Hence we can adjust these so that the surface shall contain the axes of the two given screws as generators, and that the difference of the corresponding pitches shall have the proper value. It follows that when a body has two degrees of freedom it can twist about any one of a singly infinite system of screws whose axes lie on a certain cylindroid. In particular cases the cylindroid may degenerate into a plane, the pitches being then all equal.
§ 8. Three-dimensional Statics.—A system of parallel forces can be combined two and two until they are replaced by a single resultant equal to their sum, acting in a certain line. As special cases, the system may reduce to a couple, or it may be in equilibrium.
In general, however, a three-dimensional system of forces cannot be replaced by a single resultant force. But it may be reduced to simpler elements in a variety of ways. For example, it may be reduced to two forces in perpendicular skew lines. For consider any plane, and let each force, at its intersection with the plane, be resolved into two components, one (P) normal to the plane, the other (Q) in the plane. The assemblage of parallel forces P can be replaced in general by a single force, and the coplanar system of forces Q by another single force.
If the plane in question be chosen perpendicular to the direction of the vector-sum of the given forces, the vector-sum of the components Q is zero, and these components are therefore equivalent to a couple (§ 4). Hence any three-dimensional system can be reduced to a single force R acting in a certain line, together with a couple G in a plane perpendicular to the line. This theorem was first given by L. Poinsot, and the line of action of R was called by him the central axis of the system. The combination of a force and a couple in a perpendicular plane is termed by Sir R. S. Ball a wrench. Its type, as distinguished from its absolute magnitude, may be specified by a screw whose axis is the line of action of R, and whose pitch is the ratio G/R.
 |
| Fig. 42. |
The case of two forces may be specially noticed. Let AB be the shortest distance between the lines of action, and let AA′, BB′ (fig. 42) represent the forces. Let α, β be the angles which AA′, BB′ make with the direction of the vector-sum, on opposite sides. Divide AB in O, so that
and draw OC parallel to the vector-sum. Resolving AA′, BB′ each into two components parallel and perpendicular to OC, we see that the former components have a single resultant in OC, of amount
whilst the latter components form a couple of moment
Conversely it is seen that any wrench can be replaced in an infinite number of ways by two forces, and that the line of action of one of these may be chosen quite arbitrarily. Also, we find from (2) and (3) that
The right-hand expression is six times the volume of the tetrahedron of which the lines AA′, BB′ representing the forces are opposite edges; and we infer that, in whatever way the wrench be resolved into two forces, the volume of this tetrahedron is invariable.
To define the moment of a force about an axis HK, we project the force orthogonally on a plane perpendicular to HK and take the moment of the projection about the intersection of HK with the plane (see § 4). Some convention as to sign is necessary; we shall reckon the moment to be positive when the tendency of the force is right-handed as regards the direction from H to K. Since two concurrent forces and their resultant obviously project into two concurrent forces and their resultant, we see that the sum of the moments of two concurrent forces about any axis HK is equal to the moment of their resultant. Parallel forces may be included in this statement as a limiting case. Hence, in whatever way one system of forces is by successive steps replaced by another, no change is made in the sum of the moments about any assigned axis. By means of this theorem we can show that the previous reduction of any system to a wrench is unique.
From the analogy of couples to translations which was pointed out in § 7, we may infer that a couple is sufficiently represented by a “free” (or non-localized) vector perpendicular to its plane. The length of the vector must be proportional to the moment of the couple, and its sense must be such that the sum of the moments of the two forces of the couple about it is positive. In particular, we infer that couples of the same moment in parallel planes are equivalent; and that couples in any two planes may be compounded by geometrical addition of the corresponding vectors. Independent statical proofs are of course easily given. Thus, let the plane of the paper be perpendicular to the planes of two couples, and therefore perpendicular to the line of intersection of these planes. By § 4, each couple can be replaced by two forces ±P (fig. 43) perpendicular to the plane of the paper, and so that one force of each couple is in the line of intersection (B); the arms (AB, BC) will then be proportional to the respective moments. The two forces at B will cancel, and we are left with a couple of moment P·AC in the plane AC. If we draw three vectors to represent these three couples, they will be perpendicular and proportional to the respective sides of the triangle ABC; hence the third vector is the geometric sum of the other two. Since, in this proof the magnitude of P is arbitrary, It follows incidentally that couples of the same moment in parallel planes, e.g. planes parallel to AC, are equivalent.
 |
| Fig. 43. |
 |
| Fig. 44. |
Hence a couple of moment G, whose axis has the direction (l, m, n) relative to a right-handed system of rectangular axes, is equivalent to three couples lG, mG, nG in the co-ordinate planes. The analytical reduction of a three-dimensional system can now be conducted as follows. Let (x1, y1, z1) be the co-ordinates of a point P1 on the line of action of one of the forces, whose components are (say) X1, Y1, Z1. Draw P1H normal to the plane zOx, and HK perpendicular to Oz. In KH introduce two equal and opposite forces ±X1. The force X1 at P1 with −X1 in KH forms a couple about Oz, of moment −y1X1. Next, introduce along Ox two equal and opposite forces ±X1. The force X1 in KH with −X1 in Ox forms a couple about Oy, of moment z1X1. Hence the force X1 can be transferred from P1 to O, provided we introduce couples of moments z1X1 about Oy and −y1X1, about Oz. Dealing in the same way with the forces Y1, Z1 at P1, we find that all three components of the force at P1 can be transferred to O, provided we introduce three couples L1, M1, N1 about Ox, Oy, Oz respectively, viz.
It is seen that L1, M1, N1 are the moments of the original force at P1 about the co-ordinate axes. Summing up for all the forces of the given system, we obtain a force R at O, whose components are
and a couple G whose components are
where r = 1, 2, 3 . . . Since R2 = X2 + Y2 + Z2, G2 = L2 + M2 + N2, it is necessary and sufficient for equilibrium that the six quantities X, Y, Z, L, M, N, should all vanish. In words: the sum of the projections of the forces on each of the co-ordinate axes must vanish; and, the sum of the moments of the forces about each of these axes must vanish.
If any other point O′, whose co-ordinates are x, y, z, be chosen in place of O, as the point to which the forces are transferred, we have to write x1 − x, y1 − y, z1 − z for x1, y1, z1, and so on, in the preceding process. The components of the resultant force R are unaltered, but the new components of couple are found to be
| L′ = L − yZ + zY, |
By properly choosing O′ we can make the plane of the couple
perpendicular to the resultant force. The conditions for this
are L′ : M′ : N′ = X : Y : Z, or
| L − yZ + zY | = | M − zX + xZ | = | N − xY + yX |
| X | Y | Z |
These are the equations of the central axis. Since the moment of the resultant couple is now
| G′ = | X | L′ + | Y | M′ + | Z | N′ = | LX + MY + NZ | , |
| R | R | R | R |
the pitch of the equivalent wrench is
It appears that X2 + Y2 + Z2 and LX + MY + NZ are absolute invariants (cf. § 7). When the latter invariant, but not the former, vanishes, the system reduces to a single force.
The analogy between the mathematical relations of infinitely small displacements on the one hand and those of force-systems on the other enables us immediately to convert any theorem in the one subject into a theorem in the other. For example, we can assert without further proof that any infinitely small displacement may be resolved into two rotations, and that the axis of one of these can be chosen arbitrarily. Again, that wrenches of arbitrary amounts about two given screws compound into a wrench the locus of whose axis is a cylindroid.
The mathematical properties of a twist or of a wrench have been the subject of many remarkable investigations, which are, however, of secondary importance from a physical point of view. In the “Null-System” of A. F. Möbius (1790–1868), a line such that the moment of a given wrench about it is zero is called a null-line. The triply infinite system of null-lines form what is called in line-geometry a “complex.” As regards the configuration of this complex, consider a line whose shortest distance from the central axis is r, and whose inclination to the central axis is θ. The moment of the resultant force R of the wrench about this line is − Rr sin θ, and that of the couple G is G cos θ. Hence the line will be a null-line provided
where k is the pitch of the wrench. The null-lines which are at a given distance r from a point O of the central axis will therefore form one system of generators of a hyperboloid of revolution; and by varying r we get a series of such hyperboloids with a common centre and axis. By moving O along the central axis we obtain the whole complex of null-lines. It appears also from (11) that the null-lines whose distance from the central axis is r are tangent lines to a system of helices of slope tan−1 (r/k); and it is to be noticed that these helices are left-handed if the given wrench is right-handed, and vice versa.
Since the given wrench can be replaced by a force acting through any assigned point P, and a couple, the locus of the null-lines through P is a plane, viz. a plane perpendicular to the vector which represents the couple. The complex is therefore of the type called “linear” (in relation to the degree of this locus). The plane in question is called the null-plane of P. If the null-plane of P pass through Q, the null-plane of Q will pass through P, since PQ is a null-line. Again, any plane ω is the locus of a system of null-lines meeting in a point, called the null-point of ω. If a plane revolve about a fixed straight line p in it, its null-point describes another straight line p′, which is called the conjugate line of p. We have seen that the wrench may be replaced by two forces, one of which may act in any arbitrary line p. It is now evident that the second force must act in the conjugate line p′, since every line meeting p, p′ is a null-line. Again, since the shortest distance between any two conjugate lines cuts the central axis at right angles, the orthogonal projections of two conjugate lines on a plane perpendicular to the central axis will be parallel (fig. 42). This property was employed by L. Cremona to prove the existence under certain conditions of “reciprocal figures” in a plane (§ 5). If we take any polyhedron with plane faces, the null-planes of its vertices with respect to a given wrench will form another polyhedron, and the edges of the latter will be conjugate (in the above sense) to those of the former. Projecting orthogonally on a plane perpendicular to the central axis we obtain two reciprocal figures.
In the analogous theory of infinitely small displacements of a solid, a “null-line” is a line such that the lengthwise displacement of any point on it is zero.
Since a wrench is defined by six independent quantities, it can in general be replaced by any system of forces which involves six adjustable elements. For instance, it can in general be replaced by six forces acting in six given lines, e.g. in the six edges of a given tetrahedron. An exception to the general statement occurs when the six lines are such that they are possible lines of action of a system of six forces in equilibrium; they are then said to be in involution. The theory of forces in involution has been studied by A. Cayley, J. J. Sylvester and others. We have seen that a rigid structure may in general be rigidly connected with the earth by six links, and it now appears that any system of forces acting on the structure can in general be balanced by six determinate forces exerted by the links. If, however, the links are in involution, these forces become infinite or indeterminate. There is a corresponding kinematic peculiarity, in that the connexion is now not strictly rigid, an infinitely small relative displacement being possible. See § 9.
When parallel forces of given magnitudes act at given points, the resultant acts through a definite point, or centre of parallel forces, which is independent of the special direction of the forces. If Pr be the force at (xr , yr , zr), acting in the direction (l, m, n), the formulae (6) and (7) reduce to
and
provided
| x̄ = | Σ(Px) | , ȳ = | Σ(Py) | , z̄ = | Σ(Pz) | . |
| Σ(P) | Σ(P) | Σ(P) |
These are the same as if we had a single force Σ(P) acting at the point (x̄, ȳ, z̄), which is the same for all directions (l, m, n). We can hence derive the theory of the centre of gravity, as in § 4. An exceptional case occurs when Σ(P) = 0.
If we imagine a rigid body to be acted on at given points by forces of given magnitudes in directions (not all parallel) which are fixed in space, then as the body is turned about the resultant wrench will assume different configurations in the body, and will in certain positions reduce to a single force. The investigation of such questions forms the subject of “Astatics,” which has been cultivated by Möbius, Minding, G. Darboux and others. As it has no physical bearing it is passed over here.
 |
| Fig. 45. |
§ 9. Work.—The work done by a force acting on a particle, in any infinitely small displacement, is defined as the product of the force into the orthogonal projection of the displacement on the direction of the force; i.e. it is equal to F·δs cos θ, where F is the force, δs the displacement, and θ is the angle between the directions of F and δs. In the language of vector analysis (q.v.) it is the “scalar product” of the vector representing the force and the displacement. In the same way, the work done by a force acting on a rigid body in any infinitely small displacement of the body is the scalar product of the force into the displacement of any point on the line of action. This product is the same whatever point on the line of action be taken, since the lengthwise components of the displacements of any two points A, B on a line AB are equal, to the first order of small quantities. To see this, let A′, B′ be the displaced positions of A, B, and let φ be the infinitely small angle between AB and A′B′. Then if α, β be the orthogonal projections of A′, B′ on AB, we have
ultimately. Since this is of the second order, the products F·Aα and F·Bβ are ultimately equal.
 |
 |
| Fig. 46. | Fig. 47. |
The total work done by two concurrent forces acting on a particle, or on a rigid body, in any infinitely small displacement, is equal to the work of their resultant. Let AB, AC (fig. 46) represent the forces, AD their resultant, and let AH be the direction of the displacement δs of the point A. The proposition follows at once from the fact that the sum of orthogonal projections of AB→, AC→ on AH is equal to the projection of AD→. It is to be noticed that AH need not be in the same plane with AB, AC.
It follows from the preceding statements that any two systems of forces which are statically equivalent, according to the principles of §§ 4, 8, will (to the first order of small quantities) do the same amount of work in any infinitely small displacement of a rigid body to which they may be applied. It is also evident that the total work done in two or more successive infinitely small displacements is equal to the work done in the resultant displacement.
The work of a couple in any infinitely small rotation of a rigid body about an axis perpendicular to the plane of the couple is equal to the product of the moment of the couple into the angle of rotation, proper conventions as to sign being observed. Let the couple consist of two forces P, P (fig. 47) in the plane of the paper, and let J be the point where this plane is met by the axis of rotation. Draw JBA perpendicular to the lines of action, and let ε be the angle of rotation. The work of the couple is
if G be the moment of the couple.
The analytical calculation of the work done by a system of forces in any infinitesimal displacement is as follows. For a two-dimensional system we have, in the notation of §§ 3, 4,
| Σ(Xδx + Yδy) | = Σ{X(λ − yε) + Y(μ + xε)} |
| = Σ(X)·λ + Σ(Y)·μ + Σ(xY − yX) ε | |
| = Xλ + Yμ + Nε. |
Again, for a three-dimensional system, in the notation of §§ 7, 8,
| Σ(Xδx + Yδy + Zδz) |
| = Σ{(X(λ + ηz − ζy) + Y(μ + ζx − ξx) + Z(ν + ξy − ηx)} |
| = Σ(X)·λ + Σ(Y)·μ + Σ(Z)·ν + Σ(yZ − zY)·ξ + Σ(zX − xZ)·η + Σ(xY − yX)·ζ |
| = Xλ + Yμ + Zν + Lξ + Mη + Nζ. |
This expression gives the work done by a given wrench when the body receives a given infinitely small twist; it must of course be an absolute invariant for all transformations of rectangular axes. The first three terms express the work done by the components of a force (X, Y, Z) acting at O, and the remaining three terms express the work of a couple (L, M, N).
 |
| Fig. 48. |
The work done by a wrench about a given screw, when the body twists about a second given screw, may be calculated directly as follows. In fig. 48 let R, G be the force and couple of the wrench, ε,τ the rotation and translation in the twist. Let the axes of the wrench and the twist be inclined at an angle θ, and let h be the shortest distance between them. The displacement of the point H in the figure, resolved in the direction of R, is τ cos θ − εh sin θ. The work is therefore
= Rε {(p + p′) cos θ − h sin θ},
if G = pR, τ = p′ε, i.e. p, p′ are the pitches of the two screws. The factor (p + p′) cos θ − h sin θ is called the virtual coefficient of the two screws which define the types of the wrench and twist, respectively.
A screw is determined by its axis and its pitch, and therefore involves five independent elements. These may be, for instance, the five ratios ξ : η : ζ : λ : μ : ν of the six quantities which specify an infinitesimal twist about the screw. If the twist is a pure rotation, these quantities are subject to the relation
In the analytical investigations of line geometry, these six quantities, supposed subject to the relation (4), are used to specify a line, and are called the six “co-ordinates” of the line; they are of course equivalent to only four independent quantities. If a line is a null-line with respect to the wrench (X, Y, Z, L, M, N), the work done in an infinitely small rotation about it is zero, and its co-ordinates are accordingly subject to the further relation
where the coefficients are constant. This is the equation of a “linear complex” (cf. § 8).
Two screws are reciprocal when a wrench about one does no work on a body which twists about the other. The condition for this is
if the screws be defined by the ratios ξ : η : ζ : λ : μ : ν and ξ′ : η′ : ζ′ : λ′ : μ′ : ν′, respectively. The theory of the screw-systems which are reciprocal to one, two, three, four given screws respectively has been investigated by Sir R. S. Ball.
Considering a rigid body in any given position, we may contemplate the whole group of infinitesimal displacements which might be given to it. If the extraneous forces are in equilibrium the total work which they would perform in any such displacement would be zero, since they reduce to a zero force and a zero couple. This is (in part) the celebrated principle of virtual velocities, now often described as the principle of virtual work, enunciated by John Bernoulli (1667–1748). The word “virtual” is used because the displacements in question are not regarded as actually taking place, the body being in fact at rest. The “velocities” referred to are the velocities of the various points of the body in any imagined motion of the body through the position in question; they obviously bear to one another the same ratios as the corresponding infinitesimal displacements. Conversely, we can show that if the virtual work of the extraneous forces be zero for every infinitesimal displacement of the body as rigid, these forces must be in equilibrium. For by giving the body (in imagination) a displacement of translation we learn that the sum of the resolved parts of the forces in any assigned direction is zero, and by giving it a displacement of pure rotation we learn that the sum of the moments about any assigned axis is zero. The same thing follows of course from the analytical expression (2) for the virtual work. If this vanishes for all values of λ, μ, ν, ξ, η, ζ we must have X, Y, Z, L, M, N = 0, which are the conditions of equilibrium.
The principle can of course be extended to any system of particles or rigid bodies, connected together in any way, provided we take into account the internal stresses, or reactions, between the various parts. Each such reaction consists of two equal and opposite forces, both of which may contribute to the equation of virtual work.
The proper significance of the principle of virtual work, and of its converse, will appear more clearly when we come to kinetics (§ 16); for the present it may be regarded merely as a compact and (for many purposes) highly convenient summary of the laws of equilibrium. Its special value lies in this, that by a suitable adjustment of the hypothetical displacements we are often enabled to eliminate unknown reactions. For example, in the case of a particle lying on a smooth curve, or on a smooth surface, if it be displaced along the curve, or on the surface, the virtual work of the normal component of the pressure may be ignored, since it is of the second order. Again, if two bodies are connected by a string or rod, and if the hypothetical displacements be adjusted so that the distance between the points of attachment is unaltered, the corresponding stress may be ignored. This is evident from fig. 45; if AB, A′B′ represent the two positions of a string, and T be the tension, the virtual work of the two forces ±T at A, B is T(Aα − Bβ), which was shown to be of the second order. Again, the normal pressure between two surfaces disappears from the equation, provided the displacements be such that one of these surfaces merely slides relatively to the other. It is evident, in the first place, that in any displacement common to the two surfaces, the work of the two equal and opposite normal pressures will cancel; moreover if, one of the surfaces being fixed, an infinitely small displacement shifts the point of contact from A to B, and if A′ be the new position of that point of the sliding body which was at A, the projection of AA′ on the normal at A is of the second order. It is to be noticed, in this case, that the tangential reaction (if any) between the two surfaces is not eliminated. Again, if the displacements be such that one curved surface rolls without sliding on another, the reaction, whether normal or tangential, at the point of contact may be ignored. For the virtual work of two equal and opposite forces will cancel in any displacement which is common to the two surfaces; whilst, if one surface be fixed, the displacement of that point of the rolling surface which was in contact with the other is of the second order. We are thus able to imagine a great variety of mechanical systems to which the principle of virtual work can be applied without any regard to the internal stresses, provided the hypothetical displacements be such that none of the connexions of the system are violated.
If the system be subject to gravity, the corresponding part of the virtual work can be calculated from the displacement of the centre of gravity. If W1, W2, . . . be the weights of a system of particles, whose depths below a fixed horizontal plane of reference are z1, z2, . . ., respectively, the virtual work of gravity is
where z̄ is the depth of the centre of gravity (see § 8 (14) and § 11 (6)). This expression is the same as if the whole mass were concentrated at the centre of gravity, and displaced with this point. An important conclusion is that in any displacement of a system of bodies in equilibrium, such that the virtual work of all forces except gravity may be ignored, the depth of the centre of gravity is “stationary.”
The question as to stability of equilibrium belongs essentially to kinetics; but we may state by anticipation that in cases where gravity is the only force which does work, the equilibrium of a body or system of bodies is stable only if the depth of the centre of gravity be a maximum.
Consider, for instance, the case of a bar resting with its ends on two smooth inclines (fig. 18). If the bar be displaced in a vertical plane so that its ends slide on the two inclines, the instantaneous centre is at the point J. The displacement of G is at right angles to JG; this shows that for equilibrium JG must be vertical. Again, the locus of G is an arc of an ellipse whose centre is in the intersection of the planes; since this arc is convex upwards the equilibrium is unstable. A general criterion for the case of a rigid body movable in two dimensions, with one degree of freedom, can be obtained as follows. We have seen (§ 3) that the sequence of possible positions is obtained if we imagine the “body-centrode” to roll on the “space-centrode.” For equilibrium, the altitude of the centre of gravity G must be stationary; hence G must lie in the same vertical line with the point of contact J of the two curves. Further, it is known from the theory of “roulettes” that the locus of G will be concave or convex upwards according as
| cos φ | = | 1 | + | 1 | , |
| h | ρ | ρ′ |
 |
| Fig. 49. |
where ρ, ρ′ are the radii of curvature of the two curves at J, φ is the inclination of the common tangent at J to the horizontal, and h is the height of G above J. The signs of ρ, ρ′ are to be taken positive when the curvatures are as in the standard case shown in fig. 49. Hence for stability the upper sign must obtain in (8). The same criterion may be arrived at in a more intuitive manner as follows. If the body be supposed to roll (say to the right) until the curves touch at J′, and if JJ′ = δs, the angle through which the upper figure rotates is δs/ρ + δs/ρ′, and the horizontal displacement of G is equal to the product of this expression into h. If this displacement be less than the horizontal projection of JJ′, viz. δs cosφ, the vertical through the new position of G will fall to the left of J′ and gravity will tend to restore the body to its former position. It is here assumed that the remaining forces acting on the body in its displaced position have zero moment about J′; this is evidently the case, for instance, in the problem of “rocking stones.”
The principle of virtual work is specially convenient in the theory of frames (§ 6), since the reactions at smooth joints and the stresses in inextensible bars may be left out of account. In particular, in the case of a frame which is just rigid, the principle enables us to find the stress in any one bar independently of the rest. If we imagine the bar in question to be removed, equilibrium will still persist if we introduce two equal and opposite forces S, of suitable magnitude, at the joints which it connected. In any infinitely small deformation of the frame as thus modified, the virtual work of the forces S, together with that of the original extraneous forces, must vanish; this determines S.
As a simple example, take the case of a light frame, whose bars form the slides of a rhombus ABCD with the diagonal BD, suspended from A and carrying a weight W at C; and let it be required to find the stress in BD. If we remove the bar BD, and apply two equal and opposite forces S at B and D, the equation is
 |
| Fig. 50. |
where l is the length of a side of the rhombus, and θ its inclination to the vertical. Hence
The method is specially appropriate when the frame, although just rigid, is not “simple” in the sense of § 6, and when accordingly the method of reciprocal figures is not immediately available. To avoid the intricate trigonometrical calculations which would often be necessary, graphical devices have been introduced by H. Müller-Breslau and others. For this purpose the infinitesimal displacements of the various joints are replaced by finite lengths proportional to them, and therefore proportional to the velocities of the joints in some imagined motion of the deformable frame through its actual configuration; this is really (it may be remarked) a reversion to the original notion of “virtual velocities.” Let J be the instantaneous centre for any bar CD (fig. 12), and let s1, s2 represent the virtual velocities of C, D. If these lines be turned through a right angle in the same sense, they take up positions such as CC′, DD′, where C′, D′ are on JC, JD, respectively, and C′D′ is parallel to CD. Further, if F1 (fig. 51) be any force acting on the joint C, its virtual work will be equal to the moment of F1 about C′; the equation of virtual work is thus transformed into an equation of moments.
 | |
| Fig. 12. | Fig. 51. |
 |
| Fig. 52. |
Consider, for example, a frame whose sides form the six sides of a hexagon ABCDEF and the three diagonals AD, BE, CF; and suppose that it is required to find the stress in CF due to a given system of extraneous forces in equilibrium, acting on the joints. Imagine the bar CF to be removed, and consider a deformation in which AB is fixed. The instantaneous centre of CD will be at the intersection of AD, BC, and if C′D′ be drawn parallel to CD, the lines CC′, DD′ may be taken to represent the virtual velocities of C, D turned each through a right angle. Moreover, if we draw D′E′ parallel to DE, and E′F′ parallel to EF, the lines CC′, DD′, EE′, FF′ will represent on the same scale the virtual velocities of the points C, D, E, F, respectively, turned each through a right angle. The equation of virtual work is then formed by taking moments about C′, D′, E′, F′ of the extraneous forces which act at C, D, E, F, respectively. Amongst these forces we must include the two equal and opposite forces S which take the place of the stress in the removed bar FC.
The above method lends itself naturally to the investigation of the critical forms of a frame whose general structure is given. We have seen that the stresses produced by an equilibrating system of extraneous forces in a frame which is just rigid, according to the criterion of § 6, are in general uniquely determinate; in particular, when there are no extraneous forces the bars are in general free from stress. It may however happen that owing to some special relation between the lengths of the bars the frame admits of an infinitesimal deformation. The simplest case is that of a frame of three bars, when the three joints A, B, C fall into a straight line; a small displacement of the joint B at right angles to AC would involve changes in the lengths of AB, BC which are only of the second order of small quantities. Another example is shown in fig. 53. The graphical method leads at once to the detection of such cases. Thus in the hexagonal frame of fig. 52, if an infinitesimal deformation is possible without removing the bar CF, the instantaneous centre of CF (when AB is fixed) will be at the intersection of AF and BC, and since CC′, FF′ represent the virtual velocities of the points C, F, turned each through a right angle, C′F′ must be parallel to CF. Conversely, if this condition be satisfied, an infinitesimal deformation is possible. The result may be generalized into the statement that a frame has a critical form whenever a frame of the same structure can be designed with corresponding bars parallel, but without complete geometric similarity. In the case of fig. 52 it may be shown that an equivalent condition is that the six points A, B, C, D, E, F should lie on a conic (M. W. Crofton). This is fulfilled when the opposite sides of the hexagon are parallel, and (as a still more special case) when the hexagon is regular.
When a frame has a critical form it may be in a state of stress
independently of the action of extraneous forces; moreover, the
stresses due to extraneous forces are
indeterminate, and may be infinite.
For suppose as before that one of the
bars is removed. If there are no extraneous
Fig. 53.
forces the equation of virtual work
reduces to S·δs = 0, where S is the stress
in the removed bar, and δs is the change
in the distance between the joints which
it connected. In a critical form we
have δs = 0, and the equation is satisfied
by an arbitrary value of S; a consistent
system of stresses in the remaining bars
can then be found by preceding rules. Again, when extraneous
forces P act on the joints, the equation is
where δp is the displacement of any joint in the direction of the corresponding force P. If Σ(P·δp) = 0, the stresses are merely indeterminate as before; but if Σ (P·δp) does not vanish, the equation cannot be satisfied by any finite value of S, since δs = 0. This means that, if the material of the frame were absolutely unyielding, no finite stresses in the bars would enable it to withstand the extraneous forces. With actual materials, the frame would yield elastically, until its configuration is no longer “critical.” The stresses in the bars would then be comparatively very great, although finite. The use of frames which approximate to a critical form is of course to be avoided in practice.
A brief reference must suffice to the theory of three dimensional frames. This is important from a technical point of view, since all structures are practically three-dimensional. We may note that a frame of n joints which is just rigid must have 3n − 6 bars; and that the stresses produced in such a frame by a given system of extraneous forces in equilibrium are statically determinate, subject to the exception of “critical forms.”
§ 10. Statics of Inextensible Chains.—The theory of bodies or structures which are deformable in their smallest parts belongs properly to elasticity (q.v.). The case of inextensible strings or chains is, however, so simple that it is generally included in expositions of pure statics.
It is assumed that the form can be sufficiently represented by a plane curve, that the stress (tension) at any point P of the curve, between the two portions which meet there, is in the direction of the tangent at P, and that the forces on any linear element δs must satisfy the conditions of equilibrium laid down in § 1. It follows that the forces on any finite portion will satisfy the conditions of equilibrium which apply to the case of a rigid body (§ 4).
 |
| Fig. 54. |
We will suppose in the first instance that the curve is plane. It is often convenient to resolve the forces on an element PQ (= δs) in the directions of the tangent and normal respectively. If T, T + δT be the tensions at P, Q, and δψ be the angle between the directions of the curve at these points, the components of the tensions along the tangent at P give (T + δT) cos ψ − T, or δT, ultimately; whilst for the component along the normal at P we have (T + δT) sin δψ, or Tδψ, or Tδs/ρ, where ρ is the radius of curvature.
Suppose, for example, that we have a light string stretched over a smooth curve; and let Rδs denote the normal pressure (outwards from the centre of curvature) on δs. The two resolutions give δT = 0, Tδψ = Rδs, or
The tension is constant, and the pressure per unit length varies as the curvature.
Next suppose that the curve is “rough”; and let Fδs be the tangential force of friction on δs. We have δT ± Fδs = 0, Tδψ = Rδs, where the upper or lower sign is to be taken according to the sense in which F acts. We assume that in limiting equilibrium we have F = μR, everywhere, where μ is the coefficient of friction. If the string be on the point of slipping in the direction in which ψ increases, the lower sign is to be taken; hence δT = Fδs = μTδψ, whence
if T0 be the tension corresponding to ψ = 0. This illustrates the resistance to dragging of a rope coiled round a post; e.g. if we put μ = .3, ψ = 2π, we find for the change of tension in one turn T/T0 = 6.5. In two turns this ratio is squared, and so on.
Again, take the case of a string under gravity, in contact with a smooth curve in a vertical plane. Let ψ denote the inclination to the horizontal, and wδs the weight of an element δs. The tangential and normal components of wδs are −s sinψ and −wδs cosψ. Hence
If we take rectangular axes Ox, Oy, of which Oy is drawn vertically upwards, we have δy = sin ψ δs, whence δT = wδy. If the string be uniform, w is constant, and
say; hence the tension varies as the height above some fixed level (y0). The pressure is then given by the formula
| R = T | dψ | −w cos ψ. |
| ds |
In the case of a chain hanging freely under gravity it is usually convenient to formulate the conditions of equilibrium of a finite portion PQ. The forces on this reduce to three, viz. the weight of PQ and the tensions at P, Q. Hence these three forces will be concurrent, and their ratios will be given by a triangle of forces. In particular, if we consider a length AP beginning at the lowest point A, then resolving horizontally and vertically we have
where T0 is the tension at A, and W is the weight of PA. The former equation expresses that the horizontal tension is constant.
 |
| Fig. 55. |
If the chain be uniform we have W = ws, where s is the arc AP: hence ws = T0 tan ψ. If we write T0 = wa, so that a is the length of a portion of the chain whose weight would equal the horizontal tension, this becomes
This is the “intrinsic” equation of the curve. If the axes of x and y be taken horizontal and vertical (upwards), we derive
Eliminating ψ we obtain the Cartesian equation
| y = a cosh xa | (9) |
of the common catenary, as it is called (fig. 56). The omission of the additive arbitrary constants of integration in (8) is equivalent to a special choice of the origin O of co-ordinates; viz. O is at a distance a vertically below the lowest point (ψ = 0) of the curve. The horizontal line through O is called the directrix. The relations
| s = a sinh xa, y2 = a2 + s 2, T = T0 sec ψ = wy, | (10) |
which are involved in the preceding formulae are also noteworthy.
It is a classical problem in the calculus of variations
Fig. 56.
to deduce the equation (9) from
the condition that the depth
of the centre of gravity of a
chain of given length hanging
between fixed points must be
stationary (§ 9). The length
a is called the parameter of the
catenary; it determines the
scale of the curve, all catenaries
being geometrically similar.
If weights be suspended
from various points of a hanging
chain, the intervening portions
will form arcs of equal
catenaries, since the horizontal
tension (wa) is the same for all.
Again, if a chain pass over a
perfectly smooth peg, the catenaries
in which it hangs on the two sides, though usually of
different parameters, will have the same directrix, since by
(10) y is the same for both at the peg.
As an example of the use of the formulae we may determine the maximum span for a wire of given material. The condition is that the tension must not exceed the weight of a certain length λ of the wire. At the ends we shall have y = λ, or
| λ = a cosh xa, | (11) |
and the problem is to make x a maximum for variations of a. Differentiating (11) we find that, if dx/da = 0,
| xa tanh xa | (12) |
It is easily seen graphically, or from a table of hyperbolic tangents, that the equation u tanh u = 1 has only one positive root (u = 1.200); the span is therefore
and the length of wire is
The tangents at the ends meet on the directrix, and their inclination to the horizontal is 56° 30′.
 |
| Fig. 57. |
The relation between the sag, the tension, and the span of a wire (e.g. a telegraph wire) stretched nearly straight between two points A, B at the same level is determined most simply from first principles. If T be the tension, W the total weight, k the sag in the middle, and ψ the inclination to the horizontal at A or B, we have 2Tψ = W, AB = 2ρψ, approximately, where ρ is the radius of curvature. Since 2kρ = (12AB)2, ultimately, we have
| k = 18W · AB/T. | (13) |
The same formula applies if A, B be at different levels, provided k be the sag, measured vertically, half way between A and B.
In relation to the theory of suspension bridges the case where the weight of any portion of the chain varies as its horizontal projection is of interest. The vertical through the centre of gravity of the arc AP (see fig. 55) will then bisect its horizontal projection AN; hence if PS be the tangent at P we shall have AS = SN. This property is characteristic of a parabola whose axis is vertical. If we take A as origin and AN as axis of x, the weight of AP may be denoted by wx, where w is the weight per unit length at A. Since PNS is a triangle of forces for the portion AP of the chain, we have wx/T0 = PN/NS, or
which is the equation of the parabola in question. The result might of course have been inferred from the theory of the parabolic funicular in § 2.
Finally, we may refer to the catenary of uniform strength, where the cross-section of the wire (or cable) is supposed to vary as the tension. Hence w, the weight per foot, varies as T, and we may write T = wλ, where λ is a constant length. Resolving along the normal the forces on an element δs, we find Tδψ = wδs cos ψ, whence
| ρ = | ds | = λ sec ψ. |
| dψ |
From this we derive
| x = λψ, y = λ log sec | x | , |
| λ |
where the directions of x and y are horizontal and vertical, and the origin is taken at the lowest point. The curve (fig. 58) has two vertical asymptotes x = ± 12πλ; this shows that however the thickness of a cable be adjusted there is a limit πλ to the horizontal span, where λ depends on the tensile strength of the material. For a uniform catenary the limit was found above to be 1.326λ.
 |
| Fig. 58. |
For investigations relating to the equilibrium of a string in three dimensions we must refer to the textbooks. In the case of a string stretched over a smooth surface, but in other respects free from extraneous force, the tensions at the ends of a small element δs must be balanced by the normal reaction of the surface. It follows that the osculating plane of the curve formed by the string must contain the normal to the surface, i.e. the curve must be a “geodesic,” and that the normal pressure per unit length must vary as the principal curvature of the curve.
§ 11. Theory of Mass-Systems.—This is a purely geometrical subject. We consider a system of points P1, P2 . . ., Pn, with which are associated certain coefficients m1, m2, . . . mn, respectively. In the application to mechanics these coefficients are the masses of particles situate at the respective points, and are therefore all positive. We shall make this supposition in what follows, but it should be remarked that hardly any difference is made in the theory if some of the coefficients have a different sign from the rest, except in the special case where Σ(m) = 0. This has a certain interest in magnetism.
In a given mass-system there exists one and only one point G such that
For, take any point O, and construct the vector
| OG→ = | Σ(m·OP→) | . |
| Σ(m) |
Then
Also there cannot be a distinct point G′ such that Σ(m·G′P) = 0, for we should have, by subtraction,
i.e. G′ must coincide with G. The point G determined by (1) is called the mass-centre or centre of inertia of the given system. It is easily seen that, in the process of determining the mass-centre, any group of particles may be replaced by a single particle whose mass is equal to that of the group, situate at the mass-centre of the group.
If through P1, P2, . . . Pn we draw any system of parallel planes meeting a straight line OX in the points M1, M2 . . . Mn, the collinear vectors OM→1, OM→2 . . . OM→n may be called the “projections” of OP→1, OP→2, . . . OP→n on OX. Let these projections be denoted algebraically by x1, x2, . . . xn, the sign being positive or negative according as the direction is that of OX or the reverse. Since the projection of a vector-sum is the sum of the projections of the several vectors, the equation (2) gives
| x̄=Σ(mx)Σ(m), | (5) |
if x̄ be the projection of OG→. Hence if the Cartesian co-ordinates of P1, P2, . . . Pn relative to any axes, rectangular or oblique be (x1, y1, z1), (x2, y2, z2), . . ., (xn, yn, zn), the mass-centre (x̄, ȳ, z̄) is determined by the formulae
| x̄ = | Σ(mx) | , ȳ = | Σ(my) | , z̄ = | Σ(mz) | . |
| Σ(m) | Σ(m) | Σ(m) |
If we write x = x̄ + ξ, y = ȳ + η, z = z̄ + ζ, so that ξ, η, ζ denote co-ordinates relative to the mass-centre G, we have from (6)
One or two special cases may be noticed. If three masses α, β, γ be situate at the vertices of a triangle ABC, the mass-centre of β and γ is at a point A′ in BC, such that β·BA′ = γ·A′C. The mass-centre (G) of α, β, γ will then divide AA′ so that α·AG = (β + γ) GA′. It is easily proved that
also, by giving suitable values (positive or negative) to the ratios α : β : γ we can make G assume any assigned position in the plane ABC. We have here the origin of the “barycentric co-ordinates” of Möbius, now usually known as “areal” co-ordinates. If α + β + γ = 0, G is at infinity; if α = β = γ, G is at the intersection of the median lines of the triangle; if α : β : γ = a : b : c, G is at the centre of the inscribed circle. Again, if G be the mass-centre of four particles α, β, γ, δ situate at the vertices of a tetrahedron ABCD, we find
and by suitable determination of the ratios on the left hand we can make G assume any assigned position in space. If α + β + γ + δ = O, G is at infinity; if α = β = γ = δ, G bisects the lines joining the middle points of opposite edges of the tetrahedron ABCD; if α : β : γ : δ = ΔBCD : ΔCDA : ΔDAB : ΔABC, G is at the centre of the inscribed sphere.
If we have a continuous distribution of matter, instead of a system of discrete particles, the summations in (6) are to be replaced by integrations. Examples will be found in textbooks of the calculus and of analytical statics. As particular cases: the mass-centre of a uniform thin triangular plate coincides with that of three equal particles at the corners; and that of a uniform solid tetrahedron coincides with that of four equal particles at the vertices. Again, the mass-centre of a uniform solid right circular cone divides the axis in the ratio 3 : 1; that of a uniform solid hemisphere divides the axial radius in the ratio 3 : 5.
It is easily seen from (6) that if the configuration of a system of particles be altered by “homogeneous strain” (see Elasticity) the new position of the mass-centre will be at that point of the strained figure which corresponds to the original mass-centre.
The formula (2) shows that a system of concurrent forces represented by m1·OP→1, m2·OP→2, . . . mn·OP→n will have a resultant represented by Σ(m)·OG→. If we imagine O to recede to infinity in any direction we learn that a system of parallel forces proportional to m1, m2,... mn, acting at P1, P2 . . . Pn have a resultant proportional to Σ(m) which acts always through a point G fixed relatively to the given mass-system. This contains the theory of the “centre of gravity” (§§ 4, 9). We may note also that if P1, P2, . . . Pn, and P1′, P2′, . . . Pn′ represent two configurations of the series of particles, then
where G, G′ are the two positions of the mass-centre. The forces m1·P1P1′→, m2·P2P2→′, . . . mn·PnPn′→, considered as localized vectors, do not, however, as a rule reduce to a single resultant.
We proceed to the theory of the plane, axial and polar quadratic moments of the system. The axial moments have alone a dynamical significance, but the others are useful as subsidiary conceptions. If h1, h2, . . . hn be the perpendicular distances of the particles from any fixed plane, the sum Σ(mh2) is the quadratic moment with respect to the plane. If p1, p2, . . . pn be the perpendicular distances from any given axis, the sum Σ(mp2) is the quadratic moment with respect to the axis; it is also called the moment of inertia about the axis. If r1, r2, . . . rn be the distances from a fixed point, the sum Σ(mr 2) is the quadratic moment with respect to that point (or pole). If we divide any of the above quadratic moments by the total mass Σ(m), the result is called the mean square of the distances of the particles from the respective plane, axis or pole. In the case of an axial moment, the square root of the resulting mean square is called the radius of gyration of the system about the axis in question. If we take rectangular axes through any point O, the quadratic moments with respect to the co-ordinate planes are
those with respect to the co-ordinate axes are
whilst the polar quadratic moment with respect to O is
We note that
and
In the case of continuous distributions of matter the summations in (9), (10), (11) are of course to be replaced by integrations. For a uniform thin circular plate, we find, taking the origin at its centre, and the axis of z normal to its plane, I0 = 12Ma2, where M is the mass and a the radius. Since Ix = Iy, Iz = 0, we deduce Izx = 12Ma2, Ixy = 12Ma2; hence the value of the squared radius of gyration is for a diameter 14a2, and for the axis of symmetry 12a2. Again, for a uniform solid sphere having its centre at the origin we find I0 = 35Ma2, Ix = Iy = Iz = 15Ma2, Iyz = Izx = lxy = 35Ma2; i.e. the square of the radius of gyration with respect to a diameter is 25a2. The method of homogeneous strain can be applied to deduce the corresponding results for an ellipsoid of semi-axes a, b, c. If the co-ordinate axes coincide with the principal axes, we find Ix = 15Ma2, Iy = 15Mb2, Iz = 15Mc2, whence Iyz = 15M (b2 + c2), &c.
If φ(x, y, z) be any homogeneous quadratic function of x, y, z, we have
since the terms which are bilinear in respect to x̄, ȳ, z̄, and ξ, η, ζ vanish, in virtue of the relations (7). Thus
with similar relations, and
The formula (16) expresses that the squared radius of gyration about any axis (Ox) exceeds the squared radius of gyration about a parallel axis through G by the square of the distance between the two axes. The formula (17) is due to J. L. Lagrange; it may be written
| Σ(m · OP2) | = | Σ(m · GP2) | + OG2, |
| Σ(m) | Σ(m) |
and expresses that the mean square of the distances of the particles from O exceeds the mean square of the distances from G by OG2. The mass-centre is accordingly that point the mean square of whose distances from the several particles is least. If in (18) we make O coincide with P1, P2, . . . Pn in succession, we obtain
| 0 | + m2·P1P22 | + . . . | + mn·P1Pn2 | = Σ(m · GP2) + Σ(m) · GP12, | |
| m1·P2P12 | + 0 | + . . . | + mn·P2Pn2 | = Σ(m · GP2) + Σ(m) · GP22, | |
| . . . . . . . . . | |||||
| m1·PnP12 | + m2·PnP22 | + . . . | + 0 | = Σ(m · GP2) + Σ(m) · GPn2. | |
If we multiply these equations by m1, m2 . . . mn, respectively,
and add, we find
provided the summation ΣΣ on the left hand be understood to include each pair of particles once only. This theorem, also due to Lagrange, enables us to express the mean square of the distances of the particles from the centre of mass in terms of the masses and mutual distances. For instance, considering four equal particles at the vertices of a regular tetrahedron, we can infer that the radius R of the circumscribing sphere is given by R2 = 38a2, if a be the length of an edge.
Another type of quadratic moment is supplied by the deviation-moments, or products of inertia of a distribution of matter. Thus the sum Σ(m·yz) is called the “product of inertia” with respect to the planes y = 0, z = 0. This may be expressed In terms of the product of inertia with respect to parallel planes through G by means of the formula (14); viz.:—
| Σ (m · yz) = Σ (m · ηζ) + Σ (m) · ȳz̄ | (21) |
The quadratic moments with respect to different planes through a fixed point O are related to one another as follows. The moment with respect to the plane
where λ, μ, ν are direction-cosines, is
and therefore varies as the square of the perpendicular drawn from O to a tangent plane of a certain quadric surface, the tangent plane in question being parallel to (22). If the co-ordinate axes coincide with the principal axes of this quadric, we shall have
and if we write
where M = Σ(m), the quadratic moment becomes M(a2λ2 + b2μ2 + c2ν2), or Mp2, where p is the distance of the origin from that tangent plane of the ellipsoid
| x2 | + | y2 | + | z2 | = 1, |
| a2 | b2 | c2 |
which is parallel to (22). It appears from (24) that through any
assigned point O three rectangular axes can be drawn such that
the product of inertia with respect to each pair of co-ordinate
planes vanishes; these are called the principal axes of inertia at O.
The ellipsoid (26) was first employed by J. Binet (1811), and may
be called “Binet’s Ellipsoid” for the point O. Evidently the
quadratic moment for a variable plane through O will have a
“stationary” value when, and only when, the plane coincides
with a principal plane of (26). It may further be shown that if
Binet’s ellipsoid be referred to any system of conjugate diameters
as co-ordinate axes, its equation will be
| x′2 | + | y′2 | + | z′2 | = 1, |
| a′2 | b′2 | c′2 |
provided
also that
Let us now take as co-ordinate axes the principal axes of inertia at the mass-centre G. If a, b, c be the semi-axes of the Binet’s ellipsoid of G, the quadratic moment with respect to the plane λx + μy + νz = 0 will be M(a2λ2 + b2μ2 + c2ν2), and that with respect to a parallel plane
will be M (a2λ2 + b2μ2 + c2ν2 + p2), by (15). This will have a given value Mk2, provided
Hence the planes of constant quadratic moment Mk2 will envelop the quadric
| x2 | + | y2 | + | z2 | = 1, |
| k2 − a2 | k2 − b2 | k2 − c2 |
and the quadrics corresponding to different values of k2 will be
confocal. If we write
b2 + c2 = α2, c2 + a2 = β2, a2 + b2 = γ2
the equation (31) becomes
| x2 | + | y2 | + | z2 | = 1; |
| α2 + θ | β2 + θ | γ2 + θ |
for different values of θ this represents a system of quadrics
confocal with the ellipsoid
| x2 | + | y2 | + | z2 | = 1, |
| α2 | β2 | γ2 |
which we shall meet with presently as the “ellipsoid of gyration”
at G. Now consider the tangent plane ω at any point P of a
confocal, the tangent plane ω′ at an adjacent point N′, and a
plane ω″ through P parallel to ω′. The distance between the
planes ω′ and ω″ will be of the second order of small quantities,
and the quadratic moments with respect to ω′ and ω″ will therefore
be equal, to the first order. Since the quadratic moments
with respect to ω and ω′ are equal, it follows that ω is a plane of
stationary quadratic moment at P, and therefore a principal
plane of inertia at P. In other words, the principal axes of
inertia at P are the normals to the three confocals of the system
(33) which pass through P. Moreover if x, y, z be the co-ordinates
of P, (33) is an equation to find the corresponding values of θ;
and if θ1, θ2, θ3 be the roots we find
where r 2 = x2 + y2 + z2. The squares of the radii of gyration about the principal axes at P may be denoted by k22 + k32, k32 + k12, k12 + k22; hence by (32) and (35) they are r 2 −θ1, r 2 − θ2, r 2 − θ3, respectively.
To find the relations between the moments of inertia about different axes through any assigned point O, we take O as origin. Since the square of the distance of a point (x, y, z) from the axis
| x | = | y | = | z |
| λ | μ | ν |
is x2 + y2 + z2 − (λx + μy + νz)2, the moment of inertia about
this axis is
= Aλ2 + Bμ2 + Cν2 − 2Fμν − 2Gνλ − 2Hλμ,
provided
F = Σ (myz), G = Σ (mzx), H = Σ (mxy);
i.e. A, B, C are the moments of inertia about the co-ordinate
axes, and F, G, H are the products of inertia with respect to the
pairs of co-ordinate planes. If we construct the quadric
where ε is an arbitrary linear magnitude, the intercept r which it makes on a radius drawn in the direction λ, μ, ν is found by putting x, y, z = λr, μr, νr. Hence, by comparison with (37),
The moment of inertia about any radius of the quadric (39) therefore varies inversely as the square of the length of this radius. When referred to its principal axes, the equation of the quadric takes the form
The directions of these axes are determined by the property (24), and therefore coincide with those of the principal axes of inertia at O, as already defined in connexion with the theory of plane quadratic moments. The new A, B, C are called the principal moments of inertia at O. Since they are essentially positive the quadric is an ellipsoid; it is called the momental ellipsoid at O. Since, by (12), B + C > A, &c., the sum of the two lesser principal moments must exceed the greatest principal moment. A limitation is thus imposed on the possible forms of the momental ellipsoid; e.g. in the case of symmetry about an axis it appears that the ratio of the polar to the equatorial diameter of the ellipsoid cannot be less than 1/√2.
If we write A = Mα2, B = Mβ2, C = Mγ2, the formula (37), when referred to the principal axes at O, becomes
if p denotes the perpendicular drawn from O in the direction (λ, μ, ν) to a tangent plane of the ellipsoid
| x2 | + | y2 | + | z2 | = 1 |
| α2 | β2 | γ2 |
This is called the ellipsoid of gyration at O; it was introduced into
the theory by J. MacCullagh. The ellipsoids (41) and (43) are
reciprocal polars with respect to a sphere having O as centre.
If A = B = C, the momental ellipsoid becomes a sphere; all axes through O are then principal axes, and the moment of inertia is the same for each. The mass-system is then said to possess kinetic symmetry about O.
If all the masses lie in a plane (z = 0) we have, in the notation of (25), c2 = 0, and therefore A = Mb2, B = Ma2, C = M(a2 + b2), so that the equation of the momental ellipsoid takes the form
The section of this by the plane z = 0 is similar to
| x2 | + | y2 | = 1, |
| a2 | b2 |
which may be called the momental ellipse at O. It possesses the
property that the radius of gyration about any diameter is half the
distance between the two tangents which are parallel to that diameter.
In the case of a uniform triangular plate it may be shown that the
momental ellipse at G is concentric, similar and similarly situated
to the ellipse which touches the sides of the triangle at their middle
points.
 |
| Fig. 59. |
The graphical methods of determining the moment of inertia of a plane system of particles with respect to any line in its plane may be briefly noticed. It appears from § 5 (fig. 31) that the linear moment of each particle about the line may be found by means of a funicular polygon. If we replace the mass of each particle by its moment, as thus found, we can in like manner obtain the quadratic moment of the system with respect to the line. For if the line in question be the axis of y, the first process gives us the values of mx, and the second the value of Σ(mx·x) or Σ(mx2). The construction of a second funicular may be dispensed with by the employment of a planimeter, as follows. In fig. 59 p is the line with respect to which moments are to be taken, and the masses of the respective particles are indicated by the corresponding segments of a line in the force-diagram, drawn parallel to p. The funicular ZABCD . . . corresponding to any pole O is constructed for a system of forces acting parallel to p through the positions of the particles and proportional to the respective masses; and its successive sides are produced to meet p in the points H, K, L, M, . . . As explained in § 5, the moment of the first particle is represented on a certain scale by HK, that of the second by KL, and so on. The quadratic moment of the first particle will then be represented by twice the area AHK, that of the second by twice the area BKL, and so on. The quadratic moment of the whole system is therefore represented by twice the area AHEDCBA. Since a quadratic moment is essentially positive, the various areas are to taken positive in all cases. If k be the radius of gyration about p we find
where αβ is the line in the force-diagram which represents the sum of the masses, and ON is the distance of the pole O from this line. If some of the particles lie on one side of p and some on the other, the quadratic moment of each set may be found, and the results added.
 |
| Fig. 60. |
This is illustrated in fig. 60, where the total quadratic moment is represented by the sum of the shaded areas. It is seen that for a given direction of p this moment is least when p passes through the intersection X of the first and last sides of the funicular; i.e. when p goes through the mass-centre of the given system; cf. equation (15).
§ 12. Rectilinear Motion.—Let x denote the distance OP of a moving point P at time t from a fixed origin O on the line of motion, this distance being reckoned positive or negative according as it lies to one side or the other of O. At time t + δt let the point be at Q, and let OQ = x + δx. The mean velocity of the point in the interval δt is δx/δt. The limiting value of this when δt is infinitely small, viz. dx/dt, is adopted as the definition of the velocity at the instant t. Again, let u be the velocity at time t, u + δu that at time t + δt. The mean rate of increase of velocity, or the mean acceleration, in the interval δt is then δu/δt. The limiting value of this when δt is infinitely small, viz., du/dt, is adopted as the definition of the acceleration at the instant t. Since u = dx/dt, the acceleration is also denoted by d 2x/dt2. It is often convenient to use the “fluxional” notation for differential coefficients with respect to time; thus the velocity may be represented by ẋ and the acceleration by u̇ or ẍ. There is another formula for the acceleration, in which u is regarded as a function of the position; thus du/dt = (du/dx) (dx/dt) = u(du/dx). The relation between x and t in any particular case may be illustrated by means of a curve constructed with t as abscissa and x as ordinate. This is called the curve of positions or space-time curve; its gradient represents the velocity. Such curves are often traced mechanically in acoustical and other experiments. A, curve with t as abscissa and u as ordinate is called the curve of velocities or velocity-time curve. Its gradient represents the acceleration, and the area (∫u dt) included between any two ordinates represents the space described in the interval between the corresponding instants (see fig. 62).
So far nothing has been said about the measurement of time. From the purely kinematic point of view, the t of our formulae may be any continuous independent variable, suggested (it may be) by some physical process. But from the dynamical standpoint it is obvious that equations which represent the facts correctly on one system of time-measurement might become seriously defective on another. It is found that for almost all purposes a system of measurement based ultimately on the earth’s rotation is perfectly adequate. It is only when we come to consider such delicate questions as the influence of tidal friction that other standards become necessary.
The most important conception in kinetics is that of “inertia.” It is a matter of ordinary observation that different bodies acted on by the same force, or what is judged to be the same force, undergo different changes of velocity in equal times. In our ideal representation of natural phenomena this is allowed for by endowing each material particle with a suitable mass or inertia-coefficient m. The product mu of the mass into the velocity is called the momentum or (in Newton’s phrase) the quantity of motion. On the Newtonian system the motion of a particle entirely uninfluenced by other bodies, when referred to a suitable base, would be rectilinear, with constant velocity. If the velocity changes, this is attributed to the action of force; and if we agree to measure the force (X) by the rate of change of momentum which it produces, we have the equation
| ddt (mu) = X. | (1) |
From this point of view the equation is a mere truism, its real importance resting on the fact that by attributing suitable values to the masses m, and by making simple assumptions as to the value of X in each case, we are able to frame adequate representations of whole classes of phenomena as they actually occur. The question remains, of course, as to how far the measurement of force here implied is practically consistent with the gravitational method usually adopted in statics; this will be referred to presently.
The practical unit or standard of mass must, from the nature of the case, be the mass of some particular body, e.g. the imperial pound, or the kilogramme. In the “C.G.S.” system a subdivision of the latter, viz. the gramme, is adopted, and is associated with the centimetre as the unit of length, and the mean solar second as the unit of time. The unit of force implied in (1) is that which produces unit momentum in unit time. On the C.G.S. system it is that force which acting on one gramme for one second produces a velocity of one centimetre per second; this unit is known as the dyne. Units of this kind are called absolute on account of their fundamental and invariable character as contrasted with gravitational units, which (as we shall see presently) vary somewhat with the locality at which the measurements are supposed to be made.
If we integrate the equation (1) with respect to t between the limits t, t ′ we obtain
| (2) |
The time-integral on the right hand is called the impulse of the force on the interval t ′ − t. The statement that the increase of momentum is equal to the impulse is (it maybe remarked) equivalent to Newton’s own formulation of his Second Law. The form (1) is deduced from it by putting t ′ − t = δt, and taking δt to be infinitely small. In problems of impact we have to deal with cases of practically instantaneous impulse, where a very great and rapidly varying force produces an appreciable change of momentum in an exceedingly minute interval of time.
In the case of a constant force, the acceleration u̇ or ẍ is, according to (1), constant, and we have
| d 2xdt 2 = α, | (3) |
say, the general solution of which is
| x = 12 αt 2 + At + B. | (4) |
The “arbitrary constants” A, B enable us to represent the circumstances of any particular case; thus if the velocity ẋ and the position x be given for any one value of t, we have two conditions to determine A, B. The curve of positions corresponding to (4) is a parabola, and that of velocities is a straight line. We may take it as an experimental result, although the best evidence is indirect, that a particle falling freely under gravity experiences a constant acceleration which at the same place is the same for all bodies. This acceleration is denoted by g; its value at Greenwich is about 981 centimetre-second units, or 32.2 feet per second. It increases somewhat with the latitude, the extreme variation from the equator to the pole being about 12%. We infer that on our reckoning the force of gravity on a mass m is to be measured by mg, the momentum produced per second when this force acts alone. Since this is proportional to the mass, the relative masses to be attributed to various bodies can be determined practically by means of the balance. We learn also that on account of the variation of g with the locality a gravitational system of force-measurement is inapplicable when more than a moderate degree of accuracy is desired.
We take next the case of a particle attracted towards a fixed point O in the line of motion with a force varying as the distance from that point. If μ be the acceleration at unit distance, the equation of motion becomes
| d 2xdt 2 = −μx, | (5) |
the solution of which may be written in either of the forms
| x = A cos σt + B sin σt, x = a cos (σt + ε), | (6) |
 |
| Fig. 61. |
where σ= √μ, and the two constants A, B or a, ε are arbitrary. The particle oscillates between the two positions x = ±a, and the same point is passed through in the same direction with the same velocity at equal intervals of time 2π/σ. The type of motion represented by (6) is of fundamental importance in the theory of vibrations (§ 23); it is called a simple-harmonic or (shortly) a simple vibration. If we imagine a point Q to describe a circle of radius a with the angular velocity σ, its orthogonal projection P on a fixed diameter AA′ will execute a vibration of this character. The angle σt + ε (or AOQ) is called the phase; the arbitrary elements a, ε are called the amplitude and epoch (or initial phase), respectively. In the case of very rapid vibrations it is usual to specify, not the period (2π/σ), but its reciprocal the frequency, i.e. the number of complete vibrations per unit time. Fig. 62 shows the curves of position and velocity; they both have the form of the “curve of sines.” The numbers correspond to an amplitude of 10 centimetres and a period of two seconds.
The vertical oscillations of a weight which hangs from a fixed point by a spiral spring come under this case. If M be the mass, and x the vertical displacement from the position of equilibrium, the equation of motion is of the form
| M | d 2x | = − Kx, |
| dt 2 |
provided the inertia of the spring itself be neglected. This becomes identical with (5) if we put μ = K/M; and the period is therefore 2π√(M/K), the same for all amplitudes. The period is increased by an increase of the mass M, and diminished by an increase in the stiffness (K) of the spring. If c be the statical increase of length which is produced by the gravity of the mass M, we have Kc = Mg, and the period is 2π√(c/g).
 |
| Fig. 62. |
The small oscillations of a simple pendulum in a vertical plane also come under equation (5). According to the principles of § 13, the horizontal motion of the bob is affected only by the horizontal component of the force acting upon it. If the inclination of the string to the vertical does not exceed a few degrees, the vertical displacement of the particle is of the second order, so that the vertical acceleration may be neglected, and the tension of the string may be equated to the gravity mg of the particle. Hence if l be the length of the string, and x the horizontal displacement of the bob from the equilibrium position, the horizontal component of gravity is mgx/l, whence
| d 2x | = − | gx | , |
| dt 2 | l |
The motion is therefore simple-harmonic, of period τ = 2π√(l /g). This indicates an experimental method of determining g with considerable accuracy, using the formula g = 4π2l /τ2.
In the case of a repulsive force varying as the distance from the origin, the equation of motion is of the type
| d 2x | = μx, |
| dt 2 |
the solution of which is
where n = √μ. Unless the initial conditions be adjusted so as to make A = 0 exactly, x will ultimately increase indefinitely with t. The position x = 0 is one of equilibrium, but it is unstable. This applies to the inverted pendulum, with μ = g/l, but the equation (9) is then only approximate, and the solution therefore only serves to represent the initial stages of a motion in the neighbourhood of the position of unstable equilibrium.
In acoustics we meet with the case where a body is urged towards a fixed point by a force varying as the distance, and is also acted upon by an “extraneous” or “disturbing” force which is a given function of the time. The most important case is where this function is simple-harmonic, so that the equation (5) is replaced by
| d 2x | + μx = ƒ cos (σ1t + α), |
| dt 2 |
where σ1 is prescribed. A particular solution is
| x = | ƒ | cos (σ1t + α). |
| μ − σ12 |
This represents a forced oscillation whose period 2π/σ1, coincides with that of the disturbing force; and the phase agrees with that of the force, or is opposed to it, according as σ12 < or > μ; i.e. according as the imposed period is greater or less than the natural period 2π/√μ. The solution fails when the two periods agree exactly; the formula (12) is then replaced by
| x = | ƒt | sin (σ1t + α), |
| 2σ1 |
which represents a vibration of continually increasing amplitude. Since the equation (12) is in practice generally only an approximation (as in the case of the pendulum), this solution can only be accepted as a representation of the initial stages of the forced oscillation. To obtain the complete solution of (11) we must of course superpose the free vibration (6) with its arbitrary constants in order to obtain a complete representation of the most general motion consequent on arbitrary initial conditions.
A simple mechanical illustration is afforded by the pendulum. If the point of suspension have an imposed simple vibration ξ = a cos σt in a horizontal line, the equation of small motion of the bob is
| mẍ = −mg | x − ξ | , |
| l |
This is the same as if the point of suspension were fixed, and a horizontal disturbing force mgξ/l were to act on the bob. The difference of phase of the forced vibration in the two cases is illustrated and explained in the annexed fig. 63, where the pendulum virtually oscillates about C as a fixed point of suspension. This illustration was given by T. Young in connexion with the kinetic theory of the tides, where the same point arises.
We may notice also the case of an attractive force varying inversely as the square of the distance from the origin. If μ be the acceleration at unit distance, we have
| u | du | = − | μ |
| dx | x2 |
In the case of a particle falling directly towards the earth from rest at a very great distance we have C = 0 and, by Newton’s Law of Gravitation, μ/a2 = g, where a is the earth’s radius. The deviation of the earth’s figure from sphericity, and the variation of g with latitude, are here ignored. We find that the velocity with which the particle would arrive at the earth’s surface (x = a) is √(2ga). If we take as rough values a = 21 × 106 feet, g = 32 foot-second units, we get a velocity of 36,500 feet, or about seven miles, per second. If the particles start from rest at a finite distance c, we have in (16), C = − 2μ/c, and therefore
| dx | = u = − √{ | 2μ (c − x) | }, |
| dt | cx |
the minus sign indicating motion towards the origin. If we put x = c cos2 12φ, we find
| t = | c32 | (φ + sin φ), |
| √(8μ) |
no additive constant being necessary if t be reckoned from the instant of starting, when φ = 0. The time t of reaching the origin (φ = π) is
| t1 = | π c32 | . |
| √(8μ) |
This may be compared with the period of revolution in a circular
orbit of radius c about the same centre of force, viz. 2πc32 / √μ (§ 14).
We learn that if the orbital motion of a planet, or a satellite, were
arrested, the body would fall into the sun, or into its primary, in
the fraction 0.1768 of its actual periodic time. Thus the moon
would reach the earth in about five days. It may be noticed that
if the scales of x and t be properly adjusted, the curve of positions
in the present problem is the portion of a cycloid extending from
a vertex to a cusp.
In any case of rectilinear motion, if we integrate both sides of the equation
| mududx = X, | (20) |
which is equivalent to (1), with respect to x between the limits x0, x1, we obtain
| 12 mu12 − 12 mu02 = Xdx. | (21) |
We recognize the right-hand member as the work done by the force X on the particle as the latter moves from the position x0 to the position x1. If we construct a curve with x as abscissa and X as ordinate, this work is represented, as in J. Watt’s “indicator-diagram,” by the area cut off by the ordinates x = x0, x = x1. The product 12mu2 is called the kinetic energy of the particle, and the equation (21) is therefore equivalent to the statement that the increment of the kinetic energy is equal to the work done on the particle. If the force X be always the same in the same position, the particle may be regarded as moving in a certain invariable “field of force.” The work which would have to be supplied by other forces, extraneous to the field, in order to bring the particle from rest in some standard position P0 to rest in any assigned position P, will depend only on the position of P; it is called the statical or potential energy of the particle with respect to the field, in the position P. Denoting this by V, we have δV − Xδx = 0, whence
| X = dVdx. | (22) |
The equation (21) may now be written
| 12 mu12 + V1 = 12 mu02 + V0, | (23) |
which asserts that when no extraneous forces act the sum of the kinetic and potential energies is constant. Thus in the case of a weight hanging by a spiral spring the work required to increase the length by x is V = ∫x0 Kxdx = 12Kx2, whence 12Mu2 + 12Kx2 = const., as is easily verified from preceding results. It is easily seen that the effect of extraneous forces will be to increase the sum of the kinetic and potential energies by an amount equal to the work done by them. If this amount be negative the sum in question is diminished by a corresponding amount. It appears then that this sum is a measure of the total capacity for doing work against extraneous resistances which the particle possesses in virtue of its motion and its position; this is in fact the origin of the term “energy.” The product mv2 had been called by G. W. Leibnitz the “vis viva”; the name “energy” was substituted by T. Young; finally the name “actual energy” was appropriated to the expression 12mv2 by W. J. M. Rankine.
The laws which regulate the resistance of a medium such as air to the motion of bodies through it are only imperfectly known. We may briefly notice the case of resistance varying as the square of the velocity, which is mathematically simple. If the positive direction of x be downwards, the equation of motion of a falling particle will be of the form
| du | = g − ku2; |
| dt |
this shows that the velocity u will send asymptotically to a certain limit V (called the terminal velocity) such that kV2 = g. The solution is
| u = V tanh | gt | , x = | V2 | log cosh | gt | , |
| V | g | V |
if the particle start from rest in the position x = 0 at the instant
t = 0. In the case of a particle projected vertically upwards we
have
| du | = −g − ku2, |
| dt |
the positive direction being now upwards. This leads to
| tan−1 | u | = tan−1 | u0 | − | gt | , x = | V2 | log | V2 + u02 | , |
| V | V | V | 2g | V2 + u2 |
where u0 is the velocity of projection. The particle comes to rest when
| t = | V | tan−1 | u0 | , x = | V2 | log ( 1 + | u02 | ). |
| g | V | 2g | V2 |
For small velocities the resistance of the air is more nearly proportional to the first power of the velocity. The effect of forces of this type on small vibratory motions may be investigated as follows. The equation (5) when modified by the introduction of a frictional term becomes
If k2 < 4μ the solution is
where
and the constants a, ε are arbitrary. This may be described as a simple harmonic oscillation whose amplitude diminishes asymptotically to zero according to the law e−t/τ. The constant τ is called the modulus of decay of the oscillations; if it is large compared with 2π/σ the effect of friction on the period is of the second order of small quantities and may in general be ignored. We have seen that a true simple-harmonic vibration may be regarded as the orthogonal projection of uniform circular motion; it was pointed out by P. G. Tait that a similar representation of the type (30) is obtained if we replace the circle by an equiangular spiral described, with a constant angular velocity about the pole, in the direction of diminishing radius vector. When k2 > 4μ, the solution of (29) is, in real form,
where
The body now passes once (at most) through its equilibrium position, and the vibration is therefore styled aperiodic.
To find the forced oscillation due to a periodic force we have
The solution is
| x = | ƒ | cos (σ1t + ε − ε1), |
| R |
provided
| R = { (μ − σ12)2 + k2σ12}12, tan ε1 = | kσ1 | . |
| μ − σ12 |
Hence the phase of the vibration lags behind that of the force by
the amount ε1, which lies between 0 and 12π or between 12π and π,
according as σ12 ≶ μ. If the friction be comparatively slight the
amplitude is greatest when the imposed period coincides with the
free period, being then equal to f /kσ1, and therefore very great
compared with that due to a slowly varying force of the same average
intensity. We have here, in principle, the explanation of the
phenomenon of “resonance” in acoustics. The abnormal amplitude
is greater, and is restricted to a narrower range of frequency, the
smaller the friction. For a complete solution of (34) we must of
course superpose the free vibration (30); but owing to the factor e−t/τ
the influence of the initial conditions gradually disappears.
For purposes of mathematical treatment a force which produces a finite change of velocity in a time too short to be appreciated is regarded as infinitely great, and the time of action as infinitely short. The whole effect is summed up in the value of the instantaneous impulse, which is the time-integral of the force. Thus if an instantaneous impulse ξ changes the velocity of a mass m from u to u′ we have
The effect of ordinary finite forces during the infinitely short duration of this impulse is of course ignored.
We may apply this to the theory of impact. If two masses m1, m2 moving in the same straight line impinge, with the result that the velocities are changed from u1, u2, to u1′, u2′, then, since the impulses on the two bodies must be equal and opposite, the total momentum is unchanged, i.e.
The complete determination of the result of a collision under given circumstances is not a matter of abstract dynamics alone, but requires some auxiliary assumption. If we assume that there is no loss of apparent kinetic energy we have also
Hence, and from (38),
i.e. the relative velocity of the two bodies is reversed in direction, but unaltered in magnitude. This appears to be the case very approximately with steel or glass balls; generally, however, there is some appreciable loss of apparent energy; this is accounted for by vibrations produced in the balls and imperfect elasticity of the materials. The usual empirical assumption is that
where e is a proper fraction which is constant for the same two bodies. It follows from the formula § 15 (10) for the internal kinetic energy of a system of particles that as a result of the impact this energy is diminished by the amount
| 12 (1 − e2) | m1m2 | (u1 − u2)2. |
| m1 + m2 |
The further theoretical discussion of the subject belongs to Elasticity.
This is perhaps the most suitable place for a few remarks on the theory of “dimensions.” (See also Units, Dimensions of.) In any absolute system of dynamical measurement the fundamental units are those of mass, length and time; we may denote them by the symbols M, L, T, respectively. They may be chosen quite arbitrarily, e.g. on the C.G.S. system they are the gramme, centimetre and second. All other units are derived from these. Thus the unit of velocity is that of a point describing the unit of length in the unit of time; it may be denoted by LT−1, this symbol indicating that the magnitude of the unit in question varies directly as the unit of length and inversely as the unit of time. The unit of acceleration is the acceleration of a point which gains unit velocity in unit time; it is accordingly denoted by LT−2. The unit of momentum is MLT−1; the unit force generates unit momentum in unit time and is therefore denoted by MLT−2. The unit of work on the same principles is ML2T−2, and it is to be noticed that this is identical with the unit of kinetic energy. Some of these derivative units have special names assigned to them; thus on the C.G.S. system the unit of force is called the dyne, and the unit of work or energy the erg. The number which expresses a physical quantity of any particular kind will of course vary inversely as the magnitude of the corresponding unit. In any general dynamical equation the dimensions of each term in the fundamental units must be the same, for a change of units would otherwise alter the various terms in different ratios. This principle is often useful as a check on the accuracy of an equation.
The theory of dimensions often enables us to forecast, to some extent, the manner in which the magnitudes involved in any particular problem will enter into the result. Thus, assuming that the period of a small oscillation of a given pendulum at a given place is a definite quantity, we see that it must vary as √(l/g). For it can only depend on the mass m of the bob, the length l of the string, and the value of g at the place in question; and the above expression is the only combination of these symbols whose dimensions are those of a time, simply. Again, the time of falling from a distance a into a given centre of force varying inversely as the square of the distance will depend only on a and on the constant μ of equation (15). The dimensions of μ/x2 are those of an acceleration; hence the dimensions of μ are L3T−2. Assuming that the time in question varies as axμy, whose dimensions are Lx+3yT−2y, we must have x + 3y = 0, −2y = 1, so that the time of falling will vary as a32/√μ, in agreement with (19).
The argument appears in a more demonstrative form in the theory of “similar” systems, or (more precisely) of the similar motion of similar systems. Thus, considering the equations
| d 2x | = − | μ | , | d 2x′ | = − | μ′ | , |
| dt 2 | x2 | dt ′2 | x′2 |
which refer to two particles falling independently into two distinct
centres of force, it is obvious that it is possible to have x in a constant
ratio to x′, and t in a constant ratio to t ′, provided that
| x | : | x′ | = | μ | : | μ′ | , |
| t 2 | t ′2 | x2 | x′2 |
and that there is a suitable correspondence between the initial
conditions. The relation (44) is equivalent to
| t : t ′ = | x32 | : | x′32 | , |
| μ12 | μ′12 |
where x, x′ are any two corresponding distances; e.g. they may be
the initial distances, both particles being supposed to start from rest.
The consideration of dimensions was introduced by J. B. Fourier
(1822) in connexion with the conduction of heat.
 |
| Fig. 64. |
§ 13. General Motion of a Particle.—Let P, Q be the positions of a moving point at times t, t + δt respectively. A vector OU→ drawn parallel to PQ, of length proportional to PQ/δt on any convenient scale, will represent the mean velocity in the interval δt, i.e. a point moving with a constant velocity having the magnitude and direction indicated by this vector would experience the same resultant displacement PQ→ in the same time. As δt is indefinitely diminished, the vector OU→ will tend to a definite limit OV→; this is adopted as the definition of the velocity of the moving point at the instant t. Obviously OV→ is parallel to the tangent to the path at P, and its magnitude is ds/dt, where s is the arc. If we project OV→ on the co-ordinate axes (rectangular or oblique) in the usual manner, the projections u, v, w are called the component velocities parallel to the axes. If x, y, z be the co-ordinates of P it is easily proved that
| u = | dx | , v = | dy | , w = | dz | . |
| dt | dt | dt |
The momentum of a particle is the vector obtained by multiplying
the velocity by the mass m. The impulse of a force
in any infinitely small interval of time δt is the product of the
force into δt; it is to be regarded as a vector. The total impulse
in any finite interval of time is the integral of the impulses
corresponding to the infinitesimal elements δt into which the
interval may be subdivided; the summation of which the
integral is the limit is of course to be understood in the vectorial
sense.
Newton’s Second Law asserts that change of momentum is equal to the impulse; this is a statement as to equality of vectors and so implies identity of direction as well as of magnitude. If X, Y, Z are the components of force, then considering the changes in an infinitely short time δt we have, by projection on the co-ordinate axes, δ(mu) = Xδt, and so on, or
| m | du | = X, m | dv | = Y, m | dw | = Z. |
| dt | dt | dt |
For example, the path of a particle projected anyhow under
gravity will obviously be confined to the vertical plane through
the initial direction of motion. Taking this as the plane xy,
with the axis of x drawn horizontally, and that of y vertically
upwards, we have X = 0, Y = −mg; so that
| d 2x | = 0, | d 2y | = −g. |
| dt 2 | dt 2 |
The solution is
If the initial values of x, y, ẋ, ẏ are given, we have four conditions to determine the four arbitrary constants A, B, C, D. Thus if the particle start at time t = 0 from the origin, with the component velocities u0, v0, we have
Eliminating t we have the equation of the path, viz.
| y = | v0 | x − | gx2 | . |
| u0 | 2u2 |
This is a parabola with vertical axis, of latus-rectum 2u02/g. The range on a horizontal plane through O is got by putting y = 0, viz. it is 2u0v0/g. we denote the resultant velocity at any instant by ṡ we have
Another important example is that of a particle subject to an acceleration which is directed always towards a fixed point O and is proportional to the distance from O. The motion will evidently be in one plane, which we take as the plane z = 0. If μ be the acceleration at unit distance, the component accelerations parallel to axes of x and y through O as origin will be −μx, −μy, whence
| d 2x | = −μx, | d 2y | = − μy. |
| dt 2 | dt 2 |
The solution is
where n = √μ. If P be the initial position of the particle, we may conveniently take OP as axis of x, and draw Oy parallel to the direction of motion at P. If OP = a, and ṡ0 be the velocity at P, we have, initially, x = a, y = 0, ẋ = 0, ẏ = ṡ0 whence
if b = ṡ0/n. The path is therefore an ellipse of which a, b are conjugate semi-diameters, and is described in the period 2π/√μ; moreover, the velocity at any point P is equal to √μ·OD, where OD is the semi-diameter conjugate to OP. This type of motion is called elliptic harmonic. If the co-ordinate axes are the principal axes of the ellipse, the angle nt in (10) is identical with the “excentric angle.” The motion of the bob of a “spherical pendulum,” i.e. a simple pendulum whose oscillations are not confined to one vertical plane, is of this character, provided the extreme inclination of the string to the vertical be small. The acceleration is towards the vertical through the point of suspension, and is equal to gr/l, approximately, if r denote distance from this vertical. Hence the path is approximately an ellipse, and the period is 2π √(l/g).
 |
 |
| Fig. 65. | Fig. 66. |
The above problem is identical with that of the oscillation of a particle in a smooth spherical bowl, in the neighbourhood of the lowest point. If the bowl has any other shape, the axes Ox, Oy may be taken tangential to the lines of curvature at the lowest point O; the equations of small motion then are
| d 2x | = −g | x | , | d 2y | = −g | y | , |
| dt 2 | ρ1 | dt 2 | ρ2 |
where ρ1, ρ2, are the principal radii of curvature
at O. The motion is therefore the resultant of
two simple vibrations in perpendicular directions,
of periods 2π √(ρ1/g), 2π √(ρ2/g). The
circumstances are realized in “Blackburn’s
pendulum,” which consists of a weight P
hanging from a point C of a string ACB whose
ends A, B are fixed. If E be the point in which the line of the
string meets AB, we have ρ1 = CP, ρ2 = EP. Many contrivances
for actually drawing the resulting curves have been devised.
It is sometimes convenient to resolve the accelerations in directions having a more intrinsic relation to the path. Thus, in a plane path, let P, Q be two consecutive positions, corresponding to the times t, t + δt; and let the normals at P, Q meet in C, making an angle δψ. Let v (= ṡ) be the velocity at P, v + δv that at Q. In the time δt the velocity parallel to the tangent at P changes from v to v + δv, ultimately, and the tangential acceleration at P is therefore dv/dt or s̈. Again, the velocity parallel to the normal at P changes from 0 to vδψ, ultimately, so that the normal acceleration is vdψ/dt. Since
| dv | = | dv | ds | = v | dv | , v | dψ | = v | dψ | ds | = | v 2 | , | ||
| dt | ds | dt | ds | dt | ds | dt | ρ |
where ρ is the radius of curvature of the path at P, the tangential
and normal accelerations are also expressed by v dv/ds and v 2/ρ,
respectively. Take, for example, the case of a particle moving
on a smooth curve in a vertical plane, under the action
of gravity and the pressure R of the curve. If the axes of
x and y be drawn horizontal and vertical (upwards), and if ψ
be the inclination of the tangent to the horizontal, we have
| mv | dv | = − mg sin ψ = − mg | dy | , | mv 2 | = − mg cos ψ + R. |
| ds | ds | ρ |
The former equation gives
and the latter then determines R.
In the case of the pendulum the tension of the string takes the place of the pressure of the curve. If l be the length of the string, ψ its inclination to the downward vertical, we have δs = lδψ, so that v = ldψ/dt. The tangential resolution then gives
| l | d 2ψ | = − g sin ψ. |
| dt 2 |
If we multiply by 2dψ/dt and integrate, we obtain
| ( | dψ | )2 = | 2g | cos ψ + const., |
| dt | l |
which is seen to be equivalent to (14). If the pendulum oscillate between the limits ψ = ±α, we have
| ( | δψ | )2 = | 2g | (cos ψ − cos α) = | 4g | (sin2 12α − sin2 12ψ); |
| dt | l | l |
and, putting sin 12ψ = sin 12α. sin φ, we find for the period (τ) of a complete oscillation
| τ = 4 | dt | dφ = 4√ | l | · | dφ |
| dφ | g | √(1 − sin2 12α · sin2 φ) |
| = 4√ | l | · F1 (sin 12α), |
| g |
in the notation of elliptic integrals. The function F1 (sin β) was tabulated by A. M. Legendre for values of β ranging from 0° to 90°. The following table gives the period, for various amplitudes α, in terms of that of oscillation in an infinitely small arc [viz. 2π√(l /g)] as unit.
| α/π | τ | α/π | τ |
| .1 | 1.0062 | .6 | 1.2817 |
| .2 | 1.0253 | .7 | 1.4283 |
| .3 | 1.0585 | .8 | 1.6551 |
| .4 | 1.1087 | .9 | 2.0724 |
| .5 | 1.1804 | 1.0 | ∞ |
The value of τ can also be obtained as an infinite series, by expanding the integrand in (18) by the binomial theorem, and integrating term by term. Thus
| τ = 2π √ | l | · { 1 + | 12 | sin2 12α + | 12 · 32 | sin4 12α + . . . }. |
| g | 22 | 22 · 42 |
If α be small, an approximation (usually sufficient) is
In the extreme case of α = π, the equation (17) is immediately integrable; thus the time from the lowest position is
This becomes infinite for ψ = π, showing that the pendulum only tends asymptotically to the highest position.
The variation of period with amplitude was at one time a hindrance to the accurate performance of pendulum clocks, since the errors produced are cumulative. It was therefore sought to replace the circular pendulum by some other contrivance free from this defect. The equation of motion of a particle in any smooth path is
| d 2s | = −g sin ψ, |
| dt 2 |
where ψ is the inclination of the tangent to the horizontal. If sin ψ were accurately and not merely approximately proportional to the arc s, say
 |
| Fig. 67. |
the equation (21) would assume the same form as § 12 (5). The motion along the arc would then be accurately simple-harmonic, and the period 2π √(k/g) would be the same for all amplitudes. Now equation (22) is the intrinsic equation of a cycloid; viz. the curve is that traced by a point on the circumference of a circle of radius 14k which rolls on the under side of a horizontal straight line. Since the evolute of a cycloid is an equal cycloid the object is attained by means of two metal cheeks, having the form of the evolute near the cusp, on which the string wraps itself alternately as the pendulum swings. The device has long been abandoned, the difficulty being met in other ways, but the problem, originally investigated by C. Huygens, is important in the history of mathematics.
The component accelerations of a point describing a tortuous curve, in the directions of the tangent, the principal normal, and the binormal, respectively, are found as follows. If OV→, OV′→ be vectors representing the velocities at two consecutive points P, P′ of the path, the plane VOV′ is ultimately parallel to the osculating plane of the path at P; the resultant acceleration is therefore in the osculating plane. Also, the projections of VV′→ on OV and on a perpendicular to OV in the plane VOV′ are δv and vδε, where δε is the angle between the directions of the tangents at P, P′. Since δε = δs/ρ, where δs = PP′ = vδt and ρ is the radius of principal curvature at P, the component accelerations along the tangent and principal normal are dv/dt and vdε/dt, respectively, or vdv/ds and v 2/ρ. For example, if a particle moves on a smooth surface, under no forces except the reaction of the surface, v is constant, and the principal normal to the path will coincide with the normal to the surface. Hence the path is a “geodesic” on the surface.
If we resolve along the tangent to the path (whether plane or tortuous), the equation of motion of a particle may be written
| mv | dv | = T, |
| ds |
where T is the tangential component of the force. Integrating with respect to s we find
i.e. the increase of kinetic energy between any two positions is equal to the work done by the forces. The result follows also from the Cartesian equations (2); viz. we have
whence, on integration with respect to t,
| 12m (ẋ2 + ẏ2 + ż2) | = ∫ (Xẋ + Yẏ + Zż) dt + const. |
| = ∫ (X dx + Y dy + Z dz) + const. |
If the axes be rectangular, this has the same interpretation as (24).
Suppose now that we have a constant field of force; i.e. the force acting on the particle is always the same at the same place. The work which must be done by forces extraneous to the field in order to bring the particle from rest in some standard position A to rest in any other position P will not necessarily be the same for all paths between A and P. If it is different for different paths, then by bringing the particle from A to P by one path, and back again from P to A by another, we might secure a gain of work, and the process could be repeated indefinitely. If the work required is the same for all paths between A and P, and therefore zero for a closed circuit, the field is said to be conservative. In this case the work required to bring the particle from rest at A to rest at P is called the potential energy of the particle in the position P; we denote it by V. If PP′ be a linear element δs drawn in any direction from P, and S be the force due to the field, resolved in the direction PP′, we have δV = −Sδs or
| S = − | ∂V | . |
| ∂s |
In particular, by taking PP′ parallel to each of the (rectangular) co-ordinate axes in succession, we find
| X = − | ∂V | , Y = − | ∂V | , Z = − | ∂V | . |
| ∂x | ∂y | ∂z |
The equation (24) or (26) now gives
i.e. the sum of the kinetic and potential energies is constant when no work is done by extraneous forces. For example, if the field be that due to gravity we have V = ƒmgdy = mgy + const., if the axis of y be drawn vertically upwards; hence
| 12mv 2 + mgy = const. | (30) |
This applies to motion on a smooth curve, as well as to the free motion of a projectile; cf. (7), (14). Again, in the case of a force Kr towards O, where r denotes distance from O we have V = ∫ Krdr = 12Kr 2 + const., whence
| 12mv 2 + 12Kr 2 = const. | (31) |
It has been seen that the orbit is in this case an ellipse; also that if we put μ = K/m the velocity at any point P is v = √μ. OD, where OD is the semi-diameter conjugate to OP. Hence (31) is consistent with the known property of the ellipse that OP2 + OD2 is constant.
The forms assumed by the dynamical equations when the axes of reference are themselves in motion will be considered in § 21. At present we take only the case where the rectangular axes Ox, Oy rotate in their own plane, with angular velocity ω about Oz, which is fixed. In the interval δt the projections of the line joining the origin to any point (x, y, z) on the directions of the co-ordinate axes at time t are changed from x, y, z to (x + δx) cos ω δt − (y + δy) sin ωδt, (x + δx) sin ω δt + (y + δy) cos ω δt, z respectively. Hence the component velocities parallel to the instantaneous positions of the co-ordinate axes at time t are
In the same way we find that the component accelerations are
Hence if ω be constant the equations of motion take the forms
These become identical with the equations of motion relative to fixed axes provided we introduce a fictitious force mω2r acting outwards from the axis of z, where r = √(x2 + y2), and a second fictitious force 2mωv at right angles to the path, where v is the component of the relative velocity parallel to the plane xy. The former force is called by French writers the force centrifuge ordinaire, and the latter the force centrifuge composée, or force de Coriolis. As an application of (34) we may take the case of a symmetrical Blackburn’s pendulum hanging from a horizontal bar which is made to rotate about a vertical axis half-way between the points of attachment of the upper string. The equations of small motion are then of the type
| ẍ − 2ωẏ − ω2x = −p2x, ÿ + 2ωẋ − ω2y = −q2y. | (35) |
This is satisfied by
provided
| (σ2 + ω2 − p2) A + 2σωB = 0, |
| 2σωA + (σ2 + ω2 − q2) B = 0. |
Eliminating the ratio A : B we have
It is easily proved that the roots of this quadratic in σ2 are always real, and that they are moreover both positive unless ω2 lies between p2 and q2. The ratio B/A is determined in each case by either of the equations (37); hence each root of the quadratic gives a solution of the type (36), with two arbitrary constants A, ε. Since the equations (35) are linear, these two solutions are to be superposed. If the quadratic (38) has a negative root, the trigonometrical functions in (36) are to be replaced by real exponentials, and the position x = 0, y = 0 is unstable. This occurs only when the period (2π/ω) of revolution of the arm lies between the two periods (2π/p, 2π/q) of oscillation when the arm is fixed.
§ 14. Central Forces. Hodograph.—The motion of a particle subject to a force which passes always through a fixed point O is necessarily in a plane orbit. For its investigation we require two equations; these may be obtained in a variety of forms.
Since the impulse of the force in any element of time δt has zero moment about O, the same will be true of the additional momentum generated. Hence the moment of the momentum (considered as a localized vector) about O will be constant. In symbols, if v be the velocity and p the perpendicular from O to the tangent to the path,
| pv = h, | (1) |
where h is a constant. If δs be an element of the path, pδs is twice the area enclosed by δs and the radii drawn to its extremities from O. Hence if δA be this area, we have δA = 12 pδs = 12 hδt, or
| dA | = 12h |
| dt |
Hence equal areas are swept over by the radius vector in equal times.
If P be the acceleration towards O, we have
| v | dv | = −P | dr | |
| ds | ds |
since dr /ds is the cosine of the angle between the directions of r and δs. We will suppose that P is a function of r only; then integrating (3) we find
which is recognized as the equation of energy. Combining this with (1) we have
| h2 | = C − 2 ∫ P dr, |
| p2 |
which completely determines the path except as to its orientation with respect to O.
If the law of attraction be that of the inverse square of the distance, we have P = μ/r 2, and
| h2 | = C + | 2μ | . |
| p2 | τ |
Now in a conic whose focus is at O we have
| l | = | 2 | ± | 1 | , |
| p2 | r | a |
where l is half the latus-rectum, a is half the major axis, and the upper or lower sign is to be taken according as the conic is an ellipse or hyperbola. In the intermediate case of the parabola we have a = ∞ and the last term disappears. The equations (6) and (7) are identified by putting
Since
| v 2 = | h2 | = μ ( | 2 | ± | 1 | ), |
| p2 | r | a |
it appears that the orbit is an ellipse, parabola or hyperbola, according as v 2 is less than, equal to, or greater than 2μ/r. Now it appears from (6) that 2μ/r is the square of the velocity which would be acquired by a particle falling from rest at infinity to the distance r. Hence the character of the orbit depends on whether the velocity at any point is less than, equal to, or greater than the velocity from infinity, as it is called. In an elliptic orbit the area πab is swept over in the time
| r = | πab | = | 2πa32 | , |
| 12h | √μ |
since h = μ12l12 = μ12ba−1/2 by (8).
The converse problem, to determine the law of force under which a given orbit can be described about a given pole, is solved by differentiating (5) with respect to r; thus
| P = | h2 dp | . |
| p3 dr |
In the case of an ellipse described about the centre as pole we have
| a2b2 | = a2 + b2 − r 2; |
| p2 |
hence P = μr, if μ = h2/a2b2. This merely shows that a particular ellipse may be described under the law of the direct distance provided the circumstances of projection be suitably adjusted. But since an ellipse can always be constructed with a given centre so as to touch a given line at a given point, and to have a given value of ab( = h/√μ) we infer that the orbit will be elliptic whatever the initial circumstances. Also the period is 2πab/h = 2π/√μ, as previously found.
 |
| Fig. 68. |
Again, in the equiangular spiral we have p = r sinα, and therefore P = μ/r 3, if μ = h2/sin2 α. But since an equiangular spiral having a given pole is completely determined by a given point and a given tangent, this type of orbit is not a general one for the law of the inverse cube. In order that the spiral may be described it is necessary that the velocity of projection should be adjusted to make h = √μ·sinα. Similarly, in the case of a circle with the pole on the circumference we have p2 = r 2/2a, P = μ/r 5, if μ = 8h2a2; but this orbit is not a general one for the law of the inverse fifth power.
In astronomical and other investigations relating to central forces it is often convenient to use polar co-ordinates with the centre of force as pole. Let P, Q be the positions of a moving point at times t, t + δt, and write OP = r, OQ = r + δr, ∠POQ = δθ, O being any fixed origin. If u, v be the component velocities at P along and perpendicular to OP (in the direction of θ increasing), we have
| u = lim. | δr | = | dr | , v = lim. | r δθ | = r | dθ | . |
| δt | dt | δt | dt |
Again, the velocities parallel and perpendicular to OP change
in the time δt from u, v to u − v δθ, v + u δθ, ultimately. The
component accelerations at P in these directions are therefore
| du | − v | dθ | = | d 2r | − r ( | dθ | )2, |
| dt | dt | dt 2 | dt |
| dv | + u | dθ | = | 1 | d | ( r 2 | dθ | ), | |
| dt | dt | r | dt | dt |
respectively.
In the case of a central force, with O as pole, the transverse acceleration vanishes, so that
where h is constant; this shows (again) that the radius vector sweeps over equal areas in equal times. The radial resolution gives
| d 2r | − r ( | dθ | )2 = −P, |
| dt 2 | dt |
where P, as before, denotes the acceleration towards O. If in this we put r = 1/u, and eliminate t by means of (15), we obtain the general differential equation of central orbits, viz.
| d 2u | + u = | P | . |
| dθ2 | h2u2 |
If, for example, the law be that of the inverse square, we have P = μu2, and the solution is of the form
| u = | μ | {1 + e cos (θ − α)}, |
| h2 |
where e, α are arbitrary constants. This is recognized as the polar equation of a conic referred to the focus, the half latus-rectum being h2/μ.
The law of the inverse cube P = μu3 is interesting by way of contrast. The orbits may be divided into two classes according as h2 ≷ μ, i.e. according as the transverse velocity (hu) is greater or less than the velocity √μ·u appropriate to a circular orbit at the same distance. In the former case the equation (17) takes the form
| d 2u | + m2u = 0, |
| dθ2 |
the solution of which is
The orbit has therefore two asymptotes, inclined at an angle π/m. In the latter case the differential equation is of the form
| d 2u | = m2u, |
| dθ2 |
so that
If A, B have the same sign, this is equivalent to
if the origin of θ be suitably adjusted; hence r has a maximum value α, and the particle ultimately approaches the pole asymptotically by an infinite number of convolutions. If A, B have opposite signs the form is
this has an asymptote parallel to θ = 0, but the path near the origin has the same general form as in the case of (23). If A or B vanish we have an equiangular spiral, and the velocity at infinity is zero. In the critical case of h2 = μ, we have d 2u/dθ2 = 0, and
the orbit is therefore a “reciprocal spiral,” except in the special case of A = 0, when it is a circle. It will be seen that unless the conditions be exactly adjusted for a circular orbit the particle will either recede to infinity or approach the pole asymptotically. This problem was investigated by R. Cotes (1682–1716), and the various curves obtained are known as Coles’s spirals.
A point on a central orbit where the radial velocity (dr/dt) vanishes is called an apse, and the corresponding radius is called an apse-line. If the force is always the same at the same distance any apse-line will divide the orbit symmetrically, as is seen by imagining the velocity at the apse to be reversed. It follows that the angle between successive apse-lines is constant; it is called the apsidal angle of the orbit.
If in a central orbit the velocity is equal to the velocity from infinity, we have, from (5),
| h2 | = 2 Pdr ; |
| p2 |
this determines the form of the critical orbit, as it is called. If P = μ/r n, its polar equation is
where m = 12(3 − n), except in the case n = 3, when the orbit is an equiangular spiral. The case n = 2 gives the parabola as before.
If we eliminate dθ/dt between (15) and (16) we obtain
| d 2r | − | h2 | = −P = −ƒ(r), |
| dt 2 | r 3 |
say. We may apply this to the investigation of the stability of a circular orbit. Assuming that r = a + x, where x is small, we have, approximately,
| d 2x | − | h2 | ( 1 − | 3x | ) = −ƒ(a) − xƒ′(a). |
| dt 2 | a3 | a |
Hence if h and a be connected by the relation h2 = a3ƒ(a) proper to a circular orbit, we have
| d 2x | + { ƒ′(a) + | 3 | ƒ(a) } x = 0 |
| dt 2 | a |
If the coefficient of x be positive the variations of x are simple-harmonic, and x can remain permanently small; the circular orbit is then said to be stable. The condition for this may be written
| d | { a3ƒ(a) } > 0, |
| da |
i.e. the intensity of the force in the region for which r = a, nearly, must diminish with increasing distance less rapidly than according to the law of the inverse cube. Again, the half-period of x is π/√{ƒ′(a) + 3−1ƒ(a)}, and since the angular velocity in the orbit is h/a2, approximately, the apsidal angle is, ultimately,
| π √ | ƒ(a) | , |
| aƒ′(a) + 3ƒ(a) |
or, in the case of ƒ(a) = μ/r n, π/√(3 − n). This is in agreement with
the known results for n = 2, n = −1.
We have seen that under the law of the inverse square all finite orbits are elliptical. The question presents itself whether there then is any other law of force, giving a finite velocity from infinity, under which all finite orbits are necessarily closed curves. If this is the case, the apsidal angle must evidently be commensurable with π, and since it cannot vary discontinuously the apsidal angle in a nearly circular orbit must be constant. Equating the expression (30) to π/m, we find that ƒ(a) = C/an, where n = 3 − m2. The force must therefore vary as a power of the distance, and n must be less than 3. Moreover, the case n = 2 is the only one in which the critical orbit (27) can be regarded as the limiting form of a closed curve. Hence the only law of force which satisfies the conditions is that of the inverse square.
At the beginning of § 13 the velocity of a moving point P was represented by a vector OV→ drawn from a fixed origin O. The locus of the point V is called the hodograph (q.v.); and it appears that the velocity of the point V along the hodograph represents in magnitude and in direction the acceleration in the original orbit. Thus in the case of a plane orbit, if v be the velocity of P, ψ the inclination of the direction of motion to some fixed direction, the polar co-ordinates of V may be taken to be v, ψ; hence the velocities of V along and perpendicular to OV will be dv/dt and vdψ/dt. These expressions therefore give the tangential and normal accelerations of P; cf. § 13 (12).
 |
| Fig. 69. |
In the motion of a projectile under gravity the hodograph is a vertical line described with constant velocity. In elliptic harmonic motion the velocity of P is parallel and proportional to the semi-diameter CD which is conjugate to the radius CP; the hodograph is therefore an ellipse similar to the actual orbit. In the case of a central orbit described under the law of the inverse square we have v = h/SY = h. SZ/b2, where S is the centre of force, SY is the perpendicular to the tangent at P, and Z is the point where YS meets the auxiliary circle again. Hence the hodograph is similar and similarly situated to the locus of Z (the auxiliary circle) turned about S through a right angle. This applies to an elliptic or hyperbolic orbit; the case of the parabolic orbit may be examined separately or treated as a limiting case. The annexed fig. 70 exhibits the various cases, with the hodograph in its proper orientation. The pole O of the hodograph is inside on or outside the circle, according as the orbit is an ellipse, parabola or hyperbola. In any case of a central orbit the hodograph (when turned through a right angle) is similar and similarly situated to the “reciprocal polar” of the orbit with respect to the centre of force. Thus for a circular orbit with the centre of force at an excentric point, the hodograph is a conic with the pole as focus. In the case of a particle oscillating under gravity on a smooth cycloid from rest at the cusp the hodograph is a circle through the pole, described with constant velocity.
§ 15. Kinetics of a System of Discrete Particles.—The momenta of the several particles constitute a system of localized vectors which, for purposes of resolving and taking moments, may be reduced like a system of forces in statics (§ 8). Thus taking any point O as base, we have first a linear momentum whose components referred to rectangular axes through O are
its representative vector is the same whatever point O be chosen. Secondly, we have an angular momentum whose components are
these being the sums of the moments of the momenta of the several particles about the respective axes. This is subject to the same relations as a couple in statics; it may be represented by a vector which will, however, in general vary with the position of O.
The linear momentum is the same as if the whole mass were concentrated at the centre of mass G, and endowed with the velocity of this point. This follows at once from equation (8) of § 11, if we imagine the two configurations of the system there referred to to be those corresponding to the instants t, t + δt. Thus
| Σ ( m· | PP→ | ) = Σ(m)· | GG′→ | . |
| δt | δt |
Analytically we have
| Σ(mẋ) = | d | Σ(mx) = Σ(m)· | dx̄ | , |
| dt | dt |
with two similar formulae.
Again, if the instantaneous position of G be taken as base, the angular momentum of the absolute motion is the same as the angular momentum of the motion relative to G. For the velocity of a particle m at P may be replaced by two components one of which (v̄) is identical in magnitude and direction with the velocity of G, whilst the other (v) is the velocity relative to G.
 |
| Fig. 70. |
The aggregate of the components mv̄ of momentum is equivalent to a single localized vector Σ(m)·v̄ in a line through G, and has therefore zero moment about any axis through G; hence in taking moments about such an axis we need only regard the velocities relative to G. In symbols, we have
| Σ { m(yż − zẏ) } = Σ(m)· ȳ | dz̄ | − z̄ | dȳ | + Σ { m (ηζ − ζ̇η̇) }. |
| dt | dt |
 |
| Fig. 71. |
since Σ(mξ) = 0, Σ(mξ̇) = 0, and so on, the notation being as in § 11. This expresses that the moment of momentum about any fixed axis (e.g. Ox) is equal to the moment of momentum of the motion relative to G about a parallel axis through G, together with the moment of momentum of the whole mass supposed concentrated at G and moving with this point. If in (5) we make O coincide with the instantaneous position of G, we have x̄, z̄, z = 0, and the theorem follows.
Finally, the rates of change of the components of the angular momentum of the motion relative to G referred to G as a moving base, are equal to the rates of change of the corresponding components of angular momentum relative to a fixed base coincident with the instantaneous position of G. For let G′ be a consecutive position of G. At the instant t + δt the momenta of the system are equivalent to a linear momentum represented by a localized vector Σ(m)·(v̄ + δv̄) in a line through G′ tangential to the path of G′, together with a certain angular momentum. Now the moment of this localized vector with respect to any axis through G is zero, to the first order of δt, since the perpendicular distance of G from the tangent line at G′ is of the order (δt)2. Analytically we have from (5),
| d | Σ { m (yż − zẏ) } = Σ(m)· ( ȳ | dz̄2 | − z̄ | d 2ȳ | ) + | d | Σ { m(ηζ − ζη̇) } |
| dt | dt 2 | dt 2 | dt |
If we put x̄, ȳ, z̄ = 0, the theorem is proved as regards axes
parallel to Ox.
Next consider the kinetic energy of the system. If from a fixed point O we draw vectors OV1→, OV2→ to represent the velocities of the several particles m1, m2 . . ., and if we construct the vector
| OK→ = | Σ ( m·OV→ ) |
| Σ(m) |
this will represent the velocity of the mass-centre, by (3). We
find, exactly as in the proof of Lagrange’s First Theorem (§ 11),
that
i.e. the total kinetic energy is equal to the kinetic energy of the whole mass supposed concentrated at G and moving with this point, together with the kinetic energy of the motion relative to G. The latter may be called the internal kinetic energy of the system. Analytically we have
| 12Σ { m (ẋ2 + ẏ2 + ż2) } = 12Σ(m)· { ( | dx̄ | )2 + ( | dȳ | )2 + ( | dz̄ | )2 } + 12Σ{ m(ζ2 + η̇2 + ζ̇2) }. |
| dt | dt | dt |
There is also an analogue to Lagrange’s Second Theorem, viz.
| 12Σ (m·KV2) = 12 | ΣΣ (mpmq · VpVq2) | , |
| Σm |
which expresses the internal kinetic energy in terms of the relative
velocities of the several pairs of particles. This formula is
due to Möbius.
The preceding theorems are purely kinematical. We have now to consider the effect of the forces acting on the particles. These may be divided into two categories; we have first, the extraneous forces exerted on the various particles from without, and, secondly, the mutual or internal forces between the various pairs of particles. It is assumed that these latter are subject to the law of equality of action and reaction. If the equations of motion of each particle be formed separately, each such internal force will appear twice over, with opposite signs for its components, viz. as affecting the motion of each of the two particles between which it acts. The full working out is in general difficult, the comparatively simple problem of “three bodies,” for instance, in gravitational astronomy being still unsolved, but some general theorems can be formulated.
The first of these may be called the Principle of Linear Momentum. If there are no extraneous forces, the resultant linear momentum is constant in every respect. For consider any two particles at P and Q, acting on one another with equal and opposite forces in the line PQ. In the time δt a certain impulse is given to the first particle in the direction (say) from P to Q, whilst an equal and opposite impulse is given to the second in the direction from Q to P. Since these impulses produce equal and opposite momenta in the two particles, the resultant linear momentum of the system is unaltered. If extraneous forces act, it is seen in like manner that the resultant linear momentum of the system is in any given time modified by the geometric addition of the total impulse of the extraneous forces. It follows, by the preceding kinematic theory, that the mass-centre G of the system will move exactly as if the whole mass were concentrated there and were acted on by the extraneous forces applied parallel to their original directions. For example, the mass-centre of a system free from extraneous force will describe a straight line with constant velocity. Again, the mass-centre of a chain of particles connected by strings, projected anyhow under gravity, will describe a parabola.
The second general result is the Principle of Angular Momentum. If there are no extraneous forces, the moment of momentum about any fixed axis is constant. For in time δt the mutual action between two particles at P and Q produces equal and opposite momenta in the line PQ, and these will have equal and opposite moments about the fixed axis. If extraneous forces act, the total angular momentum about any fixed axis is in time δt increased by the total extraneous impulse about that axis. The kinematical relations above explained now lead to the conclusion that in calculating the effect of extraneous forces in an infinitely short time δt we may take moments about an axis passing through the instantaneous position of G exactly as if G were fixed; moreover, the result will be the same whether in this process we employ the true velocities of the particles or merely their velocities relative to G. If there are no extraneous forces, or if the extraneous forces have zero moment about any axis through G, the vector which represents the resultant angular momentum relative to G is constant in every respect. A plane through G perpendicular to this vector has a fixed direction in space, and is called the invariable plane; it may sometimes be conveniently used as a plane of reference.
For example, if we have two particles connected by a string, the invariable plane passes through the string, and if ω be the angular velocity in this plane, the angular momentum relative to G is
where r1, r2 are the distances of m1, m2 from their mass-centre G. Hence if the extraneous forces (e.g. gravity) have zero moment about G, ω will be constant. Again, the tension R of the string is given by
| R = m1ω2r1 = | m1m2 | ω2a, |
| m1 + m2 |
where a = r1 + r2. Also by (10) the internal kinetic energy is
| 12 | m1m2 | ω2a2 |
| m1 + m2 |
The increase of the kinetic energy of the system in any interval of time will of course be equal to the total work done by all the forces acting on the particles. In many questions relating to systems of discrete particles the internal force Rpq (which we will reckon positive when attractive) between any two particles mp, mq is a function only of the distance rpq between them. In this case the work done by the internal forces will be represented by
when the summation includes every pair of particles, and each integral is to be taken between the proper limits. If we write
when rpq ranges from its value in some standard configuration A of the system to its value in any other configuration P, it is plain that V represents the work which would have to be done in order to bring the system from rest in the configuration A to rest in the configuration P. Hence V is a definite function of the configuration P; it is called the internal potential energy. If T denote the kinetic energy, we may say then that the sum T + V is in any interval of time increased by an amount equal to the work done by the extraneous forces. In particular, if there are no extraneous forces T + V is constant. Again, if some of the extraneous forces are due to a conservative field of force, the work which they do may be reckoned as a diminution of the potential energy relative to the field as in § 13.
§ 16. Kinetics of a Rigid Body. Fundamental Principles.—When we pass from the consideration of discrete particles to that of continuous distributions of matter, we require some physical postulate over and above what is contained in the Laws of Motion, in their original formulation. This additional postulate may be introduced under various forms. One plan is to assume that any body whatever may be treated as if it were composed of material particles, i.e. mathematical points endowed with inertia coefficients, separated by finite intervals, and acting on one another with forces in the lines joining them subject to the law of equality of action and reaction. In the case of a rigid body we must suppose that those forces adjust themselves so as to preserve the mutual distances of the various particles unaltered. On this basis we can predicate the principles of linear and angular momentum, as in § 15.
An alternative procedure is to adopt the principle first formally enunciated by J. Le R. d’Alembert and since known by his name. If x, y, z be the rectangular co-ordinates of a mass-element m, the expressions mẍ, mÿ, mz̈ must be equal to the components of the total force on m, these forces being partly extraneous and partly forces exerted on m by other mass-elements of the system. Hence (mẍ, mÿ, mz̈) is called the actual or effective force on m. According to d’Alembert’s formulation, the extraneous forces together with the effective forces reversed fulfil the statical conditions of equilibrium. In other words, the whole assemblage of effective forces is statically equivalent to the extraneous forces. This leads, by the principles of § 8, to the equations
| Σ(mẍ) = X, Σ(mÿ) = Y, Σ(mz̈) = Z, | |
| Σ {m (yz̈ − zÿ) } = L, Σ {m (zẍ − xz̈) } = M, Σ{m (xÿ − yẍ) } = N, |
where (X, Y, Z) and (L, M, N) are the force—and couple—constituents
of the system of extraneous forces, referred to O as base,
and the summations extend over all the mass-elements of the
system. These equations may be written
| ddt Σ(mẋ) = X, ddtΣ(mẏ) = Y, ddtΣ(mż) = Z, | |
| ddtΣ {m (yż − zẏ) } = L, ddtΣ {m (zẋ − xż) } = M, ddtΣ {m (xẏ − yẋ) } = N, ddt |
and so express that the rate of change of the linear momentum
in any fixed direction (e.g. that of Ox) is equal to the total
extraneous force in that direction, and that the rate of change
of the angular momentum about any fixed axis is equal to the
moment of the extraneous forces about that axis. If we integrate
with respect to t between fixed limits, we obtain the principles
of linear and angular momentum in the form previously given.
Hence, whichever form of postulate we adopt, we are led to
the principles of linear and angular momentum, which form in
fact the basis of all our subsequent work. It is to be noticed
that the preceding statements are not intended to be restricted
to rigid bodies; they are assumed to hold for all material systems
whatever. The peculiar status of rigid bodies is that the principles
in question are in most cases sufficient for the complete
determination of the motion, the dynamical equations (1 or 2)
being equal in number to the degrees of freedom (six) of a rigid
solid, whereas in cases where the freedom is greater we have to
invoke the aid of other supplementary physical hypotheses
(cf. Elasticity; Hydromechanics).
The increase of the kinetic energy of a rigid body in any interval of time is equal to the work done by the extraneous forces acting on the body. This is an immediate consequence of the fundamental postulate, in either of the forms above stated, since the internal forces do on the whole no work. The statement may be extended to a system of rigid bodies, provided the mutual reactions consist of the stresses in inextensible links, or the pressures between smooth surfaces, or the reactions at rolling contacts (§ 9).
§ 17. Two-dimensional Problems.—In the case of rotation about a fixed axis, the principles take a very simple form. The position of the body is specified by a single co-ordinate, viz. the angle θ through which some plane passing through the axis and fixed in the body has turned from a standard position in space. Then dθ/dt, = ω say, is the angular velocity of the body. The angular momentum of a particle m at a distance r from the axis is mωr·r, and the total angular momentum is Σ(mr 2)·ω, or Iω, if I denote the moment of inertia (§ 11) about the axis. Hence if N be the moment of the extraneous forces about the axis, we have
| ddt(Iω) = N. | (1) |
This may be compared with the equation of rectilinear motion of a particle, viz. d/dt·(Mu) = X; it shows that I measures the inertia of the body as regards rotation, just as M measures its inertia as regards translation. If N = 0, ω is constant.
As a first example, suppose we have a flywheel free to rotate about a horizontal axis, and that a weight m hangs by a vertical string from the circumferences of an axle of radius b (fig. 72).
 | |
| Fig. 72. | Fig. 73. |
Neglecting frictional resistance we have, if R be the tension of the string,
whence
| bω. = | mb2 | g. |
| 1 + mb2 |
This gives the acceleration of m as modified by the inertia of the wheel.
A “compound pendulum” is a body of any form which is free to rotate about a fixed horizontal axis, the only extraneous force (other than the pressures of the axis) being that of gravity. If M be the total mass, k the radius of gyration (§ 11) about the axis, we have
| d | ( Mk2 | dθ | ) = −Mgh sin θ, |
| dt | dt |
where θ is the angle which the plane containing the axis and the centre of gravity G makes with the vertical, and h is the distance of G from the axis. This coincides with the equation of motion of a simple pendulum [§ 13 (15)] of length l, provided l = k2/h. The plane of the diagram (fig. 73) is supposed to be a plane through G perpendicular to the axis, which it meets in O. If we produce OG to P, making OP = l, the point P is called the centre of oscillation; the bob of a simple pendulum of length OP suspended from O will keep step with the motion of P, if properly started. If κ be the radius of gyration about a parallel axis through G, we have k2 = κ2 + h2 by § 11 (16), and therefore l = h + κ2/h, whence
This shows that if the body were swung from a parallel axis through P the new centre of oscillation would be at O. For different parallel axes, the period of a small oscillation varies as √l, or √(GO + OP); this is least, subject to the condition (4), when GO = GP = κ. The reciprocal relation between the centres of suspension and oscillation is the basis of Kater’s method of determining g experimentally. A pendulum is constructed with two parallel knife-edges as nearly as possible in the same plane with G, the position of one of them being adjustable. If it could be arranged that the period of a small oscillation should be exactly the same about either edge, the two knife-edges would in general occupy the positions of conjugate centres of suspension and oscillation; and the distances between them would be the length l of the equivalent simple pendulum. For if h1 + κ2/h1 = h2 + κ2/h2, then unless h1 = h2, we must have κ2 = h1h2, l = h1 + h2. Exact equality of the two observed periods (τ1, τ2, say) cannot of course be secured in practice, and a modification is necessary. If we write l1 = h1 + κ2/h1, l2 = h2 + κ2/h2, we find, on elimination of κ,
| 12 | l1 + l2 | + 12 | l1 − l2 | = 1, |
| h1 + h2 | h1 − h2 |
whence
| 4π2 | = | 12 (τ12 + τ22) | + | 12 (τ12 − τ22) | . |
| g | h1 + h2 | h1 − h2 |
The distance h1 + h2, which occurs in the first term on the right hand
can be measured directly. For the second term we require the values
of h1, h2 separately, but if τ1, τ2 are nearly equal whilst h1, h2 are
distinctly unequal this term will be relatively small, so that an
approximate knowledge of h1, h2 is sufficient.
As a final example we may note the arrangement, often employed in physical measurements, where a body performs small oscillations about a vertical axis through its mass-centre G, under the influence of a couple whose moment varies as the angle of rotation from the equilibrium position. The equation of motion is of the type
and the period is therefore τ = 2π√(I/K). If by the attachment of another body of known moment of inertia I′, the period is altered from τ to τ′, we have τ′ = 2π√{ (I + I′)/K }. We are thus enabled to determine both I and K, viz.
The couple may be due to the earth’s magnetism, or to the torsion of a suspending wire, or to a “bifilar” suspension. In the latter case, the body hangs by two vertical threads of equal length l in a plane through G. The motion being assumed to be small, the tensions of the two strings may be taken to have their statical values Mgb/(a + b), Mga/(a + b), where a, b are the distances of G from the two threads. When the body is twisted through an angle θ the threads make angles aθ/l, bθ/l with the vertical, and the moment of the tensions about the vertical through G is accordingly −Kθ, where K = M gab/l.
For the determination of the motion it has only been necessary to use one of the dynamical equations. The remaining equations serve to determine the reactions of the rotating body on its bearings. Suppose, for example, that there are no extraneous forces. Take rectangular axes, of which Oz coincides with the axis of rotation. The angular velocity being constant, the effective force on a particle m at a distance r from Oz is mω2r towards this axis, and its components are accordingly −ω2mx, −ω2my, O. Since the reactions on the bearings must be statically equivalent to the whole system of effective forces, they will reduce to a force (X Y Z) at O and a couple (L M N) given by
L = ω2Σ(myz), M = −ω2Σ(mzx), N = 0,
where x̄, ȳ refer to the mass-centre G. The reactions do not therefore
reduce to a single force at O unless Σ(myz) = 0, Σ(msx) = 0,
i.e. unless the axis of rotation be a principal axis of inertia
(§ 11) at O. In order that the force may vanish we must also
have x̄, ȳ = 0, i.e. the mass-centre must lie in the axis of rotation.
These considerations are important in the “balancing” of
machinery. We note further that if a body be free to turn
about a fixed point O, there are three mutually perpendicular
lines through this point about which it can rotate steadily,
without further constraint. The theory of principal or “permanent”
axes was first investigated from this point of view
by J. A. Segner (1755). The origin of the name “deviation
moment” sometimes applied to a product of inertia is also
now apparent.
 |
| Fig. 74. |
Proceeding to the general motion of a rigid body in two dimensions we may take as the three co-ordinates of the body the rectangular Cartesian co-ordinates x, y of the mass-centre G and the angle θ through which the body has turned from some standard position. The components of linear momentum are then Mẋ, Mẏ, and the angular momentum relative to G as base is Iθ., where M is the mass and I the moment of inertia about G. If the extraneous forces be reduced to a force (X, Y) at G and a couple N, we have
If the extraneous forces have zero moment about G the angular velocity θ. is constant. Thus a circular disk projected under gravity in a vertical plane spins with constant angular velocity, whilst its centre describes a parabola.
We may apply the equations (9) to the case of a solid of revolution rolling with its axis horizontal on a plane of inclination α. If the axis of x be taken parallel to the slope of the plane, with x increasing downwards, we have
where κ is the radius of gyration about the axis of symmetry, a is the constant distance of G from the plane, and R, F are the normal and tangential components of the reaction of the plane, as shown in fig. 74. We have also the kinematical relation ẋ = aθ.. Hence
| ẍ = | a2 | g sin α, R = Mg cos α, F = | κ2 | Mg sin α. |
| κ2 + a2 | κ2 + a2 |
The acceleration of G is therefore less than in the case of frictionless
sliding in the ratio a2/(κ2 + a2). For a homogeneous sphere this
ratio is 57, for a uniform circular cylinder or disk 23, for a circular
hoop or a thin cylindrical shell 12.
The equation of energy for a rigid body has already been stated (in effect) as a corollary from fundamental assumptions. It may also be deduced from the principles of linear and angular momentum as embodied in the equations (9). We have
whence, integrating with respect to t,
The left-hand side is the kinetic energy of the whole mass, supposed concentrated at G and moving with this point, together with the kinetic energy of the motion relative to G (§ 15); and the right-hand member represents the integral work done by the extraneous forces in the successive infinitesimal displacements into which the motion may be resolved.
 |
| Fig. 75. |
The formula (13) may be easily verified in the case of the compound pendulum, or of the solid rolling down an incline. As another example, suppose we have a circular cylinder whose mass-centre is at an excentric point, rolling on a horizontal plane. This includes the case of a compound pendulum in which the knife-edge is replaced by a cylindrical pin. If α be the radius of the cylinder, h the distance of G from its axis (O), κ the radius of gyration about a longitudinal axis through G, and θ the inclination of OG to the vertical, the kinetic energy is 12Mκ2θ.2 + 12M·CG2·θ. 2, by § 3, since the body is turning about the line of contact (C) as instantaneous axis, and the potential energy is −Mgh cos θ. The equation of energy is therefore
Whenever, as in the preceding examples, a body or a system of bodies, is subject to constraints which leave it virtually only one degree of freedom, the equation of energy is sufficient for the complete determination of the motion. If q be any variable co-ordinate defining the position or (in the case of a system of bodies) the configuration, the velocity of each particle at any instant will be proportional to q̇, and the total kinetic energy may be expressed in the form 12Aq̇2, where A is in general a function of q [cf. equation (14)]. This coefficient A is called the coefficient of inertia, or the reduced inertia of the system, referred to the co-ordinate q.
 |
| Fig. 76. |
Thus in the case of a railway truck travelling with velocity u the kinetic energy is 12 (M + mκ2/α2)u2, where M is the total mass, α the radius and κ the radius of gyration of each wheel, and m is the sum of the masses of the wheels; the reduced inertia is therefore M + mκ2/α2. Again, take the system composed of the flywheel, connecting rod, and piston of a steam-engine. We have here a limiting case of three-bar motion (§ 3), and the instantaneous centre J of the connecting-rod PQ will have the position shown in the figure. The velocities of P and Q will be in the ratio of JP to JQ, or OR to OQ; the velocity of the piston is therefore yθ., where y = OR. Hence if, for simplicity, we neglect the inertia of the connecting-rod, the kinetic energy will be 12 (I + My2)θ. 2, where I is the moment of inertia of the flywheel, and M is the mass of the piston. The effect of the mass of the piston is therefore to increase the apparent moment of inertia of the flywheel by the variable amount My2. If, on the other hand, we take OP (= x) as our variable, the kinetic energy is 12 (M + I/y2)ẋ2. We may also say, therefore, that the effect of the flywheel is to increase the apparent mass of the piston by the amount I/y2; this becomes infinite at the “dead-points” where the crank is in line with the connecting-rod.
If the system be “conservative,” we have
where V is the potential energy. If we differentiate this with respect to t, and divide out by q̇, we obtain
| Aq̣̈ + 12 | dA | q̇2 + | dV | = 0 |
| dq | dq |
as the equation of motion of the system with the unknown reactions (if any) eliminated. For equilibrium this must be satisfied by q̇ = O; this requires that dV/dq = 0, i.e. the potential energy must be “stationary.” To examine the effect of a small disturbance from equilibrium we put V = ƒ(q), and write q = q0 + η, where q0 is a root of ƒ′ (q0) = 0 and η is small. Neglecting terms of the second order in η we have dV/dq = ƒ′(q) = ƒ″(q0)·η, and the equation (16) reduces to
where A may be supposed to be constant and to have the value corresponding to q = q0. Hence if ƒ″ (q0) > 0, i.e. if V is a minimum in the configuration of equilibrium, the variation of η is simple-harmonic, and the period is 2π √{A/ƒ″(q0) }. This depends only on the constitution of the system, whereas the amplitude and epoch will vary with the initial circumstances. If ƒ″ (q0) < 0, the solution of (17) will involve real exponentials, and η will in general increase until the neglect of the terms of the second order is no longer justified. The configuration q = q0, is then unstable.
As an example of the method, we may take the problem to which equation (14) relates. If we differentiate, and divide by θ, and retain only the terms of the first order in θ, we obtain
as the equation of small oscillations about the position θ = 0. The length of the equivalent simple pendulum is {κ2 + (h − α)2}/h.
The equations which express the change of motion (in two dimensions) due to an instantaneous impulse are of the forms
 |
| Fig. 77. |
Here u′, ν′ are the values of the component velocities of G just before, and u, ν their values just after, the impulse, whilst ω′, ω denote the corresponding angular velocities. Further, ξ, η are the time-integrals of the forces parallel to the co-ordinate axes, and ν is the time-integral of their moment about G. Suppose, for example, that a rigid lamina at rest, but free to move, is struck by an instantaneous impulse F in a given line. Evidently G will begin to move parallel to the line of F; let its initial velocity be u′, and let ω′ be the initial angular velocity. Then Mu′ = F, Iω′ = F·GP, where GP is the perpendicular from G to the line of F. If PG be produced to any point C, the initial velocity of the point C of the lamina will be
where κ2 is the radius of gyration about G. The initial centre of rotation will therefore be at C, provided GC·GP = κ2. If this condition be satisfied there would be no impulsive reaction at C even if this point were fixed. The point P is therefore called the centre of percussion for the axis at C. It will be noted that the relation between C and P is the same as that which connects the centres of suspension and oscillation in the compound pendulum.
§ 18. Equations of Motion in Three Dimensions.—It was proved in § 7 that a body moving about a fixed point O can be brought from its position at time t to its position at time t + δt by an infinitesimal rotation ε about some axis through O; and the limiting position of this axis, when δt is infinitely small, was called the “instantaneous axis.” The limiting value of the ratio ε/δt is called the angular velocity of the body; we denote it by ω. If ξ, η, ζ are the components of ε about rectangular co-ordinate axes through O, the limiting values of ξ/δt, η/δt, ζ/δt are called the component angular velocities; we denote them by p, q, r. If l, m, n be the direction-cosines of the instantaneous axis we have
If we draw a vector OJ to represent the angular velocity, then J traces out a certain curve in the body, called the polhode, and a certain curve in space, called the herpolhode. The cones generated by the instantaneous axis in the body and in space are called the polhode and herpolhode cones, respectively; in the actual motion the former cone rolls on the latter (§ 7).
 |
| Fig. 78. |
The special case where both cones are right circular and ω is constant is important in astronomy and also in mechanism (theory of bevel wheels). The “precession of the equinoxes” is due to the fact that the earth performs a motion of this kind about its centre, and the whole class of such motions has therefore been termed precessional. In fig. 78, which shows the various cases, OZ is the axis of the fixed and OC that of the rolling cone, and J is the point of contact of the polhode and herpolhode, which are of course both circles. If αbe the semi-angle of the rolling cone, β the constant inclination of OC to OZ, and ψ. the angular velocity with which the plane ZOC revolves about OZ, then, considering the velocity of a point in OC at unit distance from O, we have
where the lower sign belongs to the third case. The earth’s precessional motion is of this latter type, the angles being α = .0087″, β = 23° 28′.
If m be the mass of a particle at P, and PN the perpendicular to the instantaneous axis, the kinetic energy T is given by
where I is the moment of inertia about the instantaneous axis. With the same notation for moments and products of inertia as in § 11 (38), we have
and therefore by (1),
Again, if x, y, z be the co-ordinates of P, the component velocities of m are
by § 7 (5); hence, if λ, μ, ν be now used to denote the component angular momenta about the co-ordinate axes, we have λ = Σ {m (py − qx)y − m(rx − pz) z }, with two similar formulae, or
| λ = Ap −Hq − Gr = | ∂T | , |
| ∂p |
| μ = −Hp + Bq − Fr = | ∂T | , |
| ∂q |
| ν = −Gp − Fq + Cr = | ∂T | . |
| ∂r |
If the co-ordinate axes be taken to coincide with the principal
axes of inertia at O, at the instant under consideration, we have
the simpler formulae
It is to be carefully noticed that the axis of resultant angular momentum about O does not in general coincide with the instantaneous axis of rotation. The relation between these axes may be expressed by means of the momental ellipsoid at O. The equation of the latter, referred to its principal axes, being as in § 11 (41), the co-ordinates of the point J where it is met by the instantaneous axis are proportional to p, q, r, and the direction-cosines of the normal at J are therefore proportional to Ap, Bq, Cr, or λ, μ, ν. The axis of resultant angular momentum is therefore normal to the tangent plane at J, and does not coincide with OJ unless the latter be a principal axis. Again, if Γ be the resultant angular momentum, so that
the length of the perpendicular OH on the tangent plane at J is
| OH = | Ap | · | p | ρ + | Bq | · | q | ρ + | Cr | · | r | ρ = | 2T | · | ρ | , |
| Γ | ω | Γ | ω | Γ | ω | Γ | ω |
where ρ = OJ. This relation will be of use to us presently (§ 19).
The motion of a rigid body in the most general case may be specified by means of the component velocities u, v, w of any point O of it which is taken as base, and the component angular velocities p, q, r. The component velocities of any point whose co-ordinates relative to O are x, y, z are then
by § 7 (6). It is usually convenient to take as our base-point the mass-centre of the body. In this case the kinetic energy is given by
where M0 is the mass, and A, B, C, F, G, H are the moments and products of inertia with respect to the mass-centre; cf. § 15 (9).
The components ξ, η, ζ of linear momentum are
| ξ = M0u = | ∂T | , η = M0v = | ∂T | , ζ = M0w = | ∂T | |
| ∂u | ∂v | ∂w |
whilst those of the relative angular momentum are given by (7).
The preceding formulae are sufficient for the treatment of
instantaneous impulses. Thus if an impulse (ξ, η, ζ, λ, μ, ν)
change the motion from (u, v, w, p, q, r) to (u′, v′, w′, p′, q′, r ′)
we have
| M0 (u′ − u) = ξ, | M0 (v′ − v) = η, | M0(w′ − w) = ζ, | |
| A (p′ − p) = λ, | B (q′ − q) = μ, | C (r ′ − r) = ν, |
where, for simplicity, the co-ordinate axes are supposed to
coincide with the principal axes at the mass-centre. Hence
the change of kinetic energy is
The factors of ξ, η, ζ, λ, μ, ν on the right-hand side are proportional to the constituents of a possible infinitesimal displacement of the solid, and the whole expression is proportional (on the same scale) to the work done by the given system of impulsive forces in such a displacement. As in § 9 this must be equal to the total work done in such a displacement by the several forces, whatever they are, which make up the impulse. We are thus led to the following statement: the change of kinetic energy due to any system of impulsive forces is equal to the sum of the products of the several forces into the semi-sum of the initial and final velocities of their respective points of application, resolved in the directions of the forces. Thus in the problem of fig. 77 the kinetic energy generated is 12M (κ2 + Cq2)ω′2, if C be the instantaneous centre; this is seen to be equal to 12F·ω′·CP, where ω′·CP represents the initial velocity of P.
The equations of continuous motion of a solid are obtained by substituting the values of ξ, η, ζ, λ, μ, ν from (14) and (7) in the general equations
| dξ | = X, | dη | = Y, | dζ | = Z, | |
| dt | dt | dt | ||||
| dλ | = L, | dμ | = M, | dν | = N, | |
| dt | dt | dt |
 |
| Fig. 79. |
where (X, Y, Z, L, M, N) denotes the system of extraneous forces referred (like the momenta) to the mass-centre as base, the co-ordinate axes being of course fixed in direction. The resulting equations are not as a rule easy of application, owing to the fact that the moments and products of inertia A, B, C, F, G, H are not constants but vary in consequence of the changing orientation of the body with respect to the co-ordinate axes.
An exception occurs, however, in the case of a solid which is kinetically symmetrical (§ 11) about the mass-centre, e.g. a uniform sphere. The equations then take the forms
| M0u̇ = X, | M0v̇ = Y, | M0ẇ = Z, |
| Cṗ = L, | Cq̇ = M, | Cṙ = N, |
where C is the constant moment of inertia about any axis through the mass-centre. Take, for example, the case of a sphere rolling on a plane; and let the axes Ox, Oy be drawn through the centre parallel to the plane, so that the equation of the latter is z = −a. We will suppose that the extraneous forces consist of a known force (X, Y, Z) at the centre, and of the reactions (F1, F2, R) at the point of contact. Hence
| M0u̇ = X + F1, M0v̇ = Y + F2, 0 = Z + R, Cṗ = F2a, Cq̇ = −F1a, Cṙ = 0. |
(19) |
The last equation shows that the angular velocity about the normal to the plane is constant. Again, since the point of the sphere which is in contact with the plane is instantaneously at rest, we have the geometrical relations
by (12). Eliminating p, q, we get
The acceleration of the centre is therefore the same as if the plane were smooth and the mass of the sphere were increased by C/α2. Thus the centre of a sphere rolling under gravity on a plane of inclination a describes a parabola with an acceleration
parallel to the lines of greatest slope.
Take next the case of a sphere rolling on a fixed spherical surface. Let a be the radius of the rolling sphere, c that of the spherical surface which is the locus of its centre, and let x, y, z be the co-ordinates of this centre relative to axes through O, the centre of the fixed sphere. If the only extraneous forces are the reactions (P, Q, R) at the point of contact, we have
| Cṗ = − | a | (yR − zQ), Cq̇ = − | a | (zP − xR), Cṙ = − | a | (xQ − yP), |
| c | c | c |
the standard case being that where the rolling sphere is outside the fixed surface. The opposite case is obtained by reversing the sign of a. We have also the geometrical relations
If we eliminate P, Q, R from (22), the resulting equations are integrable with respect to t; thus
| p = − | M0a | (yż − zẏ) + α, q = − | M0a | (zẋ − xż) + β, r = − | M0a | (xẏ − yẋ) + γ, |
| Cc | Cc | Cc |
where α, β, γ are arbitrary constants. Substituting in (23) we find
| ( 1 + | M0a2 | ) ẋ = | a | (βz − γy), ( 1 + | M0a2 | ) ẏ = | a | (γx − αz), ( 1 + | M0a2 | ) ż = | a | (αy − βx). |
| C | c | C | c | C | c |
Hence αẋ + βẏ + γż = 0, or
which shows that the centre of the rolling sphere describes a circle. If the axis of z be taken normal to the plane of this circle we have α = 0, β = 0, and
| ( 1 + | M0a2 | ) ẋ = −γ | a | y, ( 1 + | M0a2 | ) ẏ = γ | a | x. |
| C | c | C | c |
The solution of these equations is of the type
where b, ε are arbitrary, and
| σ = | γa/c | . |
| 1 + M0a2/C |
The circle is described with the constant angular velocity σ.
When the gravity of the rolling sphere is to be taken into account the preceding method is not in general convenient, unless the whole motion of G is small. As an example of this latter type, suppose that a sphere is placed on the highest point of a fixed sphere and set spinning about the vertical diameter with the angular velocity n; it will appear that under a certain condition the motion of G consequent on a slight disturbance will be oscillatory. If Oz be drawn vertically upwards, then in the beginning of the disturbed motion the quantities x, y, p, q, P, Q will all be small. Hence, omitting terms of the second order, we find
| M0ẍ = P, M0ẏ = Q, R = M0g, Cṗ = −(M0ga/c) y + aQ, Cq̇ = (M0ga/c) x − aP, Cṙ = 0. |
(30) |
The last equation shows that the component r of the angular velocity retains (to the first order) the constant value n. The geometrical relations reduce to
Eliminating p, g, P, Q, we obtain the equations
(C + M0a2) ÿ − (Cna/c) x − (M0ga2/c) y = 0,
which are both contained in
| { (C + M0a2) | d 2 | − i | Cna | d | − | M0ga2 | } (x + iy) = 0. | |
| dt 2 | c | dt | c |
This has two solutions of the type x + iy = αei(σt + ε), where α, ε are
arbitrary, and σ is a root of the quadratic
If
both roots are real, and have the same sign as n. The motion of G then consists of two superposed circular vibrations of the type
in each of which the direction of revolution is the same as that of the initial spin of the sphere. It follows therefore that the original position is stable provided the spin n exceed the limit defined by (35). The case of a sphere spinning about a vertical axis at the lowest point of a spherical bowl is obtained by reversing the signs of α and c. It appears that this position is always stable.
It is to be remarked, however, that in the first form of the problem the stability above investigated is practically of a limited or temporary kind. The slightest frictional forces—such as the resistance of the air—even if they act in lines through the centre of the rolling sphere, and so do not directly affect its angular momentum, will cause the centre gradually to descend in an ever-widening spiral path.
§ 19. Free Motion of a Solid.—Before proceeding to further problems of motion under extraneous forces it is convenient to investigate the free motion of a solid relative to its mass-centre O, in the most general case. This is the same as the motion about a fixed point under the action of extraneous forces which have zero moment about that point. The question was first discussed by Euler (1750); the geometrical representation to be given is due to Poinsot (1851).
The kinetic energy T of the motion relative to O will be constant. Now T = 12Iω2, where ω is the angular velocity and I is the moment of inertia about the instantaneous axis. If ρ be the radius-vector OJ of the momental ellipsoid
drawn in the direction of the instantaneous axis, we have I = Mε4/ρ2 (§ 11); hence ω varies as ρ. The locus of J may therefore be taken as the “polhode” (§ 18). Again, the vector which represents the angular momentum with respect to O will be constant in every respect. We have seen (§ 18) that this vector coincides in direction with the perpendicular OH to the tangent plane of the momental ellipsoid at J; also that
| OH = | 2T | · | ρ | , |
| Γ | ω |
where Γ is the resultant angular momentum about O. Since ω
varies as ρ, it follows that OH is constant, and the tangent plane
at J is therefore fixed in space. The motion of the body relative
to O is therefore completely represented if we imagine the momental
ellipsoid at O to roll without sliding on a plane fixed in
space, with an angular velocity proportional at each instant to
the radius-vector of the point of contact. The fixed plane is
parallel to the invariable plane at O, and the line OH is called the
invariable line. The trace of the point of contact J on the fixed
plane is the “herpolhode.”
If p, q, r be the component angular velocities about the principal axes at O, we have
each side being in fact equal to unity. At a point on the polhode cone x : y : z = p : q : r, and the equation of this cone is therefore
| A2 ( 1 − | Γ2 | ) x2 + B2 ( 1 − | Γ2 | ) y2 + C2 ( 1 − | Γ2 | ) z2 = 0. |
| 2AT | 2BT | 2CT |
Since 2AT − Γ2 = B (A − B)q2 + C(A − C)r 2, it appears that if
A > B > C the coefficient of x2 in (4) is positive, that of z2 is
negative, whilst that of y2 is positive or negative according as
2BT ≷ Γ2. Hence the polhode cone surrounds the axis of
greatest or least moment according as 2BT ≷ Γ2. In the
critical case of 2BT = Γ2 it breaks up into two planes through
the axis of mean moment (Oy). The herpolhode curve in the
fixed plane is obviously confined between two concentric circles
which it alternately touches; it is not in general a re-entrant
curve. It has been shown by De Sparre that, owing to the
limitation imposed on the possible forms of the momental
ellipsoid by the relation B + C > A, the curve has no points of
inflexion. The invariable line OH describes another cone in the
body, called the invariable cone. At any point of this we have
x : y : z = Ap · Bq : Cr, and the equation is therefore
| 1 − | Γ2 | x2 + 1 − | Γ2 | y2 + 1 − | Γ2 | z2 = 0. |
| 2AT | 2BT | 2CT |
 |
| Fig. 80. |
The signs of the coefficients follow the same rule as in the case of (4). The possible forms of the invariable cone are indicated in fig. 80 by means of the intersections with a concentric spherical surface. In the critical case of 2BT = Γ2 the cone degenerates into two planes. It appears that if the body be sightly disturbed from a state of rotation about the principal axis of greatest or least moment, the invariable cone will closely surround this axis, which will therefore never deviate far from the invariable line. If, on the other hand, the body be slightly disturbed from a state of rotation about the mean axis a wide deviation will take place. Hence a rotation about the axis of greatest or least moment is reckoned as stable, a rotation about the mean axis as unstable. The question is greatly simplified when two of the principal moments are equal, say A = B. The polhode and herpolhode cones are then right circular, and the motion is “precessional” according to the definition of § 18. If α be the inclination of the instantaneous axis to the axis of symmetry, β the inclination of the latter axis to the invariable line, we have
| Γ cos β = C ω cos α, Γ sin β = A ω sin α, | (6) |
whence
| tan β = AC tan α. | (7) |
 |
| Fig. 81. |
Hence β ≷ α, and the circumstances are therefore those of the first or second case in fig. 78, according as A ≷ C. If ψ be the rate at which the plane HOJ revolves about OH, we have
| ψ = | sin α | ω = | C cos α | ω, |
| sin β | A cos β |
by § 18 (3). Also if χ. be the rate at which J describes the
polhode, we have ψ. sin (β − α) = χ. sin β, whence
| χ. = | sin (α − β) | ω. |
| sin α |
If the instantaneous axis only deviate slightly from the axis of
symmetry the angles α, β are small, and χ. = (A − C) A·ω; the
instantaneous axis therefore completes its revolution in the body
in the period
| 2π | = | A − C | ω. |
| χ. | A |
In the case of the earth it is inferred from the independent phenomenon of luni-solar precession that (C − A)/A = .00313. Hence if the earth’s axis of rotation deviates slightly from the axis of figure, it should describe a cone about the latter in 320 sidereal days. This would cause a periodic variation in the latitude of any place on the earth’s surface, as determined by astronomical methods. There appears to be evidence of a slight periodic variation of latitude, but the period would seem to be about fourteen months. The discrepancy is attributed to a defect of rigidity in the earth. The phenomenon is known as the Eulerian nutation, since it is supposed to come under the free rotations first discussed by Euler.
§ 20. Motion of a Solid of Revolution.—In the case of a solid of revolution, or (more generally) whenever there is kinetic symmetry about an axis through the mass-centre, or through a fixed point O, a number of interesting problems can be treated almost directly from first principles. It frequently happens that the extraneous forces have zero moment about the axis of symmetry, as e.g. in the case of the flywheel of a gyroscope if we neglect the friction at the bearings. The angular velocity (r) about this axis is then constant. For we have seen that r is constant when there are no extraneous forces; and r is evidently not affected by an instantaneous impulse which leaves the angular momentum Cr, about the axis of symmetry, unaltered. And a continuous force may be regarded as the limit of a succession of infinitesimal instantaneous impulses.
 |
| Fig. 82. |
Suppose, for example, that a flywheel is rotating with angular velocity n about its axis, which is (say) horizontal, and that this axis is made to rotate with the angular velocity ψ. in the horizontal plane. The components of angular momentum about the axis of the flywheel and about the vertical will be Cn and A ψ. respectively, where A is the moment of inertia about any axis through the mass-centre (or through the fixed point O) perpendicular to that of symmetry. If OK→ be the vector representing the former component at time t, the vector which represents it at time t + δt will be OK→′, equal to OK→ in magnitude and making with it an angle δψ. Hence KK→′ (= Cn δψ) will represent the change in this component due to the extraneous forces. Hence, so far as this component is concerned, the extraneous forces must supply a couple of moment Cnψ. in a vertical plane through the axis of the flywheel. If this couple be absent, the axis will be tilted out of the horizontal plane in such a sense that the direction of the spin n approximates to that of the azimuthal rotation ψ. . The remaining constituent of the extraneous forces is a couple Aψ.. about the vertical; this vanishes if ψ. is constant. If the axis of the flywheel make an angle θ with the vertical, it is seen in like manner that the required couple in the vertical plane through the axis is Cn sin θ ψ. . This matter can be strikingly illustrated with an ordinary gyroscope, e.g. by making the larger movable ring in fig. 37 rotate about its vertical diameter.
 |
| Fig. 83. |
If the direction of the axis of kinetic symmetry be specified by means of the angular co-ordinates θ, ψ of § 7, then considering the component velocities of the point C in fig. 83, which are θ. and sin θψ. along and perpendicular to the meridian ZC, we see that the component angular velocities about the lines OA′, OB′ are −sin θ ψ. and θ. respectively. Hence if the principal moments of inertia at O be A, A, C, and if n be the constant angular velocity about the axis OC, the kinetic energy is given by
Again, the components of angular momentum about OC, OA′ are Cn, −A sin θ ψ. , and therefore the angular momentum (μ, say) about OZ is
We can hence deduce the condition of steady precessional motion in a top. A solid of revolution is supposed to be free to turn about a fixed point O on its axis of symmetry, its mass-centre G being in this axis at a distance h from O. In fig. 83 OZ is supposed to be vertical, and OC is the axis of the solid drawn in the direction OG. If θ is constant the points C, A′ will in time δt come to positions C″, A″ such that CC″ = sin θ δψ, A′A″ = cos θ δψ, and the angular momentum about OB′ will become Cn sin θ δψ − A sin θ ψ. · cos θ δψ. Equating this to Mgh sin θ δt, and dividing out by sin θ, we obtain
as the condition in question. For given values of n and θ we have two possible values of ψ. provided n exceed a certain limit. With a very rapid spin, or (more precisely) with Cn large in comparison with √(4AMgh cos θ), one value of ψ. is small and the other large, viz. the two values are Mgh/Cn and Cn/A cos θ approximately. The absence of g from the latter expression indicates that the circumstances of the rapid precession are very nearly those of a free Eulerian rotation (§ 19), gravity playing only a subordinate part.
 |
| Fig. 84. |
Again, take the case of a circular disk rolling in steady motion on a horizontal plane. The centre O of the disk is supposed to describe a horizontal circle of radius c with the constant angular velocity ψ. , whilst its plane preserves a constant inclination θ to the horizontal. The components of the reaction of the horizontal lane will be Mcψ. 2 at right angles to the tangent line at the point of contact and Mg vertically upwards, and the moment of these about the horizontal diameter of the disk, which corresponds to OB′ in fig. 83, is Mcψ. 2. α sin θ − Mgα cos θ, where α is the radius of the disk. Equating this to the rate of increase of the angular momentum about OB′, investigated as above, we find
| ( C + Ma2 + A | a | cos θ ) ψ. 2 = Mg | a2 | cot θ, |
| c | c |
where use has been made of the obvious relation nα = cψ. . If c and θ be given this formula determines the value of ψ. for which the motion will be steady.
In the case of the top, the equation of energy and the condition of constant angular momentum (μ) about the vertical OZ are sufficient to determine the motion of the axis. Thus, we have
where ν is written for Cn. From these ψ. may be eliminated, and on differentiating the resulting equation with respect to t we obtain
| Aθ.. − | (μ − ν cos θ) (μ cos θ − ν) | − Mgh sin θ = 0. |
| A sin3 θ |
If we put θ.. = 0 we get the condition of steady precessional motion in a form equivalent to (3). To find the small oscillation about a state of steady precession in which the axis makes a constant angle α with the vertical, we write θ = α + χ, and neglect terms of the second order in χ. The result is of the form
where
(μ cos α − ν)2 } / A2 sin4 α.
When ν is large we have, for the “slow” precession σ = ν/A, and for the “rapid” precession σ = A/ν cos α = ψ. , approximately. Further, on examining the small variation in ψ. , it appears that in a slightly disturbed slow precession the motion of any point of the axis consists of a rapid circular vibration superposed on the steady precession, so that the resultant path has a trochoidal character. This is a type of motion commonly observed in a top spun in the ordinary way, although the successive undulations of the trochoid may be too small to be easily observed. In a slightly disturbed rapid precession the superposed vibration is elliptic-harmonic, with a period equal to that of the precession itself. The ratio of the axes of the ellipse is sec α, the longer axis being in the plane of θ. The result is that the axis of the top describes a circular cone about a fixed line making a small angle with the vertical. This is, in fact, the “invariable line” of the free Eulerian rotation with which (as already remarked) we are here virtually concerned. For the more general discussion of the motion of a top see Gyroscope.
§ 21. Moving Axes of Reference.—For the more general treatment of the kinetics of a rigid body it is usually convenient to adopt a system of moving axes. In order that the moments and products of inertia with respect to these axes may be constant, it is in general necessary to suppose them fixed in the solid.
We will assume for the present that the origin O is fixed. The moving axes Ox, Oy, Oz form a rigid frame of reference whose motion at time t may be specified by the three component angular velocities p, q, r. The components of angular momentum about Ox, Oy, Oz will be denoted as usual by λ, μ, ν. Now consider a system of fixed axes Ox′, Oy′, Oz′ chosen so as to coincide at the instant t with the moving system Ox, Oy, Oz. At the instant t + δt, Ox, Oy, Oz will no longer coincide with Ox′, Oy′, Oz′; in particular they will make with Ox′ angles whose cosines are, to the first order, 1, −r δt, qδt, respectively. Hence the altered angular momentum about Ox′ will be λ + δλ + (μ + δμ) (−r δt) + (ν + δν) qδt. If L, M, N be the moments of the extraneous forces about Ox, Oy, Oz this must be equal to λ + Lδt. Hence, and by symmetry, we obtain
| dλ | − r ν + qν = L, | |
| dt | ||
| dμ | − pν + r λ = M, | |
| dt | ||
| dν | − qλ + pν = N. | |
| dt |
These equations are applicable to any dynamical system whatever.
If we now apply them to the case of a rigid body moving
about a fixed point O, and make Ox, Oy, Oz coincide with the
principal axes of inertia at O, we have λ, μ, ν = Ap, Bq, Cr,
whence
| A | dp | − (B − C) qr = L, | |
| dt | |||
| B | dq | − (C − A) rp = M, | |
| C | dr | − (A − B) pq = N. | |
| dt |
If we multiply these by p, q, r and add, we get
| d | · 12 (Ap2 + Bq2 + Cr 2) = Lp + Mq + Nr, |
| dt |
which is (virtually) the equation of energy.
As a first application of the equations (2) take the case of a solid constrained to rotate with constant angular velocity ω about a fixed axis (l, m, n). Since p, q, r are then constant, the requisite constraining couple is
If we reverse the signs, we get the “centrifugal couple” exerted by the solid on its bearings. This couple vanishes when the axis of rotation is a principal axis at O, and in no other case (cf. § 17).
If in (2) we put, L, M, N = O we get the case of free rotation; thus
| A | dp | (B − C) qr, | |
| dt | |||
| B | dq | (C − A) rp, | |
| dt | |||
| C | dr | (A − B) pq. | |
| dt |
These equations are due to Euler, with whom the conception of
moving axes, and the application to the problem of free rotation,
originated. If we multiply them by p, q, r, respectively, or again
by Ap, Bq, Cr respectively, and add, we verify that the expressions
Ap2 + Bq2 + Cr 2 and A2p2 + B2q2 + C2r 2 are both constant.
The former is, in fact, equal to 2T, and the latter to Γ2, where
T is the kinetic energy and Γ the resultant angular momentum.
To complete the solution of (2) a third integral is required; this involves in general the use of elliptic functions. The problem has been the subject of numerous memoirs; we will here notice only the form of solution given by Rueb (1834), and at a later period by G. Kirchhoff (1875), If we write
| u = | dφ | , Δφ = √(1 − k2 sin2 φ), |
| Δφ |
we have, in the notation of elliptic functions, φ = am u. If we assume
we find
| ṗ = − | σp0 | qr, q̇ = | σq0 | rp, ṙ = | k2σr0 | pq. |
| q0r0 | r0p0 | p0q0 |
Hence (5) will be satisfied, provided
| −σp0 | = | B − C | , | σq0 | = | C − A | , | −k2σr0 | = | A − B | . |
| q0r0 | A | r0p0 | B | p0q0 | C |
These equations, together with the arbitrary initial values of p, q, r,
determine the six constants which we have denoted by p0, q0, r0, k2, σ, ε.
We will suppose that A > B > C. From the form of the polhode
curves referred to in § 19 it appears that the angular velocity q
about the axis of mean moment must vanish periodically. If we
adopt one of these epochs as the origin of t, we have ε = 0, and
p0, r0 will become identical with the initial values of p, r. The
conditions (9) then lead to
| q02 = | A (A − C) | p02, σ2 = | (A − C) (B − C) | r02, k2 = | A (A − B) | · | p02 | . |
| B (B − C) | AB | C (B − C) | r02 |
For a real solution we must have k2 < 1, which is equivalent to 2BT > Γ2. If the initial conditions are such as to make 2BT < Γ2, we must interchange the forms of p and r in (7). In the present case the instantaneous axis returns to its initial position in the body whenever φ increases by 2π, i.e. whenever t increases by 4K/σ, when K is the “complete” elliptic integral of the first kind with respect to the modulus k.
The elliptic functions degenerate into simpler forms when k2 = 0 or k2 = 1. The former case arises when two of the principal moments are equal; this has been sufficiently dealt with in § 19. If k2 = 1, we must have 2BT = Γ2. We have seen that the alternative 2BT ≷ Γ2 determines whether the polhode cone surrounds the principal axis of least or greatest moment. The case of 2BT = Γ2, exactly, is therefore a critical case; it may be shown that the instantaneous axis either coincides permanently with the axis of mean moment or approaches it asymptotically.
When the origin of the moving axes is also in motion with a velocity whose components are u, v, w, the dynamical equations are
| dξ | − r η + qζ = X, | dη | − pζ + r χ = Y, | dζ | − qχ + pη = Z, |
| dt | dt | dt |
| dλ | − r μ + qν − wη + vζ = L, | dμ | − pν + r λ- uζ + wξ = M, | dν | − qλ + pμ − vξ + uη = N. |
| dt | dt | dt |
To prove these, we may take fixed axes O′x′, O′y′, O′z′ coincident
with the moving axes at time t, and compare the linear
and angular momenta ξ + δξ, η + δη, ζ + δζ, λ + δλ, μ + δμ, ν + δν
relative to the new position of the axes, Ox, Oy, Oz at time t + δt
with the original momenta ξ, η, ζ, λ, μ, ν relative to O′x′, O′y′,
O′z′ at time t. As in the case of (2), the equations are applicable
to any dynamical system whatever. If the moving origin coincide
always with the mass-centre, we have ξ, η, ζ = M0u, M0v,
M0w, where M0 is the total mass, and the equations simplify.
When, in any problem, the values of u, v, w, p, q, r have been determined as functions of t, it still remains to connect the moving axes with some fixed frame of reference. It will be sufficient to take the case of motion about a fixed point O; the angular co-ordinates θ, φ, ψ of Euler may then be used for the purpose. Referring to fig. 36 we see that the angular velocities p, q, r of the moving lines, OA, OB, OC about their instantaneous positions are
by § 7 (3), (4). If OA, OB, OC be principal axes of inertia of a solid, and if A, B, C denote the corresponding moments of inertia, the kinetic energy is given by
If A = B this reduces to
cf. § 20 (1).
§ 22. Equations of Motion in Generalized Co-ordinates.—Suppose we have a dynamical system composed of a finite number of material particles or rigid bodies, whether free or constrained in any way, which are subject to mutual forces and also to the action of any given extraneous forces. The configuration of such a system can be completely specified by means of a certain number (n) of independent quantities, called the generalized co-ordinates of the system. These co-ordinates may be chosen in an endless variety of ways, but their number is determinate, and expresses the number of degrees of freedom of the system. We denote these co-ordinates by q1, q2, . . . qn. It is implied in the above description of the system that the Cartesian co-ordinates x, y, z of any particle of the system are known functions of the q’s, varying in form (of course) from particle to particle. Hence the kinetic energy T is given by
| 2T | = Σ {m (ẋ2 + ẏ2 + ż2) } |
| = a11q̇12 + a22q̇22 + . . . + 2a12q̇1q̇2 + . . ., |
where
| arr = Σ [ m { ( | ∂x | 2 + | ∂y | 2 + | ∂z | 2 } ], |
| ∂qr | ∂qr | ∂qr |
| ars = Σ { m | ∂x | ∂x | + | ∂y | ∂y | + | ∂z | ∂z | ) } = asr. | |||
| ∂qr | ∂qs | ∂qr | ∂qs | ∂qr | ∂qs |
Thus T is expressed as a homogeneous quadratic function of
the quantities q̇1, q̇2, . . . q̇n, which are called the generalized
components of velocity. The coefficients arr, ars are called the coefficients
of inertia; they are not in general constants, being
functions of the q’s and so variable with the configuration.
Again, If (X, Y, Z) be the force on m, the work done in an infinitesimal
change of configuration is
where
| Qr = Σ X | ∂x | + Y | ∂y | + Z | ∂z | . |
| ∂qr | ∂qr | ∂qr |
The quantities Qr are called the generalized components of force.
The equations of motion of m being
we have
| Σ { m ẍ | ∂x | + ÿ | ∂y | + z̈ | ∂z | ) } = Qr. |
| ∂qr | ∂qr | ∂qr |
Now
| ẋ = | ∂x | q̇1 + | ∂x | q̇2 + . . . + | ∂x | q̇n, |
| ∂q1 | ∂q2 | ∂qn |
whence
| ∂ẋ∂q̇r = ∂x∂qr | (8) |
Also
| d | ∂x | = | ∂2x | q̇1 + | ∂2x | q̇2 + . . . + | ∂2x | q̇r = | ∂ẋ | . | |
| dt | ∂qr | ∂q1∂qr | ∂q2∂qr | ∂qn∂qr | ∂qr |
Hence
| ẍ | ∂x | = | d | ẋ | ∂x | − ẋ | d | ∂x | = | d | ẋ | ∂ẋ | − ẋ | ∂ẋ | . | |
| ∂qr | dt | ∂qr | dt | ∂qr | dt | ∂q̇r | ∂qr |
By these and the similar transformations relating to y and z the
equation (6) takes the form
| d | ∂T | − | ∂T | = Qr. | |
| dt | ∂q̇r | ∂qr |
If we put r = 1, 2, . . . n in succession, we get the n independent equations of motion of the system. These equations are due to Lagrange, with whom indeed the first conception, as well as the establishment, of a general dynamical method applicable to all systems whatever appears to have originated. The above proof was given by Sir W. R. Hamilton (1835). Lagrange’s own proof will be found under Dynamics, § Analytical. In a conservative system free from extraneous force we have
where V is the potential energy. Hence
| Qr = − | ∂V | , |
| ∂qr |
and
| d | ∂T | − | ∂T | = − | ∂V | . | |
| dt | ∂q̇r | ∂qr | ∂qr |
If we imagine any given state of motion (q̇1, q̇2 . . . q̇n) through
the configuration (q1, q2, . . . qn) to be generated instantaneously
from rest by the action of suitable impulsive forces, we find on
integrating (11) with respect to t over the infinitely short duration
of the impulse
| ∂T∂q̇r = Qr′, | (15) |
where Qr′ is the time integral of Qr and so represents a generalized component of impulse. By an obvious analogy, the expressions ∂T/∂q̇r may be called the generalized components of momentum; they are usually denoted by pr thus
Since T is a homogeneous quadratic function of the velocities q̇1, q̇2, . . . q̇n, we have
| 2T = | ∂T | q̇1 + | ∂T | q̇2 + . . . + | ∂T | q̇n = p1q̇2 + p2q̇2 + . . . + pnq̇n. |
| ∂q̇1 | ∂q̇2 | ∂q̇n |
Hence
| 2dTdt | = ṗ1q̇1 + ṗ2q̇2 + . . . + ṗnq̇n + ṗ1q̈1 + ṗ2q̈2 + . . . + ṗnq̈n | |||||||||||||
| = | ∂T | + Q1 q̇1 + | ∂T | + Q2 q̇2 + . . . + | ∂T | + Qn q̇n + | ∂T | q̈1 + | ∂T | q̈2 + . . . + | ∂T | q̈n | ||
| ∂q̇1 | ∂q̇2 | ∂q̇n | ∂q̇1 | ∂q̇2 | ∂q̇n | |||||||||
| =dTdt + Q1q̇1 + Q2q̇2 + . . . + Qnq̇n, | ||||||||||||||
or
| dTdt = Q1q̇1 + Q2q̇2 + . . . + Qnq̇n. | (19) |
This equation expresses that the kinetic energy is increasing at a rate equal to that at which work is being done by the forces. In the case of a conservative system free from extraneous force it becomes the equation of energy
| ddt (T + V) = 0, or T + V = const., | (20) |
in virtue of (13).
As a first application of Lagrange’s formula (11) we may form the equations of motion of a particle in spherical polar co-ordinates. Let r be the distance of a point P from a fixed origin O, θ the angle which OP makes with a fixed direction OZ, ψ the azimuth of the plane ZOP relative to some fixed plane through OZ. The displacements of P due to small variations of these co-ordinates are δr along OP, rδθ perpendicular to OP in the plane ZOP, and r sin θ δψ perpendicular to this plane. The component velocities in these directions are therefore ṙ, rθ. , r sin θ ψ. , and if m be the mass of a moving particle at P we have
Hence the formula (11) gives
| m (r̈ − rθ. 2 − r sin2 θψ. 2) | = R, | |
| ddt (mr 2θ. ) − mr 2 · sin θ cos θψ. 2 | = Θ, | |
| ddt (mr 2 sin2 θψ. ) | = Ψ. |
The quantities R, Θ, Ψ are the coefficients in the expression
Rδr + Θδθ + Ψδψ for the work done in an infinitely small displacement;
viz. R is the radial component of force, Θ is the moment
about a line through O perpendicular to the plane ZOP, and Ψ is
the moment about OZ. In the case of the spherical pendulum
we have r = l, Θ = − mgl sin θ, Ψ = 0, if OZ be drawn vertically
downwards, and therefore
| θ.. − sin θ cos θψ. 2 | = − (g/l) sin θ, |
| sin2 θψ. | = h, |
where h is a constant. The latter equation expresses that the angular momentum ml2 sin2 θψ. about the vertical OZ is constant. By elimination of ψ. we obtain
| θ.. − h2 cos2 θ / sin3 θ = − | g | sin θ. |
| l |
If the particle describes a horizontal circle of angular radius α with constant angular velocity Ω, we have ω. = 0, h = Ω2 sin α, and therefore
| Ω2 = | g | cos α, |
| l |
as is otherwise evident from the elementary theory of uniform circular motion. To investigate the small oscillations about this state of steady motion we write θ = α + χ in (24) and neglect terms of the second order in χ. We find, after some reductions,
this shows that the variation of χ is simple-harmonic, with the period
As regards the most general motion of a spherical pendulum, it is obvious that a particle moving under gravity on a smooth sphere cannot pass through the highest or lowest point unless it describes a vertical circle. In all other cases there must be an upper and a lower limit to the altitude. Again, a vertical plane passing through O and a point where the motion is horizontal is evidently a plane of symmetry as regards the path. Hence the path will be confined between two horizontal circles which it touches alternately, and the direction of motion is never horizontal except at these circles. In the case of disturbed steady motion, just considered, these circles are nearly coincident. When both are near the lowest point the horizontal projection of the path is approximately an ellipse, as shown in § 13; a closer investigation shows that the ellipse is to be regarded as revolving about its centre with the angular velocity 23 abΩ/l2, where a, b are the semi-axes.
To apply the equations (11) to the case of the top we start with the expression (15) of § 21 for the kinetic energy, the simplified form (1) of § 20 being for the present purpose inadmissible, since it is essential that the generalized co-ordinates employed should be competent to specify the position of every particle. If λ, μ, ν be the components of momentum, we have
| λ = 1∂T | = Aθ. , | |
| μ = 1∂T | = A sin2 θψ. + C (φ. + cos θψ. ) cos θ, | |
| ν = 1∂T | = C (θ. + cos θψ. ). |
The meaning of these quantities is easily recognized; thus λ is the
angular momentum about a horizontal axis normal to the plane
of θ, μ is the angular momentum about the vertical OZ, and ν is
the angular momentum about the axis of symmetry. If M be the
total mass, the potential energy is V = Mgh cos θ, if OZ be drawn
vertically upwards. Hence the equations (11) become
| Aθ.. − A sin θ cos θψ. 2 + C (φ. + cos θψ. ) ψ. sin θ = Mgh sin θ, | |
| d/dt · { A sin2 θψ. + C(φ. + cos θψ. ) cos θ } = 0, | |
| d/dt · { C (φ. + cos θψ. ) } = 0, |
of which the last two express the constancy of the momenta μ, ν.
Hence
If we eliminate ψ. we obtain the equation (7) of § 20. The theory of disturbed precessional motion there outlined does not give a convenient view of the oscillations of the axis about the vertical position. If θ be small the equations (29) may be written
| θ.. − θω. 2 = −ν2 − 4AMgh4A2 | θ, | |
| θ2ω. = const., |
where
| ω = ψ − | ν | t. |
| 2A |
Since θ, ω are the polar co-ordinates (in a horizontal plane) of a point
on the axis of symmetry, relative to an initial line which revolves
with constant angular velocity ν/2A, we see by comparison with
§ 14 (15) (16) that the motion of such a point will be elliptic-harmonic
superposed on a uniform rotation ν/2A, provided ν2 > 4AMgh.
This gives (in essentials) the theory of the “gyroscopic pendulum.”
§ 23. Stability of Equilibrium. Theory of Vibrations.—If, in a conservative system, the configuration (q1, q2, . . . qn) be one of equilibrium, the equations (14) of § 22 must be satisfied by q̇1, q̇2 . . . q̇n = 0, whence
A necessary and sufficient condition of equilibrium is therefore that the value of the potential energy should be stationary for infinitesimal variations of the co-ordinates. If, further, V be a minimum, the equilibrium is necessarily stable, as was shown by P. G. L. Dirichlet (1846). In the motion consequent on any slight disturbance the total energy T + V is constant, and since T is essentially positive it follows that V can never exceed its equilibrium value by more than a slight amount, depending on the energy of the disturbance. This implies, on the present hypothesis, that there is an upper limit to the deviation of each co-ordinate from its equilibrium value; moreover, this limit diminishes indefinitely with the energy of the original disturbance. No such simple proof is available to show without qualification that the above condition is necessary. If, however, we recognize the existence of dissipative forces called into play by any motion whatever of the system, the conclusion can be drawn as follows. However slight these forces may be, the total energy T + V must continually diminish so long as the velocities q̇1, q̇2, . . . q̇n differ from zero. Hence if the system be started from rest in a configuration for which V is less than in the equilibrium configuration considered, this quantity must still further decrease (since T cannot be negative), and it is evident that either the system will finally come to rest in some other equilibrium configuration, or V will in the long run diminish indefinitely. This argument is due to Lord Kelvin and P. G. Tait (1879).
In discussing the small oscillations of a system about a configuration of stable equilibrium it is convenient so to choose the generalized cc-ordinates q1, q2, . . . qn that they shall vanish in the configuration in question. The potential energy is then given with sufficient approximation by an expression of the form
a constant term being irrelevant, and the terms of the first order being absent since the equilibrium value of V is stationary. The coefficients crr, crs are called coefficients of stability. We may further treat the coefficients of inertia arr, ars of § 22 (1) as constants. The Lagrangian equations of motion are then of the type
where Qr now stands for a component of extraneous force. In a free oscillation we have Q1, Q2, . . . Qn = 0, and if we assume
we obtain n equations of the type
| (c1r − σ2a1r) A1 + (c2r − σ2a2r) A2 + . . . + (cnr − σ2anr) An = 0. | (5) |
Eliminating the n − 1 ratios A1 : A2 : . . . : An we obtain the determinantal equation
where
| Δ(σ2) = | c11 − σ2a11, | c21 − σ2a21, | ..., | Cn1 − σ2anl |
| c12 − σ2a12, | c22 − σ2a22, | ..., | Cn2 − σ2an2 | |
| . | . | . . . | . | |
| . | . | . . . | . | |
| . | . | . . . | . | |
| c1n − σ2a1n, | c2n − σ2a2n, | . . ., | Cnn − σ2ann |
The quadratic expression for T is essentially positive, and the
same holds with regard to V in virtue of the assumed stability.
It may be shown algebraically that under these conditions the
n roots of the above equation in σ2 are all real and positive. For
any particular root, the equations (5) determine the ratios of
the quantities A1, A2, . . . An, the absolute values being alone
arbitrary; these quantities are in fact proportional to the minors
of any one row in the determinate Δ(σ2). By combining the
solutions corresponding to a pair of equal and opposite values
of σ we obtain a solution in real form:
 |
| Fig. 85. |
where a1, a2 . . . ar are a determinate series of quantities having to one another the above-mentioned ratios, whilst the constants C, ε are arbitrary. This solution, taken by itself, represents a motion in which each particle of the system (since its displacements parallel to Cartesian co-ordinate axes are linear functions of the q’s) executes a simple vibration of period 2π/σ. The amplitudes of oscillation of the various particles have definite ratios to one another, and the phases are in agreement, the absolute amplitude (depending on C) and the phase-constant (ε) being alone arbitrary. A vibration of this character is called a normal mode of vibration of the system; the number n of such modes is equal to that of the degrees of freedom possessed by the system. These statements require some modification when two or more of the roots of the equation (6) are equal. In the case of a multiple root the minors of Δ(σ2) all vanish, and the basis for the determination of the quantities ar disappears. Two or more normal modes then become to some extent indeterminate, and elliptic vibrations of the individual particles are possible. An example is furnished by the spherical pendulum (§ 13).
As an example of the method of determination of the normal modes we may take the “double pendulum.” A mass M hangs from a fixed point by a string of length a, and a second mass m hangs from M by a string of length b. For simplicity we will suppose that the motion is confined to one vertical plane. If θ, φ be the inclinations of the two strings to the vertical, we have, approximately,
| 2T = Ma2θ. 2 + m (aθ. + bψ. )2 | |
| 2V = Mgaθ2 + mg (aθ2 + bψ2). |
The equations (3) take the forms
| aθ.. + μbφ.. + gθ = 0, | |
| aθ.. + bφ.. + gφ = 0. |
where μ = m/(M + m). Hence
| (σ2 − g/a) aθ + μσ2bφ = 0, |
| σ2aθ + (σ2 − g/b) bφ = 0. |
The frequency equation is therefore
The roots of this quadratic in σ2 are easily seen to be real and positive. If M be large compared with m, μ is small, and the roots are g/a and g/b, approximately. In the normal mode corresponding to the former root, M swings almost like the bob of a simple pendulum of length a, being comparatively uninfluenced by the presence of m, whilst m executes a “forced” vibration (§ 12) of the corresponding period. In the second mode, M is nearly at rest [as appears from the second of equations (11)], whilst m swings almost like the bob of a simple pendulum of length b. Whatever the ratio M/m, the two values of σ2 can never be exactly equal, but they are approximately equal if a, b are nearly equal and μ is very small. A curious phenomenon is then to be observed; the motion of each particle, being made up (in general) of two superposed simple vibrations of nearly equal period, is seen to fluctuate greatly in extent, and if the amplitudes be equal we have periods of approximate rest, as in the case of “beats” in acoustics. The vibration then appears to be transferred alternately from m to M at regular intervals. If, on the other hand, M is small compared with m, μ is nearly equal to unity, and the roots of (12) are σ2 = g/(a + b) and σ2 = mg/M·(a + b)/ab, approximately. The former root makes θ = φ, nearly; in the corresponding normal mode m oscillates like the bob of a simple pendulum of length a + b. In the second mode aθ + bφ = 0, nearly, so that m is approximately at rest. The oscillation of M then resembles that of a particle at a distance a from one end of a string of length a + b fixed at the ends and subject to a tension mg.
The motion of the system consequent on arbitrary initial conditions may be obtained by superposition of the n normal modes with suitable amplitudes and phases. We have then
where
provided σ2, σ′2, σ″2, . . . are the n roots of (6). The coefficients of θ, θ′, θ″, . . . in (13) satisfy the conjugate or orthogonal relations
provided the symbols αr, αr′ correspond to two distinct roots σ2, σ′2 of (6). To prove these relations, we replace the symbols A1, A2, . . . An in (5) by α1, α2, . . . αn respectively, multiply the resulting equations by a′1, a′2, . . . a′n, in order, and add. The result, owing to its symmetry, must still hold if we interchange accented and unaccented Greek letters, and by comparison we deduce (15) and (16), provided σ2 and σ′2 are unequal. The actual determination of C, C′, C″, . . . and ε, ε′, ε″, . . . in terms of the initial conditions is as follows. If we write
we must have
| αrH + αr′H′ + αr″H″ + . . . | = [qr]0, |
| σαrH + σ′αr′H′ + σ″αr″H″ + . . . | = [q̇r]0, |
where the zero suffix indicates initial values. These equations can be at once solved for H, H′, H″, . . . and K, K′, K″, . . . by means of the orthogonal relations (15).
By a suitable choice of the generalized co-ordinates it is possible to reduce T and V simultaneously to sums of squares. The transformation is in fact effected by the assumption (13), in virtue of the relations (15) (16), and we may write
2V = cθ2 + c′θ′2 + c″θ″2 + . . . .
The new co-ordinates θ, θ′, θ″ . . . are called the normal co-ordinates of the system; in a normal mode of vibration one of these varies alone. The physical characteristics of a normal mode are that an impulse of a particular normal type generates an initial velocity of that type only, and that a constant extraneous force of a particular normal type maintains a displacement of that type only. The normal modes are further distinguished by an important “stationary” property, as regards the frequency. If we imagine the system reduced by frictionless constraints to one degree of freedom, so that the co-ordinates θ, θ′, θ″, . . . have prescribed ratios to one another, we have, from (19),
| σ2 = | cθ2 + c′θ′2 = c″θ″2 + . . . | , |
| aθ2 + a′θ′2 + a″θ″2 + . . . |
This shows that the value of σ2 for the constrained mode is intermediate
to the greatest and least of the values c/a, c′/a′, c″/a″, . . .
proper to the several normal modes. Also that if the constrained
mode differs little from a normal mode of free vibration (e.g. if
θ′, θ″, . . . are small compared with θ), the change in the frequency
is of the second order. This property can often be utilized to
estimate the frequency of the gravest normal mode of a system,
by means of an assumed approximate type, when the exact determination
would be difficult. It also appears that an estimate
thus obtained is necessarily too high.
From another point of view it is easily recognized that the equations (5) are exactly those to which we are led in the ordinary process of finding the stationary values of the function
| V (q1, q2, . . . qn) | , |
| T (q1, q2, . . . qn) |
where the denominator stands for the same homogeneous quadratic function of the q’s that T is for the q̇’s. It is easy to construct in this connexion a proof that the n values of σ2 are all real and positive.
The case of three degrees of freedom is instructive on account of the geometrical analogies. With a view to these we may write
| 2T = aẋ2 + bẏ2 + cż2 + 2fẏż + 2gżẋ + 2hẋẏ, |
| 2V = Ax2 + By2 + Cz2 + 2Fyz + 2Gzx + 2Hxy. |
It is obvious that the ratio
| V (x, y, z) |
| T (x, y, z) |
must have a least value, which is moreover positive, since the
numerator and denominator are both essentially positive. Denoting
this value by σ12, we have
| Ax1 + Hy1 + Gz1 = σ12 (ax1 + hy1 + ∂gz1), | |
| Hx1 + By1 + Fz1 = σ12 (hx1 + by1 + fz1), | |
| Gx1 + Fy1 + Cz1 = σ12 (gx1 + fy1 + cz1), |
provided x1 : y1 : z1 be the corresponding values of the ratios x:y:z. Again, the expression (22) will also have a least value when the ratios x : y : z are subject to the condition
| x1 | ∂V | + y1 | ∂V | + z1 | ∂V | = 0; |
| ∂x | ∂y | ∂z |
and if this be denoted by σ22 we have a second system of equations similar to (23). The remaining value σ22 is the value of (22) when x : y : z are chosen so as to satisfy (24) and
| x2 | ∂V | + y2 | ∂V | + z2 | ∂V | = 0; |
| ∂x | ∂y | ∂z |
The problem is identical with that of finding the common conjugate
diameters of the ellipsoids T(x, y, z) = const., V(x, y, z) = const.
If in (21) we imagine that x, y, z denote infinitesimal rotations of a
solid free to turn about a fixed point in a given field of force, it appears
that the three normal modes consist each of a rotation about
one of the three diameters aforesaid, and that the values of σ are
proportional to the ratios of the lengths of corresponding diameters
of the two quadrics.
We proceed to the forced vibrations of the system. The typical case is where the extraneous forces are of the simple-harmonic type cos (σt + ε); the most general law of variation with time can be derived from this by superposition, in virtue of Fourier’s theorem. Analytically, it is convenient to put Qr, equal to eiσt multiplied by a complex coefficient; owing to the linearity of the equations the factor eiσt will run through them all, and need not always be exhibited. For a system of one degree of freedom we have
and therefore on the present supposition as to the nature of Q
| q = Qc − σ2a. | (27) |
This solution has been discussed to some extent in § 12, in connexion with the forced oscillations of a pendulum. We may note further that when σ is small the displacement q has the “equilibrium value” Q/c, the same as would be produced by a steady force equal to the instantaneous value of the actual force, the inertia of the system being inoperative. On the other hand, when σ2 is great q tends to the value −Q/σ2a, the same as if the potential energy were ignored. When there are n degrees of freedom we have from (3)
and therefore
where a1r, a2r, . . . anr are the minors of the rth row of the determinant (7). Every particle of the system executes in general a simple vibration of the imposed period 2π/σ, and all the particles pass simultaneously through their equilibrium positions. The amplitude becomes very great when σ2 approximates to a root of (6), i.e. when the imposed period nearly coincides with one of the free periods. Since ars = asr, the coefficient of Qs in the expression for qr is identical with that of Qr in the expression for qs. Various important “reciprocal theorems” formulated by H. Helmholtz and Lord Rayleigh are founded on this relation. Free vibrations must of course be superposed on the forced vibrations given by (29) in order to obtain the complete solution of the dynamical equations.
In practice the vibrations of a system are more or less affected by dissipative forces. In order to obtain at all events a qualitative representation of these it is usual to introduce into the equations frictional terms proportional to the velocities. Thus in the case of one degree of freedom we have, in place of (26),
where a, b, c are positive. The solution of this has been sufficiently discussed in § 12. In the case of multiple freedom, the equations of small motion when modified by the introduction of terms proportional to the velocities are of the type
| d | ∂T | + B1rq̇1 + B2rq̇2 + . . . + Bnrq̇n + | ∂V | = Qr. | |
| dt | ∂q̇r | ∂qr |
If we put
this may be written
| d | ∂T | + | ∂F | + β1rq̇1 + β2rq̇2 + . . . + βnrq̇r + | ∂V | = Qr, | |
| dt | ∂q̇r | ∂q̇r | ∂qr |
provided
The terms due to F in (33) are such as would arise from frictional resistances proportional to the absolute velocities of the particles, or to mutual forces of resistance proportional to the relative velocities; they are therefore classed as frictional or dissipative forces. The terms affected with the coefficients βrs on the other hand are such as occur in “cyclic” systems with latent motion (Dynamics, § Analytical); they are called the gyrostatic terms. If we multiply (33) by q̇r and sum with respect to r from 1 to n, we obtain, in virtue of the relations βrs = −βsr, βrr = 0,
| ddt (T + V) = 2F + Q1q̇1 + Q2q̇2 + . . . + Qnq̇n. | (35) |
This shows that mechanical energy is lost at the rate 2F per unit time. The function F is therefore called by Lord Rayleigh the dissipation function.
If we omit the gyrostatic terms, and write qr = Creλt, we find, for a free vibration,
| (a1rλ2 + b1rλ + c1r) C1 + (a2rλ2 + b2rλ + c2r) C2 + . . . + (anrλ2 + bnrλ + cnr) Cn = 0. | (36) |
This leads to a determinantal equation in λ whose 2n roots are either real and negative, or complex with negative real parts, on the present hypothesis that the functions T, V, F are all essentially positive. If we combine the solutions corresponding to a pair of conjugate complex roots, we obtain, in real form,
| qr = Cαr e−t/τ cos (σt + ε − εr), | (37) |
where σ, τ, αr, εr are determined by the constitution of the system, whilst C, ε are arbitrary, and independent of r. The n formulae of this type represent a normal mode of free vibration: the individual particles revolve as a rule in elliptic orbits which gradually contract according to the law indicated by the exponential factor. If the friction be relatively small, all the normal modes are of this character, and unless two or more values of σ are nearly equal the elliptic orbits are very elongated. The effect of friction on the period is moreover of the second order.
In a forced vibration of eiσt the variation of each co-ordinate is simple-harmonic, with the prescribed period, but there is a retardation of phase as compared with the force. If the friction be small the amplitude becomes relatively very great if the imposed period approximate to a free period. The validity of the “reciprocal theorems” of Helmholtz and Lord Rayleigh, already referred to, is not affected by frictional forces of the kind here considered.
The most important applications of the theory of vibrations are to the case of continuous systems such as strings, bars, membranes, plates, columns of air, where the number of degrees of freedom is infinite. The series of equations of the type (3) is then replaced by a single linear partial differential equation, or by a set of two or three such equations, according to the number of dependent variables. These variables represent the whole assemblage of generalized co-ordinates qr; they are continuous functions of the independent variables x, y, z whose range of variation corresponds to that of the index r, and of t. For example, in a one-dimensional system such as a string or a bar, we have one dependent variable, and two independent variables x and t. To determine the free oscillations we assume a time factor eiσt; the equations then become linear differential equations between the dependent variables of the problem and the independent variables x, or x, y, or x, y, z as the case may be. If the range of the independent variable or variables is unlimited, the value of σ is at our disposal, and the solution gives us the laws of wave-propagation (see Wave). If, on the other hand, the body is finite, certain terminal conditions have to be satisfied. These limit the admissible values of σ, which are in general determined by a transcendental equation corresponding to the determinantal equation (6).
Numerous examples of this procedure, and of the corresponding treatment of forced oscillations, present themselves in theoretical acoustics. It must suffice here to consider the small oscillations of a chain hanging vertically from a fixed extremity. If x be measured upwards from the lower end, the horizontal component of the tension P at any point will be P∂y/∂x, approximately, if y denote the lateral displacement. Hence, forming the equation of motion of a mass-element, ρδx, we have
| ρδx · ÿ = δ(P · ∂y/∂x). | (38) |
Neglecting the vertical acceleration we have P = gρx, whence
| ∂2y∂t 2 = g ∂∂x x ∂y∂x. | (39) |
Assuming that y varies as eiσt we have
| ∂∂xx ∂y∂x + ky = 0. | (40) |
provided k = σ2/g. The solution of (40) which is finite for x = 0 is readily obtained in the form of a series, thus
| y = C 1 − kx12 + k2x21222 − . . . = CJ0(z), | (41) |
in the notation of Bessel’s functions, if z2 = 4kx. Since y must vanish at the upper end (x = l), the admissible values of σ are determined by
| σ2 = gz2/4l, J0(z) = 0. | (42) |
The function J0(z) has been tabulated; its lower roots are given by
approximately, where the numbers tend to the form s − 14. The frequency of the gravest mode is to that of a uniform bar in the ratio .9815 That this ratio should be less than unity agrees with the theory of “constrained types” already given. In the higher normal modes there are nodes or points of rest (y = 0); thus in the second mode there is a node at a distance .190l from the lower end.
Authorities.—For indications as to the earlier history of the subject see W. W. R. Ball, Short Account of the History of Mathematics; M. Cantor, Geschichte der Mathematik (Leipzig, 1880 . . . ); J. Cox, Mechanics (Cambridge, 1904); E. Mach, Die Mechanik in ihrer Entwickelung (4th ed., Leipzig, 1901; Eng. trans.). Of the classical treatises which have had a notable influence on the development of the subject, and which may still be consulted with advantage, we may note particularly, Sir I. Newton, Philosophiae naturalis Principia Mathematica (1st ed., London, 1687); J. L. Lagrange, Mécanique analytique (2nd ed., Paris, 1811–1815); P. S. Laplace, Mécanique céleste (Paris, 1799–1825); A. F. Möbius, Lehrbuch der Statik (Leipzig, 1837), and Mechanik des Himmels; L. Poinsot, Éléments de statique (Paris, 1804), and Théorie nouvelle de la rotation des corps (Paris, 1834).
Of the more recent general treatises we may mention Sir W. Thomson (Lord Kelvin) and P. G. Tait, Natural Philosophy (2nd ed., Cambridge, 1879–1883); E. J. Routh, Analytical Statics (2nd ed., Cambridge, 1896), Dynamics of a Particle (Cambridge, 1898), Rigid Dynamics (6th ed., Cambridge 1905); G. Minchin, Statics (4th ed., Oxford, 1888); A. E. H. Love, Theoretical Mechanics (2nd ed., Cambridge, 1909); A. G. Webster, Dynamics of Particles, &c. (1904); E. T. Whittaker, Analytical Dynamics (Cambridge, 1904); L. Arnal, Traitê de mécanique (1888–1898); P. Appell, Mécanique rationelle (Paris, vols. i. and ii., 2nd ed., 1902 and 1904; vol. iii., 1st ed., 1896); G. Kirchhoff, Vorlesungen über Mechanik (Leipzig, 1896); H. Helmholtz, Vorlesungen über theoretische Physik, vol. i. (Leipzig, 1898); J. Somoff, Theoretische Mechanik (Leipzig, 1878–1879).
The literature of graphical statics and its technical applications is very extensive. We may mention K. Culmann, Graphische Statik (2nd ed., Zürich, 1895); A. Föppl, Technische Mechanik, vol. ii. (Leipzig, 1900); L. Henneberg, Statik des starren Systems (Darmstadt, 1886); M. Lévy, La statique graphique (2nd ed., Paris, 1886–1888); H. Müller-Breslau, Graphische Statik (3rd ed., Berlin, 1901). Sir R. S. Ball’s highly original investigations in kinematics and dynamics were published in collected form under the title Theory of Screws (Cambridge, 1900).
Detailed accounts of the developments of the various branches of the subject from the beginning of the 19th century to the present time, with full bibliographical references, are given in the fourth volume (edited by Professor F. Klein) of the Encyclopädie der mathematischen Wissenschaften (Leipzig). There is a French translation of this work. (See also Dynamics.) (H. Lb.)














