A Treatise on Electricity and Magnetism/Volume 1/Chapter 13
CHAPTER XIII.
ELECTROSTATIC INSTRUMENTS.
On Electrostatic Instruments.
The instruments which we have to consider at present may be divided into the following classes:
(1) Electrical machines for the production and augmentation of electrification.
(2) Multipliers, for increasing electrification in a known ratio.
(3) Electrometers, for the measurement of electric potentials and charges.
(4) Accumulators, for holding large electrical charges.
Electrical Machines.
207.] In the common electrical machine a plate or cylinder of glass is made to revolve so as to rub against a surface of leather, on which is spread an amalgam of zinc and mercury. The surface of the glass becomes electrified positively and that of the rubber negatively. As the electrified surface of the glass moves away from the negative electrification of the rubber it acquires a high positive potential. It then comes opposite to a set of sharp metal points in connexion with the conductor of the machine. The positive electrification of the glass induces a negative electrification of the points, which is the more intense the sharper the points and the nearer they are to the glass.
When the machine works properly there is a discharge through the air between the glass and the points, the glass loses part of its positive charge, which is transferred to the points and so to the insulated prime conductor of the machine, and to any other body with which it is in electric communication.
The portion of the glass which is advancing towards the rubber has thus a smaller positive charge than that which is leaving it at the same time, so that the rubber, and the conductors in communication with it, become negatively electrified.
The highly positive surface of the glass where it leaves the rubber is more attracted by the negative charge of the rubber than the partially discharged surface which is advancing towards the rubber. The electrical forces therefore act as a resistance to the force employed in turning the machine. The work done in turning the machine is therefore greater than that spent in overcoming ordinary friction and other resistances, and the excess is employed in producing a state of electrification whose energy is equivalent to this excess.
The work done in overcoming friction is at once converted into heat in the bodies rubbed together. The electrical energy may be also converted either into mechanical energy or into heat.
If the machine does not store up mechanical energy, all the energy will be converted into heat, and the only difference between the heat due to friction and that due to electrical action is that the former is generated at the rubbing surfaces while the latter may be generated in conductors at a distance[1].
We have seen that the electrical charge on the surface of the glass is attracted by the rubber. If this attraction were sufficiently intense there would be a discharge between the glass and the rubber, instead of between the glass and the collecting points. To prevent this, flaps of silk are attached to the rubber. These become negatively electrified and adhere to the glass, and so diminish the potential near the rubber.
The potential therefore increases more gradually as the glass moves away from the rubber, and therefore at any one point there is less attraction of the charge on the glass towards the rubber, and consequently less danger of direct discharge to the rubber.
In some electrical machines the moving part is of ebonite instead of glass, and the rubbers of wool or fur. The rubber is then electrified positively and the prime conductor negatively.
The Electrophorus of Volta.
208.] The electrophorus consists of a plate of resin or of ebonite backed with metal, and a plate of metal of the same size. An insulating handle can be screwed to the back of either of these plates. The ebonite plate has a metal pin which connects the metal plate with the metal back of the ebonite plate when the two plates are in contact.
The ebonite plate is electrified negatively by rubbing it with wool or cat s skin. The metal plate is then brought near the ebonite by means of the insulating handle. No direct discharge passes between the ebonite and the metal plate, but the potential of the metal plate is rendered negative by induction, so that when it comes within a certain distance of the metal pin a spark passes, and if the metal plate be now carried to a distance it is found to have a positive charge which may be communicated to a conductor. The metal at the back of the ebonite plate is found to have a negative charge equal and opposite to the charge of the metal plate.
In using the instrument to charge a condenser or accumulator one of the plates is laid on a conductor in communication with the earth, and the other is first laid on it, then removed and applied to the electrode of the condenser, then laid on the fixed plate and the process repeated. If the ebonite plate is fixed the condenser will be charged positively. If the metal plate is fixed the condenser will be charged negatively.
The work done by the hand in separating the plates is always greater than the work done by the electrical attraction during the approach of the plates, so that the operation of charging the con denser involves the expenditure of work. Part of this work is accounted for by the energy of the charged condenser, part is spent in producing the noise and heat of the sparks, and the rest in overcoming other resistances to the motion.
On Machines producing Electrification by Mechanical Work.
209.] In the ordinary frictional electrical machine the work done in overcoming friction is far greater than that done in increasing the electrification. Hence any arrangement by which the electrification may be produced entirely by mechanical work against the electrical forces is of scientific importance if not of practical value. The first machine of this kind seems to have been Nicholson's Revolving Doubler, described in the Philosophical Transactions for 1788 as ’an instrument which by the turning of a Winch produces the two states of Electricity without friction or communication with the Earth.’
210.] It was by means of the revolving doubler that Volta succeeded in developing from the electrification of the pile an electrification capable of affecting his electrometer. Instruments on the same principle have been invented independently by Mr. C. F. Varley[2], and Sir W. Thomson.
These instruments consist essentially of insulated conductors of various forms, some fixed and others moveable. The moveable conductors are called Carriers, and the fixed ones may be called Inductors, Receivers, and Regenerators. The inductors and receivers are so formed that when the carriers arrive at certain points in their revolution they are almost completely surrounded by a con ducting body. As the inductors and receivers cannot completely surround the carrier and at the same time allow it to move freely in and out without a complicated arrangement of moveable pieces, the instrument is not theoretically perfect without a pair of re generators, which store up the small amount of electricity which the carriers retain when they emerge from the receivers.
For the present, however, we may suppose the inductors and receivers to surround the carrier completely when it is within them, in which case the theory is much simplified.
We shall suppose the machine to consist of two inductors and , and of two receivers and , with two carriers and .
Suppose the inductor to be positively electrified so that its potential is , and that the carrier is within it and is at potential . Then, if is the coefficient of induction (taken positive) between and , the quantity of electricity on the carrier will be .
If the carrier, while within the inductor, is put in connexion with the earth, then , and the charge on the carrier will be , a negative quantity. Let the carrier be carried round till it is within the receiver , and let it then come in contact with a spring so as to be in electrical connexion with . It will then, as was shewn in Art. 32, become completely discharged, and will communicate its whole negative charge to the receiver .
The carrier will next enter the inductor , which we shall suppose charged negatively. While within it is put in connexion with the earth and thus acquires a positive charge, which it carries off and communicates to the receiver , and so on.
In this way, if the potentials of the inductors remain always constant, the receivers and receive successive charges, which are the same for every revolution of the carrier, and thus every revolution produces an equal increment of electricity in the receivers.
But by putting the inductor in communication with the receiver , and the inductor with the receiver , the potentials of the inductors will be continually increased, and the quantity of electricity communicated to the receivers in each revolution will continually increase.
For instance, let the potential of and be , and that of and , , and when the carrier is within let the charge on and be , and that on the carrier , then, since the potential of the carrier is zero, being in contact with earth, its charge is . The carrier enters with this charge and communicates it to . If the capacity of and is , their potential will be changed from to .
If the other carrier has at the same time carried a charge from to , it will change the potential of and from to , if is the coefficient of induction between the carrier and , and the capacity of and . If, therefore, and be the potentials of the two inductors after half revolutions, and and after half revolutions,
If we write and , we find
Hence
It appears from these equations that the quantity continually diminishes, so that whatever be the initial state of electrification the receivers are ultimately oppositely electrified, so that the potentials of and are in the ratio of to .
On the other hand, the quantity continually increases, so that, however little may exceed or fall short of at first, the difference will be increased in a geometrical ratio in each revolution till the electromotive forces become so great that the insulation of the apparatus is overcome.
Instruments of this kind may be used for various purposes.
For producing a copious supply of electricity at a high potential, as is done by means of Mr. Varley's large machine.
For adjusting the charge of a condenser, as in the case of Thomson's electrometer, the charge of which can be increased or diminished by a few turns of a very small machine of this kind, which is then called a Replenishes
For multiplying small differences of potential. The inductors may be charged at first to an exceedingly small potential, as, for instance, that due to a thermo-electric pair, then, by turning the machine, the difference of potentials may be continually multiplied till it becomes capable of measurement by an ordinary electrometer. By determining by experiment the ratio of increase of this difference due to each turn of the machine, the original electromotive force with which the inductors were charged may be deduced from the number of turns and the final electrification.
In most of these instruments the carriers are made to revolve about an axis and to come into the proper positions with respect to the inductors by turning an axle. The connexions are made by means of springs so placed that the carriers come in contact with them at the proper instants.
211.] Sir W. Thomson[3], however, has constructed a machine for multiplying electrical charges in which the carriers are drops of water falling out of the inside of an inductor into an insulated receiver. The receiver is thus continually supplied with electricity of opposite sign to that of the inductor. If the inductor is electrified positively, the receiver will receive a continually increasing charge of negative electricity.
The water is made to escape from the receiver by means of a funnel, the nozzle of which is almost surrounded by the metal of the receiver. The drops falling from this nozzle are therefore nearly free from electrification. Another inductor and receiver of the same construction are arranged so that the inductor of the one system is in connexion with the receiver of the other. The rate of increase of charge of the receivers is thus no longer constant, but increases in a geometrical progression with the time, the charges of the two receivers being of opposite signs. This increase goes on till the falling drops are so diverted from their course by the electrical action that they fall outside of the receiver or even strike the inductor.
In this instrument the energy of the electrification is drawn from that of the falling drops.
212.] Several other electrical machines have been constructed in which the principle of electric induction is employed. Of these the most remarkable is that of Holtz, in which the carrier is a glass plate varnished with gum-lac and the inductors are pieces of pasteboard. Sparks are prevented from passing between the parts of the apparatus by means of two glass plates, one on each side of the revolving carrier plate. This machine is found to be very effective, and not to be much affected by the state of the atmosphere. The principle is the same as in the revolving doubler and the instruments developed out of the same idea, but as the carrier is an insulating plate and the inductors are imperfect conductors, the complete explanation of the action is. more difficult than in the case where the carriers are good conductors of known form and are charged and discharged at definite points.
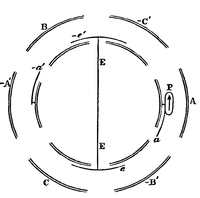
213.] In the electrical machines already described sparks occur whenever the carrier comes in contact with a conductor at a different potential from its own.
Now we have shewn that whenever this occurs there is a loss of energy, and therefore the whole work employed in turning the machine is not converted into electrification in an available form, but part is spent in producing the heat and noise of electric sparks. I have therefore thought it desirable to shew how an electrical machine may be constructed which is not subject to this loss of efficiency. I do not propose it as a useful form of machine, but as an example of the method by which the contrivance called in heat-engines a regenerator may be applied to an electrical machine to prevent loss of work.
In the figure let represent hollow fixed conductors, so arranged that the carrier passes in succession within each of them. Of these and nearly surround the carrier when it is at the middle point of its passage, but do not cover it so much.
We shall suppose to be connected with a Leyden jar of great capacity at potential , and to be connected with another jar at potential .
is one of the carriers moving in a circle from to , &c., and touching in its course certain springs, of which a and a are connected with and respectively, and are connected with the earth.
Let us suppose that when the carrier is in the middle of the coefficient of induction between and is . The capacity of in this position is greater than , since it is not completely surrounded by the receiver . Let it be .
Then if the potential of is , and that of , the charge on will be .
Now let be in contact with the spring when in the middle of the receiver , then the potential of is , the same as that of , and its charge is therefore .
If now leaves the spring it carries with it the charge . As leaves its potential diminishes, and it diminishes still more when it comes within the influence of , which is negatively electrified.
If when comes within its coefficient of induction on is , and its capacity is , then, if is the potential of the charge on is
If
then at this point the potential of will be reduced to zero.
Let at this point come in contact with the spring which is connected with the earth. Since the potential of is equal to that of the spring there will be no spark at contact.
This conductor , by which the carrier is enabled to be connected to earth without a spark, answers to the contrivance called a regenerator in heat-engines. We shall therefore call it a Regenerator.
Now let move on, still in contact with the earth-spring , till it comes into the middle of the inductor , the potential of which is . If is the coefficient of induction between and at this point, then, since the charge on will be .
When moves away from the earth-spring it carries this charge with it. As it moves out of the positive inductor towards the negative receiver its potential will be increasingly negative. At the middle of , if it retained its charge, its potential would be
and if is greater than its numerical value will be greater than that of . Hence there is some point before reaches the middle of where its potential is . At this point let it come in contact with the negative receiver-spring . There will be no spark since the two bodies are at the same potential. Let move on to the middle of still in contact with the spring, and therefore at the same potential with . During this motion it communicates a negative charge to . At the middle of it leaves the spring and carries away a charge towards the positive regenerator , where its potential is reduced to zero and it touches the earth-spring . It then slides along the earth-spring into the negative inductor , during which motion it acquires a positive charge which it finally communicates to the positive receiver , and the cycle of operations is repeated.
During this cycle the positive receiver has lost a charge and gained a charge . Hence the total gain of positive electricity is
Similarly the total gain of negative electricity is .
By making the inductors so as to be as close to the surface of the carrier as is consistent with insulation, and may be made large, and by making the receivers so as nearly to surround the carrier when it is within them, and may be made very small, and then the charges of both the Leyden jars will be increased in every revolution.
The conditions to be fulfilled by the regenerators are
and .
Since and are small the regenerators do not require to be either large or very close to the carriers.
On Electrometers and Electroscopes.
214.] An electrometer is an instrument by means of which electrical charges or electrical potentials may be measured. Instruments by means of which the existence of electric charges or of differences of potential may be indicated, but which are not capable of affording numerical measures, are called Electroscopes.
An electroscope if sufficiently sensible may be used in electrical measurements, provided we can make the measurement depend on the absence of electrification. For instance, if we have two charged bodies and we may use the method described in Chapter I to determine which body has the greater charge. Let the body be carried by an insulating support into the interior of an insulated closed vessel . Let be connected to earth and again insulated. There will then be no external electrification on . Now let be removed, and introduced into the interior of , and the electrification of tested by an electroscope. If the charge of is equal to that of there will be no electrification, but if it is greater or less there will be electrification of the same kind as that of , or the opposite kind.
Methods of this kind, in which the thing to be observed is the non-existence of some phenomenon, are called null or zero methods. They require only an instrument capable of detecting the existence of the phenomenon.
In another class of instruments for the registration of phenomena the instrument may be depended upon to give always the same indication for the same value of the quantity to be registered, but the readings of the scale of the instrument are not proportional to the values of the quantity, and the relation between these readings and the corresponding value is unknown, except that the one is some continuous function of the other. Several electrometers depending on the mutual repulsion of parts of the instrument which are similarly electrified are of this class. The use of such instruments is to register phenomena, not to measure them. Instead of the true values of the quantity to be measured, a series of numbers is obtained, which may be used afterwards to determine these values when the scale of the instrument has been properly investigated and tabulated.
In a still higher class of instruments the scale readings are proportional to the quantity to be measured, so that all that is required for the complete measurement of the quantity is a know ledge of the coefficient by which the scale readings must be multiplied to obtain the true value of the quantity.
Instruments so constructed that they contain within themselves the means of independently determining the true values of quantities are called Absolute Instruments.
Coulomb's Torsion Balance.
215.] A great number of the experiments by which Coulomb established the fundamental laws of electricity were made by measuring the force between two small spheres charged with electricity, one of which was fixed while the other was held in equilibrium by two forces, the electrical action between the spheres, and the torsional elasticity of a glass fibre or metal wire. See Art. 38.
The balance of torsion consists of a horizontal arm of gum-lac, suspended by a fine wire or glass fibre, and carrying at one end a little sphere of elder pith, smoothly gilt. The suspension wire is fastened above to the vertical axis of an arm which can be moved round a horizontal graduated circle, so as to twist the upper end of the wire about its own axis any number of degrees.
The whole of this apparatus is enclosed in a case. Another little sphere is so mounted on an insulating stem that it can be charged and introduced into the case through a hole, and brought so that its centre coincides with a definite point in the horizontal circle described by the suspended sphere. The position of the suspended sphere is ascertained by means of a graduated circle engraved on the cylindrical glass case of the instrument.
Now suppose both spheres charged, and the suspended sphere in equilibrium in a known position such that the torsion-arm makes an angle with the radius through the centre of the fixed sphere. The distance of the centres is then , where is the radius of the torsion-arm, and if is the force between the spheres the moment of this force about the axis of torsion is .
Let both spheres be completely discharged, and let the torsion-arm now be in equilibrium at an angle with the radius through the fixed sphere.
Then the angle through which the electrical force twisted the torsion-arm must have been , and if is the moment of the torsional elasticity of the fibre, we shall have the equation
Hence, if we can ascertain , we can determine , the actual force between the spheres at the distance .
To find , the moment of torsion, let be the moment of inertia of the torsion-arm, and the time of a double vibration of the arm under the action of the torsional elasticity, then
.
In all electrometers it is of the greatest importance to know what force we are measuring. The force acting on the suspended sphere is due partly to the direct action of the fixed sphere, but partly also to the electrification, if any, of the sides of the case.
If the case is made of glass it is impossible to determine the electrification of its surface otherwise than by very difficult measurements at every point. If, however, either the case is made of metal, or if a metallic case which almost completely encloses the apparatus is placed as a screen between the spheres and the glass case, the electrification of the inside of the metal screen will depend entirely on that of the spheres, and the electrification of the glass case will have no influence on the spheres. In this way we may avoid any indefiniteness due to the action of the case.
To illustrate this by an example in which we can calculate all the effects, let us suppose that the case is a sphere of radius , that the centre of motion of the torsion-arm coincides with the centre of the sphere and that its radius is ; that the charges on the two spheres are and and that the angle between their positions is ; that the fixed sphere is at a distance from the centre, and that is the distance between the two small spheres.
Neglecting for the present the effect of induction on the distribution of electricity on the small spheres, the force between them will be a repulsion
and the moment of this force round a vertical axis through the centre will be
The image of due to the spherical surface of the case is a point in the same radius at a distance with a charge , and the moment of the attraction between and this image about the axis of suspension is
If , the radius of the spherical case, is large compared with and the distances of the spheres from the centre, we may neglect the second and third terms of the factor in the denominator. The whole moment tending to turn the torsion-arm may then be written
Electrometers for the Measurement of Potentials.
216.] In all electrometers the moveable part is a body charged with electricity, and its potential is different from that of certain of the fixed parts round it. When, as in Coulomb's method, an insulated body having a certain charge is used, it is the charge which is the direct object of measurement. We may, however, connect the balls of Coulomb's electrometer, by means of fine wires, with different conductors. The charges of the balls will then depend on the values of the potentials of these conductors and on the potential of the case of the instrument. The charge on each ball will be approximately equal to its radius multiplied by the excess of its potential over that of the case of the instrument, provided the radii of the balls are small compared with their distances from each other and from the sides or opening of the case.
Coulomb's form of apparatus, however, is not well adapted for measurements of this kind, owing to the smallness of the force between spheres at the proper distances when the difference of potentials is small. A more convenient form is that of the Attracted Disk Electrometer. The first electrometers on this principle were constructed by Sir W. Snow Harris[4]. They have since been brought to great perfection, both in theory and construction, by Sir W. Thomson[5].
When two disks at different potentials are brought face to face with a small interval between them there will be a nearly uniform electrification on the opposite faces and very little electrification on the backs of the disks, provided there are no other conductors or electrified bodies in the neighbourhood. The charge on the positive disk will be approximately proportional to its area, and to the difference of potentials of the disks, and inversely as the distance between them. Hence, by making the areas of the disks large and the distance between them small, a small difference of potential may give rise to a measurable force of attraction.
The mathematical theory of the distribution of electricity over two disks thus arranged is given at Art. 202, but since it is impossible to make the case of the apparatus so large that we may suppose the disks insulated in an infinite space, the indications of the instrument in this form are not easily interpreted numerically.
217.] The addition of the guard-ring to the attracted disk is one of the chief improvements which Sir W. Thomson has made on the apparatus.
Instead of suspending the whole of one of the disks and determining the force acting upon it, a central portion of the disk is separated from the rest to form the attracted disk, and the outer ring forming the remainder of the disk is fixed. In this way the force is measured only on that part of the disk where it is most regular, and the want of uniformity of the electrification near the

edge is of no importance, as it occurs on the guard-ring and not on the suspended part of the disk.
Besides this, by connecting the guard-ring with a metal case surrounding the back of the attracted disk and all its suspending apparatus, the electrification of the back of the disk is rendered impossible, for it is part of the inner surface of a closed hollow conductor all at the same potential.
Thomson's Absolute Electrometer therefore consists essentially of two parallel plates at different potentials, one of which is made so that a certain area, no part of which is near the edge of the plate, is moveable under the action of electric force. To fix our ideas we may suppose the attracted disk and guard-ring uppermost. The fixed disk is horizontal, and is mounted on an insulating stem which has a measurable vertical motion given to it by means of a micrometer screw. The guard-ring is at least as large as the fixed disk; its lower surface is truly plane and parallel to the fixed disk. A delicate balance is erected on the guard-ring to which is suspended a light moveable disk which almost fills the circular aperture in the guard-ring without rubbing against its sides. The lower surface of the suspended disk must be truly plane, and we must have the means of knowing when its plane coincides with that of the lower surface of the guard-ring, so as to form a single plane interrupted only by the narrow interval between the disk and its guard-ring.
For this purpose the lower disk is screwed up till it is in contact with the guard-ring, and the suspended disk is allowed to rest upon the lower disk, so that its lower surface is in the same plane as that of the guard-ring. Its position with respect to the guard-ring is then ascertained by means of a system of fiducial marks. Sir W. Thomson generally uses for this purpose a black hair attached to the moveable part. This hair moves up or down just in front of two black dots on a white enamelled ground and is viewed along with these dots by means of a piano convex lens with the plane side next the eye. If the hair as seen through the lens appears straight and bisects the interval between the black dots it is said to be in its sighted position, and indicates that the suspended disk with which it moves is in its proper position as regards height. The horizontality of the suspended disk may be tested by comparing the reflexion of part of any object from its upper surface with that of the remainder of the same object from the upper surface of the guard-ring.
The balance is then arranged so that when a known weight is placed on the centre of the suspended disk it is in equilibrium in its sighted position, the whole apparatus being freed from electrification by putting every part in metallic communication. A metal case is placed over the guard-ring so as to enclose the balance and suspended disk, sufficient apertures being left to see the fiducial marks.
The guard-ring, case, and suspended disk are all in metallic communication with each other, but are insulated from the other parts of the apparatus.
Now let it be required to measure the difference of potentials of two conductors. The conductors are put in communication with the upper and lower disks respectively by means of wires, the weight is taken off the suspended disk, and the lower disk is moved up by means of the micrometer screw till the electrical attraction brings the suspended disk down to its sighted position. We then know that the attraction between the disks is equal to the weight which brought the disk to its sighted position.
If be the numerical value of the weight, and the force of gravity, the force is , and if is the area of the suspended disk, the distance between the disks, and the difference of the potentials of the disks,
or
If the suspended disk is circular, of radius , and if the radius of the aperture of the guard-ring is , then
, and .
218.] Since there is always some uncertainty in determining the micrometer reading corresponding to , and since any error
[6] in the position of the suspended disk is most important when is small, Sir W. Thomson prefers to make all his measurements depend on differences of the electromotive force . Thus, if and are two potentials, and and the corresponding distances,
For instance, in order to measure the electromotive force of a galvanic battery, two electrometers are used.
By means of a condenser, kept charged if necessary by a replenisher, the lower disk of the principal electrometer is maintained at a constant potential. This is tested by connecting the lower disk of the principal electrometer with the lower disk of a secondary electrometer, the suspended disk of which is connected with the earth. The distance between the disks of the secondary electrometer and the force required to bring the suspended disk to its sighted position being constant, if we raise the potential of the condenser till the secondary electrometer is in its sighted position, we know that the potential of the lower disk of the principal electrometer exceeds that of the earth by a constant quantity which we may call .
If we now connect the positive electrode of the battery to earth, and connect the suspended disk of the principal electrometer to the negative electrode, the difference of potentials between the disks will be , if is the electromotive force of the battery. Let be the reading of the micrometer in this case, and let be the reading when the suspended disk is connected with earth, then
In this way a small electromotive force may be measured by the electrometer with the disks at conveniently measurable distances. When the distance is too small a small change of absolute distance makes a great change in the force, since the
force varies inversely as the square of the distance, so that any error in the absolute distance introduces a large error in the result unless the distance is large compared with the limits of error of the micrometer screw.
The effect of small irregularities of form in the surfaces of the disks and of the interval between them diminish according to the inverse cube and higher inverse powers of the distance, and what ever be the form of a corrugated surface, the eminences of which just reach a plane surface, the electrical effect at any distance which is considerable compared to the breadth of the corrugations, is the same as that of a plane at a certain small distance behind the plane of the tops of the eminences. See Arts. 197, 198.
By means of the auxiliary electrification, tested by the auxiliary electrometer, a proper interval between the disks is secured.
The auxiliary electrometer may be of a simpler construction, in which there is no provision for the determination of the force of attraction in absolute measure, since all that is wanted is to secure a constant electrification. Such an electrometer may be called a gauge electrometer.
This method of using an auxiliary electrification besides the electrification to be measured is called the Heterostatic method of electrometry, in opposition to the Idiostatic method in which the whole effect is produced by the electrification to be measured.
In several forms of the attracted disk electrometer, the attracted disk is placed at one end of an arm which is supported by being attached to a platinum wire passing through its centre of gravity and kept stretched by means of a spring. The other end of the arm carries the hair which is brought to a sighted position by altering the distance between the disks, and so adjusting the force of the electric attraction to a constant value. In these electro meters this force is not in general determined in absolute measure, but is known to be constant, provided the torsional elasticity of the platinum wire does not change.
The whole apparatus is placed in a Leyden jar, of which the inner surface is charged and connected with the attracted disk and guard-ring. The other disk is worked by a micrometer screw and is connected first with the earth and then with the conductor whose potential is to be measured. The difference of readings multiplied by a constant to be determined for each electrometer gives the potential required.
219.] The electrometers already described are not self-acting, but require for each observation an adjustment of a micrometer screw, or some other movement which must be made by the observer. They are therefore not fitted to act as self-registering instruments, which must of themselves move into, the proper position. This condition is fulfilled by Thomson s Quadrant Electrometer.
The electrical principle on which this instrument is founded may be thus explained:–
and are two fixed conductors which may be at the same or at different potentials. is a moveable conductor at a high potential, which is so placed that part of it is opposite to the surface of and part opposite to that of , and that the proportions of these parts are altered as moves.
For this purpose it is most convenient to make moveable about an axis, and make the opposed surfaces of , of , and of portions of surfaces of revolution about the same axis.
In this way the distance between the surface of and the opposed surfaces of or of remains always the same, and the motion of in the positive direction simply increases the area opposed to and diminishes the area opposed to .
If the potentials of and are equal there will be no force urging from to , but if the potential of differs from that of more than from that of , then will tend to move so as to increase the area of its surface opposed to .
By a suitable arrangement of the apparatus this force may be made nearly constant for different positions of within certain limits, so that if is suspended by a torsion fibre, its deflexions will be nearly proportional to the difference of potentials between and multiplied by the difference of the potential of from the mean of those of and .
is maintained at a high potential by means of a condenser provided with a replenisher and tested by a gauge electrometer, and and are connected with the two conductors the difference of whose potentials is to be measured. The higher the potential of the more sensitive is the instrument. This electrification of , being independent of the electrification to be measured, places this electrometer in the heterostatic class.
We may apply to this electrometer the general theory of systems of conductors given in Arts. 93, 127.
Let denote the potentials of the three conductors respectively. Let be their respective capacities, the coefficient of induction between and , that between and , and that between and . All these coefficients will in general vary with the position of , and if is so arranged that the extremities of and are not near those of as long as the motion of is confined within certain limits, we may ascertain the form of these coefficients. If represents the deflexion of from towards , then the part of the surface of opposed to will diminish as increases. Hence if is kept at potential 1 while and are kept at potential , the charge on will be , where and are constants, and is the capacity of .
If and are symmetrical, the capacity of is .
The capacity of is not altered by the motion, for the only effect of the motion is to bring a different part of opposite to the interval between and . Hence .
The quantity of electricity induced on when is raised to potential unity is .
The coefficient of induction between and is .
The coefficient of induction between and is not altered by the motion of , but remains .
Hence the electrical energy of the system is
and if is the moment of the force tending to increase ,
or

In the present form of Thomson's Quadrant Electrometer the conductors and are in the form of a cylindrical box completely divided into four quadrants, separately insulated, but joined by wires so that two opposite quadrants are connected with and the two others with .
The conductor is suspended so as to be capable of turning about a vertical axis, and may consist of two opposite flat quadrantal arcs supported by their radii at their extremities. In the position of equilibrium these quadrants should be partly within and partly within , and the supporting radii should be near the middle of the quadrants of the hollow base, so that the divisions of the box and the extremities and supports of may be as far from each other as possible.
The conductor is kept permanently at a high potential by being connected with the inner coating of the Leyden jar which forms the case of the instrument. and are connected, the first with the earth, and the other with the body whose potential is to be measured.
If the potential of this body is zero, and if the instrument be in adjustment, there ought to be no force tending to make move, but if the potential of is of the same sign as that of , then will tend to move from to with a nearly uniform force, and the suspension apparatus will be twisted till an equal force is called into play and produces equilibrium. For deflexions within certain limits the deflexions of will be proportional to the product
By increasing the potential of the sensibility of the instrument may be increased, and for small values of the force will be nearly proportional to .
On the Measurement of Electric Potential.
220.] In order to determine large differences of potential in absolute measure we may employ the attracted disk electrometer, and compare the attraction with the effect of a weight. If at the same time we measure the difference of potential of the same conductors by means of the quadrant electrometer, we shall ascertain the absolute value of certain readings of the scale of the quadrant electrometer, and in this way we may deduce the value of the scale readings of the quadrant electrometer in terms of the potential of the suspended part, and the moment of torsion of the suspension apparatus.
To ascertain the potential of a charged conductor of finite size we may connect the conductor with one electrode of the electro meter, while the other is connected to earth or to a body of constant potential. The electrometer reading will give the potential of the conductor after the division of its electricity between it and the part of the electrometer with which it is put in contact. If denote the capacity of the conductor, and that of this part of the electrometer, and if denote the potentials of these bodies before making 1 contact, then their common potential after making contact will be
Hence the original potential of the conductor was
If the conductor is not large compared with the electrometer, will be comparable with , and unless we can ascertain the values of and the second term of the expression will have a doubtful value. But if we can make the potential of the electrode of the electrometer very nearly equal to that of the body before making contact, then the uncertainty of the values of and will be of little consequence.
If we know the value of the potential of the body approximately, we may charge the electrode by means of a 'replenisher' or otherwise to this approximate potential, and the next experiment will give a closer approximation. In this way we may measure the potential of a conductor whose capacity is small compared with that of the electrometer.
To Measure the Potential at any Point in the Air.
221.] First Method. Place a sphere, whose radius is small compared with the distance of electrified conductors, with its centre at the given point. Connect it by means of a fine wire with the earth, then insulate it, and carry it to an electrometer and ascertain the total charge on the sphere.
Then, if be the potential at the given point, and the radius of the sphere, the charge on the sphere will be , and if be the potential of the sphere as measured by an electrometer when placed in a room whose walls are connected with the earth, then
whence
or the potential of the air at the point where the centre of the sphere was placed is equal but of opposite sign to the potential of the sphere after being connected to earth, then insulated, and brought into a room.
This method has been employed by M. Delmann of Creuznach in measuring the potential at a certain height above the earth s surface.
Second Method. We have supposed the sphere placed at the given point and first connected to earth, and then insulated, and carried into a space surrounded with conducting matter at potential zero.
Now let us suppose a fine insulated wire carried from the electrode of the electrometer to the place where the potential is to be measured. Let the sphere be first discharged completely. This may be done by putting it into the inside of a vessel of the same metal which nearly surrounds it and making it touch the vessel. Now let the sphere thus discharged be carried to the end of the wire and made to touch it. Since the sphere is not electrified it will be at the potential of the air at the place. If the electrode wire is at the same potential it will not be affected by the contact, but if the electrode is at a different potential it will by contact with the sphere be made nearer to that of the air than it was before. By a succession of such operations, the sphere being alternately discharged and made to touch the electrode, the potential of the electrode of the electrometer will continually approach that of the air at the given point.
222.] To measure the potential of a conductor without touching it, we may measure the potential of the air at any point in the neighbourhood of the conductor, and calculate that of the conductor from the result. If there be a hollow nearly surrounded by the conductor, then the potential at any point of the air in this hollow will be very nearly that of the conductor.
In this way it has been ascertained by Sir W. Thomson that if two hollow conductors, one of copper and the other of zinc, are in metallic contact, then the potential of the air in the hollow surrounded by zinc is positive with reference to that of the air in the hollow surrounded by copper.
Third Method. If by any means we can cause a succession of small bodies to detach themselves from the end of the electrode, the potential of the electrode will approximate to that of the surrounding air. This may be done by causing shot, filings, sand, or water to drop out of a funnel or pipe connected with the electrode. The point at which the potential is measured is that at which the stream ceases to be continuous and breaks into separate parts or drops.
Another convenient method is to fasten a slow match to the electrode. The potential is very soon made equal to that of the air at the burning end of the match. Even a fine metallic point is sufficient to create a discharge by means of the particles of the air when the difference of potentials is considerable, but if we wish to reduce this difference to zero, we must use one of the methods stated above.
If we only wish to ascertain the sign of the difference of the potentials at two places, and not its numerical value, we may cause drops or filings to be discharged at one of the places from a nozzle connected with the other place, and catch the drops or filings in an insulated vessel. Each drop as it falls is charged with a certain amount of electricity, and it is completely discharged into the vessel. The charge of the vessel therefore is continually accumulating, and after a sufficient number of drops have fallen, the charge of the vessel may be tested by the roughest methods. The sign of the charge is positive if the potential of the nozzle is positive relatively to that of the surrounding air.
MEASUREMENT OF SURFACE-DENSITY OF ELECTRIFICATION.
Theory of the Proof Plane.
223.] In testing the results of the mathematical theory of the distribution of electricity on the surface of conductors, it is necessary to be able to measure the surface-density at different points of the conductor. For this purpose Coulomb employed a small disk of gilt paper fastened to an insulating stem of gum-lac. He applied this disk to various points of the conductor by placing it so as to coincide as nearly as possible with the surface of the conductor. He then removed it by means of the insulating stem, and measured the charge of the disk by means of his electrometer.
Since the surface of the disk, when applied to the conductor, nearly coincided with that of the conductor, he concluded that the surface-density on the outer surface of the disk was nearly equal to that on the surface of the conductor at that place, and that the charge on the disk when removed was nearly equal to that on an area of the surface of the conductor equal to that of one side of the disk. This disk, when employed in this way, is called Coulomb's Proof Plane.
As objections have been raised to Coulomb's use of the proof plane, I shall make some remarks on the theory of the experiment.
The experiment consists in bringing a small conducting body into contact with the surface of the conductor at the point where the density is to be measured, and then removing the body and determining its charge.
We have first to shew that the charge on the small body when in contact with the conductor is proportional to the surface- density which existed at the point of contact before the small body was placed there.
We shall suppose that all the dimensions of the small body, and especially its dimension in the direction of the normal at the point of contact, are small compared with either of the radii of curvature of the conductor at the point of contact. Hence the variation of the resultant force due to the conductor supposed rigidly electrified within the space occupied by the small body may be neglected, and we may treat the surface of the conductor near the small body as a plane surface.
Now the charge which the small body will take by contact with a plane surface will be proportional to the resultant force normal to the surface, that is, to the surface-density. We shall ascertain the amount of the charge for particular forms of the body.
We have next to shew that when the small body is removed no spark will pass between it and the conductor, so that it will carry its charge with it. This is evident, because when the bodies are in contact their potentials are the same, and therefore the density on the parts nearest to the point of contact is extremely small. When the small body is removed to a very short distance from the conductor, which we shall suppose to be electrified positively, then the electrification at the point nearest to the small body is no longer zero but positive, but, since the charge of the small body is positive, the positive electrification close to the small body will be less than at other neighbouring points of the surface. Now the passage of a spark depends in general on the magnitude of the resultant force, and this on the surface-density. Hence, since we suppose that the conductor is not so highly electrified as to be discharging electricity from the other parts of its surface, it will not discharge a spark to the small body from a part of its surface which we have shewn to have a smaller surface-density.
224.] We shall now consider various forms of the small body.
Suppose it to be a small hemisphere applied to the conductor so as to touch it at the centre of its flat side.
Let the conductor be a large sphere, and let us modify the form of the hemisphere so that its surface is a little more than a hemisphere, and meets the surface of the sphere at right angles. Then we have a case of which we have already obtained the exact solution. See Art. 168.
If and be the centres of the two spheres cutting each other at right angles, a diameter of the circle of intersection, and the centre of that circle, then if is the potential of a conductor whose outer surface coincides with that of the two spheres, the quantity of electricity on the exposed surface of the sphere is
and that on the exposed surface of the sphere is
the total charge being the sum of these, or
If and are the radii of the spheres, then, when is large compared with , the charge on is to that on in the ratio of
Now let be the uniform surface-density on when is removed, then the charge on is
and therefore the charge on is
or, when is very small compared with , the charge on the hemisphere is equal to three times that due to a surface-density extending over an area equal to that of the circular base of the hemisphere.
It appears from Art. 175 that if a small sphere is made to touch an electrified body, and is then removed to a distance from it, the mean surface-density on the sphere is to the surface-density of the body at the point of contact as is to 6, or as 1.645 to 1.
225.] The most convenient form for the proof plane is that of a circular disk. We shall therefore shew how the charge on a circular disk laid on an electrified surface is to be measured.
For this purpose we shall construct a value of the potential function so that one of the equipotential surfaces resembles a circular flattened protuberance whose general form is somewhat like that of a disk lying on a plane.
Let be the surface-density of a plane, which we shall suppose to be that of .
The potential due to this electrification will be
Now let two disks of radius be rigidly electrified with surface-densities and . Let the first of these be placed on the plane of with its centre at the origin, and the second parallel to it at the very small distance .
Then it may be shewn, as we shall see in the theory of magnetism, that the potential of the two disks at any point is , where is the solid angle subtended by the edge of either disk at the point. Hence the potential of the whole system will be
The forms of the equipotential surfaces and lines of induction are given on the left-hand side of Fig. XX, at the end of Vol. II.

Let us trace the form of the surface for which . This surface is indicated by the dotted line.
Putting the distance of any point from the axis of , then, when is much less than , and is small,
Hence, for values of considerably less than , the equation of the zero equipotential surface is
or
Hence this equipotential surface near the axis is nearly flat.
Outside the disk, where is greater than , is zero when is zero, so that the plane of is part of the equipotential surface.
To find where these two parts of the surface meet, let us find at what point of this plane .
When is very nearly equal to
Hence, when
The equipotential surface is therefore composed of a disklike figure of radius , and nearly uniform thickness , and of the part of the infinite plane of which lies beyond this figure.
The surface-integral over the whole disk gives the charge of electricity on it. It may be found, as in the theory of a circular current in Part IV, to be
The charge on an equal area of the plane surface is , hence the charge on the disk exceeds that on an equal area of the plane in the ratio of
to unity,
where is the thickness and the radius of the disk, being supposed small compared with .
On Electric Accumulators and the Measurement of Capacity.
226.] An Accumulator or Condenser is an apparatus consisting of two conducting surfaces separated by an insulating dielectric medium.
A Leyden jar is an accumulator in which an inside coating of tinfoil is separated from the outside coating by the glass of which the jar is made. The original Leyden phial was a glass vessel containing water which was separated by the glass from the hand which held it.
The outer surface of any insulated conductor may be considered as one of the surfaces of an accumulator, the other being the earth or the walls of the room in which it is placed, and the intervening air being the dielectric medium.
The capacity of an accumulator is measured by the quantity of electricity with which the inner surface must be charged to make the difference between the potentials of the surfaces unity.
Since every electrical potential is the sum of a number of parts found by dividing each electrical element by its distance from a point, the ratio of a quantity of electricity to a potential must have the dimensions of a line. Hence electrostatic capacity is a linear quantity, or we may measure it in feet or metres without ambiguity.
In electrical researches accumulators are used for two principal purposes, for receiving and retaining large quantities of electricity in as small a compass as possible, and for measuring definite quantities of electricity by means of the potential to which they raise the accumulator.
For the retention of electrical charges nothing has been devised more perfect than the Leyden jar. The principal part of the loss arises from the electricity creeping along the damp uncoated surface of the glass from the one coating to the other. This may be checked in a great degree by artificially drying the air within the jar, and by varnishing the surface of the glass where it is exposed to the atmosphere. In Sir W. Thomsons electroscopes there is a very small percentage of loss from day to day, and I believe that none of this loss can be traced to direct conduction either through air or through glass when the glass is good, but that it arises chiefly from superficial conduction along the various insulating stems and glass surfaces of the instrument.
In fact, the same electrician has communicated a charge to sulphuric acid in a large bulb with a long neck, and has then hermetically sealed the neck by fusing it, so that the charge was completely surrounded by glass, and after some years the charge was found still to be retained.
It is only, however, when cold, that glass insulates in this way, for the charge escapes at once if the glass is heated to a temperature below 100°C.
When it is desired to obtain great capacity in small compass, accumulators in which the dielectric is sheet caoutchouc, mica, or paper impregnated with paraffin are convenient.
227.] For accumulators of the second class, intended for the measurement of quantities of electricity, all solid dielectrics must be employed with great caution on account of the property which they possess called Electric Absorption.
The only safe dielectric for such accumulators is air, which has this inconvenience, that if any dust or dirt gets into the narrow space between the opposed surfaces, which ought to be occupied only by air, it not only alters the thickness of the stratum of air, but may establish a connexion between the opposed surfaces, in which case the accumulator will not hold a charge.
To determine in absolute measure, that is to say in feet or metres, the capacity of an accumulator, we must either first ascertain its form and size, and then solve the problem of the distribution of electricity on its opposed surfaces, or we must compare its capacity with that of another accumulator, for which this problem has been solved.
As the problem is a very difficult one, it is best to begin with an accumulator constructed of a form for which the solution is known. Thus the capacity of an insulated sphere in an unlimited space is known to be measured by the radius of the sphere.
A sphere suspended in a room was actually used by MM. Kohlrausch and Weber, as an absolute standard with which they compared the capacity of other accumulators.
The capacity, however, of a sphere of moderate size is so small when compared with the capacities of the accumulators in common use that the sphere is not a convenient standard measure.
Its capacity might be greatly increased by surrounding the sphere with a hollow concentric spherical surface of somewhat greater radius. The capacity of the inner surface is then a fourth proportional to the thickness of the stratum of air and the radii of the two surfaces.
Sir W. Thomson has employed this arrangement as a standard of capacity, but the difficulties of working the surfaces truly spherical, of making them truly concentric, and of measuring their distance and their radii with sufficient accuracy, are considerable.
We are therefore led to prefer for an absolute measure of capacity a form in which the opposed surfaces are parallel planes.
The accuracy of the surface of the planes can be easily tested, and their distance can be measured by a micrometer screw, and may be made capable of continuous variation, which is a most important property of a measuring instrument.
The only difficulty remaining arises from the fact that the planes must necessarily be bounded, and that the distribution of electricity near the boundaries of the planes has not been rigidly calculated. It is true that if we make them equal circular disks, whose radius is large compared with the distance between them, we may treat the edges of the disks as if they were straight lines, and calculate the distribution of electricity by the method due to Helmholtz, and described at Art. 202. But it will be noticed that in this case part of the electricity is distributed on the back of each disk, and that in the calculation it has been supposed that there are no conductors in the neighbourhood, which is not and cannot be the case in a small instrument.
228.] We therefore prefer the following arrangement, due to Sir W. Thomson, which we may call the Guard-ring arrangement, by means of which the quantity of electricity on an insulated disk may be exactly determined in terms of its potential.
The Guard-ring Accumulator.

is a cylindrical vessel of conducting material of which the outer surface of the upper face is accurately plane. This upper surface consists of two parts, a disk , and a broad ring surrounding the disk, separated from it by a very small interval all round, just sufficient to prevent sparks passing. The upper surface of the disk is accurately in the same plane with that of the guard-ring. The disk is supported by pillars of insulating material . is a metal disk, the under surface of which is accurately plane and parallel to . The disk is considerably larger than . Its distance from is adjusted and measured by means of a micrometer screw, which is not given in the figure.
This accumulator is used as a measuring instrument as follows:–
Suppose to be at potential zero, and the disk and vessel both at potential . Then there will be no electrification on the back of the disk because the vessel is nearly closed and is all at the same potential. There will be very little electrification on the edges of the disk because is at the same potential with the disk. On the face of the disk the electrification will be nearly uniform, and therefore the whole charge on the disk will be almost exactly represented by its area multiplied by the surface-density on a plane, as given at Art. 124.
In fact, we learn from the investigation at Art. 201 that the charge on the disk is
where is the radius of the disk, that of the hole in the guard-ring, the distance between and , and a quantity which cannot exceed .
If the interval between the disk and the guard-ring is small compared with the distance between and , the second term will be very small, and the charge on the disk will be nearly
Now let the vessel be put in connexion with the earth. The charge on the disk will no longer be uniformly distributed, but it will remain the same in quantity, and if we now discharge we shall obtain a quantity of electricity, the value of which we know in terms of , the original difference of potentials and the measurable quantities and .
On the Comparison of the Capacity of Accumulators.
229.] The form of accumulator which is best fitted to have its capacity determined in absolute measure from the form and dimensions of its parts is not generally the most suitable for electrical experiments. It is desirable that the measures of capacity in actual use should be accumulators having only two conducting surfaces, one of which is as nearly as possible surrounded by the other. The guard-ring accumulator, on the other hand, has three independent conducting portions which must be charged and discharged in a certain order. Hence it is desirable to be able to compare the capacities of two accumulators by an electrical process, so as to test accumulators which may afterwards serve as secondary standards.
I shall first shew how to test the equality of the capacity of two guard-ring accumulators.
Let be the disk, the guard-ring with the rest of the conducting vessel attached to it, and the large disk of one of these accumulators, and let , and be the corresponding parts of the other.
If either of these accumulators is of the more simple kind, having only two conductors, we have only to suppress or , and to suppose to be the inner and the outer conducting surface. in this case being understood to surround .
Let the following connexions be made.
Let be kept always connected with , and with , that is, let each guard-ring be connected with the large disk of the other condenser.
(1) Let be connected with and and with , the electrode of a Leyden jar, and let be connected with and and with the earth.
(2) Let and be insulated from .
(3) Let be insulated from and , and from and .
(4) Let and be connected with and and with the earth.
(5) Let be connected with .
(6) Let and be connected with an electroscope .
We may express these connexions as follows:–
Here the sign of equality expresses electrical connexion, and the vertical stroke expresses insulation.
In (1) the two accumulators are charged oppositely, so that is positive and negative, the charges on and being uniformly distributed on the upper surface opposed to the large disk of each accumulator.
In (2) the jar is removed, and in (3) the charges on and are insulated.
In (4) the guard-rings are connected with the large disks, so that the charges on and , though unaltered in magnitude, are now distributed over their whole surface.
In (5) is connected with . If the charges are equal and of opposite signs, the electrification will be entirely destroyed, and in (6) this is tested by means of the electroscope .
The electroscope will indicate positive or negative electrification according as or has the greater capacity.
By means of a key of proper construction, the whole of these operations can be performed in due succession in a very small fraction of a second, and the capacities adjusted till no electrification can be detected by the electroscope, and in this way the capacity of an accumulator may be adjusted to be equal to that of any other, or to the sum of the capacities of several accumulators, so that a system of accumulators may be formed, each of which has its capacity determined in absolute measure, i. e. in feet or in metres, while at the same time it is of the construction most suitable for electrical experiments.
This method of comparison will probably be found useful in determining the specific capacity for electrostatic induction of different dielectrics in the form of plates or disks. If a disk of the dielectric is interposed between and , the disk being considerably larger than , then the capacity of the accumulator will be altered and made equal to that of the same accumulator when and are nearer together. If the accumulator with the dielectric plate, and with and at distance , is of the same capacity as the same accumulator without the dielectric, and with and at distance , then, if is the thickness of the plate, and its specific dielectric inductive capacity referred to air as a standard,
The combination of three cylinders, described in Art. 127, has been employed by Sir W. Thomson as an accumulator whose capacity may be increased or diminished by measurable quantities.
The experiments of MM. Gibson and Barclay with this apparatus are described in the Proceedings of the Royal Society, Feb. 2, 1871, and Phil. Trans., 1871, p. 573. They found the specific inductive capacity of paraffin to be 1.975, that of air being unity.
- ↑ It is probable that in many cases where dynamical energy is converted into heat by friction, part of the energy may be first transformed into electrical energy and then converted into heat as the electrical energy is spent in maintaining currents of short circuit close to the rubbing surfaces. See Sir W. Thomson. 'On the Electrodynamic Qualities of Metals'. Phil. Trans., 1856, p. 650.
- ↑ Specification of Patent, Jan. 27, 1860, No. 206.
- ↑ Proc. R. S., June 20, 1867.
- ↑ Phil Trans. 1834.
- ↑ See an excellent report on Electrometers by Sir W. Thomson. Report of the British Association, Dundee, 1867.
- ↑ Let us denote the radius of the suspended disk by , and that of the aperture of the guard-ring by , then the breadth of the annular interval between the disk and the ring will be .
If the distance between the suspended disk and the large fixed disk is , and the difference of potentials between these disks is , then, by the investigation in Art. 201, the quantity of electricity on the suspended disk will be
where
, or
If the surface of the guard-ring is not exactly in the plane of the surface of the suspended disk, let us suppose that the distance between the fixed disk and the guard-ring is not but , then it appears from the investigation in Art. 225 that there will be an additional charge of electricity near the edge of the disk on account of its height above the general surface of the guard-ring. The whole charge in this case is therefore
and in the expression for the attraction we must substitute for , the area of the disk, the corrected quantitywhere
- = radius of suspended disk,
- = radius of aperture in the guard-ring,
- = distance between fixed and suspended disks,
- = distance between fixed disk and guard-ring,
- .
When is small compared with we may neglect the second term, and when is small we may neglect the last term.




























































































































































































