An Introduction to the Study of the Maya Hieroglyphs/Chapter 5
It has been suggested that this work be split into multiple pages. If you'd like to help, please review the style guidelines and help pages. |
CHAPTER V
THE INSCRIPTIONS
The present chapter will be devoted to the interpretation of texts drawn from monuments, a process which consists briefly in the application to the inscriptions[1] of the material presented in Chapters III and IV.

Fig. 66. Diagram showing the method of designating particular glyphs in a text.
Before proceeding with this discussion it will first be necessary to explain the method followed in designating particular glyphs in a text. We have seen (p. 23) that the Maya glyphs were presented in parallel columns, which are to be read two columns at a time, the order of the individual glyph-blocks[2] in each pair of columns being from left to right and from top to bottom. For convenience in referring to particular glyphs in the texts, the vertical columns of glyph-blocks are lettered from left to right, thus, A, B, C, D, etc., and the horizontal rows numbered from top to bottom, thus, 1, 2, 3, 4, etc. For example, in figure 66 the glyph-blocks in columns A and B are read together from left to right and top to bottom, thus, A1 B1, A2 B2, A3 B3, etc. When glyph-block B10 is reached the next in order is C1, which is followed by D1, C2 D2, C3 D3, etc. Again, when D10 is reached the next in order is E1, which is followed by F1, E2 F2, E3 F3, etc. In this way the order of reading proceeds from left to right and from top to bottom, in pairs of columns, that is, G H, I J, K L, and M N throughout the inscription, and usually closes with the glyph-block in the lower right-hand corner, as N10 in figure 66. By this simple system of coordinates any particular glyph in a text may be readily referred to when the need arises. Thus, for example, in figure 66 glyph α is referred to as D3; glyph β as F6; glyph γ as K4; glyph δ as N10. In a few texts the glyph-blocks are so irregularly placed that it is impracticable to designate them by the above coordinates. In such cases the order of the glyph-blocks will be indicated by numerals, 1, 2, 3, etc. In two Copan texts, Altar S (fig. 81) and Stela J (pl. 15), made from the drawings of Mr. Maudslay, his numeration of the glyphs has been followed. This numeration appears in these two figures.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 6

GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF BAR AND DOT NUMERALS AND NORMAL-FORM PERIOD GLYPHS
Texts Recording Initial Series
Because of the fundamental importance of Initial Series in the Maya system of chronology, the first class of texts represented will illustrate this method of dating. Moreover, since the normal forms for the numerals and the period glyphs will be more easily recognised by the beginner than the corresponding head variants, the first Initial Series given will be found to have all the numerals and period glyphs expressed by normal forms.[3]
In plate 6 is figured the drawing of the Initial Series[4] from Zoömorph P at Quirigua, a monument which is said to be the finest piece of aboriginal sculpture in the western hemisphere. Our text opens with one large glyph, which occupies the space of four glyph-blocks, A1-B2.[5] Analysis of this form shows that it possesses all the elements mentioned on page 65 as belonging to the so-called Initial-series introducing glyph, without which Initial Series never seem to have been recorded in the inscriptions. These elements are: (1) the trinal superfix, (2) the pair of comblike lateral appendages, (3) the normal form of the tun sign, (4) the trinal subfix, and (5) the variable central element. As stated above, all these appear in the large glyph A1-B2. Moreover, a comparison of A1-B2 with the introducing glyphs given in figure 24 shows that these forms are variants of one and the same sign. Consequently, in A1-B2 we have recorded an Initial-series introducing glyph. The use of this sign is so highly specialized that, on the basis of its occurrence alone in a text, the student is perfectly justified in assuming that an Initial Series will immediately follow.[6] Exceptions to this rule are so very rare (see p. 67) that the beginner will do well to disregard them altogether.
The next glyph after the introducing glyph in an Initial Series is the cycle sign, the highest period ever found in this kind of count[7]. The cycle sign in the present example appears in A3 with the coefficient 9 (1 bar and 4 dots). Although the period glyph is partially effaced in the original enough remains to trace its resemblance to the normal form of the cycle sign shown in figure 25, a-c. The outline of the repeated Cauac sign appears in both places. We have then, in this glyph, the record of 9 cycles[8]. The glyph following the cycle sign in an Initial Series is always the katun sign, and this should appear in B3, the glyph next in order. This glyph is quite clearly the normal form of the katun sign, as a comparison of it with figure 27, a, b, the normal form for the katun, will show. It has the normal-form numeral 18 (3 bars and 3 dots) prefixed to it, and this whole glyph therefore signifies 18 katuns. The next glyph should record the tuns, and a comparison of the glyph in A4 with the normal form of the tun sign in figure 29, a, b, shows this to be the case. The numeral 5 (1 bar prefixed to the tun sign) shows that this period is to be used 5 times; that is, multiplied by 5. The next glyph (B4) should be the uinal sign, and a comparison of B4 with figure 31, a-c, the normal form of the uinal sign, shows the identity of these two glyphs. The coefficient of the uinal sign contains as its most conspicuous element the clasped hand, which suggests that we may have 0 uinals recorded in B4. A comparison of this coefficient with the sign for zero in figure 54 proves this to be the case. The next glyph (A5) should be the kin sign, the lowest period involved in recording Initial Series. A comparison of A5 with the normal form of the kin sign in figure 34, a, shows that these two forms are identical. The coefficient of A5 is, moreover, exactly like the coefficient of B4, which, we have seen, meant zero, hence glyph A5 stands for 0 kins. Summarizing the above, we may say that glyphs A3-A5 record an Initial-series number consisting of 6 cycles, 18 katuns, 5 tuns, 0 uinals, and 0 kins, which we may write thus: 9.18.5.0.0 (see p. 138, footnote 1).
Now let us turn to Chapter IV and apply the several steps there given, by means of which Maya numbers may be solved. The first step on page 134 was to reduce the given number, in this case 9.18.5.0.0, to units of the first order; this may be done by multiplying the recorded coefficients by the numerical values of the periods to which they are respectively attached. These values are given in Table XIII, and the sum of the products arising from their multiplication by the coefficients recorded in the Initial Series in plate 6, A are given below:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3 = | 18 × | 7,200 = | 129,600 |
| A4 = | 5 × | 360 = | 1,800 |
| B4 = | 0 × | 20 = | 0 |
| A5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,427,400 | |||
Therefore 1,427,400 will be the number used in the following calculations.
The second step (see step 2, p. 135) is to determine the starting point from which this number is counted. According to rule 2, page 136, if the number is an Initial Series the starting point, although never recorded, is practically always the date 4 Ahau 8 Cumhu. Exceptions to this rule are so very rare that they may be disregarded by the beginner, and it may be taken for granted, therefore, in the present case, that our number 1,427,400 is to be counted from the date 4 Ahau 8 Cumhu.
The third step (see step 3, p. £136) is to determine the direction of the count, whether forward or backward. In this connection it was stated that the general practice is to count forward, and that the student should always proceed upon this assumption. However, in the present case there is no room for uncertainty, since the direction of the count in an Initial Series is governed by an invariable rule. In Initial Series, according to the rule on page 137, the count is always forward, consequently 1,427,400 is to be counted forward from 4 Ahau 8 Cumhu.
The fourth step (see step 4, p. 138) is to count the given number from its starting point; and the rules governing this process will be found on pages 139-143. Since our given number (1,427,400) is greater than 18,980, or 1 Calendar Round, the preliminary rule on page 143 applies in the present case, and we may therefore subtract from 1,427,400 all the Calendar Rounds possible before proceeding to count it from the starting point. By referring to Table XVI, it appears that 1,427,400 contains 75 complete Calendar Rounds, or 1,423,500; hence, the latter number may be subtracted from 1,427,400 without affecting the value of the resulting terminal date: 1,427,400 - 1,423,500 = 3,900. In other words, in counting forward 3,900 from 4 Ahau 8 Cumhu, the same terminal date will be reached as though we had counted forward 1,427,400.[9]
In order to find the coefficient of the day of the terminal date, it is necessary, by rule 1, page 139, to divide the given number or its equivalent by 13; 3,900 ÷ 13 = 300. Now since there is no fractional part in the resulting quotient, the numerator of an assumed fractional part will be 0; counting forward 0 from the coefficient of the day of the starting point, 4 (that is, 4 Ahau 8 Cumhu), we reach 4 as the coefficient of the day of the terminal date.
In order to find the day sign of the terminal date, it is necessary, under rule 2, page 140, to divide the given number or its equivalent by 20; 3,900 ÷ 20 = 195. Since there is no fractional part in the resulting quotient, the numerator of an assumed fractional part will be 0; counting forward 0 in Table I, from Ahau, the day sign of the starting point (4 Ahau 8 Cumhu), we reach Ahau as the day sign of the terminal date. In other words, in counting forward either 3,900 or 1,427,400 from 4 Ahau 8 Cumhu, the day reached will be 4 Ahau. It remains to show what position in the year this day 4 Ahau distant 1,427,400 from the date 4 Ahau 8 Cumhu, occupied.
In order to find the position in the year which the day of the terminal date occupied, it is necessary, under rule 3, page 141, to divide the given number or its equivalent by 365; 3,900 ÷ 365 = 10250⁄365. Since the numerator of the fractional part of the resulting quotient is 250, to reach the year position of the day of the terminal date desired it is necessary to count 250 forward from 8 Cumhu, the year position of the day of the starting point 4 Ahau 8 Cumhu. It appears from Table XV, in which the 365 positions of the year are given, that after position 8 Cumhu there are only 16 positions in the year—11 more in Cumhu and 5 in Uayeb. These must be subtracted, therefore, from 250 in order to bring the count to the end of the year; 250 - 16 = 234, so 234 is the number of positions we must count forward in the new year. It is clear that the first 11 uinals in the year will use up exactly 220 of our 234 positions (11 × 20 = 220), and that 14 positions will be left, which must be counted in the next uinal, the 12th. But the 12th uinal of the year is Ceh (see Table XV); counting forward 14 positions in Ceh, we reach 13 Ceh, which is, therefore, the month glyph of our terminal date. In other words, counting 250 forward from 8 Cumhu, position 13 Ceh is reached. Assembling the above values, we find that by calculation we have determined the terminal date of the Initial Series in plate 6, A, to be 4 Ahau 13 Ceh.
At this point there are several checks which the student may apply to his result in order to test the accuracy of his calculations; for instance, in the present example if 115, the difference between 365 and 250 (115 + 250 = 365) is counted forward from position 13 Ceh, position 8 Cumhu will be reached if our calculations were correct. This is true because there are only 365 positions in the year, and having reached 13 Ceh in counting forward 250 from 8 Cumhu, counting the remaining 115 days forward from day reached by 250, that is, 13 Ceh, we should reach our starting point (8 Cumhu) again. Another good check in the present case would be to count backward 250 from 13 Ceh; if our calculations have been correct, the starting point 8 Cumhu will be reached. Still another check, which may be applied is the following: From Table VII it is clear that the day sign Ahau can occupy only positions 3, 8, 13, or 18 in the divisions of the year;[10] hence, if in the above case the coefficient of Ceh had been any other number but one of these four, our calculations would have been incorrect.
We come now to the final step (see step 5, p. 151), the actual finding of the glyphs in our text which represent the two parts of the terminal date—the day and its corresponding position in the year. If we have made no arithmetical errors in calculations and if the text itself presents no irregular and unusual features, the terminal date recorded should agree with the terminal date obtained by calculation.
It was explained on page 152 that the two parts of an Initial-series terminal date are usually separated from each other by several intervening glyphs, and further that, although the day part follows immediately the last period glyph of the number (the kin glyph), the month part is not recorded until after the close of the Supplementary Series, usually a matter of six or seven glyphs. Returning to our text (pl. 6, A), we find that the kins are recorded in A5, therefore the day part of the terminal date should appear in B5. The glyph in B5 quite clearly records the day 4 Ahau by means of 4 dots prefixed to the sign shown in figure 16, e'-g', which is the form for the day name Ahau, thereby agreeing with the value of the day part of the terminal date as determined by calculation. So far then we have read our text correctly. Following along the next six or seven glyphs, A6-C1a, which record the Supplementary Series,[11] we reach in C1a a sign similar to the forms shown in figure 65. This glyph, which always has a coefficient of 9 or 10, was designated on page 152 the month-sign "indicator," since it usually immediately precedes the month sign in Initial-series terminal dates. In C1a it has the coefficient 9 (4 dots and 1 bar) and is followed in C1b by the month part of the terminal date, 13 Ceh. The bar and dot numeral 13 appears very clearly above the month sign, which, though partially effaced, yet bears sufficient resemblance to the sign for Ceh in figure 19, u, v, to enable us to identify it as such.
Our complete Initial Series, therefore, reads: 9.18.5.0.0 4 Ahau 13 Ceh, and since the terminal date recorded in B5, C1b agrees with the terminal date determined by calculation, we may conclude that this text is without error and, furthermore, that it records a date, 4 Ahau 13 Ceh, which was distant 9.18.5.0.0 from the starting point of Maya chronology. The writer interprets this text as signifying that 9.18.5.0.0 4 Ahau 13 Ceh was the date on which Zoömorph P at Quirigua was formally consecrated or dedicated as a time-marker, or in other words, that Zoömorph P was the monument set up to mark the hotun, or 5-tun period, which came to a close on the date 9.18.5.0.0 4 Ahau 13 Ceh of Maya chronology.[12]
In plate 6, B, is figured a drawing of the Initial Series on Stela 22 at Naranjo.[13] The text opens in A1 with the Initial-series introducing glyph, which is followed in B1 B3 by the Initial-series number 9.12.15.13.7. The five period glyphs are all expressed by their corresponding normal forms, and the student will have no difficulty in identifying them and reading the number, as above recorded.
By means of Table XIII this number may be reduced to units of the 1st order, in which form it may be more conveniently used. This reduction, which forms the first step in the process of solving Maya numbers (see step 1, p. 134), follows:
| B1 = | 9 × | 144,000 = | 1,296,000 |
| A2 = | 12 × | 7,200 = | 86,400 |
| B2 = | 15 × | 360 = | 5,400 |
| A3 = | 13 × | 20 = | 260 |
| B3 = | 7 × | 1 = | 7 |
| ———— | |||
| 1,388,067 | |||
And 1,388,067 will be the number used in the following calculations.
The next step is to find the starting point from which 1,388,067 is counted (see step 2, p. 135). Since this number is an Initial Series, in all probability its starting point will be the date 4 Ahau 8 Cumhu; at least it is perfectly safe to proceed on that assumption.
The next step is to find the direction of the count (see step 3, p. 136); since our number is an Initial Series, the count can only be forward (see rule 2, p. 137).[14]
Having determined the number to be counted, the starting point from which the count commences, and the direction of the count, we may now proceed with the actual process of counting (see step 4, p. 138).
Since 1,388,067 is greater than 18,980 (1 Calendar Round), we may deduct from the former number all the Calendar Rounds possible (see preliminary rule, page 143). According to Table XVI it appears that 1,388,067 contains 73 Calendar Rounds, or 1,385,540; after deducting this from the given number we have left 2,527 (1,388,067 - 1,385,540), a far more convenient number to handle than 1,388,067.
Applying rule 1 (p. 139) to 2,527, we have: 2,527 ÷ 13 = 1945⁄13, and counting forward 5, the numerator of the fractional part of the quotient, from 4, the day coefficient of the starting point, 4 Ahau 8 Cumhu, we reach 9 as the day coefficient of the terminal date.
Applying rule 2 (p. 140) to 2,527, we have: 2,527 ÷ 20 = 1267⁄20; and counting forward 7, the numerator of the fractional part of the quotient, from Ahau, the day sign of our starting point, 4 Ahau 8 Cumhu, in Table I, we reach Manik as the day sign of the terminal date. Therefore, the day of the terminal date will be 9 Manik.
Applying rule 3 (p. 141) to 2,527, we have: 2,527 ÷ 365 = 6337⁄365; and counting forward 337, the numerator of the fractional part of the quotient, from 8 Cumhu, the year position of the starting point, 4 Ahau 8 Cumhu, in Table XV, we reach 0 Kayab as the year position of the terminal date. The calculations by means of which 0 Kayab is reached are as follows: After 8 Cumhu there are 16 positions in the year, which we must subtract from 337; 337 - 16 = 321, which is to be counted forward in the new year. This number contains just 1 more than 16 uinals, that is, 321 = (16 × 20) + 1; hence it will reach through the first 16 uinals in Table XV and to the first position in the 17th uinal, 0 Kayab. Combining this with the day obtained above, we have for our terminal date determined by calculation, 9 Manik 0 Kayab.
The next and last step (see step 5, p. 151) is to find the above date in the text. In Initial Series (see p. 152) the two parts of the terminal date are generally separated, the day part usually following immediately the last period glyph and the month part the closing glyph of the Supplementary Series. In plate 6, B, the last period glyph, as we have seen, is recorded in B3; therefore the day should appear in A4. Comparing the glyph in A4 with the sign for Manik in figure 16, j, the two forms are seen to be identical. Moreover, A4 has the bar and dot coefficient 9 attached to it, that is, 4 dots and 1 bar; consequently it is clear that in A4 we have recorded the day 9 Manik, the same day as reached by calculation. For some unknown reason, at Naranjo the month glyphs of the Initial-series terminal dates do not regularly follow the closing glyphs of the Supplementary Series; indeed, in the text here under discussion, so far as we can judge from the badly effaced glyphs, no Supplementary Series seems to have been recorded. However, reversing our operation, we know by calculation that the month part should be 0 Kayab, and by referring to figure 49 we find the only form which can be used to express the 0 position with the month signs—the so-called "spectacles" glyph—which must be recorded somewhere in this text to express the idea 0 with the month sign Kayab. Further, by referring to figure 19, d'-f', we may fix in our minds the sign for the month Kayab, which should also appear in the text with one of the forms shown in figure 49.
Returning to our text once more and following along the glyphs after the day in A4, we pass over B4, A5, and B5 without finding a glyph resembling one of the forms in figure 49 joined to figure 19, d'-f'; that is, 0 Kayab. However, in A6 such a glyph is reached, and the student will have no difficulty in identifying the month sign with d'-f' in the above figure. Consequently, we have recorded in A4, A6 the same terminal date, 9 Manik 0 Kayab, as determined by calculation, and may conclude, therefore, that our text records without error the date 9.12.15.13.7 9 Manik 0 Kayab[15] of Maya chronology.
The next text presented (pl. 6, C) shows the Initial Series from Stela I at Quirigua.[16] Again, as in plate 6, A, the introducing glyph occupies the space of four glyph-blocks, namely, A1-B2. Immediately after this, in A3-A4, is recorded the Initial-series number 9.18.10.0.0, all the period glyphs and coefficients of which are expressed by normal forms. The student's attention is called to the form for 0 used with the uinal and kin signs in A4a and A4b, respectively, which differs from the form for 0 recorded with the uinal and kin signs in plate 6, A, B4, and A5, respectively. In the latter text the 0 uinals and 0 kins were expressed by the hand and curl form for zero shown in figure 54; in the present text, however, the 0 uinals and 0 kins are expressed by the form for 0 shown in figure 47, a new feature.
Reducing the above number to units of the 1st order by means of Table XIII, we have:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3a = | 18 × | 7,200 = | 129,600 |
| B3b = | 10 × | 360 = | 3,600 |
| A4a = | 0 × | 20 = | 0 |
| A4b = | 0 × | 1 = | 0 |
| ———— | |||
| 1,429,200 | |||
Deducting from this number all the Calendar Rounds possible, 75 (see Table XVI), it may be reduced to 5,700 without affecting its value in the present connection.
Applying rules 1 and 2 (pp. 139 and 140, respectively) to this number, the day reached will be found to be 10 Ahau; and by applying rule 3 (p. 141), the position of this day in the year will be found to be 8 Zac. Therefore, by calculation we have determined that the terminal date reached by this Initial Series is 10 Ahau 8 Zac. It remains to find this date in the text. The regular position for the day in Initial-series terminal dates is immediately following the last period glyph, which, as we have seen above, was in A4b. Therefore the day glyph should be B4a. An inspection of this latter glyph will show that it records the day 10 Ahau, both the day sign and the coefficient being unusually clear, and practically unmistakable. Compare B4a with figure 16, e'-g', the sign for the day name Ahau. Consequently the day recorded agrees with the day determined by calculation. The month glyph in this text, as mentioned on page 157, footnote 1, occurs out of its regular position, following immediately the day of the terminal date.
As mentioned on page 153, when the month glyph in Initial-series terminal dates is not to be found in its usual position, it will be found in the regular position for the month glyphs in all other kinds of dates in the inscriptions, namely, immediately following the day glyph to which it belongs. In the present text we found that the day, 10 Ahau, was recorded in B4a; hence, since the month glyph was not recorded in its regular position, it must be in B4b, immediately following the day glyph. By comparing the glyph in B4b with the month signs in figure 19, it will be found exactly like the month sign for Zac (s-t), and we may therefore conclude that this is our month glyph and that it is Zac. The coefficient of B4b is quite clearly 8 and the month part therefore reads, 8 Zac. Combining this with the day recorded in B4a, we have the date 10 Ahau 8 Zac, which corresponds with the terminal date determined by calculation. The whole text therefore reads 9.18.10.0.0 10 Ahau 8 Zac.

Fig. 67. Signs representing the hotun, or 5-tun, period.

The next Initial Series presented (see pl. 6, D) is from Stela 24 at Naranjo.[18] The text opens with the introducing glyph, which is in the same relative position as the introducing glyph in the other Naranjo text (pl. 6, B) at A1. Then follows regularly in B1-B3 the number 9.12.10.5.12, the numbers and period glyphs of which are all expressed by normal forms. By this time the student should have no difficulty in recognizing these and in determining the number as given above. Reducing this according to rule 1, page 134, the following result should be obtained:
| B1 = | 9 × | 144,000 = | 1,296,000 |
| A2 = | 12 × | 7,200 = | 86,400 |
| B2 = | 10 × | 360 = | 3,600 |
| A3 = | 5 × | 20 = | 100 |
| B3 = | 12 × | 1 = | 12 |
| ———— | |||
| 1,386,112 | |||
Deducting[19] from this number all the Calendar Rounds possible, 73 (see preliminary rule, p. 143, and Table XVI), we may reduce it to 572 without affecting its value in so far as the present calculations are concerned (1,386,112 - 1,385,540). First applying rule 1, page 139, and next rule 2, page 140, to this number (572), the student will find the day reached to be 4 Eb. And applying rule 3, page 141, he will find that the year position reached will be 10 Yax;[20] hence, the terminal date as determined by calculation will be 4 Eb 10 Yax.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 7

GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF BAR AND DOT NUMERALS AND HEAD-VARIANT PERIOD GLYPHS
Turning again to the text (pl. 6, D), the next step (see step 5, p. 151) is to find the glyphs representing the above terminal date. In this connection it should be remembered that the day part of an Initial-series terminal date usually follows immediately the last period glyph of the number. The glyph in A4, therefore, should record the day reached. Comparing this form with the several day signs in figure 16, it appears that A4 more closely resembles the sign for Eb (fig. 16, s-u) than any of the others, hence the student may accept Eb as the day sign recorded in A4. The 4 dots prefixed to this sign show that the day 4 Eb is here indicated. The month sign, as stated on page 152, usually follows the last glyph of the Supplementary Series; passing over B4, A5, B5, and A6, we reach the latter glyph in B6. Compare the left half of B6 with the forms given in figure 65. The coefficient 9 or 10 is expressed by a considerably effaced head numeral. Immediately following the month-sign "indicator" is the month sign itself in A7. The student will have little difficulty in tracing its resemblance to the month Yax in figure 19, q, r, although in A7 the Yax element itself appears as the prefix instead of as the superfix, as in q and r, just cited. This difference, however, is immaterial. The month coefficient is quite clearly 10,[21] and the whole terminal date recorded will read 4 Eb 10 Yax, which corresponds exactly with the terminal date determined by calculation. We may accept this text, therefore, as recording the Initial-series date 9.12.10.5.12 4 Eb 10 Yax of Maya chronology.
In the foregoing examples nothing but normal-form period glyphs have been presented, in order that the first exercises in deciphering the inscriptions may be as easy as possible. By this time, however, the student should be sufficiently familiar with the normal forms of the period glyphs to be able to recognize them when they are present in the text, and the next Initial Series figured will have its period glyphs expressed by head variants.
In A, plate 7, is figured the Initial Series from Stela B at Copan.[22] The introducing glyph appears at the head of the inscription in A1 and is followed by a head-variant glyph in A2, to which is prefixed a bar and dot coefficient of 9. By its position, immediately following the introducing glyph, we are justified in assuming that A2 records 9 cycles, and after comparing it with d-f, figure 25, where the head variant of the cycle sign is shown, this assumption becomes a certainty. Both heads have the same clasped hand in the same position, across the lower part of the face, which, as explained on page 68, is the essential element of the cycle head; therefore, A2 records 9 cycles. The next glyph, A3, should be the katun sign, and a comparison of this form with the head variant for katun in e-h, figure 27, shows this to be the case. The determining characteristic (see p. 69) is probably the oval in the top of the head, which appears in both of these forms for the katun. The katun coefficient is 15 (3 bars). The next glyph, A4, should record the tuns, and by comparing this form with the head variant for the tun sign in e-g, figure 29, this also is found to be the case. Both heads show the same essential characteristic—the fleshless lower jaw (see p. 70). The coefficient is 0 (compare fig. 47). The uinal head in A5 is equally unmistakable. Note the large curl protruding from the back part of the mouth, which was said (p. 71) to be the essential element of this sign. Compare figure 31, d-f, where the head variant for the uinal is given. The coefficient of A5 is like the coefficient of A4 (0), and we have recorded, therefore, 0 uinals. The closing period glyph of the Initial Series in A6 is the head variant for the kin sign. Compare this form with figure 34, e-g, where the kin head is figured. The determining characteristic of this head is the subfixial element, which appears also in the normal form for the kin sign (see fig. 34, a). Again, the coefficient of A6 is like the coefficient of A4 and A5, hence we have recorded here 0 kins.
The number recorded by the head-variant period glyphs and normal-form numerals in A2-A6 is therefore 9.15.0.0.0; reducing this by means of Table XIII, we have:
| A2 = | 9 × | 144,000 = | 1,296,000 |
| A3 = | 15 × | 7,200 = | 108,000 |
| A4 = | 0 × | 360 = | 0 |
| A5 = | 0 × | 20 = | 0 |
| A6 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,404,000 | |||
Deducting from this number all the Calendar Rounds possible, 73 (see Table XVI), it may be reduced to 18,460. Applying to this number rules 1 and 2 (pp. 139 and 140, respectively), the day reached will be found to be 4 Ahau. Applying rule 3 (p. 141), the position of 4 Ahau in the year will be found to be 13 Yax. Therefore the terminal date determined by calculation will be 4 Ahau 13 Yax.
According to step 5 (p. 151), the day reached should follow immediately the last period glyph, which in this case was in A6; hence the day should be recorded in A7. This glyph has a coefficient 4, but the glyph does not resemble either of the forms for Ahau shown in B5, plate 6, A, or in B4a, C of the same plate. However, by comparing this glyph with the second variant for the day sign Ahau in figure 16, h'-i', the two forms will be found to be identical, and we may accept A7 as recording the day 4 Ahau. Immediately following in A8 is the month sign, again out of its usual place as in plate 6, C. Comparing it with the month signs in figure 19, it will be found to exactly correspond with the sign for Yax in q-r. The coefficient is 13. Therefore the terminal date recorded, 4 Ahau 13 Yax, agrees with the terminal date reached by calculation, and the whole Initial Series reads 9.15.0.0.0 4 Ahau 13 Yax. This date marks the close not only of a hotun in the Long Count, but of a katun as well.
In B, plate 7, is figured the Initial Series from Stela A at Copan.[23] The introducing glyph appears in A1 B1, and is followed by the Initial-series number in A2-A4. The student will have no difficulty in picking out the clasped hand in A2, the oval in the top of the head in B2, the fleshless lower jaw in A3, the large mouth curl in B3, and the flaring subfix in A4, which are the essential elements of the head variants for the cycle, katun, tun, uinal, and kin, respectively. Compare these glyphs with figures 25, d-f, 27, e-h, 29, e-g, 31, d-f, and 34, e-g, respectively. The coefficients of these period glyphs are all normal forms and the student will have no difficulty in reading this number as 9.14.19.8.0.[24]
Reducing this by means of Table XIII to units of the 1st order, we have:
| A2 = | 9 × | 144,000 = | 1,296,000 |
| B2 = | 14 × | 7,200 = | 108,000 |
| A3 = | 19 × | 360 = | 6,840 |
| B3 = | 8 × | 20 = | 160 |
| A4 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,403,800 | |||
Deducting from this all the Calendar Rounds possible, 73 (see Table XVI), and applying rules 1 and 2 (pp. 139 and 140, respectively), to the remainder, the day reached will be 12 Ahau. And applying rule 3 (p. 141), the month reached will be 18 Cumhu, giving for the terminal date as reached by calculation 12 Ahau 18 Cumhu. The day should be recorded in B4, and an examination of this glyph shows that its coefficient is 12, the day coefficient reached by calculation. The glyph itself, however, is unlike the forms for Ahau previously encountered in plate 6, A, B5 and C, B4b, and in plate 7, A, A7. Turning now to the forms for the day sign Ahau in figure 16, it is seen that the form in A4 resembles the third variant j' or k', the grotesque head, and it is clear that the day 12 Ahau is here recorded. At first sight the student might think that the month glyph follows in A5, but a closer inspection of this form shows that this is not the case. In the first place, since the day sign is Ahau the month coefficient must be either 3, 8, 13, or 18, not 7, as recorded (see Table VII), and, in the second place, the glyph itself in A5 bears no resemblance whatsoever to any of the month signs in figure 19. Consequently the month part of the Initial-series terminal date of this text should follow the closing glyph of the Supplementary Series. Following along the glyphs next in order, we reach in A9 a glyph with a coefficient 9, although the sign itself bears no resemblance to the month-glyph "indicators" heretofore encountered (see fig. 65).
The glyph following, however, in A9b is quite clearly 18 Cumhu (see fig. 19, g'-h'), which is the month part of the terminal date as reached by calculation. Therefore, since A9a has the coefficient 9 it is probable that it is a variant of the month-glyph "indicator";[25] and consequently that the month glyph itself follows, as we have seen, in B9. In other words, the terminal date recorded, 12 Ahau 18 Cumhu, agrees with the terminal date reached by calculation, and the whole text, so far as it can be deciphered, reads 9.14.19.8.0 12 Ahau 18 Cumhu. The student will note that this Initial Series precedes the Initial Series in plate 7, A by exactly 10 uinals, or 200 days. Compare A and B, plate 7.
In plate 8, A, is figured the Initial Series from Stela 6 at Copan.[26] The introducing glyph occupies the space of four glyph-blocks, A1-B2, and there follows in A3-B4a the Initial-series number 9.12.10.0.0. The cycle glyph in A3 is partially effaced; the clasped hand, however, the determining characteristic of the cycle head, may still be distinguished. The katun head in B3 is also unmistakable, as it has the same superfix as in the normal form for the katun. At first sight the student might read the bar and dot coefficient as 14, but the two middle crescents are purely decorative and have no numerical value, and the numeral recorded here is 12 (see pp. 88-91). Although the tun and uinal period glyphs in A4a and A4b,[27] respectively, are effaced, their coefficients may be distinguished as 10 and 0, respectively. In such a case the student is perfectly justified in assuming that the tun and uinal signs originally stood here. In B4a the kin period glyph is expressed by its normal form and the kin coefficient by a head-variant numeral, the clasped hand of which indicates that it stands for 0 (see fig. 53, s-w).[28] The number here recorded is 9.12.10.0.0.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 8
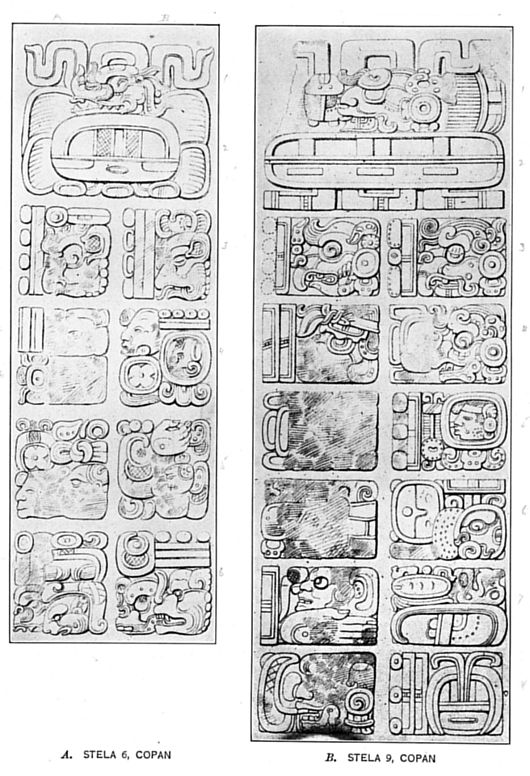
GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF BAR AND DOT NUMERALS AND HEAD-VARIANT PERIOD GLYPHS
Reducing this to units of the 1st order by means of Table XIII, we have:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3 = | 12 × | 7,200 = | 86,400 |
| A4a = | 10 × | 360 = | 3,600 |
| A4b = | 0 × | 20 = | 0 |
| B4a = | 0 × | 1 = | 0 |
| ———— | |||
| 1,386,000 | |||
Deducting from this number all the Calendar Rounds possible, 73 (see Table XVI), and applying to the remainder rules 1, 2, and 3 (pp. 139-141), respectively, the date reached by the resulting calculations will be 9 Ahau 18 Zotz. Turning to our text again, the student will have little difficulty in identifying B4b as 9 Ahau, the day of the above terminal date. The form Ahau here recorded is the grotesque head, the third variant j' or k' in figure 16. Following the next glyphs in order, A5-A6, the closing glyph of the Supplementary Series is reached in B6a. Compare this glyph with the forms in figure 65. The coefficient of B6a is again a head-variant numeral, as in the case of the kin period glyph in B4a, above. The fleshless lower jaw and other skull-like characteristics indicate that the numeral 10 is here recorded. Compare B6a with figure 52, m-r. Since B6a is the last glyph of the Supplementary Series, the next glyph B6b should represent the month sign. By comparing the latter form with the month signs in figure 19 the student will readily recognize that the sign for Zotz in e or f is the month sign here recorded. The coefficient 18 stands above. Consequently, B4b and B6b represent the same terminal date, 9 Ahau 18 Zotz, as reached by calculation. This whole Initial Series reads 9.12.10.0.0 9 Ahau 18 Zotz, and according to the writer's view, the monument upon which it occurs (Stela 6 at Copan) was the period stone for the hotun which began with the day 9.12.5.0.1 4 Imix 4 Xul[29] and ended with the day 9.12.10.0.0 9 Ahau 18 Zotz, here recorded.
In plate 8, B, is figured the Initial Series from Stela 9 at Copan.[30] The introducing glyph stands in A1-B2 and is followed by the five period glyphs in A3-A5. The cycle is very clearly recorded in A3, the clasped hand being of a particularly realistic form. Although the coefficient is partially effaced, enough remains to show that it was above 5, having had originally more than the one bar which remains, and less than 11, there being space for only one more bar or row of dots. In all the previous Initial Series the cycle coefficient was 9, consequently it is reasonable to assume that 4 dots originally occupied the effaced part of this glyph. If the use of 9 cycles in this number gives a terminal date which agrees with the terminal date recorded, the above assumption becomes a certainty. In B3 six katuns are recorded. Note the ornamental dotted ovals on each side of the dot in the numeral 6. Although the head for the tun in A4 is partially effaced, we are warranted in assuming that this was the period originally recorded here. The coefficient 10 appears clearly. The uinal head in B4 is totally unfamiliar and seems to have the fleshless lower jaw properly belonging to the tun head; from its position, however, the 4th in the number, we are justified in calling this glyph the uinal sign. Its coefficient denotes that 0 uinals are recorded here. Although the period glyph in A5 is also entirely effaced, the coefficient appears clearly as 0, and from position again, 5th in the number, we are justified once more in assuming that 0 kins were originally recorded, here. It seems at first glance that the above reading of the number A3-A5 rests on several assumptions:
1. That the cycle coefficient was originally 9.
2. That the effaced glyph in A4 was a tun head.
3. That the irregular head in B4 is a uinal head.
4. That the effaced glyph in A5 was a kin sign.
The last three are really certainties, since the Maya practice in recording Initial Series demanded that the five period glyphs requisite—the cycle, katun, tun, uinal, and kin—should follow each other in this order, and in no other. Hence, although the 3d, 4th, and 5th glyphs are either irregular or effaced, they must have been the tun, uinal, and kin signs, respectively. Indeed, the only important assumption consisted in arbitrarily designating the cycle coefficient 9, when, so far as the appearance of A3 is concerned, it might have been either 6, 7, 8, 9, or 10. The reason for choosing 9 rests on the overwhelming evidence of antecedent probability. Moreover, as stated above, if the terminal date recorded agrees with the terminal date determined by calculation, using the cycle coefficient as 9, our assumption becomes a certainty. Designating the above number as 9.6.10.0.0 then and reducing this by means of Table XIII, we obtain:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3 = | 6 × | 7,200 = | 43,200 |
| A4 = | 10 × | 360 = | 3,600 |
| B4 = | 0 × | 20 = | 0 |
| A5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,342,800 | |||
Deducting from this number all the Calendar Rounds possible, 70 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the date determined by the resulting calculations will be 8 Ahau 13 Pax. Turning to our text again, the student will have little difficulty in recognizing the first part of this date, the day 8 Ahau, in B5. The numeral 8 appears clearly, and the day sign is the profile-head h' or i', the second variant for Ahau in figure 16. The significance of the element standing between the numeral and the day sign is unknown. Following along through A6, B6, A7, B7, the closing glyph of the Supplementary Series is reached in A8. The glyph itself is on the left and the coefficient, here expressed by a head variant, is on the right. The student will have no difficulty in recognizing the glyph and its coefficient by comparing the former with figure 65, and the latter with the head variant for 10 in figure 52, m-r. Note the fleshless lower jaw in the head numeral in both places. The following glyph, B8, is one of the clearest in the entire text. The numeral is 13, and the month sign on comparison with figure 19 unmistakably proves itself to be the sign for Pax in c'. Therefore the terminal date recorded in B5, B8, namely, 8 Ahau 13 Pax, agrees with the terminal date determined by calculation; it follows, further, that the effaced cycle coefficient in A3 must have been 9, the value tentatively ascribed to it in the above calculations. The whole Initial Series reads 9.6.10.0.0 8 Ahau 13 Pax.
Some of the peculiarities of the numerals and signs in this text are doubtless due to its very great antiquity, for the monument presenting this inscription, Stela 9, records the next to earliest Initial Series[31] yet deciphered at Copan.[32] Evidences of antiquity appear in the glyphs in several different ways. The bars denoting 5 have square ends and all show considerable ornamentation. This type of bar was an early manifestation and gave way in later times to more rounded forms. The dots also show this greater ornamentation, which is reflected, too, by the signs themselves. The head forms show greater attention to detail, giving the whole glyph a more ornate appearance. All this embellishment gave way in later times to more simplified forms, and we have represented in this text a stage in glyph morphology before conventionalization had worn down the different signs to little more than their essential elements.

Fig. 68. Initial Series showing bar and dot numerals and head-variant period glyphs: A, Stela C (west side), Quirigua; B, Stela M, Copan.
In figure 68, A, is figured the Initial Series on the west side of Stela C at Quirigua.[33] The introducing glyph in A1-B2 is followed by the number in A3-A5, which the student will have no difficulty in reading except for the head-variant numeral attached to the kin sign in A5. The clasped hand in this glyph, however, suggests that 0 kins are recorded here, and a comparison of this form with figure 53, s-w, confirms the suggestion. The number therefore reads 9.1.0.0.0. Reducing this number by means of Table XIII to units of the 1st order, we obtain:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3 = | 1 × | 7,200 = | 7,200 |
| A4 = | 0 × | 360 = | 0 |
| B4 = | 0 × | 20 = | 0 |
| A5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,303,200 | |||
Deducting from this number all the Calendar Rounds possible, 68 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, we reach for the terminal date 6 Ahau 13 Yaxkin. Looking for the day part of this date in B5, we find that the form there recorded bears no resemblance to 6 Ahau, the day determined by calculation. Moreover, comparison of it with the day signs in figure 16 shows that it is unlike all of them; further, there is no bar and dot coefficient. These several points indicate that the day sign is not the glyph in B5, also that the day sign is, therefore, out of its regular position. The next glyph in the text, A6, instead of being one of the Supplementary Series is the day glyph 6 Ahau, which should have been recorded in B5. The student will readily make the same identification after comparing A6 with figure 16, e'-g'. A glance at the remainder of the text, will show that no Supplementary Series is recorded, and consequently that the month glyph will be found immediately following the day glyph in B6. The form in B6 has a coefficient 13, one of the four (3, 8, 13, 18) which the month must have, since the day sign is Ahau (see Table VII). A comparison of the form in B6 with the month signs in figure 19 shows that the month Yaxkin in k or l is the form here recorded; therefore the terminal date recorded agrees with the terminal date reached by calculation, and the text reads 9.1.0.0.0 6 Ahau 13 Yaxkin.[34]
In figure 68, B, is shown the Initial Series on Stela M at Copan.[35] The introducing glyph appears in A1 and the Initial-series number in B1a-B2a. The student will note the use of both normal-form and head-variant period glyphs in this text, the cycle, tun, and uinal in B1a, A2a, and A2b, respectively, being expressed by the latter, and the katun and kin in B1b and B2a, respectively, by the former. The number recorded is 9.16.5.0.0, and this reduces to units of the first order, as follows (see Table XIII):
| B1a = | 9 × | 144,000 = | 1,296,000 |
| B1b = | 16 × | 7,200 = | 115,200 |
| A2a = | 5 × | 360 = | 1,800 |
| A2b = | 0 × | 20 = | 0 |
| B2a = | 0 × | 1 = | 0 |
| ———— | |||
| 1,413,000 | |||
Deducting from this number all the Calendar Rounds possible, 74 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached by the resulting calculations will be 8 Ahau 8 Zotz. Turning to our text, the student will have no difficulty in recognizing in B2b the day 8 Ahau. The month glyph in this inscription irregularly follows immediately the day glyph. Compare the form in A3a with the month signs in figure 19 and it will be found to be the sign for Zotz (see fig. 19, e-f). The coefficient is 8 and the whole glyph represents the month part 8 Zotz, the same as determined by calculation. This whole Initial Series reads 9.16.5.0.0 8 Ahau 8 Zotz.
The Maya texts presented up to this point have all been drawings of originals, which are somewhat easier to make out than either photographs of the originals or the originals themselves. However, in order to familiarize the student with photographic reproductions of Maya texts a few will be inserted here illustrating the use of bar and dot numerals with both normal-form and head-variant period glyphs, with which the student should be perfectly familiar by this time.
In plate 9, A, is figured a photograph of the Initial Series on the front of Stela 11 at Yaxchilan.[36] The introducing glyph appears in A1 B1; 9 cycles in A2; 16 katuns in B2, 1 tun in A3, 0 uinals in B3, and 0 kins in B4. The student will note the clasped hand in the cycle head, the oval in the top of the katun head, the large mouth curl in the uinal head, and the flaring postfix in the kin head. The tun is expressed by its normal form. The number here recorded is 9.16.1.0.0, and reducing this to units of the first order by means of Table XIII, we have:
| A2 = | 9 × | 144,000 = | 1,296,000 |
| B2 = | 16 × | 7,200 = | 115,200 |
| A3 = | 1 × | 360 = | 360 |
| B3 = | 0 × | 20 = | 0 |
| A4 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,411,560 | |||
Deducting from this number all the Calendar Rounds possible, 74 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), to the remainder, the terminal date reached by the resulting calculations will be 11 Ahau 8 Tzec. The day part of this date is very clearly recorded in B4 immediately after the last period glyph, and the student will readily recognize the day 11 Ahau in this form. Following along the glyphs of the Supplementary Series in C1 D1, C2 D2, the closing glyph is reached in C3b. It is very clear and has a coefficient of 9. The glyph following (D3) should record the month sign. A comparison of this form with the several month signs in figure 19 shows that Tzec is the month here recorded. Compare D3 with figure 19, g-h. The month coefficient is 8. The terminal date, therefore, recorded in B4 and D3 (11 Ahau 8 Tzec) agrees with the terminal date determined by calculation, and this whole text reads 9.16.1.0.0 11 Ahau 8 Tzec. The meaning of the element between the tun coefficient and the tun sign in A3, which is repeated again in D3 between the month coefficient and the month sign, is unknown.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 9

GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF BAR AND DOT NUMERALS AND HEAD-VARIANT PERIOD GLYPHS
In plate 9, B, is figured the Initial Series on an altar in front of Structure 44 at Yaxchilan.[37] The introducing glyph appears in A1 B1 and is followed by the number in A2-A4. The period glyphs are all expressed as head variants and the coefficients as bar and dot numerals. Excepting the kin coefficient in A4, the number is quite easily read as 9.12.8.14.? An inspection of our text shows that the coefficient must be 0, 1, 2, or 3. Let us work out the terminal dates for all four of these values, commencing with 0, and then see which of the resulting terminal days is the one actually recorded in A4. Reducing the number 9.12.8.14.0 to units of the first order by means of Table XIII, we have:
| A2 = | 9 × | 144,000 = | 1,296,000 |
| B2 = | 12 × | 7,200 = | 86,400 |
| A3 = | 8 × | 360 = | 2,880 |
| B3 = | 14 × | 20 = | 280 |
| A4 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,385,560 | |||
Deducting from this number all the Calendar Rounds possible, 73 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), to the remainder, the terminal day reached will be 11 Ahau 3 Pop. Therefore the Initial-series numbers 9.12.8.14.1, 9.12.8.14.2, and 9.12.8.14.3 will lead to the three days immediately following 9.12.8.14.0 11 Ahau 3 Pop. Therefore our four possible terminal dates will be:
| 9.12.8.14.0 | 11 Ahau | 3 Pop |
| 9.12.8.14.1 | 12 Imix | 4 Pop ← |
| 9.12.8.14.2 | 13 Ik | 5 Pop |
| 9.12.8.14.3 | 1 Akbal | 6 Pop |
Now let us look for one of these four terminal dates in the text. The day reached by an Initial Series is almost invariably recorded immediately after the last period glyph; therefore, if this inscription is regular, the day glyph should be B4. This glyph probably has the coefficient 12 (2 bars and 2 numerical dots), the oblong element between probably being ornamental only. This number must be either 11 or 12, since if it were 13 the 3 dots would all be of the same size, which is not the case. An inspection of the coefficient in B4 eliminates from consideration, therefore, the last two of the above four possible terminal dates, and reduces the possible values for the kin coefficient in A4 to 0 or 1. Comparing the glyph in B4 with the day signs in figure 16, the form here recorded will be found to be identical with the sign for Imix in figure 16, a. This eliminates the first terminal date above and leaves the second, the day part of which we have just seen appears in B4. This further proves that the kin coefficient in A4 is 1. The final confirmation of this identification will come from the month glyph, which must be 4 Pop if we have correctly identified the day as 12 Imix. If, on the other hand, the day were 11 Ahau, the month glyph would be 3 Pop. Passing over A5 B5, A6 B6, C1 D1, and C2, we, reach in D2a the closing glyph of the Supplementary Series, here showing the coefficient 9. Compare this form with figure 65. The month glyph, therefore, should appear in D2b. The coefficient of this glyph is very clearly 4, thus confirming our identification of B4 as 12 Imix. (See Table VII.) And finally, the month glyph itself is Pop. Compare D2b with figure 19, a. The whole Initial Series in plate 9, B, therefore reads 9.12.8.14.1 12 Imix 4 Pop.
In plate 10, is figured the Initial Series from Stela 3 at Tikal.[38] The introducing glyph, though somewhat effaced, may still be recognized in A1. The Initial-series number follows in B1-B3. The head-variant period glyphs are too badly weathered to show the determining characteristic in each case, except the uinal head in A3, the mouth curl of which appears clearly, and their identification rests on their relative positions with reference to the introducing glyph. The reliability of this basis of identification for the period glyphs of Initial Series has been thoroughly tested in the texts already presented and is further confirmed in this very inscription by the uinal head. Even if the large mouth curl of the head in A3 had not proved that the uinal was recorded here, we should have assumed this to be the case because this glyph, A3, is the fourth from the introducing glyph. The presence of the mouth curl therefore confirms the identification based on position. The student will have no difficulty in reading the number recorded in B1-B3 as 9.2.13.0.0.
Reducing this number by means of Table XIII to units of the first order, we obtain:
| B1 = | 9 × | 144,000 = | 1,296,000 |
| A2 = | 2 × | 7,200 = | 14,400 |
| B2 = | 13 × | 360 = | 4,680 |
| A3 = | 0 × | 20 = | 0 |
| B3 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,315,080 | |||
Deducting all the Calendar Rounds possible from this number, 69 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 4 Ahau 13 Kayab. It remains to find this date in the text. The glyph in A4, the proper position for the day glyph, is somewhat effaced, though the profile of the human head may yet be traced, thus enabling us to identify this form as the day sign Ahau. Compare figure 16, h', i'. The coefficient of A4 is very clearly 4 dots, that is, 4, and consequently this glyph agrees with the day as determined by calculation, 4 Ahau. Passing over B4, A5, B5, and A6, we reach in B6 the closing glyph of the Supplementary Series, here recorded with a coefficient of 9. Compare B6 with figure 65. The month glyph follows in A7 with the coefficient 13. Comparing this latter glyph with the month signs in figure 19, it is evident that the month Kayab (fig. 19, d'-f') is recorded in A7, which reads, therefore, 13 Kayab. Hence the whole text records the Initial Series 9.2.13.0.0 4 Ahau 13 Kayab.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 10

GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF BAR AND DOT NUMERALS AND HEAD-VARIANT PERIOD GLYPHS—STELA 3, TIKAL
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 11

GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF BAR AND DOT NUMERALS AND HEAD-VARIANT PERIOD GLYPHS—STELA A (EAST SIDE), QUIRIGUA
This Initial Series is extremely important, because it records the earliest contemporaneous[39] date yet found on a monument[40] in the Maya territory.
In plate 11 is figured the Initial Series from the east side of Stela A at Quirigua.[41] The introducing glyph appears in A1-B2 and the Initial-series number in A3-A5. The student will have little difficulty in picking out the clasped hand in A3, the oval in the top of the head in B3, the fleshless lower jaw in A4, the mouth curl in B4, as the essential characteristic of the cycle, katun, tun, and uinal heads, respectively. The kin head in A5 is the banded-headdress variant (compare fig. 34, i, j), and this completes the number, which is 9.17.5.0.0. Reducing this by means of Table XIII to units of the first order, we have:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3 = | 17 × | 7,200 = | 122,400 |
| A4 = | 5 × | 360 = | 4,680 |
| B4 = | 0 × | 20 = | 1,800 |
| A5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,420,200 | |||
Deducting from this number all the Calendar Rounds possible, 73 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal day reached will be found to be 6 Ahau 13 Kayab.
In B5 the profile variant of the day sign, Ahau, is clearly recorded (fig. 16, h', i'), and to it is attached a head-variant numeral. Comparing this with the head-variant numerals in figures 51-53, the student will have little difficulty in identifying it as the head for 6 (see fig. 51, t-v). Note the so-called "hatchet eye" in A5, which is the determining characteristic of the head for 6 (see p. 99). Passing over A6 B6, A7 B7, A8 B8, we reach in A9 the closing glyph of the Supplementary Series, here showing the head-variant coefficient 10 (see fig. 52, m-r). In B9, the next glyph, is recorded the month 13 Kayab (see fig. 19, d'-f'). The whole Initial Series therefore reads 9.17.5.0.0 6 Ahau 13 Kayab.
All the Initial Series heretofore presented have had normal-form numerals with the exception of an incidental head-variant number here and there. By this time the student should have become thoroughly familiar with the use of bar and dot numerals in the inscriptions and should be ready for the presentation of texts showing head-variant numerals, a more difficult group of glyphs to identify.
In plate 12, A, is figured the Initial Series on the tablet from the Temple of the Foliated Cross at Palenque.[42] The introducing glyph appears in A1 B2, and is followed by the Initial-series number in A3-B7. The student will have little difficulty in identifying the heads in B3, B4, B5, B6, and B7 as the head variants for the cycle, katun, tun, uinal, and kin, respectively. The head in A3 prefixed to the cycle glyph in B3 has for its determining characteristic the forehead ornament composed of more than one part (here, of two parts). As explained on page 97, this is the essential element of the head for 1. Compare A3 with figure 51, a-e, and the two glyphs will be found to be identical. We may conclude, therefore, that in place of the usual 9 cycles heretofore encountered in Initial Series, we have recorded in A3-B3 1 cycle.[43] The katun coefficient in A4 resembles closely the cycle coefficient except that its forehead ornament is composed of but a single part, a large curl. As explained on page 97, the heads for 1 and 8 are very similar, and are to be distinguished from each other only by their forehead ornaments, the former having a forehead ornament composed of more than one part, as in A3, and the latter a forehead ornament composed of but one part, as here in A4. This head, moreover, is very similar to the head for 8 in figure 52, a-f; indeed, the only difference is that the former has a fleshless lower jaw. This is the essential element of the head for 10 (see p. 100); when applied to the head for any other numeral it increases the value of the resulting head by 10. Therefore we have recorded in A4 B4, 18 (8 + 10) katuns. The tun coefficient in A5 has for its determining characteristic the tun headdress, which, as explained on page 99, is the essential element of the head for 5 (see fig. 51, n-s). Therefore A5 represents 5, and A5 B5, 5 tuns. The uinal coefficient in A6 has for its essential elements the large bulging eye, square irid, and snaglike front tooth. As stated on page 98, these characterize the head for 4, examples of which are given in figure 51, j-m. Consequently, A6 B6 records 4 uinals. The kin coefficient in A7 is quite clearly 0. The student will readily recognize the clasped hand, which is the determining characteristic of the 0 head (see p. 101 and fig. 53, s-w). The number recorded in A3-B7 is, therefore, 1.18.5.4.0. Reducing this number to units of the 1st order by means of Table XIII, we obtain:
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 12

GLYPHS REPRESENTING INITIAL SERIES, SHOWING USE OF HEAD-VARIANT NUMERALS AND PERIOD GLYPHS
| A3B3 = | 1 × | 144,000 = | 144,000 |
| A4B4 = | 18 × | 7,200 = | 129,600 |
| A5B5 = | 5 × | 360 = | 1,800 |
| A6B6 = | 4 × | 20 = | 80 |
| A7B7 = | 0 × | 1 = | 0 |
| ———— | |||
| 275,480 | |||
Deducting from this number all the Calendar Rounds possible, 14 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal date reached will be 1 Ahau 13 Mac. Of this date, the day part, 1 Ahau, is recorded very clearly in A8 B8. Compare the head in A8 with the head in A3, which, we have seen, stood for 1 and also with figure 51, a-e, and the head in B8 with figure 16, h', i', the profile head for the day sign Ahau. This text is irregular in that the month glyph follows immediately the day glyph, i.e., in A9. The glyph in A9 has a coefficient 13, which agrees with the month coefficient determined by calculation, and a comparison of B9 with the forms for the months in figure 19 shows that the month Mac (fig. 19, w, x) is here recorded. The whole Initial Series therefore reads 1.18.5.4.0 1 Ahau 13 Mac.
In plate 12, B, is figured the Initial Series on the tablet from the Temple of the Sun at Palenque.[44] The introducing glyph appears in A1-B2 and is followed by the Initial-series number in A3-B7. The student will have no difficulty in identifying the period glyphs in B3, B4, B5, B6, and B7; and the cycle, katun, and tun coefficients in A3, A4, and A5, respectively, will be found to be exactly like the corresponding coefficients in the preceding Initial Series (pl. 12, A, A3, A4, A5), which, as we have seen, record the numbers 1, 18, and 5, respectively. The uinal coefficient in A6, however, presents a new form. Here the determining characteristic is the banded headdress, or fillet, which distinguishes the head for 3, as explained on page 98 (see fig. 51 h, i). We have then in A6 B6 record of 3 uinals. The kin coefficient in A7 is very clearly 6. Note the "hatchet eye," which, as explained on page 99, is the essential element of this head numeral, and also compare it with figure 51, t-v. The number recorded in A3-B7 therefore is 1.18.5.3.6. Reducing this to units of the first order by means of Table XIII, we obtain:
| A3B3 = | 1 × | 144,000 = | 144,000 |
| A4B4 = | 18 × | 7,200 = | 129,600 |
| A5B5 = | 5 × | 360 = | 1,800 |
| A6B6 = | 3 × | 20 = | 60 |
| A7B7 = | 6 × | 1 = | 6 |
| ———— | |||
| 275,466 | |||
Deducting from this number all the Calendar Rounds possible, 14 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141), respectively, to the remainder, the terminal date reached will be 13 Cimi 19 Ceh. If this inscription is regular, the day part of the above date should follow in A8 B8, the former expressing the coefficient and the latter the day sign. Comparing A8 with the head numerals in figures 51-53, it will be found to be like the second variant for 13 in figure 52, x-b', the essential element of which seems to be the pendulous nose surmounted by a curl, the protruding mouth fang, and the large bulging eye. Comparing the glyph in B8 with the day signs in figure 16, it will be seen that the form here recorded is the day sign Cimi (fig. 16, h, i). Therefore A8 B8 expresses the day 13 Cimi. The month glyph is recorded very irregularly in this text, since it occurs neither immediately after the Supplementary Series or the day sign, but the second glyph after the day sign, in B9. A comparison of this form with figure 19, u-v, shows that the month Ceh is recorded here. The coefficient is 19. Why the glyph in A9 should stand between the day and its month glyph is unknown; this case constitutes one of the many unsolved problems in the study of the Maya glyphs. This whole Initial Series reads 1.18.5.3.6 13 Cimi 19 Ceh.
The student will note that this Initial Series records a date 14 days earlier than the preceding Initial Series (pl. 12, A). That two dates should be recorded which were within 14 days of each other, and yet were more than 3,000 years earlier than practically all other Maya dates, is a puzzling problem. These two Initial Series from the Temple of the Sun and that of the Foliated Cross at Palenque, together with a Secondary-series date from the Temple of the Cross in the same city, have been thoroughly reviewed by Mr. Bowditch (1906). The conclusions he reaches and the explanation he offers to account for the occurrence of three dates so remote as these are very reasonable, and, the writer believes, will be generally accepted by Maya students.

Fig. 69. Initial Series showing head-variant numerals and period glyphs: A, House C of the Palace Group at Palenque; B, Stela P at Copan.
In figure 69, A, is shown the Initial Series inscribed on the rises and treads of the stairway leading to House C in the Palace at Palenque.[45] The introducing glyph is recorded in A1, and the Initial-series number follows in B1-B3. The student will readily recognize the period glyphs in B1b, A2b, B2b, A3b, and B3b. The head expressing the cycle coefficient in B1a has for its essential element the dots centering around the corner of the mouth. As explained on page 100, this characterizes the head for 9 (see fig. 52, g-l, where variants for the 9 head are figured). In B1, therefore, we have recorded 9 cycles, the number almost always found in Initial Series as the cycle coefficient. The essential element of the katun coefficient in A2a is the forehead ornament composed of a single part. This denotes the head for 8 (see p. 100, and fig. 52, a-f; also compare A2a with the heads denoting 18 in the two preceding examples, pl. 12, A, A4, and pl. 12, B, A4, each of which shows the same forehead ornament). The tun coefficient in B2a is exactly like the cycle coefficient just above it in B1a; that is, 9, having the same dotting of the face near the corner of the mouth. The uinal coefficient in A3a is 13. Compare this head numeral with A8, plate 12, B, which also denotes 13, and also with figure 52, x-b'. The essential elements (see p. 101) are the large pendulous nose surmounted by a curl, the bulging eye, and the mouth fang, the last mentioned not appearing in this case. Since the kin coefficient in B3a is somewhat effaced, let us call it 0 for the present[46] and proceed to reduce our number 9.8.9.13.0 to units of the first order by means of Table XIII:
| B1 = | 9 × | 144,000 = | 1,296,000 |
| A2 = | 8 × | 7,200 = | 57,600 |
| B2 = | 9 × | 360 = | 3,240 |
| A3 = | 13 × | 20 = | 260 |
| B3 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,357,100 | |||
Deducting from this number all the Calendar Rounds possible, 71 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, we reach as the terminal date 8 Ahau 13 Pop. Now let us examine the text and see what is the terminal date actually recorded. In A4b the student will have little difficulty in recognizing the profile variant of the day sign Ahau (see fig. 16, h', i'). This at once gives us the missing value for the kin coefficient in B3, for the day Ahau can never be reached in an Initial Series if the kin coefficient is other than 0. Similarly, the day Imix can never be reached in Initial Series if the kin coefficient is other than 1, etc. Every one of the 20 possible kin coefficients, 0 to 19, has a corresponding day to which it will always lead, that is, Ahau to Cauac, respectively (see Table I). Thus, if the kin coefficient in an Initial-series number were 5, for example, the day sign of the resulting terminal date must be Chicchan, since Chicchan is the fifth name after Ahau in Table I. Thus the day sign in Initial-series terminal dates may be determined by inspection of the kin coefficient as well as by rule 2 (p. 140), though, as the student will see, both are applications of the same principle, that is, deducting all of the 20s possible and counting forward only the remainder. Returning to our text, we can now say without hesitation that our number is 9.8.9.13.0 and that the day sign in A4b is Ahau. The day coefficient in A4a is just like the katun coefficient in A2a, having the same determining characteristic, namely, the forehead ornament composed of one part. A comparison of this ornament with the ornament on the head for 8 in A2a will show that the two forms are identical. The bifurcate ornament surmounting the head in A4a is a part of the headdress, and as such should not be confused with the forehead ornament. The failure to recognize this point might cause the student to identify A4a as the head for 1, that is, having a forehead ornament composed of more than one part, instead of the head for 8. The month glyph, which follows in B4b, is unfortunately effaced, though its coefficient in B4a is clearly the head for 13. Compare B4a with the uinal coefficient in A3a and with the heads for 13 in figure 52, x-b'. As recorded, therefore, the terminal date reads 8 Ahau 13 ?, thus agreeing in every particular so far as it goes with the terminal date reached by calculation, 8 Ahau 13 Pop. In all probability the effaced sign in B4b originally was the month Pop. The whole Initial Series therefore reads 9.8.9.13.0 8 Ahau 13 Pop.
In figure 69, B, is shown the Initial Series from Stela P at Copan.[47] The introducing glyph appears in A1-B2 and is followed by the Initial-series number in A3-B4. The student will readily identify A3, B3, and A4 as 9 cycles, 9 katuns, and 10 tuns, respectively. Note the beard on the head representing the number 9 in both A3a and B3a. As explained on page 100, this characteristic of the head for 9 is not always present (see fig. 52, g-i). The uinal and kin glyphs have been crowded together into one glyph-block, B4, the uinal appearing in B4a and the kin in B4b. Both their coefficients are 0, which is expressed in each case by the form shown in figure 47. The whole number recorded is 9.9.10.0.0; reducing this to units of the first order by means of Table XIII, we obtain:
| A3 = | 9 × | 144,000 = | 1,296,000 |
| B3 = | 9 × | 7,200 = | 64,800 |
| A4 = | 10 × | 360 = | 3,600 |
| B4a = | 0 × | 20 = | 0 |
| B4b = | 0 × | 1 = | 0 |
| ———— | |||
| 1,364,400 | |||
Deducting from this number all of the Calendar Rounds possible, 71 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 2 Ahau 13 Pop. In A5a the day 2 Ahau is very clearly recorded, the day sign being expressed by the profile variant and the 2 by two dots (incorrectly shown as one dot in the accompanying drawing).[48] Passing over A5b, B5, and A6 we reach in B6a the closing glyph of the Supplementary Series, and in the following glyph, B6b, the month part of this terminal date. The coefficient is 13, and comparing the sign itself with the month signs in figure 19, it will be seen that the form in a (Pop) is the month recorded here. The whole Initial Series therefore reads 9.9.10.0.0 2 Ahau 13 Pop.

Fig. 70. Initial Series, showing head-variant numerals and period glyphs, from Zoömorph G at Quirigua.
In figure 70 is illustrated the Initial Series from Zoömorph G at Quirigua.[49] The introducing glyph appears in A1-B2 and is followed in C1-H1 by the Initial-series number. Glyphs C1 D1 record 9 cycles. The dots on the head for 9 in C1 are partially effaced. In C2 is the katun coefficient and in D2 the katun sign. The determining characteristic of the head for 7 appears in C2, namely, the scroll passing under the eye and projecting upward and in front of the forehead. See page 100 and figure 51, w. It would seem, then, at first sight that 7 katuns were recorded in C2 D2. That this was not the case, however, a closer examination of C2 will show. Although the lower part of this glyph is somewhat weathered, enough still remains to show that this head originally had a fleshless lower jaw, a character increasing its value by 10. Consequently, instead of having 7 katuns in C2 D2 we have 17 (7 + 10) katuns. Compare C2 with figure 53, j-m. In E1 F1, 15 tuns are recorded. The tun headdress in E1 gives the value 5 to the head there depicted (see fig. 51, n-s) and the fleshless lower jaw adds 10, making the value of E1 15. Compare figure 53, b-e, where examples of the head for 15 are given. Glyphs E2 and F2 represent 0 uinals and G1 H1 0 kins; note the clasped hand in E2 and G1, which denotes the 0 in each case. This whole number therefore reads 9.17.15.0.0. Reducing this to units of the first order by means of Table XIII, we have:
| C1 | D1 = | 9 × | 144,000 = | 1,296,000 |
| C2 | D2 = | 17 × | 7,200 = | 122,400 |
| E1 | F1 = | 15 × | 360 = | 5,400 |
| E2 | F2 = | 0 × | 20 = | 0 |
| G1 | H1 = | 0 × | 1 = | 0 |
| ———— | ||||
| 1,423,800 | ||||
Deducting from this number all the Calendar Rounds possible, 75 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), to the remainder, the terminal day reached will be 5 Ahau 3 Muan. The day is recorded in G2 H2. The day sign in H2 is quite clearly the grotesque head variant for Ahau in figure 16, j'-k'. The presence of the tun headdress in G2 indicates that the coefficient here recorded must have been either 5 or 15, depending on whether or not the lower part of the head originally had a fleshless lower jaw or not. In this particular case there is no room for doubt, since the numeral in G2 is a day coefficient, and day coefficients as stated in Chapter III, can never rise above 13. Consequently the number 15 can not be recorded in G2, and this form must stand for the number 5.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 13

OLDEST INITIAL SERIES AT COPAN—STELA 15
Passing over I1 J1, I2 J2, K1 Ll, K2 L2, we reach in M1 the closing glyph of the Supplementary Series, here shown with a coefficient of 10, the head having a fleshless lower jaw. The month sign follows in N1. The coefficient is 3 and by comparing the sign itself with the month glyphs in figure 19, it will be apparent that the sign for Muan in a' or b' is recorded here. The Initial Series of this monument therefore is 9.17.15.0.0 5 Ahau 3 Muan.
In closing the presentation of Initial-series texts which show both head-variant numerals and period glyphs, the writer has thought best to figure the Initial Series on Stela 15 at Copan, because it is not only the oldest Initial Series at Copan, but also the oldest one known in which head-variant numerals are used[50] (see pl. 13). The introducing glyph appears at A1-B2. There follows in A3 a number too much effaced to read, but which, on the basis of all our previous experience, we are justified in calling 9. Similarly B3 must be the head variant of the cycle sign. The numeral 4 is clearly recorded in A4. Note the square irid, protruding fang, and mouth curl. Compare A4 with figure 51, j-m. Although the glyph in B4 is too much effaced to read, we are justified in assuming that it is the head variant of the katun sign. The glyph in A5 is the numeral 10. Note the fleshless lower jaw and other characteristics of the death's-head. Again we are justified in assuming that B5 must be the head variant of the tun sign. The glyphs A6, B6 clearly record 0 uinals. Note the clasped hand denoting zero in A6, and the curling mouth fang of the uinal period glyph in B6. This latter glyph is the full-figure form of the uinal sign[51] (a frog). Compare B6 with figure 33, which shows the uinal sign on Stela D at Copan. The stela is broken off just below the uinal sign and its coefficient; and therefore the kin coefficient and sign, the day coefficient and sign, and the month coefficient and sign, are missing. Assembling the four periods present, we have 9.4.10.0.?. Calling the missing kin coefficient 0, and reducing this number to units of the first order by means of Table XIII, we have:
| A3 B3 = | 9 × | 144,000 = | 1,296,000 |
| A4 B4 = | 4 × | 7,200 = | 28,800 |
| A5 B5 = | 10 × | 360 = | 3,600 |
| A6 B6 = | 0 × | 20 = | 0 |
| 0 × | 1 = | 0 | |
| ———— | |||
| 1,328,400 | |||
Deducting from this number all the Calendar Rounds possible, 69 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 12 Ahau 8 Mol. This date is reached on the assumption that the missing kin coefficient was zero. This is a fairly safe assumption, since when the tun coefficient is either 0, 5, 10, or 15 (as here) and the uinal coefficient is 0 (as here), the kin coefficient is almost invariably zero. That is, the close of an even hotun in the Long Count is recorded.
While at Copan in May, 1912, the writer was shown a fragment of a stela which he was told was a part of this monument (Stela 15). This showed the top parts of two consecutive glyphs, the first of which very clearly had a coefficient of 12 and the one following of 8. The glyphs to which these coefficients belonged were missing, but the coincidence of the two numbers 12 (?) 8 (?) was so striking when taken into consideration with the fact that these were the day and month coefficients reached by calculation, that the writer was inclined to accept this fragment as the missing part of Stela 15 which showed the terminal date. This whole Initial Series therefore reads: 9.4.10.0.0 12 Ahau 8 Mol. It is chiefly interesting because it shows the earliest use of head-variant numerals known.
In the foregoing texts plate 12, A, B, figure 69, A, B, and figure 70, the head-variant numerals 0, 1, 3, 4, 5, 6, 8, 9, 10, 13, 14, 15, 17, and 18 have been given, and, excepting the forms for 2, 11, and 12, these include examples of all the head numerals.[52] No more texts specially illustrating this type of numeral will be presented, but when any of the head numerals not figured above (2, 7, 11, 12, 16, and 19) occur in future texts their presence will be noted.
Before taking up the consideration of unusual or irregular Initial Series the writer has thought best to figure one Initial Series the period glyphs and numerals of which are expressed by full-figure forms. As mentioned on page 68, such inscriptions are exceedingly rare, and such glyphs, moreover, are essentially the same as head-variant forms, since their determining characteristics are restricted to their head parts, which are exactly like the corresponding head-variant forms. This fact will greatly aid the student in identifying the full-figure glyphs in the following text.
In plate 14 is figured the Initial Series from Stela D at Copan.[53] The introducing glyph is recorded in A1. The variable central element in keeping with the other glyphs of the inscription appears here as a full figure, the lower part of which is concealed by the tun-sign.[54]
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 14

INITIAL SERIES ON STELA D, COPAN, SHOWING FULL-FIGURE NUMERAL GLYPHS AND PERIOD GLYPHS
The Initial-series number itself appears in B1-B3. The cycle sign is a grotesque bird, designated by Mr. Bowditch a parrot, an identification which the hooked beak and claws strongly suggest. The essential element of the cycle sign, however, the clasped hand, appears only in the head of this bird, where the student will readily find it. Indeed, the head of this full-figure form is nothing more nor less than a head-variant cycle glyph, and as such determines the meaning of the whole figure. Compare this head with figure 25, d-f, or with any of the other head-variant cycle forms figured in the preceding texts. This grotesque "cycle bird," perhaps the parrot, is bound to the back of an anthropomorphic figure, which we have every reason to suppose records the cycle coefficient. An examination of this figure will show that it has not only the dots on the lower part of the cheek, but also the beard, both of which are distinctive features of the head for 9. Compare this head with figure 52, g-l, or with any other head variants for the numeral 9 already figured. Bearing in mind that the heads only present the determining characteristics of full-figure glyphs, the student will easily identify B1 as recording 9 cycles.
The katun and its coefficient are represented in A2, the former by a grotesque bird, an eagle according to Mr. Bowditch, and the latter by another anthropomorphic figure. The period glyph shows no essential element recognizable as such, and its identification as the katun sign therefore rests on its position, immediately following the cycle sign. The head of the full figure, which represents the katun coefficient, shows the essential element of the head for 5, the tun headdress. It has also the fleshless lower jaw of the head for 10. The combination of these two elements in one head, as we have seen, indicates the numeral 15, and A2 therefore records 15 katuns. Compare the head of this anthropomorphic figure with figure 53, b-e.
The tun and its coefficient are represented in B2. The former again appears as a grotesque bird, though in this case of undetermined nature. Its head, however, very clearly shows the essential element of the head-variant tun sign, the fleshless lower jaw. Compare this form with figure 29, e-g, and the other head-variant tun signs already illustrated. The head of the anthropomorphic figure, which denotes the tun coefficient, is just like the head of the anthropomorphic figure in the preceding glyph (A2), except that in B2 the head has no fleshless lower jaw.
Since the head in A2 with the fleshless lower jaw and the tun headdress represents the numeral 15, the head in B2 without the former but with the latter represents the numeral 5. Compare the head of the anthropomorphic figure in B2 with figure 51, n-s. It is clear, therefore, that 5 tuns are recorded in B2.
The uinal and its coefficient in A3 are equally clear. The period glyph here appears as a frog (Maya, uo), which, as we have seen elsewhere, may have been chosen to represent the 20-day period because of the similarity of its name, uo, to the name of this period, u, or uinal. The head of the anthropomorphic figure which clasps the frog's foreleg is the head variant for 0. Note the clasped hand across the lower part of the face, and compare this form with figure 53, s-w. The whole glyph, therefore, stands for 0 uinals.
In B3 are recorded the kin and its coefficient. The period glyph here is represented by an anthropomorphic figure with a grotesque head. Its identity, as representing the kins of this number, is better established from its position in the number than from its appearance, which is somewhat irregular. The kin coefficient is just like the uinal coefficient—an anthropomorphic figure the head of which has the clasped hand as its determining characteristic. Therefore B3 records 0 kins.
The whole number expressed by B1-B3 is 9.15.5.0.0; reducing this by means of Table XIII to units of the first order, we have:
| B1 = | 9 × | 144,000 = | 1,296,000 |
| A2 = | 15 × | 7,200 = | 108,000 |
| B2 = | 5 × | 360 = | 1,800 |
| A3 = | 0 × | 20 = | 0 |
| B3 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,405,800 | |||
Deducting from this number all the Calendar Rounds possible, 74 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141 respectively), to the remainder, the terminal date reached will be 10 Ahau 8 Chen.
The day part of this terminal date is recorded in A4. The day sign Ahau is represented as an anthropomorphic figure, crouching within the customary day-sign cartouche. The head of this figure is the familiar profile variant for the day sign Ahau, seen in figure 16, h', i'. This cartouche is clasped by the left arm of another anthropomorphic figure, the day coefficient, the head of which is the skull, denoting the numeral 10. Note the fleshless lower jaw of this head and compare it with the same element in figure 52, m-r. This glyph A4 records, therefore, the day reached by the Initial Series, 10 Ahau.
The position of the month glyph in this text is most unusual. Passing over B4, the first glyph of the Supplementary Series, the month glyph follows it immediately in A5. The month coefficient appears again as an anthropomorphic figure, the head of which has for its determining characteristic the forehead ornament composed of one part, denoting the numeral 8. Compare this head with the heads for 8, in figure 52, a-f. The month sign itself appears as a large grotesque head, the details of which present the essential elements of the month here recorded—Chen. Compare with figure 19, o, p.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 15

INITIAL SERIES ON STELA J, COPAN

The student will note that this Initial Series records a date just 5 tuns later than the Initial Series on Stela B at Copan (pl. 7, A). According to the writer's opinion, therefore, Stelæ B and D marked two successive hotuns at this city.
We come now to the consideration of Initial Series which are either unusual or irregular in some respect, examples of which it is necessary to give in order to familiarize the student with all kinds of texts.
The Initial Series in plate 15, A,[55] is figured because of the very unusual order followed by its glyphs. The sequence in which these succeed each other is given in B of that plate. The scheme followed seems to have been that of a mat pattern. The introducing glyph appears in position 0 (pl. 15, B), and the student will readily recognize it in the same position in A of the same plate. The Initial Series number follows in 1, 2, 3, 4, and 5 (pl. 15, B). Referring to these corresponding positions in A, we find that 9 cycles are recorded in 1, and 13 katuns in 2. At this point the diagonal glyph- band passes under another band, emerging at 3, where the tun sign with a coefficient of 10 is recorded. Here the band turns again and, crossing backward diagonally, shows 0 uinals in 4. At this point the band passes under three diagonals running in the opposite direction, emerging at position 5, the glyph in which are recorded 0 kins.
This number 9.13.10.0.0 reduces by means of Table XIII to units of the first order, as follows:
| 1 = | 9 × | 144,000 = | 1,296,000 |
| 2 = | 13 × | 7,200 = | 93,600 |
| 3 = | 10 × | 360 = | 3,600 |
| 4 = | 0 × | 20 = | 0 |
| 5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,393,200 | |||
Deducting from this number all the Calendar Rounds possible, 73 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 7 Ahau 3 Cumhu. Referring again to plate 15, B, for the sequence of the glyphs in this text, it is clear that the day of this terminal date should be recorded in 6, immediately after the kins of the Initial-series number in 6. It will be seen, however, in plate 15, A, that glyph 6 is effaced, and consequently the day is missing. Passing over 7, 8, 9, 10, and 11, in A and B of the plate named, we reach in the lower half of 12 the closing glyph of the Supplementary Series here shown with a coefficient of 10. Compare this form with figure 65. The month glyph, therefore, should follow in the upper half of 13.[56] This glyph is very clearly the form for the month Cumhu (see fig. 19, g', h'), and it seems to have attached to it the bar and dot coefficient 8. A comparison of this with the month coefficient 3, determined above by calculation, shows that the two do not agree, and that the month coefficient as recorded exceeds the month coefficient determined by calculation, by 5, or in Maya notation, 1 bar. Since the Initial-series number is very clearly 9.13.10.0.0, and since this number leads to the terminal date 7 Ahau 3 Cumhu, it would seem that the ancient scribes had made an error in this text, recording 1 bar and 3 dots instead of 3 dots alone. The writer is inclined to believe, however, that the bar here is only ornamental and has no numerical value whatsoever, having been inserted solely to balance this glyph. If it had been omitted, the month sign would have had to be greatly elongated and its proportions distorted in order to fill completely the space available. According to the writer's interpretation, this Initial Series reads 9.13.10.0.0 7 Ahau 3 Cumhu.
The opposite face of the above-mentioned monument presents the same interlacing scheme, though in this case the glyph bands cross at right angles to each other instead of diagonally.
The only other inscription in the whole Maya territory, so far as the writer knows, which at all parallels the curious interlacing pattern of the glyphs on the back of Stela J at Copan, just described, is Stela H at Quirigua, illustrated in figure 71.[57] The drawing of this inscription appears in a of this figure and the key to the sequence of the glyphs in b. The introducing glyph occupies position 1 and is followed by the Initial Series in 2-6. The student will have little difficulty in identifying 2, 3, and 4 as 9 cycles, 16 katuns, and 0 tuns, respectively. The uinal and kin glyphs in 5 and 6, respectively, are so far effaced that in order to determine the values of their coefficients we shall have to rely to a large extent on other inscriptions here at Quirigua. For example, every monument at Quirigua which presents an Initial Series marks the close of some particular hotun in the Long Count; consequently, all the Initial Series at Quirigua which record these Katun endings have 0 for their uinal and kin coefficients.[58] This absolute uniformity in regard to the uinal and kin coefficients in all the other Initial Series at Quirigua justifies the assumption that in the text here under discussion 0 uinals and 0 kins were originally recorded in glyphs 5 and 6, respectively. Furthermore, an inspection of the coefficients of these two glyphs in figure 71, a, shows that both of them are of the same general size and shape as the tun coefficient in 4, which, as we have seen, is very clearly 0. It is more than probable that the uinal and kin coefficients in this text were originally 0, like the tun coefficient, and that through weathering they have been eroded down to their present shape. In figure 72, a, is shown the tun coefficient and beside it in b, the uinal or kin coefficient. The dotted parts in b are the lines which have disappeared through erosion, if this coefficient was originally 0. It seems more than likely from the foregoing that the uinal and kin coefficients in this number were originally 0, and proceeding on this assumption, we have recorded in glyphs 2-6, figure 71, a, the number 9.16.0.0.0.

Fig. 71. Initial Series on Stela H, Quirigua: a, Mat pattern of glyph sequence; b, key to sequence of glyphs in a.
Reducing this to units of the first order by means of Table XIII, we have:
| 5 = | 9 × | 144,000 = | 1,296,000 |
| 6 = | 16 × | 7,200 = | 115,200 |
| 7 = | 0 × | 360 = | 0 |
| 8 = | 0 × | 20 = | 0 |
| 9 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,411,200 | |||
Deducting from this number all the Calendar Rounds possible, 74 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date 2 Ahau 13 Tzec will be reached.
Fig. 72. The tun, uinal, and kin coefficients on Stela H, Quirigua: a, Tun coefficient; b, suggested restoration of the uinal and kin coefficients like the tun coefficient.
In spite of some weathering, the day part of the terminal date appears in glyph 7 immediately after the kin glyph in 6. The coefficient, though somewhat eroded, appears quite clearly as 2 (2 dots separated by an ornamental crescent). The day sign itself is the profile variant for Ahau shown in figure 16, h', i'. The agreement of the day recorded with the day determined by calculations based on the assumption that the kin and uinal coefficients are both 0, of itself tends to establish the accuracy of these assumptions. Passing over 8, 9, 10, 11, 12, 13, and 14, we reach in 15 the closing glyph of the Supplementary Series, and in 16 probably, the month glyph. This form, although badly eroded, presents no features either in the outline of its coefficient or in the sign itself which would prevent it representing the month part 13 Tzec. The coefficient is just wide enough for three vertical divisions (2 bars and 3 dots), and the month glyph itself is divided into two parts, a superfix comprising about one-third of the glyph and the main element the remaining two-thirds. Compare this form with the sign for Tzec in figure 19, g, h. Although this text is too much weathered to permit absolute certainty with reference to the reading of this Initial Series, the writer nevertheless believes that in all probability it records the date given above, namely, 9.16.0.0.0 2 Ahau 13 Tzec. If this is so, Stela H is the earliest hotun-marker at Quirigua.[59]
The student will have noticed from the foregoing texts, and it has also been stated several times, that the cycle coefficient is almost invariably 9. Indeed, the only two exceptions to this rule in the inscriptions already figured are the Initial Series from the Temples of the Foliated Cross and the Sun at Palenque (pl. 12, A and B, respectively), in which the cycle coefficient in each case was 1. As explained on page 179, footnote 1, these two Initial Series refer probably to mythological events, and the dates which they record were not contemporaneous with the erection of the temples on whose walls they are inscribed; and, finally, Cycle 9 was the first historic period of the Maya civilization, the epoch which witnessed the rise and fall of all the southern cities.
As explained on page 179, footnote 2, however, there are one or two Initial Series which can hardly be considered as referring to mythological events, even though the dates which they record fall in a cycle earlier than Cycle 9. It was stated, further, in the same place that these two Initial Series were not found inscribed on large monuments but on smaller antiquities, one of them being a small nephrite figure which has been designated the Tuxtla Statuette, and the other a nephrite plate, designated the Leyden Plate; and, finally, that the dates recorded on these two antiquities probably designated contemporaneous events in the historic period of the Maya civilization.
Fig. 73. The Initial Series on the Tuxtla Statuette, the oldest Initial Series known (in the early part of Cycle 8).

Fig. 74. The introducing glyph (?) of the Initial Series on the Tuxtla Statuette.
These two minor antiquities have several points in common. Both are made of the same material (nephrite) and both have their glyphs incised instead of carved. More important, however, than these similarities is the fact that the Initial Series recorded on each of them has for its cycle coefficient the numeral 8; in other words, both record dates which fell in the cycle immediately preceding that of the historic period, or Cycle 9. Finally, at least one of these two Initial Series (that on the Leyden Plate), if indeed not both, records a date so near the opening of the historic period, which we may assume occurred about 9.0.0.0.0 8 Ahau 13 Ceh in round numbers, that it may be considered as belonging to the historic period, and hence constitutes the earliest historical inscription from the Maya territory.
The Initial Series on the first of these minor antiquities, the Tuxtla Statuette, is shown in figure 73.[60] The student will note at the outset one very important difference between this Initial Series—if indeed it is one, which some have doubted—and those already presented. No period glyphs appear in the present example, and consequently the Initial-series number is expressed by the second method (p. 129), that is, numeration by position, as in the codices. See the discussion of Initial Series in the codices in Chapter VI (pp. 266-273), and plates 31 and 32. This at once distinguishes the Initial Series on the Tuxtla Statuette from every other Initial Series in the inscriptions now known. The number is preceded by a character which bears some general resemblance to the usual Initial-series introducing glyph. See figure 74. The most striking point of similarity is the trinal superfix, which is present in both signs. The student will have little difficulty in reading the number here recorded as 8 cycles, 6 katuns, 2 tuns, 4 uinals, and 17 kins, that is, 8.6.2.4.17; reducing this to units of the first order by means of Table XIII, we have:
| 8 × | 144,000 = | 1,152,000 |
| 6 × | 7,200 = | 43,200 |
| 2 × | 360 = | 720 |
| 4 × | 20 = | 80 |
| 17 × | 1 = | 17 |
| ———— | ||
| 1,196,017 | ||
Solving this Initial-series number for its terminal date, it will be found to be 8 Caban 0 Kankin. Returning once more to our text (see fig. 73), we find the day coefficient above reached, 8, is recorded just below the 17 kins and appears to be attached to some character the details of which are, unfortunately, effaced. The month coefficient 0 and the month sign Kankin do not appear in the accompanying text, at least in recognizable form. This Initial Series would seem to be, therefore, 8.6.2.4.17 8 Caban 0 Kankin, of which the day sign, month coefficient, and month sign are effaced or unrecognizable. In spite of its unusual form and the absence of the day sign, and the month coefficient and sign the writer is inclined to accept the above date as a contemporaneous Initial Series.[61]

Fig. 75. Drawings of the Initial Series: A, On the Leyden Plate. This records a Cycle-8 date and next to the Tuxtla Statuette Initial Series, is the earliest known. B, On a lintel from the Temple of the Initial Series, Chichen Itza. This records a Cycle-10 date, and is one of the latest Initial Series known.
The other Initial Series showing a cycle coefficient 8 is on the Leyden Plate, a drawing of which is reproduced in figure 75, A. This Initial Series is far more satisfactory than the one just described, and its authenticity, generally speaking, is unquestioned. The student will easily identify A1-B2 as an Initial-series introducing glyph, even though the pair of comblike appendages flanking the central element and the tun tripod are both wanting. Compare this form with figure 24. The Initial-series number, expressed by normal-form numerals and head-variant period glyphs, follows in A3-A7. The former are all very clear, and the number may be read from them in spite of certain irregularities in the corresponding period glyphs. For example, the katun head in A4 has the clasped hand, which is the distinguishing characteristic of the cycle head, and as such should have appeared in the head in A3. Neither the tun head in A5 nor the kin head in A7 shows an essential element heretofore found distinguishing these particular period glyphs. Indeed, the only period glyph of the five showing the usual essential element is the uinal head in A6, where the large mouth curl appears very clearly. However, the number recorded here may be read as 8.14.3.1.12 from the sequence of the coefficients—that is, their position with reference to the introducing glyph—a reading, moreover, which is confirmed by the only known period glyph, the uinal sign, standing in the fourth position after the introducing glyph.
Reducing this number to units of the first order by means of Table XIII, we have:
| A3 = | 8 × | 144,000 = | 1,152,000 |
| A4 = | 14 × | 7,200 = | 100,800 |
| A5 = | 3 × | 360 = | 1,080 |
| A6 = | 1 × | 20 = | 20 |
| A7 = | 12 × | 1 = | 12 |
| ———— | |||
| 1,253,912 | |||
Deducting from this number all the Calendar Rounds possible, 66 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 1 Eb 0 Yaxkin. The day part of this date is very clearly recorded in A8, the coefficient 1 being expressed by one dot, and the day sign itself having the hook surrounded by dots, and the prominent teeth, both of which are characteristic of the grotesque head which denotes the day Eb. See figure 16, s-u.
The month glyph appears in A9a, the lower half of which unmistakably records the month Yaxkin. (See fig. 19, k, l.) Note the yax and kin elements in each. The only difficulty here seems to be the fact that a bar (5) is attached to this glyph. The writer believes, however, that the unexplained element (
The fact that there are some few irregularities in this text confirms rather than invalidates the antiquity which has been ascribed to it by the writer. Dating from the period when the Maya were just emerging from savagery to the arts and practices of a semicivilized state, it is not at all surprising that this inscription should reflect the crudities and uncertainties of its time. Indeed, it is quite possible that at the very early period from which it probably dates (8.14.3.1.12 1 Eb 0 Yaxkin) the period glyphs had not yet become sufficiently conventionalized to show individual peculiarities, and their identity may have been determined solely by their position with reference to the introducing glyph, as seemingly is the case in some of the period glyphs of this text.
The Initial Series on the Leyden Plate precedes the Initial Series on Stela 3 at Tikal, the earliest contemporaneous date from the monuments, by more than 160 years, and with the possible exception of the Tuxtla Statuette above described, probably records the earliest date of Maya history. It should be noted here that Cycle-8 Initial Series are occasionally found in the Dresden Codex, though none are quite so early as the Initial Series from the Tuxtla Statuette.
Passing over the Initial Series whose cycle coefficient is 9, many of which have already been described, we come next to the consideration of Initial Series whose cycle coefficient is 10, a very limited number indeed. As explained in Chapter I, the southern cities did not long survive the opening of Cycle 10, and since Initial-series dating did not prevail extensively in the later cities of the north, Initial Series showing 10 cycles are very unusual.
In figure 75, B, is shown the Initial Series from the Temple of the Initial Series at Chichen Itza, the great metropolis of northern Yucatan. This inscription is not found on a stela but on the under side of a lintel over a doorway leading into a small and comparatively insignificant temple. The introducing glyph appears in A1-B2 and is followed by the Initial-series number in A3-A5. The student will have little difficulty in deciphering all of the coefficients except that belonging to the kin in A5, which is a head-variant numeral, and the whole number will be found to read 10.2.9.1.?. The coefficient of the day of the terminal date is very clearly 9 (see B5) and the month part, 7 Zac (see A6). We may now read this Initial Series as 10.2.9.1.? 9? 7 Zac; in other words, the kin coefficient and the day sign are still indeterminate. First substituting 0 as the missing value of the kin coefficient, the terminal date reached will be 10.2.9.1.0 13 Ahau 18 Yax. But according to Table XV, position 18 Yax is just 9 days earlier than position 7 Zac, the month part recorded in A6. Consequently, in order to reach 7 Zac from 10.2.9.1.0 13 Ahau 18 Yax, 9 more days are necessary. Counting these forward from 10.2.9.1.0 13 Ahau 18 Yax, the date reached will be 10.2.9.1.9 9 Muluc 7 Zac, which is the date recorded on this lintel. Compare the day sign with figure 16, m, n, and the month sign with figure 19, s, t.

Fig. 76. The Cycle-10 Initial Series from Quen Santo (from drawings): A, Stela 1; B, Stela 2. There is less than a year's difference in time between the Chichen Itza Initial Series and the Initial Series in B.
Two other Initial Series whose cycle coefficient is 10 yet remain to be considered, namely, Stelæ 1 and 2 at Quen Santo.[62] The first of these is shown in figure 76, A, but unfortunately only a fragment of this monument has been recovered. In A1-B2 appears a perfectly regular form of the introducing glyph (see fig. 24), and this is followed in A3-B4 by the Initial-series number itself, with the exception of the kin, the glyph representing which has been broken off. The student will readily identify A3 as 10 cycles, noting the clasped hand on the head-variant period glyph, and B3 as 2 katuns. The glyph in A4 has very clearly the coefficient 5, and even though it does not seem to have the fleshless lower jaw of the tun head, from its position alone—after the unmistakable katun sign in B3 we are perfectly justified in assuming that 5 tuns are recorded here. Both the coefficient and the glyph in B4 are unfamiliar. However, as the former must be one of the numerals 0 to 19, inclusive, since it is not one of the numerals 1 to 19, inclusive, it is clear that it must be a new form for 0. The sign to which it is attached bears no resemblance to either the normal form for the uinal or the head variant; but since it occupies the 4th position after the introducing glyph, B4, we are justified in assuming that 0 uinals are recorded here. Beyond this we can not proceed with certainty, though the values for the missing parts suggested below are probably those recorded on the lost fragments of the monument. As recorded in A3-B4 this number reads 10.2.5.0.?. Now, if we assume that the missing term is filled with 0, we shall have recorded the end of an even hotun in the Long Count, and this monument becomes a regular hotun-marker. That this monument was a hotun-marker is corroborated by the fact that Stela 2 from Quen Santo very clearly records the close of the hotun next after 10.2.5.0.0, which the writer believes this monument marks. For this reason it seems probable that the glyph which stood in A5 recorded 0 kins.
Reducing this number to units of the first order by means of Table XIII, we obtain:
| A3 | = | 10 × | 144,000 = | 1,440,000 |
| B3 | = | 2 × | 7,200 = | 14,400 |
| A4 | = | 5 × | 360 = | 1,800 |
| B4 | = | 0 × | 20 = | 0 |
| A5[63] | = | 0 × | 1 = | 0 |
| ———— | ||||
| 1,456,200 | ||||
Deducting from this number all the Calendar Rounds possible, 76 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 9 Ahau 18 Yax, and the whole Initial Series originally recorded on this monument was probably 10.2.5.0.0 9 Ahau 18 Yax.
In figure 76, B, is shown Stela 2 from Quen Santo. The workmanship on this monument is somewhat better than on Stela 1 and, moreover, its Initial Series is complete. The introducing glyph appears in A1-B2 and is followed by the Initial-series number in A3-A5. Again, 10 cycles are very clearly recorded in A3, the clasped hand of the cycle head still appearing in spite of the weathering of this glyph. The katun sign in B3 is almost entirely effaced, though sufficient traces of its coefficient remain to enable us to identify it as 2. Note the position of the uneffaced dot with reference to the horizontal axis of the glyph. Another dot the same distance above the axis would come as near the upper left-hand corner of the glyph-block as the uneffaced dot does to the lower left-hand corner. Moreover, if 3 had been recorded here the uneffaced dot would have been nearer the bottom. It is clear that 1 and 4 are quite out of the question and that 2 remains the only possible value of the numeral here. We are justified in assuming that the effaced period glyph was the katun sign. In A4 10 tuns are very clearly recorded; note the fleshless lower jaw of the tun head. The uinal head with its characteristic mouth curl appears in B4. The coefficient of this latter glyph is identical with the uinal coefficient in the preceding text (see fig. 76, A) in B4, which we there identified as a form for 0. Therefore we must make the same identification here, and B4 then becomes 0 uinals. From its position, if not from its appearance, we are justified in designating the glyph in A5 the head for the kin period; since the coefficient attached to this head is the same as the one in the preceding glyph (B4), we may therefore conclude that 0 kins are recorded here. The whole number expressed in A3-A5 is therefore 10.2.10.0.0. Reducing this to units of the first order by means of Table XIII, we have:
| A3 = | 10 × | 144,000 = | 1,440,000 |
| B3 = | 2 × | 7,200 = | 14,400 |
| A4 = | 10 × | 360 = | 3,600 |
| B4 = | 0 × | 20 = | 0 |
| A5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,458,000 | |||
Deducting from this number all the Calendar Rounds possible, 76 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 2 Ahau 13 Chen. Although the day sign in B5 is effaced, the coefficient 2 appears quite clearly. The month glyph is recorded in A6. The student will have little difficulty in restoring the coefficient as 13, and the month glyph is certainly either Chen, Yax, Zac, or Ceh (compare fig. 19, o and p, q and r, s and t, and u and v, respectively). Moreover, since the month coefficient is 13, the day sign in B5 can have been only Chicchan, Oc, Men, or Ahau (see Table VII); since the kin coefficient in A5 is 0, the effaced day sign must have been Ahau. Therefore the Initial Series on Stela 2 at Quen Santo reads 10.2.10.0.0 2 Ahau 13 Chen and marked the hotun immediately following the hotun commemorated by Stela 1 at the same site.
The student will note also that the date on Stela 2 at Quen Santo is less than a year later than the date recorded by the Initial Series on the Temple lintel from Chichen Itza (see fig. 75, B). And a glance at the map in plate 1 will show, further, that Chichen Itza and Quen Santo are separated from each other by almost the entire length (north and south) of the Maya territory, the former being in the extreme northern part of Yucatan and the latter considerably to the south of the central Maya cities. The presence of two monuments so close together chronologically and yet so far apart geographically is difficult to explain. Moreover, the problem is further complicated by the fact that not one of the many cities lying between has yielded thus far a date as late as either of these.[64] The most logical explanation of this interesting phenomenon seems to be that while the main body of the Maya moved northward into Yucatan after the collapse of the southern cities others retreated southward into the highlands of Guatemala; that while the northern emigrants were colonizing Yucatan the southern branch was laying the foundation of the civilization which was to flourish later under the name of the Quiche and other allied peoples; and finally, that as Chichen Itza was a later northern city, so Quen Santo was a later southern site, the two being at one period of their existence at least approximately contemporaneous, as these two Initial Series show.
It should be noted in this connection that Cycle-10 Initial Series are occasionally recorded in the Dresden Codex, though the dates in these cases are all later than those recorded on the Chichen Itza lintel and the Quen Santo stelæ. Before closing the presentation of Initial-series texts it is first necessary to discuss two very unusual and highly irregular examples of this method of dating, namely, the Initial Series from the east side of Stela C at Quirigua and the Initial Series from the tablet in the Temple of the Cross at Palenque. The dates recorded in these two texts, so far as known,[65] are the only ones which are not counted from the starting point of Maya chronology, the date 4 Ahau 8 Cumhu.
In figure 77, A, is shown the Initial Series on the east side of Stela C at Quirigua.[66] The introducing glyph appears in A1-B2, and is followed by the Initial-series number in A3-A5. The student will easily read this as 13.0.0.0.0. Reducing this number to units of the first order by means of Table XIII, we have:
| A3 = | 13 × | 144,000 = | 1,872,000 |
| B3 = | 0 × | 7,200 = | 0 |
| A4 = | 0 × | 360 = | 0 |
| B4 = | 0 × | 20 = | 0 |
| A5 = | 0 × | 1 = | 0 |
| ———— | |||
| 1,872,000 | |||
Deducting from this number all the Calendar Rounds possible, 98[67] (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141), respectively, to the remainder, the terminal date reached should be, under ordinary circumstances, 4 Ahau 3 Kankin. An inspection of our text, however, will show that the terminal date recorded in B5-A6 is unmistakably 4 Ahau 8 Cumhu, and not 4 Ahau 3 Kankin. The month part in A6 is unusually clear, and there can be no doubt that it is 8 Cumhu. Compare A6 with figure 19, g', h'. If we have made no mistake in calculations, then it is evident that 13.0.0.0.0 counted forward from the starting point of Maya chronology, 4 Ahau 8 Cumhu, will not reach the terminal date recorded. Further, since the count in Initial Series has never been known to be backward,[68] we are forced to accept one of two conclusions: Either the starting point is not 4 Ahau 8 Cumhu, or there is some error in the original text. However, there is one way by means of which we can ascertain the date from which the number 13.0.0.0.0 is counted. The terminal date reached by the count is recorded very clearly as 4 Ahau 8 Cumhu. Now, if we reverse our operation and count the given number, 13.0.0.0.0, backward from the known terminal date, 4 Ahau 8 Cumhu, we reach the starting point from which the count proceeds.

Fig. 77. Initial Series which proceed from a date prior to 4 Ahau 8 Cumhu, the starting point of Maya chronology: A, Stela C (east side) at Quirigua; B, Temple of the Cross at Palenque.
Deducting from this number, as before, all the Calendar Rounds possible, 98 (see p. 203, footnote 3), and applying rules 1, 2, and 3 (pp. 139, 140, 141, respectively) to the remainder, remembering that in each operation the direction of the count is backward, not forward,—the starting point will be found to be 4 Ahau 8 Zotz. This is the first Initial Series yet encountered which has not proceeded from the date 4 Ahau 8 Cumhu, and until the new starting point here indicated can be substantiated it will be well to accept the correctness of this text only with a reservation. The most we can say at present is that if the number recorded in A3-A5, 13.0.0.0.0, be counted forward from 4 Ahau 8 Zotz as a starting point, the terminal date reached by calculation will agree with the terminal date as recorded in B5-A6, 4 Ahau 8 Cumhu.
Let us next examine the Initial Series on the tablet from the Temple of the Cross at Palenque, which is shown in figure 77, B.[69] The introducing glyph appears in A1-B2, and is followed by the Initial-series number in A3-B7. The period glyphs in B3, B4, B5, B6, and B7 are all expressed by their corresponding normal forms, which will be readily recognized. Passing over the cycle coefficient in A3 for the present, it is clear that the katun coefficient in A4 is 19. Note the dots around the mouth, characteristic of the head for 9 (fig. 52, g-l), and the fleshless lower jaw, the essential element of the head for 10 (fig. 52, m-r). The combination of the two gives the head in A4 the value of 19. The tun coefficient in A5 is equally clear as 13. Note the banded headdress, characteristic of the head for 3 (fig. 51, h, i), and the fleshless lower jaw of the 10 head, the combination of the two giving the head for 13 (fig. 52, w).[70] The head for 4 and the hand zero sign appear as the coefficient of the uinal and kin signs in A6 and A7, respectively. The number will read, therefore, ?.19.13.4.0. Let us examine the cycle coefficient in A3 again. The natural assumption, of course, is that it is 9. But the dots characteristic of the head for 9 are not to be found here. As this head has no fleshless lower jaw, it can not be 10 or any number above 13, and as there is no clasped hand associated with it, it can not signify 0, so we are limited to the numbers, 1, 2, 3, 4, 5,[71] 6, 7, 8, 11, 12, and 13, as the numeral here recorded. Comparing this form with these numerals in figures 51 and 52, it is evident that it can not be 1, 3, 4, 5, 6, 7, 8, or 13, and that it must therefore be 2, 11, or 12. Substituting these three values in turn, we have 2.19.13.4.0, 11.19.13.4.0, and 12.19.13.4.0 as the possible numbers recorded in A3-B7, and reducing these numbers to units of the first order and deducting the highest number of Calendar Rounds possible from each, and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to their remainders, the terminal dates reached will be:
| 2.19.13.4.0 | 5 Ahau 3 Pax |
| 11.19.13.4.0 | 9 Ahau 8 Yax |
| 12.19.13.4.0 | 8 Ahau 13 Pop |
If this text is perfectly regular and our calculations are correct, one of these three terminal dates will be found recorded, and the value of the cycle coefficient in A3 can be determined.
The terminal date of this Initial Series is recorded in A8-B9 and the student will easily read it as 8 Ahau 18 Tzec. The only difference between the day coefficient and the month coefficient is that the latter has a fleshless lower jaw, increasing its value by 10. Moreover, comparison of the month sign in B9 with g and h, figure 19, shows unmistakably that the month here recorded is Tzec. But the terminal date as recorded does not agree with any one of the three above terminal dates as reached by calculation and we are forced to accept one of the two conclusions which confronted us in the preceding text (fig. 77, A): Either the starting point of this Initial Series is not the date 4 Ahau 8 Cumhu, or there is some error in the original text.[72]
Assuming that the ancient scribes made no mistakes in this inscription, let us count backward from the recorded terminal date, 8 Ahau 18 Tzec, each of the three numbers 2.19.13.4.0, 11.19.13.4.0, and 12.19.13.4.0, one of which, we have seen, is recorded in A3-B7.
Reducing these numbers to units of the first order by means of Table XIII, and deducting all the Calendar Rounds possible from each (see Table XVI), and, finally, applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), to the remainders, the starting points will be found to be:
| 7 Ahau 3 Mol | for 2.19.13.4.0 |
| 3 Ahau 18 Mac | for 11.19.13.4.0 |
| 4 Ahau 8 Zotz | for 12.19.13.4.0 |
Which of these starting points are we to accept as the one from which this number is counted? The correct answer to this question will give at the same time the value of the cycle coefficient, which, as we have seen, must be 2, 11, or 12. Most Maya students have accepted as the starting point of this Initial-series number the last of the three dates above given, 4 Ahau 8 Zotz, which involves also the identification of the cycle coefficient in A3 as 12. The writer has reached the same conclusion from the following points:
1. The cycle coefficient in A3, except for its very unusual headdress, is almost identical with the other two head-variant numerals, whose values are known to be 12. These three head numerals are shown side by side in figure 52, t-v, t being the form in A3 above, inserted in this figure for the sake of comparison. Although these three heads show no single element or characteristic that is present in all (see p. 100), each is very similar to the other two and at the same time is dissimilar from all other head-variant numerals. This fact warrants the conclusion that the head in A3 represents the numeral 12, and if this is so the starting point of the Initial Series under discussion is 4 Ahau 8 Zotz.
2. Aside from the fact that 12 seems to be the best reading of the head in A3, and consequently that the starting point of this number is 4 Ahau 8 Zotz, the writer believes that 4 Ahau 8 Zotz should be selected, if for no other reason than that another Initial Series has been found which proceeds from this same date, while no other Initial Series known is counted from either 7 Ahau 3 Mol or 3 Ahau 18 Mac.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 16

INITIAL SERIES AND SECONDARY SERIES ON LINTEL 21, YAXCHILAN
As we have seen in discussing the preceding text, from the east side of Stela C at Quirigua (fig. 77, A), the Initial Series there recorded was counted from the same starting point, 4 Ahau 8 Zotz, as the Initial Series from the Temple of the Cross at Palenque, if we read the latter as 12.19.13.4.0. This coincidence, the writer believes, is sufficient to warrant the identification of the head in A3 (fig. 77, B) as the head numeral 12 and the acceptance of this Initial Series as proceeding from the same starting point as the Quirigua text just described, namely, the date 4 Ahau 8 Zotz. With these two examples the discussion of Initial-series texts will be closed.
Texts Recording Initial Series and Secondary Series
It has been explained (see pp. 74-76) that in addition to Initial-series dating the Maya had another method of expressing their dates, known as Secondary Series, which was used when more than one date had to be recorded on the same monument. It was stated, further, that the accuracy of Secondary-series dating depended solely on the question whether or not the Secondary Series was referred to some date whose position in the Long Count was fixed either by the record of its Initial Series or in some other way. The next class of texts to be presented will be those showing the use of Secondary Series in connection with an Initial Series, by means of which the Initial-series values of the Secondary-series dates, that is, their proper positions in the Long Count, may be worked out even though they are not recorded in the text.
The first example presented will be the inscription on Lintel 21 at Yaxchilan, which is figured in plate 16.[73] As usual, when an Initial Series is recorded, the introducing glyph opens the text and this sign appears in A1, being followed by the Initial-series number itself in B1-B3. This the student will readily decipher as 9.0.19.2.4, recording apparently a very early date in Maya history, within 20 years of 9.0.0.0.0 8 Ahau 13 Ceh, the date arbitrarily fixed by the writer as the opening of the first great period.
Reducing this number by means of Table XIII to units of the first order[74] and deducting all the Calendar Rounds possible, 68 (see Table XVI), and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the terminal date reached will be 2 Kan 2 Yax. This date the student will find recorded in A4 and A7a, glyph B6b being the month-sign "indicator," or the closing glyph of the Supplementary Series, here shown with the coefficient 9. Compare the day sign in A4a with the sign for Kan in figure 16, f, and the month sign in A7a with the sign for Yax in figure 19, q, r. We have then recorded in A1-A4[75], and A7a the Initial-series date 9.0.19.2.4 2 Kan 2 Yax. At first sight it would appear that this early date indicates the time at or near which this lintel was inscribed, but a closer examination reveals a different condition. Following along through the glyphs of this text, there is reached in C3-C4 still another number in which the normal forms of the katun, tun, and uinal signs clearly appear in connection with bar and dot coefficients. The question at once arises, Has the number recorded here anything to do with the Initial Series, which precedes it at the beginning of this text?
Let us first examine this number before attempting to answer the above question. It is apparent at the outset that it differs from the Initial-series numbers previously encountered in several respects:
1. There is no introducing glyph, a fact which at once eliminates the possibility that it might be an Initial Series.
2. There is no kin period glyph, the uinal sign in C3 having two coefficients instead of one.
3. The order of the period glyphs is reversed, the highest period, here the katun, closing the series instead of commencing it as heretofore.
It has been explained (see p. 129) that in Secondary Series the order of the period glyphs is almost invariably the reverse of that shown by the period glyphs in Initial Series; and further, that the former are usually presented as ascending series, that is, with the lowest units first, and the latter invariably as descending series, with the highest units first. It has been explained also (see p. 128) that in Secondary Series the kin period glyph is usually omitted, the kin coefficient being attached to the left of the uinal sign. Since both of these points (see 2 and 3, above) are characteristic of the number in C3-C4, it is probable that a Secondary Series is recorded here, and that it expresses 5 kins, 16 uinals, 1 tun, and 15 katuns. Reversing this, and writing it according to the notation followed by most Maya students (see p. 138, footnote 1), we have as the number recorded by C3-C4, 15.1.16.5.
Reducing this number to units of the first order by means of Table XIII, we have:
| C4 = | 15 × | 7,200 = | 108,000 |
| D3 = | 1 × | 360 = | 360 |
| C3 = | 16 × | 20 = | 320 |
| C3 = | 5 × | 1 = | 5 |
| ——— | |||
| 108,685 | |||
Since all the Calendar Rounds which this number contains, 5 (see Table XVI) may be deducted from it without affecting its value, we can further reduce it to 13,785 (108,685 - 94,900), and this will be the number used in the following calculations.
It was stated (on p. 135) in describing the direction of the count that numbers are usually counted forward from the dates next preceding them in a text, although this is not invariably true. Applying this rule to the present case, it is probable that the Secondary-series number 15.1.16.5, which we have reduced to 13,785 units of the first order, is counted forward from the date 2 Kan 2 Yax, the one next preceding it in our text, a date, moreover, the Initial-series value of which is known.
Remembering that this date 2 Kan 2 Yax is our new starting point, and that the count is forward, by applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), to 13,785, the new terminal date reached will be 7 Muluc 17 Tzec; and this date is recorded in C5-D5. Compare C5 with the sign for the day Muluc in figure 16, m, n, and D5 with the sign for the month Tzec in figure 19, g, h. Furthermore, by adding the Secondary-series number 15.1.16.5 to 9.0.19.2.4 (the Initial-series number which fixes the position of the date 2 Kan 2 Yax in the Long Count), the Initial-series value of the terminal date of the Secondary Series (calculated and identified above as 7 Muluc 17 Tzec) can also be determined as follows:
| 9. | 0. | 19. | 2. | 4 | 2 Kan 2 Yax | Initial Series |
| 15. | 1. | 16. | 5 | Secondary-series number | ||
| 9. | 16. | 1. | 0. | 9 | 7 Muluc 17 Tzec | Initial Series of the Secondary-series terminal date 7 Muluc 17 Tzec |
The student may verify the above calculations by treating 9.16.1.0.9 as a new Initial-series number, and counting it forward from 4 Ahau 8 Cumhu, the starting point of Maya chronology. The terminal date reached will be found to be the same date as the one recorded in C5-D5, namely, 7 Muluc 17 Tzec.
What is the meaning then of this text, which records two dates nearly 300 years apart?[76] It must be admitted at the outset that the nature of the events which occurred on these two dates, a matter probably set forth in the glyphs of unknown meaning in the text, is totally unknown. It is possible to gather from other sources, however, some little data concerning their significance. In the first place, 9.16.1.0.9 7 Muluc 17 Tzec is almost surely the "contemporaneous date" of this lintel, the date indicating the time at or near which it was formally dedicated or put into use. This point is established almost to a certainty by the fact that all the other dates known at Yaxchilan are very much nearer to 9.16.1.0.9 7 Muluc 17 Tzec in point of time than to 9.0.19.2.4 2 Kan 2 Yax, the Initial-series date recorded on this lintel. Indeed, while they range from 9 days[77] to 75 years from the former, the one nearest the latter is more than 200 years later. This practically proves that 9.16.1.0.9 7 Muluc 17 Tzec indicates the "contemporaneous time" of this lintel and that 9.0.19.2.4 2 Kan 2 Yax referred to some earlier event which took place perhaps even before the founding of the city. And finally, since this inscription is on a lintel, we may perhaps go a step further and hazard the conclusion that 9.16.1.0.9 7 Muluc 17 Tzec records the date of the erection of the structure of which this lintel is a part.
We may draw from this inscription a conclusion which will be found to hold good in almost all cases, namely, that the last date in a text almost always indicates the "contemporaneous time" of the monument upon which it appears. In the present text, for example, the Secondary-series date 7 Muluc 17 Tzec, the Initial-series value of which was found to be 9.16.1.0.9, is in all probability its contemporaneous date, or very near thereto. It will be well to remember this important point, since it enables us to assign monuments upon which several different dates are recorded to their proper periods in the Long Count.
The next example illustrating the use of Secondary Series with an Initial Series is the inscription from Stela 1 at Piedras Negras, figured in plate 17.[78] The order of the glyphs in this text is somewhat irregular. It will be noted that there is an uneven number of glyph columns, so that one column will have to be read by itself. The natural assumption would be that A and B, C and D, and E and F are read together, leaving G, the last column, to be read by itself. This is not the case, however, for A, presenting the Initial Series, is read first, and then B C, D E, and F G, in pairs. The introducing glyph of the Initial Series appears in A1 and is followed by the Initial-series number 9.12.2.0.16 in A2-A6. The student should be perfectly familiar by this time with the processes involved in counting this number from its starting point, and should have no difficulty in determing by calculation the terminal date recorded in A7, C2, namely, 5 Cib 14 Yaxkin.[79] Compare A7 with the sign for Cib in figure 16, z, and C2 with the sign for Yaxkin in figure 19, k, l. The Initial Series recorded in A1-A7, C2 is 9.12.2.0.16 5 Cib 14 Yaxkin.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 17

INITIAL SERIES AND SECONDARY SERIES ON STELA 1, PIEDRAS NEGRAS
Passing over the glyphs in B3-E1, the meanings of which are unknown, we reach in D2 E2 a number showing very clearly the tun and uinal signs, the latter having two coefficients instead of one. Moreover, the order of these period glyphs is reversed, the lower standing first in the series. As explained in connection with the preceding text, these points are both characteristic of Secondary-series numbers, and we may conclude therefore that D2 E2 records a number of this kind. Finally, since the kin coefficient in Secondary Series usually appears on the left of the uinal sign, we may express this number in the commonly accepted notation as follows: 12.9.15. Reducing this to units of the first order, we have:
| E2 = | 12 × | 360 = | 4,320 |
| D2 = | 9 × | 20 = | 180 |
| D2 = | 15 × | 1 = | 15 |
| —— | |||
| 4,515 | |||
Remembering that Secondary-series numbers are usually counted from the dates next preceding them in the texts, in this case 5 Cib 14 Yaxkin, and proceeding according to rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal date of the Secondary Series reached will be 9 Chuen 9 Kankin, which is recorded in F1 G1, though unfortunately these glyphs are somewhat effaced. Moreover, since the position of 5 Cib 14 Yaxkin in the Long Count is known, that is, its Initial-series value, it is possible to determine the Initial-series value of this new date, 9 Chuen 9 Kankin:
| 9. | 12. | 2. | 0. | 16 | 5 Cib 14 Yaxkin |
| 12. | 9. | 15 | |||
| 9. | 12. | 14. | 10. | 11 | 9 Chuen 9 Kankin |
But the end of this text has not been reached with the date 9 Chuen 9 Kankin in F1 G1. Passing over F2 G2, the meanings of which are unknown, we reach in F3 an inverted Ahau with the coefficient 5 above it. As explained on page 72, this probably signifies 5 kins, the inversion of the glyph changing its meaning from that of a particular day sign, Ahau, to a general sign for the kin day period (see fig. 34, d). The writer recalls but one other instance in which the inverted Ahau stands for the kin sign—on the north side of Stela C at Quirigua.
We have then another Secondary-series number consisting of 5 kins, which is to be counted from some date, and since Secondary-series numbers are usually counted from the date next preceding them in the text, we are justified in assuming that 9 Chuen 9 Kankin is our new starting point.
Counting 5 forward from this date, according to rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal date reached will be 1 Cib 14 Kankin, and this latter date is recorded in G3-G4. Compare G3 with the sign for Cib in A7 and in figure 16, z, and G4 with the sign for Kankin in figure 19, y, z. Moreover, since the Initial-series value of 9 Chuen 9 Kankin was calculated above as 9.12.14.10.11, the Initial-series value of this new date, 1 Cib 14 Kankin, also can be calculated from it:
| 9. | 12. | 14. | 10. | 11 | 9 Chuen 9 Kankin |
| 5 | |||||
| 9. | 12. | 14. | 10. | 16 | 1 Cib 14 Kankin |
Passing over G5 as unknown, we reach in G6-G7 another Secondary-series number. The student will have little difficulty in identifying G6 as 2 uinals, 5 kins, and G7 as 1 katun. It will be noted that no tun sign appears in this number, which is a very unusual condition. By far the commoner practice in such cases in which 0 units of some period are involved is to record the period with a coefficient 0. However, this was not done in the present case, and since no tuns are recorded, we may conclude that none were involved, and G6-G7 may be written 1.(0).2.5. Reducing this number to units of the first order, we have:
| G7 = | 1 × | 7,200 = | 7,200 |
| ([80]) = | 0 × | 360 = | 0 |
| G6 = | 2 × | 20 = | 40 |
| G6 = | 5 × | 1 = | 5 |
| —— | |||
| 7,245 | |||
Remembering that the starting point from which this number is counted is the date next preceding it, 1 Cib 14 Kankin, and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal date reached will be 5 Imix 19 Zac; this latter date is recorded in G8-G9. Compare G8 with the sign for Imix in figure 16, a, b, and G9 with the sign for Zac in figure 19, s, t. Moreover, since the Initial Series of 1 Cib 14 Kankin was obtained by calculation from the date next preceding it, the Initial Series of 5 Imix 19 Zac may be determined in the same way.
| 9. | 12. | 14. | 10. | 16 | 1 Cib 14 Kankin |
| 1. | 0.[80] | 2. | 5 | ||
| 9. | 13. | 14. | 13. | 1 | 5 Imix 19 Zac |
With the above date closes the known part of this text, the remaining glyphs, G10-G12, being of unknown meaning.
Assembling all the glyphs deciphered above, the known part of this text reads as follows:
| 9. | 12. | 2. | 0. | 16 | A1-A7, C2 | 5 Cib 14 Yaxkin |
| 12. | 9. | 15 | D2 E2 | |||
| 9. | 12. | 14. | 10. | 11 | F1 G1 | 9 Chuen 9 Kankin |
| 5 | F3 | |||||
| 9. | 12. | 14. | 10. | 16 | G3 G4 | 1 Cib 14 Kankin |
| 1. | 0.[80] | 2. | 5 | G6 G7 | ||
| 9. | 13. | 14. | 13. | 1 | G8 G9 | 5 Imix 19 Zac |
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 18

INITIAL SERIES (A) AND SECONDARY SERIES (B) ON STELA K, QUIRIGUA
We have recorded here four different dates, of which the last, 9.13.14.13.1 5 Imix 19 Zac, probably represents the actual date, or very near thereto, of this monument.[81] The period covered between the first and last of these dates is about 32 years, within the range of a single lifetime or, indeed, of the tenure of some important office by a single individual. The unknown glyphs again probably set forth the nature of the events which occurred on the dates recorded.
In the two preceding texts the Secondary Series given are regular in every way. Not only was the count forward each time, but it also started in every case from the date immediately preceding the number counted. This regularity, however, is far from universal in Secondary-series texts, and the following examples comprise some of the more common departures from the usual practice.
In plate 18 is figured the Initial Series from Stela K at Quirigua.[82] The text opens on the north side of this monument (see pl. 18, A) with the introducing glyph in A1-B2. This is followed by the Initial-series number 9.18.15.0.0 in A3-B4, which leads to the terminal date 3 Ahau 3 Yax. The day part of this date the student will find recorded in its regular position, A5a. Passing over A5b and B5, the meanings of which are unknown, we reach in A6 a Secondary-series number composed very clearly of 10 uinals and 10 kins (10.10), which reduces to the following number of units of the first order:
| A6 = | 10 × | 20 = | 200 |
| A6 = | 10 × | 1 = | 10 |
| —— | |||
| 210 | |||
The first assumption is that this number is counted forward from the terminal date of the Initial Series, 3 Ahau 3 Yax, and performing the operations indicated in rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) the terminal date reached will be 5 Oc 8 Uo. Now, although the day sign in B6b is clearly Oc (see fig. 16, o-q), its coefficient is very clearly 1, not 5, and, moreover, the month in A7a is unmistakably 18 Kayab (see fig. 19, d'-f'). Here then instead of finding the date determined by calculation, 5 Oc 8 Uo, the date recorded is 1 Oc 18 Kayab, and consequently there is some departure from the practices heretofore encountered.
Since the association of the number 10.10 is so close with (1) the terminal date of the Initial Series, 3 Ahau 3 Yax, and (2) the date 1 Oc 18 Kayab almost immediately following it, it would almost seem as though these two dates must be the starting point and terminal date, respectively, of this number. If the count is forward, we have just proved that this can not be the case; so let us next count the number backward and see whether we can reach the date recorded in B6b-A7a (1 Oc 18 Kayab) in this way.
Counting 210 backward from 3 Ahau 3 Yax, according to rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal date reached will be 1 Oc 18 Kayab, as recorded in B6b-A7. In other words, the Secondary Series in this text is counted backward from the Initial Series, and therefore precedes it in point of time. This will appear from the Initial-series value of 1 Oc 18 Kayab, which may be determined by calculation:
| 9. | 18. | 15. | 0. | 0 | 3 Ahau 3 Yax |
| 10. | 10 | ||||
| 9. | 18. | 14. | 7. | 10 | 1 Oc 18 Kayab |
This text closes on the south side of the monument in a very unusual manner (see pl. 18, B). In B3a appears the month-sign indicator, here recorded as a head variant with a coefficient 10, and following immediately in B3b a Secondary-series number composed of 0 uinals and 0 kins, or, in other words, nothing. It is obvious that in counting this number 0.0, or nothing, either backward or forward from the date next preceding it in the text, 1 Oc 18 Kayab in B6b-A7a on the north side of the stela, the same date 1 Oc 18 Kayab will remain. But this date is not repeated in A4, where the terminal date of this Secondary Series, 0.0, seems to be recorded. However, if we count 0.0 from the terminal date of the Initial Series, 3 Ahau 3 Yax, we reach the date recorded in A4, 3 Ahau 3 Yax,[83] and this whole text so far as deciphered will read:
| 9. | 18. | 15. | 0. | 0 | 3 Ahau 3 Yax |
| 10. | 10 | backward | |||
| 9. | 18. | 14. | 7. | 10 | 1 Oc 18 Kayab |
| 0. | 0 | forward from Initial Series | |||
| 9. | 18. | 15. | 0. | 0 | 3 Ahau 3 Yax |
The reason for recording a Secondary-series number equal to zero, the writer believes, was because the first Secondary-series date 1 Oc 18 Kayab precedes the Initial-series date, which in this case marks the time at which this monument was erected. Hence, in order to have the closing date on the monument record the contemporaneous time of the monument, it was necessary to repeat the Initial-series date; this was accomplished by adding to it a Secondary-series date denoting zero. Stela K is the next to the latest hotun-marker at Quirigua following immediately Stela I, the Initial series of which marks the hotun ending 9.18.10.0.0 10 Ahau 8 Zac (see pl. 6, C).
Mr. Bowditch (1910: p. 208) has advanced a very plausible explanation to account for the presence of the date 9.18.14.7.10 1 Oc 18 Kayab on this monument. He shows that at the time when Stela K was erected, namely, 9.18.15.0.0 3 Ahau 3 Yax, the official calendar had outrun the seasons by just 210 days, or exactly the number of days recorded in A6, plate 18, A (north side); and further, that instead of being the day 3 Yax, which occurred at Quirigua about the beginning of the dry season,[84] in reality the season was 210 days behind, or at 18 Kayab, about the beginning of the rainy season. This very great discrepancy between calendar and season could not have escaped the notice of the priests, and the 210 days recorded in A6 may well represent the days actually needed on the date 9.18.15.0.0 3 Ahau 3 Yax to bring the calendar into harmony with the current season. If this be true, then the date 9.18.14.7.0 1 Oc 18 Kayab represented the day indicated by the sun when the calendar showed that the 3d hotun in Katun 18 of Cycle 9 had been completed. Mr. Bowditch suggests the following free interpretation of this passage: "The sun has just set at its northern point[85] and we are counting the day 3 Yax—210 days from 18 Kayab—which is the true date in the calendar according to our traditions and records for the sun to set at this point on his course." As stated above, the writer believes this to be the true explanation of the record of 210 days on this monument.

Fig. 78. The Initial Series on Stela J, Quirigua.
In figures 78 and 79 are illustrated the Initial Series and Secondary Series from Stela J at Quirigua.[86] For lack of space the introducing glyph in this text has been omitted; it occupies the position of six glyph-blocks, however, A1-B3, after which the Initial-series number 9.16.5.0.0 follows in A4-B8. This leads to the terminal date 8 Ahau 8 Zotz, which is recorded in A9, B9, B13, the glyph in A13 being the month-sign indicator here shown with the coefficient 9. Compare B9 with the second variant for Ahau in figure 16 h', i', and B13 with the sign for Zotz in figure 19, e, f. The Initial-series part of this text therefore in A1-B9, B13, is perfectly regular and reads as follows: 9.16.5.0.0 8 Ahau 8 Zotz. The Secondary Series, however, are unusual and differ in several respects from the ones heretofore presented.

Fig. 79. The Secondary Series on Stela J, Quirigua.
The first Secondary Series inscribed on this monument (see fig. 79, A) is at B1-B2. This series the student should readily decipher as 3 kins, 13 uinals, 11 tuns, and 0 katuns, which we may write 0.11.13.3. This number presents one feature, which, so far as the writer knows, is unique in the whole range of Maya texts. The highest order of units actually involved in this number is the tun, but for some unknown reason the ancient scribe saw fit to add the katun sign also, B2, which, however, he proceeded to nullify at once by attaching to it the coefficient 0. For in so far as the numerical value is concerned, 11.13.3 and 0.11.13.3 are equal. The next peculiarity is that the date which follows this number in B3-A4 is not its terminal date, as we have every reason to expect, but, on the contrary, its starting point. In other words, in this Secondary Series the starting point follows instead of precedes the number counted from it. This date is very clearly 12 Caban 5 Kayab; compare B3 with the sign for Caban in figure 16, a', b', and A4 with the sign for Kayab in figure 19, d'-f'. So far as Stela J is concerned there is no record of the position which this date occupied in the Long Count; that is, there are no data by means of which its Initial Series may be calculated. Elsewhere at Quirigua, however, this date is recorded twice as an Initial Series and in each place it has the same value, 9.14.13.4.17. We may safely conclude, therefore, that the date in A3-B4 is 9.14.13.4.17 12 Caban 5 Kayab, and use it in our calculations as such. Reducing 0.11.13.3 to units of the first order, we have:
| B2 = | 0 × | 7,200 = | 0 |
| A2 = | 11 × | 360 = | 3,960 |
| B1 = | 13 × | 20 = | 260 |
| B1 = | 3 × | 1 = | 3 |
| —— | |||
| 4,223 | |||
Applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to this number, the terminal date reached will be 10 Ahau 8 Chen, which is nowhere recorded in the text (see fig. 79, A).
The Initial Series corresponding to this date, however, may be calculated from the Initial Series which we have assigned to the date 12 Caban 5 Kayab:
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab |
| 0. | 11. | 13. | 3 | ||
| 9. | 15. | 5. | 0. | 0 | 10 Ahau 8 Chen |
Although the date 9.15.5.0.0 10 Ahau 8 Chen is not actually recorded at Quirigua, it is reached on another monument by calculation just as here. It has a peculiar fitness here on Stela J in that it is just one katun earlier than the Initial Series on this monument (see fig. 78), 9.16.5.0.0 8 Ahau 8 Zotz.
The other Secondary Series on this monument (see fig. 79, B) appears at B1-A2, and records 18 tuns, 3 uinals, and 14 kins, which we may write thus: 18.3.14. As in the preceding case, the date following this number in B2-A3 is its starting point, not its terminal date, a very unusual feature, as has been explained. This date is 6 Cimi 4 Tzec—compare B2 with the sign for Cimi in figure 16, h, i, and A3 with the sign for Tzec in figure 19, g, h—and as far as Stela J is concerned it is not fixed in the Long Count. However, elsewhere at Quirigua this date is recorded in a Secondary Series, which is referred back to an Initial Series, and from this passage its corresponding Initial Series is found to be 9.15.6.14.6 6 Cimi 4 Tzec. Reducing the number recorded in B1-A2, 18.3.14, to units of the first order, we have:
| A2 = | 18 × | 360 = | 6,480 |
| B2 = | 3 × | 20 = | 60 |
| B2 = | 14 × | 1 = | 14 |
| —— | |||
| 6,554 | |||
Applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the number, the terminal date reached will be 8 Ahau 8 Zotz, which does not appear in figure 79, B. The Initial Series corresponding to this date may be calculated as follows:
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec |
| 18. | 3. | 14 | |||
| 9. | 16. | 5. | 0. | 0 | 8 Ahau 8 Zotz |
But this was the Initial Series recorded on the reverse of this monument, consequently the Secondary-series dates, both of which have preceded the Initial-series date in point of time, bring this count up to the contemporaneous time of this monument, which was 9.16.5.0.0 8 Ahau 8 Zotz. In view of the fact that the Secondary Series on Stela J are both earlier than the Initial Series, the chronological sequence of the several dates is better preserved by regarding the Initial Series as being at the close of the inscription instead of at the beginning, thus:
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab | Figure 79, A, | B3-A4 |
| 0. | 11. | 13. | 3 | B1-B2 | |||
| [9. | 15. | 5. | 0. | 0] | 10 Ahau 8 Chen[87] | ||
| [1. | 14. | 6] | [88] | ||||
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec | Figure 79, B, | B2-A3 |
| 18. | 3. | 14 | B1-A2 | ||||
| 9. | 16. | 5. | 0. | 0 | 8 Ahau 8 Zotz | Figure 78 | A1-B9, B13 |
By the above arrangement all the dates present in the text lead up to 9.16.5.0.0 8 Ahau 8 Zotz as the most important date, because it alone records the particular hotun-ending which Stela J marks. The importance of this date over the others is further emphasized by the fact that it alone appears as an Initial Series.
The text of Stela J illustrates two points in connection with Secondary Series which the student will do well to bear in mind: (1) The starting points of Secondary-series numbers do not always precede the numbers counted from them, and (2) the terminal dates and starting points are not always both recorded.
The former point will be illustrated in the following example:
In plate 19, A, is figured the Initial Series from the west side of Stela F at Quirigua.[89] The introducing glyph appears in A1-B2 and is followed by the Initial-series number in A3-A5. This is expressed by head variants and reads as follows: 9.14.13.4.17. The terminal date reached by this number is 12 Caban 5 Kayab, which is recorded in B5-A6. The student will readily identify the numerals as above by comparing them with the forms in figures 51-53, and the day and month signs by comparing them with figures 16, a', b', and 19, d'-f', respectively. The Initial Series therefore reads 9.14.13.4.17 12 Caban 5 Kayab.[90]
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 19

INITIAL SERIES (A) AND SECONDARY SERIES (B) ON STELA F (WEST SIDE), QUIRIGUA
Passing over B6-A10, the meanings of which are unknown, we reach in B10 the Secondary-series number 13.9.9. Reducing this to units of the first order, we have:
| B10b = | 13 × | 360 = | 4,680 |
| B10a = | 9 × | 20 = | 180 |
| B10a = | 9 × | 1 = | 9 |
| —— | |||
| 4,869 | |||
Assuming that our starting point is the date next preceding this number in the text, that is, the Initial-series terminal date 12 Caban 5 Kayab in B5-A6, and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal day reached will be 6 Cimi 4 Tzec. This date the student will find recorded in plate 19, B, B11b-A12a. Compare B11b with the sign for Cimi in figure 16, h, i, and A12a with the sign for Tzec in figure 19, g, h. Moreover, since the Initial-series value of the starting point 12 Caban 5 Kayab is known, the Initial-series value of the terminal date 6 Cimi 4 Tzec may be calculated from it:
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab |
| 13. | 9. | 9 | |||
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec[91] |
In A15 is recorded the date 3 Ahau 3 Mol (compare A15a with fig. 16, k', i', and A15b with fig. 19, m, n) and in A17 the date 4 Ahau 13 Yax (compare A17a with fig. 16, e'-g' and A17b with fig. 19, q, r). This latter date, 4 Ahau 13 Yax, is recorded elsewhere at Quirigua in a Secondary Series attached to an Initial Series, where it has the Initial-series value 9.15.0.0.0. This value we may assume, therefore, belongs to it in the present case, giving us the full date 9.15.0.0.0 4 Ahau 13 Yax. For the present let us pass over the first of these two dates, namely, 3 Ahau 3 Mol, the Initial Series of which as well as the reason for its record here will better appear later.
In B17-A18a is recorded another Secondary-series number composed of 3 kins, 13 uinals, 16 tuns, and 1 katun, which we may write thus: 1.16.13.3. The student will note that the katun coefficient in A18a is expressed by an unusual form, the thumb. As explained on page 103, this has a numerical value of 1. Again, our text presents another irregular feature. Instead of being counted either forward or backward from the date next preceding it in the text; that is, 4 Ahau 13 Yax in A17, this number is counted from the date following it in the text, like the two Secondary-series numbers in Stela J, just discussed. This starting date recorded in A18b B18a is 12 Caban 5 Kayab, which, as we have seen, is also the date recorded by the Initial Series in plate 19, A, A1-A6. We are perfectly justified in assuming, therefore, that the 12 Caban 5 Kayab in A18b-B18a had the same Initial-series value as the 12 Caban 5 Kayab in plate 19, A, B5-A6, namely, 9.14.13.4.17. Reducing the number in B17-A18a, namely, 1.16.13.3, to units of the first order, we have:
| A18a = | 1 × | 7,200 = | 7,200 |
| B17b = | 16 × | 360 = | 5,760 |
| B17a = | 13 × | 20 = | 260 |
| B17a = | 3 × | 1 = | 3 |
| ——— | |||
| 13,223 | |||
Remembering that this number is to be counted forward from the date 12 Caban 5 Kayab, and applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively), the terminal date reached will be 1 Ahau 3 Zip, which is recorded in A19. Compare the coefficient of the day sign in A19a with the coefficient of the katun sign in A18a, and the day sign itself with the profile variant for Ahau in figure 16, h', i'. For the month sign, compare A19b with figure 19, d. But since the Initial-series value of the starting point is known, we may calculate from it the Initial-series value of the new terminal date:
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab |
| 1. | 16. | 13. | 3 | ||
| 9. | 16. | 10. | 0. | 0 | 1 Ahau 3 Zip |
Passing over to the east side of this monument, the student will find recorded there the continuation of this inscription (see pl. 20).[92] This side, like the other, opens with an introducing glyph A1-B2, which is followed by an Initial Series in A3-A5. Although this number is expressed by head variants, the forms are all familiar, and the student will have little difficulty in reading it as 9.16.10.0.0. The terminal date which this number reaches is recorded in B5-B8; that is, 1[93] Ahau 3 Zip, the "month indicator" appearing as a head variant in A8 with the head-variant coefficient 10. But this date is identical with the date determined by calculation and actually recorded at the close of the inscription on the other side of this monument, and since no later date is recorded elsewhere in this text, we may conclude that 9.16.10.0.0 1 Ahau 3 Zip represents the contemporaneous time of Stela F, and hence that it was a regular hotun-marker. Here again, as in the case of Stela J at Quirigua, the importance of the "contemporaneous date" is emphasized not only by the fact that all the other dates lead up to it, but also by the fact that it is expressed as an Initial Series.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 20

INITIAL SERIES ON STELA F (EAST SIDE), QUIRIGUA
Fig. 80. Glyphs which may disclose the nature of the events that happened at Quirigua on the dates: a, 9. 14. 13. 4. 17 12 Caban 5 Kayab; b, 9. 15. 6. 14. 6 6 Cimi 4 Tzec.
We have explained all the dates figured except 3 Ahau 3 Mol in plate 19, B, A15, the discussion of which was deferred until after the rest of the inscription had been considered. It will be remembered in connection with Stela J (figs. 78, 79) that one of the dates reached in the course of the calculations was just 1 katun earlier than the date recorded by the Initial Series on the same monument. Now, one of the Initial-series values corresponding to the date 3 Ahau 3 Mol here under discussion is 9.15.10.0.0, exactly 1 katun earlier than the Initial-series date on Stela F. In other words, if we give to the date 3 Ahau 3 Mol in A15 the value 9.15.10.0.0, the cases are exactly parallel. While it is impossible to prove that this particular Initial Series was the one which the ancient scribes had in mind when they recorded this date 3 Ahau 3 Mol, the writer believes that the coincidence and parallel here presented are sufficient to warrant the assumption that this is the case. The whole text reads as follows:
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab | Plate 19, A, A1-A6 |
| 13. | 9. | 9 | Plate 19, A, A10 | |||
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec | Plate 19, B, B11b-A12a |
| [9. | 15. | 10. | 0. | 0] | 3 Ahau 3 Mol | Plate 19, B, A15 |
| [9. | 15. | 0. | 0. | 0] | 4 Ahau 13 Yax | Plate 19, B, A17 |
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab | Plate 19, B, A18b B18a |
| 1. | 16. | 13. | 3 | Plate 19, B, B17 A18a | ||
| 9. | 16. | 10. | 0. | 0 | 1 Ahau 3 Zip | Plate 19, B, A19 |
| (repeated as Initial Series on east side of monument) | ||||||
| 9. | 16. | 10. | 0. | 0 | 1 Ahau 3 Zip | Plate 20, A1-B5-B8 |
The student will note the close similarity between this inscription and that on Stela J (figured in figs. 78 and 79), a summary of which appears on page 239. Both commence with the same date, 9.14.13.4.17 12 Caban 5 Kayab; both show the date 9.15.6.14.6 6 Cimi 4 Tzec; both have dates which are just 1 katun in advance of the hotuns which they mark; and finally, both are hotun-markers, Stela J preceding Stela F by just 1 hotun. The date from which both proceed, 9.14.13.4.17 12 Caban 5 Kayab, is an important one at Quirigua, being the earliest date there. It appears on four monuments, namely, Stelæ J, F, and E, and Zoömorph G. Although the writer has not been able to prove the point, he is of the opinion that the glyph shown in figure 80, a, tells the meaning of the event which happened on this date, which is, moreover, the earliest date at Quirigua which it is possible to regard as being contemporaneous. Hence, it is not improbable that it might refer to the founding of the city or some similar event, though this is of course a matter of speculation. The fact, however, that 9.14.13.4.17 12 Caban 5 Kayab is the earliest date on four different hotun-markers shows that it was of supreme importance in the history of Quirigua. This concludes the discussion of texts showing the use of Secondary Series with Initial Series.
Texts Recording Period Endings
It was explained in Chapter III (p. 77) that in addition to Initial-series dating and Secondary-series dating, the Maya used still another method in fixing events, which was designated Period-ending dating. It was explained further that, although Period-ending dating was less exact than the other two methods, it served equally well for all practical purposes, since dates fixed by it could not recur until after a lapse of more than 18,000 years, a considerably longer period than that covered by the recorded history of mankind. Finally, the student will recall that the katun was said to be the period most commonly used in this method of dating.
The reason for this is near at hand. Practically all of the great southern cities rose, flourished, and fell within the period called Cycle 9 of Maya chronology. There could have been no doubt throughout the southern area which particular cycle was meant when the "current cycle" was spoken of. After the date 9.0.0.0.0 8 Ahau 13 Ceh had ushered in a new cycle there could be no change in the cycle coefficient until after a lapse of very nearly 400 (394.250 +) years. Consequently, after Cycle 9 had commenced many succeeding generations of men knew no other, and in time the term "current cycle" came to mean as much on a monument as "Cycle 9." Indeed, in Period-ending dating the Cycle 9 was taken for granted and scarcely ever recorded. The same practice obtains very generally to-day in regard to writing the current century, such expressions as July 4, '12, December 25, '13, being frequently seen in place of the full forms July 4, 1912, A. D., December 25, 1913, A. D.; or again, even more briefly, 7/4/12 and 12/25/13 to express the same dates, respectively. The desire for brevity, as has been explained, probably gave rise to Period-ending dating in the first place, and in this method the cycle was the first period to be eliminated as superfluous for all practical purposes. No one could have forgotten the number of the current cycle.
When we come to the next lower period, however, the katun, we find a different state of affairs. The numbers belonging to this period were changing every 20 (exactly, 19.71 +) years; that is, three or four times in the lifetime of many individuals; hence, there was plenty of opportunity for confusion about the number of the katun in which a particular event occurred. Consequently, in order to insure accuracy the katun is almost always the unit used in Period-ending dating.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 21

EXAMPLES OF PERIOD-ENDING DATES IN CYCLE 9
In plate 21 are figured a number of Period-ending dates, the glyphs of which have been ranged in horizontal lines, and are numbered from left to right for convenience in reference. The true positions of these glyphs in the texts from which they have been taken are given in the footnotes in each case. In plate 21, A, is figured a Period-ending date from Stela 2 at Copan.[94] The date 12 Ahau 8 Ceh appears very clearly in glyphs 1 and 2. Compare the month sign with figure 19, u, v. There follows in 3 a glyph the upper part of which probably represents the "ending sign" of this date. By comparing this form with the ending signs in figure 37 its resemblance to figure 37, o, will be evident. Indeed, figure 37, o, has precisely the same lower element as glyph 3. In glyph 4 follows the particular katun, 11, whose end fell on the date recorded in glyphs 1 and 2. The student can readily prove this for himself by reducing the Period-ending date here recorded to its corresponding Initial Series and counting the resulting number forward from the common starting point, 4 Ahau 8 Cumhu, as follows: Since the cycle glyph is not expressed, we may fill this omission as the Maya themselves filled it, by supplying Cycle 9. Moreover, since the end of a katun is recorded here, it is clear that all the lower periods—the tuns, uinals, and kins—will have to appear with the coefficient 0, as they are all brought to their respective ends with the ending of any katun. Therefore we may write the Initial-series number corresponding to the end of Katun 11, as 9.11.0.0.0. Treating this number as an Initial Series, that is, first reducing it to units of the first order, then deducting from it all the Calendar Rounds possible, and finally applying rules 1, 2, and 3 (pp. 139, 140, and 141, respectively) to the remainder, the student will find that the terminal date reached will be the same as the date recorded in glyphs 1 and 2, namely, 12 Ahau 8 Ceh. In other words, the Katun 11, which ended on the date 12 Ahau 8 Ceh, was 9.11.0.0.0 12 Ahau 8 Ceh, and both indicate exactly the same position in the Long Count. The next example (pl. 21, B) is taken from the tablet in the Temple of the Foliated Cross at Palenque.[95] In glyph 1 appears the date 8 Ahau 8 Uo (compare the month form with fig. 19, b, c) and in glyph 3 the "ending" of Katun 13. The ending sign here is the variant shown in figure 37, a-h, and it occurs just above the coefficient 13. These two glyphs therefore record the fact that Katun 13 ended with the day 8 Ahau 8 Uo. The student may again test the accuracy of the record by changing this Period-ending date to its corresponding Initial-series number, 9.13.0.0.0, and performing the various operations indicated in such cases. The resulting Initial-series terminal date will be the same as the date recorded in glyphs 1 and 2, 8 Ahau 8 Uo.
In plate 21, C, is figured a Period-ending date taken from Stela 23 at Naranjo.[96] The date 6 Ahau 13 Muan appears very clearly in glyphs 1 and 2 (compare the month form with fig. 19, a', b'). Glyph 3 is the ending sign, here showing three common "ending elements," (1) the clasped hand; (2) the element with the curl infix; (3) the tassel-like postfix. Compare this form with the ending signs in figure 37, l-q, and with the zero signs in figure 54. In glyph 4 is recorded the particular katun, 14, which came to its end on the date recorded in 1 and 2. The element prefixed to the Katun 14 in glyph 4 is also an ending sign, though it always occurs as a prefix or superfix attached to the sign of the period whose close is recorded. Examples illustrating its use are shown in figure 37, a-h, with which the ending element in glyph 4 should be compared. The glyphs 1 to 4 in plate 21, C, therefore record that Katun 14 came to an end on the date 6 Ahau 13 Muan. As we have seen above, this could be shown to correspond with the Initial Series 9.14.0.0.0 6 Ahau 13 Muan.
This same date, 6 Ahau 13 Muan ending Katun 14, is also recorded on Stela 16 at Tikal (see pl. 21, D).[97] The date itself appears in glyphs 1 and 2 and is followed in 3 by a sign which is almost exactly like the ending sign in glyph 3 just discussed (see pl. 21, C). The subfixes are identical in both cases, and it is possible to distinguish the lines of the hand element in the weathered upper part of the glyph in 3. Compare glyph 3 with the ending signs in figure 37, l-q, and with the zero signs in figure 54. As in the preceding example, glyph 4 shows the particular katun whose end is recorded here—Katun 14. The period glyph itself appears as a head variant to which is prefixed the same ending prefix or superfix shown with the period glyph in the preceding example. See also figure 37, a-h. As above stated, the Initial Series corresponding to this date is 9.14.0.0.0 6 Ahau 13 Muan.
One more example will suffice to illustrate the use of katun Period-ending dates. In plate 21, E, is figured a Period-ending date from Stela 4 at Copan.[98] In glyphs 1 and 2 appears the date 4 Ahau 13 Yax (compare the month in glyph 2 with fig. 19, q, r), which is followed by the ending sign in 3. This is composed of the hand, a very common "ending" element (see fig. 37, j, k) with a grotesque head superfix, also another "ending sign" (see i, r, u, v of the plate just named). In glyph 4 follows the particular katun (Katun 15) whose end is here recorded. This date corresponds to the Initial Series 9.15.0.0.0 4 Ahau 13 Yax.
Cases where tun endings are recorded are exceedingly rare. The bare statement that a certain tun, as Tun 10, for example, had come to its end left much to be desired in the way of accuracy, since there was a Tun 10 in every katun, and consequently any given tun recurred after an interval of 20 years; in other words, there were three or four different Tun 10's to be distinguished from one another in the average lifetime. Indeed, to keep them apart at all it was necessary either to add the particular katun in which each fell or to add the date on which each closed. The former was a step away from the brevity which probably prompted the use of Period-ending dating in the first place, and the latter imposed too great a task on the memory, that is, keeping in mind the 60 or 70 various tun endings which the average lifetime included. For these reasons tun-ending dates occur but rarely, only when there was little or no doubt concerning the particular katun in which they fell.
In plate 21, F, is figured a tun-ending date from the tablet in the Temple of the Inscription at Palenque.[99] In glyph 1 appears an ending sign showing the hand element and the grotesque flattened head (for the latter see fig. 37, i, r, u, v), both common ending signs. The remaining element, another grotesque head with a flaring postfix, is an unusual variant of the tun head found only at Palenque (see fig. 29, h). The presence of the tun sign with these two ending signs indicates probably that some tun ending follows. Glyphs 2 and 3 record the date 5 Ahau 18 Tzec, and glyph 4 records Tun 13. We have here then the record of a Tun 13, which ended on the date 5 Ahau 18 Tzec. But which of the many Tun 13s in the Long Count was the one that ended on this particular date? To begin with, we are perfectly justified in assuming that this particular tun occurred somewhere in Cycle 9, but this assumption does not aid us greatly, since there were twenty different Tun 13s in Cycle 9, one for each of the twenty katuns. However, in the full text of the inscription from which this example is taken, 5 Ahau 3 Chen is the date next preceding, and although the fact is not recorded, this latter date closed Katun 8 of Cycle 9. Moreover, shortly after the tun-ending date here under discussion, the date "3 Ahau 3 Zotz, end of Katun 9," is recorded. It seems likely, therefore, that this particular Tun 13, which ended on the date 5 Ahau 18 Tzec, was 9.8.13.0.0 of the Long Count, after 9.8.0.0.0 but before 9.9.0.0.0. Reducing this number to units of the first order, and applying the several rules given for solving Initial Series, the terminal date of 9.8.13.0.0 will be found to agree with the terminal date recorded in glyphs 2 and 3, namely, 5 Ahau 18 Tzec, and this tun ending corresponded, therefore, to the Initial Series 9.8.13.0.0 5 Ahau 18 Tzec.
Another tun-ending date from Stela 5 at Tikal is figured in plate 21, G.[100] In glyphs 1 and 2 the date 4 Ahau 8 Yaxkin appears, the month sign being represented as a head variant, which has the essential elements of the sign for Yaxkin (see fig. 19, k, l). Following this in glyph 3 is Tun 13, to which is prefixed the same ending-sign variant as the prefixial or superfixial elements in figure 37, i, r, u, v. We have recorded here then "Tun 13 ending on 4 Ahau 8 Yaxkin," though there seems to be no mention elsewhere in this inscription of the number of the katun in which this particular tun fell. By referring to Great Cycle 54 of Goodman's Tables (Goodman, 1897), however, it appears that Tun 13 of Katun 15 of Cycle 9 closed with this date 4 Ahau 8 Yaxkin, and we may assume, therefore, that this is the correct position in the Long Count of the tun-ending date here recorded. This date corresponds to the Initial Series 9.15.13.0.0 4 Ahau 8 Yaxkin.
There is a very unusual Period-ending date on the west side of Stela C at Quirigua[101] (see pl. 21, H). In glyphs 1 and 2 appears the number 0 kins, 0 uinals, 5 tuns, and 17 katuns, which we may write 17.5.0.0 and following this in glyphs 3 and 4 is the date 6 Ahau 13 Kayab. At first sight this would appear to be a Secondary Series, the number 17.5.0.0 being counted forward from some preceding date to reach the date 6 Ahau 13 Kayab recorded just after it. The next date preceding this on the west side of Stela C at Quirigua is the Initial-series terminal date 6 Ahau 13 Yaxkin, illustrated together with its corresponding Initial-series number in figure 68, A. However, all attempts to reach the date 6 Ahau 13 Kayab by counting either forward or backward the number 17.5.0.0 from the date 6 Ahau 13 Yaxkin will prove unsuccessful, and we must seek another explanation for the four glyphs here under discussion. If this were a Period-ending date it would mean that Tun 5 of Katun 17 came to an end on the date 6 Ahau 13 Kayab. Let us see whether this is true. Assuming that our cycle coefficient is 9, as we have done in all the other Period-ending dates presented, we may express glyphs 1 and 2 as the following Initial-series number, provided they represent a period ending, not a Secondary-series number: 9.17.5.0.0. Reducing this number to units of the 1st order, and applying the rules previously given for solving Initial Series, the terminal date reached will be 6 Ahau 13 Kayab, identical with the date recorded in glyphs 3 and 4. We may conclude, therefore, that this example records the fact that "Tun 5 of Katun 17 ended on the date 6 Ahau 13 Kayab," this being identical with the Initial Series 9.17.5.0.0 6 Ahau 13 Kayab.
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 22

EXAMPLES OF PERIOD-ENDING DATES IN CYCLES OTHER THAN CYCLE 9
The foregoing Period-ending dates have all been in Cycle 9, even though this fact has not been recorded in any of the above examples. We come next to the consideration of Period-ending dates which occurred in cycles other than Cycle 9.
In plate 22, A, is figured a Period-ending date from the tablet in the Temple of the Cross at Palenque.[102] In glyphs 1 and 2 appears the date 4 Ahau 8 Cumhu (compare the month form in glyph 2 with fig. 19, g', h'), and in glyph 3 an ending sign (compare glyph 3 with the ending signs in fig. 37, l-q, and with the zero signs in fig. 54). There follows in glyph 4, Cycle 13. These four glyphs record the fact, therefore, that Cycle 13 closed on the date 4 Ahau 8 Cumhu, the starting point of Maya chronology. This same date is again recorded on a round altar at Piedras Negras (see pl. 22, B).[103] In glyphs 1 and 2 appears the date 4 Ahau 8 Cumhu, and in glyph 3a the ending sign, which is identical with the ending sign in the preceding example, both having the clasped hand, the subfix showing a curl infix, and the tassel-like postfix. Compare also figure 37, l-q, and figure 54. Glyph 3b clearly records Cycle 13. The dates in plate 22, A, B, are therefore identical. In both cases the cycle is expressed by its normal form.
In plate 22, C, is figured a Period-ending date from the tablet in the Temple of the Foliated Cross at Palenque.[104] In glyph 1 appears an ending sign in which the hand element and tassel-like postfix show clearly. This is followed in glyph 2 by Cycle 2, the clasped hand on the head variant unmistakably indicating the cycle head. Finally, in glyphs 3 and 4 appears the date 2 Ahau 3 Uayeb (compare the month form with fig. 19, i').[105] The glyphs in plate 22, C, record, therefore, the fact that Cycle 2 closed on the date 2 Ahau 3 Uayeb, a fact which the student may prove for himself by converting this Period-ending date into its corresponding Initial Series and solving the same. Since the end of a cycle is recorded here, it is evident that the katun, tun, uinal, and kin coefficients must all be 0, and our Initial-series number will be, therefore, 2.0.0.0.0. Reducing this to units of the 1st order and proceeding as in the case of Initial Series, the terminal date reached will be 2 Ahau 3 Uayeb, just as recorded in glyphs 3 and 4. The Initial Series corresponding to this Period-ending date will be 2.0.0.0.0 2 Ahau 3 Uayeb.
These three Period-ending dates (pl. 22, A-C) are not to be considered as referring to times contemporaneous with the erection of the monuments upon which they are severally inscribed, since they precede the opening of Cycle 9, the first historic epoch of the Maya civilization, by periods ranging from 2,700 to 3,500 years. As explained elsewhere, they probably referred to mythological events. There is a date, however, on a tablet in the Temple of the Cross at Palenque which falls in Cycle 8, being fixed therein by an adjoining Period-ending date that may have been historical. This case is figured in plate 22, G.[106] In glyphs 4 and 5 appears the date 8 Ahau 13 Ceh (compare the month form in glyph 5 with fig. 16, u, v). This is followed in glyph 6 by a sign which shows the same ending element as the forms in figure 37, i, r, u, v, and this in turn is followed by Cycle 9 in glyph 7. The date recorded in this case is Cycle 9 ending on the date 8 Ahau 13 Ceh, which corresponds to the Initial Series 9.0.0.0.0 8 Ahau 13 Ceh.
Now, in glyphs 1 and 2 is recorded the date 2 Caban 10 Xul (compare the day sign with fig. 16, a', b', and the month sign with fig. 19, i, j), and following this date in glyph 3 is the number 3 kins, 6 uinals, or 6.3. This looks so much like a Secondary Series that we are justified in treating it as such until it proves to be otherwise. As the record stands, it seems probable that if we count this number 6.3 in glyph 3 forward from the date 2 Caban 10 Xul in glyphs 1 and 2, the terminal date reached will be the date recorded in glyphs 4 and 5; that is, the next date following the number. Reducing 6.3 to units of the first order, we have:
| Glyph 3 = | 6 × | 20 = | 120 |
| Glyph 3 = | 3 × | 1 = | 3 |
| —— | |||
| 123 | |||
Counting this number forward from 2 Caban 10 Xul according to the rules which apply in such cases, the terminal day reached will be 8 Ahau 13 Ceh, exactly the date which is recorded in glyphs 4 and 5. But this latter date, we have just seen, is declared by the text to have closed Cycle 9, and therefore corresponded with the Initial Series 9.0.0.0.0 8 Ahau 13 Ceh. Hence, from this known Initial Series we may calculate the Initial Series of the date 2 Caban 10 Xul by subtracting from 9.0.0.0.0 the number 6.3, by which the date 2 Caban 10 Xul precedes the date 9.0.0.0.0 8 Ahau 13 Ceh:
| 9. | 0. | 0. | 0. | 0 | 8 Ahau 13 Ceh |
| 6. | 3 | ||||
| 8. | 19. | 19. | 11. | 17 | 2 Caban 10 Xul |
This latter date fell in Cycle 8, as its Initial Series indicates. It is quite possible, as stated above, that this date may have referred to some actual historic event in the annals of Palenque, or at least of the southern Maya, though the monument upon which it is recorded probably dates from an epoch at least 200 years later.
In a few cases Cycle-10 ending dates have been found. Some of these are surely "contemporaneous," that is, the monuments upon which they appear really date from Cycle 10, while others are as surely "prophetic," that is, the monuments upon which they are found antedate Cycle 10. Examples of both kinds follow.
In plate 22, E, is figured a Period-ending date from Stela 8 at Copan.[107] Glyphs 1 and 2 declare the date 7 Ahau 18 ?, the month sign in glyph 2 being effaced. In glyph 3 is recorded Cycle 10, the cycle sign being expressed by its corresponding head variant. Note the clasped hand, the essential characteristic of the cycle head. Above this appears the same ending sign as that shown in figure 37, a-h, and it would seem probable, therefore, that these three glyphs record the end of Cycle 10. Let us test this by changing the Period-ending date in glyph 3 into its corresponding Initial-series number and then solving this for the resulting terminal date. Since the end of a cycle is here indicated, the katun, tun, uinal, and kin coefficients must be 0 and the Initial-series number will be, therefore, 10.0.0.0.0. Reducing this to units of the first order and applying the rules indicated in such cases, the resulting terminal date will be found to be 7 Ahau 18 Zip. But this agrees exactly with the date recorded in glyphs 1 and 2 so far as the latter go, and since the two agree so far as they go, we may conclude that glyphs 1-3 in plate 22, E, express "Cycle 10 ending on the date 7 Ahau 18 Zip." Although this is a comparatively late date for Copan, the writer is inclined to believe that it was "contemporaneous" rather than "prophetic."
The same can not be said, however, for the Cycle-10 ending date on Zoömorph G at Quirigua (see pl. 22, F). Indeed, this date, as will appear below, is almost surely "prophetic" in character. Glyphs 1 and 2 record the date 7 Ahau 18 Zip (compare the month form in glyph 2 with fig. 19, d) and glyph 3 shows very clearly "the end of Cycle 10." Compare the ending prefix in glyph 4 with the same element in fig. 37, a-h. Hence we have recorded here the fact that "Cycle 10 ended on the date 7 Ahau 18 Zip," a fact proved also by calculation in connection with the preceding example. Does this date represent, therefore, the contemporaneous time of Zoömorph G, the time at which it was erected, or at least dedicated? Before answering this question, let us consider the rest of the text from which this example is taken. The Initial Series on Zoömorph G at Quirigua has already been shown in figure 70, and, according to page 187, it records the date 9.17.15.0.0 5 Ahau 3 Muan. On the grounds of antecedent probability, we are justified in assuming at the outset that this date therefore indicates the epoch or position of Zoömorph G in the Long Count, because it alone appears as an Initial Series. In the case of all the other monuments at Quirigua,[108] where there is but one Initial Series in the inscription, that Initial Series marks the position of the monument in the Long Count. It seems likely, therefore, judging from the general practice at Quirigua, that 9.17.15.0.0 5 Ahau 3 Muan was the contemporaneous date of Zoömorph G, not 10.0.0.0.0 7 Ahau 18 Zip, that is, the Initial Series corresponding to the Period-ending date here under discussion (see pl. 22, F).[109]
Other features of this text point to the same conclusion. In addition to the Initial Series on this monument there are upward of a dozen Secondary-series dates, all of which except one lead to 9.17.15.0.0 5 Ahau 3 Muan. Moreover, this latter date is recorded thrice in the text, a fact which points to the conclusion that it was the contemporaneous date of this monument.
There is still another, perhaps the strongest reason of all, for believing that Zoömorph G dates from 9.17.15.0.0 5 Ahau 3 Muan rather than from 10.0.0.0.0 7 Ahau 18 Zip. If assigned to the former date, every hotun from 9.15.15.0.0 9 Ahau 18 Xul to 9.19.0.0.0 9 Ahau 18 Mol has its corresponding marker or period-stone at Quirigua, there being not a single break in the sequence of the fourteen monuments necessary to mark the thirteen hotun endings between these two dates. If, on the other hand, the date 10.0.0.0.0 7 Ahau 18 Zip is assigned to this monument, the hotun ending 9.17.15.0.0 5 Ahau 3 Muan is left without its corresponding monument at this city, as are also all the hotuns after 9.19.0.0.0 9 Ahau 18 Mol up to 10.0.0.0.0 7 Ahau 18 Zip, a total of four in all. The perfect sequence of the monuments at Quirigua developed by regarding Zoömorph G as dating from 9.17.15.0.0 5 Ahau 3 Muan, and the very fragmentary sequence which arises if it is regarded as dating from 10.0.0.0.0 7 Ahau 18 Zip, is of itself practically sufficient to prove that the former is the correct date, and when taken into consideration with the other points above mentioned leaves no room for doubt.
If this is true, as the writer believes, the date "Cycle 10 ending on 7 Ahau 18 Zip" on Zoömorph G is "prophetic" in character, since it did not occur until nearly 45 years after the erection of the monument upon which it was recorded, at which time the city of Quirigua had probably been abandoned, or at least had lost her prestige.
Another Cycle-10 ending date, which differs from the preceding in that it is almost surely contemporaneous, is that on Stela 11 at Seibal, the latest of the great southern sites.[110] This is figured in plate 22, D. Glyphs 1 and 2 show very clearly the date 7 Ahau 18 Zip, and glyph 3 declares this to be "at the end of Cycle 10."[111] Compare the ending-sign superfix in glyph 3 with figure 37, a-h. This glyph is followed by 1 katun in 4, which in turn is followed by the date 5 Ahau 3 Kayab in 5 and 6. Finally, glyph 7 declares "The end of Katun 1." Counting forward 1 katun from 10.0.0.0.0 7 Ahau 18 Zip, the date reached will be 5 Ahau 3 Kayab, as recorded by 5 and 6, and the Initial Series corresponding to this date will be 10.1.0.0.0 5 Ahau 3 Kayab, as declared by glyph 7. See below:
| 10. | 0. | 0. | 0. | 0 | 7 Ahau 18 Zip |
| 1. | 0. | 0. | 0 | ||
| 10. | 1. | 0. | 0. | 0 | 5 Ahau 3 Kayab |
| End of Katun 1. | |||||
This latter date is found also on Stelæ 8, 9, and 10, at the same city.
Another Cycle-10 ending date which was probably "prophetic", like the one on Zoömorph G at Quirigua, is figured on Altar S at Copan (see fig. 81). In the first glyph on the left appears an Initial-series introducing glyph; this is followed in glyphs 1-3 by the Initial-series number 9.15.0.0.0, which the student will find leads to the terminal date 4 Ahau 13 Yax recorded in glyph 4. This whole Initial Series reads, therefore, 9.15.0.0.0 4 Ahau 13 Yax. In glyph 6a is recorded 5 katuns and in glyph 7 the date 7 Ahau 18 Zip, in other words, a Secondary Series.[112] Reducing the number in glyph 6a to units of the first order, we have:
| 6a = | 5 × | 7,200 = | 36,000 | |
| 0 × | 360 = | 0 | ||
| Not recorded | 0 × | 20 = | 0 | |
| 0 × | 1 = | 0 | ||
| ——— | ||||
| 36,000 | ||||

Fig. 81. The Initial Series, Secondary Series, and Period-ending date on Altar S, Copan.
Counting this number forward from the date 4 Ahau 13 Yax, the terminal date reached will be found to agree with the date recorded in glyph 7, 7 Ahau 18 Zip. But turning to our text again, we find that this date is declared by glyph 8a to be at the end of Cycle 10. Compare the ending sign, which appears as the superfix in glyph 8a, with figure 37, a-h. Therefore the Secondary-series date 7 Ahau 18 Zip, there recorded, closed Cycle 10. The same fact could have been determined by adding the Secondary-series number in glyph 6a to the Initial-series number of the starting point 4 Ahau 13 Yax in glyphs 1-3:
| 9. | 15. | 0. | 0. | 0 | 4 Ahau 13 Yax |
| 5. | (0. | 0. | 0) | ||
| 10. | 0. | 0. | 0. | 0 | 7 Ahau 18 Zip |
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 23

INITIAL SERIES, SECONDARY SERIES, AND PERIOD-ENDING DATES ON STELA 3, PIEDRAS NEGRAS
The "end of Cycle 10" in glyph 8a is merely redundancy. The writer believes that 9.15.0.0.0 4 Ahau 13 Yax indicates the present time of Altar S rather than 10.0.0.0.0 7 Ahau 18 Zip, and that consequently the latter date was "prophetic" in character, as was the same date on Zoömorph G at Quirigua. One reason which renders this probable is that the sculpture on Altar S very closely resembles the sculpture on Stelæ A and B at Copan, both of which date from 9.15.0.0.0 4 Ahau 13 Yax. A possible explanation of the record of Cycle 10 on this monument is the following: On the date of this monument, 9.15.0.0.0 4 Ahau 13 Yax, just three-fourths of Cycle 9 had elapsed. This important fact would hardly have escaped the attention of the old astronomer-priests, and they may have used this monument to point out that only a quarter cycle, 5 katuns, was left in Cycle 9. This concludes the discussion of Cycle-10 Period-ending dates.
The student will note in the preceding example (fig. 81) that Initial-series, Secondary-series, and Period-ending dating have all been used together in the same text, glyphs 1-4 recording an Initial-series date, glyphs 6a and 7, a Secondary-series date, and glyphs 7 and 8a, a Period-ending date. This practice is not at all unusual in the inscriptions and several texts illustrating it are figured below.
Texts Recording Initial Series, Secondary Series, and Period Endings
In plate 23 is shown the inscription on Stela 3 at Piedras Negras. The introducing glyph appears in A1 and is followed by the Initial-series number 9.12.2.0.16 in B1-B3. This number reduced to units of the first order and counted forward from its starting point will be found to reach the terminal date 5 Cib 14 Yaxkin, which the student will readily recognize in A4-B7; the "month-sign indicator" appearing very clearly in A7, with the coefficient 9 affixed to it. Compare the day sign in A4 with figure 16, z, and the month sign in B7 with figure 19, k, l. The Initial Series recorded in A1-A4, B7 reads, therefore, 9.12.2.0.16 5 Cib 14 Yaxkin. In C1 D1 is recorded the number 0 kins, 10 uinals, and 12 tuns; that is, 12.10.0, the first of several Secondary Series in this text. Reducing this to units of the first order and counting it forward from the terminal date of the Initial Series, 5 Cib 14 Yaxkin, the terminal date of the Secondary Series will be found to be 1 Cib 14 Kankin, which the student will find recorded in C2b D2a. The Initial-series value of this latter date may be calculated as follows:
| 9. | 12. | 2. | 0. | 16 | 5 Cib 14 Yaxkin |
| 12. | 10. | 0 | |||
| 9. | 12. | 14. | 10. | 16 | 1 Cib 14 Kankin |
Following along the text, the next Secondary-series number appears in D4-C5a and consists of 10 kins,[113] 11 uinals, 1 tun, and 1 katun; that is, 1.1.11.10. Reducing this number to units of the first order and counting it forward from the date next preceding it in the text, that is, 1 Cib 14 Kankin in C2b D2a, the new terminal date reached will be 4 Cimi 14 Uo, which the student will find recorded in D5-C6. Compare the day sign in D5 with figure 16, h, i, and the month sign in C6 with figure 19, b, c. The Initial-series value of this new date may be calculated from the known Initial-series value of the preceding date:
| 9. | 12. | 14. | 10. | 16 | 1 Cib 14 Kankin |
| 1. | 1. | 11. | 10 | ||
| 9. | 13. | 16. | 4. | 6 | 4 Cimi 14 Uo |
The third Secondary Series appears in E1 and consists of 15 kins,[114] 8 uinals, and 3 tuns, or 3.8.15. Reducing this number to units of the first order and counting it forward from the date next preceding it in the text, 4 Cimi 14 Uo, in D5-C6, the new terminal date reached will be 11 Imix 14 Yax, which the student will find recorded in E2 F2. The day sign in E2 appears, as is very unusual, as a head variant of which only the headdress seems to show the essential element of the day sign Imix. Compare E2 with figure 16, a, b, also the month sign in F2 with figure 19, q, r. The Initial Series of this new terminal date may be calculated as above:
| 9. | 13. | 16. | 4. | 6 | 4 Cimi 14 Uo |
| 3. | 8. | 15 | |||
| 9. | 13. | 19. | 13. | 1 | 11 Imix 14 Yax |
The fourth and last Secondary Series in this text follows in F6 and consists of 19 kins and 4 uinals, that is, 4.19. Reducing this number to units of the first order and counting it forward from the date next preceding it in the text, 11 Imix 14 Yax in E2 F2, the new terminal date reached will be 6 Ahau 13 Muan, which the student will find recorded in F7-F8. Compare the month sign in F8 with figure 19, a' b'. But the glyph following this date in F9 is very clearly an ending sign; note the hand, tassel-like postfix, and subfixial element showing the curl infix, all of which are characteristic ending elements (see figs. 37, l-q, and 54). Moreover, in F10 is recorded "the end of Katun 14." Compare the ending prefix in this glyph with figure 37, a-h. This would seem to indicate that the date in F7-F8, 6 Ahau 13 Muan, closed Katun 14 of Cycle 9 of the Long Count. Whether this be true or not may be tested by finding the Initial-series value corresponding to 6 Ahau 13 Muan, as above:
| 9. | 13. | 19. | 13. | 1 | 11 Imix 14 Yax |
| 4. | 19 | ||||
| 9. | 14. | 0. | 0. | 0 | 6 Ahau 13 Muan |
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 24

INITIAL SERIES, SECONDARY SERIES, AND PERIOD-ENDING DATES ON STELA E (WEST SIDE), QUIRIGUA
This shows that the date 6 Ahau 13 Muan closed Katun 14, as glyphs F9-F10 declare. This may also be verified by changing "the end of Katun 14" recorded in F9-F10 into its corresponding Initial-series value, 9.14.0.0.0, and solving for the terminal date. The day reached by these calculations will be 6 Ahau 13 Muan, as above. This text, in so far as it has been deciphered, therefore reads:
| 9. | 12. | 2. | 0. | 16 | 5 Cib 14 Yaxkin | A1-A4, B7 |
| 12. | 10. | 0 | C1 D1 | |||
| 9. | 12. | 14. | 10. | 16 | 1 Cib 14 Kankin | C2b D2a |
| 1. | 1. | 11. | 10 | D4-C5a | ||
| 9. | 13. | 16. | 4 | . 6 | 4 Cimi 14 Uo | D5-C6 |
| 3. | 8. | 15 | E1 | |||
| 9. | 13. | 19. | 13. | 1 | 11 Imix 14 Yax | E2 F2 |
| 4. | 19 | F6 | ||||
| 9. | 14. | 0. | 0. | 0 | 6 Ahau 13 Muan | F7-F8 |
| End of Katun 14 | F9-F10 | |||||
The inscription just deciphered is worthy of special note for several reasons. In the first place, all its dates and numbers are not only exceedingly clear, thus facilitating their identification, but also unusually regular, the numbers being counted forward from the dates next preceding them to reach the dates next following them in every case; all these features make this text particularly well adapted for study by the beginner. In the second place, this inscription shows the three principal methods employed by the Maya in recording dates, that is, Initial-series dating, Secondary-series dating, and Period-ending dating, all combined in the same text, the example of each one being, moreover, unusually good. Finally, the Initial Series of this inscription records identically the same date as Stela 1 at Piedras Negras, namely, 9.12.2.0.16 5 Cib 14 Yaxkin. Compare plate 23 with plate 17. Indeed, these two monuments, Stelæ 1 and 3, stand in front of the same building. All things considered, the inscription on Stela 3 at Piedras Negras is one of the most satisfactory texts that has been found in the whole Maya territory.
Another example showing the use of these three methods of dating in one and the same text is the inscription on Stela E at Quirigua, illustrated in plate 24 and figure 82.[115] This text begins with the Initial Series on the west side. The introducing glyph appears in A1-B3 and is followed by the Initial-series number 9.14.13[116].4.17 in A4-A6. Reducing this number to units of the first order, remembering the correction in the tun coefficient in A5 noted below, and applying the rules previously given for solving Initial Series, the terminal date reached will be 12 Caban 5 Kayab. This the student will readily recognize in B6-B8b, the form in B8a being the "month sign indicator," here shown with a head-variant coefficient 10. Compare B6 with figure 16, a', b', and B8b with figure 19, d'-f'. This Initial Series therefore should read as follows: 9.14.13.4.17 12 Caban 5 Kayab. Following down the text, there is reached in B10b-A11a, a Secondary-series number consisting of 3 kins, 13 uinals, and 6 tuns, that is, 6.13.3. Counting this number forward from the date next preceding it in the text, 12 Caban 5 Kayab, the date reached will be 4 Ahau 13 Yax, which the student will find recorded in B11. Compare the month form in B11b with figure 19, q, r. But since the Initial-series value of 12 Caban 5 Kayab is known, the Initial-series value of 4 Ahau 13 Yax may be calculated from it as follows:
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab |
| 6. | 13. | 3 | |||
| 9. | 15. | 0. | 0. | 0 | 4 Ahau 13 Yax |

Fig. 82. The Initial Series on Stela E (east side), Quirigua.
The next Secondary-series number appears in B12, plate 24, B, and consists of 6 kins, 14 uinals, and 1 tun, that is, 1.14.6.[117] The student will find that all efforts to reach the next date recorded in the text, 6 Cimi 4 Tzec in A13b B13a, by counting forward 1.14.6 from 4 Ahau 13 Yax in B11, the date next preceding this number, will prove unsuccessful. However, by counting backward 1.14.6 from 6 Cimi 4 Tzec, he will find the date from which the count proceeds is 10 Ahau 8 Chen, though this latter date is nowhere recorded in this text. We have seen elsewhere, on Stela F for example (pl. 19, A, B), that the date 6 Cimi 4 Tzec corresponded to the Initial-series number 9.15.6.14.6; consequently, we may calculate the position of the unrecorded date 10 Ahau 8 Chen in the Long Count from this known Initial Series, by subtracting[118] 1.14.6 from it:
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec |
| 1. | 14. | 6 | |||
| 9. | 15. | 5. | 0. | 0 | 10 Ahau 8 Chen |
We now see that there are 5 tuns, that is, 1 hotun, not recorded here, namely, the hotun from 9.15.0.0.0 4 Ahau 13 Yax, to 9.15.5.0.0 10 Ahau 8 Chen, and further, that the Secondary-series number 1.14.6 in B12 is counted from the unexpressed date 10 Ahau 8 Chen to reach the terminal date 6 Cimi 4 Tzec recorded in A13b B13a.
The next Secondary-series number appears in A14b B14 and consists of 15 kins, 16 uinals, 1 tun, and 1 katun, that is, 1.1.16.15. As in the preceding case, however, all efforts to reach the date following this number, 11 Imix 19 Muan in A15b B15a, by counting it forward from 6 Cimi 4 Tzec, the date next preceding it in the text, will prove unavailing. As before, it is necessary to count it backward from 11 Imix 19 Muan to determine the starting point. Performing this operation, the starting point will be found to be the date 7 Cimi 9 Zotz. Since neither of these two dates, 11 Imix 19 Muan and 7 Cimi 9 Zotz, occurs elsewhere at Quirigua, we must leave their corresponding Initial-series values indeterminate for the present.
The last Secondary Series in this text is recorded in A17b B17a and consists of 19 kins,[119] 4 uinals, and 8 tuns. Reducing this number to units of the first order and counting it forward from the date next preceding it in the text, 11 Imix 19 Muan in A15b B15a, the terminal date reached will be 13 Ahau 18 Cumhu, which the student will find recorded in A18. Compare the month sign with figure 19, g', h'. But immediately following this date in B18a is Katun 17 and in the upper part of B18b the hand-denoting ending. These glyphs A18 and B18 would seem to indicate, therefore, that Katun 17 came to an end on the date 13 Ahau 18 Cumhu. That they do, may be proved beyond all doubt by changing this period ending into its corresponding Initial-series number 9.17.0.0.0 and solving for the terminal date. This will be found to be 13 Ahau 18 Cumhu, which is recorded in A18. This latter date, therefore, had the following position in the Long Count: 9.17.0.0.0 13 Ahau 18 Cumhu. But having determined the position of this latter date in the Long Count, that is, its Initial-series value, it is now possible to fix the positions of the two dates 11 Imix 19 Muan and 7 Cimi 9 Zotz, which we were obliged to leave indeterminate above. Since the date 13 Ahau 18 Cumhu was derived by counting forward 8.4.19 from 11 Imix 19 Muan, the Initial-series value of the latter may be calculated by subtracting 8.4.19 from the Initial-series value of the former:
| 9. | 17. | 0. | 0. | 0 | 13 Ahau 18 Cumhu |
| 8. | 4. | 19 | |||
| 9. | 16. | 11. | 13. | 1 | 11 Imix 19 Muan |
And since the date 11 Imix 19 Muan was reached by counting forward 1.1.16.15 from 7 Cimi 9 Zotz, the Initial-series value of the latter may be calculated by subtracting 1.1.16.15 from the now known Initial-series value of the former:
| 9. | 16. | 11. | 13. | 1 | 11 Imix 19 Muan |
| 1. | 1. | 16. | 15 | ||
| 9. | 15. | 9. | 14. | 6 | 7 Cimi 9 Zotz |
Although this latter date is not recorded in the text, the date next preceding the number 1.1.16.15 is 6 Cimi 4 Tzec, which corresponded to the Initial Series 9.15.6.14.6 6 Cimi 4 Tzec, as we have seen, a date which was exactly 3 tuns earlier than 7 Cimi 9 Zotz, 9.15.9.14.6 - 9.15.6.14.6 = 3.0.0.
The inscription on the west side closes then in A18 B18 with the record that Katun 17 ended on the date 13 Ahau 18 Cumhu. The inscription on the east side of this same monument opens with this same date expressed as an Initial Series, 9.17.0.0.0 13 Ahau 18 Cumhu. See figure 82, A1-A6, A7,[120] and A10.
The reiteration of this date as an Initial Series, when its position in the Long Count had been fixed unmistakably on the other side of the same monument by its record as a Period-ending date, together with the fact that it is the latest date recorded in this inscription, very clearly indicates that it alone designated the contemporaneous time of Stela E, and hence determines the fact that Stela E was a hotun-marker. This whole text, in so far as deciphered, reads as follows:
| West side: | 9.14.13.[121]4.17 | 12 Caban 5 Kayab | Plate 24, A, A1-B5, B8b | ||||
| 6. | 13. | 3 | Plate 24, A, B10b-A11a | ||||
| 9. | 15. | 0. | 0. | 0 | 4 Ahau 13 Yax | Plate 25, A, B11 | |
| [5. | 0. | 0] | Undeclared | ||||
| 9. | 15. | 5. | 0. | 0 | 10 Ahau 8 Chen | " | |
| 1. | 14. | 6 | Plate 24, B, B12 | ||||
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec | Plate 24, B, A13b, B13a | |
| [3. | 0. | 0] | Undeclared | ||||
| 9. | 15. | 9. | 14. | 6 | 7 Cimi 9 Zotz | " | |
| 1. | 1. | 16. | 15 | Plate 24, B, A14b B14 | |||
| 9. | 16. | 11. | 13. | 1 | 11 Imix 19 Muan | Plate 24, B, A15b B15a | |
| 8. | 4. | 19 | Plate 24, B, A17b B17a | ||||
| 9. | 17. | 0. | 0. | 0 | 13 Ahau 18 Cumhu | Plate 24, B, A18 | |
| End of Katun 17 | Plate 24, B, B18 | ||||||
| East side: | 9. | 17. | 0. | 0. | 0 | 13 Ahau 18 Cumhu | Figure 82, A1-A6, A7, A10 |
Comparing the summary of the inscription on Stela E at Quirigua, just given, with the summaries of the inscriptions on Stelæ J and F, and Zoömorph G, at the same city, all four of which are shown side by side in Table XVII,[122] the interrelationship of these four monuments appears very clearly.
Table XVII. INTERRELATIONSHIP OF DATES ON STELÆ E, F, AND J AND ZOÖMORPH G, QUIRIGUA
| Date | Stela J | Stela F | Stela E | Zoömorph G | |||||
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab | X | X | X | X |
| 9. | 15. | 0. | 0. | 0 | 4 Ahau 13 Yax | - | X | X | - |
| 9. | 15. | 5. | 0. | 0 | 10 Ahau 8 Chen | X | - | X | - |
| 9. | 15. | 6. | 14. | 6 | 6 Cimi 4 Tzec | X | X | X | X |
| 9. | 15. | 9. | 14. | 6 | 7 Cimi 9 Zotz | - | - | X | - |
| 9. | 15. | 10. | 0. | 0 | 3 Ahau 3 Mol | - | X | - | - |
| 9. | 16. | 5. | 0. | 0 | 8 AHAU 8 ZOTZ | X | - | - | - |
| 9. | 16. | 10. | 0. | 0 | 1 AHAU 8 ZIP | - | X | - | - |
| 9. | 16. | 11. | 13. | 1 | 11 Imix 19 Muan | - | - | X | - |
| 9. | 17. | 0. | 0. | 0 | 13 AHAU 18 CUMHU | - | - | X | - |
| 9. | 17. | 15. | 0. | 0 | 5 AHAU 3 MUAN | - | - | - | X |
In spite of the fact that each one of these four monuments marks a different hotun in the Long Count, and consequently dates from a different period, all of them go back to the same date, 9.14.13.4.17 12 Caban 5 Kayab, as their original starting point (see above). This date would almost certainly seem, therefore, to indicate some very important event in the annals of Quirigua. Moreover, since it is the earliest date found at this city which can reasonably be regarded as having occurred during the actual occupancy of the site, it is not improbable that it may represent, as explained elsewhere, the time at which Quirigua was founded.[123] It is necessary, however, to caution the student that the above explanation of the date 9.14.13.4.17 12 Caban 5 Kayab, or indeed any other for that matter, is in the present state of our knowledge entirely a matter of conjecture.
Passing on, it will be seen from Table XVII that two of the monuments, namely, Stelæ E and F, bear the date 9.15.0.0.0 4 Ahau 3 Yax, and two others, Stelæ E and J, the date 9.15.5.0.0 10 Ahau 8 Chen, one hotun later. All four come together again, however, with the date 9.15.6.14.6 6 Cimi 4 Tzec, which is recorded on each. This date, like 9.14.13.4.17 12 Caban 5 Kayab, designates probably another important event in Quirigua history, the nature of which, however, again escapes us. After the date 9.15.6.14.6 6 Cimi 4 Tzec, these monuments show no further correspondences, and we may pass over the intervening time to their respective closing dates with but scant notice, with the exception of Zoömorph G, which records a half dozen dates in the hotun that it marks, 9.17.15.0.0 5 Ahau 3 Muan. (These latter are omitted from Table XVII.)
This concludes the presentation of Initial-series, Secondary-series, and Period-ending, dating, with which the student should be sufficiently familiar by this time to continue his researches independently.
It was explained (see p. 76) that, when a Secondary-series date could not be referred ultimately to either an Initial-series date or a Period-ending date, its position in the Long Count could not be determined with certainty, and furthermore that such a date became merely one of the 18,980 dates of the Calendar Round and could be fixed only within a period of 52 years. A few examples of Calendar-round dating are given in figure 83 and plate 25. In figure 83, A, is shown a part of the inscription on Altar M at Quirigua.[124] In A1 B1 appears a number consisting of 0 kins, 2 uinals, and 3 tuns, that is, 3.2.0, and following this in A2b B2, the date 4 Ahau 13 Yax, and in A3b B3 the date 6 Ahau 18 Zac. Compare the month glyphs in B2 and B3 with q and r, and s and t, respectively, of figure 19. This has every appearance of being a Secondary Series, one of the two dates being the starting point of the number 3.2.0, and the other its terminal date. Reducing 3.2.0 to units of the first order, we have:
| B1 = | 3 × | 360 = | 1,080 |
| A1 = | 2 × | 20 = | 40 |
| A1 = | 0 × | 1 = | 0 |
| —— | |||
| 1,120 | |||
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 25

CALENDAR-ROUND DATES ON ALTAR 5, TIKAL
Counting this number forward from 4 Ahau 13 Yax, the nearest date to it in the text, the terminal date reached will be found to be 6 Ahau 18 Zac, the date which, we have seen, was recorded in A3b B3. It is clear, therefore, that this text records the fact that 3.2.0 has been counted forward from the date 4 Ahau 13 Yax and the date 6 Ahau 18 Zac has been reached, but there is nothing given by means of which the position of either of these dates in the Long Count can be determined; consequently either of these dates will be found recurring like any other Calendar-round date, at intervals of every 52 years. In such cases the first assumption to be made is that one of the dates recorded the close of a hotun, or at least of a tun, in Cycle 9 of the Long Count. The reasons for this assumption are quite obvious.

Fig. 83. Calendar-round dates: A, Altar M, Quirigua; B, Altar Z, Copan.
The overwhelming majority of Maya dates fall in Cycle 9, and nearly all inscriptions have at least one date which closed some hotun or tun of that cycle. Referring to Goodman's Tables, in which the tun endings of Cycle 9 are given, the student will find that the date 4 Ahau 13 Yax occurred as a tun ending in Cycle 9, at 9.15.0.0.0 4 Ahau 13 Yax, in which position it closed not only a hotun but also a katun. Hence, it is probable, although the fact is not actually recorded, that the Initial-series value of the date 4 Ahau 13 Yax in this text is 9.15.0.0.0 4 Ahau 13 Yax, and if this is so the Initial-series value of the date 6 Ahau 18 Zac will be:
| 9. | 15. | 0. | 0. | 0 | 4 Ahau 13 Yax |
| 3. | 2. | 0 | |||
| 9. | 15. | 3. | 2. | 0 | 6 Ahau 18 Zac |
In the case of this particular text the Initial-series value 9.15.0.0.0 might have been assigned to the date 4 Ahau 13 Yax on the ground that this Initial-series value appears on two other monuments at Quirigua, namely, Stelæ E and F, with this same date.
In figure 83, B, is shown a part of the inscription from Altar Z at Copan.[125] In A1 B1 appears a number consisting of 1 kin, 8 uinals, and 1 tun, that is, 1.8.1, and following this in B2-A3 is the date 13 Ahau 18 Cumhu, but no record of its position in the Long Count. If 13 Ahau 18 Cumhu is the terminal date of the number 1.8.1, the starting point can be calculated by counting this number backward, giving the date 12 Cauac 2 Zac. On the other hand, if 13 Ahau 18 Cumhu is the starting point, the terminal date reached by counting 1.8.1 forward will be 1 Imix 9 Mol. However, since an ending prefix appears just before the date 13 Ahau 18 Cumhu in A2 (compare fig. 37, a-h), and since another, though it must be admitted a very unusual ending sign, appears just after this date in A3 (compare the prefix of B3 with the prefix of fig. 37, o, and the subfix with the subfixes of l-n and q of the same figure), it seems probable that 13 Ahau 18 Cumhu is the terminal date and also a Period-ending date. Referring to Goodman's Tables, it will be found that the only tun in Cycle 9 which ended with the date 13 Ahau 18 Cumhu was 9.17.0.0.0 13 Ahau 18 Cumhu, which not only ended a hotun but a katun as well.[126]If this is true, the unrecorded starting point 12 Cauac 2 Zac can be shown to have the following Initial-series value:
| 9. | 17. | 0. | 0. | 0 | 13 Ahau 18 Cumhu |
| 1. | 8. | 1 | Backward | ||
| 9. | 16. | 18. | 9. | 19 | 12 Cauac 2 Zac |
In each of the above examples, as we have seen, there was a date which ended one of the katuns of Cycle 9, although this fact was not recorded in connection with either. Because of this fact, however, we were able to date both of these monuments with a degree of probability amounting almost to certainty. In some texts the student will find that the dates recorded did not end any katun, hotun, or even tun, in Cycle 9, or in any other cycle, and consequently such dates can not be assigned to their proper positions in the Long Count by the above method.
The inscription from Altar 5 at Tikal figured in plate 25 is a case in point. This text opens with the date 1 Muluc 2 Muan in glyphs 1 and 2 (the first glyph or starting point is indicated by the star). Compare glyph 1 with figure 16, m, n, and glyph 2 with figure 19, a', b'. In glyphs 8 and 9 appears a Secondary-series number consisting of 18 kins, 11 uinals, and 11 tuns (11.11.18). Reducing this number to units of the first order and counting it forward from the date next preceding it in the text, 1 Muluc 2 Muan in glyphs 1 and 2, the terminal date reached will be 13 Manik 0 Xul, which the student will find recorded in glyphs 10 and 11. Compare glyph 10 with figure 16, j, and glyph 11 with figure 19, i, j. The next Secondary-series number appears in glyphs 22 and 23, and consists of 19 kins, 9 uinals, and 8 tuns (8.9.19). Reducing this to units of the first order and counting forward from the date next preceding it in the text, 13 Manik 0 Xul in glyphs 10 and 11, the terminal date reached will be 11 Cimi 19 Mac, which the student will find recorded in glyphs 24 and 25. Compare glyph 24 with figure 16, h, i, and glyph 25 with figure 19, w, x. Although no number appears in glyph 26, there follows in glyphs 27 and 28 the date 1 Muluc 2 Kankin, which the student will find is just three days later than 11 Cimi 19 Mac, that is, one day 12 Manik 0 Kankin, two days 13 Lamat 1 Kankin, and three days 1 Muluc 2 Kankin.
In spite of the fact that all these numbers are counted regularly from the dates next preceding them to reach the dates next following them, there is apparently no glyph in this text which will fix the position of any one of the above dates in the Long Count. Moreover, since none of the day parts show the day sign Ahau, it is evident that none of these dates can end any uinal, tun, katun, or cycle in the Long Count, hence their positions can not be determined by the method used in fixing the dates in figure 83, A and B.
There is, however, another method by means of which Calendar-round dates may sometimes be referred to their proper positions in the Long Count. A monument which shows only Calendar-round dates may be associated with another monument or a building, the dates of which are fixed in the Long Count. In such cases the fixed dates usually will show the positions to which the Calendar-round dates are to be referred.
Taking any one of the dates given on Altar 5 in plate 25, as the last, 1 Muluc 2 Kankin, for example, the positions at which this date occurred in Cycle 9 may be determined from Goodman's Tables to be as follows:
| 9. | 0. | 16. | 5. | 9 | 1 Muluc 2 Kankin |
| 9. | 3. | 9. | 0. | 9 | 1 Muluc 2 Kankin |
| 9. | 6. | 1. | 13. | 9 | 1 Muluc 2 Kankin |
| 9. | 8. | 14. | 8. | 9 | 1 Muluc 2 Kankin |
| 9. | 11. | 7. | 3. | 9 | 1 Muluc 2 Kankin |
| 9. | 13. | 19. | 16. | 9 | 1 Muluc 2 Kankin |
| 9. | 16. | 12. | 11. | 9 | 1 Muluc 2 Kankin |
| 9. | 19. | 5. | 6. | 9 | 1 Muluc 2 Kankin |
Next let us ascertain whether or not Altar 5 was associated with any other monument or building at Tikal, the date of which is fixed unmistakably in the Long Count. Says Mr. Teobert Maler, the discoverer of this monument:[127] "A little to the north, fronting the north side of this second temple and very near it, is a masonry quadrangle once, no doubt, containing small chambers and having an entrance to the south. In the middle of this quadrangle stands Stela 16 in all its glory, still unharmed, and in front of it, deeply buried in the earth, we found Circular Altar 5, which was destined to become so widely renowned." It is evident from the foregoing that the altar we are considering here, called by Mr. Maler "Circular Altar 5," was found in connection with another monument at Tikal, namely, Stela 16. But the date on this latter monument has already been deciphered as "6 Ahau 13 Muan ending Katun 14" (see pl. 21, D; also p. 224), and this date, as we have seen, corresponded to the Initial Series 9.14.0.0.0 6 Ahau 13 Muan.
Our next step is to ascertain whether or not any of the Initial-series values determined above as belonging to the date 1 Muluc 2 Kankin on Altar 5 are near the Initial Series 9.14.0.0.0 6 Ahau 13 Muan, which is the Initial-series date corresponding to the Period-ending date on Stela 16. By comparing 9.14.0.0.0 with the Initial-series values of 1 Muluc 2 Kankin given above the student will find that the fifth value, 9.13.19.16.9, corresponds with a date 1 Muluc 2 Kankin, which was only 31 days (1 uinal and 11 kins) earlier than 9.14.0.0.0 6 Ahau 13 Muan. Consequently it may be concluded that 9.13.19.16.9 was the particular day 1 Muluc 2 Kankin which the ancient scribes had in mind when they engraved this text. From this known Initial-series value the Initial-series values of the other dates on Altar 5 may be obtained by calculation. The texts on Altar 5 and Stela 16 are given below to show their close connection:
| Altar 5 | ||||||
| 9. | 12. | 19. | 12. | 9 | 1 Muluc 2 Muan | glyphs 1 and 2 |
| 11. | 11. | 18 | glyphs 8 and 9 | |||
| 9. | 13. | 11. | 6. | 7 | 13 Manik 0 Xul | glyphs 10 and 11 |
| 8. | 9. | 19 | glyphs 22 and 23 | |||
| 9. | 13. | 19. | 16. | 6 | 11 Cimi 19 Mac | glyphs 24 and 25 |
| (3) | undeclared | |||||
| 9. | 13. | 19. | 16. | 9 | 1 Muluc 2 Kankin | glyphs 27 and 28 |
| (1. | 11) | (Time between the two monuments, 31 days.) | ||||
| Stela 16 | ||||||
| 9. | 14. | 0. | 0. | 0 | 6 Ahau 13 Muan | A1-A4 |
Sometimes, however, monuments showing Calendar-round dates stand alone, and in such cases it is almost impossible to fix their dates in the Long Count. At Yaxchilan in particular Calendar-round dating seems to have been extensively employed, and for this reason less progress has been made there than elsewhere in deciphering the inscriptions.
Errors in the Originals
Before closing the presentation of the subject of the Maya inscriptions the writer has thought it best to insert a few texts which show actual errors in the originals, mistakes due to the carelessness or oversight of the ancient scribes.

Fig. 84. Texts showing actual errors in the originals: A, Lintel, Yaxchilan; B, Altar Q, Copan; C, Stela 23, Naranjo.
Errors in the original texts may be divided into two general classes: (1) Those which are revealed by inspection, and (2) those which do not appear until after the indicated calculations have been made and the results fail to agree with the glyphs recorded.
An example of the first class is illustrated in figure 84, A. A very cursory inspection of this text—an Initial Series from a lintel at Yaxchilan—will show that the uinal coefficient in C1 represents an impossible condition from the Maya point of view. This glyph as it stands unmistakably records 19 uinals, a number which had no existence in the Maya system of numeration, since 19 uinals are always recorded as 1 tun and 1 uinal.[128] Therefore the coefficient in C1 is incorrect on its face, a fact we have been able to determine before proceeding with the calculation indicated. If not 19, what then was the coefficient the ancient scribe should have engraved in its place? Fortunately the rest of this text is unusually clear, the Initial-series number 9.15.6.?.1 appearing in B1-D1, and the terminal date which it reaches, 7 Imix 19 Zip, appearing in C2 D2. Compare C2 with figure 16, a, b, and D2 with figure 19, d. We know to begin with that the uinal coefficient must be one of the eighteen numerals 0 to 17, inclusive. Trying 0 first, the number will be 9.15.6.0.1, which the student will find leads to the date 7 Imix 4 Chen. Our first trial, therefore, has proved unsuccessful, since the date recorded is 7 Imix 19 Zip. The day parts agree, but the month parts are not the same. This month part 4 Chen is useful, however, for one thing, it shows us how far distant we are from the month part 19 Zip, which is recorded. It appears from Table XV that in counting forward from position 4 Chen just 260 days are required to reach position 19 Zip. Consequently, our first trial number 9.15.6.0.1 falls short of the number necessary by just 260 days. But 260 days are equal to 13 uinals; therefore we must increase 9.15.6.0.1 by 13 uinals. This gives us the number 9.15.6.13.1. Reducing this to units of the first order and solving for the terminal date, the date reached will be 7 Imix 19 Zip, which agrees with the date recorded, in C2 D2. We may conclude, therefore, that the uinal coefficient in C1 should have been 13, instead of 19 as recorded.
Another error of the same kind—that is, one which may be detected by inspection—is shown in figure 84, B. Passing over glyphs 1, 2, and 3, we reach in glyph 4 the date 5 Kan 13 Uo. Compare the upper half of 4 with figure 16, f, and the lower half with figure 19, b, c. The coefficient of the month sign is very clearly 13, which represents an impossible condition when used to indicate the position of a day whose name is Kan; for, according to Table VII, the only positions which the day Kan can ever occupy in any division of the year are 2, 7, 12, and 17. Hence, it is evident that we have detected an error in this text before proceeding with the calculations indicated. Let us endeavor to ascertain the coefficient which should have been used with the month sign in glyph 4 instead of the 13 actually recorded. These glyphs present seemingly a regular Secondary Series, the starting point being given in 1 and 2, the number in 3, and the terminal date in 4. Counting this number 3.4 forward from the starting point, 6 Ahau 13 Kayab, the terminal date reached will be 5 Kan 12 Uo. Comparing this with the terminal date actually recorded, we find that the two agree except for the month coefficient. But since the date recorded represents an impossible condition, as we have shown, we are justified in assuming that the month coefficient which should have been used in glyph 4 was 12, instead of 13. In other words, the craftsman to whom the sculpturing of this inscription was intrusted engraved here 3 dots instead of 2 dots, and 1 ornamental crescent, which, together with the 2 bars present, would have given the month coefficient determined by calculation, 12. An error of this kind might occur very easily and indeed in many cases may be apparent rather than real, being due to weathering rather than to a mistake in the original text.
Some errors in the inscriptions, however, can not be detected by inspection, and develop only after the calculations indicated have been performed, and the results are found to disagree with the glyphs recorded. Errors of this kind constitute the second class mentioned above. A case in point is the Initial Series on the west side of Stela E at Quirigua, figured in plate 24, A. In this text the Initial-series number recorded in A4-A6 is very clearly 9.14.12.4.17, and the terminal date in B6-B8b is equally clearly 12 Caban 5 Kayab. Now, if this number 9.14.12.4.17 is reduced to units of the first order and is counted forward from the same starting point as practically all other Initial Series, the terminal date reached will be 3 Caban 10 Kayab, not 12 Caban 5 Kayab, as recorded. Moreover, if the same number is counted forward from the date 4 Ahau 8 Zotz, which may have been another starting point for Initial Series, as we have seen, the terminal date reached will be 3 Caban 10 Zip, not 12 Caban 5 Kayab, as recorded. The inference is obvious, therefore, that there is some error in this text, since the number recorded can not be made to reach the date recorded. An error of this kind is difficult to detect, because there is no indication in the text as to which glyph is the one at fault. The first assumption the writer makes in such cases is that the date is correct and that the error is in one of the period-glyph coefficients. Referring to Goodman's Table, it will be found that the date 12 Caban 5 Kayab occurred at the following positions in Cycle 9 of the Long Count:
| 9. | 1. | 9. | 11. | 17 | 12 Caban 5 Kayab |
| 9. | 4. | 2. | 6. | 17 | 12 Caban 5 Kayab |
| 9. | 6. | 15. | 1. | 17 | 12 Caban 5 Kayab |
| 9. | 9. | 7. | 14. | 17 | 12 Caban 5 Kayab |
| 9. | 12. | 0. | 9. | 17 | 12 Caban 5 Kayab |
| 9. | 14. | 13. | 4. | 17 | 12 Caban 5 Kayab |
| 9. | 17. | 5. | 17. | 17 | 12 Caban 5 Kayab |
| 9. | 19. | 18. | 12. | 17 | 12 Caban 5 Kayab |
An examination of these values will show that the sixth in the list, 9.14.13.4.17, is very close to the number recorded in our text, 9.14.12.4.17. Indeed, the only difference between the two is that the former has 13 tuns while the latter has only 12. The similarity between these two numbers is otherwise so close and the error in this event would be so slight—the record of 2 dots and 1 ornamental crescent instead of 3 dots—that the conclusion is almost inevitable that the error here is in the tun coefficient, 12 having been recorded instead of 13. In this particular case the Secondary Series and the Period-ending date, which follow the Initial-series number 9.14.12.4.17, prove that the above reading of 13 tuns for the 12 actually recorded is the one correction needed to rectify the error in this text.
Another example indicating an error which can not be detected by inspection is shown in figure 84, C. In glyphs 1 and 2 appears the date 8 Eznab 16 Uo (compare glyph 1 with fig. 16, c', and glyph 2 with fig. 19, b, c). In glyph 3 follows a number consisting of 17 kins and 4 uinals (4.17). Finally, in glyphs 4 and 5 is recorded the date 2 Men 13 Yaxkin (compare glyph 4 with fig. 16, y, and glyph 5 with fig. 19, k, l). This has every appearance of being a Secondary Series, of which 8 Eznab 16 Uo is the starting point, 4.17, the number to be counted, and 2 Men 13 Yaxkin the terminal date. Reducing 4.17 to units of the first order and counting it forward from the starting point indicated, the terminal date reached will be 1 Men 13 Yaxkin. This differs from the terminal date recorded in glyphs 4 and 5 in having a day coefficient of 1 instead of 2. Since this involves but a very slight change in the original text, we are probably justified in assuming; that the day coefficient in glyph 4 should have been 1 instead of 2 as recorded.
One more example will suffice to show the kind of errors usually encountered in the inscriptions. In plate 26 is figured the Initial Series from Stela N at Copan. The introducing glyph appears in A1 and is followed by the Initial-series number 9.16.10.0.0 in A2-A6, all the coefficients of which are unusually clear. Reducing this to units of the first order and solving for the terminal date, the date reached will be 1 Ahau 3 Zip. This agrees with the terminal date recorded in A7-A15 except for the month coefficient, which is 8 in the text instead of 3, as determined by calculation. Assuming that the date recorded is correct and that the error is in the coefficient of the period glyphs the next step is to find the positions in Cycle 9 at which the date 1 Ahau 8 Zip occurred. Referring to Goodman's Tables, these will be found to be:
| 9. | 0. | 8. | 11. | 0 | 1 Ahau 8 Zip |
| 9. | 3. | 1. | 6. | 0 | 1 Ahau 8 Zip |
| 9. | 5. | 14. | 1. | 0 | 1 Ahau 8 Zip |
| 9. | 8. | 6. | 14. | 0 | 1 Ahau 8 Zip |
| 9. | 10. | 19. | 9. | 0 | 1 Ahau 8 Zip |
| 9. | 13. | 12. | 4. | 0 | 1 Ahau 8 Zip |
| 9. | 16. | 4. | 17. | 0 | 1 Ahau 8 Zip |
| 9. | 18. | 17. | 12. | 0 | 1 Ahau 8 Zip |
BUREAU OF AMERICAN ETHNOLOGYBULLETIN 57 PLATE 26

INITIAL SERIES ON STELA N, COPAN, SHOWING ERROR IN MONTH COEFFICIENT
The number in the above list coming nearest to the number recorded in this text (9.16.10.0.0) is the next to the last, 9.16.4.17.0. But in order to reach this value of the date 1 Ahau 8 Zip (9.16.4.17.0) with the number actually recorded, two considerable changes in it are first necessary, (1) replacing the 10 tuns in A4 by 4 tuns, that is, changing 2 bars to 4 dots, and (2) replacing 0 uinals in A5 by 17 uinals, that is, changing the 0 sign to 3 bars and 2 dots. But these changes involve a very considerable alteration of the original, and it seems highly improbable, therefore, that the date here intended was 9.16.4.17.0 1 Ahau 8 Zip. Moreover, as any other number in the above list involves at least three changes of the number recorded in order to reach 1 Ahau 8 Zip, we are forced to the conclusion that the error must be in the terminal date, not in one of the coefficients of the period glyphs. Let us therefore assume in our next trial that the Initial-series number is correct as it stands, and that the error lies somewhere in the terminal date. But the terminal date reached in counting 9.16.10.0.0 forward in the Long Count will be 1 Ahau 3 Zip, as we have seen on the preceding page, and this date differs from the terminal date recorded by 5—1 bar in the month coefficient. It would seem probable, therefore, that the bar to the left of the month sign in A15 should have been omitted, in which case the text would correctly record the date 9.16.10.0.0 1 Ahau 3 Zip.
The student will note that in all the examples above given the errors have been in the numerical coefficients, and not in the signs to which they are attached; in other words, that although the numerals are sometimes incorrectly recorded, the period, day, and month glyphs never are.
Throughout the inscriptions, the exceptions to this rule are so very rare that the beginner is strongly advised to disregard them altogether, and to assume when he finds an incorrect text that the error is in one of the numerical coefficients. It should be remembered also in this connection that errors in the inscriptions are exceedingly rare, and a glyph must not be condemned as incorrect until every effort has been made to explain it in some other way.
This concludes the presentation of texts from the inscriptions. The student will have noted in the foregoing examples, as was stated in Chapter II, that practically the only advances made looking toward the decipherment of the glyphs have been on the chronological side. It is now generally admitted that the relative ages[129] of most Maya monuments can be determined from the dates recorded upon them, and that the final date in almost every inscription indicates the time at or near which the monument bearing it was erected, or at least formally dedicated. The writer has endeavored to show, moreover, that many, if indeed not most, of the monuments, were "time markers" or "period stones," in every way similar to the "period stones" which the northern Maya are known to[130] have erected at regularly recurring periods. That the period which was used as this chronological unit may have varied in different localities and at different epochs is not at all improbable. The northern Maya at the time of the Spanish Conquest erected a "period stone" every katun, while the evidence presented in the foregoing texts, particularly those from Quirigua and Copan, indicates that the chronological unit in these two cities at least was the hotun, or quarter-katun period. Whatever may have been the chronological unit used, the writer believes that the best explanation for the monuments found so abundantly in the Maya area is that they were "period stones," erected to commemorate or mark the close of successive periods.
That we have succeeded in deciphering, up to the present time, only the calendric parts of the inscriptions, the chronological skeleton of Maya history as it were, stripped of the events which would vitalize it, should not discourage the student nor lead him to minimize the importance of that which is already gained. Thirty years ago the Maya inscriptions were a sealed book, yet to-day we read in the glyphic writing the rise and fall of the several cities in relation to one another, and follow the course of Maya development even though we can not yet fill in the accompanying background. Future researches, we may hope, will reconstruct this background from the undeciphered glyphs, and will reveal the events of Maya history which alone can give the corresponding chronology a human interest.
- ↑ As used throughout this work, the word "inscriptions" is applied only to texts from the monuments.
- ↑ The term glyph-block has been used instead of glyph in this connection because in many inscriptions several different glyphs are included in one glyph-block. In such cases, however, the glyphs within the glyph-block follow precisely the same order as the glyph-blocks themselves follow in the pairs of columns, that is, from left to right and top to bottom.
- ↑ Initial Series which have all their period glyphs expressed by normal forms are comparatively rare; consequently the four examples presented in pl. 6, although they are the best of their kind, leave something to be desired in other ways. In pl. 6, A, for example, the month sign was partially effaced though it is restored in the accompanying reproduction; in B of the same plate the closing glyph of the Supplementary Series (the month-sign indicator) is wanting, although the month sign itself is very clear. Again, in D the details of the day glyph and month glyph are partially effaced (restored in the reproduction), and in C, although the entire text is very clear, the month sign of the terminal date irregularly follows immediately the day sign. However, in spite of these slight irregularities, it has seemed best to present these particular texts as the first examples of Initial Series, because their period glyphs are expressed by normal forms exclusively, which, as pointed out above, are more easily recognized on account of their greater differentiation than the corresponding head variants.
- ↑ In most of the examples presented in this chapter the full inscription is not shown, only that part of the text illustrating the particular point in question being given. For this reason reference will be made in each case to the publication in which the entire inscription has been reproduced. The full text on Zoömorph P at Quirigua will be found in Maudslay, 1889-1902: II, pls. 53, 54, 55, 56, 57, 59, 63, 64.
- ↑ All glyphs expressed in this way are to be understood as inclusive. Thus A1-B2 signifies 4 glyphs, namely, A1, B1, A2, B2,
- ↑ The introducing glyph, so far as the writer knows, always stands at the beginning of an inscription, or in the second glyph-block, that is, at the top. Hence an Initial Series can never precede it.
- ↑ The Initial Series on Stela 10 at Tikal is the only exception known. See pp. 123-127.
- ↑ As will appear in the following examples, nearly all Initial Series have 9 as their cycle coefficient.
- ↑ In the present case therefore so far as these calculations are concerned, 3,900 is the equivalent of 1,427,400.
- ↑ It should be remembered in this connection, as explained on pp. 47, 55, that the positions in the divisions of the year which the Maya called 3, 8, 13, and 18 correspond in our method of naming the positions of the days in the months to the 4th, 9th, 14th, and 19th positions, respectively.
- ↑ As stated in footnote 1, p. 152, the meaning of the Supplementary Series has not yet been worked out.
- ↑ The reasons which have led the writer to this conclusion are given at some length on pp. 33-36.
- ↑ For the full text of this inscription see Maler, 1908 b: pl. 36.
- ↑ Since nothing but Initial-series texts will be presented in the plates and figures immediately following, a fact which the student will readily detect by the presence of the introducing glyph at the head of each text, it is unnecessary to repeat for each new text step 2 (p. 135) and step 3 (p. 136), which explain how to determine the starting point of the count and the direction of the count, respectively; and the student may assume that the starting point of the several Initial Series hereinafter figured will always be the date 4 Ahau 8 Cumhu and that the direction of the count will always be forward.
- ↑ As will appear later, in connection with the discussion of the Secondary Series, the Initial-series date of a monument does not always correspond with the ending date of the period whose close the monument marks. In other words, the Initial-series date is not always the date contemporaneous with the formal dedication of the monument as a time-marker. This point will appear much more clearly when the function of Secondary Series has been explained.
- ↑ For the full text of this inscription see Hewett, 1911: pl. XXXV C.
- ↑ So far as the writer knows, the existence of a period containing 5 tuns has not been suggested heretofore. The very general practice of closing inscriptions with the end of some particular 5-tun period in the Long Count, as 9.18.5.0.0, or 9.18.10.0.0, or 9.18.15.0.0, or 9.19.0.0.0, for example, seems to indicate that this period was the unit used for measuring time in Maya chronological records, at least in the southern cities. Consequently, it seems likely that there was a special glyph to express this unit.
- ↑ For the full text of this inscription see Maler, 1908 b: pl. 39.
- ↑ The student should note that from this point steps 2 (p. 139) and 3 (p. 140) have been omitted in discussing each text (see p. 162, footnote 3).
- ↑ In each of the above cases—and, indeed, in all the examples following—the student should perform the various calculations by which the results are reached, in order to familiarize himself with the workings of the Maya chronological system.
- ↑ The student may apply a check at this point to his identification of the day sign in A4 as being that for the day Eb. Since the month coefficient in A7 is surely 10 (2 bars), it is clear from Table VII that the only days which can occupy this position in any division of the year are Ik, Manik, Eb, and Caban. Now, by comparing the sign in A4 with the signs for Ik, Manik, and Caban, c, j, and a', b', respectively, of fig. 16, it is very evident that A4 bears no resemblance to any of them; hence, since Eb is the only one left which can occupy a position 10, the day sign in A4 must be Eb, a fact supported by the comparison of A4 with fig. 16, s-u, above.
- ↑ The full text of this inscription will be found in Maudslay, 1889-1901: I, pls. 35-37.
- ↑ The full text of this inscription is given in Maudslay, 1889-1902: I, pls. 27-30.
- ↑ Note the decoration on the numerical bar.
- ↑ So far as known to the writer, this very unusual variant for the closing glyph of the Supplementary Series occurs in but two other inscriptions in the Maya territory, namely, on Stela N at Copan. See pl. 26, Glyph A14, and Inscription 6 of the Hieroglyphic Stairway at Naranjo, Glyph A1 (?). (Maler, 1908 b: pl. 27.)
- ↑ For the full text of this inscription see Maudslay, 1889-1902: I, pls. 105-107.
- ↑ In this glyph-block, A4, the order of reading is irregular; instead of passing over to B4a after reading A4a (the 10 tuns), the next glyph to be read is the sign below A4a, A4b, which records 0 uinals, and only after this has been read does B4a follow.
- ↑ Texts illustrating the head-variant numerals in full will be presented later.
- ↑ The preceding hotun ended with the day 9.12.5.0.0 3 Ahau 3 Xul and therefore the opening day of the next hotun, 1 day later, will be 9.12.5.0.1 4 Imix 4 Xul.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: I, pls. 109, 110.
- ↑ The oldest Initial Series at Copan is recorded on Stela 15, which is 40 years older than Stela 9. For a discussion of this text see pp. 187, 188.
- ↑ An exception to this statement should be noted in an Initial Series on the Hieroglyphic Stairway, which records the date 9.5.19.3.0 8 Ahau 3 Zotz. The above remark applies only to the large monuments, which, the writer believes, were period-markers. Stela 9 is therefore the next to the oldest "period stone" yet discovered at Copan. It is more than likely, however, that there are several older ones as yet undeciphered.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: II, pls. 17-19.
- ↑ Although this date is considerably older than that on Stela 9 at Copan, its several glyphs present none of the marks of antiquity noted in connection with the preceding example (pl. 8, B). For example, the ends of the bars denoting 5 are not square but round, and the head-variant period glyphs do not show the same elaborate and ornate treatment as in the Copan text. This apparent contradiction permits of an easy explanation. Although the Initial Series on the west side of Stela C at Quirigua undoubtedly refers to an earlier date than the Initial Series on the Copan monument, it does not follow that the Quirigua monument is the older of the two. This is true because on the other side of this same stela at Quirigua is recorded another date, 9.17.5.0.0 6 Ahau 13 Kayab, more than three hundred years later than the Initial Series 9.1.0.0.0 6 Ahau 13 Yaxkin on the west side, and this later date is doubtless the one which referred to present time when this monument was erected. Therefore the Initial Series 9.1.0.0.0 6 Ahau 13 Yaxkin does not represent the period which Stela C was erected to mark, but some far earlier date in Maya history.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: I, pl. 74.
- ↑ For the full text of this inscription see Maler, 1903: II, No. 2, pls. 74, 75.
- ↑ For the full text of this inscription see Maler, 1903: II, No. 2, pl. 79, 2.
- ↑ For the full text of this inscription see Maler, 1911: V, No. 1, pl. 15.
- ↑ As used throughout this book, the expression "the contemporaneous date" designates the time when the monument on which such a date is found was put into formal use, that is, the time of its erection. As will appear later in the discussion of the Secondary Series, many monuments present several dates between the extremes of which elapse long periods. Obviously, only one of the dates thus recorded can represent the time at which the monument was erected. In such inscriptions the final date is almost invariably the one designating contemporaneous time, and the earlier dates refer probably to historical, traditional, or even mythological events in the Maya past. Thus the Initial Series 9.0.19.2.4 2 Kan 2 Yax on Lintel 21 at Yaxchilan, 9.1.0.0.0 6 Ahau 13 Yazkin on the west side of Stela C at Quirigua, and 9.4.0.0.0 13 Ahau 18 Yax from the Temple of the Inscriptions at Palenque, all refer probably to earlier historical or traditional events in the past of these three cities, but they do not indicate the dates at which they were severally recorded. As Initial Series which refer to purely mythological events may be classed the Initial Series from the Temples of the Sun, Cross, and Foliated Cross at Palenque, and from the east side of Stela C at Quirigua, all of which are concerned with dates centering around or at the beginning of Maya chronology. Stela 3 at Tikal (the text here under discussion), on the other hand, has but one date, which probably refers to the time of its erection, and is therefore contemporaneous.
- ↑ There are one or two earlier Initial Series which probably record contemporaneous dates; these are not inscribed on large stone monuments but on smaller antiquities, namely, the Tuxtla Statuette and the Leyden Plate. For the discussion of these early contemporaneous Initial Series, see pp. 194-198.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: II, pls. 4-7.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: IV, pls. 80-82.
- ↑ As explained on p. 179, footnote 1, this Initial Series refers probably to some mythological event rather than to any historical occurrence. The date here recorded precedes the historic period of the Maya civilization by upward of 3,000 years.
- ↑ For the full text of this inscription see Maudslay, 1889-1902; IV, pls. 87-89.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: IV, pl. 23.
- ↑ It is clear that if all the period coefficients above the kin have been correctly identified, even though the kin coefficient is unknown, by designating it 0 the date reached will be within 19 days of the date originally recorded. Even though its maximum value (19) had originally been recorded here, it could have carried the count only 19 days further. By using 0 as the kin coefficient, therefore, we can not be more than 19 days from the original date.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: I, pls. 88, 89.
- ↑ While at Copan the writer made a personal examination of this monument and found that Mr. Maudslay's drawing is incorrect as regards the coefficient of the day sign. The original has two numerical dots between two crescents, whereas the Maudslay drawing shows one numerical dot between two distinct pairs of crescents, each pair, however, of different shape.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: II, pls. 41-44.
- ↑ For the text of this monument see Spinden, 1913: VI, pl. 23, 2.
- ↑ For the discussion of full-figure glyphs, see pp. 65-73.
- ↑ The characteristics of the heads for 7, 14, 16, and 19 will be found in the heads for 17, 4, 6, and 9, respectively.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: I, pls. 47, 48.
- ↑ The student will note also in connection with this glyph that the pair of comblike appendages usually found are here replaced by a pair of fishes. As explained on pp. 65-66, the fish represents probably the original form from which the comblike element was derived in the process of glyph conventionalization. The full original form of this element is therefore in keeping with the other full-figure forms in this text.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: I, pls. 66-71.
- ↑ The student should remember that in this diagonal the direction of reading is from bottom to top. See pl. 15, B, glyphs 7, 8, 9, 10, 11, 12, etc. Consequently the upper half of 13 follows the lower half in this particular glyph.
- ↑ For the full text of this inscription see Hewett, 1911: pl. XXII B.
- ↑ A few monuments at Quirigua, namely, Stelæ F, D, E, and A, have two Initial Series each. In A both of the Initial Series have 0 for the coefficients of their uinal and kin glyphs, and in F, D, E, the Initial Series which shows the position of the monument in the Long Count, that is, the Initial Series showing the katun ending which it marks, has 0 for its uinal and kin coefficients.
- ↑ In 1913 Mr. M. D. Landry, superintendent of the Quirigua district, Guatemala division of the United Fruit Co., found a still earlier monument about half a mile west of the main group. This has been named Stela S. It records the katun ending prior to the one on Stela H, i. e., 9.15.15.0.0 9 Ahau 18 Xul.
- ↑ For the full text of this inscription see Holmes, 1907: pp. 691 et seq., and pls. 34-41.
- ↑ For a full discussion of the Tuxtla Statuette, including the opinions of several writers as to its inscription, see Holmes, 1907: pp. 691 et seq. The present writer gives therein at some length the reasons which have led him to accept this inscription as genuine and contemporaneous.
- ↑ For the full text of these inscriptions, see Seler, 1902-1908: II, 253, and 1901 c: I, 23, fig. 7. During his last visit to the Maya territory the writer discovered that Stela 11 at Tikal has a Cycle-10 Initial Series, namely, 10.2.0.0.0. 3 Ahau 3 Ceh.
- ↑ Missing.
- ↑ At Seibal a Period-ending date 10.1.0.0.0 5 Ahau 3 Kayab is clearly recorded, but this is some 30 years earlier than either of the Initial Series here under discussion, a significant period just at this particular epoch of Maya history, which we have every reason to believe was filled with stirring events and quickly shifting scenes. Tikal, with the Initial Series 10.2.0.0.0 3 Ahau 3 Ceh, and Seibal with the same date (not as an Initial Series, however) are the nearest, though even these fall 10 years short of the Quen Santo and Chichen Itza Initial Series.
- ↑ Up to the present time no successful interpretation of the inscription on Stela C at Copan has been advanced. The inscription on each side of this monument is headed by an introducing glyph, but in neither case is this followed by an Initial Series. A number consisting of 11.14.5.1.0 is recorded in connection with the date 6 Ahau 18 Kayab, but as this date does not appear to be fixed in the Long Count, there is no way of ascertaining whether it is earlier or later than the starting point of Maya chronology. Mr. Bowditch (1910: pp. 195-196) offers an interesting explanation of this monument, to which the student is referred for the possible explanation of this text. A personal inspection of this inscription failed to confirm, however, the assumption on which Mr. Bowditch's conclusions rest. For the full text of this inscription, see Maudslay, 1889-1902: I, pls. 39-41.
- ↑ For the full text of this inscription, see ibid.: II, pls. 16, 17, 19.
- ↑ Table XVI contains only 80 Calendar Rounds (1,518,400), but by adding 18 Calendar Rounds (341,640) the number to be subtracted, 98 Calendar Rounds (1,860,040), will be reached.
- ↑ Counting 13.0.0.0.0 backward from the starting point of Maya chronology, 4 Ahau 8 Cumhu, gives the date 4 Ahau 8 Zotz, which is no nearer the terminal date recorded in B5-A6 than the date 4 Ahau 3 Kankin reached by counting forward.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: IV, pls. 73-77.
- ↑ As noted in Chapter IV, this is one of the only two heads for 13 found in the inscriptions which is composed of the essential element of the 10 head applied to the 3 head, the combination of the two giving 13. Usually the head for 13 is represented by a form peculiar to this number alone and is not built up by the combination of lower numbers as in this case.
- ↑ Although at first sight the headdress resembles the tun sign, a closer examination shows that it is not this element.
- ↑ Similarly, it could be shown that the use of every other possible value of the cycle coefficient will not give the terminal date actually recorded.
- ↑ For the full text of this inscription see Maler, 1903: II, No. 2, pl. 56.
- ↑ From this point on this step will be omitted, but the student is urged to perform the calculations necessary in each case to reach the terminal dates recorded.
- ↑ Since the introducing glyph always accompanies an Initial Series, it has here been included as a part of it, though, as has been explained elsewhere, its function is unknown.
- ↑ The number 15.1.16.5 is equal to 108,685 days, or 297½ years.
- ↑ It is interesting to note in this connection that the date 9.16.1.0.0 11 Ahau 8 Tzec, which is within 9 days of 9.16.1.0.9 7 Muluc 17 Tzec, is recorded in four different inscriptions at Yaxchilan, one of which (see pl. 9, A) has already been figured.
- ↑ For the full text of this inscription see Maler, 1901: II, No. 1, pl. 12.
- ↑ The month-sign indicator appears in B2 with a coefficient 10.
- ↑ 80.0 80.1 80.2 Not expressed.
- ↑ The writer has recently established the date of this monument as 9.13.15.0.0 13 Ahau 18 Pax, or 99 days later than the above date.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: II, pls. 47-49.
- ↑ Although the details of the day and month signs are somewhat effaced, the coefficient in each case is 3, agreeing with the coefficients in the Initial-series terminal date, and the outline of the month glyph suggests that it is probably Yax. See fig. 19, q, r.
- ↑ Since the Maya New Year's day, 0 Pop, always fell on the 16th of July, the day 3 Yax always fell on Jan. 15th, at the commencement of the dry season.
- ↑ Since 0 Pop fell on July 16th (Old Style), 18 Kayab fell on June 19th, which is very near the summer solstice, that is, the seeming northern limit of the sun, and roughly coincident with the beginning of the rainy season at Quirigua.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: II, pl. 46.
- ↑ Bracketed dates are those which are not actually recorded but which are reached by numbers appearing in the text.
- ↑ Although not recorded, the number 1.14.6 is the distance from the date 9.15.5.0.0 reached by the Secondary Series on one side to the starting point of the Secondary Series on the other side, that is, 9.15.6.14.6 6 Cimi 4 Tzec.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: II, pls. 37, 39, 40. For convenience in figuring, the lower parts of columns A and B are shown in B instead of below the upper part. The numeration of the glyph-blocks, however, follows the arrangement in the original.
- ↑ This is one of the two Initial Series which justified the assumptions made in the previous text that the date 12 Caban 5 Kayab, which was recorded there, had the Initial-series value 9.14.13.4.17, as here.
- ↑ This is the text in which the Initial-series value 9.15.6.14.6 was found attached to the date 6 Cimi 4 Tzec.
- ↑ For the full text of this inscription see Maudslay, 1889-1902: II, pls. 38, 40.
- ↑ The frontlet seems to be composed of but one element, indicating for this head the value 8 instead of 1. However, as the calculations point to 1, it is probable there was originally another element to the frontlet.
- ↑ See Maudslay, 1889-1902: I, pl. 102, west side, glyphs A5b-A7a.
- ↑ See ibid.: IV, pl. 81, glyphs N15 O15.
- ↑ See Maler, 1908 b: IV, No. 2, pl. 38, east side, glyphs A17-B18.
- ↑ See ibid., 1911: V, pl. 26, glyphs A1-A4.
- ↑ See Maudslay, 1889-1902: I, pl. 104, glyphs A7, B7.
- ↑ See Maudslay, 1889-1902: IV, pl. 60, glyphs M1-N2.
- ↑ Maler, 1911: V, pl. 17, east side, glyphs A4-A5.
- ↑ See Maudslay, 1889-1902: II, pl. 19, west side, glyphs B10-A12.
- ↑ See Maudslay, 1889-1902: IV, pl. 75, glyphs D3-C5.
- ↑ See Maler, 1901: II, No. 1, pl. 8, glyphs A1-A2.
- ↑ See Maudslay, op. cit., pl. 81, glyphs C7-D8.
- ↑ It will be remembered that Uayeb was the name for the xma kaba kin, the 5 closing days of the year. Dates which fall in this period are exceedingly rare, and in the inscriptions, so far as the writer knows, have been found only at Palenque and Tikal.
- ↑ See Maudslay, 1889-1902: IV, pl. 77, glyphs P14-R2. Glyphs Q15-P17 are omitted from pl. 22, G, as they appear to be uncalendrical.
- ↑ See Maudslay, 1889-1902: I, pl. 100, glyphs C1 D1, A2.
- ↑ This excludes Stela C, which has two Initial Series (see figs. 68 and 77), though neither of them, as explained on p. 175, footnote 1, records the date of this monument. The true date of this monument is declared by the Period-ending date figured in pl. 21, H, which is 9.17.0.0.0 6 Ahau 13 Kayab. (See p. 226.)
- ↑ See Maudslay, 1889-1902: II, pl. 44, west side, glyphs G4 H4, F5.
- ↑ The dates 10.2.5.0.0 9 Ahau 18 Yax and 10.2.10.0.0 2 Ahau 13 Chen on Stelæ 1 and 2, respectively, at Quen Santo, are purposely excluded from this statement. Quen Santo is in the highlands of Guatemala (see pl. 1) and is well to the south of the Usamacintla region. It rose to prominence probably after the collapse of the great southern cities and is to be considered as inaugurating a new order of things, if not indeed a new civilization.
- ↑ See Maler, 1908 a: IV, No. 1, pl. 9, glyphs E2, F2, A3, and A4.
- ↑ The student will note that the lower periods (the tun, uinal, and kin signs) are omitted and consequently are to be considered as having the coefficient 0.
- ↑ The usual positions of the uinal and kin coefficients in D4a are reversed, the kin coefficient 10 standing above the uinal sign instead of at the left of it. The calculations show, however, that 10, not 11, is the kin coefficient.
- ↑ In this number also the positions of the uinal and kin coefficients are reversed.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: II, pls. 28-32.
- ↑ The student will note that 12, not 13, tuns are recorded in A5. As explained elsewhere (see pp. 247, 248), this is an error on the part of the ancient scribe who engraved this inscription. The correct tun coefficient is 13, as used above.
- ↑ This Secondary-series number is doubly irregular. In the first place, the kin and uinal coefficients are reversed, the latter standing to the left of its sign instead of above, and in the second place, the uinal coefficient, although it is 14, has an ornamental dot between the two middle dots.
- ↑ Since we counted backward 1.14.6 from 6 Cimi 4 Tzec to reach 10 Ahau 8 Chen, we must subtract 1.14.6 from the Initial-series value of 6 Cimi 4 Tzec to reach the Initial-series value of 10 Ahau 8 Chen.
- ↑ It is obvious that the kin and uinal coefficients are reversed in A17b since the coefficient above the uinal sign is very clearly 19, an impossible value for the uinal coefficient in the inscriptions, 19 uinals always being written 1 tun, 1 uinal. Therefore the 19 must be the kin coefficient. See also p. 110, footnote 1.
- ↑ The first glyph of the Supplementary Series, B6a, very irregularly stands between the kin period glyph and the day part of the terminal date.
- ↑ Incorrectly recorded as 12. See pp. 247, 248.
- ↑ In this table the numbers showing the distances have been omitted and all dates are shown in terms of their corresponding Initial-series numbers, in order to facilitate their comparison. The contemporaneous date of each monument is given in bold-faced figures and capital letters, and the student will note also that this date not only ends a hotun in each case but is, further, the latest date in each text.
- ↑ The Initial Series on the west side of Stela D at Quirigua is 9.16.13.4.17 8 Caban 5 Yaxkin, which was just 2 katuns later than 9.14.13.4.17 12 Caban 5 Kayab, or, in other words, the second katun anniversary, if the term anniversary may be thus used, of the latter date.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: II, pl. 50.
- ↑ For the full text of this inscription, see Maudslay, 1889-1902: I, pl. 112.
- ↑ Every fourth hotun ending in the Long Count was a katun ending at the same time, namely:
9. 16. 0. 0. 0 2 Ahau 13 Tzec 9. 16. 5. 0. 0 8 Ahau 8 Zotz 9. 16. 10. 0. 0 1 Ahau 3 Zip 9. 16. 15. 0. 0 7 Ahau 18 Pop 9. 17. 0. 0. 0 13 Ahau 18 Cumhu etc. - ↑ Maler, 1911: No. 1, p. 40.
- ↑ For a seeming exception to this statement, in the codices, see p. 110, footnote 1.
- ↑ That is, the age of one compared with the age of another, without reference to their actual age as expressed in terms of our own chronology.
- ↑ See Chapter II for the discussion of this point and the quotations from contemporary authorities, both Spanish and native, on which the above statement is based.
