Cathode Rays
THE
LONDON, EDINBURGH, AND DUBLIN
PHILOSOPHICAL MAGAZINE
AND
JOURNAL OF SCIENCE.
[FIFTH SERIES.]
OCTOBER 1897.
XL. Cathode rays. By J. J. THOMSON, M.A., F.R.S., Cavendish Professor of Experimental Physics, Cambridge[1].
THE experiments[2] discussed in this paper were undertaken in the hope of gaining some information as to the nature of the Cathode Rays. The most diverse opinions are held as to these rays; according to the almost unanimous opinion of German physicists they are due to some process in the æther to which—inasmuch as in a uniform magnetic field their course is circular and not rectilinear—no phenomenon hitherto observed is analogous: another view of these rays is that, so far from being wholly ætherial, they are in fact wholly material, and that they mark the paths of particles of matter charged with negative electricity. It would seem at first sight that it ought not to be difficult to discriminate between views so different, yet experience shows that this is the case, as amongst the physicists who have most deeply studied the subject can be found supporters of either theory.
The electrified-particle theory has for purposes of research a great advantage over the ætherial theory, since it is definite and its consequences can be predicted; with the ætherial theory it is impossible to predict what will happen under any given circumstances, as on this theory we are dealing with hitherto unobserved phenomena in the æther, of whose laws we are ignorant.
The following experiments were made to test some of the consequences of the electrified-particle theory.
Charge carried by the Cathode Rays.
If these rays are negatively electrified particles, then when they enter an enclosure they ought to carry into it a charge of negative electricity. This has been proved to be the case by Perrin, who placed in front of a plane cathode two coaxial metallic cylinders which were insulated from each other: the outer of these cylinders was connected with the earth, the inner with a gold-leaf electroscope. These cylinders were closed except for two small holes, one in each cylinder, placed so that the cathode rays could pass through them into the inside of the inner cylinder. Perrin found that when the rays passed into the inner cylinder the electroscope received a charge of negative electricity, while no charge went to the electroscope when the rays were deflected by a magnet so as no longer to pass through the hole.
This experiment proves that something charged with negative electricity is shot off from the cathode, travelling at right angles to it, and that this something is deflected by a magnet; it is open, however, to the objection that it does not prove that the cause of the electrification in the electroscope has anything to do with the cathode rays. Now the supporters of the ætherial theory do not deny that electrified particles are shot off from the cathode; they deny, however, that these charged particles have any more to do with the cathode rays than a rifle-ball has with the flash when a rifle is fired. I have therefore repeated Perrin’s experiment in a form which is not open to this objection. The arrangement used was as follows:— Two coaxial cylinders (fig. 1) with slits in them are placed in a bulb connected with the discharge-tube; the cathode rays from the cathode A pass into the bulb through a slit in a metal plug fitted into the neck of the tube; this plug is connected with the anode and is put to earth. The cathode rays thus do not fall upon the cylinders unless they are deflected by a magnet. The outer cylinder is connected with the earth, the inner with the electrometer. When the cathode rays (whose path was traced by the phosphorescence on the glass) did not fall on the slit, the electrical charge sent to the electrometer when the induction-coil producing the rays was set in action was small and irregular; when, however, the rays were bent by a magnet so as to fall on the slit there was a large charge of negative electricity sent to the electrometer. I was surprised at the magnitude of the charge; on some occasions enough negative electricity went through the narrow slit into the inner cylinder in one second to alter the potential of a capacity of 1.5 microfarads by 20 volts. If the rays were so
Fig. 1.

much bent by the magnet that they overshot the slits in the cylinder, the charge passing into the cylinder again to a very small fraction of its value when the aim was true. Thus this experiment shows that however we twist and deflect the cathode rays by magnetic forces, the negative electrification follows the same path as the rays, and that this negative electrification is indissolubly connected with the cathode rays.
When the rays are turned by the magnet so as to pass through the slit into the inner cylinder, the deflexion of the electrometer connected with this cylinder increases up to a certain value, and then remains stationary although the rays continue to pour into the cylinder. This is due to the fact that the gas in the bulb becomes a conductor of electricity when the cathode rays pass through it, and thus, though the inner cylinder is perfectly insulated when the rays are not passing, yet as soon as the rays pass through the bulb the air between the inner cylinder and the outer one becomes a conductor, and the electricity escapes from the inner cylinder to the earth. Thus the charge within the inner cylinder does not go on continually increasing; the cylinder settles down into a state of equilibrium in which the rate at which it gains negative electricity from the rays is equal to the rate at which it loses it by conduction through the air. If the inner cylinder has initially a positive charge it rapidly loses that charge and acquires a negative one; while if the initial charge is a negative one, the cylinder will leak if the initial negative potential is numerically greater than the equilibrium value.
Deflexion of the Cathode Rays by an Electrostatic Field.
An objection very generally urged against the view that the cathode rays are negatively electrified particles, is that hitherto no deflexion of the rays has been observed under a small electrostatic force, and though the rays are deflected when they pass near electrodes connected with sources of large differences of potential, such as induction-coils or electrical machines, the deflexion in this ease is regarded by the supporters of the ætherial theory as due to the discharge passing between the electrodes, and not primarily to the electrostatic field. Hertz made the rays travel between two parallel plates of metal placed inside the discharge-tube, but found that they were not deflected when the plates were connected with a battery of storage-cells; on repeating this experiment I at first got the same result, but subsequent experiments showed that the absence of deflexion is due to the conductivity conferred on the rarefied gas by the cathode rays. On measuring this conductivity it was found that it diminished very rapidly as the exhaustion increased; it seemed then that on trying Hertz's experiment at very high exhaustions there might be a chance of detecting the deflexion of the cathode rays by an electrostatic force.
The apparatus used is represented in fig. 2.
Fig. 2.

The rays from the cathode C pass through a slit in the anode A, which is a metal plug fitting tightly into the tube and connected with the earth; after passing a second slit in another earth-connected metal plug B, they travel between two parallel aluminium plates about 5 cm. long by 2 broad and at a distance of 1.5 cm. apart; they then fall on the end of the tube and produce a narrow well-defined phosphorescent patch. A scale pasted on the outside of the tube serves to measure the deflexion of this patch. At high exhaustions the rays were deflected when the two aluminium plates were connected with the terminals of a battery of small storage-cells; the rays were depressed when the upper plate was connected with the negative pole of the battery, the lower with the positive, and raised when the upper plate was connected with the positive, the lower with the negative pole. The deflexion was proportional to the difference of potential between the plates, and I could detect the deflexion when the potential-difference was as small as two volts. It was only when the vacuum was a good one that the deflexion took place, but that the absence of deflexion is due to the conductivity of the medium is shown by what takes place when the vacuum has just arrived at the stage at which the deflexion begins. At this stage there is a deflexion of the rays when the plates are first connected with the terminals of the battery, but if this connexion is maintained the patch of phosphorescence gradually creeps back to its undeflected position. This is just what would happen if the space between the plates were a conductor, though a very bad one, for then the positive and negative ions between the plates would slowly diffuse, until the positive plate became coated with negative ions, the negative plate with positive ones; thus the electric intensity between the plates would vanish and the cathode rays be free from electrostatic force. Another illustration of this is afforded by what happens when the pressure is low enough to show the deflexion and a large difference of potential, say 200 volts, is established between the plates; under these circumstances there is a large deflexion of the cathode rays, but the medium under the large electromotive force breaks down every now and then and a bright discharge passes between the plates; when this occurs the phosphorescent patch produced by the cathode rays jumps back to its undeflected position. When the cathode rays are deflected by the electrostatic field, the phosphorescent band breaks up into several bright bands separated by comparatively dark spaces; the phenomena are exactly analogous to those observed by Birkeland when the cathode rays are deflected by a magnet, and called by him the magnetic spectrum.
A series of measurements of the deflexion of the rays by the electrostatic force under various circumstances will be found later on in the part of the paper which deals with the velocity of the rays and the ratio of the mass of the electrified particles to the charge carried by them. It may, however, be mentioned here that the deflexion gets smaller as the pressure diminishes, and when in consequence the potential-difference in the tube in the neighbourhood of the cathode increases.
Conductivity of a Gas through which Cathode Rays are passing.
The conductivity of the gas was investigated by means of the apparatus shown in fig. 2. The upper plate D was connected with one terminal of a battery of small storage-cells, the other terminal of which was connected with the earth; the other plate E was connected with one of the coatings of a condenser of one microfarad capacity, the other coating of which was to earth; one pair quadrants of an electrometer was also connected with E, the other pair of quadrants being to earth. When the cathode rays are passing between the plates the two pairs of quadrants of the electrometer are first connected with each other, and then the connexion between them was broken. If the space between the plates were a non-conductor, the potential of the pair of quadrants not connected with the earth would remain zero and the needle of the electrometer would not move; if, however, the space between the plates were a conductor, then the potential of the lower plate would approach that of the upper, and the needle of the electrometer would be deflected. There is always a deflexion of the electrometer, showing that current passes between the plates. The magnitude of the current depends very greatly upon the pressure of the gas; so much so, indeed, that it is difficult to obtain consistent readings in consequence of the changes which always occur in the pressure when the discharge passes through the tube.
We shall first take the case when the pressure is only just low enough to allow the phosphorescent patch to appear at the end of the tube; in this case the relation between the current between the plates and the initial difference of potential is represented by the curve shown in fig. 3. In this
Fig. 3.
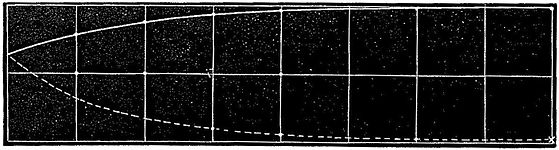
figure the abscissæ represent the initial difference of potential between the plates, each division representing two volts, and the ordinates the rise in potential of the lower plate in one minute each division again representing two volts. The quantity of electricity which has passed between the plates in one minute is the quantity required to raise 1 microfarad to the potential-difference shown by the curve. The upper and lower curve relates to the case when the upper plate is connected with the negative and positive pole respectively of the battery.
Even when there is no initial difference of potential between the plates the lower plate acquires a negative charge from the impact on it of some of the cathode rays.
We see from the curve that the current between the plates soon reaches a value where it is only slightly affected by an increase in the potential-difference between the plates; this is a feature common to conduction through gases traversed by Röntgen rays, by uranium rays, by ultra-violet light, and, as we now see, by cathode rays. The rate of leak is not greatly different whether the upper plate be initially positively or negatively electrified.
The current between the plates only lasts for a short time; it ceases long before the potential of the lower plate approaches that of the upper. Thus, for example, when the potential of the upper plate was about 400 volts above that of the earth, the potential of the lower plate never rose above 6 volts: similarly, if the upper plate were connected with the negative pole of the battery, the fall in potential of the lower plate was very small in comparison with the potential-difference between the upper plate and the earth.
These results are what we should expect if the gas between the plates and the plug B (fig. 2) were a very much better conductor than the gas between the plates, for the lower plate will be in a steady state when the current coming to it from the upper plate is equal to the current going from it to the plug: now if the conductivity of the gas between the plate and the plug is much greater than that between the plates, a small difference of potential between the lower plate and the plug will be consistent with a large potential-difference between the plates.
So far we have been considering the case when the pressure is as high as is consistent with the cathode rays reaching the end of the tube; we shall now go to the other extreme and consider the case when the pressure is as low as is consistent with the passage of a discharge through the bulb. In this case, when the plates are not connected with the battery we get a negative charge communicated to the lower plate, but only very slowly in comparison with the effect in the previous case. When the upper plate is connected with the negative pole of a battery, this current to the lower plate is only slightly increased even when the difference of potential is as much as 400 volts: a small potential-difference of about 20 volts seems slightly to decrease the rate of leak. Potential-differences much exceeding 400 volts cannot be used, as though the dielectric between the plates is able to sustain them for some little time, yet after a time an intensely bright arc flashes across between the plates and liberates so much gas as to spoil the vacuum. The lines in the spectrum of this glare are chiefly mercury lines; its passage leaves very peculiar markings on the aluminium plates.
If the upper plate was charged positively, then the negative charge communicated to the lower plate was diminished, and stopped when the potential-difference between the plates was about 20 volts; but the lowest pressure, however great (up to 400 volts) the potential-difference, there was no leak of positive electricity to the lower plate at all comparable with the leak of negative electricity to this plate when the two plates were disconnected from the battery. In fact at this very low pressure all the facts are consistent with the view that the effects are due to the negatively electrified particles travelling along the cathode rays, the rest of the gas possessing little conductivity. Some experiments were made with a tube similar to that shown in fig. 2, with the exception that the second plug B was absent, so that a much greater number of cathode rays passed between the plates. When the upper plate was connected with the positive pole of the battery a luminous discharge with well-marked striations passed between the upper plate and the earth-connected plug through which the cathode rays were streaming; this occurred even though the potential-difference between the plate and the plug did not exceed 20 volts. Thus it seems that if we supply cathode rays from an external source to the cathode a small potential-difference is sufficient to produce the characteristic discharge through a gas.
Magnetic Deflexion of the Cathode Rays in Different Gases.
The deflexion of the cathode rays by the magnetic field was studied with the aid of the apparatus shown in fig. 4. The cathode was placed in a side-tube fastened on to a bell-jar; the opening between this tube and the bell-jar was closed by a metallic plug with a slit in it; this plug was connected with the earth and was used as the anode. The cathode rays passed through the slit in this plug into the bell-jar, passing in front of a vertical plate of glass ruled into small squares. The bell-jar was placed between two large parallel coils arranged as a Helmholtz galvanometer. The course of the rays was determined by taking photographs of the bell-jar when the cathode rays were passing through it; the divisions on the plate enabled the path of the rays to be determined. Under the action of the magnetic field the narrow beam of cathode rays spreads out into a broad fan-shaped luminosity in the gas. The luminosity in this fan is not uniformly
Fig. 4.

distributed, but is condensed along certain lines. The phosphorescence on the glass is also not uniformly distributed; it is much spread out, showing that the beam consists of rays which are not all deflected to the same extent by the magnet. The luminosity on the glass is crossed by bands along which the luminosity is very much greater than in the adjacent parts. These bright and dark bands are called by Birkeland, who first observed them, the magnetic spectrum. The brightest spots on the glass are by no means always the terminations of the brightest streaks of luminosity in the gas; in fact, in some cases a very bright spot on the glass is not connected with the cathode by any appreciable luminosity, though there may be plenty of luminosity in other parts of the gas. One very interesting point brought out by the photographs is that in a given magnetic field, and with a given mean potential-difference between the terminals, the path of the rays is independent of the nature of the gas. Photographs were taken of the discharge in hydrogen, air, carbonic acid, methyl iodide, i.e., in gases whose densities range from 1 to 70, and yet, not only were the paths of the most deflected rays the same in all cases, but even the details, such as the distribution of the bright and dark spaces, were the same; in fact, the photographs could hardly be distinguished from each other. It is to be noted that the pressures were not the same; the pressures in the different gases were adjusted so the mean potential-differences between the cathode and the anode were the same in all the gases. When the pressure of a gas is lowered, the potential-difference between the terminals increases, and the deflexion of the rays produced by a magnet diminishes, or at any rate the deflexion of the rays when the phosphorescence is a maximum diminishes. If an air-break is inserted an effect of the same kind is produced.
In the experiments with different gases, the pressures were as high as was consistent with the appearance of the phosphorescence on the glass, so as to ensure having as much as possible of the gas under consideration in the tube.
As the cathode rays carry a charge of negative electricity, are deflected by an electrostatic force as if they were negatively electrified, and are acted on by a magnetic force in just the way in which this force would act on a negatively electrified body moving along the path of these rays, I can see no escape from the conclusion that they are charges of negative electricity carried by particles of matter. The question next arises, What are these particles? are they atoms, or molecules, or matter in a still finer state of subdivision? To throw some light on this point, I have made a series of measurements of the ratio of the mass of these particles to the charge carried by it. To determine this quantity, I have used two independent methods. The first of these is as follows:— Suppose we consider a bundle of homogeneous cathode rays. Let m be the mass of each of the particles, e the charge carried by it. Let N be the number of particles passing across any section of the beam in a given time; then Q the quantity of electricity carried by these particles is given by the equation
We can measure Q if we receive the cathode rays in the inside of a vessel connected with an electrometer. When these rays strike against a solid body, the temperature of the body is raised; the kinetic energy of the moving particles being converted into heat; if we suppose that all this energy is converted into heat, then if we measure the increase in the temperature of a body of known thermal capacity caused by the impact of these rays, we can determine W, the kinetic energy of the particles, and if v is the velocity of the particles,
If ρ is the radius of curvature of the path of these rays in a uniform magnetic field H, then
where I is written for Hρ for the sake of brevity. From these equations we get
Thus, if we know the values of Q, W, and I, we can deduce the values of v and m/e.
To measure these quantities, I have used tubes of three different types. The first I tried is like that represented in fig. 2, except that the plates E and D are absent, and two coaxial cylinders are fastened to the end of the tube. The rays from the cathode C fall on the metal plug B, which is connected with the earth, and serves for the anode; a horizontal slit is cut in this plug. The cathode rays pass through this slit, and then strike against the two coaxial cylinders at the end of the tube; slits are cut in these cylinders, so that the cathode rays pass into the inside of the inner cylinder. The outer cylinder is connected with the earth, the inner cylinder, which is insulated from the outer one, is connected with an electrometer, the deflexion of which measures Q, the quantity of electricity brought into the inner cylinder by the rays. A thermo-electric couple is placed behind the slit in the inner cylinder; this couple is made of very thin strips of iron and copper fastened to very fine iron and copper wires. These wires passed through the cylinders, being insulated from them, and through the glass to the outside of the tube, where they were connected with a low-resistance galvanometer, the deflexion of which gave data for calculating the rise of temperature of the junction produced by the impact against it of the cathode rays. The strips of iron and copper were large enough to ensure that every cathode ray which entered the inner cylinder struck against the junction. In some of the tubes the strips of iron and copper were placed end to end, so that some of the rays struck against the iron, and others against the copper; in others, the strip of one metal was placed in front of the other; no difference, however, could be detected between the results got with those two arrangements. The strips of iron and copper were weighed, and the thermal capacity of the junction calculated. In one set of junctions this capacity was 5x10-3, in another 3x10-3. If we assume that the cathode rays which strike against the junction give their energy up to it, the deflexion of the galvanometer gives us W or ½Nmv2. The value of I, i.e., Hρ, where ρ is the curvature of the path of the rays in a magnetic field of strength H was found as follows:— The tube was fixed between two large circular coils placed parallel to each other, and separated by a distance equal to the radius of either; these coils produce a uniform magnetic field, the strength of which is got by measuring with an ammeter the strength of the current passing through them. The cathode rays are thus in a uniform field, so that their path is circular. Suppose that the rays, when deflected by a magnet, strike against the glass of the tube at E
Fig. 5.

(fig. 5), then, if ρ is the radius of the circular path of the rays,
;
thus, if we measure CE and AC we have the means of determining the radius of curvature of the path of the rays.
The determination of ρ is rendered to some extent uncertain, in consequence of the pencil of rays spreading out under the action of the magnetic field, so that the phosphorescent patch at E is several millimetres long; thus values of ρ differing appreciably from each other will be got by taking E at different points of this phosphorescent patch. Part of this patch was, however, generally considerably brighter than the rest; when this was the case, E was taken as the brightest point; when such a point of maximum brightness did not exist, the middle of the patch was taken for E. The uncertainty in the value of ρ thus introduced amounted sometimes to about 20 per cent.; by this I mean that if we took E first at one extremity of the patch and then at the other, we should get values of ρ differing by this amount.
The measurement of Q, the quantity of electricity which enters the inner cylinder, is complicated by the cathode rays making the gas through which they pass a conductor, so that though the insulation of the inner cylinder was perfect when the rays were off, it was not so when they were passing through the space between the cylinders; this caused some of the charge communicated to the inner cylinder to leak away so that the actual charge given to the cylinder by the cathode rays was larger than that indicated by the electrometer. To make the error from this cause as small as possible, the inner cylinder was connected to the largest capacity available, 1.5 microfarad, and the rays were only kept on for a short time, about 1 or 2 seconds, so the alteration in potential of the inner cylinder was not large, ranging in the various experiments from about .5 to 5 volts. Another reason why it is necessary to limit the duration of the rays to as short a time as possible, is to avoid the correction for the loss of heat from the thermo-electric junction by conduction along the wires; the rise in temperature of the junction was of the order 2° C.; a series of experiments showed that with the same tube and the same gaseous pressure Q and W were proportional to each other when the rays were not kept on too long.
Tubes of this kind gave satisfactory results, the chief drawback being that sometimes in consequence of the charging up of the glass of the tube, a secondary discharge started from the cylinder to the walls of the tube, and the cylinders were surrounded by glow; when this glow appeared, the readings were very irregular; the glow could, however, be got rid of by pumping and letting the tube rest for some time. The results got with this tube are given in the Table under the heading Tube 1.
The second type of tube was like that used for photographing the path of the rays (fig. 4); double cylinders with a thermo-electric junction like those used in the previous tube were placed in the line of fire of the rays, the inside of the belljar was lined with copper gauze connected with the earth, This tube gave very satisfactory results; we were never troubled with any glow round the cylinders, and the readings were most concordant; the only drawback was that as some of the connexions had to be made with sealing-wax, it was not possible to get the highest exhaustions with this tube, so that the range of pressure for this tube is less than that for tube 1. The results got with this tube are given in the Table under the heading Tube 2.
The third type of tube was similar to the first, except that the openings in the two cylinders were made very much smaller; in this tube the slits in the cylinders were replaced by small holes, about 1.5 millim. in diameter. In consequence of the smallness of the openings, the magnitude of the effects was very much reduced; in order to get measurable results it was necessary to reduce the capacity of the condenser in connexion with the inner cylinder to .15 microfarad, and to make the galvanometer exceedingly sensitive, as the rise in temperature of the thermo-electric junction was in these experiments only about .5° C. on the average. The results obtained in this tube are given in the Table under the heading Tube 3.
The results of a series of measurements with these tubes are given in the following Table:—
| Gas. | Value of W/Q. | I. | m/e | v. |
| Tube 1. | ||||
| Air......................... | 4.60×1011 | 230 | .57 ×10-7 | 4.0×109 |
| Air......................... | 1.80× 1212 | 350 | .34 ×10-7 | 1.0×1010 |
| Air......................... | 6.10×1011 | 230 | .43 ×10-7 | 5.4×109 |
| Air......................... | 2.50×1012 | 400 | .32 ×10-7 | 1.2×1010 |
| Air......................... | 5.50×1011 | 230 | .48 ×10-7 | 4.8×109 |
| Air......................... | 1.00×1012 | 285 | .40 ×10-7 | 7.0×109 |
| Air......................... | 1.00×1012 | 285 | .40 ×10-7 | 7.0×109 |
| Hydrogen ............. | 6.00×1012 | 205 | .35 ×10-7 | 6.0×109 |
| Hydrogen ............. | 2.10×1012 | 460 | .50 ×10-7 | 9.2×109 |
| Carbonic acid ....... | 8.40×1011 | 260 | .40 ×10-7 | 7.5×109 |
| Carbonic acid ....... | 1.47×1012 | 340 | .40 ×10-7 | 8.5×109 |
| Carbonic acid ....... | 3.00×1012 | 480 | .39 ×10-7 | 1.3×1010 |
| Tube 2. | ||||
| Air......................... | 2.80×1011 | 175 | .53×10-7 | 3.3×109 |
| Air......................... | 4.40×1011 | 195 | .47×10-7 | 4.1×109 |
| Air......................... | 3.50×1011 | 181 | .47×10-7 | 3.8×109 |
| Hydrogen ............. | 2.80×1011 | 175 | .53×10-7 | 3.3×109 |
| Air......................... | 2.50×1011 | 160 | .51×10-7 | 3.1×109 |
| Carbonic acid ....... | 2.00×1011 | 148 | .54×10-7 | 2.5×109 |
| Air......................... | 1.80×1011 | 151 | .63×10-7 | 2.3×109 |
| Hydrogen ............. | 2.80×1011 | 175 | .53×10-7 | 3.3×109 |
| Hydrogen ............. | 4.40×1011 | 201 | .46×10-7 | 4.4×109 |
| Air......................... | 2.50×1011 | 176 | .61×10-7 | 2.8×109 |
| Air......................... | 4.20×1011 | 200 | .48×10-7 | 4.1×109 |
| Tube 3. | ||||
| Air......................... | 2.50×1011 | 220 | .9 ×10-7 | 2.4×109 |
| Air......................... | 3.50×1011 | 225 | .7 ×10-7 | 3.2×109 |
| Hydrogen ............. | 3.00×1011 | 250 | 1.0 ×10-7 | 2.5×109 |
It will be noticed that, the value of m/e is considerably greater for Tube 3, where the opening is a small hole, than for Tubes 1 and 2, where the opening is a slit of much greater area. I am of opinion that the values of m/e got from Tubes 1 and 2 are too small, in consequence of the leakage from the inner cylinder to the outer by the gas being rendered a conductor by the passage of the cathode rays.
It will be seen from these tables that the value of m/e is independent of the nature of the gas. Thus, for the first tube the mean for air is .40×10-7, for hydrogen .42×10-7, and for carbonic acid gas .4×10-7; for the second tube the mean for air is .52×10-7, for hydrogen .50×10-7, and for carbonic acid gas .54×10-7.
Experiments were tried with electrodes made of iron instead of aluminium; this altered the appearance of the discharge and the value of v at the some pressure, the values of m/e were, however, the same in the two tubes; the effect produced by different metals on the appearance of the discharge will be described later on.
In all the preceding experiments, the cathode rays were first deflected from the cylinder by a magnet, and it was then found that there was no deflexion either of the electrometer or the galvanometer, so that the deflexions observed were entirely due to the cathode rays; when the glow mentioned previously surrounded the cylinders there was a deflexion of the electrometer even when the cathode rays were deflected from the cylinder.
Before proceeding to discuss the results of these measurements I shall describe another method of measuring the quantities m/e and v of an entirely different kind from the preceding; this method is based upon the deflexion of the cathode rays in an electrostatic field. If we measure the deflexion experienced by the rays when traversing a given length under a uniform electric intensity, and the deflexion of the rays when they traverse a given distance under a uniform magnetic field, we can find the values of m/e and v in the following way:-
Let the space passed over by the rays under a uniform electric intensify F be l, the time taken for the rays to traverse this space is l/v, the velocity in the direction of F is therefore
so that ϑ, the angle through which the rays are deflected when they leave the electric field and enter a region free from electric force, is given by the equation
If, instead of the electric intensity, the rays are acted on by a magnetic force H at right angles to the rays, and extending across the distance l, the velocity at right angles to the original path of the rays is
so that ϕ, the angle through which the rays are deflected when they leave the magnetic field, is given by the equation
From these equations we get
and
In the actual experiments H was adjusted so that, ϕ=ϑ; in this case the equations become
The apparatus used to measure v and m/e by this means is that represented in fig. 2. The electric field was produced by connecting the two aluminium plates to the terminals of a battery of storage-cells. The phosphorescent patch at the end of the tube was deflected, and the deflexion measured by a scale pasted to the end of the tube. As it was necessary to darken the room to see the phosphorescent patch, a needle coated with luminous paint was placed so that by a screw it could be moved up and down the scale; this needle could be seen when the room was darkened, and it was moved until it coincided with the phosphorescent patch. Thus, when light was admitted, the deflexion of the phosphorescent patch could be measured.
The magnetic field was produced by placing outside the tube two coils whose diameter was equal to the length of the plates; the coils were placed so that they covered the space occupied by the plates, the distance between the coils was equal to the radius of either. The mean value of the magnetic force over the length l was determined in the following way: a narrow coil C whose length was l, connected with a ballistic galvanometer, was placed between the coils; the plane of the windings of C was parallel to the planes of the coils; the cross section of the coil was a rectangle 5 cm. by 1 cm. A given current was sent through the outer coils and the kick α of the galvanometer observed when this current was reversed. The coil C was then placed at the centre of two very large coils, so as to be in a field of uniform magnetic force: the current through the large coils was reversed and the kick β of the galvanometer again observed; by comparing α and β we can get the mean value of the magnetic force over a length l; this was found to be
60×ι,
where ι is the current flowing through the coils.
A series of experiments was made to see if the electrostatic deflexion was proportional to the electric intensity between the plates; this was found to be the case. In the following experiments the current through the coils was adjusted so that the electrostatic deflexion was the same as the magnetic:-
| Gas. | θ. | H. | F. | l. | m/e. | v. |
| Air..................... | 8/110 | 5.5 | 1.5×1010 | 5 | 1.3×10-7 | 2.8×109 |
| Air..................... | 9.5/110 | 5.4 | 1.5×1010 | 5 | 1.1×10-7 | 2.8×109 |
| Air..................... | 13/110 | 6.6 | 1.5×1010 | 5 | 1.2×10-7 | 2.3×109 |
| Hydrogen.......... | 9/110 | 6.3 | 1.5×1010 | 5 | 1.5×10-7 | 2.5×109 |
| Carbonic acid... | 11/110 | 6.9 | 1.5×1010 | 5 | 1.5×10-7 | 2.2×109 |
| Air..................... | 6/110 | 5.0 | 1.8×1010 | 5 | 1.3×10-7 | 3.6×109 |
| Air..................... | 7/110 | 3.6 | 1×1010 | 5 | 1.1×10-7 | 2.8×109 |
The cathode in the first five experiments was aluminium, in the last two experiments it was made of platinum; in the last experiment Sir William Crookes's method of getting rid of the mercury vapour by inserting tubes of pounded sulphur, sulphur iodide, and copper filings between the bulb and the pump was adopted. In the calculation of m/e and v no allowance has been made for the magnetic force due to the coil in the region outside the plates; in this region the magnetic force will be in the opposite direction to that between the plates, and will tend to bend the cathode rays in the opposite direction: thus the effective value of H will be smaller than the value used in the equations so that the values of m/e are larger, and those of v less than would be if this correction were applied. This method of determining the values of m/e and v is much less laborious and probably more accurate than the former method; it cannot, however, be used over so wide a range of pressures.
From these determinations we see that the value of m/e is independent of the nature of the gas, and that its value 10-7 is very small compared with the value 10-4, which is the smallest value of this quantity previously known, and which is the value for the hydrogen ion in electrolysis.
Thus for the carriers of the electricity in the cathode rays m/e is very small compared with its value in electrolysis. The smallness of m/e may be due to the smallness of m or the largeness of e, or to a combination of these two. That the carriers of the charges in the cathode rays are small compared with ordinary molecules is shown, I think, by Lenard's results as to the rate at which the brightness of the phosphorescence produced by these rays diminishes with the length of path travelled by the ray. If we regard this phosphorescence as due to the impact of the charged particles, the distance through which the rays must travel before the phosphorescence fades to a given fraction (say 1/e, where e = 2.71) of its original intensity, will be some moderate multiple of the mean free path. Now Lenard found that this distance depends solely upon the density of the medium, and not upon its chemical nature or physical state. In air at atmospheric pressure the distance was about half a centimetre, and this must be comparable with the mean free path of the carriers through air at atmospheric pressure. But the mean free path of the molecules of air is a quantity of quite a different order. The carrier, then, must be small compared with ordinary molecules.
The two fundamental points about these carriers seem to me to be (1) these carriers are the same whatever the gas through which the discharge passes, (2) that the mean free paths depend upon nothing but the density of the medium traversed by these rays.
It might be supposed that the independence of the mass of the carriers of the gas through which the discharge passes was due to the mass concerned being the quasi mass which a charged body possesses in virtue of the electric field set up in its neighbourhood; moving the body involves the production of a varying electric field, and, therefore, of a certain amount of energy which is proportional to the square of the velocity. This causes the charged body to behave as if its mass were increased by a quantity, which for a charged sphere is (‘Recent Researches in Electricity and Magnetism'), where e is the charge and α the radius of the sphere. If we assume that it is this mass which we are concerned with in the cathode rays, since m/e would vary as e/α, it affords no clue to the explanation of either of the properties (1 and 2) of these rays. This is not by any means the only objection to this hypothesis, which I only mention to show that it has not been overlooked.
The explanation which seems to me to account in the most simple and straightforward manner for the facts is founded on a view of the constitution of the chemical elements which has been favourably entertained by many chemists: this view is that the atoms of the different chemical elements are different aggregations of atoms of the same kind. In the form in which this hypothesis was enunciated by Prout, the atoms of the different elements were hydrogen atoms; in this precise form the hypothesis is not tenable, but if we substitute for hydrogen some unknown primordial substance X, there is nothing known which is inconsistent with this hypothesis, which is one that has been recently supported by Sir Norman Lockyer for reasons derived from the study of the stellar spectra.
If, in the very intense electric field in the neighbourhood of the cathode, the molecules of the gas are dissociated and are split up, not into the ordinary chemical atoms, but into these primordial atoms, which we shall for brevity call corpuscles; and if these corpuscles are charged with electricity and projected from the cathode by the electric field, they would behave exactly like the cathode rays. They would evidently give a value of m/e which is independent of the nature of the gas and its pressure, for the carriers are the same whatever the gas may be; again, the mean free paths of these corpuscles would depend upon the density of the medium through which they pass. For the molecules of the medium are composed of a number of such corpuscles separated by considerable spaces; now the collision between a single corpuscle and the molecule will not be between the corpuscles and the molecule as a whole, but between this corpuscle and the individual corpuscles which form the molecule; thus the number of collisions the particle makes as it moves through a crowd of these molecules will be proportional, not to the number of the molecules in the crowd, but to the number of the individual corpuscles. The mean free path is inversely proportional to the number of collisions in unit time, and so inversely proportional to the number of corpuscles in unit volume; now as these corpuscles are all of the same mass, the number of corpuscles in unit volume will be proportional to the mass of unit volume, that is the mean free path will be inversely proportional to the density of the gas. We see, too, that so long as the distance between neighbouring corpuscles is large compared with the linear dimensions of a corpuscle the mean free path will be independent of the way they are arranged, provided the number in unit volume remains constant, that is the mean free path will depend only on the density of the medium traversed by the corpuscles, and will be independent of its chemical nature and physical state: this from Lenard's very remarkable measurements of the absorption of the cathode rays by various media, must be a property possessed by the carriers of the charges in the cathode rays.
Thus on this view we have in cathode rays matter in a new state, a state in which the subdivision of matter is carried very much further than in the ordinary gaseous state: a state in which all matter — that is, matter derived from different sources such as hydrogen, oxygen, &c.- is of one and the same kind; this matter being the substance from which all the chemical elements are built up.
With appliances of ordinary magnitude, the quantity of matter produced by means of the dissociation at the cathode is so small as to almost to preclude the possibility of any direct chemical investigation of its properties. Thus the coil I used would, I calculate, if kept going uninterruptedly night and day for a year, produce only about one three-millionth part of a gramme of this substance.
The smallness of the value of m/e is, I think, due to the largeness of e as well as the smallness of m. There seems to me to be some evidence that the charges carried by the corpuscles in the atom are large compared with those carried by the ions of an electrolyte. In the molecule of HCl, for example, I picture the components of the hydrogen atoms as held together by a great number of tubes of electrostatic force; the components of the chlorine are similarly held together, while only one stray tube binds the hydrogen atom to the chlorine atom. The reason for attributing this high charge to the constituents of the atom is derived from the values of the specific inductive capacity of gases: we may imagine that the specific inductive capacity of a gas is due to the setting in the electric field of the electric doublet formed by the two oppositely electrified atoms which form the molecule of the gas. The measurements of the specific inductive capacity show, however, that this is very approximately an additive quantity: that is, that we can assign a certain value to each element, and find the specific inductive capacity of HCl by adding the value for hydrogen to the value for chlorine; the value of H2O by adding twice the value for hydrogen to the value for oxygen, and so on. Now the electrical moment of the doublet formed by a positive charge on one atom of the molecule and a negative charge on the other atom would not be an additive property; if, however, each atom had a definite electrical moment, and this were large compared with the electrical moment of the two atoms in the molecule, then the electrical moment of any compound, and hence its specific inductive capacity, would be an additive property. For the electrical moment of the atom, however, to be large compared with that of the molecule, the charge on the corpuscles would have to be very large compared with those on the ion.
If we regard the chemical atom as an aggregation of a number of primordial atoms, the problem of finding the configurations of stable equilibrium a number of equal particles acting on each other according to some law of force — whether that of Boscovich, where the force between them is a repulsion when they are separated by less than a certain critical distance, and an attraction when they are separated by a greater distance, or even the simpler case of a number of mutually repellent particles held together by a central force — is of great interest in connexion with the relation between the properties of an element and its atomic weight. Unfortunately the equations which determine the stability of such a collection of particles increase so rapidly in complexity with the number of particles that, a general mathematical investigation is scarcely possible. We can, however, obtain a good deal of insight into the general laws which govern such configurations by the use of models, the simplest of which is the floating magnets of Professor Mayer. In this model the magnets arrange themselves in equilibrium under their mutual repulsions and a central attraction caused by the pole of a large magnet placed above the floating magnets.
A study of the forms taken by these magnets seems to me to be suggestive in relation to the periodic law. Mayer showed that when the number of floating magnets did not exceed 5 they arranged themselves at the corners of a regular polygon— 5 at the corners of a pentagon, 4 at the corners a square, and so on. When the numbers exceeds 5, however, this law no longer holds: thus 6 magnets do not arrange themselves at the corners of a hexagon, but divide into two systems, consisting of 1 in the middle surrounded by 5 at the corners of a pentagon. For 8 we have two in the inside and 6 outside; this arrangement in two systems, an inner and an outer, lasts up to 18 magnets. After this we have three systems: an inner, a middle, and an outer; for a still larger number of magnets we have four systems, and so on.
Mayer found the arrangement of magnets was as follows:—
| 000 | 000 | 000 | 000 | 000 |
| 00 | ||||
where, for example, means an arrangement with one magnet in the middle, then a ring of six, then a ring of ten, and a ring of twelve outside.
Now suppose that a certain property is associated with two magnets forming a group by themselves; we should have this property with 2 magnets, again with 8 and 9, again with 19 and 20, and again with 34, 35, and so on. If we regard the system of magnets as a model of an atom, the number of magnets being proportional to the atomic weight, we should have this property occurring in elements of atomic weight 2, (8,9), 19, 20, (34, 35). Again, any property conferred by three magnets forming a system by themselves would occur with atomic weights 3, 10, and 11; 20, 21, 22, 23, and 24; 35, 36, 37 and 39; in fact, we should have something quite analogous to the periodic law, the first series corresponding to the arrangement of the magnets in a single group, the second series to the arrangement in two groups, the third series in three groups, and so on.
Velocity of the Cathode Rays.
The velocity of the cathode rays is variable, depending upon the potential-difference between the cathode and anode, which is a function of the pressure of the gas — the velocity increases as the exhaustion improves; the measurements given above show, however, that all the pressures at which experiments were made the velocity exceeded 109 cm./sec. This velocity is much greater than the value 2×107 which I previously obtained (Phil. Mag. Oct. 1894) by measuring directly the interval which separated the appearance of luminosity at two places on the walls of the tube situated at different distances from the cathode.
In my earlier experiments the pressure was higher than in the experiments described in this paper, so that the velocity of the cathode rays would on this account be less. The difference between the two results is, however, too great to be wholly explained in this way, and I attribute the difference to the glass requiring to be bombarded by the rays for a finite time before becoming phosphorescent, this time depending upon the intensity of the bombardment. As this time diminishes with the intensity of bombardment, the appearance of phosphorescence at the piece of glass most removed from the cathode would be delayed beyond the time taken for the rays to pass from one place to the other by the difference in time taken by the glass to become luminous; the apparent velocity measured in this way would thus be less than the true velocity. In the former experiments endeavours were made to diminish this effect by making the rays strike the glass at the greater distance from the cathode less obliquely than they struck the glass nearer to the cathode; the obliquity was adjusted until the brightness of the phosphorescence was approximately equal in the two cases. In view, however, of the discrepancy between the results obtained in this way and those obtained by the later method, I think that it was not successful in eliminating the lag caused by the finite time required by the gas to light up.
Experiments with Electrodes of Different Materials.
In the experiments described in this paper the electrodes were generally made of aluminium. Some experiments, however, were made with iron and platinum electrodes.
Though the value of m/e came out the same whatever the material of the electrode, the appearance of the discharge varied greatly; and as the measurements showed, the potential-difference between the cathode and anode depended greatly upon the metal used for the electrode; the pressure being the same in all cases.
To test this point further I used a tube like that shown in fig. 6, where a, b, c are cathodes made of different metals, the anodes being in all cases platinum wires. The cathodes were disks of aluminium, iron, lead, tin, copper, mercury, sodium amalgam, and silver chloride; the potential-difference
between the cathode and anode was measured by Lord Kelvin's vertical voltmeter, and also by measuring the length of spark in air which, when placed parallel with the anode and cathode, seemed to allow the discharge to go as often through the spark-gap as through the tube. With this arrangement the pressures were the same for all the cathodes. The potential- difference between the anode and cathode and the equivalent spark-length depended greatly upon the nature of the cathode. The extent of the variation in potential may be estimated from the following table:-
| Cathode. | Mean Potential-Difference between Cathode and Anode. | |
| Aluminium..... | 001800 volts. | |
| Lead............. | 210000" | |
| Tin................ | 240000" | |
| Copper......... | 260000" | |
| Iron.............. | 290000" | |
The potential-difference when the cathode was made of sodium amalgam or silver chloride was less even than that of aluminium.
The order of many of the metals changed about very capriciously, experiments made at intervals of a few minutes frequently giving quite different results. From the abrupt way in which these changes take place I am inclined to think that gas absorbed by the electrode has considerable influence on the passage of the discharge.
I have much pleasure in thanking Mr. Everitt for the assistance he has given me in the preceding investigation.
Cambridge, Aug. 7, 1897.







































