Climatic Cycles and Tree-Growth/Chapter 8
Significance of cycles.—It has already been stated that three characteristics were observed in the curves of tree-growth: (1) correlation with rainfall; (2) correlation with sunspots; (3) general periodic variation. In the first and second of these the trees are compared directly with existing records, but in the third the tree record is available over hundreds and even thousands of years during which no human observations were recorded. Thus, if previous inferences are correct, the trees may reasonably be expected to give us some knowledge of prehistoric conditions. In the first attempt to secure such knowledge, the method which promises the most certain results is the analysis of ring variations in terms of cycles.
Correlatively, the study of cycles is of special value in climatic investigations. Such studies are undertaken for the purpose of predicting the future. The basis of daily or short-distance prediction is found in the conditions existing about the country at a given moment and a knowledge of the usual movement of storm areas. A basis for long-distance prediction is now generally sought in climatic cycles. Such cycles may or may not be permanent. Perhaps they are nothing more enduring than a series of wave systems on a water surface. Yet for the navigator a knowledge of the existing system is important, and so for the purpose of weather prediction we need to know the nature of the pulsations actually operating, and each one should be studied minutely. For this purpose the very long tree records and their presumably fair accuracy seem especially advantageous, since they give us a range in centuries which the meteorological records, with few exceptions, give only in decades.
A special and rapid method of carrying on the study of cycles has been developed in the periodograph which has been used in checking fully all the results in the present chapter. But after its recent completion and trial the fact became clear to the writer that its real service will be in a complete and thorough examination of all curves obtained, in order to derive a quantitative statement of the extension in time and space shown by each cycle. This in itself is a long process. Moreover, preliminary analysis of many tree curves reveals a very complex system of short-period variations in the trees, some of evident significance and some of little-known value as yet. The study of this complex of short periods together with other problems naturally suggested in the course of the work is reserved for the future; we shall now touch upon a few of the most important results reached in the analyses already accomplished.
Predominant cycles.—With the understanding that the study of cycles is not yet complete, it may be stated at once that the more conspicuous and general cycles at once apparent in the trees are directly related to the solar period. They are as follows:
| 5 | to | 6 | years | approximate | half | sunspot | period. |
| 10 | to | 13 | " | " | full | " | " |
| 21 | to | 24 | " | " | double | " | " |
| 32 | to | 35 | " | " | triple | " | " |
| 100 | to | 105 | " | " | triple-triple | " | " |
There are few if any periods over 20 years not in this list, but under 20 years several are fairly persistent, such as 19-, 14-, 10-, and 7-year periods. There is also a period of about 2 years which causes a frequent alternation of size in successive rings, giving a "see-saw" or "zig-zag" effect in the appearance of the curve. The discussion in this chapter, however, will be confined to the solar group of periods above listed and to a preliminary statement regarding the 2-year period. As the larger of these solar periods are very nearly simple multiples of the 11-year period, it is naturally suspected that they are or should be real multiples of the sunspot period. Hence I feel at liberty to speak of the "double sunspot period" or the "triple sunspot period" without committing myself to its exact length.
Locality and solar cycles. — Compared to the multitudes of meteorological districts about the world, the few isolated localities which have here been investigated seem very insignificant. The wet-climate trees near the Baltic Sea show variations following almost perfectly, the curve of sunspot numbers. The Scotch pines just south of the sea have had good care since they were planted about 90 years ago. This care has prevented the excessive competition between individuals which characterize natural forests, and perhaps for that reason they give this remarkable record of external conditions. The trees to the north of the Baltic include spruces as well as Scotch pines, and show the same reaction. Both these groups are in comparatively level country and far from mountains. The group of pines from the Swedish province of Dalarne show the 11-year period somewhat less clearly. They were nearer the backbone of mountains which extends down the Scandinavian peninsula. The older trees of this group show evidence of a triple sunspot period. The groups growing in the mountains and in the inner fjords of Norway show extensive variations and even reversals. Some of the individual trees exhibit the sunspot period very well, while some show it inverted and some divide it into two crests. The older trees show evidence of an inverted double period.
The trees near sea-level, both at Christiania and on the outer coast of Norway, return again to the 11-year period. The former do not cross-identify well and the latter show occasional variations, such as double-crested period, inversion, etc. Variations of this kind were noted in different radii of the same tree. The trees from the south of England show slight relation to the solar cycle. They show more prominently other variations, which, taken between 1870 and 1900, may have given rise to Lockyer's 3.8-year period (1905, 1906). The full tree record becomes more accordant on a 3.5-year period. In this group there appears to be a slight relation to London rainfall of a direct character, that is, the growth is larger with increased rain. Naturally in such a well-cultivated region there may have been large differences due to treatment of the soil, drainage, and so forth. The other two European groups, one from Pilsen in Bohemia and one from the north slopes of the Alps in southern Bavaria, do not show consistent agreement with the solar variation. Yet the former shows a double sunspot period which is illustrated below.
Coming to the American continent, the Vermont group may also be considered as growing in a wet climate. It shows a very strong single-creasted solar period, but the maxima come 3 years early during the last century. During the preceding century, when the trees were younger, the tree maximum is only 1 year early. The rainfall in this region shows the solar period also, but it is roughly inverted with respect to the tree curve. The Oregon group must be considered as in the wet climate of the temperate zone. It is near the Pacific coast and has abundant rain or snow. The solar cycle is probably in it, but it is not so conspicuous as other short cycles. When these trees are summed up on the 11-year period, they show about 10 per cent total variation with maximum and minimum coinciding with the Vermont group and therefore anticipating the sunspot maximum by 3 years.
The sequoias grow farther south and experience the heavy precipitation of the temperate-zone winter combined with dry-climate summer conditions — that is, the summers are mostly clear, but have occasional sharp local showers, often with lightning. The tree-growth shows a relation to the rainfall in the great valley below and therefore we could expect some similarity to the Arizona pines. This does exist, but the exact 11.4-year cycle shown in the pines is less evident in the sequoias, though unmistakably there. The analysis of the long sequoia record will be shown below. In it several cycles between 7 and 15 years predominate in places. The 11-year period is plainly evident through most of the record and for some centuries is the predominant cycle, but for long periods other slightly differing cycles, such as 10 years, 12.6 years, or 13 years, are more evident. It is as yet impossible to say whether at these times there was a real change in the sunspot period, whether some subordinate period is operating in the sun, or whether only local conditions of some kind are the controlling factor.
The yellow pines of northern Arizona are dry-climate trees. They have a modified winter precipitation of the temperate zone. Spring and autumn have the complete dryness of the "horse latitudes," and the summers have the characteristic subtropical torrential thunderstorms. Rain is the controlling factor in these trees. The trees show a double-crested 11.4-year period through nearly all the 500 years of their record. This will be illustrated below. A 7-year period is also frequently observed, and the combination of the 7-year and 11-year periods may be the cause of these trees showing the double sunspot period prominently through most of their record by interfering to suppress alternate 11-year maxima. A triple sunspot period is very evident in the last 200 years, but is practically lost in the preceding 300. The pines and sequoias agree in showing a long period of about 100 years. The record of the pines is not long enough to give it much precision, and 120 years fits it more nearly. The 3,200 years of the sequoias analyze best at 101 years.
Illustrations of cycles — Two methods of illustrating cycles in the tree curves are used here. One is the usual method of showing the plotted curves together with another curve indicating the cycle, so that agreements and disagreements may be noted. To this method also belongs the integrated or summated curve, which shows the mean variation in the desired period. The other method is by aid of various periodograph diagrams. These diagrams may similarly be divided into the differential pattern, in which variations from the cycle at any time may be noted, and the periodogram proper, which gives roughly the mean form of the cycles in a considerable range of periods. This form of presentation, being new and yet carrying more information than the former, will be given with some explanation after the curves themselves have been shown.
The 11-year cycle. — Only two tree records, the yellow pine and the sequoia, extend back of the first telescopic observations of sunspots. It is of peculiar interest to see whether the trees which carry the rainfall record back so far with a comparatively high degree of accuracy show the same cycle. In nearly all parts of the yellow-pine curve there are suggestions of an 11-year cycle. By tracing this throughout the record, the period is found to have a length of about 11.4 years, which is sufficiently close to the length of the sunspot cycle to be considered identical with it. This exact figure is not yet considered final, as future intensive study of the short-period variations in the trees may throw more light upon it. Taking 11.4 years as the probable length, the average total variation is found to be some 16 per cent of the mean growth. The period is generally double-crested with two well-developed maxima and minima, but they are rarely symmetrical. During the 120 years from 1410 to 1530 it shows most remarkable regularity. This feature, which was observed as soon as the smoothed curve was examined, is shown in figure 32. The tree curve in this diagram has been reduced to departures from its own mean and smoothed by Hann's formula. The short period is immediately evident, even without the 5.7-year cycle plotted below. This bit of record in the yellow pines and the 90 years of record in the wet-climate Scotch pines near the Baltic Sea give the finest examples of rhythmic growth yet found in the trees.

Fig. 32.—Smoothed curve of Arizona pines showing the half-sunspot period for 120 years.
In order to test for possible variations in the sunspot curve during these 500 years, the tree record from 1420 to 1909 has been divided into 8 periods of approximately 60 years each and the form of the 11-year period obtained in each. This is shown in figure 33. From this it appears that the 11-year cycle is not uniform throughout the whole 490 years covered by the curve. In general the cycle shows 2 maxima and 2 minima. From 1420 to 1660 the second minimum is generally the deeper. For the next 60 years the curve flattens out in a striking manner. From 1730 to 1790 the curve again shows variations, but they are not well related to this cycle. After 1790 there are again 2 minima, but on the whole the first is more conspicuous.
The 11-year cycle in sequoia. — The question of agreement between the sequoia and the yellow pine is a vital one. Although the sequoias grow in a locality some 450 miles distant, there is a similarity in the rainfall of the two places. Some attempt has been made to cross-identify the rings in the two groups, and the puzzling fact was revealed that from 1400 to about 1580 no certain identity could be found, though after that date it was evident in many places. The difficulty has been partly removed by applying this same method of analysis to the last 500 years of the sequoia. The result is shown in the dotted lines of figure 33. It is evident that from 1420 to 1476 the second maximum of the pines is almost entirely lacking in the sequoias. The same is true of the interval from 1602 to 1658. The sequoias show strikingly the flattening of the curve from 1670 or 1680 to 1727. In the remainder of the curves the sequoias show better rhythm in the sunspot cycle than do the pines.
Taking the evidence as a whole, it seems likely that the sunspot cycle has been operating since 1400 A. D., with some possible interference for a considerable interval about the end of the seventeenth century. Correlation curves. — Figure 34 is arranged to show certain relations of special interest in this connection. At the top was found the mean pine and sequoia curves for 490 years averaged on an 11.4-year period. Below these the mean 11.4-year period for the last 60-year interval is given for each tree. This is required for proper comparison with the short interval of climatic records. Next the rainfall and temperature observed on the southern California coast are plotted, and last of all the inverted sunspot curve for a corresponding period. There appears to be a marked relationship between these curves. Even the subordinate crest, which sometimes shows in the change from maximum to mini-
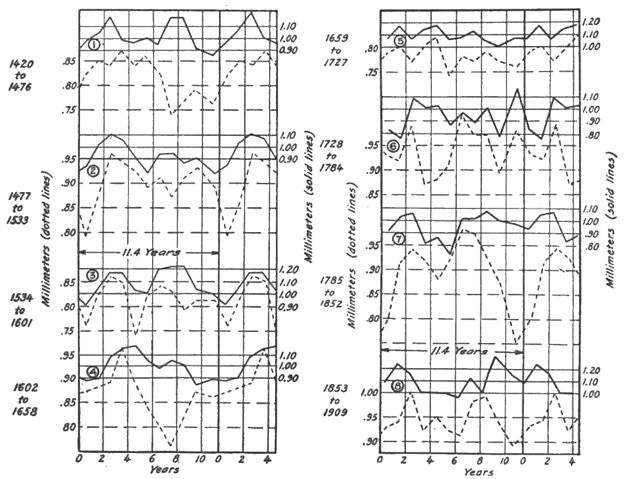
Fig. 33.—Changes in the 11-year period in 500 years. Solid line, Arizona pine; dotted line, sequoia.
mum of sunspots, matches the suppressed second crest of temperature and the full second crest of rainfall and tree-growth. This would seem impossible in the absence of a physical relation between them.
Double and triple cycles. — The first tabulation of the Arizona pines covered a period of only 200 years and included 25 trees. There were a few errors of identification in some of these trees, sufficient to flatten
1 The correction for the ring 1580 was made too late for insertion in this figure. The two dotted curves between 1420 and 1533, therefore, should be moved one year to the left, while the third dotted curve between 1534 and 1601 becomes slightly modified. A slight change in the first Arizona curve is required by a correction at 1463 A. D. the curve a little but not enough to change the pronounced fluctuations amply shown in recent analysis. This 200-year record showed a very clear combination of the double and triple sun-spot periods. This was illustrated at the time in a drawing which is largely reproduced in figure 35. Curve No. 1 is a triple solar cycle 32.8 years in length;

Fig. 34.—Correlation curves in the 11-year cycle.
No. 2 is a double cycle 21.2 years long, and the third curve is a simple combination of the two. The fourth curve is the tree-growth, showing fluctuations which admirably combine these two periods. All subsequent analysis of these trees has entirely supported this result, as shown in the periodograph work below. When the length of curve was extended from 200 years to 500 years, the double solar period was found to prevail through almost the entire length, but the triple period does not appear to have affected the tree-growth in the earlier 300 years.
Two other plain examples of the double solar type are illustrated in figures 36 and 37. The former gives the double cycle shown in a scattered group of trees of considerable age from the inner fjords and mountains of Norway. The earlier half of the curve includes 6 trees and the later half 8. The cycle beneath makes evident a well-developed rhythm in these trees. Figure 37 shows a very regular double sun-spot rhythm in the sequoias. There are many similar rhythms apparent in the sequoias, but as yet little study has been made of them. This one shows 80 years of the section D-12, whose identification was for a

Fig. 35.—Early curve of Arizona pines from 1700 to 1900 A. D. (No. 4), compared with double and triple sunspot cycles combined (No. 3).

Fig. 36.—Double sunspot period in tree-growth at inner fjords of Norway; lower curve a 22.8 year cycle.

Fig. 37.—Double sunspot rhythm in sequoia, D-12 about 300 A. D.
(Material obtained in 1919 shows the dates in this figure to be too large by 27 years.)
long time uncertain on account of its complacent character and badly compressed rings. The rhythmic character is so evident that no cycle needs to be placed below the curve. The period is estimated at 20 to 22 years.
A triple solar cycle is shown in figure 38, giving the condensed curve of a single 400-year-old Norwegian tree. The upper curve gives the mean growth, and the lower curve is a simple 34-year cycle. The rhythmic character of the growth was clearly seen in the measures immediately after their completion, and the period at once suggested the Bruckner cycle of 35 years. This interesting tree has been mentioned on pages 34 and 41.
A 2-year cycle — In the cross-identification of the trees used in this investigation, a constantly recurring feature has been a marked alternation in size of successive rings, giving them an appearance of being arranged in pairs. In the plotted curves this produces a zig-zag or see-saw effect. Usually such effect lasts a few years and then disappears or reverses, but the example illustrated in figure 39 shows unusual persistence. It is taken from D-22 from 750 B. C. to 660 B. C. The even dates show less growth than the odd almost continuously for 60 years, but for the next 30 years the reverse is the case. This is

Fig. 38.—Triple sunspot cycle in a single tree from northern Norway. Lower curve, a 34-year cycle.
evidently due to a short period of about 2 years in length. It has not yet been fully studied, but it is prominent in the European groups and in the Vermont group. It frequently shows a duration of a little less than 7 years in one phase, with odd dates greater in growth than even dates, and then for the next 7 years reverses its phase. This 14-year cycle is the series of beats the 2-year cycle produces by interfering with
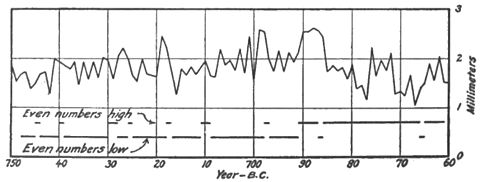
Fig. 39.—D-22 at 760 to 660 B. C, showing a 2-year period.[1]
the exact annual and biennial effects in the tree. Hence, by a simple process, its length is found to be in effect frequently 21 or 28 months. Comparison has been made with the rainfall records near the Vermont group (Douglass, 1915:181) and a variable period has been found
averaging near the larger figure. It should more properly be called a "broken" period perhaps, since it is made up of different periods for different intervals, first one and then another predominating. The methods used in the search for this 2-year period have revealed frequently a solar cycle also, and there seems to be some obscure connection between the two.
PERIODOGRAPH ANALYSES.
Differential patterns. — The periodograms, as already shown, indicate the different cycles operating within a certain range. Any one cycle together with others close to it may be studied more minutely on the differential pattern produced when the instrument is set at the desired period. Plates 12 and 10, b, are arranged to illustrate this and at the same time show the solar cycles in several of the groups. A periodic effect equal in length to the setting of the instrument is indicated by a vertical row of light crests or dark spaces. These rows may be seen in any of the patterns. If the row of crests points downward to the right, its period is greater than the setting of the instrument; if to the left, the period is less. The straightness of the row indicates the regularity of the period. Plate 12, q, is made from the standard 5-year period with a setting at 5.0 years. The first pattern in plate 12 shows the regularity of the sunspot period since 1610 A. D. The interval in the latter part of the eighteenth century, when the cycle was reduced to less than 10 years, is distinguished by a bending of the row toward the left. This is followed by a deflection toward the right during the interval of readjustment from 1790 to 1830. The direction of any row becomes an exact measure of its period.
If a period is constant, the row of crests is straight. A zigzag row made up of short, straight parts means that one period after another becomes predominant. A curved row means a constantly changing period. Some examples of apparent curved rows may be picked out in the sequoia pattern. A curved row may indicate some other function than a simple period. Pattern R in plate 12 is made to illustrate a logarithmic variable, beginning at the top as a 5-year period and changing by a constant percentage increase to a 10-year period at the bottom. The instrument is set at 8.0 years.
The 11-year cycle. — The first 6 patterns in plate l2 illustrate this cycle. The first gives the sunspot numbers from 1610 to 1910, including the uncertain ones from 1610 to 1750. Pattern B gives the fine vertical row shown by the 6 groups of trees from north Europe. This was shown as a curve in figure 25, page 77. The qualitative test of the entire 80 European trees is shown in pattern C. This may be seen as a curve in figure 26. The small secondary maxima at several of the minima show as light crests between the main rows. Pattern D shows a 12-year period in south Sweden during the past 50 years, preceded by several maxima at about 8.5-year intervals. Pattern E gives the Vermont analysis. The solar cycle shows well for the last 150 years, but is preceded by a 9.2-year cycle for about 50 years, and then by the solar cycle again. This tree curve is shown in figure 27, page 78.
The Arizona pines are given in pattern F. The double-crested solar cycle shows in the larger part of it, but is best developed in the upper and lower thirds. By sighting along these vertical rows, a dark line in the upper third, indicating the more pronounced minimum, comes in straight line with the lesser dark minimum line in the lower third, indicating a transfer of emphasis from one-half of the 11-year cycle to the other half in passing the seventeenth century. This was noted above in connection with the analysis of the same record by a series of curves in figure 33, page 103. Further study of this pattern, however, gives information as to how and when that change took place.
Changes in the 11-year tree-cycle of Arizona—A careful examination of an early differential pattern of the Flagstaff tree record gave the following probable history of the 11-year variation in Arizona:
| Years. | Period. | Remarks. |
|---|---|---|
| 1395-1550 | 11.3 | Double crests throughout, except 1476 and 1487, where the second crest fails. |
| 1550-1595 | 14.3 | Heavy double crest. |
| 1595-1661 | 11.0=0.5 | Heavy single crests with trace of double diminishing to small variable singles. |
| 1661-1667 | 16.0(?) | Possibly 1 long interval. |
| 1677-1770 | 12.5 | Double crests mostly; going to 10.8 from 1702 to 1722. |
| 1770-1793 | 9.0 | Sharp single crest continuing second crest of preceding double. |
| 1793-1817 | Doubtful. | |
| 1817-1910 | 11.6 | Rather broad, heavy crests, sometimes double; 1864 has too little and 1875 too much crest. |
The interval from 1830 to the present time divides also extremely well on a 21.0-year period, and fairly well in one of 7.3 years.
In obtaining this result no comparison was made with the sunspot record. So the following is of interest:
| Trees. | Sunspots. | ||
|---|---|---|---|
| Years. | Period. | Years. | Period. |
| 1595-1661 | 11.0=0.5 years | 1615.5 to 1660.0 | 11.1 (?) years. |
| 1661-1677 | 16(?) | 1660.0 to 1675.0 | 15.0 |
| 1677-1770 | 12.5 mostly and 10.8 | 1675.0 to 1769.7 | 10.5 |
| 1770-1793 | 9.0 | 1769.7 to 1788.1 | 9.2 |
| 1793-1817 | Doubtful. | 1788.1 to 1816.4 | 14.15 |
| 1817-1910 | 11.6, 21.0, or 7.3 | 1816.4 to 1905 | 11.08 |
DOUGLASS PLATE 12

| DIFFERENTIAL PATTERNS. | |
|
a. Sunspot Nos. 1610-1910 at 11.4. |
j. Norway, N-2, 400 years at 33.0. |
The agreement seems to the writer to justify the conclusion that the tree record may indicate a possible sunspot period of 11.3 years from 1400 to 1550 and of 14.3 from the latter date to 1600.
Sequoia pattern. — Pattern B in plate 10, opposite page 94, is naturally the most interesting in respect to age, as it gives the sequoia analysis for 3,200 years. The solar cycle subject to slight variations may be dimly seen in large parts of it. It shows with some prominence during the first 500 years of our era, then for a few hundred years near the year 1000 A. D., and for a long interval in the first 500 years of the record. There is opportunity for extensive study of these short periods, interpreting them by the aid of more widely scattered groups and other kinds of trees, and when possible by weather records.

Fig. 40.—Two differential patterns of Huntington's preliminary 2000-year sequoia record. The most prominent cycle is about 105 years in length, shown in the upper diagram.
Other solar cycles. — Plate 12, g to p, shows the multiples of the solar cycle. Pattern G gives the Arizona tree record analyzed at 23.5 years. It shows a slightly irregular vertical row of crests. This is best seen by tipping the pattern so that the eye views it from a low angle instead of perpendicularly as in ordinary reading. A line slanting down to the left giving a period at nearly 22.2 years would answer quite as well. The lower third is somewhat broken by the triple sunspot period showing in it. The same record is analyzed at 33.0 years in pattern N. In this pattern the lower third shows the triple cycle in vertical rows and the double cycle shows in rows slanting strongly down to the left. Patterns H and I in plate 12 show the excellent double sunspot rhythm in the long Norwegian and shorter Austrian records, whose curves were given in figures 36 and 24 respectively, pages 105 and 77. Pattern J shows the 33-year cycle of the 400-year tree, N-2, from near the Arctic Circle in Norway. The Vermont hemlocks are shown in pattern K. Here is found a good rhythm with a change in phase about 100 years ago. The Swedish curve shows a good rhythm at 37 years. Several intervals of triple solar cycle appear in the 1,000 years of early sequoia growth in pattern M. All the 8 patterns G to N are taken from special curves prepared on a one-fifth scale, using 5-year sums in the plot.
The 100-year cycle. — Only two tree records are long enough to be tested for a cycle of this length. The sequoia gives a very excellent alinement at a period of 101 years, shown even better in the upper pattern of figure 40. The pattern of the present plate shows an increase to about 125 years in the last 600 years, which corresponds to the best analysis of the 500-year Arizona curve. This latter is at 120 years as shown in pattern P. Both of these are made from special curves plotted on one twenty-fifth of the usual scale.
Illustration by the periodograph. — The illustrations of periodograph analysis given above are practically the first made with this instrument and are therefore crude in many respects. Its advantage in the study of simple and obvious cycles such as the sunspot numbers is not at once apparent to the eye and its efficiency becomes evident only when one tries to select the exact period and state its accuracy. But one can foresee a useful application of this instrument in the study of mixed periods, such as appear in tree-growth here considered or in rainfall and other meteorological elements, a field as yet almost untouched on account of its complexity. However, in the brief presentation of its work given above, it is evident that the periodograph is found to corroborate and extend the results of the previous direct study of curves and to confirm the evidence there given of the great extent and importance of the solar cycles in the growth of trees. SUMMARY.
In the foregoing investigation the following conclusions have been reached:
(1) The variations in the annual rings of individual trees over considerable areas exhibit such uniformity that the same rings can be identified in nearly every tree and the dates of their formation established with practical certainty.
(2) In dry climates the ring thicknesses are proportional to the rainfall with an accuracy of 70 per cent in recent years and this accuracy presumably extends over centuries; an empirical formula can be made to express still more closely this relationship between tree-growth and rainfall; the tree records therefore give us reliable indications of climatic cycles and of past climatic conditions.
(3) The tree's years for such records begins in the autumn.
(4) Double rings are caused by spring drought and are indicative of the distribution of rainfall throughout the year.
(5) Tree records may be used in the intensive study of the location of homogeneous meteorological conditions and in outlining meteorological districts.
(6) Certain areas of wet-climate trees in northern Europe give an admirable record of the sunspot numbers and some American wet-climate trees give a similar record, but with their maxima 1 to 3 years in advance of the solar maxima. It is possible to identify living trees giving this remarkable record and to ascertain the exact conditions under which they grow.
(7) Practically all the groups of trees investigated show the sunspot cycle or its multiples; the solar cycle becomes more certain and accurate as the area of homogeneous region increases or the time of a tree record extends farther back; this suggests the possibility of determining the climatic and vegetational reaction to the solar cycle in different parts of the world.
(8) A most suggestive correlation exists in the dates of maxima and minima found in tree-growth, rainfall, temperature and solar phenomena. The prevalence of the solar cycle or its multiples, the greater accuracy as area or time are extended, and this correlation in dates point toward a physical connection between solar activity and terrestrial weather.
(9) The tree curves indicate a complex combination of short periods including a prominent cycle of about 2 years.
(10) An instrument has been constructed, which promises special facility in the analysis of such periods.
The items enumerated above point to the general conclusion that near at hand and readily available in our forest areas is written a story of climatic cycles and solar relationship which in part at least is interpreted by the methods illustrated in the foregoing pages. In the summer of 1919 a trip was made to the sequoia groves with three objects in view: (1) settling an uncertainty regarding the ring provisionally called 1580a; (2) gathering material bearing on the relation of short-period cycles to topography; (3) investigating the causes of enlarged or gross rings. It is only the first of these topics which has an important bearing on the foregoing chapters.
The region near the General Grant National Park was visited and 12 new trees were very carefully selected as to their water-supply, drainage, and distance from other trees, and short radial samples were cut from them. It did not seem necessary to have these include more than the last 500 years of growth. The radial piece, therefore, was made very small, but especial attention was given to procuring a continuous and reliable record. Critical examination showed at once that occurrence of the ring 1580a was dependent on locality. The trees from the uplands, where identification was easy, largely failed to show the ring, but in specimens from swampy basins, where cross-identification was difficult and sometimes uncertain, the ring was nearly always present. A complete decision, therefore, in favor of its real existence was satisfactorily obtained and the necessary corrections were made in the foregoing text and in the tabular matter which follows. It seems likely that the year 1580, which this ring represents, was phenomenally deficient in moisture in the locality of these giant trees.
In addition to the 12 new trees added to the sequoia group, a cutting was made from the stump D-12, which had hitherto defied all attempts at satisfactory dating. A small piece going back about 800 years was cut from a part of the circumference, entirely free from compressed rings, about 4 feet away from the full sample cut in 1915. At the time of cutting, great care was taken to insure proper cross-identification between the inner end of the new piece and the former sample. But in the laboratory the new piece proved to carry a very excellent series of rings and the identification was everywhere very easy and sure, and all doubt about the dating of that particular tree to its earliest ring in 135 A. D., several inches away from its original center, was removed; therefore, it may now be included among those whose dating is entirely reliable.
A new group of 5 very old trees from near Flagstaff, has settled an uncertainty regarding the years 1463 and 1464 in the yellow pines (too late, however, to rectify figure 3 on page 25). It is now possible to carry a very fair cross-identification between the pines of Arizona and the sequoias of California through the whole five centuries of the former.
- ↑ The corrections found in 1919 make these dates one year earlier.