Effect of Reflection from a Moving Mirror on the Velocity of Light
EFFECT OF REFLECTION FROM A MOVING MIRROR
ON THE VELOCITY OF LIGHT
BY A. A. MICHELSON
According to the undulatory theory of light the velocity of light is independent of the velocity of the source, and of the velocity of a mirror at which it is reflected.
According to the emission theory the resultant velocity from a moving source is increased by the component of the velocity of the source. But it appears that different forms of emission theory require different results on reflection from a moving mirror. If the light corpuscles are reflected as projectiles from an elastic wall, then the velocity of light should be increased by twice the component of the velocity of the mirror.[1]
The following arrangement was devised for the purpose of deciding the question experimentally.
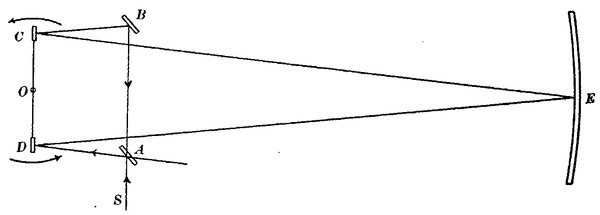
Fig. 1.—Diagram of apparatus
Light from a source at S falls on a lightly silvered mirror A. The reflected pencil goes to a revolving mirror D, thence to the concave mirror E, to the second mirror C revolving about the same axis O, whence it proceeds to the plane mirror B and is reflected back to A. The transmitted pencil pursues the same path in the opposite direction, returning via DA to the starting-point, where it meets the first pencil, producing interference fringes which are observed by means of a telescope with micrometer eyepiece.
According to the undulatory theory the velocity of light is unaffected by the velocity of the mirror while the emission theory[2] requires that
where is the velocity of light after reflection, V the velocity before reflection and v the component of the velocity of the mirror in the direction of the reflected pencil, and r = 2 according to the elastic impact theory; while r = 1 if the mirror surface acts as a new source.
The time occupied by the pencil DEC is
while that taken by the pencil CED is
where D is the distance OE, d = distance the revolving mirror moves while light passes over DEC, and V1 the resultant velocity of the first pencil, V2 that of the second.
The difference in time is therefore
But
whence[3]
The corresponding displacement of the interference fringes is
| For | ||
| " | ||
| " |
The experiment was tried under the following conditions.
The revolving mirrors were mounted on the shaft of an electric motor the speed of which (measured by a speed counter) could be varied from zero to 1800 revolutions per minute. The distance between centers of the mirrors was l = 26.5 cm;[4] the distance OE was 608 cm. The light of the carbon arc (in one experiment, sunlight) was filtered through a gelatine film transmitting light of mean wave-length λ = 0μ.60.
The formula for the displacement,
if n is turns per sec.
or
if N is turns per min.
gives with these data and r = 0 a displacement of 3.76 fringes for 1000 revolutions per minute.
Following is a table of results of observations reduced to this speed.
It appears therefore that within the limit of error of experiment (say 2 per cent) the velocity of a moving mirror is without influence on the velocity of light reflected from its surface.
Assuming that the effect is actually nil, this interference method may be used to measure the velocity of light with an order of accuracy equal to that of the improved Foucault method or of the "combination" method proposed in an article in the Phil. Mag., March 1902. Any one of these three methods is capable of furnishing results of the order of accuracy of one part in one hundred thousand; and differential measurements (e.g., with the light of the
| Δ | Weight | |
| 1… 2… 3… 4… 5… 6… 7… |
3.8 3.1 3.2 4.3 3.8 3.93 3.83 |
1 1 1 2 2 3 4 |
| 3.81 = weighted mean 3.76 = calculated displacement | ||
two limbs of the sun) can be obtained with a still higher degree of precision; and thus the effect of a moving source on the velocity of light could be determined.
- Ryerson Physical Laboratory
- University of Chicago
- ↑ An alternative hypothesis, that the velocity of light should be increased by the component of the velocity of the mirror, is suggested by R. C. Tolman but shown to be inadmissible. (R. C. Tolman, "Some Emission Theories of Light," Physical Review, August 1912).
- ↑ According to the theory of Ritz (Annales de chimie et de physique, Ser. VIII, 13, 1908) the velocity of light is not affected by reflection from a moving mirror, but is affected by the motion of the source.
- ↑ Omitting quantities of the second order; v should be replaced by v cos α, but since a is only 3°, the factor cos α may be taken equal to unity.
- ↑ This agrees within less than 1 per cent with the distance calculated from the measured distance AB of the interferometer mirrors.
![]()
This work is in the public domain in the United States because it was published before January 1, 1929.
The longest-living author of this work died in 1931, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 92 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
![]()
Public domainPublic domainfalsefalse




![{\displaystyle T_{1}-T_{2}=2\left[{\frac {D+d}{V+rv}}-{\frac {D-d}{V-rv}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0fb8c8259798131a2050643624001cc261cfc39)










