Optimum height for the bursting of a 105mm shell
BALLISTIC RESEARCH LABORATORY
MEMORANDUM REPORT NO. 139
SC/mo
Aberdeen Proving Ground, Md.
April 15, 1943
OPTIMUM HEIGHT FOR THE BURSTING OF A 105MM SHELL
1. The statement of the problem and its solution: It is required to find the height at which it is most advantageous to have a 105mm shell burst in order that the maximum injury may be inflicted on personnel.
It is found (as a result of the calculations to be presented) that the height at which it it most advantageous to have the shell burst is 75 feet.
2. Basis for the calculations: The experimental data on which the calculations were based are those of Mr. Tolch who has analyzed both the angular distribution of the fragments when a 105mm shell bursts and the distribution in weight of these fragments.
Regarding the angular distribution it appears that the greater proportion of the fragments in the lateral spray is confined to an annular cone with semi-angle of 7-1/2. We shall see later that the precise value of this semi-angle defining the angular width of the spray has no special influence on our results.

Regarding the distribution with mass of the fragments, Mr. Tolch's results can be relied upon for the heavier fragments (), while for the smaller fragments the reliability becomes steadily less on account of the necessary incompleteness in the recovery of these fragments. In order, therefore, to obtain a reasonable extrapolation of the distribution for the smaller masses, the total mass contributed by the fragments in the various mass groups was plotted against the mass of the fragment and from a smooth curve drawn through these points, a distribution was derived which formed the basis of further calculations. The observed and the derived distributions are compared in Table I. From this table, Table II giving the number of fragments in the downward lateral spray with masses greater than a given value was derived.
| m in lbs. | Observed | Derived |
| 0.005 | 250 | 484 |
| 0.007 | 340 | |
| 0.009 | 200 | 260 |
| 0.015 | 146 | 146 |
| 0.025 | 79 | 80 |
| 0.035 | 51 | 52 |
| 0.045 | 45 | 36 |
| 0.055 | 27 | 27 |
| 0.065 | 16 | 20 |
| 0.075 | 10 | 16 |
| 0.085 | 9 | 13 |
| 0.095 | 8 | 11 |
| 0.105 | 13 | 9 |
| 0.115 | 23 | 8 |
| 0.125 | 6 | |
| 0.135 | 6 | |
| 0.145 | 5 | |
| 0.155 | 4 | |
| 0.165 | 3 | |
| 0.175 | 2 | |
| 0.185 | 1 |
TABLE II
Number of fragments in the downward lateral spray with masses greater than m
| m | |
| 0.003 | 1176 |
| 0.005 | 765 |
| 0.007 | 523 |
| 0.009 | 353 |
| 0.015 | 223 |
| 0.025 | 150 |
| 0.035 | 110 |
| 0.045 | 88 |
| 0.055 | 66 |
| 0.065 | 52 |
| 0.075 | 42 |
| 0.085 | 34 |
| 0.095 | 27 |
| 0.105 | 22 |
| 0.115 | 18 |
| 0.125 | 13 |
| 0.135 | 10 |
| 0.145 | 7 |
| 0.155 | 5 |
| 0.165 | 3 |
3. The effectiveness and the ranges of the fragments of different masses: Another factor which it is necessary to decide on before we can estimate the height at which it it most advantageous to have the shell burst is concerned with the range and the effectiveness of a fragment of a given mass.
We shall suppose that a fragment is effective if it has a sufficient velocity to penetrate an inch of wood. Using a formula due to Welch (who has experimented on the penetration of wood by fragments of various masses) we find that a fragment of mass (in lbs.) will be effective if it has a velocity greater than where
(1)
where is expressed in lbs. and in ft/sec.
Now the velocity with which the fragments are shot off from a 105mm shell is of the order of 3500 ft/sec. Consequently, a fragment of this shell which has a given mass will be effective only if it has traversed a range less than a certain value To determine this maximum range as a function of the mass of the fragment the following formulae (again based on Welch) were used:
(2)
and
(3)
Using the foregoing formulae the following table was derived.
| m in lbs. | range in ft. | m in lbs. | range in ft. |
| 0.0005 | 17 | 0.025 | 551 |
| 0.001 | 40 | 0.030 | 630 |
| 0.002 | 73 | 0.040 | 769 |
| 0.004 | 119 | 0.050 | 895 |
| 0.006 | 156 | 0.060 | 1006 |
| 0.008 | 209 | 0.080 | 1202 |
| 0.010 | 253 | 0.100 | 1376 |
| 0.015 | 368 | 0.200 | 2046 |
| 0.020 | 466 | 0.400 | 2801 |
In deriving Table III, we have, as we have already stated, used the British results on the retardation in air and the penetration into wood of fragments. However, it is now held that Welch's formula underestimates (possibly by a factor ) the retardation in air. On the other hand it appears that using Welch's results both for the penetration in air and in wood we are led to consistent results. Thus Inglis using a different criterion for effectiveness (namely that a fragment to be effective must have 150 ft. lbs. of energy) and using a retardation factor in air which is two thirds of Welch's finds ranges of the order of 70, 110 and 280 ft. for masses 0.0023, 0.0040 and 0.0095 lbs., respectively. These ranges of Inglis should be compared with the values we have derived namely 80, 120 and 250 ft., respectively. The agreement is satisfactory.
4. The estimate of the optimum height. The estimate of the optimum height was made on the basis of the following model.

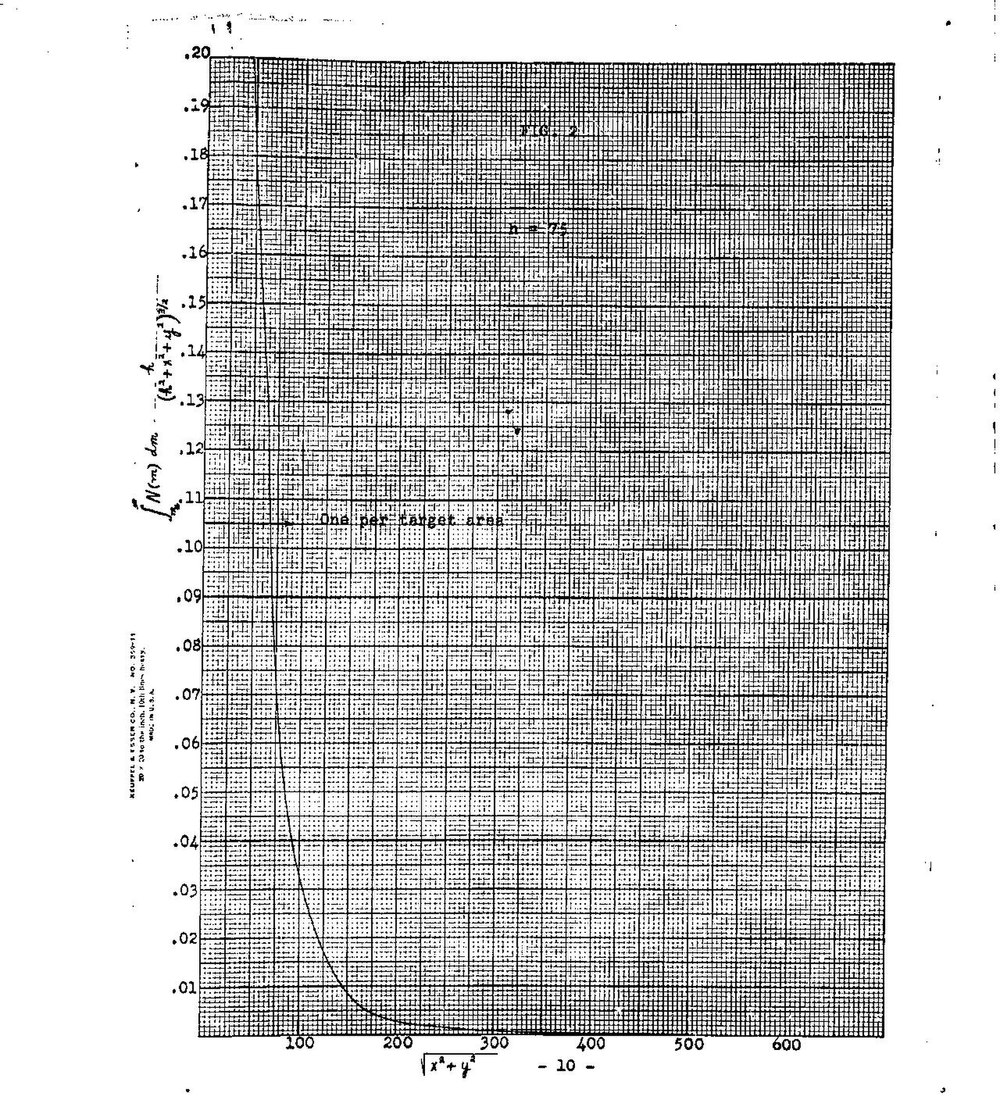
Let the shell explode at a height from the ground. We shall suppose further the lateral spray is symmetrical with respect to the plane. Then the surface density of the fragments which arrive at the point and which are effective is given by
(4)
Now let denote the effective area of a target. Then the area on the ground sprayed by fragments can be divided, in general, into two regions: An inner region I in which is greater than and an outer region II in which is less than . Under these circumstances it is clear that in region I where we are super effective in the sense that the entire personnel in this region may be expected to be seriously affected. In the other region the probability of hitting a particular target is proportional to . Thus the number of casualties is given by
(5)
where denotes the number of targets per unit area and
(6)
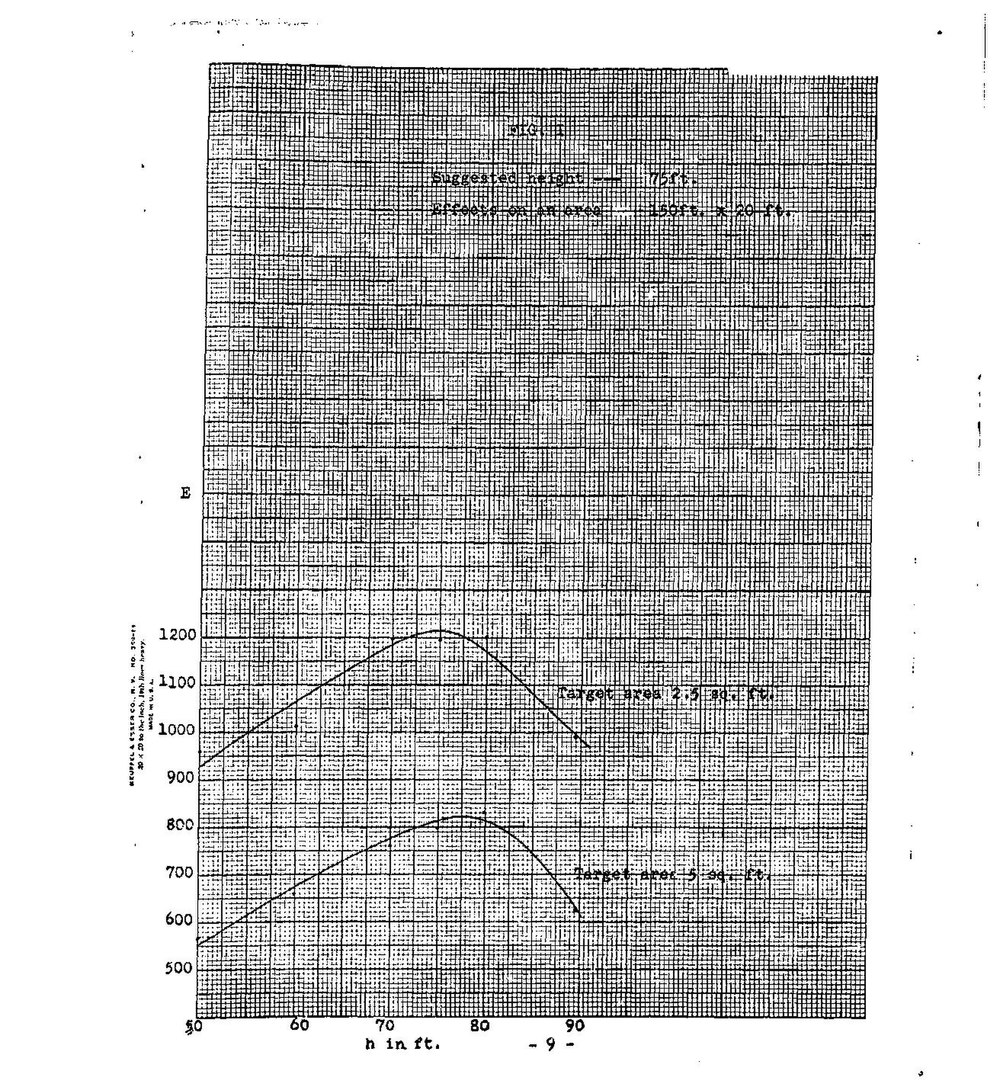
In Table IV the density (apart from the factor ) is tabulated for various values of . Finally the values of derived on the basis of the results of Table IV are plotted in Fig. 1. It is seen that within the uncertainties of the problem the optimum height is about 75 ft. for a wide range of target areas.
| h=50 | h=60 | h=70 | h=75 | h=80 | h=90 | h=120 | |
| 25 | - | - | - | - | - | 0.1380 | 0.0586 |
| 50 | - | - | - | - | - | 0.0955 | 0.0459 |
| 75 | - | 0.0874 | 0.0745 | 0.0722 | 0.0673 | 0.0559 | 0.0318 |
| 100 | 0.0376 | 0.0378 | 0.0338 | 0.0334 | 0.0324 | 0.0330 | 0.0189 |
| 125 | 0.0166 | 0.0169 | 0.0176 | 0.0174 | 0.0176 | 0.0168 | 0.0127 |
| 150 | 0.0076 | 0.0084 | 0.0089 | 0.0091 | 0.0093 | 0.0089 | 0.0079 |
| 175 | 0.0041 | 0.0047 | 0.0051 | 0.0050 | 0.0052 | 0.0052 | 0.0050 |
| 200 | 0.0023 | 0.0027 | 0.0029 | 0.0030 | 0.0030 | 0.0031 | 0.0033 |
| 250 | 0.0010 | 0.0011 | 0.0013 | 0.0014 | 0.0014 | 0.0015 | 0.0017 |
| 300 | 0.00049 | 0.00057 | 0.00065 | 0.00069 | 0.00072 | 0.00078 | 0.00092 |
| 400 | 0.00016 | 0.00018 | 0.00021 | 0.00022 | 0.00024 | 0.00026 | 0.00033 |
| 500 | 0.00007 | 0.00008 | 0.00009 | 0.00010 | 0.00010 | 0.00011 | 0.00014 |
| 600 | 0.00003 | 0.00004 | 0.00004 | 0.00005 | 0.00005 | 0.00005 | 0.00007 |
| 700 | 0.00002 | 0.00002 | 0.00002 | 0.00002 | 0.00003 | 0.00003 | 0.00004 |
| 800 | 0.00001 | 0.00001 | 0.00001 | 0.00001 | 0.00001 | 0.00002 | 0.00002 |
5. Some General Remarks: We have seen that the height at which it is most advantageous to have a 105mm shell burst is about 75 ft. for wide limits in the effective area of the target involved. The reason for this rough independence can be understood in terms of the following considerations:
Essentially the existence of an optimum height for burst depends on the extent to which the area on the ground where we are super-efficient (region I of §4) can be reduced. It cannot however be concluded that the optimum height corresponds to reducing this area to zero. For the fragments which are most numerous are those with small masses and these have ranges of the order of itself. Thus, when , the fragments which are effective (i.e., with velocities greater than [Cf. eq. 1]) and which arrive on the ground directly below the point of burst must have masses greater than 0.0021 lb. (cf. Table III). Fragments with in this neighborhood are the most numerous, but their effect is confined to a very small area. Accordingly we must go to somewhat larger masses (with correspondingly longer ranges) to be really efficient. In other words, at the optimum height we must necessarily be super efficient in the regions directly below the point of burst. In other words the area over which we are super efficient must be reduced as much as is compatible with the circumstances of the problem.
The considerations of the preceding paragraph account also for relative insensitiveness of the optimum height with the target area within limits. For while a reduction in the effective target area requires a greater surface density of fragments this can be achieved by even a slight reduction in since by so doing we bring into range the smaller fragments which increase in number very rapidly with decreasing mass.
Again, it it clear that since a change in the half angle of the spray can be formally incorporated into the calculations as a change in target area, the optimum height is relatively insensitive also to changes in . For a given total number of fragments, the surface density varies inversely as . Hence, other things being equal a change in alters the surface densities by a constant factor and the final efficiency will be clearly the same if were kept unaltered but the target area increased by the same factor.
In our calculations we have assumed that the spray is symmetrical with respect to the plane. A tilt of this spray with the vertical by a small angle can be taken into account by using for the optimum height the value
the angle of tilt of the spray with the vertical).
Considering all the uncertainties of the problem we may suggest as the optimum height for burst a value of 75 ft. In doubtful cases it might be safer to go down to as much as 70 ft. and in any event greater heights should be avoided as far as possible.
We may finally remark that if the shell bursts at 75 ft above the ground, the area which is effectively sprayed by the fragments is
and
Accordingly, when firing, it would be advantageous to have the shells burst at about 150 ft apart sideways and 20 ft. apart depth-wise (See Fig. 2)
This paper is devoted to determining the height at which it is most advantageous to have 105mm shell burst in order that the maximum injury may be inflicted on personnel. On the basis of the experimental data of Tolch on the fragmentation of the 105mm shell it is concluded that the optimum height is about 75 ft. Also when the shell does burst at this height, it effectively covers an area of 150 ft by 20 ft.
COMMENTS ON THE RELATION OF THE PRECEDING REPORT TO RECENT OBSERVATIONS AT FORT BRAGG.
Recent experiments on the effect of ricochet and time fire of 105mm H.E. Shells against personnel, conducted by the Field Artillery Board at Fort Bragg, indicate an optimum altitude of burst as 45 feet instead of the 75 feet suggested by the computations of Dr. Chandrasekhar. This brings up the question of the reason for this experimental discrepancy.
The main reason appears to be that the computations of Dr. Chandrasekhar were presumably based on a tacit assumption of more deeply entrenched personnel, protected against fragments coming in at oblique angles, whereas the dummies used in the experiments at Fort Bragg came to within a few inches of the surface. This assumption would affect the computed optimum altitude of burst in two ways. First, obviously a very low burst could only injure personnel in a very small area. Thus whereas in the experiments at Fort Bragg, a burst at an altitude of 15-30 feet is found effective over a rather wide area, deeply entrenched horizontal personnel would be exposed to such a burst over a region perhaps 8 feet in diameter. And also, oblique hits have longer trajectories, and hence less striking velocity. This would explain the apparent decrease in striking velocity of small fragments from altitudes above 40 feet observed at Fort Bragg. It is usually supposed that this deceleration becomes important only for ranges of 70-100 feet; these would be consistent for fragments travelling obliquely at angles of 30°-45° with the horizontal.
Thus Dr. Chandrasekhar's conclusions should apply to entrenched personnel, screened against oblique hits.
Garrett Birkhoff
![]()
This work is in the public domain in the United States because it is a work of the United States federal government (see 17 U.S.C. 105).
![]()
Public domainPublic domainfalsefalse





































