Page:EB1911 - Volume 02.djvu/568

35. Diagram of Multiplication.—The process of multiplication is performed in order to obtain such results as the following:—

If 1 boy receives 7 apples,
then 3 boys receive 21 apples;

or

If 1s. is equivalent to 12d.,
then 5s. is equivalent to 60d.

The essential portions of these statements, from the arithmetical point of view, may be exhibited in the form of the diagrams A and B:—

or more briefly, as in C or C′ and D or D′:—

the general arrangement of the diagram being as shown in E or E′:—

Multiplication is therefore equivalent to completion of the diagram by entry of the product.

36. Multiple-Tables.—The diagram C or D of § 35 is part of a complete table giving the successive multiples of the particular unit. If we take several different units, and write down their successive multiples in parallel columns, preceded by the number-series, we obtain a multiple-table such as the following:—

1	1	2	9	1s.   5d.	3 yds. 2 ft.	17359	. . . . .
2	2	4	18	2s. 10d.	7 yds. 1 ft.	34718	. . . . .
3	3	6	27	4s.   3d.	11 yds. 0 ft.	52077	. . . . .
4	4	8	36	5s.   8d.	14 yds. 2 ft.	69436	. . . . .
5	5	10	45	7s.   1d.	16 yds. 1 ft.	86795	. . . . .
.	.	.	.	.	.	.	. . . . .
.	.	.	.	.	.	.	. . . . .
.	.	.	.	.	.	.	. . . . .
.	.	.	.	.	.	.	. . . . .

It is to be considered that each column may extend downwards indefinitely.

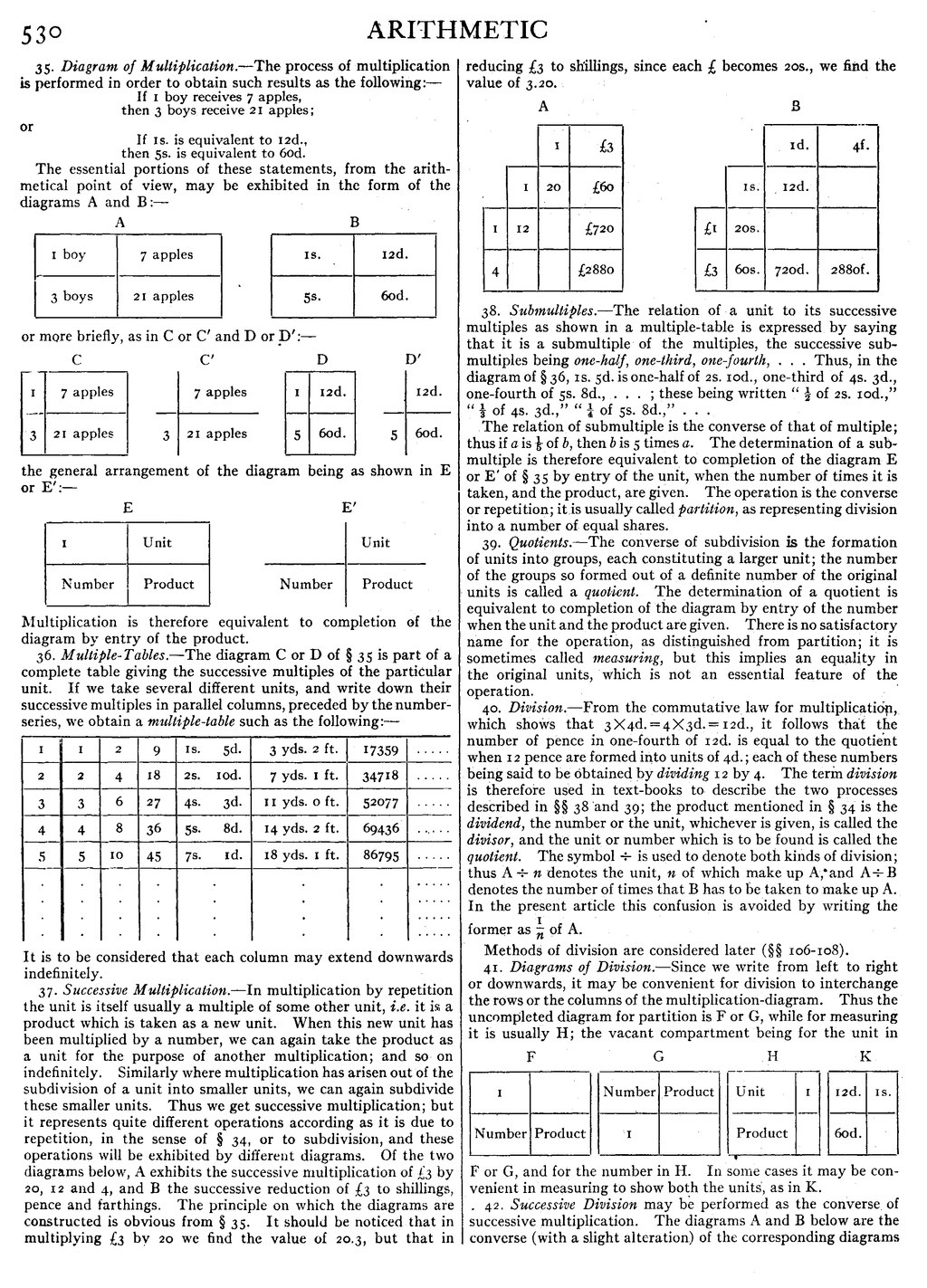
37. Successive Multiplication.—In multiplication by repetition the unit is itself usually a multiple of some other unit, i.e. it is a product which is taken as a new unit. When this new unit has been multiplied by a number, we can again take the product as a unit for the purpose of another multiplication; and so on indefinitely. Similarly where multiplication has arisen out of the subdivision of a unit into smaller units, we can again subdivide these smaller units. Thus we get successive multiplication; but it represents quite different operations according as it is due to repetition, in the sense of § 34, or to subdivision, and these operations will be exhibited by different diagrams. Of the two diagrams below, A exhibits the successive multiplication of £3 by 20, 12 and 4, and B the successive reduction of £3 to shillings, pence and farthings. The principle on which the diagrams are constructed is obvious from § 35. It should be noticed that in multiplying £3 by 20 we find the value of 20·3, but that in reducing £3 to shillings, since each £ becomes 20s., we find the value of 3·20.

38. Submultiples.—The relation of a unit to its successive multiples as shown in a multiple-table is expressed by saying that it is a submultiple of the multiples, the successive submultiples being one-half, one-third, one-fourth, . . . Thus, in the diagram of § 36, 1s. 5d. is one-half of 2s. 10d., one-third of 4s. 3d., one-fourth of 5s. 8d., . . .; these being written “1/2 of 2s. 10d.,” “1/3 of 4s. 3d.,” “1/4 of 5s. 8d,”. . .

The relation of submultiple is the converse of that of multiple; thus if a is 1/5 of b, then b is 5 times a. The determination of a submultiple is therefore equivalent to completion of the diagram E or E′ of § 35 by entry of the unit, when the number of times it is taken, and the product, are given. The operation is the converse of repetition; it is usually called partition, as representing division into a number of equal shares.

39. Quotients.—The converse of subdivision is the formation of units into groups, each constituting a larger unit; the number of the groups so formed out of a definite number of the original units is called a quotient. The determination of a quotient is equivalent to completion of the diagram by entry of the number when the unit and the product are given. There is no satisfactory name for the operation, as distinguished from partition; it is sometimes called measuring, but this implies an equality in the original units, which is not an essential feature of the operation.

40. Division.—From the commutative law for multiplication, which shows that 3 × 4d. = 4 × 3d. = 12d., it follows that the number of pence in one-fourth of 12d. is equal to the quotient when 12 pence are formed into units of 4d.; each of these numbers being said to be obtained by dividing 12 by 4. The term division is therefore used in text-books to describe the two processes described in §§ 38 and 39; the product mentioned in § 34 is the dividend, the number or the unit, whichever is given, is called the divisor, and the unit or number which is to be found is called the quotient. The symbol ÷ is used to denote both kinds of division; thus A ÷ n denotes the unit, n of which make up A, and A ÷ B denotes the number of times that B has to be taken to make up A. In the present article this confusion is avoided by writing the former as 1/n of A.

Methods of division are considered later (§§ 106-108).

41. Diagrams of Division.—Since we write from left to right or downwards, it may be convenient for division to interchange the rows or the columns of the multiplication-diagram. Thus the uncompleted diagram for partition is F or G, while for measuring it is usually H; the vacant compartment being for the unit in F or G, and for the number in H. In some cases it may be convenient in measuring to show both the units, as in K.

42. Successive Division may be performed as the converse of successive multiplication. The diagrams A and B below are the converse (with a slight alteration) of the corresponding diagrams