(see Thermodynamics), dp/dt = λ/t(v2−v1), where p and t denote
the pressure and temperature, λ the heat required to change unit
mass of the systems from one phase to the other, and v2−v1
the resulting change in volume. The phase rule combined with the
latent heat equation contains the whole theory of chemical and
physical equilibrium.
Application to Solutions.—In a system containing a solution we have to deal with two components at least. The simplest case is that of water and a salt, such as sodium chloride, which crystallizes without water. To obtain a non-variant system, we must assemble four phases—two more than the number of components. The four phases are (1) crystals of salt, (2) crystals of ice, (3) a saturated solution of the salt in water, and (4) the vapour, which is that practically of water alone, since the salt is non-volatile at the temperature in question. Equilibrium between these phases is obtained at the freezing point of the saturated solution under the pressure of the vapour. At that pressure and temperature the four phases can co-exist, and, as long as all of them are present, the pressure and temperature will remain steady. Thus a mixture of ice, salt and the saturated solution has a constant freezing point, and the composition of the solution is constant and the same as that of the mixed solids which freeze out on the abstraction of heat. This constancy both in freezing point and composition formerly was considered as a characteristic of a pure chemical compound', and hence these mixtures were described as components and given the name of “cryohydrates.”
In representing on a diagram the phenomena of equilibrium in a two-component system we require a third axis along which to plot the composition of a variable phase. It is usual to take three axes at right angles to each other to represent pressure, temperature and the composition of the variable phase. On a plane figure this solid diagram must be drawn in perspective, the third axis C being imagined to lie out of the plane of the paper. The phase-rule diagram that we construct is then a sketch of a solid model, the lines of which do not really lie in the plane of the paper.

Fig. 2.
Let us return to the case of the system of salt and water. At the cryohydric point O we have four phases in equilibrium at a definite pressure, temperature and composition of the liquid phase. The condition of the system is represented by a single point on the diagram. If heat be added to the mixture ice will melt and salt dissolve in the water so formed. If the supply of ice fails first the temperature will rise, and, since solid salt remains, we pass along a curve OA giving the relation between temperature and the vapour pressure of the saturated solution. If, on the other hand, the salt of the cryohydrate fails before the ice the water given by the continued fusion dilutes the solution, and we pass along the curve OB which shows the freezing points of a series of solutions of constantly increasing dilution. If the process be continued till a very large quantity of ice be melted the resulting solution is so dilute that its freezing point B is identical with that of the pure solvent. Again, starting from O, by the abstraction of heat we can remove all the liquid and travel along the curve OD of equilibrium between the two solids (salt and ice) and the vapour. Or, by increasing the pressure, we eliminate the vapour and obtain the curve OF giving the relation between pressure, freezing point and composition when a saturated solution is in contact with ice and salt.
If the salt crystallizes with a certain amount of water as well as with none, we get a second point of equilibrium between four phases. Sodium sulphate, for instance, crystallizes below 32.6° as Na2SO4⋅10H2O, and above that temperature as the anhydrous solid Na2SO4. Taking the point O to denote the state of equilibrium between ice, hydrate, saturated solution and vapour, we pass along OA till a new solid phase, that of Na2SO4, appears at 32.6°; from this point arise four curves, analogous to those diverging from the point O.
For the quantitative study of such systems in detail it is convenient to draw plane diagrams which are theoretically projections of the curves of the solid phase rule diagram on one or other of these planes. Experiments on the relation between temperature and concentration are illustrated by projecting the curve OA of fig. 2 on the tc-plane. The pressure at each point should be that of the vapour, but since the solubility of a solid does not change much with pressure, measurements under the constant atmospheric pressure give a curve practically identical with the theoretical one.

Fig. 3.
Fig. 3 gives the equilibrium between sodium sulphate and water in this way. B is the freezing point of pure water, O that of a saturated solution of Na2SO4⋅10H2O. The curve OP represents the varying solubility of the hydrate as the temperature rises from the cryohydric point to 32.6°. At that temperature crystals of the anhydrous Na2SO4 appear, and a new fixed equilibrium exists between the four phases—hydrate, anhydrous salt, solution and vapour. As heat is supplied, the hydrate is transformed gradually into the anhydrous salt and water. When this process is complete the temperature rises, and we pass along a new curve giving the equilibrium between anhydrous crystals, solution and vapour. In this particular case the solubility decreases with rise of temperature. This behaviour is exceptional.
Two Liquid Components.—The more complete phenomena of mutual solubility are illustrated by the case of phenol and water.

Fig. 4.
In fig. 4 A represents the freezing point of pure water, and AB the freezing point curve showing the depression of the freezing point as phenol is added. At B is a non-variant system made up of ice, solid phenol, saturated solution and vapour. BCD is the solubility curve of phenol in water. At C a new liquid phase appears—the solution of water in liquid phenol, the solubility of which is represented by the curve DE. At D the composition of the two liquids becomes identical, and at temperatures above D, 68°C the liquids are soluble in each other in all proportions, and only one liquid phase can exist. If the two substances are soluble in each other in all proportions at all temperatures above their melting points we get a diagram reduced to the two fusion curves cutting each other at a non-variant point. This behaviour is illustrated by the case of silver and copper (fig. 5). At the non-variant point the two metals freeze out together and the composition of the liquid is the same as that of the mixed solid which crystallizes from it. The solid is then known as a eutectic alloy.
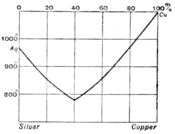
Fig. 5.
A liquid in which the composition is nearly that of the eutectic shows the changes in the rate of fall of temperature as it is allowed to cool. First a small quantity of one of the pure components begins to crystallize out, and the rate of cooling is thereby diminished owing to the latent heat liberated by the change of state. This process continues till the composition of the liquid phase reaches that of the eutectic, when the whole mass solidifies on the further loss of heat without change of temperature, giving a very definite freezing point. The process of cooling is thus represented by a path which runs vertically downwards till it cuts the
