for the intrinsic energy of a system will contain terms depending on the area of contact between different phases, and, for a given mass of material, the area will be greater if the substance is finely divided. Hence the conditions necessary to secure equilibrium when the solid phase is present are not the same as those necessary to cause crystallization to start in a number of crystals at first excessively minute in size. The corresponding phenomenon in the case of vapours is well known. Dust-free air will remain supersaturated with water-vapour in conditions where a dense cloud would be formed in presence of solid dust- nuclei or electric ions which serve the same purpose.
If a solution of a salt be stirred as it cools in an open vessel, a thin shower of crystals appears at or about the saturation temperature. These crystals grow steadily, but do not increase in number. When the temperature has fallen about io° C. below this point of saturation, a dense shower of new crystals appear suddenly. This shower may be dense enough to make the liquid quite opaque. These phenomena have been studied by H. A. Miers and Miss F. Isaac. If the solution be confined in a sealed glass tube, the first thin shower is not formed, and the system remains liquid till the secondary dense shower comes down. From this and other evidence it has been shown that the first thin shower in open vessels is produced by the accidental presence of tiny crystals obtained from the dust of the air, while the second dense shower marks the point of spon- taneous crystallization, where the decrease in total available energy caused by solidification becomes greater than the increase due to the large surface of contact between the liquid and the potentially existing multitudinous small crystals of the shower.
If the temperature at which this dense spontaneous shower of crystals is found be determined for different concentrations of solution, we can plot a " supersolubility curve," which is found generally to run roughly parallel to the " solubility curve " of steady equilibrium between liquid and already existing solid. When two substances are soluble in each other in all proportions, we get solubility curves like those of copper and silver shown in fig. 5. We should expect to find supersolubility curves lying below the solubility curves, and this result has been realized experimentally for the supersolubility curves of mixtures of salol (phenyl salicylate) and betol (/3-naphthol salicylate) represented by the dotted lines of fig. 12.
In practical cases of crystallization in nature, it is probable that these phenomena of supersaturation often occur. If a liquid mixture
of A and B (fig. 12) were inocu- lated with crystals of A when its composition was that represented by x, cooled very slowly and stirred, the conditions would be those of equilibrium throughout. When the temperature sank to a, on the freezing point curve, crystals of pure A would appear. The residual liquid would thus become richer in B, and the tem- perature and composition would pass along the curve till E, the eutectic point, was reached. The 100 liquid then becomes saturated " with B also, and, if inoculated with B crystals, will deposit B alongside of A, till the whole mass is solid. But, if no solid be present initially, or if the cooling be rapid, the liquid of composition x becomes supersaturated and may cool till the supersaturation curve is reached at b, and a cloud of A crystals comes down. The temperature may then rise and the concentration of B increase in the liquid in a manner represented by some such line as b f. The conditions may then remain those of equilibrium along the curve / E, but before reaching / the solution may become supersaturated with B and deposit B crystals spontaneously. The eutectic point may never be reached. The possibility of these phenomena should be borne in mind when attempts are made to interpret the structure of crystalline bodies in terms of the theory of equilibrium.
Osmotic Pressure. — The phase rule combined with the latent heat equation enables us to trace the general phenomena of equilibrium in solutions, and to elucidate and classify cases even of great complexity. But other relations between the different properties of solutions have been investigated by another series of conceptions which we shall proceed to develop. Some botanical experiments made about 1870 suggested the idea of semi-permeable membranes, i.e. membranes which allow a solvent to pass freely but are impervious to a solute when dissolved in that solvent. It was found, for instance, that a film of insoluble copper ferrocyanide, deposited in the walls of a
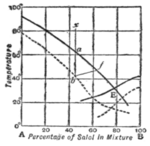
Fig. 12.
porous vessel by the inward diffusion and meeting of solutions of copper sulphate and potassium ferrocyanide, would allow water to pass, but retained sugar dissolved in that liquid. It was found, too, when water was placed on one side of such a membrane, and a sugar solution in a confined space on the other, that water entered the solution till a certain pressure was set up when equilibrium resulted.
The importance of these experiments from the point of view of the theory of solution, lay in the fact that they suggested the con- ception of a perfect or ideal semi-permeable partition, and that of an equilibrium pressure representing the excess of hydrostatic pressure required to keep a solution in equilibrium with its pure solvent through such a partition. Artificial membranes are seldom or never perfectly semi-permeable — some leakage of solute nearly always occurs, but the imperfections of actual membranes need no more prevent our use of the ideal conception than the faults of real engines invalidate the theory of ideal thermodynamics founded on the conception of a perfect, reversible, frictionless, heat engine. Further, in the free surface the solutions of an involatile solute in a volatile solvent, through which surface the vapour of the solvent alone can pass, and in the boundary of a crystal of pure ice in a solution, we have actual surfaces which are in effect perfectly semi- permeable. Thus the results of our investigations based on ideal conceptions are applicable to the real phenomena of evaporation and freezing.
Dilute Solutions. — Before considering the more complicated case of a concentrated solution, we will deal with one which is very dilute, when the theoretical relations are much simplified. The vapour pressure of a solution may be p^ssare. measured experimentally by two methods. It may be compared directly with that of the pure solvent, as the vapour- pressure of a pure liquid is determined, by placing solvent and solution respectively above the mercury in two barometer tubes, and comparing the depressions of the mercury with the height of a dry barometer at the same temperature. This method was used by Raoult. On the other hand, a current of dry air may be passed through the series of weighed bulbs containing solution and solvent respectively, and the loss in weight of each determined. The loss in the solution bulbs gives the mass of solvent absorbed from the solution, and the loss in the solvent bulbs the additional mass required to raise the vapour pressure in the air-current to equilibrium with the pure solvent. The relative lowering of vapour pressure of the solution compared with that of the solvent is measured by the ratio of the extra mass absorbed from the solvent bulbs to the total mass absorbed from both series of bulbs. Experiments by this method have been made by W. Ostwald and J. Walker, and by Lord Berkeley and E. G. J. Hartley.
The vapour pressure of the solution of a non- volatile solute is less than the vapour pressure of the pure solvent. Hence if two vessels, one filled with solvent and one with solution, be placed side by side in an exhausted chamber, vapour will evapo- rate from the solvent and condense on the solution. The solution will thus gain solvent,, and will grow more and more dilute. Its volume will also increase, and thus its upper surface will rise in the vessel. But as we ascend in an atmosphere the pressure diminishes; hence the pressure of the vapour in the chamber is less the higher we go, and thus eventually w T e reach a state of equilibrium where the column of vapour is in equilibrium at the appropriate level both with solvent and solution. Neglecting the very small buoyancy of the vapour, the hydrostatic pressure P at the foot of the column of solution is h g p where h is the height of the column and p the mean density of the solution. If the height be not too great, we may assume the density of the vapour to be uniform, and write the difference in vapour pressure at the surfaces of the solvent and of the solution as p — p'= hgcr. Hence we find that p — p' =P<r/p for a very dilute solution, where the difference p—p' is small and the height of the balancing column of solution small.
In practice the time required to reach these various conditions of equilibrium would be too great for experimental demonstration, but the theoretical consideration of vapour pressures is of funda- mental importance. Let us suppose that we possess a partition such as that described above, which is permeable to the solvent but not to the solute when dissolved in it, and let us connect the solution and solvent of fig. 13 with each other through such a partition. If solvent were to flow one way or the other through the partition, the
