subject, and it must suffice to say here that the measurement of the minute elastic tides of the solid earth has at length been achieved. The results recently obtained by Dr O. Hecker at Potsdam constitute a conspicuous advance on all the previous attempts.
The tides of an imperfectly elastic or viscous globe are obviously subject to frictional resistance, and the like is true of the tides of an actual ocean. In either case it is clear that the system must be losing energy, and this leads to results of so much general interest that we propose to give a short sketch of the subject, deferring to chapter VIII. a more rigorous investigation. It is unfortunately impossible to give even an outline of the principles involved without the use of some technical terms:
In fig. 5 the paper is supposed to be the plane of the orbit of a satellite M revolving in the direction of the arrow about the planet C, which rotates in the direction of the arrow about an General Explanation of Tidal Friction. axis perpendicular to the paper. The rotation of the planet is supposed to be more rapid than that of the satellite, so that the day is shorter than the month. Let us suppose that the planet is either entirely fluid, or has an ocean of such depth that it is high-water under or nearly under the satellite. When there is no friction, with the satellite at m, the planet is elongated into the ellipsoidal shape shown, cutting the mean sphere, which is dotted. The tidal protuberances
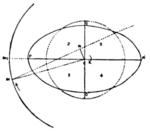
Fig. 5.
are drawn with much exaggeration and the satellite is shown as very close to the planet in order to illustrate the principle more clearly. Now, when there is friction in the fluid motion, the tide is retarded, and high-tide occurs after the satellite has passed the meridian. Then, if we keep the same figure to represent the tidal deformation, the satellite must be at M, instead of at m. If we number the four quadrants as shown, the satellite must be in quadrant I. The protuberance P is nearer to the satellite than P', and the deficiency Q is farther away than the deficiency Q'. Hence the resultant action of the planet on the satellite must be in some such direction as MN. The action of the satellite on the planet is equal and opposite, and the force in NM, not being through the planet's centre, must produce a retarding couple on the planet's rotation, the magnitude of which depends on the length of the arm CN. This tidal frictional couple varies as the height of the tide, and as the satellite's distance. The magnitude of the tidal protuberances varies inversely as the cube of the distance Planet's Rotation Retarded. of the satellite, and the difference between the attractions of the satellite on the nearer and farther protuberances also varies inversely as the cube of the distance. Accordingly the tidal frictional couple varies as the inverse sixth power of the satellite's distance. Let us now consider its effect on the satellite. If the force acting on M be resolved along and perpendicular to the direction CM, the perpendicular component tends to accelerate the satellite's velocity. It alone would carry the satellite farther from C than it would be dragged back by the central force towards C. The satellite would describe a spiral, the coils of which would be very nearly circular and very nearly coincident. If now we resolve the central component force along CM tangentially and perpendicular to the spiral, the tangential component tends to retard the velocity of the satellite, whereas the disturbing force, already considered, tends to accelerate it. With the gravitational Satellite's Velocity Retarded. law of force between the two bodies the retardation must prevail over the acceleration[1] The action of tidal friction may appear somewhat paradoxical, but it is the exact converse of the acceleration of the linear and angular velocity and the diminution of distance of a satellite moving through a resisting medium. The latter result is generally more familiar than the action of tidal friction, and it may help the reader to realize the result in the present case. Tidal friction then diminishes planetary rotation, increases the satellite's distance and diminishes the orbital angular velocity. The comparative rate of diminution of the two angular velocities is generally very different. If the satellite be close to the planet the rate of increase of the satellite's periodic time or month is large compared with the rate of increase of the period of planetary rotation or day; but if the satellite is far off the converse is true. Hence, if the satellite starts very near the planet, with the month a little longer than the day, as the satellite recedes, the month soon increases so that it contains many days. The number of days in the month attains a maximum and then diminishes. Finally the two angular velocities subside to a second identity, the day and month being identical and both very long.
We have supposed that the ocean is of such depth that the tides are direct; if, however, they are inverted, with low-water under or nearly under the satellite, friction, instead of retarding, accelerates the tide; and it would be easy by drawing another figure to see that the whole of the above conclusions would hold equally true with inverted tides.
Attempts have been made to estimate the actual amount of the retardation of the earth's rotation, but without much success. It must be clear from the sketch just given that the effect of tidal friction is that the angular motion of the moon round the earth is retarded, but not to so great an extent as the earth's rotation. Thus a terrestrial observer, who regards the earth as a perfect timekeeper, would look on the real retardation of the moon's angular motion as being an acceleration. Now there is a true acceleration of the moon's angular motion which depends on a slow change in the eccentricity of the earth's orbit round the sun. After many thousands of years this acceleration will be reversed and it will become a retardation, but it will continue for a long time from now into the future; thus it is indistinguishable to us at present from a permanent acceleration. The amount of this true acceleration may be derived from the theories of the motions of the moon and of the earth when correctly developed. Laplace conceived that its observed amount was fully explained in this way, but John Couch Adams showed that Laplace had made a mistake and had only accounted for half of it. It thus appeared that there was an unexplained portion which might be only apparent and might be attributed to the effects of tidal friction.
The time and place of an eclipse of the sun depend on the motions of the moon and earth. Accordingly the records of ancient eclipses, which occurred centuries before the Christian era, afford exceedingly delicate tests of the motions of the moon and earth. At the time when Thomson and Tait's Natural Philosophy[2] was first published it was thought that all the numerical data were known with sufficient precision to render it possible to give a numerical estimate of the retardation of the earth's rotation. But the various revisions of the lunar theory which have been made since that date throw the whole matter into doubt. It seems probable that there is some portion of the acceleration of the moon's motion which is unexplained by gravitation, and may therefore be attributed to tidal friction, but its amount is uncertain. We can only say that the amount is very small. It is, however, not impossible that this smallness may be due to counteracting influences which tend to augment the speed of the earth's rotation; such an augmentation would result from shrinkage of the earth's mass through cooling. However this matter may stand, it does not follow that, because the changes produced by tidal friction in a man's lifetime or in many generations of man are almost insensible, the same must be true when we deal with millions of years. It follows that it is desirable to trace the effects of tidal friction back to their beginnings.
We have seen above that this cause will explain the repulsion of a satellite from a position close to the planet to a more remote distance. Now when we apply these considerations to the moon and earth we find that the moon must once have been nearly in contact with the earth. This very remarkable initial configuration of the two bodies seems to point to the origin of the moon by detachment from the earth.
Further details concerning this speculation in cosmogony are given below in chapter VIII.[3]
§ 10. Bibliography.—Many works on popular astronomy contain a few paragraphs on the tides, but the treatment is generally so meagre as to afford no adequate idea of the whole subject.
A complete list of works both general and technical bearing on the theory of the tides, from the time of Newton down to 1881, is contained in vol. ii. of the Bibliographie de l'astronomie by J. C. Houzeau and A. Lancaster (1882). This list does not contain papers on the tides of particular ports, and we are not aware of the existence of any catalogue of works on practical observation, reduction of observations, prediction and tidal instruments. The only general work on the tides, without mathematics, is George Darwin's Tides and Kindred Phenomena in the Solar Systems.[4] This book treats of all the subjects considered in the present article (with references to original sources), and also others such as seiches (q.v.) and the bore (q.v.).
The most extensive monograph on the tides is A Manual of Tides by Mr Rollin A. Harris, published by the United States Coast Survey in a series of parts, of which pt. i. appeared in 1897, and pt. iv.
- ↑ This way of presenting the action of tidal friction is due to Sir George G. Stokes.
- ↑ See that work (ed. 1883), § 830; P. H. Cowell, M. N. R. Ast. Soc. (1905), lxv. 861.
- ↑ For a discussion of the subject without mathematics, see G. H. Darwin's Tides.
- ↑ London (1898) and with important changes (1901, 1911); (Boston, 1898); translations: German, by A. Pockels (Leipzig, 1902, 1911); Italian, by G. Magrini (Turin, 1905), with appendices by translator; Magyar, by Radó von Kövesligethy (Budapest, 1904), with appendices by translator.
