To this let EH be taken equal, and ELKH will be always a parallelogram. And therefore the point K is always placed in the side HK (given by position) of that parallelogram. Q.E.D.
Cor. Because the figure EFLC is given in kind, the three right lines EF, EL, and EC, that is, GD, HK, and EC, will have given ratios to each other.
LEMMA XXIV.
- If three right lines, two whereof are parallel, and given by position, touch any conic section; I say, that the semi-diameter of the section which is parallel to those two is a mean proportional between the segments of those two that are intercepted between the points of contact and the third tangent.
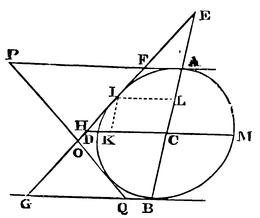
Let AF, GB be the two parallels touching the conic section ADB in A and B; EF the third right line touching the conic section in I, and meeting the two former tangents in F and G, and let CD be the semi-diameter of the figure parallel to those tangents; I say, that AF, CD, BG are continually proportional.
For if the conjugate diameters AB, DM meet the tangent FG in E and H, and cut one the other in C, and the parallelogram IKCL be completed; from the nature of the conic sections, EC will be to CA as CA to CL; and so by division, EC - CA to CA - CL, or EA to AL; and by composition, EA to EA + AL or EL, as EC to EC + CA or EB; and therefore (because of the similitude of the triangles EAF, ELI, ECH, EBG) AF is to LI as CH to BG. Likewise, from the nature of the conic sections, LI (or CK) is to CD as CD to CH; and therefore (ex æquo perturbatè) AF is to CD as CD to BG. Q.E.D.
Cor. 1. Hence if two tangents FG, PQ, meet two parallel tangents AF, BG in F and G, P and Q, and cut one the other in O; AF (ex æquo perturbatè) will be to BQ as AP to BG, and by division, as FP to GQ, and therefore as FO to OG.
Cor. 2. Whence also the two right lines PG, FQ drawn through the points P and G, F and Q, will meet in the right line ACB passing through the centre of the figure and the points of contact A, B.
LEMMA XXV.
- If four sides of a parallelogram indefinitely produced touch any conic section, and are cut by a fifth tangent; I say, that, taking those segments of any two conterminous sides that terminate in opposite angles of the parallelogram, either segment is to the side from which it is cut off as that part of the other conterminous side which is intercepted between the point of contact and the third side is to the other segment.
