Popular Science Monthly/Volume 10/April 1877/The Ball-Paradox
| THE BALL-PARADOX. |
By THOMAS S. CRANE, Mechanical Engineer.
THE exhibitors of the atmospheric air-brake, at the Centennial, attached a tube to the air-reservoir for the purpose of showing the immense pressure employed.
The current rushing from the small orifice of the tube sustains balls of varying gravities, according to the pressure applied.
Once, on accidentally resting the base from which the tube springs upon something lying on the table, it was found that, although no longer vertical, the current of air still held the ball in suspension, the ball revolving rapidly, and apparently hanging to the jet of air, which strikes the sphere at its upper side.

Fig. 1.
It also makes little difference in the result whether the ball be a solid glass one an inch and a half in diameter, or a hollow rubber ball, or a solid wooden one three or four inches in diameter, the only variation being the distance at which the spherical body is held from the orifice.
When a glass ball with interior colored lines, such as children play with, is gently held in the current until the air has the sphere well in its power, it will rotate partly back and forth at first, and, when really revolved by the force of the air, has an uncertain axis of rotation until it has been turning for some time. The jet of air will also sustain a larger ball of lighter gravity behind the glass one, the former hanging on the lower side of the jet behind the heavier and smaller one.
These phenomena have excited so much attention that the following is offered as an illustration of the principles involved, and in explanation of the various points noted above:
The current of air sustains the ball by removing the atmospheric pressure from the ball where it strikes it; the unbalanced pressure of the air on the opposite side then forcing the ball toward the current, as shown by the arrow marked D in Fig. 1. The friction of the jet J against the ball tends to throw it in the direction indicated by C. To balance these two forces, we have the action of gravity, shown at G, which, being a constant factor, must be exactly neutralized by the forces named for the ball to remain suspended.
This adjustment, nice as it is, can be easily effected by placing the ball near enough to the jet at first; for, the pressure D being ample to sustain the ball in any position (else the experiment cannot be performed), the force of the jet will inevitably drive the ball away to a point where the power in that direction is just able to balance the force of gravity—the ball being evidently lifted, in spite of gravity, so long as it moves in the direction of the jet, and the force C naturally diminishing as the distance from the orifice J increases.

Fig. 2.
To make it clear that it is the ordinary atmospheric pressure that supports the ball, let us imagine it exposed to two forces (as shown in Fig. 2), acting on opposite sides of the sphere. The atmospheric pressures that act on all other sides of the sphere are ignored, as they perfectly balance one another.
If a ball B (Fig. 2) is secured to the top of a spiral spring S, attached to a platform P,, and a jet of water V projected vertically upon it, the spring will be compressed until its resistance is equal to the force of the jet. In that position the ball resembles a sphere exposed to atmospheric pressure above and below.
Now, let an horizontal jet of water H be thrown against the vertical jet V, as shown in Fig. 3, and its action, opposed to the spring S, must cease at once, and the unbalanced pressure of the spring raise the ball into the position shown in Fig. 3.
The situation of the ball in Fig. 3 is now equivalent to that in Fig. 1, where the air-jet J, passing over one side of the ball, calls into action the pressure D at right angles to the jet. Were the sphere B in Fig. 1 placed in the centre of the jet, no such action could result; and, if the ball were placed there, its gravity would be un-balanced until the ball fell to one side of the jet, and the supporting power of the air evoked.
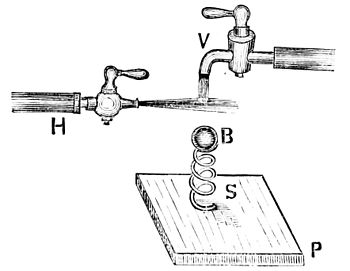
Fig. 3.
To prove that a current of air moving parallel with any surface destroys the atmospheric pressure at that point, take a visiting-card and bend the ends at right angles with the card, so as to turn up one quarter of an inch at each end. Now place the card near the edge of a smooth table, supported by the two ends like a little bench, and try the effect of blowing violently between the card and the table in a direction parallel to both. The current will destroy the atmospheric pressure beneath the card, and the unbalanced pressure above will force the middle of the card downward. Or, take another card and fit a quill or straw tightly into a hole cut in the centre. Try to displace another card laid loosely over the first by blowing upward against it. If a pin is stuck through the centre of the second card, into the opening of the quill, to keep it from sliding off, it will be found that no effort will blow the upper card from the first, as the current of air passing out between the cards destroys the atmospheric pressure between them, calling into play a force upon their outside surfaces that presses them tightly together. The arrangement of the cards is shown in Fig. 4.
It is thus evident that a pressure perpendicular to any surface can be displaced by one acting parallel to it.
An experiment illustrated in Fig. 5, and successfully performed while writing these lines, will settle all doubts, if any remain, upon this puzzling point.
Attach a pith-ball to a short piece of thread, and, knotting the other end, slip the knot in a slit in one end of a quill so as to secure it firmly, and retain the ball about an inch from the other end of the

Fig. 4.
quill, as shown in Fig. 5. Now blow through the quill Q steadily, and the ball B can be made to hang from or upon the under side of the jet J, being prevented by the string S from blowing away, and the atmospheric pressure A balancing the gravity G of the light ball. As the atmosphere presses nearly fifteen pounds upon a square inch, a ball one-quarter of a pound in weight would be balanced by the full pressure of the air upon a surface only 1/60 of an inch in area. It remains to notice the rapid revolutions of the ball and its uncertain axis of rotation when first suspended in the jet.

Fig. 5.
Few balls being perfectly round, or of uniform density, will revolve on their own centres under such conditions, but on the shortest axis passing through their centre of gravity (seldom the centre of form).
It is easy to show that all bodies freely suspended tend to revolve on their shortest axis, by tying a string a yard long to a door-key, just under the head, so that it will hang nearly vertical. If the string be now rapidly twisted by the thumbs and forefingers of both hands, the key wiil assume an horizontal position, and the string revolve in the form of a cone.
The friction of the jet must, therefore, tend to rotate a ball on an axis at right angles to the path of the jet, and, if this axis is not the shortest one passing through its centre of gravity, several oscillations, back and forth, must occur before the necessary adjustment is made.
When two balls of different densities are sustained by the same jet, it seems plain that each is sustained by the pressure of the air on the side opposite to the contact of the jet, for it is evident that, farther from the orifice, the jet has less power to displace the atmospheric pressure, and at that point the lighter ball only can be sustained.
In its rapid revolutions in such a jet of air as we have described, a light and hollow India-rubber ball affords a beautiful illustration of the flattening of the earth's poles by its revolutions on a free axis.