Popular Science Monthly/Volume 21/June 1882/The Stereoscope: Its Theory II
| THE STEREOSCOPE: ITS THEORY. |
By W. LE CONTE STEVENS.
II.
ALL of the forms under which the stereoscope has come into general use have been devised with a view to creating to the utmost the illusion of natural binocular perspective by reproducing as nearly as possible the conditions of natural vision. That this end is not successfully attained is painfully felt by those who linger too long over an attractive collection of stereographs. To secure comfortable vision the muscles of the eyes must suffer no unusual strain. It is not easy to explain briefly how such strain is necessarily implied in the use of this instrument. Suffice it to say that, in looking at a point a few inches distant, the ciliary muscle which surrounds the crystalline lens in each eye is strongly contracted, and so is the muscle on the inner side of each eyeball. These contractions usually accompany each other, and to dissociate them is always more or less painful. The stereograph is but a few inches distant, but, because there are two pictures, the convergence of the visual lines is much less than normal; indeed, optic divergence is not unfrequently necessary. The unconscious interpretation which is put upon the retinal sensation is due partly to imagination; but also largely to the temporary condition of the muscles of the eyes. This includes not only the ciliary but also the rectus muscles, external and internal, by which the eyeballs are controlled, as the angle between the visual lines is varied. The effect of varying this angle is best studied with a modification of Wheatstone's stereoscope, which the writer has constructed for this purpose. A pair of conjugate pictures are chosen, which present as little as possible of mathematical perspective. A stereograph of the moon, divided at the middle, is one of the best for this purpose. The twin photographs are placed upon cross-bars (Fig. 12) which rest on graduated arms that are pivoted at the proper point in the base of a cubical block to which the mirrors are cemented. These arms move in contact with part of a circle, marked off in degrees at the circumference, the center of this being in the pivot. If the two arms make a straight line, and the pictures are properly adjusted, the visual lines must be parallel, for the eyes to receive the reflected rays. If pulled forward toward the observer, the visual lines must converge in order to retain single vision, and the angle of convergence is at once obtained from the circle. If pushed slightly back, as represented in the figure, single vision can be retained only by optic divergence. Most eyes that are healthy will be found capable of enduring a few degrees of such divergence. The real distance of the object is thus kept unchanged, and the card appears always directly across the visual line. The variations in apparent size and distance of the binocular image are very striking, while the perspective in the picture remains clear but also variable. If the stereograph be that of a reversed cone, this becomes apparently shallow, small, and near, or deep, large, and remote, according
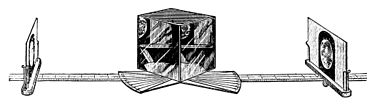
Fig. 12.—The Graduated Reflecting Stereoscope.
as the excess of strain is upon the internal or the external rectus muscles. This instrument, indeed, is useful in quite a variety of binocular experiments. The visual effects are the same as those from an adjustable stereoscope with semi-lenses, but the limits of variation are far wider, and it is a decided advantage to obtain direct measurement of the optic angle.
Such experiments show very conclusively that the current theory of visual triangulation, whatever may be its application to normal binocular vision, has to be entirely discarded as an explanation of stereoscopic vision. As a theory it is beautifully simple, and at first glance appears eminently satisfactory; the only objection to it in relation to the stereoscope consists in the fact that it is untrue. Its expression may be found in most of our text-books of physics, and the diagram usually employed in explaining the stereoscope is that of Fig. 13, which is taken from Helmholtz's "Physiological Optics," the only change being in the avoidance of Greek lettering. This slight change also is made in the following translation from the French edition of this work, which received the last corrections of the distinguished author, who is universally recognized as the highest living authority on the subject of which it treats. After describing the arrangement of the prism-like semi-lenses, he writes: "The two drawings are placed, side by side, upon the same sheet. The right eye, R, looks upon the drawing, a b, through the prism, p; the left eye, L, looks upon the drawing. a' b', through the prism, p'; the partition, g, prevents each eye from seeing the drawing intended for the other. The rays, c p and c' p', sent forth by the drawings, are refracted by the prisms, following the directions p R and p' L, the prolongations of which cut each other at C. The convexity of the surfaces of the prisms has the effect of diminishing at the same time the divergence of the sheafs of rays, so that each eye sees at A B an image of the drawing that is presented to it. The object appears in relief at A B."
This explanation is distinctly geometric, the locality of each point of the image perceived being determined by intersection of visual lines,
R C and L C, as the attention is successively directed to different points in the field of view. If accepted at all, it must be accepted fully. If we suppose the semi-lenses removed, and that R and L together represent a binocular camera, the diagram shows the exact  Fig. 13.—Theory of Visual Triangulation. relation between this and an object to be pictured, and the admirable mathematical discussion which Helmholtz gives subsequently in full is strictly applicable. But, if the observer's eyes be too near together, or the stereographic interval be too great, the relation between the visual lines ceases to be the same as that between the camera axes, and we no longer have the conditions under which the geometric discussion can be applied. It is but due to Helmholtz to add that he closes with the following remark: "These conditions are not generally fulfilled for the photographic proofs and the stereoscopes of commerce." The same credit can not be given to the writers of the ordinary text-books. This qualification is of the last importance, for without it the theory is absurd, the apparent position of the image determined by intersection of visual lines being behind the observers head when optic divergence is induced, and at an infinite distance when they are parallel. But, even when camera axes and visual lines bear the same relation among themselves, the abnormal muscular condition necessitated in stereoscopic vision introduces a disturbing element. The theory is hence not applicable at all to the stereoscope, but must be limited to the discussion of the binocular camera.
Fig. 13.—Theory of Visual Triangulation. relation between this and an object to be pictured, and the admirable mathematical discussion which Helmholtz gives subsequently in full is strictly applicable. But, if the observer's eyes be too near together, or the stereographic interval be too great, the relation between the visual lines ceases to be the same as that between the camera axes, and we no longer have the conditions under which the geometric discussion can be applied. It is but due to Helmholtz to add that he closes with the following remark: "These conditions are not generally fulfilled for the photographic proofs and the stereoscopes of commerce." The same credit can not be given to the writers of the ordinary text-books. This qualification is of the last importance, for without it the theory is absurd, the apparent position of the image determined by intersection of visual lines being behind the observers head when optic divergence is induced, and at an infinite distance when they are parallel. But, even when camera axes and visual lines bear the same relation among themselves, the abnormal muscular condition necessitated in stereoscopic vision introduces a disturbing element. The theory is hence not applicable at all to the stereoscope, but must be limited to the discussion of the binocular camera.
With a view to enabling persons with untrained eyes easily to perform many of the experiments through which variation in appearance of the binocular image is produced by varying the conditions under which the same stereograph is viewed, the writer has devised an adjustable stereoscope (Fig. 14), which presents the additional very important advantage of rendering vision as nearly painless as it can be with the ideal stereograph, even although the stereographic interval on the one employed be so great as to produce only confusion, or strain of the eyes, when the common form of stereoscope is used. Instead of being fixed in position, the semi-lenses are lightly rested in a pair of boxes, with openings in front and rear so as to transmit the light. Attached to the partition between them are a pair of springs against which the thin edges of the semi-lenses are pressed by adjusting-screws in contact with their thick bases. By turning these so that the glasses are pressed as close as possible together, the light which enters the eyes passes through the thicker part of each glass, where the planes that may be supposed to touch the opposite curved faces are nearly parallel. The rays are hence but little deviated in transmission, and the condition is the same as that in the ordinary stereoscope. Vision is then as comfortable as can ever be expected, when the stereographic interval is less than three inches. If it exceed this limit, the pain produced by the muscular strain of optic divergence, which would now be necessary, is prevented by giving a few

Fig. 14.—The Adjustable Stereoscope. Adjustment for Natural Perspective.
leftward turns to each screw. The semi-lenses are at once pressed farther apart by the springs, the rays pass through at points where the opposite surfaces are more inclined to each other, and they are hence more deviated, so as to enter the eyes still without imposing the necessity of divergence. Indeed, if the stereographic interval be small, and free play be given to the springs, uncomfortable convergence may be induced at will. Under this condition a stereograph may be employed on which the interval is as great as four inches. If, while viewing the combined image, the semi-lenses be screwed closer together, the eyes will continue to adapt themselves, while fusion of images is retained, and any degree of divergence is thus induced that the observer may be disposed to endure. If the stereograph has been properly selected to illustrate the effects of muscle-reading, the image will appear to increase in depth as the visual lines diverge.
In front of the partition between the lens-cases are a pair of folding metal screens, of such width that when pressed flat against the wood they will hide from each eye the picture on the side belonging to the other, but when folded, as shown in Fig. 15 s, the whole stereo-graph becomes visible to each eye. On a movable cross-bar there is another folding-screen of wood, which is shown pressed down in Fig. 14, and raised in Fig. 15. In the former condition it does not obstruct any part of the field of view, but in the latter it hides from each eye the half of the stereograph on its own side, and permits that on the other side to be seen through the opening at the middle. By now lifting the cover of the cases containing the semi-lenses, these glasses may be removed, and their places supplied with a pair of wedge-shaped prisms, which are introduced with their bases, instead of their sharp

Fig. 15.—The Adjustable Stereoscope. Adjustment for Reversed Perspective.
edges, against the springs, while the screens are arranged as in Fig. 15. Pushing the cross-bar, intended to hold the picture, out to the farther end, a stereograph is put upon it that has been specially selected to show the effects of binocular perspective. Any stereograph in which mathematical perspective is not strong may be employed—that of the moon is excellent. Looking at this now through the prisms, instead of appearing convex it presents the aspect of a lustrous hollow hemisphere of crystal, through which on its farther side are seen the familiar dead sea-bottoms and jagged volcanic ridges. Our prisms and windowed screen have apparently turned the moon into a cup by bringing into each eye the picture originally intended for the other. On folding down the windowed screen, two extra moons spring into view. Comparing the middle concave image with the flat ones upon the two sides, it appears smaller and nearer, and this disparity is increased by pulling the stereograph nearer. As it approaches it grows shallower and slightly elliptic, the horizontal diameter becoming shorter; for, as the card is brought nearer, its plane becomes more oblique to the direction of the rays, which leave it to be refracted by the prisms before entering the eye. To the combined Cyclopean eye, while each circle must appear as an ellipse because viewed obliquely, the illusion is that there is no obliquity of vision, but that a narrow cup is suspended directly in front; while the pictures that are really in front of each separate eye appear, without relief, out at the two sides.
If the attention be carefully directed successively to the foreground and background when binocularly viewing a properly constructed outline stereograph, it will be found that perfectly distinct vision of the whole picture at any given moment is not usually possible. The distance between corresponding background points exceeds that between similar foreground points. This excess we shall call the stereoscopic displacement. If it be considerable, a pair of corresponding background points must be seen double, or imperfectly combined, when the foreground is distinct. In transferring the attention, then, to the background, slight associated contraction of the external rectus muscles is necessary to secure perfect combination of corresponding points, and this instantly suggests the idea of greater distance for these. Thus, as the attention is given to different parts of the picture, the tension in the muscles of the eyes is continually varying, and this is one important element in determining our binocular perception of solidity. Unless the attention be very carefully given to it, we are apt to overlook the successive duplication in different parts of the field of view. If the stereoscopic displacement be small, the perception of such duplication may be quite impossible, while the appearance of solidity, or of perspectiveness, as it has been called, remains distinct. The stereograph, represented in Fig. 16, has been specially constructed to exhibit a variety of different stereoscopic displacements. It may be viewed either with cross-vision, or with the aid of a card placed edgwise upon the triple line at the middle, or by placing the page in front of the semi-lenses of a stereoscope. Supposing the last of these methods to be employed, there will be seen at the top of the field of view a truncated cone, with a dot at the center of its lower base, and a pair of projections from the circumference of the

Fig. 16.—Stereograph illustrating the Binocular Combination or Lines.
The two halves of this stereograph are strikingly dissimilar, but the principle which it illustrates enables us to secure stereoscopy with a pair of absolutely similar figures by so adjusting these in position that advantage may be taken of the almost spherical surface of the back of each eye. The geometric explanation of this is unsuited to the present article.[1] It may be sufficient to state that, if the two pictures be oppositely inclined to the visual lines, instead of being directly across these, the retinal images must be dissimilar, and the subjective combination of these must hence present the appearance of relief, which may be varied at will by varying the inclination of the cards.
The theory of associated muscular action which has been illustrated, while undoubtedly true, is still not sufficient by itself to explain all the phenomena of stereoscopy. The perception of distinct relief is possible when the card is illuminated with the electric spark. No motion of the eyes is attainable during so minute an interval. It is possible also, when the stereoscopic displacement is so small, that not the slightest duplication of images can be distinguished with even the keenest vision. When this displacement is large, the play of the eyes is necessary to the completeness of the perception; but, in any case, the illusion is complex. The perception of double images is doubtless one important element; but when these are too minute to be distinguished, we are driven to other resources for an explanation.
Every one has noticed that each instrument in an orchestra has its own peculiar quality of sound, each singer in the cast of an opera his own vocal timbre. The explanation of this is no longer a mystery since Helmholtz analyzed, by the aid of resonators, what had eluded analysis by the unaided ear, and showed that the difference in quality between tones, nominally the same from different sources, is due to minute modifications upon sensations, corresponding to small air-waves accompanying those which produce the fundamental tone. By a well-known system of graphic representation, let the curve in Fig. 17 stand for the fundamental note; if this be simple, the curve is perfectly regular. But in fact it is accompanied by a group of smaller waves

Fig. 17.—Simple Sound Waves.

Fig. 18.—Complex Sound Waves.
(Fig. 18, a b) when all are graphically combined, the curve is modified (Fig. 18, c d), and so is the actual sensation. With the same fundamental a different series of overtones would have produced a different resultant curve and sensation. The first of these resultants may represent c' from a soprano's voice, the other c' from that of the tenor, each sending into the ear 264 complex thrills per second. Without being absolutely unisonant, they constitute a pair of dissimilar musical sounds that coalesce harmoniously. A well-trained ear may pick out some of the overtones without the aid of resonators, and perceive in the background a few duplicated sound-images; but the great majority of them are so faint that their presence can not be perceived apart from each other, or from the fundamental to which they give character. The rich combination of all stands out in strong musical relief, compared with what each voice alone would yield, or with the sweet but thin sound of a tuning-fork that sings forth the same fundamental pitch.
This principle relates to the combination of sensations, whatever may be the cause of dissimilarity among the components of the group. We have not the data from which a binocular image can be graphically expressed as a curve, for the dissimilarity of the components is not due to interference of waves of light. But the facts suggest kinship between the modes of sensation in the two cases. The dissimilar groups of light-images arouse sensations that are simultaneously conveyed to the brain, and the proper interpretation at once comes as the product of past experience. All we can affirm is, that experience has taught us to interpret retinal sensations which are slightly different in the two eyes, as the signs of an external object possessing three dimensions in space, when the images are produced upon parts of the concave surfaces which bear to each other the relations that would be imposed by the presence of such an object if naturally viewed. Such experience has been acquired by each of us individually, and probably with exceeding rapidity in consequence of inherited tendencies. It is therefore not necessary that the localization of what we see in the stereoscope should be limited to cases of optic convergence, or the perception of relief to those in which double images can be distinguished.
Our discussion has led us from the domain of physics to the confines of metaphysics. Explanations are at best only relative, and the psychologist, the physiologist, and the physicist must join hands in working out the problems of binocular vision. The progress made during the last half-century invites the hope that much may yet be accomplished before the next century brings us its morning greeting.
- ↑ See "American journal of Science" for April, 1882, p. 297, and May, 1882, p. 359.