Popular Science Monthly/Volume 63/June 1903/Hertzian Wave Wireless Telegraphy I
THE
POPULAR SCIENCE
MONTHLY
JUNE, 1903.
| HERTZIAN WAVE WIRELESS TELEGRAPHY. I.[1] |
By Dr. J. A. FLEMING, F.R.S.,
PROFESSOR OF ELECTRICAL ENGINEERING, UNIVERSITY COLLEGE, LONDON.
THE immense public interest which has been aroused of late years in the subject of telegraphy without connecting wires has undoubtedly been stimulated by the achievements of Mr. Marconi in effecting communication over great distances by means of Hertzian waves. The periodicals and daily journals, which are the chief avenues through which information reaches the public, whilst eager to describe in a» sensational manner these wonderful applications of electrical principles, have done little to convey an intelligible explanation of them. Hence it appeared probable that a service would be rendered by an endeavor to present an account of the present condition of electric wave telegraphy in a manner acceptable to those unversed in the advanced technicalities of the subject, but acquainted at least with the elements of electrical science. It is the purpose of these articles to attempt this task. We shall, however, limit the discussion to an account of the scientific principles underlying the operation of this particular form of wireless telegraphy, omitting, as far as possible, references to mere questions of priority and development.
The practical problem of electric wave wireless telegraphy, which has been variously called Hertzian wave telegraphy, Marconi telegraphy, or spark telegraphy (Funkentelegraphie), is that of the production of an effect called an electric wave or train of electric waves, which can be sent out from one place, controlled, detected at another place, and interpreted into an alphabetic code. Up to the present time, the chief part of that intercommunication has been effected by means of the Morse code, in which a group of long and short signs form the letter or symbol. Some attempts have been made with more or less success to work printing telegraphs and even writing or drawing telegraphs by Hertzian waves, but have not passed beyond the experimental stage, whilst wireless telephony by this means is still a dream of the future.
We shall, in the first place, consider the transmitting arrangements and, incidentally, the nature of the effect or wave transmitted; in the second place, the receiving appliances; and finally, discuss the problem of the isolation or secrecy of the intelligence conveyed between any two places.
The transmitter used in Hertzian wave telegraphy consists essentially of a device for producing electric waves of a type which will travel over the surface of the land or sea without speedy dissipation, and the important element in this arrangement is the radiator, by which these waves are sent out. It will be an advantage to begin by explaining the electrical action of the radiator, and then proceed to discuss the details of the transmitting appliances.
It will probably assist the reader to arrive most easily at a general idea of the functions of the various portions of the transmitting arrangements, and in particular of the radiator, if we take as our starting point an analogy which exists between electric wave generation for telegraphic purposes and air wave generation for sound signal purposes. Most persons have visited some of the large lighthouses which exist around our coasts and have there seen a steam or air siren, as used for the production of sound signals during fogs. If they have examined this appliance, they will know that it consists, in the first place, of a long metal tube, generally with a trumpet-shaped mouthpiece. At the bottom of this tube there is a fixed plate with holes in it, against which revolves another similarly perforated plate. These two plates separate a back chamber or wind chest from the tube, and the wind chest communicates with a reservoir of compressed air or a high-pressure steam boiler. In the communication pipe there is a valve which can be suddenly opened for a longer or shorter time. When the movable plate revolves, the coincidence or non-coincidence of the holes in the two plates opens or shuts the air passage way very rapidly. Hence when the blast of air or steam is turned on, the flow is cut up by the revolving plates into a series of puffs which inflict blows upon the stationary air in the siren tube. If these blows come at the rate. say of a hundred a second, they give rise to aerial oscillations in the tube, which impress the ear as a deep, musical note or roar; and this continuous sound can be cut up by closing the valve intermittently into long and short periods, and so caused to signal a letter according to the Morse code, denoting the name of the lighthouse. In this case the object is to produce: first, aerial vibrations in the tube, giving rise to a train of powerful air waves; secondly, to intermit this wave-train so as to produce an intelligible signal; and thirdly, to transmit this wave as far as possible through space.
The production of a sound or air wave can only be achieved by administering a very sudden blow to the general mass of the air in the tube. This impulse must be sufficient to call into operation the inertia and elastic qualities of the air. It is found, moreover, that the amplitude of the resulting wave, or the loudness of the sound, is increased by suitably proportioning the length of the siren pipe and the frequency of the air puffs; whilst the distance at which it is heard depends also in some degree upon the form of the mouthpiece.
Inside the siren tube, when it is in operation, the air molecules are in rapid vibratory motion in the direction of the length of the tube. If we could at any one instant examine the distribution and changes of air pressure in the tube, we should find that at some places there are large, and at others small, variations in air pressure. These latter places are called the nodes of pressure. At the pressure nodes, however, we should find large variations in the velocity of the air particles, and these points are called the antinodes of velocity. In those places at which the pressure variation is greatest, the velocity changes are least, and vice versa. Outside the tube, as a result of these air motions in it, we have a hemispherical air wave produced, which travels out from the mouthpiece as a center; and if we could examine the distribution of air pressure and velocity through all external space, we should find a distribution which is periodic in space as well as time, constituting the familiar phenomenon of an air wave.
Turning then to consider the production of an electric, instead of an air wave, we notice in the first place that the medium with which we are concerned is the ether filling all space. This ether permits the production of physical changes in it which are analogous to, but not identical in nature with, the pressures and movements which constitute a sound wave. The Hertzian radiator is an appliance for acting on the ether as the siren acts on the air. It produces a wave in it, and it can be shown that all the parts of the above described siren apparatus have their electrical equivalents in the transmitter employed in Hertzian wave wireless telegraphy.
To understand the nature of an electric wave we must consider, in the first place, some properties of the ether. In this medium we can at any place produce a state called electric displacement or ether strain, as we can produce compression or rarefaction in air; and, just as the latter changes are said to be created by mechanical force, so the former is said to be due to electric force. We can not define more clearly the nature of this ether strain or displacement until we know much more about the structure of the ether than we do at present. We can picture to ourselves the operation of compressing air as an approximation of the air molecules, but the difficulty of comprehending the nature of an electric wave arises from the fact that we can not yet definitely resolve the notion of electric strain into any simpler or more familiar ideas.
We have to be content, therefore, to disguise our present ignorance by the use of some descriptive term, such as electric strain, electrostatic strain or ether strain, to describe the directed condition of the space around a body in a state of electrification which is produced by electric force. This electric strain is certainly not of the nature of a compression in the ether, but much more akin to a twist or rotational strain in a solid body.
For our present purpose it is not so necessary to postulate any particular theory of the ether as it is to possess some consistent hypothesis, in terms of which we can describe the phenomena which will concern us. These effects are, as we shall see, partly states of electrification on the surface or distributions of electric current in wires or rods, and partly conditions in the space outside them, which we are led to recognize as distributions of electric strain and of an associated effect called magnetic flux.
We find such a theory at hand at the present time in the electronic theory of electricity, which has now been sufficiently developed and popularized to make it useful as a descriptive hypothesis.[2] This theory has the great recommendation that it offers a means of abolishing the perplexing dualism of ether and ponderable matter, and gives a definite and, in a sense, objective meaning to the word electricity. In this physical speculation, the chief subject of contemplation is the electron, or ultimate particle of negative electricity, which, when associated in greater or less number with a matrix of some description, forms the atom of ponderable matter. To avoid further hypothesis, this matrix may be called the co-electron; and we shall adopt the view that a single chemical atom is a union of a co-electron with a surrounding envelope or group of electrons, one or more of the latter being detachable. We need not stop to speculate on the structure of the atomic core or co-electron, whether it is composed of positive and negative electrons or of something entirely different. The single electron is the indivisible unit or atomic element of so-called negative electricity, and the neutral chemical atom deprived of one electron is the unit of positive electricity. On this hypothesis, the chemical atom is to be regarded as a microcosm, a sort of a solar system in miniature, the component electrons being capable of vibration relatively to the atomic center of mass. Furthermore, from this point of view it is the electron which is the effective cause of radiation. It alone has a grip on the ether whereby it is able to establish wave motion in the latter.
Dr. Larmor has developed in considerable detail an hypothesis of the nature of an electron which makes it the center or convergence-point of lines of a self-locked ether strain of a torsional type. The notion of an atom merely as a 'center of force' was one familiar to Faraday and much supported by Boscovich and others. The fatal objection to the validity of this notion as originally stated was that it offers no possibility of explaining the inertia of matter. On the electronic hypothesis, the source of all inertia is the inertia of the ether, and until we are able to dissect this last quality into anything simpler than the time-element involved in the production of an ether strain or displacement, we must accept it as an ultimate fact, not more elucidated because we speak of it as the inductance of the electron.
We postulate, therefore, the following ideas: We have to think of the ether as a homogeneous medium in which a strain of some kind, most probably of a rotational type, is possible. This strain appears only under the influence of an appropriate stress called the electric force, and disappears when the force is removed. Hence to create this strain necessitates the expenditure of energy. An electron is a center or convergence-point of lines of permanent ether strain of such nature that it can not release itself. To obtain some idea of the nature of such a structure, let us imagine a flat steel band formed into a ring by welding the ends together. There is then no torsional strain. If, however, we suppose the band cut in one place, one end then given half a turn and the cut ends again welded, we shall have on the band a self-locked twist, which can be displaced on the band, but which can not release itself or be released except by cutting the ring. Hence we see that to make an electron in an ether possessing torsional elasticity would require creative energy, and when made, the electron can not destroy itself except by occupying simultaneously the same place as an electron of opposite type. Every electron extends, therefore, as Faraday said of the atom, throughout the universe, and the properties that we find in the electron are only there because they are first in the universal medium, the ether. Every line of ether or electric strain must, therefore, be a self-closed line, or else it must terminate on an electron and a co-electron.
So far we have only considered the electron at rest. If, however, it moves, it can be mathematically demonstrated that it must give rise to a second form of ether strain which is related to the electric strain as a twist is related to a thrust or a vortex ring to a squirt in liquid or a rotation to a linear progression. The ether strain which results from the lateral movement of lines of electric strain is called the magnetic-flux, and it can be mathematically shown that the movement of an electron, consisting when at rest of a radial convergence of lines of electric strain, must be accompanied by the production of self-closed lines of magnetic flux, distributed in concentric circles or rings round it, the planes of these circles being perpendicular to the direction of motion of the electron.
This electronic hypothesis, therefore, affords a basis on which we can build up a theory affording an explanation of the nature of the intimate connection known to exist between ether, matter and electricity. The electron is the connecting link between them all, for it is in itself a center of convergent ether strain; isolated, it presents itself as electricity of the negative or resinous kind; and, in combination with co-electrons and other electrons, it forms the atoms of ponderable matter. At rest the electron or the co-electron constitutes an electric charge, and when in motion it is an electric current. A steady flux or drift of electrons in one direction and co-electrons in the opposite direction is a continuous electric current, whilst their mere oscillation about a mean position is an alternating current. Furthermore, the vibration of an electron, if sufficiently rapid, enables it to establish what are called electric waves in the ether, but which are really detached and self-closed lines of ether strain distributed in a periodic manner through space.
We have, therefore, to start with, three conceptions concerning the electron, viz: Its condition when at rest; its state when in uniform motion; and its operations when in vibration or rapid oscillation. In the first case, by our fundamental supposition, it consists of lines of ether strain of a type called the electric strain, radiating uniformly in all directions. When in uniform motion, it can be shown that these lines of electric strain tend to group themselves in a plane perpendicular to the line of motion drawn through the electron, and their lateral motion generates another class of strain called the magnetic strain, disposed in concentric circles described round the electron and lying in this equatorial plane.
The proof of the above propositions can not be given verbally, but requires the aid of mathematical analysis of an advanced kind. The reader must be referred for the complete demonstration to the writings of Professor J. J, Thomson[3] and Mr. Oliver Heaviside.[4]
In the third case, when the electron vibrates, we have a state in which self-closed lines of electric strain and magnetic flux are thrown off and move away through the ether, constituting electric radiation. The manner in which this happens was first described by Hertz in a paper on 'Electric Oscillations treated according to the Method of Maxwell.'[5] As this phenomenon lies at the very root of Hertzian wave wireless telegraphy, we must spend a moment or two in its careful examination.
Let us imagine two metal rods placed in line and constituting what is called a linear oscillator. Let these rods have adjacent ends separated by a very small air space, and let one rod be charged with positive and the other with negative electricity. On the electronic theory this is explained by stating that there is an accumulation of electrons in one and of co-electrons in the other. These charges create a distribution of electric strain throughout their neighborhood, which follows approximately the same law of distribution as the lines of magnetic force of a bar magnet, and may be roughly represented as in Fig. 1. Suppose then that the air gap is destroyed,  Fig. 1. Lines of Electric Strain between a Positive and Negative Electron at Rest. these charges move towards each other and disappear by uniting, the lines of electric strain then collapse, and as they shrink in give rise to circular lines of magnetic flux embracing the rods. This external distribution of magnetism constitutes an electric current in the rods produced by the movement of the two opposite electric charges. At this stage it may be explained that the electrons or atoms of electricity can in some cases make their way freely between the atoms of ponderable matter. The former are incomparably smaller than the latter, and in those cases in which this electronic movement can take place easily, we call the material a good conductor.
Fig. 1. Lines of Electric Strain between a Positive and Negative Electron at Rest. these charges move towards each other and disappear by uniting, the lines of electric strain then collapse, and as they shrink in give rise to circular lines of magnetic flux embracing the rods. This external distribution of magnetism constitutes an electric current in the rods produced by the movement of the two opposite electric charges. At this stage it may be explained that the electrons or atoms of electricity can in some cases make their way freely between the atoms of ponderable matter. The former are incomparably smaller than the latter, and in those cases in which this electronic movement can take place easily, we call the material a good conductor.
Suppose then the electric charges reappear in reversed positions and go through an oscillatory motion. The result in the external space would be the alternate production of lines of electric strain and magnetic flux, the direction of these lines being reversed each half cycle. Inside the rods we have a movement of electrons and co-electrons to and fro, electric charges at the ends of the rods alternating with electric currents in the rods, the charges being at a maximum when the current is zero, and the current at a maximum when the charges have for the moment disappeared. Outside the rods we have a corresponding set of charges, lines of electric strain stretching from end to end of the rod, alternating with rings of magnetic flux embracing the rod. So far we have supposed the oscillation to be relatively a slow one.
Imagine next that the to and fro movement of the electrons or charges is sufficiently rapid to bring into play the inertia quality of the medium. We then have a different state of affairs. The lines of strain in the external medium can not contract or collapse quickly

enough to keep up with the course of events, or movements of the electrons in the rods, and hence their regular contraction and absorption is changed into a process of a different kind. As the electrons and coelectrons, i. e., the electric charges, vibrate to and fro, the lines of electric strain connecting them are nipped in and thrown off as completely independent and closed lines of electric strain, and at each successive alternation, groups or batches of these loops of strain are detached from the rod, and, so to speak, take on an independent existence. The whole process of the formation of these self-closed lines of electric strain is best understood by examining a series of diagrams which roughly represent the various stages of the process. In Fig. 2 we have a diagram (a) the curved line in which delineates approximately the form of one line of electric strain round a linear oscillator, with spark gap in the center, one half being charged positively and the other negatively. Let us then suppose that the insulation of the spark gap is destroyed, so that the opposite electric charges rush together and oscillate to and fro. The strain lines at each oscillation are then crossed or decussate, and the result, as shown in Fig. 2, d, is that a portion of the energy of the field is thrown off in the form of self-closed lines of strain (see Fig. 2, e). At each oscillation of the charges the direction of the lines of strain springing from end to end of the radiator is reversed. It is a general property of lines of strain, whether electric or magnetic, that there is a tension along the line and a pressure at right angles. In other words, these lines of electric strain are like elastic threads, they tend to contract in the direction of their length and press sideways on each other when in the same direction. Hence it is not difficult to see that as each batch of self-closed lines of strain is thrown off, the direction of the strain round each loop is alternately in one direction and in the other. Hence these loops of electric strain press each other out, and each one that is formed squeezes the already formed loops further and further from the radiator. The loops, therefore, march away into space (see Fig. 2, f). If we imagine ourselves standing at a little distance at a point on the equatorial line and able to see these loops of strain as they pass, we should recognize a procession of loops, consisting of alternately directed strain lines marching past. This movement through the ether of self-closed lines of electric strain constitutes what is called electric radiation.
Hence along a line drawn perpendicular to the radiator through its center, there is a distribution of electric strain normal to that line, which is periodic in space and in time. Moreover, in addition to these lines of electric strain, there are at right angles to them another set of self-closed lines of magnetic flux. Alternated between the instants when the electric charges at the ends of the radiator are at their maximum, we have instants when the radiator rod is the seat of an electric current, and hence the field round it is filled with circular lines of magnetic flux coaxial with the radiator. As the current alternates in direction each half period, these rings of magnetic flux alternate in direction as regards the flux, and hence we must complete our mental picture of the space round the radiator rods when the charges are oscillating by supposing it filled with concentric rings of magnetic flux which are periodically reversed in direction, and have their maximum values at those instants and places where the lines of electric strain have their zero values. Accordingly, along the equatorial line we have two sets of strains in the ether, distributed periodically in space and in time. First, the lines of electric strain in the plane of the radiator, and secondly, the lines of magnetic flux at right angles to these. At any one point in space these two changes, the strain and the flux, succeed each other periodically, being, however, at right angles in direction. At any one moment these two effects are distributed periodically or cyclically through space, and these changes in time and space constitute an electric wave or electromagnetic wave.
We may then summarize the above statements by saying that the most recent hypothesis as to the nature of electrical action and of electricity itself is briefly comprised in the following statements: The universally diffused medium called the ether has had created in it certain centers of strain or radiating points from which proceed lines of strain, and these centers of force are called electrons. Electrons must, therefore, be of two kinds, positive and negative, according to the direction of the strain radiating from the center. These electrons in their free condition constitute what we call electricity, and the electrons themselves are the atoms of electricity which, in one sense, is, therefore, as much material as that which we call ordinary gross or ponderable matter.
Collocations of these electrons constitute the atoms of gross matter, and we must consider that the individuality of any atom is not determined merely by the identity of the electrons composing it, but by the permanence of their arrangement or form. In any mass of material substance there is probably a continual exchange of electrons from one atom to another, and hence at any one given moment, whilst a number of the electrons are an association forming material atoms, there will be a further number of isolated but intermingled electrons, which are called the free electrons. In substances which we call good conductors, we must imagine that the free electrons have the power of moving freely through or between the material atoms, and this movement of the electrons constitutes a current of electricity; whilst a superfluity of electrons of either type in any one mass of matter constitutes what we call a charge of electricity. Hence an electrical oscillation, which is merely a very rapid alternating current taking place in a conductor, is on this hypothesis assumed to consist in a rapid movement to and fro of the free electrons. We may picture to ourselves, therefore, a rod of metal in which electrical oscillations are taking place, as similar to an organ pipe or siren tube in which movements of the air particles are taking place to and fro, the free electrons corresponding with the air particles.
Owing to the nature of the structure of an electron, it follows, however, that every movement of an electron is accompanied by changes in the distribution of the electric strain or ether strain taking place throughout all surrounding space, and, as already explained, certain very rapid movements of the electrons have the effect of detaching closed lines of strain in the ether which move off through space, forming, when cyclically distributed, an electric wave.
We may next proceed to apply these principles to the explanation of the action of the simplest form of Hertzian wave telegraphic radiator, viz., the Marconi aerial wire. In its original form this consists of a long vertical insulated wire A, the lower end  Fig. 3. Simple Marconi Radiator. B, battery; I, induction coil; K, signalling key; S, spark gap; A, aerial wire; E, earth plate. of which is attached to one of the spark balls S of an induction coil I, the other spark' ball being connected to earth E, and the two spark balls being placed a few millimeters apart (see Fig. 3). When the coil is set in action, oscillatory or Hertzian sparks pass between the balls, electric oscillations are set up in the wire and electric waves are radiated from it. Deferring for the moment a more detailed examination of the operations of the coil and at the spark gap, we may here say that the action which takes place in the aerial wire is as follows: The wire is first charged to a high potential, let us suppose, with negative electricity. We may imagine this process to consist in forcing additional electrons into it, the induction coil acting as an electron pump. Up to a certain pressure the spark gap is a perfect insulator, but at a critical pressure, which for spark gap lengths of four or five millimeters and balls about one centimeter in diameter approximates to three thousand volts per millimeter, the insulation of the air gives way, and the charge in the wire rushes into the earth. In consequence, however, of the inertia of the medium or of the electrons, the
Fig. 3. Simple Marconi Radiator. B, battery; I, induction coil; K, signalling key; S, spark gap; A, aerial wire; E, earth plate. of which is attached to one of the spark balls S of an induction coil I, the other spark' ball being connected to earth E, and the two spark balls being placed a few millimeters apart (see Fig. 3). When the coil is set in action, oscillatory or Hertzian sparks pass between the balls, electric oscillations are set up in the wire and electric waves are radiated from it. Deferring for the moment a more detailed examination of the operations of the coil and at the spark gap, we may here say that the action which takes place in the aerial wire is as follows: The wire is first charged to a high potential, let us suppose, with negative electricity. We may imagine this process to consist in forcing additional electrons into it, the induction coil acting as an electron pump. Up to a certain pressure the spark gap is a perfect insulator, but at a critical pressure, which for spark gap lengths of four or five millimeters and balls about one centimeter in diameter approximates to three thousand volts per millimeter, the insulation of the air gives way, and the charge in the wire rushes into the earth. In consequence, however, of the inertia of the medium or of the electrons, the 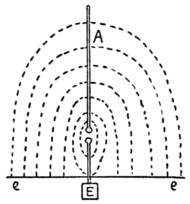 Fig. 4. Lines of Electric Strain (Dotted Lines) extending between a Marconi Aerial A and the earth ee before discharge.charge, so to speak, overshoots the mark, and the wire is then left with a charge of opposite sign. This again in turn rebounds, and so the wire is discharged by a series of electrical oscillations, consisting of alternations of* static charge and electric discharge. We may fasten our attention either on the events taking place in the vertical wire or in the medium outside, but the two sets of phenomena are inseparably connected and go on together. When the aerial wire is statically charged, we may describe it by saying that there is an accumulation of electrons or coelectrons in it. Outside the wire there is, however, a distribution of electric strain, the strain lines proceeding from the wire to the earth (see Fig. 4).
Fig. 4. Lines of Electric Strain (Dotted Lines) extending between a Marconi Aerial A and the earth ee before discharge.charge, so to speak, overshoots the mark, and the wire is then left with a charge of opposite sign. This again in turn rebounds, and so the wire is discharged by a series of electrical oscillations, consisting of alternations of* static charge and electric discharge. We may fasten our attention either on the events taking place in the vertical wire or in the medium outside, but the two sets of phenomena are inseparably connected and go on together. When the aerial wire is statically charged, we may describe it by saying that there is an accumulation of electrons or coelectrons in it. Outside the wire there is, however, a distribution of electric strain, the strain lines proceeding from the wire to the earth (see Fig. 4).
The wire has capacity with respect to the earth, and it acts like the inner coating of a Leyden jar, of which the dielectric is the air and ether around it, and the outer coating is the earth's surface. When the discharge takes place, we may consider that electrons rush out of the wire and then rush back again into it. At the moment when the electrons rush out of or into the aerial wire, we say there is an electric current flowing into or out of the wire, and this electron movement, therefore, creates the magnetic flux which is distributed in concentric circles round the wire. This current, and, therefore, motion of electrons, can be proved to exist by its heating effect upon a fine wire inserted in series with the aerial, and in the case of large aerials it may have a mean value of many amperes and a maximum value of hundreds of amperes. Inside the aerial wire we have, therefore, alternations of electric potential or charge and electric current, or we may call it electron-pressure and electron-movement.
There is, therefore, an oscillation of electrons in the aerial wire, just as in the case of an organ pipe there is an oscillation of air molecules in the pipe. Outside the aerial we have variations and distributions of electric strain and magnetic flux.  Fig. 5. Amplitude of pressure Variation in a Closed Organ Pipe, indicated by the ordinates of the dotted Dotted Line xy. The resemblance between the closed organ-pipe and the simple Marconi aerial is, in fact, very complete. In the case of the closed organ-pipe, we have a longitudinal oscillation of air molecules in the pipe. At the open end or mouthpiece, where we have air moving in and out, the air movement is alternating and considerable, but there is little or no variation of air pressure. At the upper or closed end of the pipe we have great variation of air pressure, but little or no air movement (see Fig. 5).
Fig. 5. Amplitude of pressure Variation in a Closed Organ Pipe, indicated by the ordinates of the dotted Dotted Line xy. The resemblance between the closed organ-pipe and the simple Marconi aerial is, in fact, very complete. In the case of the closed organ-pipe, we have a longitudinal oscillation of air molecules in the pipe. At the open end or mouthpiece, where we have air moving in and out, the air movement is alternating and considerable, but there is little or no variation of air pressure. At the upper or closed end of the pipe we have great variation of air pressure, but little or no air movement (see Fig. 5).
Compare this now with the electrical phenomena of the aerial. At the spark ball or lower end we have little or no variation of potential or electron pressure, but we nave electrons rushing into and out of the aerial each half oscillation, forming the electric discharge or current. At the upper or insulated end we have little or no current, but great variations of potential or electron pressure. Supposing we could examine the wire inch by inch, all the way up from the spark balls at the bottom to the top, we should find at each stage of our journey that the range of variation and maximum value of the current in the wire became less and those of the potential became greater. At the bottom we have nearly zero potential or no electric pressure, but large current, and at the top end, no current, but great variation of potential.
We can represent the amplitude of the current and potential values along the aerial by the ordinates of a dotted line so drawn that its distance from the aerial represents the potential oscillation or current oscillation at that point (see Fig. 6).
This distribution of potential and current along the wire does not necessarily imply that any one electron moves far from its normal position. The actual movement of any particular air molecule in the case of a sound wave is  Fig. 6. (a) Distribution of Electric Pressure in a Marconi Aerial A, (b) Distribution of Electric Current in a Marconi Aerial, as shown by the Ordinates of the dotted Line xy. probably very small, and reckoned in millionths of an inch. So also we must suppose that any one electron may have a small individual amplitude of movement, but the displacement is transferred from one to another. Conduction in a solid may be effected by the movement of free electrons intermingled with the chemical atoms, but any one electron may be continually passing from a condition of freedom to one of combination.
Fig. 6. (a) Distribution of Electric Pressure in a Marconi Aerial A, (b) Distribution of Electric Current in a Marconi Aerial, as shown by the Ordinates of the dotted Line xy. probably very small, and reckoned in millionths of an inch. So also we must suppose that any one electron may have a small individual amplitude of movement, but the displacement is transferred from one to another. Conduction in a solid may be effected by the movement of free electrons intermingled with the chemical atoms, but any one electron may be continually passing from a condition of freedom to one of combination.
So much for the events inside the wire, but now outside the wire its electric charge is represented by lines of electric strain springing from the aerial to the earth. It must be remembered that every line of strain terminates on an electron or a co-electron. Hence when the discharge or spark takes place between the spark balls, the rapid movement of the electrons in the wire is accompanied by a redistribution and movement of the lines of strain outside. As the negative charge flows out of the aerial the ends of the strain lines abutting on to it run down the wire and are transferred to the earth, and at the next instant this semi-loop of electric or ether strain, with its ends on the earth, is pushed out sideways from the wire by the growth of a new set of lines of ether strain in an opposite direction. The process is best understood by consulting a series of diagrams which represent the distribution and approximate form of a few of the strain lines at successive instants (see Fig. 7). In between the lines of formation of the successive strain lines between the aerial and the earth, corresponding to the successive alternate electric charges of the aerial with opposite sign, there are a set of concentric rings of magnetic flux formed round it which are alternately in opposite directions, and these expand out, keeping step with the progress of the detached strain loops and having their planes at right angles to the latter. As the semi-loops of electric strain march outwards with their feet on the ground, these strain lines must always be supposed to terminate on electrons, but not continually on the same electrons. Since the earth is a conductor, we must suppose that there is a continual migration of the electrons forming the atoms of the earth, and that when one electron enters an atom, another leaves it. Hence corresponding to the electric wave in the space above, there are electrical changes in the ground beneath. This view is confirmed by the well-known fact that the achievement of Hertzian wave telegraphy is much dependent on the nature of the surface over which it is conducted, and can be carried on more easily over good conducting material, like sea water, than over badly conducting dry land.

The matter may be viewed, however, from another standpoint. Good conductors are opaque to Hertzian waves; in other words, are non-absorptive. The energy of the electric wave is not so rapidly absorbed when it glides over a sea surface as when it is passing over a surface which is an indifferent conductor, like dry land. In fact, it is possible by the improvement of the signals to detect a heavy fall of rain in the space between two stations separated only by dry land. It is, however, clear that on the electronic theory the progression of the lines of electric strain can only take place if the surface over which they move is a fairly good conductor, unless these lines of strain form completely closed loops. Hence we may sum up by saying that there are three sets of phenomena to which we must pay attention in formulating any complete theory of the aerial. The first is the operation taking place in the vertical wire, which is described by saying that electrical oscillations or vibratory movements of electrons are taking place in it, and, on our adopted theory, it may be said to consist in a longitudinal vibration of electrons of such a nature that we may appropriately call the aerial an ether organ pipe. Then in the next place, we have the distribution and movement of the lines of electric strain and magnetic flux in the space outside the wire, constituting the electric wave; and lastly, there are the electrical changes in the conductor over which the wave travels, which is the earth or water surrounding the aerial. In subsequently dealing with the details of transmitting arrangements, attention will be directed to the necessity for what telegraphists call 'a good earth' in connection with Hertzian wave telegraphy. This only means that there must be a perfectly free egress and ingress for the electrons leaving or entering the aerial, so that nothing hinders their access to the conducting surface over which the wave travels. There must be nothing to stop or throttle the rush of electrons into or out of the aerial wire, or else the lines of strain can not be detached and travel away.
We may next consider more particularly the energy which is available for radiation and which is radiated. In the original form of simple Marconi aerial, the aerial itself when insulated forms one coating or surface of a condenser, the dielectric being the air and ether around it, and the other conductor being the earth. The electric energy stored up in it just before discharge takes place is numerically equal to the product of the capacity of the aerial and half the square of the potential to which it is charged.
If we call C the capacity of the aerial in microfarads, and V the potential in volts to which it is raised before discharge, then the energy storage in joules E is given by the equation.
Since one joule is nearly equal to three quarters of a foot-pound, the energy storage in foot-pounds F is roughly given by the rule . For spark lengths of the order of five to fifteen millimeters, the disruptive voltage in air of ordinary pressure is at the rate of 3,000 volts per millimeter. Hence if S stands for the spark length in millimeters, and C for the aerial capacity in microfarads, it is easy to see that the energy storage in foot-pound is
If the aerial consists of a stranded wire formed of 7⁄22 and has a length of 150 feet, and is insulated and held vertically with its lower end near the earth, it would have a capacity of about one three tenthousandths of a microfarad or 0.0003 mfd.[6] Hence if it is used as a Marconi aerial and operated with a spark gap of one centimeter in length, the energy stored up in the wire before each discharge would be only one tenth (0.1) of a foot-pound.
By no means can all of this energy be radiated as Hertzian waves; part of it is dissipated as heat and light in the spark, and yet such an aerial can, with a sensitive receiver such as that devised by Mr. Marconi, make itself felt for a hundred miles over sea in every direction. This fact gives us an idea of the extremely small energy which, when properly imparted to the ether, can effect wireless telegraphy over immense distances. Of course, the minimum telegraphic signal, say the Morse dot, may involve a good many, perhaps half a dozen, discharges of the wire, but even then the amount of energy concerned in affecting the receiver at the distant place is exceedingly small.
The problem, therefore, of long distance telegraphy by Hertzian waves is largely, though not entirely, a matter of associating sufficient energy with the aerial wire or radiator. There are obviously two things which may be done; first, we may increase the capacity of the aerial, and secondly, we may increase the charging voltage or, in other words, lengthen the spark gap. There is, however, a well-defined limit to this last achievement. If we lengthen the spark gap too much, its resistance becomes too great and the spark ceases to be oscillatory. We can make a discharge, but we obtain no radiation. When using an induction coil, about a centimeter or at most a centimeter and a half is the limiting length of oscillatory sparks; in other words, our available potential difference is restricted to 30,000 or 40,000 volts. By other appliances we can, however, obtain oscillatory sparks having a voltage of 100,000 or 200,000 volts, and so obtain what Hertz called 'active sparks' five or six centimeters in length.
Turning then to the question of capacity, we may enquire in the next place how the capacity of an aerial wire can be increased. This has generally been done by putting up two or more aerial wires in contiguity and joining them together, and so making arrangements called in the admitted slang of the subject 'multiple aerials.' The measurement of the capacity of insulated wires can be easily carried out by means of an appliance devised by the author and Mr. W. C. Clinton, consisting of a rotating commutator which alternately charges the insulated wire at a source of known electromotive force and then discharges it through a galvanometer. If this galvanometer is subsequently standardized, so that the ampere value of its deflection is known, we can determine easily the capacity C of the aerial or insulated conductor, reckoned in microfarads, when it is charged to a potential of V volts, and discharged n times a second through a galvanometer. The series of discharges are equivalent to a current, of which the value in amperes A is given by the equation,
and hence if the value of the current resulting is known, we have the capacity of the aerial or conductor expressed in microfarads, given by the formula,
A series of experiments made on this plan have revealed the fact that if a number of vertical insulated wires are hung up in the air and rather near together, the electrical capacity of the whole of the wires in parallel is not nearly equal to the sum of their individual capacities. If a number of parallel insulated wires are separated by a distance equal to about 3 per cent, of their length, the capacity of the whole lot together varies roughly as the square root of their number. Thus, if we call the capacity of one vertical wire in free space, unity, then the capacity of four wires placed rather near together will only be about twice that of one wire, and that of twenty-five wires will only be about five times one wire.

This approximate rule has been confirmed by experiments made with long wires one hundred or two hundred feet in length in the open air. Hence it points to the fact that the ordinary plan of endeavoring to obtain a large capacity by putting several wires in parallel and not very far apart is very uneconomical in material. The diagrams in Fig. 8 show the various methods which have been employed by Mr. Marconi and others in the construction of such multiple wire aerials. If, for instance, we put four insulated stranded 7⁄22 wires, each 100 feet long, about six feet apart, all being held in a vertical position, the capacity of the four together is not much more than twice that of a single wire. In the same manner, if we arrange 150 similar wires, each 100 feet long, in the form of a conical aerial, the wires being distributed at the top round a circle 100 feet in diameter, the whole group will not have much more than twelve times the capacity of one single wire, although it weighs 150 times as much.
The author has designed an aerial in which the wires, all of equal length, are arranged sufficiently far apart not to reduce each other's capacity.
As a rough guide in practice, it may be borne in mind that a wire about one 'tenth of an inch in diameter and one hundred feet long, held vertical and insulated, with its bottom end about six feet from the ground, has a capacity of 0.0003 of a microfarad, if no other earthed vertical conductors are very near it. The moral of all this is that the amount of electric energy which can be stored up in a simple Marconi aerial is very limited, and is not much more than one tenth of a joule or one fourteenth of a foot-pound, per hundred feet of 7⁄22 wire. The astonishing thing is that with so little storage of energy it should be possible to transmit intelligence to a distance of a hundred miles without connecting wires.
One consequence, however, of the small amount of energy which can be accumulated in a simple Marconi aerial is that this energy is almost entirely radiated in one oscillation or wave. Hence, strictly speaking, a simple aerial of this type does not create a train of waves in the ether, but probably at most a single impulse or two.
We shall later on consider some consequences which follow from this fact. Meanwhile, it may be explained that there are methods by which not only a much larger amount of energy can be accumulated in connection with an aerial, but more sustained oscillations created than by the original Marconi method. One of these methods originated with Professor Braun, of Strasburg, and a modification was first described by Mr. Marconi in a lecture before the Society of Arts of London.[7] In this method the charge in the aerial is not created by the direct application to it of the secondary electromotive force of an induction coil, but by means of an induced electromotive force created in the aerial by an oscillation transformer. The method due to Professor Braun is as follows: A condenser or Leyden jar has one terminal, say its inside, connected to one spark ball of an induction coil. The other spark ball is connected to the outside of the Leyden jar or condenser through the primary coil of a transformer of a particular kind, called an oscillation transformer (see Fig. 9). The spark balls are brought within a few millimeters of each other. When the coil is set in operation, the jar is charged and discharged through the spark gap, and electrical oscillations are set up in the circuit consisting of the dielectric of the jar, the primary coil of the oscillation trans former and the spark gap. The secondary  Fig. 9. Marconi-Braun System of inducing Electromotive Force in an Aerial A. B, battery; K key, I, induction coil; S spark gap; C, Leyden jar; E, earth plate; ps, oscillator transformer. circuit of this oscillation transformer is connected in between the earth and the insulated aerial wire; hence when the oscillations take place in the primary circuit, they induce other oscillations in the aerial circuit. But the arrangement is not very effective unless, as is shown by Mr. Marconi, the two circuits of the oscillation transformer are tuned together.
Fig. 9. Marconi-Braun System of inducing Electromotive Force in an Aerial A. B, battery; K key, I, induction coil; S spark gap; C, Leyden jar; E, earth plate; ps, oscillator transformer. circuit of this oscillation transformer is connected in between the earth and the insulated aerial wire; hence when the oscillations take place in the primary circuit, they induce other oscillations in the aerial circuit. But the arrangement is not very effective unless, as is shown by Mr. Marconi, the two circuits of the oscillation transformer are tuned together.
We shall return presently to the consideration of this form of transmitter; meanwhile, we may notice that by means of such an arrangement it is possible to create in the aerial a far greater charging electromotive force than would be the case if the aerial were connected directly to one terminal of the secondary circuit of the induction coil, the other terminal being to earth, and the two terminals connected as usual by spark balls. By the inductive arrangement it is possible to create in an aerial electromotive forces which are equivalent to a spark of a foot in length, and when the length of the aerial is also properly proportioned, the potential along it will increase all the way up, until at the top or insulated end of the aerial it may reach an amount capable of giving sparks several feet in length. From the remarks already made on the analogy between the closed organ-pipe and the Marconi aerial wire, it will be seen that the wave which is radiated from the aerial must have a wave length four times that of the aerial, if the aerial is vibrating in its fundamental manner. It is also possible to create electrical oscillations in a vertical wire which are the harmonics of the fundamental. All musicians are aware that in the case of an organ-pipe, if the pipe is blown gently it sounds a note which is called the fundamental of the pipe. The celebrated mathematician, Daniel Bernouilli, discovered that an organ-pipe can be made to yield a succession of musical notes by properly varying the pressure of the current of air blown into it. If the pipe is an open pipe, and if we call the frequency of the primary note obtained when the pipe is gently blown, unity, then when we blow more strongly, the pipe yields notes which are the harmonics of the fundamental one; that is to say, notes which have frequencies represented by the numbers 2, 3, 4, 5, etc. If, however, the pipe is closed at the top, then over-blowing the pipe makes it yield the odd harmonics or the tones which are related to the primary tone in the ratio of 3, 5, 7, etc., to unity. Accordingly, if a stopped pipe gives as its fundamental the note C, its first overtone will be the fifth above the octave or G′.
As already remarked, the aerial wire or radiator as used in Marconi telegraphy may be looked upon as a kind of ether organ-pipe or siren tube, and its electrical phenomena are in every respect similar to the acoustic phenomena of the ordinary closed organ-pipe. When the aerial is sounding its fundamental ether note, the conditions which pertain are that there is a current flowing into the aerial at the lower end, but at that point the variation in potential is very small, whereas at the upper end there is no current but the variations of potential are very large. Accordingly, we say that at the upper end of the aerial there is an antinode of potential and a node of current, and at the bottom, an antinode of current and a node of potential. By altering the frequency of the electrical impulses we can create in the aerial an arrangement of nodes of current or potential corresponding to the overtones of a closed organ-pipe. But whatever may be the arrangement, the conditions must always hold, that there is a node of current at the upper end and an antinode of current at the lower end. In other words, there are large variations of current at the place where the aerial terminates on the spark gap and no current at the upper end. The first harmonic is formed where there is a node of potential at one third of the length of the aerial from the top. In this case, we have a node of potential not only at the lower end of the wire, but at two thirds of the way up. In the same way we can create in the closed organ-pipe by properly overblowing the pipe, a region about two thirds of the way up the pipe, where the pressure changes in the air are practically no greater than they are at the mouthpiece. We can make evident visually in a beautiful manner the existence of similar stationary electrical waves in an aerial by means of an ingenious arrangement devised by Dr. Georg Seibt, of Berlin. It consists of a very long, silk covered copper wire A (see Fig. 10) wound in a close spiral of single layer round a wooden rod six feet long and about two inches in diameter. This rod is insulated, and at the lower end the wire is connected to a Leyden jar circuit, consisting of a Leyden jar or jars and an inductance coil L, the inductance of which can be varied. Oscillations are set up in this jar circuit by means of an induction coil discharge, and the lower end of the long spiral wire is attached to one point on the jar circuit. In this manner we can communicate to the bottom end of the long spiral wire a scries of electric impulses, the time period of which depends upon the capacity of the jar and the inductance of the discharge circuit. We can, moreover, vary this frequency over wide limits. Parallel to the long spiral wire is suspended another copper wire E (see Fig. 10), and between this wire and the silk-covered copper wire discharges  Fig. 10. Seibt's Apparatus for showing Stationary Waves in Long Solenoid A. I, induction coil; S, spark gap L, inductance coil; C1C2, Leyden jars; E, earth wire. take place due to the potential difference between each part of the wire and this long aerial wire. If we arrange matters so that the impulses communicated to the bottom end of the long spiral wire correspond to its fundamental note or periodic time, then in a darkened room we shall see a luminous glow or discharge between the vertical wire and the spiral wire, which increases in intensity all the way up to the top of the spiral wire. The luminosity of this brush discharge at any point is evidence of the potential of the spiral wire at that point, and its distribution clearly demonstrates that the difference of potential between the spiral wire and the aerial increases all the way up from the bottom to the top of the spiral wire. In the next place, by making a little adjustment and by varying the inductance of the jar circuit, we can increase the frequency of the impulses which are falling upon the spiral wire; and then it will be noticed that the distribution of the brush discharge or luminosity is altered, and that there is a maximum now at about
Fig. 10. Seibt's Apparatus for showing Stationary Waves in Long Solenoid A. I, induction coil; S, spark gap L, inductance coil; C1C2, Leyden jars; E, earth wire. take place due to the potential difference between each part of the wire and this long aerial wire. If we arrange matters so that the impulses communicated to the bottom end of the long spiral wire correspond to its fundamental note or periodic time, then in a darkened room we shall see a luminous glow or discharge between the vertical wire and the spiral wire, which increases in intensity all the way up to the top of the spiral wire. The luminosity of this brush discharge at any point is evidence of the potential of the spiral wire at that point, and its distribution clearly demonstrates that the difference of potential between the spiral wire and the aerial increases all the way up from the bottom to the top of the spiral wire. In the next place, by making a little adjustment and by varying the inductance of the jar circuit, we can increase the frequency of the impulses which are falling upon the spiral wire; and then it will be noticed that the distribution of the brush discharge or luminosity is altered, and that there is a maximum now at about 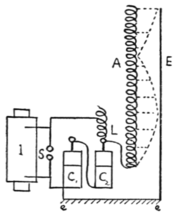 Fig. 11. Harmonic Oscillations in Long Solenoid shown with Seibt's Apparatus. one third of the height of the spiral wire, and a dark place at about two thirds of the height, and another bright place at the top, thus showing that we have a node of potential at about two thirds the way up the wire (see Fig. 11), and we have therefore set up in the spiral wire electrical oscillations corresponding to the first overtone. It is possible to show in the same way the existence of the second harmonic in the coil, but the luminosity then becomes too faint to be seen at a distance.
Fig. 11. Harmonic Oscillations in Long Solenoid shown with Seibt's Apparatus. one third of the height of the spiral wire, and a dark place at about two thirds of the height, and another bright place at the top, thus showing that we have a node of potential at about two thirds the way up the wire (see Fig. 11), and we have therefore set up in the spiral wire electrical oscillations corresponding to the first overtone. It is possible to show in the same way the existence of the second harmonic in the coil, but the luminosity then becomes too faint to be seen at a distance.
An interesting form of aerial devised by Professor Slaby, of Berlin, depends for its action entirely on the fact that the electrical oscillations set up in it which radiate are harmonics of the fundamental tone.
A closed vertical loop A1A2 (see Fig. 12) is formed by erecting two parallel insulated wires vertically a few feet apart and joining them together at the top. At the bottom these wires are connected, with the secondary terminals of an induction coil,  Fig. 12 Non- radiative Closed Loop Aerial. a condenser C or Leyden jar being bridged across the terminals and a pair of spark balls S inserted in one side of the loop. It will readily be seen that on setting the coil in action, oscillations will take place in these vertical wires, but that if the oscillations are simply the fundamental note of the system, then at any moment corresponding to a current going up one side of the loop of wire, there must be a current coming down the other. Accordingly, an arrangement of this kind, forming what is called a closed circuit, will not radiate or radiates but very feebly. Professor Slaby found, however, that it might be converted into a powerful radiator if we give the two sides of the loop unequal capacity or inductance, and at the same time earth one of the lower ends of the loop, as shown in Fig. 13. By this means it is possible to set up in the loop electrical overtones or harmonics of the fundamental oscillation, and if we cause the system to vibrate so as to produce its first odd harmonic, there is a potential node at the lower end of both vertical sides of the loop, a potential node on both vertical sides at two thirds of the way up, and a potential antinode at the summit of the loop; then, under these circumstances, the closed loop of wire is in the same electrical condition as if two simple Marconi aerials, both emitting their first odd harmonic
Fig. 12 Non- radiative Closed Loop Aerial. a condenser C or Leyden jar being bridged across the terminals and a pair of spark balls S inserted in one side of the loop. It will readily be seen that on setting the coil in action, oscillations will take place in these vertical wires, but that if the oscillations are simply the fundamental note of the system, then at any moment corresponding to a current going up one side of the loop of wire, there must be a current coming down the other. Accordingly, an arrangement of this kind, forming what is called a closed circuit, will not radiate or radiates but very feebly. Professor Slaby found, however, that it might be converted into a powerful radiator if we give the two sides of the loop unequal capacity or inductance, and at the same time earth one of the lower ends of the loop, as shown in Fig. 13. By this means it is possible to set up in the loop electrical overtones or harmonics of the fundamental oscillation, and if we cause the system to vibrate so as to produce its first odd harmonic, there is a potential node at the lower end of both vertical sides of the loop, a potential node on both vertical sides at two thirds of the way up, and a potential antinode at the summit of the loop; then, under these circumstances, the closed loop of wire is in the same electrical condition as if two simple Marconi aerials, both emitting their first odd harmonic  Fig. 13. Slaby's Loop Radiator. oscillation, were placed side by side and joined together at the top.
Fig. 13. Slaby's Loop Radiator. oscillation, were placed side by side and joined together at the top.
It is a little difficult without the employment of mathematical analysis to explain precisely the manner in which earthing one side of the loop or making the loop unsymmetrical as regards inductance has the effect of creating overtones in it. The following rough illustration may, however, be of some assistance. Imagine a long spiral metallic spring supported horizontally by threads. Let this represent a conductor, and let any movement to or fro of a part of the spring represent a current in that conductor. Suppose we take hold of the spring at one end, we can move it bodily to and fro as a whole. In this case, every part of the spring is moving one way or the other in the same manner at the same time. This corresponds with the case in which the discharge of the condenser through the uniform loop conductor is a flow of electricity, all in one direction one way or the other. The current is in the same direction in all parts of the loop at the same time, and, therefore, if the current is going up one side of the loop it is at the same time coming down the other side. Hence the two sides of the loop are always in exact opposition as regards the effect of the current in them on the external space, and the loop does not radiate. Returning again to the case of the spring. Supposing that we add a weight to one end of the spring by attaching to it a metal ball, and then move the other end to and fro with certain periodic motion, it will be found quite easy to set up in the spring a pulsatory motion resembling the movement of the air in an open organ-pipe. Under these circumstances both ends of the spring will be moving inwards or outwards at the same time, and the central portions of the spring, although being pressed and expanded slightly, are moving to and fro very little. This corresponds in the case of the looped aerial with a current flowing up or down both sides at the same time; in other words, when this mode of electrical oscillation is established in the loop, its electrical condition is just that of two simple Marconi aerials joined together at the top and vibrating in their fundamental manner. Accordingly, if one side of the double loop is earthed, we then have an arrangement which radiates waves. Professor Slaby found that by giving one side of the loop less inductance than the other, and at the same time earthing the side having greater inductance at the bottom, he was able to make an arrangement which radiated, not in virtue of the normal oscillations of the condenser, but in virtue of the harmonic oscillations set up in the conductor itself. The mathematical theory of this radiator has been very fully developed by Dr. Georg Seibt.
It will be seen, therefore, that there are several ways in which we may start into existence oscillations in an aerial. First, the aerial may be insulated, and we may charge it to a high potential and allow this charge suddenly to rush out. Although this process gives rise to a disturbance in the ether, as already explained, it is analogous to a pop or explosion in the air, rather than to a sustained musical note. The exact acoustic analogue would be obtained if we imagine a long pipe pumped full of air and then suddenly opened at one end. The air would rush out, and, communicating a blow to the outer air, would create an atmospheric disturbance appreciated as a noise or small explosion. This is what happens when we cut the string and let the cork fly out from a bottle of champagne. At the same time, the inertia of the air rushing out of the tube would cause it to overshoot the mark, and a short time after opening the valve the tube, so far from containing compressed air, would contain air slightly rarefied near its mouth, and this rarefication would travel back up the tube in the form of wave motion, and, being reflected as condensation at the closed end, travel down again; and so after being reflected once or twice at the open or closed end, become damped out very rapidly in virtue of both air friction and the radiation of the energy. In the case, however, of the ordinary organ-pipe, we do not depend merely upon a store of compressed air put into the pipe, but we have a store of energy to draw upon in the form of the large amount of compressed air contained in a wind chest, which is being continually supplied by the bellows. This store of compressed air is fed into the organ-pipe with the result that we obtain a continuous radiation of sound waves. The first case, in which the only store of energy is the compressed air originally contained in the pipe, illustrates the operation of the simple Marconi aerial. The second case, in which there is a larger store of energy to draw upon, the organ-pipe being connected to a wind chest, illustrates the Marconi-Braun method in which an aerial is employed to radiate a store of electric energy contained in a condenser, gradually liberated by the aerial in the form of a series of electrical oscillations and waves. In this arrangement the condenser corresponds to the wind chest, and it is continually kept full of electrical energy by means of the induction coil or transformer, which answers to the bellows of the organ. From the condenser, electrical energy is discharged each time the spark discharge passes at a spark gap in the form of electrical oscillations set up in the primary circuit of an oscillation transformer. The secondary circuit of this transformer is connected in between the earth and the aerial, and therefore may be considered as part of it, and, accordingly, the energy which is radiated from the aerial is not simply that which is stored up in it in virtue of its own small capacity, but that which is stored up in the much larger capacity represented by the primary condenser or, as it may be called, the electrical wind chest. By the second arrangement we have therefore the means of radiating more or less continuous trains of electric waves, corresponding with each spark discharge. To create powerful oscillations in the aerial, one condition of success is that there shall be an identity in time-period between the circuit of the aerial and that of the primary condenser. The aerial is an open circuit which has capacity with respect to the earth, and it has also inductance, partly due to the wire of the aerial and partly due to the secondary circuit of the oscillation transformer in series with it. The primary circuit or spark circuit has capacity, viz., the capacity of the energy-storing condenser, and it has also inductance, viz., the inductance of the primary circuit of the oscillation transformer. We shall consider at a later stage more particularly the details of syntonising arrangements, but meanwhile it may be said that one condition for setting up powerful waves by means of the above arrangement is that the electrical time-period of both the two circuits mentioned shall be the same. This involves adjusting the inductance and capacity so that the product of conductance and capacity for each of these two circuits is numerically the same. Instead of employing an oscillation transformer between the condenser circuit and the aerial, the aerial may be connected directly to some point on the condenser circuit at which the potential oscillations are large, and we have then another arrangement devised by Professor Braun (see Fig. 14). In this case, in order to accumulate large potential  Fig. 14. Braun's Radiator. B, battery; I, induction coil; K, key; S, spark gap; L, inductance coil; C, condenser; A, aerial. oscillations at the top of the aerial, it is, as we have seen, necessary that the length of the aerial shall be one quarter the length of the wave. If therefore the electrical oscillations in the condenser circuit are at the rate of N per second, in other words, have a frequency N, the wave-length corresponding to this frequency is given by the expression,
Fig. 14. Braun's Radiator. B, battery; I, induction coil; K, key; S, spark gap; L, inductance coil; C, condenser; A, aerial. oscillations at the top of the aerial, it is, as we have seen, necessary that the length of the aerial shall be one quarter the length of the wave. If therefore the electrical oscillations in the condenser circuit are at the rate of N per second, in other words, have a frequency N, the wave-length corresponding to this frequency is given by the expression,
The number is the value in centimeters per second of the velocity of the electromagnetic wave, and is identical with that of light. The corresponding resonant length of the aerial is therefore one fourth of this wave-length, or . Generally speaking, however, it will be found that with any length of aerial which is practicable, say 200 feet or 6,000 cms., this proportion necessitates rather a high frequency in the primary oscillation circuit. In the case considered, viz., for an aerial 200 feet in height, the oscillations in the primary circuit must have a frequency of one and a quarter million. This high frequency can only be obtained either by greatly reducing the inductance of the primary discharge circuit, or reducing the capacity. If we reduce the capacity, we thereby greatly reduce the storage of energy, and it is not practicable to reduce the inductance below a certain amount.
Summing up, it may be said that there are three, and as far as the writer is aware, at present only three, modes of exciting the electrical oscillations in an aerial wire. First, the aerial may itself be used as an electrical reservoir and charged to a high potential and suddenly discharged to the earth. This is the original Marconi method. The second method, due to Braun, consists of attaching the aerial to some point on an oscillation circuit consisting of a condenser, an inductance coil and a spark gap, in series with one another, and charging and discharging the condenser across the spark gap so as to create alterations of potential at some point on the oscillation circuit. The length of the aerial must then be so proportioned as above described that it is resonant to this frequency. Thirdly, we may employ the arrangement involving an oscillation transformer, in which the oscillations in the primary condenser circuit are made to induce others in the aerial circuit, the time-period of the two circuits being the same. This method may be called the Braun-Marconi method. Professor Slaby has combined together in a certain way the original Marconi simple aerial with the resonant quarter-wave-length wire of Braun. He constructs what he calls a multiplicator, which is really a wire wound into a loose spiral connected at one point to an oscillation circuit consisting of a condenser inductance, the length of this wire being proportioned so that there is a great resonance or multiplication of tension or potential at its free end. This free end is then attached to the lower end of an ordinary Marconi aerial, and serves to charge it with a higher potential than could be obtained by the use of the induction coil directly attached to it.
(To he continued.)
- ↑ This series of articles is based on the Cantor lectures delivered before the Society of Arts, London, in March, 1903. The lectures were attended by many of the leading British scientific men and electrical engineers, and attracted wide attention as the most complete and authoritative statement hitherto made of wireless telegraphy. In writing the articles for The Popular Science Monthly, the author has omitted advanced technicalities in order that the substance may be suitable for the general reader.—Editor.
- ↑ For a more detailed account of this hypothesis, the reader is referred to an article by the present writer entitled: 'The Electronic Theory of Electricity,' published in the Popular Science Monthly for May, 1902.
- ↑ See J. J. Thomson, 'Recent Researches in Electricity and Magnetism,' Chapter I., 16.
- ↑ See O. Heaviside, 'Electromagnetic Theory,' Vol. I., p. 54.
- ↑ Wiedemann's Annalen, 36, p. 1, 1889. Or in his republished papers, 'Electric Waves,' p. 137. English translation by D. E. Jones.
- ↑ The fraction 7/22 here denotes a stranded wire formed of seven strands, each single wire having a diameter expressed by the number 22 on the British standard wire gauge.
- ↑ G. Marconi, 'Syntonic Wireless Telegraphy,' Journal of the Society of Arts, Vol. XLIX., p. 501, 1901.






