Popular Science Monthly/Volume 74/June 1909/The Tides: Their Causes and Representation
THE
POPULAR SCIENCE
MONTHLY
JUNE, 1909
| THE TIDES: THEIR CAUSES AND REPRESENTATION |
By ROLLIN ARTHUR HARRIS
THE UNITED STATES COAST AND GEODETIC SURVEY, WASHINGTON, D. C.
Historical Note on the Tidal Problem
THE so-called problem of the tides has for ages engaged the attention of observing and thinking men. Before Newton established the law of universal gravitation, the whole subject was surrounded with an air of mystery, although the fact had long been recognized by many that in some manner the tides are governed by the moon or the moon and sun. Such views were held by Pytheas of Massilia, Seleucus of Babylonia, Posidonius the Stoic philosopher, Cæsar, Cicero, Strabo, Seneca, Pliny the elder, Lucan, Claudianus and Macrobius.
The ancients say little as to the agency whereby the moon is enabled to exert an influence upon the waters of the globe; but winds produced by the moon, vapors surrounding the moon and the special power of the moon to replenish moist bodies, are severally mentioned as being the probable means.
However, before Newton's great discovery, several philosophers had gone so far as to suggest or assert that the tides are due to an attractive force of the moon analogous to magnetic attraction. Among these were Scaliger, Gilbert, the College of Jesuits at Coimbra, Antonio de Dominis, Stevin and especially Kepler.
Of course, not all ancient or medieval theorists admitted the moon to be the cause of the tides. Some of the many other causes brought forward were: The discharging of rivers into the sea; variations in depths and densities of the sea; the surface of the sea not being everywhere upon the same level; the respiration of the earth; submarine caverns; submarine heat; submarine vapors, exhalations, or fermentations; power exerted by a supernatural being; whirlpools and eddies; and the non-uniform motion of the earth or of its various parts.
When Newton had made public his capital discovery, and had shown that the magnitudes or ranges of the tides increase and decrease in accordance with the varying attractions of the moon and sun, the tidal problem was supposed to be nearing a solution. Indeed, Newton thought that he could see in the observed times of tides upon certain shores a justification of his theoretical considerations. His work, however, was only a beginning. Since his time, eminent mathematicians, astronomers and physicists—including Bernoulli, Maclaurin, Euler, Lalande, Laplace, Young, Lubbock, Whewell, Airy, Ferrel, Kelvin, Darwin, Lévy and Hough—have addressed themselves to this subject; while others, like Lagrange, Stokes, Rayleigh, Lamb and Poincaré, have dealt rather with the underlying mathematical and physical problems.
Since it has been universally recognized that the tides result from the attraction of the moon and sun, the popular mind has taken little interest in the manner in which these forces operate in order to produce the tides. The apparent hopelessness of the task has doubtless deterred many investigators from devoting to it a full measure of their attention. In fact, as will be shown below, there is no such thing as "the tidal problem" analogous to the astronomers' "problem of three bodies." The tide involves a number of problems, and to even discover what these problems are requires a good knowledge of the forms, sizes and depths of the oceans, together with a knowledge of the tide-producing forces. The observed tides themselves render great assistance in this matter; for their times and ranges indicate the ways in which the various oceans probably oscillate, and so, in a measure, the underlying tidal problems requiring solution.
General Belief in a Westwardly-progressing Tide Wave
Various theories were instrumental in leading to the belief of a general westward progression of the tide. As before the Copernican system of astronomy became known or generally accepted, the tides were made to accord with the Ptolemaic system then prevailing, so for some time before and after the publication of Newton's "Principia," the tides were made dependent upon the vortices of Descartes's theory.
The Ptolemaic system of astronomy assumed the center of the earth to be the fixed center of the universe around which revolved a series of concentric spheres. The outermost of these was styled the primum mobile; this by its westward motion imparted westward motion to the stars and other heavenly bodies, to the atmosphere, and even to the waters of the oceans. And so before the law of gravitation was established, the notion became prevalent that water had a westward motion (ab oriente in occidentem or ab ortu in occasum) around the globe; and because the flood stream, rather than the ebb, was the one chiefly considered, the flood stream (and so the progression of the tidal wave) was commonly supposed to partake of this westward motion. The theory of a westerly motion of the waters thus had its origin in the assumed motion of the primum mobile. The flood tide was associated with this westward motion by Scaliger and Bacon. Kepler also asserts that the flood has a westerly direction, although, as already stated, he attributes the tides to the attraction of the moon.
Descartes's vortex theory also gave a westward progression to the tidal wave because he assumed that low water would always occur when the moon crossed the local meridian.
Newton, Bernoulli and Laplace evidently contemplated tide waves progressing westward around the earth, completing the circuit in 24 lunar hours, or 24 hours and 50 minutes solar time, although they were aware that the land masses must produce many irregularities in this hypothetical motion.
In order to see how any tide wave progresses, it is necessary to reduce to a common time. This is generally taken as Greenwich lunar time. Consequently, if tides in a given locality are found to follow the meridian passage of the moon by a certain interval (expressed in lunar hours), this interval must be increased by the longitude, expressed in hours, if the place be in west longitude and decreased if in east longitude. Places having high water at the same tidal hour are said to lie upon the same cotidal line.
The first extensive charts of cotidal lines were constructed by Whewell about 75 years ago; and these charts, or these charts slightly modified, have been in common use in atlases and astronomies ever since.
The Importance of Stationary Waves suggested
The analogy between the tides and the oscillatory motion of water in a vase, or other vessel, had been noted by many even before the moon's attraction had been universally recognized as the principal and primary cause of the phenomenon. But in order that the water should oscillate, it must first be disturbed from its position of equilibrium. Galileo imagined that he had found this necessary disturbance in the non-uniform motion of different parts of the earth as it rotates upon its axis and revolves about the sun.
César d'Arcons (1667) supposes the solid earth to move a short distance back and forth along its axis, thus causing the flood in the northern hemisphere to appear to move from south to north and the ebb in the reverse direction. According to his views the entire Atlantic Ocean is a huge vessel of water, the surface rising and falling considerably at the two ends (i. e., in high latitudes), but having little vertical motion near the middle (i. e., in equatorial regions), where he logically infers the horizontal motion to be great.
John Bryanston (1683) supposes the moon to produce in the earth a small east-and-west libration, not detected by astronomers, and this motion of the earth to cause the waters of the oceans to oscillate like water contained in vessels of various shapes and sizes.
While not questioning the fact established by Newton that the tides are primarily due to the attraction of the moon and sun. Admiral Fitz Roy attempts to explain the tides upon the assumption of stationary waves extending in an east-and-west direction across various portions of the several oceans. His wide experience as a navigator had familiarized him with the fact that throughout some extended regions of the ocean, the tides occur at nearly one and the same time; also that even for islands remote from the land, the amount of rise and fall is quite various.
Sir George B. Airy was the first person to make an extensive mathematical study of wave motion implied in tidal phenomena. While he does not point out how the ocean tides are produced, he shows that certain dependent bodies of water, and in particular the Irish Sea, must contain stationary waves. He establishes the theoretical result that the tides in a north-and-south canal extending from the equator to either pole must consist of a stationary wave.
William Ferrel suggests that, because of their unusual size, the tides of the North Atlantic may depend upon stationary waves extending in an east-and-west direction across the ocean; and, in particular, upon one extending between the coasts of Ireland and those of Newfoundland.
These, and other writers who have expressed similar views, failed to consider that an imperfectly bounded strip of the sea must have considerable width (as well as a suitable length) in order to make a stationary wave possible. They also failed to make any connection between the known tidal forces and the times of the tide.
This brings us to the subject proper, which involves an approximate explanation of the dominant ocean tides, it being manifestly unreasonable to expect accurate mathematical solutions of the problems involved.
It should be noted in passing that although Dr. Berghaus propounded no theories concerning the tides, his cotidal chart constructed in 1889 marks a radical departure from those previously constructed, and is in itself highly suggestive.
The Tide-producing Forces
The tide-producing forces of moon and sun can be computed from well-established astronomical data, and there are no uncertainties connected with their determination, at least to a moderate degree of refinement. In this place it is necessary to say only a few words descriptive of these forces. The tide-producing force of the moon upon a particle of unit mass is the difference between the moon's attraction upon this mass and upon a unit mass situated at the earth's center; or

Fig. 1. The diagram shows the magnitude and direction of the tidal forces at each half lunar hour for various north latitudes. Such a force is represented by a line drawn from the center to the periphery of the ellipse having a given latitude. At the equator the mean value of the semi-diurnal force at 9 or 3 o'clock is equal to one thirteen-millionth part of the force of gravity at the earth's surface. The diurnal forces shown in the figure are those occurring upon the day when the moon's declination is greatest either north or south.
it is the difference between the moon's attraction upon the given unit mass and the moon's attraction upon the entire earth divided by the mass of the earth. Because the depths of the oceans are small in comparison with the length of the earth's radius, and because of the smallness of the tidal forces, only the horizontal components of such forces are effective in the production of tides; and so these may, without impropriety, be spoken of as the tidal forces.
The vertical forces alter the intensity of the earth's gravity upon the waters of the ocean in a way similar to the alteration which would be occasioned were the density of the waters to undergo a fluctuation having a range of less than one ten-millionth part of itself. Now the greatest known ocean depth occurs near Guam Island and measures 5,269 fathoms or 31,614 feet; and it is obvious that the small density fluctuation just mentioned, and so the vertical forces, can create no sensible disturbance in the existing ocean.
For simplicity's sake, we shall here ignore that alternation in the forces which depends upon the declination of the moon, and is responsible for what is called the "diurnal inequality" in the tides. We shall also, as a rule, ignore that portion of the tidal forces resulting from the sun's attraction.
It is evident that at moonrise or moonset at a given point or locality upon the earth's equator, the horizontal forces vanish because the given point is then (very nearly) as remote from the moon as is the earth's center. On account of the moon's parallax, the moon at the times of rise or set does exert a downward disturbing force at the given point or locality; but, as already stated, this does not concern the tides. When the moon is on the meridian above or below the horizon, the disturbing force is all vertical and so the horizontal component does not exist. Therefore the tidal forces vanish four times during each lunar day. From moonrise to moon culmination, the force is directed eastward; and from culmination to moonset, westward. Also from moonset to lower culmination, the force is directed eastward, and from lower culmination to moonrise, westward.
For a point not upon the equator, there is also a meridional periodic force. In north latitude this force has its maximum southward value at the time of either culmination, and its maximum northward value at moonrise and moonset. The reverse of this is true for a point situated in the southern hemisphere.
In accordance with what has been said, a suspended plumb bob will, at the equator, make two complete oscillations daily in an east-and-west direction. The average amount of deviation either way from its undisturbed position will be about one thirteen-millionth part of the length of the line measured from the point of suspension to the center of inertia of the bob.
Equilibrium or Lake Tides
The surface of a small and sufficiently deep body of water will arrange itself normal to the direction of apparent gravity; that is, normal to the direction of terrestrial gravity when disturbed by the moon and sun, or, in other words, normal to the disturbed plumb line. If such a body of water be situated upon the earth's equator, high water will occur at its east end three lunar hours before the upper or lower culmination of the moon and low water, three hours after such times. When it is high water at the east end, it will be low water at the west end, and vice versâ. The amount of the rise and fall (i. e., the range of tide) at either end will be one thirteen-millionth part of the length of the body of water. If the body of water be not upon the equator, the range of tide will be somewhat less, and the times of high water around its margin will be progressive, following the order of the hands of a watch in the northern hemisphere and the opposite order in the southern. At the center of gravity of the surface of such a body will be a point having no rise and fall of tide, and so styled a "no-tide point." Tides produced in this way are called "equilibrium tides"; the minute tide found in Lake Superior constitutes an excellent example of this class. The observed rise and fall of the lunar tide at Duluth amounts to 1.6 inches, while the value computed directly from the forces amounts to 1.4 inches.
As commonly taught in schools and colleges, the expression "equilibrium tide" is used to denote a fluctuation in the ocean's surface resulting from an instantaneous arrangement of all water particles such that the surface of the ocean is everywhere apparently level, or normal to the direction of the earth's gravity when slightly disturbed by the action of the moon. It is taught that, but for the resistance caused by the continents and ocean bed, high water at a given place would occur when the moon crosses the local meridian. As may be gathered from what follows, this conception is fundamentally wrong. The semidaily fluctuation of the ocean's surface does not even approximate towards a surface of equilibrium, because the inertia of the water, and the shallowness of the ocean, when its depths are compared with its horizontal dimensions or with the distance from the surface to the center of the earth, prevent such adjustment from taking place in anything like the half-daily period.
Oscillatory or Ocean Tides
Most tides are not equilibrium tides; they are waves either stationary or progressive. The forces just described act upon portions of the oceans which are susceptible of taking up stationary oscillations having about the same period as the period of the forces. In this way the dominant tides originate. But irregularities in depth and coast line, particularly openings through the latter, cause the tides generated in these ocean basins to send off progressive waves into other parts of the oceans and into seas, gulfs, bays and tidal rivers.
By a stationary oscillation is meant a mode of motion which can be readily set up and maintained in a tank, vase or other artificial vessel of water. High water at one end of a rectangular body of water occurs when it is low water at the other end, if the simplest mode of oscillation be under consideration. Between the two ends is a line, styled "nodal line," along which there is neither rise nor fall but across which the horizontal motion of the liquid particles is comparatively great. In order that a large and regular oscillation may be maintained, it is necessary that the natural period of the basin of water be very nearly equal to the period of the applied forces: just as a resonator must have certain dimensions if a particular musical tone is to be reinforced by its presence. An oscillation is best sustained if the phases (or time-angles) of the forces, all parts of the system being considered, agree, as well as may be, with the phases of the velocities of the water particles. This furnishes a clue to the times of the tides when one knows the times of the vanishing of the forces.
Obviously, if two rectangular basins performing simultaneous oscillations in accordance with their simplest modes be put together end-to-end, and the partition between them removed, the whole body may be made to so oscillate that high water will occur simultaneously at the two ends, while it will be low water over the central portion. The nodal lines will remain in the same positions as before, crossing the individual bodies midway between their real and virtual ends., or the new body at points one quarter of the body's length from either end. The individual bodies each comprise a half wave-length of the whole-wave system to which they now belong. The oscillation in each of the individual bodies is said to be "uninodal" and that in the whole body, "binodal."
No-tide Points
Points shown upon the charts (Figs. 5, 6 and 7) from which the cotidal lines radiate, are no-tide points; that is, points at each of which there is no rise and fall of tide. In the oceans these points are due to the fact that the times of the tides around them and which times are dependent upon stationary or progressive waves, or both, must take successively all values from one to twelve, because in open water sudden changes in time can not occur.
In narrow arms of the sea, no-tide points may result from dependent stationary oscillations influenced by the deflecting force of the earth's rotation. This, for the northern hemisphere, is such that if we always face the direction towards which the flood or ebb stream is flowing, water will be piled up upon the side of the channel then situated upon the right, and drawn away from the opposite bank. The reverse of this occurs for channels situated in south latitude.
Atlantic-Ocean Tides
A body of water resembling the artificial one just described is the portion of the Atlantic Ocean (shown by one form of shading) extending from South America to southern Greenland and resting against the western coast of Africa and Europe. A section of this basin or
Fig. 2. This diagram shows the binodal oscillation going on in the North Atlantic Ocean. When it is high water at either end, it is low water off Morocco and vice versâ. The depth of the southern portion being greater than the depth of the northern, a half wave-length in the former exceeds a half wave-length in the latter—the period in each case being very nearly 12 lunar hours.
system is shown by means of a diagram (Fig. 2). One nodal line passes near the Cape Verde Islands and another lies westerly from Ireland. When it is high water on the coasts of Guiana and Brazil, it is also high water around southern Greenland, and it is then low water along the coast of Morocco, Spain and Portugal. The Roman numerals upon the small map of the world show that high water occurs at eight o'clock, Greenwich  Fig. 3. This diagram shows that the Bay of Bengal measures a quarter of a wave-length to its nodal line extending eastward from Ceylon. Its tide depends directly upon that tide of the Indian Ocean which lies to the southward of the nodal line. lunar time, for the South American and Greenland ends of this basin and at two o'clock for the central or Morocco portion. On account of the extensive openings to the eastward and northward of this basin or system, progressive waves are formed which contribute to the tides around the British Isles and Arctic Archipelago, and are chiefly responsible for the tides of the Arctic Ocean. Since progressive waves can not arise suddenly, their effects are felt over a large portion of the system now under consideration, and they tend to obscure the theoretical nodal lines which cross it.
Fig. 3. This diagram shows that the Bay of Bengal measures a quarter of a wave-length to its nodal line extending eastward from Ceylon. Its tide depends directly upon that tide of the Indian Ocean which lies to the southward of the nodal line. lunar time, for the South American and Greenland ends of this basin and at two o'clock for the central or Morocco portion. On account of the extensive openings to the eastward and northward of this basin or system, progressive waves are formed which contribute to the tides around the British Isles and Arctic Archipelago, and are chiefly responsible for the tides of the Arctic Ocean. Since progressive waves can not arise suddenly, their effects are felt over a large portion of the system now under consideration, and they tend to obscure the theoretical nodal lines which cross it.
The tides along the Atlantic Coast of the United States are produced in the body of water which extends from this coast to the Antarctic Continent by way of Cape of Good Hope. This is shown upon the smaller chart of the world (Fig. 4) by one of the types of shading. The northern portion of this region is not greatly influenced by progressive waves because the openings through its northwestern, or United-States, boundary are not large. Consequently, the theoretical nodal line running northeasterly from the Lesser Antilles is not obscured. Referring now to the cotidal chart of the Atlantic Ocean (Fig. 5), it will be seen that the mean range of tide, as shown by Arabic numerals, is seven feet along the coast of Georgia, between two and three feet for the Bahamas, one foot for the outer coast of Porto Rico, and little or nothing some leagues farther eastward. Hence the observational proof of the existence of one end of this nodal line.
When it is high water along the Atlantic Coast of the United States, it should be low water between Brazil and western Africa; that is, because the tidal hour is twelve for the former locality, it should be six for the latter. Doubtless such is the case for the portion of the tide depending upon the system now under consideration. But the system previously considered, viz., that extending from Guiana and Brazil to southern Greenland, gives eight for the tidal hour off the Brazilian coast. This explains why the observed times of tide between western Africa and Brazil fall between six and eight o'clock.
All along the southeastern coast of Brazil, the tidal hour is six, while west of Cape of Good Hope it is about twelve—but not exactly twelve because this locality is influenced by a progressive wave due to the existence of the Gulf of Guinea,
Farther south, along the Antarctic Continent, the tidal hour is doubtless six, but no observations are available for verifying this conclusion.
It may be noted here, and before going farther, that upon the small chart of the world (Fig. 4), the unshaded water areas are such that forces acting upon them, and them alone, can produce little tide either in such areas themselves or in other parts of the oceans. In other words, if they possess tides, these will depend upon the tides existing in such portions of the oceans as are comparatively well suited for their production. Heavy lines upon the chart indicate outer boundaries of systems. If rigid walls were erected along the outer boundaries of any particular system, the forces would incite tides of considerable size in the waters bounded by the walls and the shore lines; the tides of the system, if kept down by resistance, would nearly agree in their times of occurrence with the tides actually existing. These hypothetical bodies of water, together with such landward dependencies as have their tides occurring simultaneously with those of the body proper and upon which the forces act, are shaded by means of light parallel lines. In a particular ocean, the systems are distinguished by the directions given to the lines of shading. Double shading indicates an overlapping of systems.
The waters surrounding the British Isles have, as a rule, large tides accompanied by swift tidal streams. They depend chiefly upon the rise and fall of that part of the ocean situated to the southwestward of these isles. 
Fig. 4. Systems for the Semi-daily Tides. The shaded portions of this chart represent the regions most concerned in the production of tides, together with landward dependencies which possess tides simultaneous with those of the systems proper. The Roman numerals refer to Greenwich lunar time of high water. The values upon Fig. 4. are nearly those which would result from theoretical considerations. The values upon Figs. 5, 6, 7 and 8 are made to agree with observation as nearly as possible. The Arabic numerals on Figs. 5, 6, 7 and 8 denote mean ranges in feet of the observed semi-daily tide. The Roman numerals are placed upon that side of a cotidal line towards which the wave appears to progress.
The diminution of the mean range of tide in going westward from Portugal indicates the existence of a no-tide point westward from the Azores. Other no-tide points occur in European and American arms of the Atlantic Ocean. The no-tide point between Holland and England was first pointed out by Dr. Whewell and the one in the Adriatic Sea by Dr. Sterneck.
Indian-Ocean Tides
The Indian Ocean contains two strips of water well suited to the production of tides. The first extends from the northwestern coast of Australia to the coast of Somali Land and Arabia, the second, from the southern coast of Australia to the southern coast of Africa and Madagascar—the southern edge of this strip resting upon the Antarctic Continent. The tides of the Bay of Bengal depend upon those generated in the first strip, while the horizontal shading in the area between Madagascar and Hindustan, taken in connection with the tidal hours, indicates that an oscillation exists in this area which depends chiefly upon the rise and fall of the tide at the southern end of Mozambique Channel.
The stationary character of the tide in the Bay of Bengal is shown not only upon the small chart of the world, but also upon the chart of cotidal lines which covers the Indian Ocean (Fig. 6). A vertical section is shown by means of a diagram (Fig. 3).
The distance southward from the southern coast of Australia to the Antarctic Continent is less than a half wave-length of the lunar tide. It is more nearly equal to a half wave-length of the solar tide. Consequently the tides due to this oscillation are chiefly solar, and the tidal hours are enclosed in parentheses for the sake of distinction.
Fig. 6 shows that a great diversity of ranges of tide occurs in the Indian Ocean. Between Ceylon and Sumatra the mean range of tide is about one foot, while at the head of the Gulf of Martaban the range is nearly 14 feet. In the mouths of the Ganges the mean range is nearly 10 feet. At the southern extremity of Hindustan Peninsula the mean range of tide is about 1.5 feet while at the head of the Gulf of Cambay it is 23 feet. On the western coast of Madagascar the range of tide is 8 or 10 feet, while at Tamatave, upon the eastern coast, it is 1.5 feet. At Freemantle, near the southwestern corner of Australia, the range of the semidaily tide is 0.4 foot, while at Collier Bay and King Sound on the northwestern coast the mean range of tide is about 24 feet.
Between Madagascar and Hindustan is a no-tide point where the rise and fall of the semidaily tide vanishes.
Pacific-Ocean Tides
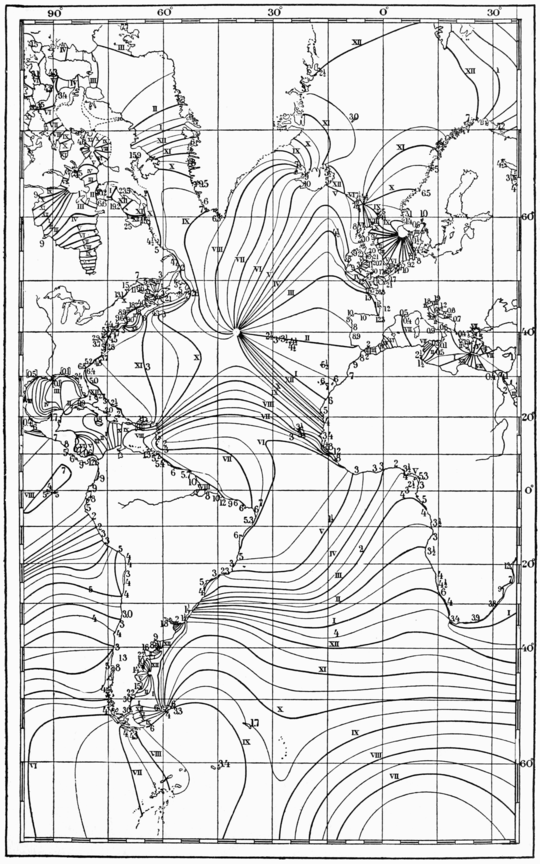
Fig. 5.

Fig. 6.

Fig. 7.
shading (Fig. 4). The region occupied by the first comprises a triangular body of water covering the greater portion of the North Pacific Ocean, and also a trapezoidal body extending in a southeasterly direction to the coast of Chile. The nodal line near Acapulco, Mexico, is
very apparent from observation, as can be seen upon consulting the chart of cotidal lines for the Pacific Ocean (Fig. 7). The same chart shows the stationary character of the oscillation by the fact that at the three angles of this huge triangle—that is, in Panama Bay, the Gulf
of Alaska and off the coast of Luzon—the tide occurs at nearly one and the same time, while the amount of rise and fall is considerable. Also, that for a considerable area around each of these angles, the time of tide changes slowly in going from place to place. The range of tide gradually decreases from the Gulf of Alaska, where it is about eight feet, to the western groups of the Aleutian Islands—the range off Rat Islands being less than two feet.
The South Pacific system embraces an L-shaped region extending from the coast of California and Lower California to the shoals and islands north of New Zealand, thence southeasterly to southern Chile and Graham Land.
Three no-tide points occur in mid-ocean, one occurs in Norton Sound, Alaska, one near either end of the Sea of Japan, and one in the Gulf of Pechili.
Tides at the Isthmus of Panama and Elsewhere
Referring now to the cotidal maps of the world, it appears that the mean range of tide at Panama is 12.6 feet, while at Colon, just across the isthmus, it is only 0.6 foot. That a great difference between the tides at these two points exists was mentioned by Oviedo y Valdez as long ago as 1526, and the question as to the reasons therefor has been frequently raised even up to the present time. Upon consulting the small chart of the world, it will be seen that Panama is situated at one angle of the triangular area where the rise and fall would naturally be greatest.
On the other hand, the tides which enter the Caribbean Sea from the ocean must be small because of the proximity of the nodal line setting out from the Lesser Antilles (Fig. 4). The time and range of the small tide at Colon indicate that it belongs to the equilibrium tides of the Caribbean Sea itself.
Likewise the small tides in the southwestern portion of the Gulf of Mexico are equilibrium tides belonging to the gulf.
The tides in the eastern portion of the Mediterranean are equilibrium tides of that body.
The tides in the Red Sea consist partly of a bodily oscillation of that sea and partly of a progressive wave from the Indian Ocean.
The tides found along the South American coast, from Cape Horn to Rio de la Plata, are derived from the tides of the Pacific Ocean, as is apparent from the chart of cotidal lines for the Atlantic Ocean. The range of tide is about thirty feet at the eastern end of Magellan Strait and less than two feet at Buenos Aires.
Dependent Stationary Wave
It has already been noted that a dependent stationary wave occupies the Bay of Bengal. Such waves are found in the following arms of the sea: The English Channel; the Irish Sea; the Adriatic Sea; the Gulf of St. Lawrence; the Gulf of Maine, including the Bay of Fundy; Long Island Sound; Bahia Grande; the Gulf of California; the Gulf of Georgia; and Norton Sound. These waves are accompanied by progressive waves, setting inwardly; and the effects of the deflecting force of the earth's rotation upon the moving waters are generally more or less apparent. As a consequence, nodal lines, such as characterize simple stationary waves, are more or less concealed in the bodies of water just mentioned.
Tides in the Vicinity of New York
Turning now to the chart of cotidal lines for New York Harbor and approaches (Fig. 8), several items may be noted:
The tidal hour changes rapidly along the southeastern coast of Nantucket Island. Here the range of tide is small. Over Cape Cod Bay the time of tide is simultaneous, and the mean range exceeds nine feet. Through Muskeget Channel the tidal hour changes rapidly and the currents are hydraulic in character; i. e., the flood and ebb are not oscillatory, but simply flow towards the body of water which is temporarily the lower. A similar remark is approximately true for Vineyard Sound. Over Buzzards Bay the tide is nearly simultaneous, indicating the stationary character of the tide wave. A similar remark is approximately true for Narragansett Bay.
The proposed Cape Cod Ship Canal will connect the waters of Cape Cod Bay at a locality where the average rise and fall of the tide is nearly ten feet with those of Buzzards Bay, where the average range scarcely exceeds four feet. The difference in level due to the tides will suffice to produce in this canal, a tidal current having an ordinary maximum velocity of three knots per hour.
In the eastern portion of Long Island Sound the time of tide changes rapidly and the range of tide is small. Over the greater portion of the Sound the tide is nearly simultaneous; and the mean range exceeds seven feet at the western end. The time and range of tide change rapidly through East River, and the tidal currents are hydraulic and strong. West of the northern end of Blackwells Island, the ordinary maximum velocity is five knots. Before the Hell Gate channel was cleared of reefs and submerged rocks, the currents were a source of much inconvenience and danger to all shipping passing through the East River. The time and range of tide change rapidly in Fire Island Inlet, and the tidal currents are hydraulic and strong. A similar remark is true for Barnegat Inlet. The tide in Raritan Bay consists chiefly of a stationary wave. The tidal currents in Arthur Kill and Kill van Kull are nearly hydraulic. The tide in the Hudson River consists chiefly of a progressive wave.
Attention has been called to these local details for the purpose of showing how varied the tidal phenomena may be within a comparatively limited region, and that detailed cotidal maps can be constructed with accuracy only after tidal observations have been made at a great number of points along the shores and upon the islands included in the area to be represented. The gauging of the tide away from land has seldom been undertaken; but there are indications that in the future such work will be carried out on an extensive scale.
Concluding Remarks
From the cotidal maps of the world, the reader can draw his own conclusions concerning the resemblance between the tides as they must approximately occur in nature and the hypothetical tides progressing westerly around the globe according to the popular conception of today and which, as we have seen, existed at the time when the Ptolemaic System held sway over the astronomy of medieval times. He will find no indications of tide waves having crests coincident with meridians and progressing westward at the rate of fifteen degrees of longitude per lunar hour. He will see that even a general westerly progression of the tide around the globe has no existence in fact.
The dictum of Aristotle, Pliny, Newton and others, that large tides are found in large seas, can be tested by means of these charts. The truth of this is manifest when the tides of the Mediterranean Sea are compared with those of the North Atlantic Ocean, but no such rule applies when the tides of the North Atlantic Ocean are compared with those of the Pacific Ocean and especially with those of the South Pacific Ocean.
The reader may ask. How does it happen that even rude approximations to the tides in nature have been so slow in their development? The answer is, Definite or applicable theories concerning the causes of existing tides were impossible before the depths of the oceans had become generally known. And so, before a few decades ago, tidal theories were developed with reference to certain assumed or hypothetical cases. This remark is no disparagement of the labors of such men as Newton, Laplace and Airy, and which compel the admiration of all persons interested in tidal matters. In fact, the comparative simplicity of the hypotheses upon which their theories were founded, placed tidal work squarely upon a scientific basis and enabled these intellectual giants to press their investigations a long way towards completion.
As to the construction of cotidal lines for the various oceans, it may be said that this implies, not only a rational approximate theory, but also a multitude of carefully-made tidal observations; such observations are, even to-day, either wanting or defective in many portions of the globe despite the efforts of individuals, expeditions, learned societies, institutions and governments.

