Popular Science Monthly/Volume 75/July 1909/Some Practical Aspects of Gyrostatic Action

by William Suddards Franklin

Layout 4

SOME PRACTICAL ASPECTS OF GYROSTATIC ACTION

By Professor W. S. FRANKLIN

LEHIGH UNIVERSITY

THE Brennan monorail car and the Schlick device for the prevention of rolling of ships at sea have recently attracted popular attention to the gyrostat, and gyrostatic action has recently become vitally interesting to a large group of men because an automobile-engine fly-wheel shows serious gyrostatic reactions when the automobile rounds a curve rapidly or rises suddenly upon a bump in the road. The following discussion will therefore be welcomed by many readers. Let no one imagine that gyrostatic action is mysterious and difficult to analyze; it is really quite simple^[1] and the discussion of Fig. 10 makes this action as clear, physically, as the simple inertia reaction of a heavily loaded wagon or boat. The formula for calculating the numerical value of the torque reaction of a gyrostat, as given at the end of this paper, is simple enough for any one to use.

The rotation of a wheel on an axis is called spin, and the axle upon which the wheel rotates is called the axle of spin. The spin of a wheel may be completely represented in both magnitude and 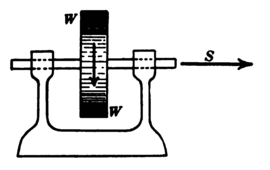Fig. 1. direction by an arrow drawn parallel to the axle of spin, pointing in the direction in which a right-handed screw would travel if turned with the spinning wheel, and having a length which represents the number of revolutions per second of the wheel. Thus, the arrow S^[2] Fig. 1, represents the spin of the wheel WW. Let the arrow S', Fig. 2, represent the spin of a body, imagine a large turning force to act upon the body for a short time, and let the arrow S" represent the spin which would be produced by the turning force if the body had been initially at rest. The actual resultant spin of the body will be represented in magnitude and in direction by the arrow R.^[3] That is to say, after the large turning force has acted for a short time the body will be found spinning about R as an axis, and the number of revolutions per second will be represented by the length of R. The geometrical relationship between the arrows S', S", and R is completely represented in the triangle OMN of Fig. 2, which triangle is shown by itself in Fig. 3.

A turning force is usually called a torque, thus the turning or

Fig. 2.

Fig. 3.

twisting force which is exerted upon a screw driver is a torque. A torque may be completely represented by an arrow drawn parallel to the axis of the torque, pointing in the direction in which a right-handed screw would travel if turned by the torque, and having a length which represents the magnitude or value Fl of the torque to scale. Thus the arrow T in Fig. 4 represents the torque due to the two forces FF.

The effect of an unbalanced torque upon a body is to produce a spin-velocity about the same axis as the torque, the amount produced

Fig. 4.

being proportional to the time the torque continues to act and inversely proportional to what is called the moment of inertia of the body, (a) The simplest case is where the axis of the torque is parallel to the axis of already existing spin as shown in Fig. 5, which represents a wheel and axle set spinning by pulling a cord which is wound around the axle. In this case the axle of spin remains stationary, and the magnitude of the spin increases steadily as long as the torque continues to act. (b) The general case is where the axis of the torque makes any angle whatever with the axis of the already existing spin. Thus, let the arrow S, Fig. 6, represent the already existing spin of a body, and let the arrow T represent a torque acting upon the body. Then the arrow ΔS represents the amount of spin produced by T during a short interval of time, and the diagonal arrow S' represents the actual spin of the body after the torque T has acted for a short interval of time.

(c) The case where the axis of torque is always at right angles to the axis of spin is the most important case, and this case is exemplified in the ordinary gyrostat, which is a wheel and axle supported in a

Fig. 5.

Fig. 6.

movable frame as shown in Fig. 7. By taking hold of the frame it is impossible to exert a torque upon the wheel except about an axis perpendicular to OS, friction at pivots being ignored. If the frame be suspended by a string as shown in Fig. 7 (side view), the pull of the earth combined with the pull of the string constitutes a torque as indicated by the arrow T in Fig. 7 (top view). The effect of this torque during a short interval of time is to produce a certain amount of spin, or spin-momentum, ΔS about T as an axis, and the resultant axis of spin

Fig. 7.

becomes S' as shown in the diagram Fig. 7. The unbalanced torque T, due to the weight of the wheel and frame in Fig. 7, causes the frame and wheel to sweep round and round in a horizontal plane about the supporting string as' an axis. This kind of motion of an axis of spin due to a torque which is at each instant at right angles to the axis of spin is called precession, and the axis PP, Fig. 7, about which the axis of spin rotates is called the axis of precession.

A familiar form of gyrostat is shown in Fig. 8. It consists of a spinning wheel mounted in a metal ring which rests on a pivot O. The pull of the earth on the wheel and ring produces an unbalanced torque about an axis which is at right angles to the axis of spin, and this torque causes the axis of spin to sweep around the pivot O as described in connection with Fig. 7. Precessional motion is illustrated

Fig. 8.

Fig. 9.

in the simplest kind of way by the ordinary top. Fig. 9 shows a top spinning about an inclined axis S. The weight of the top together with the reaction of the floor against the point of the top produces a torque the axis of which is at right angles to the plane of the paper

Fig. 10.

in Fig 9, and the effect of this torque is to cause the axis of spin to sweep around the vertical axis PP (the axis of precession).

The above discussion furnishes a sufficient basis for the consideration of the various practical aspects of gyrostatic action, but it is interesting to see how the precessional motion of the gyrostat in Fig. 8 (sweeping of axis of spin about a vertical axis through O) brings about inertia reactions of the various particles of the spinning wheel which keep the wheel from falling under the pull of gravity; it is only necessary to show that to produce precessional motion there must act upon the gyrostat-wheel an unbalanced torque (the torque due to the pull of gravity upon the overhanging frame and wheel in Fig. 8). Fig. 10 represents a disk spinning in the direction of the curved arrows (in the front view), the spin being represented by the straight arrow S in the side view. Imagine the axle of spin to sweep slowly

style="margin:0 auto 0 auto;font-size:85%;line-height:110%;text-align:center;font-variant:small-caps;border-collapse:collapse;background-color:transparent;" |width=220|Fig. 11. |width=220|Fig. 12. |}

around the vertical line CD in the direction of the curved arrows PP. This sweeping of the axle of spin about the line CD constitutes precessional motion, and CD is the axis of precession. Consider the front view of the spinning disk in Fig. 10; every particle in the upper half of the disk has a component of its velocity towards the right, and every particle in the lower half of the disk has a component of it» velocity towards the left. After a short interval of time the precessional motion moves the edge E of the disk forwards and the edge E' of the disk backwards in the figure, so that the velocity of every particle in the upper half of the disk is turned slightly backwards and the velocity of every particle in the lower half of the disk is turned slightly forwards, that is to say, every particle in the upper half of the disk has received a slight backward component of velocity and every particle in the lower half of the disk has received a slight forward component of velocity. Therefore, during the short interval of time, every particle of the upper half of the disk must have been gaining velocity backwards and every particle in the lower half of the disk must have been gaining velocity forwards, so that unbalanced forces must have been pushing backwards on every particle in the upper half of the disk and pulling forwards on every particle in the lower half of the disk, or, in other words, a torque must have been acting about the line EE' as an axis as shown by the two arrows FF in the side view.

 

Gyrostatic Action of the Fly-wheel of the Automobile Engine

Figs. 11 and 12 show top views of an automobile, the curved dotted arrows represent the turning of the automobile around a curve, and the

Fig. 13.

Fig. 14.

straight arrows S represent the spin of the fly-wheel shaft. The arrow S in the vector diagram of Fig. 11 or 12 represents the spin-momentum of the fly-wheel at a given instant, the arrow S' represents the spin-momentum at a later instant, ΔS represents the increment of spin-momentum, and the arrow T represents the torque which must act upon the fly-wheel shaft.

To produce this torque the bearing a must push upwards on the engine shaft and the bearing b must push downwards on the engine shaft, or, in other words, the engine shaft must push downwards on the bearing a and pull upwards on the bearing b, so that the gyrostatic reaction of the fly-wheel causes the outer wheels OO of the automobile to be pushed against the ground excessively as the automobile turns round a curve.

Figs. 11 and 12 represent the case in which the top of the spinning fly-wheel is moving forwards, and Figs. 13 and 14 represent the case in which the top of the spinning fly-wheel is moving backwards. In Figs. 13 and 14 the gyrostatic action of the fly-wheel causes the inner wheels II of the automobile to be forced against the ground excessively, as may be seen by studying the vector diagrams in Figs. 13 and 14.

Fig. 15.

Fig. 16.

Figs. 15 and 16 represent the case in which the fly-wheel shaft is parallel to the length of the car. In Fig. 15 the car is represented as turning to the right, the arrow S in the vector diagram represents the spin-momentum of the fly-wheel at a given instant, S' represents the spin-momentum at a later instant, ΔS represents the increment of spin-momentum, and T represents the torque which must act upon the fly-wheel shaft. To produce the torque T, the bearing a must push upwards upon the engine shaft and the bearing b must push downwards on the engine shaft, or, in other words, the engine shaft must push downwards on bearing a and upwards on bearing b. Therefore the front wheels FF of the automobile are pushed against the ground with excessive force by the gyrostatic reaction of the fly-wheel in Fig. 15. When the automobile is turning to the left, as shown in Fig. 16, the gyrostatic reaction of the fly-wheel causes the rear wheels BB of the automobile to be pushed against the ground with excessive force.

When an automobile runs over a bump in the road, no gyrostatic action is produced if the engine shaft is crosswise of the car, but very severe gyrostatic action may be produced if the engine shaft is fore and aft, as shown in Fig. 17. In the vector diagram of Fig. 17,

Fig. 17.

S represents the spin-momentum of the fly-wheel at a given instant, S'represents the spin-momentum at a later instant, ΔS represents the increment of spin-momentum, and the arrow T represents the torque which must act upon the fly-wheel shaft. In order to produce the torque T, the bearing a must push the front end of the engine axle to the left (with reference to the driver), and the bearing b must push the rear end of the engine axle to the right (with reference to the driver); or, in other words, the front end of the engine axle pushes to the right against the bearing a, and the rear end of the engine axle pushes to the left against the bearing b. Thus, there is a tendency for the front end of the car to be suddenly thrown to the right, when the car rises upon the bump, and the supporting springs of the car body are subjected to a skew action which is apt to break them.

There has been designed and placed upon the market an automobile in which the engine shaft is vertical. This obviates all gyrostatic action in the turning of curves, but it does not reduce the severe gyrostatic reactions when the car runs over a bump.

 

Gyrostatic Action on Board Ship

Fig. 18 is a top view of a side-wheel steamer which is represented as turning to the right as indicated by the curved dotted arrow. The arrow S in the vector diagram represents the spin-momentum of the paddle wheels and shaft at a given instant, S' represents the spin-momentum at a later instant, ΔS represents the increment of spin-momentum, and the arrow T represents the torque which must act upon the paddle-wheel shaft. To produce this torque the bearing a must push upwards on the crank shaft, and the Fig. 18. bearing b must push downwards on the crank shaft, or in other words, the crank shaft must push downwards on bearing a and upwards on bearing b, so that the gyrostatic reaction of the paddle wheels and crank shaft causes the boat to list, sinking the side OO of the boat deeper into the water as it turns round in the direction of the curved arrow in Fig. 18.

Fig. 19 is a side view of a boat driven by a steam turbine and propeller. The most serious gyrostatic action occurs in this case when the boat is pitching violently in a rough sea, and Fig. 19 is intended to represent the bow of the boat as rising as represented by the curved dotted arrow. Under these conditions the arrow S in the vector diagram represents the spin-momentum of the steam turbine and propeller shaft at a given instant, S' represents the spin-momentum at a later

Fig. 19.

instant, ΔS represents the increment of spin-momentum, and the arrow T represents the torque which must act on the propeller shaft. This torque is exerted upon the propeller shaft by the bearings as indicated by the arrows FF' in the top view, Fig. 20. The high speed and great weight of the rotating parts of a steam turbine represent a very great spin-momentum (arrows S and S' in Fig. 19

Fig. 20.

very long) so that the increment of spin-momentum ΔS which corresponds to a given angular movement of the ship is very considerable, and the torque T is great. Therefore the forces FF' in Fig. 20 may be very great. These forces are transmitted to the bearings of the propeller shaft through the hull of the vessel from the middle and forward parts of the vessel, and therefore excessive stresses may be brought into existence in the hull. It is supposed that the loss of the

Fig. 21.

British torpedo boat Viper several years ago in a rough sea was due to this action.

Figs. 21 and 22 represent the details of the gyrostatic action of a high-speed steam engine, such as is used for driving dynamos on board ship, the shaft of the engine being athwartship. In Fig. 21 the ship is represented as rolling in the direction of the curved dotted arrow, and T in the vector diagram represents the torque which must act upon the engine shaft. The details of this torque action are shown in Fig. where the arrows FF in the top view represent the forces with which the bearings must act upon the engine shaft to produce the torque T.

Fig. 22.

 

Gyrostatic Action of a Rolling Disk

Fig. 23 represents a penny rolling along a floor. The forces FF in the side view (the tendency of the penny to fall over) constitute a torque which is represented by the arrow T in the top view. This torque produces during a short interval of time an increment of spin-momentum

Fig. 23.

ΔS which, added to the existing spin-momentum S, gives the resultant spin-momentum S' in the direction of which the axis of the penny is found to be turned. The result is that the penny rolls along a circular path as represented by the dotted curve in the top view, Fig. 23. The wheels of a bicycle exhibit a gyrostatic reaction when the handle bar is turned, and although this gyrostatic action helps to maintain the equilibrium of the rider, it is very small in its effect as compared with the linear momentum of the rider and bicycle frame.

Fig. 24.

Fig. 24 is a top view of an axle and pair of drive wheels of a locomotive rounding a railway curve. The arrow S in the vector diagram represents the spin-momentum of the axle and drivers at a given instant, S' represents the spin-momentum at a later instant, ΔS represents the increment of spin-momentum, and T represents the torque which must act upon the axle because of its precession. To exert this torque the outer rail must push up with an excessive force against the outer driver, or, in other words, the outer driver must be forced downwards against the outer rail with more force than that which is due to the locomotive alone as it is rounding a curve. That is to say, the gyrostatic action of the drivers of a locomotive exaggerates the excess of pressure on the outer rail while the locomotive is rounding a curve.

 

Gyrostatic Action of the Boomerang

The most familiar type of boomerang is a pair of crossed sticks twisted very slightly at the ends like the vanes of a windmill. This type of boomerang, which we will call the propeller-wheel type, is essentially similar in its action to the boomerang of the native Australians. The boomerang is thrown through the air with a spinning motion about an axis at right angles to the plane of the crossed pair of sticks, and the peculiar flight of the boomerang is due to the forces exerted upon the boomerang by the air.

Forces are exerted upon the moving boomerang very much as if it were a disk traveling approximately edgewise through the air and forces are exerted upon the boomerang by virtue of its propeller-wheel shape and because of its combined spinning and edgewise motion. The effects of these two sets of forces will be described separately and their combined action will then be made use of in explaining the actual motion of the boomerang.

A disk moving approximately edgewise through the air is in an unstable condition, if the disk starts to glance to one side or the other the air exerts a turning force or torque upon it which tends to turn it with its side flat against the air. This may be shown by dropping a thin paper disk through the air or by blowing a blast of air against a disk which is pivoted about a diameter as an axis. Fig. 25 represents

Fig. 25.

a thin metal disk DD which is thrown in the direction of the arrow V and at the same time set spinning in the direction of the curved arrow S, the thrower standing at MM. Figs. 26 and 27 are top views

Fig. 26.

of the disk. Fig. 26 shows the disk starting to glance to the right (with reference to the thrower at M), and Fig. 27 shows the disk starting to glance to the left (with reference to the thrower at M). This glancing action of the disk causes the air to exert upon the

Fig. 27.

disk a torque about a vertical axis in Figs. 26 and 27, which torque is represented by the forces FF in Fig. 26 and by the forces F'F' in Fig. 27. This torque would turn the disk flatwise against the air if the disk were not spinning, but the effect of the torque on the spinning disk is to cause precession, the axis of spin of the disk in Figs. 26 and 27 turns towards the vertical, bringing the right-hand side (with reference to the thrower) of the disk in Fig. 26 upwards and bringing the left-hand side of the disk in Fig. 27 upwards.

Fig. 28 represents a propeller-wheel boomerang. In the following discussion the propeller is supposed to be right-handed, that is to say, if it were set spinning in the direction of the curved arrow S in Fig. 28, it would blow air towards the reader like a desk fan. Fig. 28 represents the boomerang as it leaves the hands of the thrower, who is supposed to be standing at MM, V being the direction in which the boomerang is thrown, and the curved arrow S representing the direction in which the boomerang is set spinning. The upper vane of the

Fig. 28.

boomerang in Fig. 28 is traveling forwards at a greater velocity than the lower vane, because the forward velocity of the upper vane is the velocity of forward motion of the boomerang plus a forward velocity Sr which is due to the spinning motion of the boomerang, whereas the forward velocity of the lower vane is the forward velocity of the boomerang minus Sr. Fig. 29 is a top view of the boomerang as it leaves the hand of the thrower at M, V is the velocity of forward motion of the boomerang, and the arrow S represents the spin of the boomerang. The arrow F represents the force with which the air pushes sidewise against the upper vane because of propeller action. A force pushes sidewise in the same 'direction on the lower vane because of propeller action, but the sidewise force on the upper vane is the greater because of the greater velocity of the upper vane. The inequality of these forces constitutes a torque upon the boomerang, and this torque is represented by the arrow T in Fig. 29. The effect of this torque during a short interval of time is to produce an increment of spin-momentum AS, and the addition of this increment of spin momentum to the previously existing spin-momentum S gives a resultant spin-momentum S'. That is to say, the effect of the torque T is to cause the axis of spin to sweep around in the direction of the curved dotted arrow.

Fig. 29.

Fig. 30 shows a view as seen from above of an actual flight of the boomerang. The boomerang leaves the thrower at M with its plane approximately vertical, and the effect of the torque T of Fig. 29 is to cause the axis of spin of the boomerang to sweep about a vertical axis as represented by the curved dotted arrow in Fig. 29, thus tending to make the boomerang glance around a circular horizontal path. At the same time the boomerang acts more or less like a disk as represented in Figs. 25 and 27, and this action slowly brings the axis of spin of the boomerang into a vertical position (plane of boomerang horizontal). As the plane of the boomerang comes into an approximately horizontal position toward the end of its circular flight, the torque which is produced by propeller action (see Figs. 28 and 29) produces precessional motion which tends to raise the forward edge a and lower the backward edge b of the boomerang, thus causing the boomerang to tend to glance upwards. This tendency of the boomerang to glance upwards is helped by the propeller action of the boomerang, that is to say, the boomerang, spinning in the direction of the arrows SS, Fig. 30, tends to climb upwards through the air. The result is that the curve of flight as shown in Fig. 30 is approximately a horizontal circle, the drooping of the curve of flight which would normally be produced by

Fig. 30.

gravity being counteracted by the tendency of the boomerang to glance upwards and the tendency of the boomerang to climb upwards as specified.

 

The Device of Otto Schlick for the Prevention of Rolling of Ships at Sea

Fig. 31 represents a spinning wheel hung upon a vertical axis from a hinge which permits the axis to swing to and fro in the plane of the keel of the ship (plane of paper in Fig. 31), the lower end of the axle being guided between two parallel bars. If the spin-momentum of the wheel were sufficiently great, all rolling motion of the ship could be eliminated, and the ship would heel over into a position for which the average heeling or rolling torque would be equal to zero; thus, the spin-momentum produced by an unbalanced torque T' would be completely absorbed by the precessional motion of the spinning wheel as its axis of spin turns in the direction of the curved dotted arrow P', and the spin-momentum produced by an unbalanced torque T" would

Fig. 31.

be completely absorbed by the precessional motion of the spinning wheel as its axis of spin turns in the direction of the curved dotted arrow P".

Fig. 32.

To completely hinder the rolling motion of a ship in this way would require the use of a very large wheel rotating at high speed. Thus a rolling torque (T' or T" in Fig. 31) equivalent to 200 tons placed 10 feet to one side of the axis of the ship and continuing for only one tenth of a second would represent the whole amount of spin-momentum contained in a solid steel disk 2 feet thick, 10 feet in diameter and rotating at a speed of 144 revolutions per minute; and therefore this amount of rolling torque continued for one tenth of a second would bring the axle of such a wheel into a horizontal position so that any further continuation of the torque would cause the ship to roll.

The rolling motion of a ship, however, is largely an oscillatory motion which is slowly built up by a succession of waves in synchronism with the proper period of rolling motion, and excessive rolling may therefore be prevented by an action which tends to hinder the oscillations by friction. A very considerable amount of frictional damping may be produced by a moderately small gyrostat arranged as shown in Pig. 32 (plane of paper in Pig. 32 is a vertical plane containing the keel of the ship). In this case the rolling motion of the ship causes the pendant wheel and axle to oscillate to and fro in the plane of the keel, and these oscillations are hindered by the motion of a piston in a dash-pot as indicated in the figure.

 

The Brennan Monorail Car

Before discussing the Brennan gyrostatic mechanism for maintaining the equilibrium of a monorail car, let us consider the action of the apparatus shown in Figs. 33 to 36, a gyrostat wheel mounted in a frame aa which in turn is pivoted in a larger frame BB, the whole

Fig. 33.

Fig. 34.

being supported upon two legs, one behind the other, as seen in the figures. Standing in the position shown in Fig. 33, the framework is acted upon by the unbalanced pull of the earth which produces a torque; the spin-momentum which is continually produced by this torque is absorbed by a precessional motion P of the gyrostat wheel as it turns from the position shown in Fig. 33 to the position shown in Fig. 34, and the reaction of this precessional motion produces the two forces FF, Fig. 33, which keep the frame from falling over. When the gyrostat wheel reaches the position shown in Fig. 34, however, the precession ceases and the frame-structure falls over. Standing in the position shown in Fig. 35, the framework is acted upon by the unbalanced pull of the earth, which produces a torque, the spin momentum which is continually produced by this torque is absorbed by the precessional motion P' of the gyrostat wheel as it turns from the position shown in Fig. 35 to the position shown in Fig. 36, and the reaction of this precessional motion produces the two forces F'F', Fig. 35, which keep the frame from falling over. When the gyrostat

Fig. 35.

Fig. 36.

wheel reaches the position shown in Fig. 36, however, the precession ceases and the frame-structure falls over. Suppose the handle h in Figs. 33 and 34 to be forcibly turned in the direction of the precessional motion P. This hastened precession causes the reactions FF to be more than enough to hold the inclined frame in position, and the result is to bring the frame into a vertical position, or, if the precession is hastened sufficiently, to throw the frame-structure over into the reverse position as shown in Fig. 35, thus starting the reversed precession P'. This hastened precession is the essential feature of the Brennan gyrostatic mechanism and it is brought about automatically as explained in the following discussion.

The essential features of the Brennan mechanism are shown in Fig. 37. The car body BB' supports a rocker-axle which is parallel to the rail or rope W upon which the car stands. A steel frame FFFF is supported upon the rocker-axle O, and the two gyrostat wheels are carried in two smaller frames ff and f'f' which are free to turn about the precession axles P and P'. The axles of spin of the gyrostat wheels are ss and s's', and these axles project as shown at A and A'. The two gyrostat wheels spin in the direction of motion of the hands of a clock as seen from the outer ends of the axles of spin A and A', respectively. The precession axles P and P' are geared together by sectors of gear wheels G and G'. The frame FFFF is hindered from turning about the rocker-axis by the tables H, L, H' and L'; the tables H and L' extend backwards from the plane of the paper, and the tables L and H' extend forwards from the plane of the paper.

Fig. 37.

The action of this mechanism is as follows: Suppose side B' of the car body to be the heavier. The pull of gravity on this heavier side produces spin-momentum about the rail W as an axis, and this spin momentum is absorbed by the precessional motion of the gyrostat wheels, causing both ends of the axles of spin A and A' to move away from the reader in the figure. The unbalanced car, however, in tending to tip over (side B' overloaded), brings the projecting axle A into contact with the table H, the rolling action of the axle A upon the table H hastens the precessional motion, and this hastened precession raises the side B' and lowers the side B of the car-frame, as explained in connection with Figs. 33 to 36. This action continues until side B is heavier than side B′, when the reversed unbalanced condition of the car body causes a reversed precessional movement of the gyrostat wheels. This reversed precession continues steadily and unhastened so long as the heavy side B is balanced by the contact of the idle wheel i′ with the table L′, that is, until the projecting ends of the axles of spin A and A′ are brought forwards (in the figure) into the plane of the paper. Then the continuation of the reversed precession brings the axle A′ upon the table H′, the reversed precessional motion is then hastened, and this hastened precession raises the side B and lowers the side B′ of the car-frame, thus bringing the car-frame into its initial unbalanced condition (side B′ heavier than side B). The above-described action is then repeated, and so on.

The stability of the Brennan car is due to the hastened precession which is caused by rolling action of one or the other of the projecting axles of spin upon the tables H and H′, while the axles of spin are departing from a line at right angles to the length of the car, and to the steady and unhastened precession, while the axles of spin are moving towards a line at right angles to the length of the car. The hastened precession on the one hand quickly alters the condition of balance of the car so as to limit the departure of the axles of spin from a line at right angles to the length of the car, and the steady and unhastened precession, on the other hand, insures the complete return of the axles of spin to a line at right angles to the length of the car.

The hastened precession is accomplished with great friction losses by the rolling axles A and A′ in Fig. 37, and it is reported that Brennan is working upon an automatic motor-driven mechanism to produce the hastened precession without exhausting the energy of the gyrostat wheels.

Two devices like Fig. 37 with their rocker-axles at right angles to each other would hold a one-legged body in equilibrium; indeed, such a double mechanism would make it possible to use a one-wheeled car, but the wheel would have to have a deep double flange to make it roll along a rope or rail. Such a one-wheeled car, a sort of hyper-wheelbarrow car, would be of no value for practical use, and, indeed, most of us believe that Brennan's two-wheeled car is nothing more than a scientific toy.

 

Calculation of Torque-Reaction Due to Precession

Let n be the revolutions per second of a spinning wheel, P the revolutions per second (or the fraction of a revolution per second) of the axis of spin due to the precession, and K the moment of inertia of the spinning wheel in pound $\times$ feet squared. Then the torque reaction is equal to $\scriptstyle 4\pi ^{2}nPK$ poundal-feet or $\scriptstyle {\frac {1}{2}}\pi ^{2}nPK$ pound-feet.^[4]

1. When the angular velocity of precession is small as compared with the velocity of spin and when the gyrostat wheel is symmetrical with respect to its axis of spin.
2. To appreciate the geometrical meaning of the arrows S, ΔS and T in the vector diagrams given in this paper, the reader should thrust his hand in the direction of the arrow head and move the hand as if turning a right-handed screw.
3. This proposition is entirely correct if by spin we understand that spin momentum is meant; the spin-velocity of a body is sometimes greatly complicated by its lack of symmetry, and these complications are ignored in the present discussion.
4. See Franklin and MacNutt'a "Elements of Mechanics," p. 150.