Popular Science Monthly/Volume 78/April 1911/The Genesis of the Law of Gravity
THE
POPULAR SCIENCE
MONTHLY
APRIL, 1911
| THE GENESIS OF THE LAW OF GRAVITY |
By Professor JOHN C. SHEDD
OLIVET COLLEGE, OLIVET, MICH.
SINCE the earliest ages man has been interested in the world outside of himself. Thunderstorms, waterfalls, winds, waves, fire, the starry heavens have aroused his wonder, admiration or fear.
During the earlier stages of racial development the simplest phenomenon was explained by reference to some arbitrary power, and soon gods and demigods were conceived of as presiding over the agencies of nature. Later men who had wrested some of her secrets from nature or had won some victory over her were exalted to the position of heroes and worshipped, while their exploits, greatly magnified, became part of the legendary history of the race. Slowly man began to realize that there is a constancy about nature that may be expressed in general statements. These statements were often vaguely expressed as, "Nature abhors a vacuum," "Water and fire are antagonistic," "There are three elements, earth, air and water" or "earth, fire and water." These crude beginnings led to more careful and more systematic study of nature, and to more exact statements of what we now call the laws of nature.
It took long ages—perhaps we have not even yet reached the goal—for man to realize that the content of his study is here objective, so that the method of study must be inductive and not deductive. This being the case, the conclusions arrived at must be allowed to shape themselves regardless of consequences to antecedent beliefs. Thus it happened that the study of nature has been for ages hampered by many a prejudice and by many a "Thou shalt not" from churchman and philosopher.
Another and perhaps greater impediment than the inertia of the human mind was the ravage wrought by war and time. Could each age have the full benefit of all preceding ages, could man in very truth be "the heir of all the ages," there would be no lost arts and the world would not have to learn over and over again lessons once mastered.
A last impediment may be mentioned, peculiar perhaps to problems "like the discovery of the law under discussion. It is hard for a worker in any field not to attempt to reach forward to the final solution of his problem. This is true even if the data for generalization be most meager. Thus it has happened time after time that ill-formed theories have been advanced even by great minds. Indeed the very greatness of the man whose name the theory bears proves an added obstacle. Thus the dicta of Aristotle held sway for centuries and even Galileo's brilliant experiments at the leaning tower of Pisa could scarce overcome the false Aristotelian theory of falling bodies. Another example is Newton's theory of light which survived at least a hundred years, simply because it was Newton's,
We shall in the present paper seek to trace the history of the problem which found its final answer in Newton's Law of Universal Gravitation. This law may be stated in the following familiar terms: "Every particle of matter attracts every other particle of matter with a force proportional to the mass of each and to the inverse square of the distance between them."
In tracing the history of how the race came into a clear knowledge of this law we find two streams with their headwaters far back in history, slowly gathering volume age by age and finally uniting and bearing the world on to the long-sought-for goal. The first of these streams may be called the study of pure motion, or of kinematics, the second the study of the causes of motion, or of dynamics. The first is best illustrated by the history of astronomy as developed down to the seventeenth century, while the second is best illustrated by the history of mechanics during the same period.
In astronomy we shall pay attention only to those persons whose work has a bearing upon the present problem. The first name of worth seems to be that of Thales of Miletus (640-546 B.C.). With remarkable clearness he maintained the sphericity of the earth, the present theory of lunar eclipses, and the correct view regarding the source of the light received from the earth's satellite. He also suggested that the stars may be regarded as being of the same material as the earth. Thales was followed by his disciple, Anaximander (611-547), who was the first of the ancients to view the heavens with the eye of a philosopher. His name should be immortal, for it was he who first suggested that the earth moves about the sun as a center, a doctrine which became one of the tenets of the Ionian school.
Perhaps rapid progress might have been made in the explanation by natural causes of the phenomena of the heavens, but soon the jealous ire of the Athenians was aroused in behalf of their gods. As a result, history would have claimed the first martyr to scientific truth in the person of Anaxagoras (500-428), had not the great Pericles interposed in his behalf. Even so, the death penalty was but exchanged for that of banishment.
Another disciple of Thales was the illustrious Pythagoras (578-400), who not only held the views of his master, but, from observations on the altitude of the stars, measured in different places, demonstrated that the earth was round, or, at least, not flat. He conceived Venus to be both the morning and evening star—a view lost sight of, later, as shown by the double name, Lucifer and Hesperus, long applied to this planet. Most remarkable, perhaps, was his doctrine of the diurnal rotation of the earth and its annual motion about the sun. Less substantial, but longer-lived, was his fanciful notion of the harmony of the spheres. He conceived each planet as held in place by being fixed in a celestial crystalline sphere which, in its rotation about the sun as center, carried the planet with it. Having observed that the planets move at different rates, it followed that the various spheres had different rates of rotation, and Pythagoras believed that some law controlled their motions. This he expressed by supposing that each sphere emitted sounds or notes like the strings of a harp, and the harmony was expressed by the belief that the several notes united in a beautiful celestial harmony of most exquisite music. More fantastic than suggestive, yet here in the far-away dawn of scientific history is the foreshadowing of the great thought which two millenniums later was given in Newton's universal law of gravitation.
The fate of Anaxagoras warned Pythagoras against being too overt in his public teaching, so that much that he taught was under the seal of secrecy. He also sought greater freedom by removing from Samos to Italy.
It might be expected that with so much to build upon the genius of Aristotle (384-322) would have accomplished great things in astronomical science. But not so! For some reason he rejected the theories of Pythagoras and, although he is said to have come into possession of great stores of Chaldean observations, on the capture of Babylon by Alexander the Great, he made no use of them. Perhaps the task of
mastering these treasures was too great, perhaps his studies in anatomy and metaphysics prevented, but be that as it may, it must be acknowledged that his few pronouncements on physical science were for the most part erroneous and proved hindrances and not helps to those who followed him.
With the founding of the schools of Alexandria in the palmy days of the Ptolemys astronomy became a science. It was during this period that simultaneous measurements were made upon the altitude of the sun at Alexandria and Syene. At the latter place the sun at the summer solstice was on the zenith and at the former place 7° 12' therefrom. From this and the known distance between stations the circumference of the earth was calculated as 250,000 stadia or 28,000 miles. This measurement was first made by Eratosthenes (276396) and places him in the first rank in the Hall of Fame.
The centuries immediately preceding and following the beginning of the Christian era mark the rise both of astronomy and of geometry. It was probably due to progress in the latter science that Hipparchus (190-120 B.C.) and, later, Ptolemy (A.D. 120-170), were led to propound the system that still bears their names. This was a far more ambitious system than any that had preceded it, and sought, for the first time perhaps, to describe the exact path of the heavenly bodies. From our vantage point of wider knowledge it is easy to see its absurdities. Hasty judgment, however, must not be passed either upon its founders or upon the system itself.
In the first place, it was based upon observations; in other words, it was a generalization from data.
Secondly, it satisfactorily explained the observations contained in the premises.
Thirdly, it made possible the forecasting of eclipses.
The characteristics of the system may be given as follows:
1. The earth is a globe set immovable at the center of the celestial sphere—which sphere carries the fixed stars and revolves once per day.
2. The size of the earth is insignificant in comparison with that of the celestial sphere.
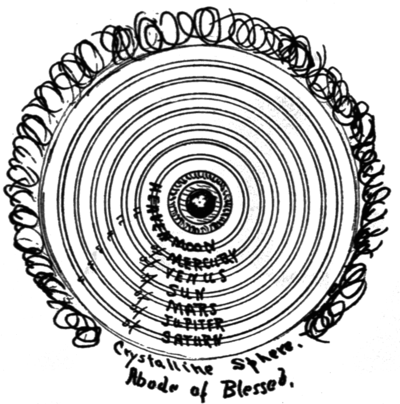
3. Seven planets revolve around the earth in the following order—the moon, Mercury, Venus, the Sun, Mars, Jupiter, Saturn.
4. The moon and sun move in excentric circles, the rest in epicycles. Of the several considerations that must have induced the Alexandrian school to adopt this system we may note:
I. The Pythagorean system called for a moving earth, the Ptolemaic did not.
II. The observed motions of the planets were explained by the Ptolemaic system, and, while it is true that the Pythagorean system was capable of this also, it does not appear that the test by actual calculation had been made.
III. The system seemed adequate, was geocentric and appealed to the popular imagination.
Some of the more obvious criticisms of the system may be mentioned:
I. The ancients believed the sun to be larger than the earth—it would be more likely to be the center of the system.
II. The diurnal motion of the earth offered a simple explanation of the apparent motion of the heavens—the simple should prevail when opposed to the complex.
III. The Pythagorean system gave the same law of motion (the circle) to all the members of the system, while in the Ptolemaic system the moon and sun moved in circles and the rest in epicycles.
The cumbersome Ptolemaic system, having been adopted, became with the passage of time deeply rooted in the philosophy and religion of the race. Its complexity became greater and greater, for with more accurate observations came the necessity of adding "cycle on epicycle, orb on orb" to keep track of the required corrections. It is not surprising, therefore, to find Alphonso X., in the thirteenth century, when contemplating the system, exclaiming, "if the Deity had called him to His councils at the creation of the world, he could have given Him good advice." Indeed the system finally crumbled and fell from the very weight of its superstructure.
"We have spoken of the ravages of time and of war as hindering the progress of knowledge. We have now to note the greatest calamity that has in modern history overtaken the cause of human knowledge. In the third century before Christ, was founded the Alexandrian library with its treasures of art, of literature and of science collected from every part of the known world. Century by century it grew, and could it have survived what untold treasures would have been ours to-day! But in the seventh century a.d. the Caliph Omar in a day reduced to ashes this storehouse of wisdom, and by one act set the world back a thousand years. Perhaps this disaster can be overrated; perhaps, in the dissemination of copies of the old masters, the Alexandrian library had done its real work; but to me it seems otherwise; for many a priceless gem of literature and of science must have perished in the wanton Arab's destruction. As a single example, it is doubtless due to this cause that we have none of the astronomical writings of Hipparchus.
To Alphonso X., of Castile, belongs the honor of being the first European monarch to foster astronomy. In the thirteenth century he founded a college in Toledo, and gathered together savants from all parts of his realm. From the Arabs they acquired much both in mathematics and in astronomy. Original sources were also sought out in the Greek. Other schools were rapidly established and centers of scientific culture formed. Among the notable workers and thinkers of the thirteenth and fourteenth centuries were Roger Bacon (1214-1292) in Cambridge and Paris, John Müller of Königsberg (1436-1476), and Leonardo da Vinci (1452-1519), the artist philosopher of Florence. In the early part of the sixteenth century the illustrious Copernicus appears (1473-1543). Copernicus, or Copernic, had a keen mind and a firm belief in what may be called the simplicity of nature. On examining the Ptolemaic system he was embarrassed by its epicycles and excentrics, producing, as they did, complexity where he believed there should be simplicity. He, therefore, turned with relief to the ancient ideas of Pythagoras, and of his system he says:
Under the hand of Copernic this system was elaborated and shaped 80 as to acquire a dignity equal to that of the older system, and, but for the retarding hand of superstition and bigotry, the dawning day might have rapidly advanced.
As it was, Copernic, fearful perhaps of the fate of Roger Bacon, taught in private a few select pupils, and only on his death bed did he see his printed work (1543). Copernic's sudden death was all that saved him from the hands of his enemies. As it was, his book was soon proscribed and his theory placed under the ban of the church.
With the printing of Copernic's work the battle between the geocentric and helio-centric hypotheses may be said to have been fairly joined. Copernic himself foresaw the coming conflict. He also saw
that the real conflict would be, not with astronomers, but with churchmen. In the dedication of his book he says:
Sir Oliver Lodge, in summing up the life-work of this pioneer of science, says:
Mr. E, J. C. Morton in a biography of Copernic says:
Kopernicus can not be said to have flooded with light the dark places of nature—in the way that one stupendous mind subsequently did—but still, as we look back through the long vista of the history of science, the dim, Titanic figure of the old monk seems to rear itself out of the dull flats around it, pierces with its head the mists that overshadow them, and catches the first gleam of the rising sun,
". . . like some iron peak, by the Creator
Fired with the red glow of the rushing morn."
It is not to be supposed that there were not weighty objections to be urged against the Copernican system. Of these three may be noted:
1. If it be true that the earth moves, why do not the configurations of the stars change with the changing seasons? It is evident that the grouping of the stars depends upon the distance of the earth from them, and if the earth moves the groups of stars in front of the earth's motion should appear to open out while those behind should appear to close up. We now know the correct answer, that is, that the 184 millions of miles making up the diameter of the earth's orbit is lost in the immensity of stellar space and its effect can only be detected by the most refined of modern methods,
2. If the earth moves about the sun. Mercury and Venus should show phases as does the moon.
The only answer Copernicus could make was that, wore the powers of man's eyesight sufficiently increased, this would doubtless be found to be the case. Seventy years later, Galileo furnished the required proof.
Before looking so far ahead, two important workers must be noted. The first of these is the Danish astronomer, Tycho Brahé (1545-1601), who is well called the father of instrumental astronomy. His aid in the solution of the present problem did not consist in the advocacy of the Copernican system—for he rejected it—but in his patient, faithful gathering of data. His tables of planetary motions and his star tables were the most extensive and the most accurate of his time. Even when judged by the standards of to-day they are to be viewed with respect. When we remember that the telescope and microscope were then unknown, respect rises to admiration and wonder. So careful was he that not a single mistake due to carelessness has ever been detected in his work.
From 1576 to 1597 Tycho Brahé worked in his well-equipped observatory at Uraniburg on the island of Huen. For twenty years this temple of science was the greatest center of its sort in Europe. Philosophers, statesmen and even kings visited him in his island home. Year by year the great tables of observations grew until further additions seemed but repetitions of oft-told tales. Indeed, the tables grew beyond the ability of their maker to interpret, and some keener mind was needed to unfold their hidden meaning. The possessor of such a mind was even then living in Austria in the person of John Kepler.
John Kepler was born and reared in poverty, and all his life had to struggle to keep actual want from the door. There could scarcely be a greater contrast than that presented by these two men: Brahé, the favored son of fortune, possessing all that wealth and princely favor could procure, acknowledged as the foremost philosopher of his day; Kepler, with nothing to commend him to notice save a passion for knowledge and longing to learn the hidden meaning of equations and formulae and mystic numbers. The common bond between them was the love of the truth and the capacity for taking infinite pains. For the progress of the race each of these men needed the other, and dame fortune's immediate problem was the bringing them together.
By so doing it would be possible for Brahé to pass on to Kepler the completion of his own work, and at the same time train him for an even greater task.
In 1590 James I., of England, visited Denmark and spent eight days with Tycho and his wonderful instruments. On leaving he presented the astronomer with various gifts, and among these was a pet dog of which the astronomer became very fond. Now this canine became the innocent cause of much trouble to his master, for it seems that one day the chancellor of Denmark brutally kicked the poor beast. This was too much for Tycho's temper—never very even—and he roundly berated the chancellor for his cruelty. Of course there is more to the story than just this, but at all events Tycho made a powerful enemy. who, after the death of the king, stripped the astronomer of all his estates and drove him penniless from the kingdom. For two years he was without a home, but in 1599 found refuge and a pension with Emperor Rudolph II., of Bohemia. Becoming established in Prague, he set up his instruments, and soon students flocked to him again. Among them came the poor youth, Kepler, who soon made himself invaluable to his master. In return, Tycho was kind to Kepler, and together they labored until the former's death in 1601.
With the advent of Kepler (1571-1630) the real problem of gravity together with its solution took definite form. Always a firm believer in the unity and simplicity of the solar system, Kepler rejected the teaching of Tycho Brahé and adopted Copernicus's scheme in toto. Next, he set about bringing order out of the mass of observations accumulated (for the most part) by Brahé. He took infinite pains, testing by actual calculation every hypothesis or rule that he could think of. For example, he tried circular orbits with constant velocities for the planets and the sun at the center. Finding that this did not fit the facts, he placed the sun a little off center and tried again, but the theory did not yet fit the observed facts. "After incredible labor, through innumerable wrong guesses, and six years of almost incessant calculation" the truth began to dawn upon him, until he was able to enunciate three laws which have since gone by his name. The first of these to yield itself to his zeal was the so-called second law which gives the rule governing the velocity of the planet in its orbit.
Law II., The radius vector sweeps out equal areas in equal times. Having determined, as he believed, the law of speed, he next inquired into the exact shape of the orbit. Here "however, the geometrical and mathematical difficulties of calculation threatened to become overwhelming," and as the days dragged into months he had every reason to become disheartened. By day he worked, by night he dreamed of his problem, and it is said that the hint which led to its solution came to him as he slept and awoke him. Arising at once, he lighted his lamp and set to work anew at his calculations. Step by step he progressed, and finally, in a paroxysm of delight, he proved what is now known as Kepler's first law.
Law I., The planets move in ellipses with the sun at one focus. To these two laws Kepler nine years later in 1618 added a third.
Law III., The square of the time of revolution of each planet is proportional to the cube of its mean distance from the sun.
In these three statements Kepler brought order out of chaos and reduced to system a heterogeneous mass of observations and records. When we remember that these laws of Kepler's furnished Newton not only a point of departure, but also gave him a criterion by which to test his results, we begin to see that without Kepler, Newton might not have been possible. Lodge says of him:
A man of keen imagination, indomitable perseverance and uncompromising love of truth, Kepler overcame ill-health, poverty and misfortune, and placed himself in the very highest rank of scientific men. His laws so extraordinarily discovered introduced order and simplicity into what else would have been a chaos of detailed observations; and they served as a secure basis for the splendid erection made on them by Newton.
While Kepler was laying the enduring foundations of the Copernican theory, Galileo (1564-1642), was carrying on an open propaganda in Italy. In 1609 he perfected the telescope, and with it, night by night, questioned the heavens. The mountains on the moon, the satellites of Jupiter, sun-spots, the strange appearance of Saturn due to its rings, the changing phases of Venus, were discoveries rapidly announced to an astonished public. Some of the discoveries, such as those relating to Saturn and Venus, were of such an astonishing and revolutionary nature that Galileo first published them in the form of anagrams. The one announcing the phases of Venus, when deciphered, reads as follows: "Cynthiæ Figuras Æmulatur Mater Amonun." Freely translated: "Venus emulates the phases of the moon." The immediate result of Galileo's brilliant work was to convince all unbiased minds of the truth and to array the church in solid phalanx against both him and his system. Of Galileo personally we have not time to speak—suffice it to say that he was made to suffer most cruelly for his beliefs.
In the year he died (1642) was born—on Christmas Day—the man
who was destined to establish forever the truths for which so many had toiled and suffered before him.
We have tried to follow one of the lines of succession leading up to Newton, giving, as it were, his pedigree upon the side of astronomy. It is a noble line: Pythagoras, Eratosthenes, Hipparchus, Ptolemy, Copernicus, Brahé, Kepler, Galileo, with many lesser names unmentioned. There is another line of succession to be traced, and to this I invite your attention for a brief moment—for I have kept you all too long from the main theme of the paper.
In the study of mechanics as in the study of astronomy we must begin with the Greeks. Thus, we find Aristotle attempting to teach the law of falling bodies, and also giving the reason why heavy bodies sink while light ones arise. All his statements relating to mechanics are erroneous and some are positively childish.
The first real student of mechanics was Archimedes (287-312 B.C.) To him we owe the foundations of the science. For example, to him we owe the theory of the lever, from which he developed the idea of the center of gravity. He was especially interested in the subject of hydrostatics, and established principles that are of universal application to-day. His practical applications are best illustrated in the engines of war which he devised to aid in the defense of Syracuse. So effective were these that the Romans took the city not by assault but by starvation. For fifteen hundred years thereafter practically no advance was made. In 1462 the Turks took Constantinople, and fugitive Greeks
carried Greek manuscripts westward to Europe. These stray documents gave a fresh impetus to science as they did to letters. The first one really to grasp the subject of mechanics and develop it was Galileo (1564-1642). To him we owe the true theory of falling bodies, the law of the pendulum, the theory of projectiles and two of the three great laws of motion, which were put into their final form by Newton himself.
Two stories about Galileo will serve to show what manner of man he was and also to illustrate his methods. In 1583, while worshipping in the cathedral in Pisa, he chanced to notice the swaying of the great chandelier, the lamps of which had been freshly lighted. From watching its stately vibration he fell to timing it, using as a standard his pulse-beat. Thus there dawned upon him one of the laws of the pendulum—that the time of vibration is independent of the arc of motion. How many thousands of times had that same chandelier been observed swinging to and fro, and yet it had awaited the coming of Galileo to read its inner meaning!
On the question of falling bodies Galileo ran counter to Aristotle. That philosopher had taught that bodies in falling acquire velocity in proportion to their weight. Galileo found by a simple but careful study that all bodies acquire the same velocity in falling. With the imprudence of youth he forthwith proclaimed the errors of Aristotle from the house-tops, much to the scandal of his classical friends. In answer to their protests he proposed an experiment, and this experiment was made. The faculty of the University of Pisa together with the interested or curious of the city gathered at the leaning tower—"Pisa's leaning miracle," as Whittier calls it. From the top and at the overhanging side Galileo let fall a one-pound and a one-hundred-pound shot. The two shot started, fell—and struck the ground together. As Lodge exclaims, "The simultaneous clang of those two weights sounded the death-knell of the old system of philosophy and heralded the birth of the new." And yet, it is recorded that while some saw, and were convinced, others—nor is their race extinct to-day—saw, but, consulting their copies of Aristotle, disbelieved.
Following in Galileo's foot-steps—perhaps more cautiously lest he be made to suffer for it—Huygens (1629-1699) further developed and extended the science of mechanics. In particular may be noted his development of the theory of circular motion; the invention, or at least perfection, of the pendulum clock, and this determination of the acceleration of gravity from pendulum observations, a method which is to-day the most accurate one in use. Huygens shares with Galileo all the honors due a scholar and original worker of the first rank. They resemble each other in character, in method and in the great value of their labors.
As bearing upon the law of gravitation the theory of circular motion was of the very greatest value. Without it, Newton must either have failed in his task or have discovered these principles for himself. As a matter of fact he did the latter. Huygens was also the first to grasp the significance of the following occurrence. In 1671 Jean Richter, in the course of astronomical work, carried a pendulum clock from Paris to Cayenne in South America. The clock kept correct time in Paris, but at the latter station it daily fell two and a half minutes behind mean solar time. The pendulum was shortened to correct it, but on returning to Paris it was found to gain time at the same rate that it had before lost it. Huygens at once correctly explained this as due to the rotation of the earth on its axis; thus furnishing the first experimental evidence of the earth's rotation.
The span of Galileo's life was from 1664 to 1642. He died discredited by his church, deprived of his liberty and afflicted with blindness. His enemies thought that they had vanquished him and his ideas. They even attempted to blot out his memory from among men by refusing to allow his grave to be marked. How little they knew! Already through Huygens the new knowledge had made great advances; and in the very year of Galileo's death was born the man whose mighty intellect was to flood with light the dark places of nature and to carry Galileo's work to a proud completion.
The year 1660 was in England an important year for science. This is the year of the founding of the Royal Society, and in the same year Isaac Newton, a young man of eighteen, entered the University of Cambridge from the town of Woolsthorpe in Lincolnshire. In 1663 the society received a royal charter, and some time after King Charles is said to have sent it a weighty problem with which to test its powers. "Why is it," said the king, "that the same fish weighs less when alive and swimming in a pan of water, than when dead and floating on its surface?" There must have been rapid improvement in the caliber of its meetings, for in 1665 its members are listening to Robert Boyle's brilliant papers on the air-pump and the barometer.
In the meantime, Isaac Newton, destined for twenty-five years to be president of the society, was pursuing his studies at Cambridge and in 1665 was given the A.B. degree. This and the following year were the years of the great plague. For a time the Royal Society took refuge in Oxford, while the University at Cambridge was, in the fall of 1666 "sent down," the students and faculty scattering to escape contagion.
Newton returned home, his mind teeming with new ideas and hard problems. He had already mastered the most advanced scientific works of his time—Kepler's "Optics," Descartes's "Analytical Geometry" and Wallis's "Arithmetica Infinitorum." In reading, Newton was in the habit of noting what seemed to him capable of improvement. At this time (1666) he had already projected experiments in optics which were to be the first of his achievements to make him known to the world. In mathematics he had originated the binomial theorem and had laid the foundations of the infinitesimal calculus. Armed with this new weapon of analysis, Newton pushed his mathematical researches in many directions, solving with ease problems that had so far baffled attack. Whatever he touched turned to gold under his hand. So rapidly did his mind work that he seems not to have needed to work out each step in detail; his printed papers sometimes read like a list of answers to difficult propositions. For example, he presents a classification of cubic curves, giving seventy classes in all. Yet in all this list there is no suggestion of the process by which the results were obtained. Among the books that Newton read was Galileo's "Dialogues on Motion," and here as elsewhere he found abundant material for work. In this field of mechanics his mind worked with its usual clearness and rapidity. He restated the laws of motion in such clear and simple terms that for two and a half centuries no word or line has been changed. Bringing to bear his new calculus he readily solved the problem of falling bodies, and in 1666 discovered the laws of circular motion, seven years before they were published by Huygens in 1673.
To such a wide reader and deep thinker as Newton, the problem of "gravity" would appeal with keen interest. It would have been but natural that he should have gathered together all that was available of the literature of the subject. Thus he was familiar with Kepler's views expressed in the following citation:
The true theory of gravity is founded on the following axioms. Gravity is a mutual affection between cognate bodies toward union or conjunction, similar to the magnetic virtue. . . . If the moon and the earth were not retained in their orbits by their animal force or some other equivalent, the earth would mount to the moon by a fifty-fourth part of their distance from each other, and the moon would fall toward the earth through the other fifty-three parts, that is, assuming that the substance of the earth is of the same density. . ., The sphere of the attractive virtue which is in the moon extends to the earth and entices up the waters, but as the moon flies rapidly across the zenith and the waters can not follow so quickly, a flow of the ocean is occasioned toward the westward. If the attractive virtue of the moon extends to the earth, it follows, with greater reason, that the attractive virtue of the earth extends to the moon and much farther, and, in short, nothing which consists of earthy substance, however constituted, although thrown up to any height, can ever escape the powerful operation of this attractive virtue.
Borelli (1608-1679) also expresses views no less explicit, and, in his work, "On the Satellites of Jupiter," distinctly attributes the revolutions of the heavenly bodies to the force of gravity. So also Bullialdus wrote "that all force respecting the sun as its center, and depending upon matter, must be in a reciprocally duplicate ratio of the distance from the center." This last sentence is quoted from one of Newton's letters, and shows how carefully he had read on the subject.
Of Newton's immediate contemporaries, Robert Hooke and Edmund Halley were actively working in this field. Hooke (1635-1702) especially is ambitious to secure the honor of the solution of the problem the answer to which he reads almost exactly right, but the proof of which—poor man—he can not give. Failing in the demonstration himself, he talks on the subject, about the subject, and all over the subject, in the meetings of the Royal Society, in his papers and in his letters. So full of it is he that he imagines that whatever any one else does is stolen from him. Finally Sir Cristopher Wren offers him a prize if in two months he will produce the boasted of solution. None is forthcoming and history must write Hooke down as a most ardent worker and ingenious man, but as totally unequal to the great task imposed upon Newton.
Halley is more modest; he applies the laws of circular motion published by Huygens in 1671, sees clearly that the Inw of inverse squares
must hold good, does hold good for the circular orbit; sees also from Kepler's third law that if it can be applied to the elliptical orbit as well then all the planets immediately fall into that celestial harmony predicted by Pythagoras two millenniums before. The law holds for the circle, does it not hold for the ellipse also? We can imagine with what nervous eagerness Halley argues the question with Wren and Hooke and then—Heaven-inspired thought—posts him down to Cambridge to consult Newton. This was in August, 1684.
We must now rapidly review Newton's own work during the twenty years following his graduation from Cambridge in 1665. From the very beginning he was interested in this particular problem of gravity, but it was only one of many. Moreover, his was not a mind to stop short of the full and complete solution. This force of gravity—if it be this force that governs the universe—must be expressed by an exact law; he sees more clearly than any one else what is involved. So he ponders over the problem, and one day—would that we knew the date—he is seated in his garden studying, beside him his books and papers. In the sky is the pale moon and as Newton gazes upon her he ponders
on the world-old problem, this riddle of the ages. What force holds that moon forever circling about the earth? An apple falls to the ground beside him and its thud awakens a train of thought in his mind. Can it be the same force in the two cases—is the moon but a larger apple forever falling toward the earth, urged by the force of gravity, and forever receding from the earth, urged by her own uniform motion? Fascinated by the thought, Newton sets to calculating. He has studied out the laws of uniform motion and of accelerated motion—now he combines the two and gets the law of circular motion. He draws a circle to represent the moon's orbit and calculates by what amount the moon ought to fall toward the earth in a minute, assuming that its distance from the earth is that given in the books. In his own words he finds the figures "to answer pretty nearly," But this does not satisfy him; to a mind like Newton's "pretty nearly" is as bad as "not at all," so he lays aside his papers until more exact data are at hand. He has, however, made the first stage of the journey toward the goal. This was in the plague year, 1666. As soon as the university is again convened, Newton returns to Cambridge and for a number of years is engrossed in the study of optics. In 1672 he is momentarily reminded of the problem while editing a revised edition of Varenius's "Geography." In this he gives the accepted value for the earth's degree sixty-one and one half miles. This was probably the value Newton used in his calculations of 1666 and which fitted "pretty well," as he said. In 1679-80 Newton has an unwilling and one-sided correspondence with Hooke relating to the theory of projectiles, and in which the subject of gravity is involved.
We may be sure that during these years Newton had many times analyzed the grand problem of solar gravity and had carefully noted just what was involved therein. We may even venture to note what must have been his thoughts. If, he would say to himself, it be gravity that rules the motion of the moon, then I must prove the following:
1. Gravity must act on all kinds of matter alike, for the earth is a composite body, and presumably the moon also.
2. We know with a fair degree of accuracy that the moon is sixty-one earth-radii from us, but to make any calculation, this distance must be known in feet. Hence it is important that measurements of the size of the earth be made with the greatest care.
3. The same law should extend to the planets also, but the planetary orbits are ellipses, hence I must prove that the ellipse is a possible or necessary orbit under such a law of force.
4. I must determine some point from which measurements of distance between earth and moon are to be made, e. g., shall it be from the centers of these bodies? Also, does the same law of force hold good over the whole distance, or is it modified as the surface of the earth or moon is approached?
Whether or no Newton set the matter in orderly array, it is clear from his papers and letters that each of these points was considered. Thus he proves the first point by an exhaustive series of experiments on pendulums in which he varies the material of which the pendulum is made, proving clearly, "by experiments made with the greatest accuracy, the quantity of matter in bodies to be proportional to their weights." The converse must also be true—the weight or pull of gravity on bodies is proportional to their mass or quantity of matter.[1] The second point Newton did not himself attack, but in 1682, when attending a meeting of the Royal Society in London, he heard of Picard's recent measurements of the earth's degree. On returning to Cambridge he inserted the new value in his old calculations of 1665, measuring the distance from earth center to moon center. Finding as he advanced that the result was manifestly going to produce the long-wished-for answer, he found it impossible—so the story goes—to proceed. With the aid of a friend the calculation was completed, and Newton had reached another milestone on the way towards his cherished goal. The figures tally exactly—has he not solved the problem and may he not proclaim the answer to a waiting world? None but Newton knew the distance yet to be traveled before complete success should be his. Nothing short of this could satisfy his truth-loving mind, and the world must wait. The third point may be stated thus: "Given a central force varying as the inverse square of the distance, show that the orbit is an ellipse with the force-center at one focus." This Newton did before the year 1684, for in August of this year, when Halley, disgusted with Hooke's bombast, came to Cambridge, he asked Newton without delay the following question: "What path will a body describe if it be attracted by a center with a force varying as the inverse square of the distance?" To this Newton at once replied, "An ellipse with the center of force at one focus." "How on earth do you know?" exclaimed Halley in amazement and delight. "Why, I have calculated it," and Newton rummaged for the paper. Failing to find it, he promised to forward it to Halley by post. This promise Newton fulfilled in November. It is not known how much ground was covered in this paper, but, of course, the desired demonstration of the third point above noted was given. Newton must now have realized that he must solve the fourth point and thus complete the work so nearly finished. Something of this may have been expressed in his letters to Halley, for in December, 1684, Halley again visited him and urged him to continue his investigations. Thus far he had shown that Kepler's laws called for the inverse square law of gravity—that Picard's value of the earth's radius fitted exactly into the theory. It but remained to prove that he is correct in taking the distance from center to center of the earth and moon. For weeks and months he works over this proof and finally, some time in 1685, it yields to his unremitting toil. The approximate date of the achievement we know from a letter of Newton's to Halley dated June 26, 1686, in which he says, "I never extended the duplicate proportion lower than to the superfices of the earth, and before a certain demonstration I found the last year, have suspected it not to reach accurately enough down so low." The answer, mathematically proved in Prop. LXXIV. of Book I. of the "Principia," is that a sphere attracts all outside bodies as if its mass were concentrated at its center.
Thus he reached his goal at last, and after twenty years of work, ranging over many subjects, the key of the universe lies in Newton's hand. Surely, now, he will publish it and proclaim its discovery to the world. Not so; he must first have the joy of undisturbed possession. Also there is much more to be done. The law he has proved is an "open sesame" to wider knowledge. Or, to change the figure, it is as if a mountain climber, who has toiled upward and upward, now stands at last on the topmost height. As he is climbing he thinks that if he can but gain the summit it will be enough—he will be content and rest. The toiling climber does not realize what awaits him at the top, until the whole panorama of plain and mountain, of crag and canyon, bursts upon his astonished sight. With this before him he forgets his toil, forgets to rest and devours the view. So with Newton, having at last mastered the central law upon which the universe swings, he saw the members of the solar system sweeping in orderly grandure through space, he saw this law governing every motion of every satellite and comet, accounting for the nutations and perturbations, which before seemed to make order impossible. He saw it causing the tides with the rising and setting of the sun and moon. All this and more he saw, and we can not wonder that instead of rushing into print, he shut himself up and worked and thought and wrote, and calculated and worked and thought and wrote.
For two years he labored, sleeping little, eating little, always lost in thought. Often, it is said, on rising, he would sit for hours half dressed upon his bedside. Often for days, he would seem oblivious to all external events. The following story well illustrates his abstraction. One day a friend. Dr. Stukely, called and found Newton's solitary dinner ready on the table. After waiting a long while, Dr. Stukely thought to play a joke on Newton, which he proceeded to do by eating his dinner for him. Having done so, he rearranged the table, covering the dishes so that it would not appear that anything had happened. At length Newton appeared, and, after greeting his friend, sat down to dinner, but, on lifting the cover, said in surprise, "Dear me! I thought I had not dined, but I see I have."
So it went on for two full years, until Newton felt that his work was done. He divided it into three books. The first is entitled The Mathematical Principles of Natural Philosophy, and comprises about two hundred and fifty pages. It reminds one of a geometry, with its propositions, theorems, scholiums and problems. The first book is divided into fourteen sections and contains ninety-seven propositions, fifty theorems and forty-seven problems. Book II. discusses The Motions of Bodies. Here are found fifty-three propositions, forty-one theorems and twelve problems. Book III. has fewer diagrams, less mathematics and more discussion. The principles of natural philosophy are applied to the explanation of the solar system, and such topics as comets and tides are carefully treated. There are forty-two propositions, twenty-two problems and twenty theorems. The whole work covers 507 printed pages, and has a total of 192 propositions, 113 problems and 79 theorems, besides lemmas and scholiums in abundance.
Oliver Lodge in an outline of the "Principia" selects seventeen points for special emphasis. Of these a few may be reviewed.
1. Newton shows from Kepler's laws the following: (a) From the first law, that the law of gravity is inversely as the square of the distance, (b) From the second law, that this force is directed toward the sun as center, (c) From the third law, that all the planets are acted on by the same law of gravity; i. e., that the law of gravity extends to the uttermost confines of the solar system.
2. From the length of the year and the distance of any planet from the sun Newton calculates the planet's mass, using the earth's mass as a unit.
3. He recognized the comets as members of the solar family and showed how to calculate their orbits.[2]
4. He showed that the earth, as a result of its rotation, must be flattened at the poles, and calculated the amount (28 miles).
5. He laid the foundation for a complete theory of the tides.
We have but noted the high lights, as it were, of Newton's work. No wonder that he became lost to external events as his mind grappled with problem after problem, and one by one lay bare the secrets of the universe. As an example of the style in which the "Principia" is written, we may quote from the beginning of the third book where he lays down rules for reasoning in philosophy:
Rule I. We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances. To this purpose the philosophers say that nature is pleased with simplicity and affects not the pomp of superfluous causes.
The "Principia" was finished in the spring of 1686. It was published by order of the Royal Society, being issued from the press in July, 1687. Newton, from being a little-known member of the faculty of Cambridge, was at once recognized as the foremost scientist of the world. Honors were showered upon him. He was sent to parliament. He was elected president of the Royal Society. The queen made him a knight of the realm. He was given a lucrative position under government and moved to London. His work for science was finished, and for forty years he reaped the reward of his labors.
What Newton accomplished in optics and in mathematics would entitle him to high rank in the world of science. Of his work in mathematics the German scholar, Leibnitz, said, "Taking mathematics from the beginning of the world to the time when Newton lived, what he had done was much the better half."
The work included in the "Principia" was most of it done between 1680 and 1686. By far the greater part was done during the last two years of this short period, or between the forty-second and forty-fourth years of his age. This work, in its scope, in its far-reaching importance, and in the order of mind required for its accomplishment, raises Newton not merely to the first rank of the world's great minds, but compels the world to admit no second in his class. His genius shone resplendent even in his own day. We have already quoted Leibnitz. A French admirer wrote to an English correspondent, "Does Mr. Newton eat, drink, sleep like other men? I picture him to myself as a celestial genius, entirely removed from the restrictions of ordinary matter." Says Lagrange (1736-1813), a great French mathematician, "Newton was the greatest genius that ever existed, and the most fortunate, for we can not find more than once a system of the world to establish." The English writer, Whewell (1794-1866), writes, "The (Law of Gravitation) is indisputably and incomparably the greatest scientific discovery ever made, whether we look at the advance which it involved, the extent of truth disclosed, or the fundamental and satisfactory nature of this truth." Pope in a striking epigram expresses the same thought:
Nature and Nature's laws lay hid in night;
God said, Let Newton be, and all was light.
La Place, who did much work along the lines laid down by Newton, says of the "Principia": "The universality and generality of the discoveries it contains, the number of profound and original views respecting the system of the universe it presents, and all presented with so much elegance, will insure to it a lasting preeminence over all other productions of the human mind."
Sir Oliver Lodge says of Newton: "In science the impression he makes upon me is only expressed by the words 'inspired,' 'superhuman.'"
Of his own work Newton says: "I know not what the world will think of my labors, but to myself it seems that I have been but as a child playing on the seashore; now finding some pebble rather more polished, and now some shell rather more agreeably variegated than another, while the immense ocean of truth extended itself unexplored before me." When asked how he made his discoveries, he replied: "By always thinking unto them. I keep the subject constantly before me, and wait till the first dawnings open slowly by little and little into a full and clear light." Commenting upon this somewhat modest remark Lodge says: "That is the way—quiet, steady, continuous thinking, uninterrupted and unharassed brooding. Much may be done under these conditions; much ought to be sacrificed to obtain these conditions. All the best thinking work of the world has been thus done."
In closing, let us pause and consider the state of knowledge before and after Newton. Before him are the foreshadowings of Copernicus, the dim gropings of Kepler, the elementary truths of Galileo, the flashes of Borelli and Huygens, the fantastic speculations of Descartes; after him is a magnificent and comprehensive system of well-ordered knowledge. As we contemplate this we can understand the significance of the inscription on Newton's tomb. "Let mortals congratulate themselves that so great an ornament of the human race has existed."