Popular Science Monthly/Volume 79/November 1911/Mathematics and Engineering in Nature
| MATHEMATICS AND ENGINEERING IN NATURE |
By Professor ARNOLD EMCH
UNIVERSITY OF ILLINOIS
WHEN up on the heights, among the imposing wilderness of rocks, crags and pines, the mountaineer is struck by the roaring sound of a storm, he may observe clearly that the weather-beaten trees of a mountain forest, like other organic beings, have to defend themselves against the external attacks of nature. In other words, they have to make provisions to grow in spite of precarious circumstances and to resist many violent disturbances. The adaptability of organic beings to surrounding conditions and the existence of special means of resistance against inner and outer enemies are well known biological facts. That nature in its domain of activity, however, also makes extended use of such principles to which the engineer is accustomed in carrying out his projects, seems to be less generally known. In many instances nature is far in advance of the best human efforts in regard to rational construction. To the eye of the attentive observer, nature even may show pictures which in a beautiful manner reveal definite geometric configurations and relations.
It is not surprising that this should be the case, and might be expected. The axioms of geometry are abstract statements of primitive experiences in space. In fact, according to Picard,[1] geometry may be called the theory of space and, as such, has its origin in experience. Geometric configurations as exhibited by nature are therefore necessarily in accord with the results deduced from the geometric premises. Conversely, within the space of our experience the theorems deduced in ordinary geometry are not contradicted by nature. This statement does, of course, not exclude the possibility of other consistent theories of space, as, for instance, established in the so-called non-Euclidean geometries. The tremendous advantage of the ordinary, or Euclidean geometry, lies in the relative simplicity and adequacy of its application to physical space. As Painlevé[2] states, the science of mechanics, in the philosophical aspect of its foundations, does not differ from that of geometry. Its axioms also are derived from primitive experiences. No science can be created by purely formalistic logic.
Returning to the innumerable objects of natural growth, I shall confine myself to a description of the architectural and mechanical features of a few most conspicuous examples.
The contour-lines of a column or tower, all of whose horizontal  Fig. 1. cross-sections are subject to constant specific stresses, are geometrically defined by cubic parabolas. This form results from the law of stresses under the given conditions, and may be seen in the contour of heavily supporting bridge piers, the Eiffel tower in Paris and numerous other structures. Precisely the same problem nature has solved in building the trunks of tall trees. The famous coniferous trees of California (Fig. 1) offer the best illustration for this principle. The reason for this lies in the fact that the maximum strength of the material used in one and the same engineering structure, or in a tree, being a known constant, it is evidently of the greatest economic advantage to make the specific stresses throughout as uniform as possible.
Fig. 1. cross-sections are subject to constant specific stresses, are geometrically defined by cubic parabolas. This form results from the law of stresses under the given conditions, and may be seen in the contour of heavily supporting bridge piers, the Eiffel tower in Paris and numerous other structures. Precisely the same problem nature has solved in building the trunks of tall trees. The famous coniferous trees of California (Fig. 1) offer the best illustration for this principle. The reason for this lies in the fact that the maximum strength of the material used in one and the same engineering structure, or in a tree, being a known constant, it is evidently of the greatest economic advantage to make the specific stresses throughout as uniform as possible.
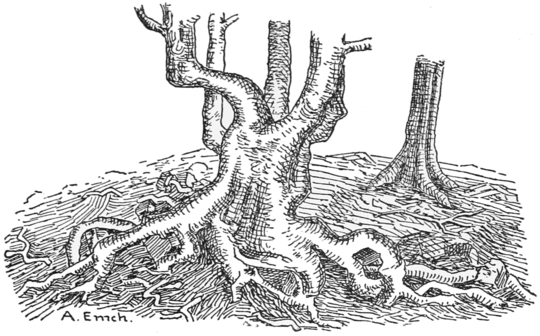
To resist great lateral bending forces, or moments caused by strong and irregular winds, the large trees of the forest are equipped with powerful wind-struts near the base and extending to the anchoring roots (Pigs. 2 and 3). The same thing the architect does when he provides for buttresses in Gothic buildings, or when he reinforces the base of a column to secure lateral stability. The more the trees are exposed to the winds, the larger the crown, the more the principle of buttresses and pillars assumes its functions. Wherever winds from a certain direction prevail, one notices plainly that in such a region the wind-struts of the trees on the side opposite to the attack of the wind are most strongly developed. In mountainous regions where on account of the rough character of the surface, the winds are very turbulent and are making their attacks in violent gusts from all directions, one may observe wonderful and grotesque shapes of root-stocks. In a seemingly almost impossible manner the roots crawl over each other, over rocks and around irregular cliffs, simply to find in a crack some ground for anchorage (Fig. 3).
From a technical standpoint also the cell structure of trees and other plants must be considered as a wonderful manifestation of the resources of nature.[3]
In this respect, the stalk of a rye-plant may be mentioned as a typical example. This plant meets the same requirements that are necessary in the construction of a high tower. The base of the whole structure is subject to the pressure of the entire load above, and must be able to resist it by compressive strength. Horizontally inserted beams, carrying loads, must have strength to resist bending. There are, furthermore, forces of gravity and all kinds of strains, caused by shearing and torsional forces, which must be accounted for. Considering the fact that in the growth of a rye-plant nature provides completely for the resistance against this complicated system of stresses, and comparing
this kind of engineering with corresponding human efforts, then even the famous and much admired Eiffel tower appears as a relatively large and clumsy structure.
According to Francé,[4] a rye stalk has an average height of 1,500 millimeters and a diameter of 3 mm. at the base. This, transformed to the proportions of architecture, means that nature has here established a structure which in comparison is 33 times the height of one of the towers of the Cathedral of Cologne. Imagine now that at the top of such a colossal tower a proportionally large and heavy ear of rye be pendling, and we get an idea of the amount of compressive, tensile and bending strength a plant-stalk may acquire. We become aware that the plant, with extreme perfection, applies the same principles with which the engineer is working. One discovers relations which the engineer finds in studying moments of inertia, bending moments, etc., in beams, girders, columns, and all kinds of trusses. Thus the plant produces extremely complex structural phenomena, which, from the standpoint of the engineer, reveal a masterful knowledge of the laws of mechanics and the consequent economy of materials. The same statement applies to the physiological problems of zoology.
While in the foregoing examples special stress was put on the relative identity of mechanical principles in engineering and nature, it will, in the next place, be interesting to show that in many cases the laws of rational construction and design are at a glance geometrically apparent.
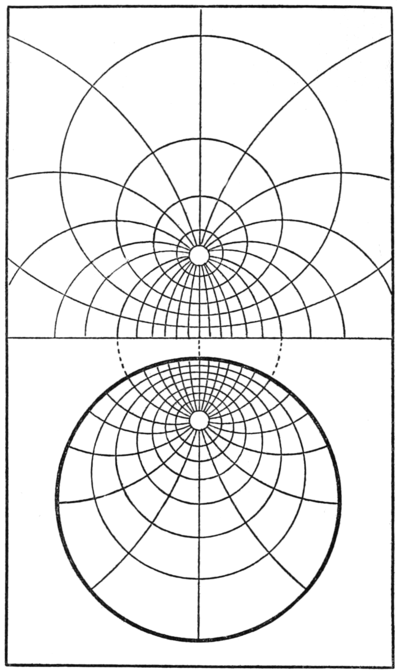
If we think of the cross-section of a tree, further growth must necessarily occur in directions normal to the surface of the last year ring. This causes the year-rings and pith-rays to form a system of orthogonal trajectories. In Fig. 4 such a system, consisting of two conjugate pencils of circles, is shown, and is caused by a rate of growth greater in one direction than another.
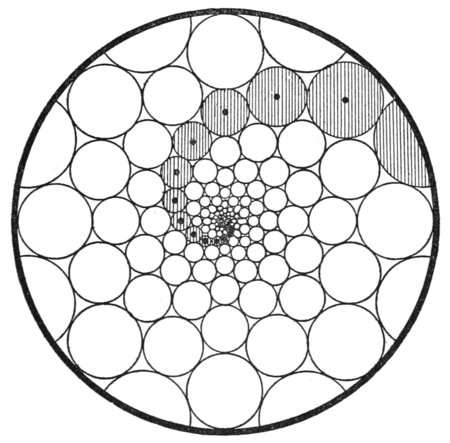
The inner yellow portion of a daisy (Chrysanthemum leucanthemum) exhibits a beautiful geometrical arrangement of its elements. By the mathematical principle of conformal transformations it can easily be proved that the best distribution of the elements is obtained when the lines appearing in the configuration of the flower (Fig. 5) are logarithmic spirals.[5]
In a similar manner the location of the leaves along the stem of a plant is determined by remarkable numerical relations.[6] The fraction n/m expressing the parts of the circumference by which consecutive leaves are separated are constant for each species and are the successive approximations of the continued fraction
| 1 | ||||||
| 1 | + | 1 | ||||
| 1 | + | 1 | ||||
| 1 | + | ..., | ||||
i. e., 1, 12, 23, 35, 58, 812, …, which, on the other hand, are also the terms of a special Lame's series. Arranging the leaves according to these fractions, nature insures for each species the best distribution of light and masses, and consequently the best growth.
Helical motion in the growth of certain plants around supporting poles may be explained mechanically. The outer parts exposed to the light grow faster than the inner portions, with the resulting tendency to bend the stem around the pole. This, combined with the upward growth, produces the spiral motion. The fact that most climbing plants, with a few exceptions (hops, Polygonum convolvulus, etc.), show left-handed twisting may be circumscribed by calling it "geotropism."
| a | Fig. 6. | b |
This, however, does not give a mechanical reason for it; not more so than for the left-handed spirals of snail-shells. In the Rocky Mountains I have often noticed this peculiar tendency in the uniform twisting of the fibers of the Lodge Pole pine.
The plain appearance of geometric configurations and relations is, of course, not limited to plant life alone; mineralogy, zoology and geology also offer many examples of this kind.
The forms of crystals, for instance, may be derived abstractly from certain considerations in the theory of groups.
Mendel's law of heredity has in recent years become of extreme importance as a powerful means of research.[7] The abstract form of this law is derived from combinatory analysis, as will appear from the following experiment of L. Cuénot.[8] All individuals of the offspring resulting from the crossing of the ordinary gray mouse with the albino mouse are gray; the gray element G dominates, while the white element W is hidden by the gray. Crossing individuals of the offspring, among the new offspring there will be gray and white specimens, and the ratio
of their respective numbers is generally 3 to 1. To explain this fact, first observed by Mendel, the hypothesis is made that in crossing the specific sexual elements merely associate and do not form a new uniform individual element. Among the G- and W- elements, in equal numbers, the following combinations are possible during the act of generation:
G and G,
G and W,
W and G,
W and W.
Each of these combinations is the starting point for a new individual. It will be gray if there is a dominant G in the combination. Hence, among the offspring there will be three gray and one white. The result may be expressed by the formula
which is corroborated by similar experiments of other investigators.
In graphic statics, one of the most valuable branches of structural engineering, may be found the reason for the peculiar distribution of the substance in the upper portion of a thigh-bone along orthogonal trajectories (Fig. 6 a). This is in analogy with the problem of a cranelike structure, as diagrammatically shown in Fig. 6 b. It is well known that the curves of maximum compression and tension in a strained body form an orthogonal system,[9] and it seems natural that in order to insure greatest strength, cell matter should be deposited according to this system.
An orthogonal system formed by the stream lines and lines of greatest tension, which appear as lateral cracks and crevasses, is shown in most glacial movements (Fig. 7). The directions of corresponding stresses and sections upon which they act form an involutoric pencil of rays. The case where the field is exclusively subject to tensions only leads to elliptic involutions around all points. Every involutoric pencil admits of a rectangular pair, corresponding to the maximum and minimum stresses; tensions in this case. The effect of this condition is shown in Fig. 8, representing the cracks of a mud-bed or on a heavily varnished surface which is drying up. In this case only tensile normal stresses act on the rectangular pair. One is a maximum, the other a minimum. After a crack has formed, the maximal stress and strain normal to the crack has been relieved, so that the former minimal normal tension along the crack becomes now the maximum. The next rupture will therefore be orthogonal to the first crack. The reason for this peculiar configuration is thus found by the methods of projective geometry.[10]
A great number of other examples from the realms of natural history might be added which all would give further evidence of the fact, that the whole evolution of the inventive and creative human intellect is reflected by the well-perceived phenomena of nature.
By the laws of the universe the human mind is forced to repeat the same logic conclusions, according to which the rest of the organic world and nature in general manifest themselves.
- ↑ "De la méthode dans les sciences," pp. 1-30, Paris, 1909.
- ↑ "De la méthode dans les sciences," pp. 336-407.
- ↑ Schwender, "Mechanische Probleme der Botanik," Leipzig, 1909.
- ↑ "Illustrierte Zeitung," 1909.
- ↑ Emch, "L'Enseignement Mathématique," Vol. 7, p. 722 (1910).
- ↑ Strassburger, "Lehrbuch der Botanik für Hoehschulen," pp. 31-35.
- ↑ Lang, "Uber die Mendelschen Gesetze, etc.," Schweiz. Naturf. Gesellsch., Luzern, 1905.
- ↑ Revue Scientifique, Paris, 1906.
- ↑ Ritter, "Graphische Statik," Vol. 1, pp. 128-134.
- ↑ Emch, "An Introduction to Projective Geometry and its Applications," pp. 239-241, New York, 1905.