Rational Psychrometric Formulae/Paper
RATIONAL PSYCHROMETRIC FORMULAE
THEIR RELATION TO THE PROBLEMS OF METEOROLOGY AND OF AIR CONDITIONING
By Willis H. Carrier, Buffalo, N. Y.
Associate Member of the Society
A specialized engineering field has recently developed, technically known as air conditioning, or the artificial regulation of atmospheric moisture. The application of this new art to many varied industries has been demonstrated to be of greatest economic importance. When applied to the blast furnace, it has increased the net profit in the production of pig iron from $0.50 to $0.70 per ton, and in the textile mill it has increased the output from 5 to 15 per cent, at the same time greatly improving the quality and the hygienic conditions surrounding the operative. In many other industries, such as lithographing, the manufacture of candy, bread, high explosives and photographic films, and the drying and preparing of delicate hygroscopic materials, such as macaroni and tobacco, the question of humidity is equally important. While air conditioning has never been properly applied to coal mines, the author is convinced that if this were made compulsory, the greater number of mine explosions would be prevented.
2Although of so much practical as well as scientific importance the laws governing many of the phenomena of atmospheric moisture are but partially understood, while the present engineering data pertaining thereto are both inaccurate and incomplete. Accepted data used in psychrometric calculations are based largely on empirical formulae, which are incorrect as well as limited in their range. Recent investigators have determined the most important properties of water vapor with final accuracy. At the same time, sufficient error has been shown in previous steam data, especially at atmospheric temperatures, to warrant the revision of all calculations based thereon.
3It is the purpose of this paper to apply these final data to the development of rational formulae for the solution of all problems pertaining to the phenomena of atmospheric moisture as related to psychrometry and to air conditioning. Original data are given in proof of fundamental relations as well as in determination of errors in standard psychrometric instruments. The author hopes these results may prove to be of permanent value.4In order to establish a logical basis for the presentation of these data and the derivation of the rational formulae, the established principles and laws governing atmospheric moisture will be reviewed and the present methods of determining atmospheric humidity discussed.
VAPOR PRESSURE AND LAW OF PARTIAL PRESSURES
5Water vapor exists in the air purely as a mixture in relation to its other elements. This vapor, according to Dalton's law, is capable of exerting a certain maximum vapor pressure dependent entirely on its temperature and regardless of the presence of other gases or vapors. For example, assume 1 cu. ft. saturated with vapor of alcohol at 100 deg. cent, having a vapor pressure of 1697.6 mm., and add isothermally to this 1 cu. ft. saturated with water vapor at 100 deg. cent, having a vapor pressure of 760 mm. This will give 1 cu. ft. of the mixture saturated with both water vapor and alcohol vapor at 100 deg. cent., having as a total pressure the sum of the two separate saturated vapor pressures, or 2457.6 mm. Similarly, an equal volume of a third saturated vapor might be added without affecting the other two. But if, on the other hand, it is attempted to include isothermally an additional amount of either of the saturated vapors, a corresponding condensation of the particular vapor added would result. In the same manner, an unlimited amount of a gas, such as air, could be added isothermally to a cubic foot of water vapor without affecting its condition of saturation, giving a combined pressure equal to the gas pressure plus the vapor pressure.
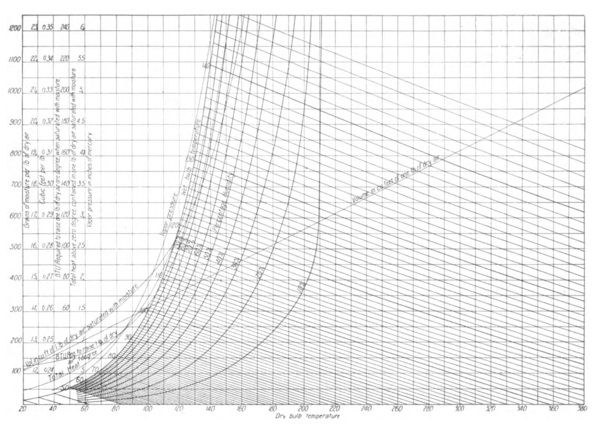
6The established temperature-pressure relationship of saturated water vapor is shown by curve (1) on the charts, Figs. 1 and 2. This is the well-known temperature-pressure curve of steam.
PARTIAL SATURATION
7When the temperature of a definite weight of saturated vapor is increased isobarometrically, it is said to be superheated. Its specific volume is increased, in accordance with the law of gases, in direct proportion to the increase of absolute temperature, while its density is changed in an inverse proportion, as shown in Fig. 3; that is, , where and are the densities corresponding to the absolute temperatures and , respectively, and is the degree of superheat. If is the density of saturated vapor at temperature , then the ratio is said to be the per cent of saturation, or more exactly, the per cent of isothermal saturation. When these relationships are considered with respect to water vapor in
air, this ratio is termed the per cent of relative humidity, while the densities , , , etc., customarily expressed in grains of moisture per cubic foot, are termed absolute humidities.
DEW POINT
8It should be noted that although the total weight of the water vapor remains the same, the absolute humidity , is less than the absolute humidity ,. However, if water vapor, or air containing water vapor, having a temperature , and an absolute humidity of , be cooled to , it will become saturated, and if cooled further, moisture will be precipitated. Therefore is termed the dew point of air having a temperature and an absolute humidity, , or a corresponding relative humidity, . Therefore, the dew point may be defined as the minimum temperature to which air of a given moisture content may be cooled without precipitation of moisture.
9Usually it is more convenient to determine the absolute and relative humidities from the temperature-pressure curve by comparing the vapor pressures. The per cent of humidity is , but it may also be shown to be equal to ; i.e.
[1]
where , is the pressure of saturated vapor corresponding to the dew point , and is the vapor pressure at saturation corresponding to temperature . It also follows that
[2]
Proof of these relationships is given in Appendix No. 1.
METHODS OF MEASURING ATMOSPHERIC HUMIDITY
10Determinations of atmospheric moisture may be made by four distinct methods:
11Chemical Method. A measured quantity of air is drawn through some de-hydrating solution, such as concentrated sulphuric acid, until the moisture is completely removed and the increase in the weight of the solution noted.
12Hygroscopic Method. This method is chiefly useful in an approximate determination of the relative humidity directly. It is known that nearly all animal and vegetable substances containing albumen or cellulose, and also many mineral salts are very sensitive to changes in atmospheric moisture. The moisture content of such materials at equilibrium is found to bear a direct relation to the existing amount of moisture in the atmosphere.
13The per cent of moisture which they will freely absorb, however, is not exactly the same for the same percentage of humidity for different temperatures. This relationship of moisture content of various textiles to different atmospheric humidities and temperatures has been very thoroughly investigated by Schloessing in France. Fig. 4 exhibits some of the relationships thus determined.
14It is therefore to be seen that the moisture content of the air will be approximately indicated by measuring the increase in weight of a skein of silk, or other textile, whose dry weight has been definitely determined. Such an instrument for the measurement of humidity has been devised by William D. Hartshorne of Lawrence, Mass.
15The action of the hair hygrometer depends upon its linear expansion due both to humidity and temperature. The accuracy of this type of hygrometer was thoroughly investigated by Regnault. It may be calibrated to give a fairly accurate indication of humidity throughout a considerable range of temperature. However, the elasticity of the hair or any similar fiber is not permanent and any instrument operating on this principle requires frequent calibration and readjustment. Therefore it can be used only in connection with some instrument giving absolute determinations.
16In his investigations of atmospheric humidity, Regnault found that a solution of calcium chloride exposed to the air would assume a density in proportion to the relative humidity. If the air became drier, it would evaporate moisture from the solution, increasing its density. If, on the other hand, the humidity of the air increased, moisture would be absorbed by the solution until it reached an equilibrium.
17A test was made by the writer in May 1902, to determine the moisture-absorbing properties of calcium-chloride brine for the purpose of air conditioning. It was found that with a constant humidity of the air, the rate of absorption varied directly in proportion to its change in density, and that the density of the solution decreased to a point where absorption stopped. In connection with this test an interesting phenomenon was observed relative to the conversion of the latent heat into sensible heat of the moisture thus absorbed. By measuring the increase in temperature, it was found possible to account very closely for the calculated latent heat of the moisture removed. The temperature of the solution was, furthermore, considerably higher than the final temperature of the air. This may be explained by the assumption that the absorption and consequent heat transformation occurred at the surface film where the air in the film and the liquid were heated to an equal temperature, and that not all of the air came into direct contact with the liquid. This is the direct inverse of phenomena occurring in evaporation with incomplete saturation. Here the temperature of the air is lowered to correspond with the increase in latent heat by evaporation, while the water always remains at a lower temperature than the partially saturated air.
18In 1909, in connection with a test made upon a humidifying plant for conditioning tobacco, similar phenomena were noted. It was found that the ventilation of cool, dry tobacco with moist air produced a rapid rise in temperature both of the air and of the tobacco, which rose to a much higher temperature than the air.
19Dew-Point Method. The dew-point method was first brought into use by Daniels and by Regnault, and adopted by the United States Weather Bureau in the determination of the values used in their psychrometric tables. The dew point is measured directly by observing the temperature at which moisture begins to form upon an artificially cooled mirror surface. Determination by this method is extremely delicate and when suitable precautions are taken, is considered very accurate. However, it is questionable whether the true dew point is ever quite as low as indicated by this method. The temperature is usually taken by a thermometer placed in a thin silver tube filled with sulphuric ether or other volatile liquid, which produces cold by evaporation. The temperature of the exterior of this tube is undoubtedly at the true dew point, but it is questionable whether the thermometer at the center of the tube registers this dew point with absolute accuracy. The exterior surface of the tube must often be cooled 25 or even 50 deg. below atmospheric temperature in order to reach the dew point.
20In any case a considerable quantity of heat must pass through the tube to the cooling medium from the external air by convection, and to a less extent from external objects by radiation. The internal resistance to the transfer of heat of a thin plate of metal, forming the wall of the tube, is in itself negligible; however, as any one who has studied the subject of heat transmission will recognize, the surface resistances are appreciable. On the outside, there is the resistance of the surface exposed to the water vapor at low tension, and, on the inside, the more considerable resistance of the liquid surface. There is therefore every reason to believe that the interior ether is at a slightly lower temperature than the exterior dew point. This conclusion conforms with conditions demonstrated by other observers in tests upon the temperature of the exterior of radiating or connecting surfaces. The extreme accuracy of the results obtained by the dew-point method at high temperatures and low humidities would, therefore, seem greatly in question.
21Evaporative or Psychrometric Method. The evaporative or psychrometric method has not heretofore, to the writer's knowledge, been definitely accepted as an absolute means of moisture determination, but as will be demonstrated, is independent of and preferable to all other methods in scope and accuracy. It is of special interest in relation to the art of air conditioning, because the same fundamental phenomena are involved and subject to the same theory. It is of service not only in the art of air conditioning, but also a departure in the science of meteorology. It provides a method, remarkable for simplicity and accuracy, for the determination of the specific heat of air, which present methods have failed to establish, within an unquestioned accuracy of 2 per cent.
22This method of moisture determination depends upon the cooling effect produced by the evaporation of moisture in a partially saturated atmosphere. This is usually measured by covering the bulb of an ordinary mercurial thermometer with a cloth or wick saturated with water and comparing its temperature with that of a thermometer unaffected by evaporation. The covered bulb is termed the wet-bulb thermometer, and the difference between the wet and dry-bulb readings is termed the wet-bulb depression. The temperature of the wet bulb is affected in a measure by radiation from surrounding objects. It is therefore very susceptible to air currents which serve to increase the evaporation and therefore decrease the percentage of error due to radiation. On this account, the earlier and more convenient form of hygrometer using a stationary wet bulb is very unreliable, considerable correction being necessary for radiation. The sling psychrometer advocated by the United States Weather Bureau overcomes this error to a great extent by increasing the ventilation and consequent rate of evaporation to such a degree that the heat received by radiation becomes a small percentage of the total heat transformation.
23The most reliable tables based on the stationary wet-bulb hygrometer are those by James Glaisher (1847)[1]. The tables of the United States Weather Bureau based upon an empirical formula deduced by Prof. Wm. Ferrel from simultaneous determinations with the sling psychrometer and the dew-point instrument are more reliable, and are now generally used. The limitations of this formula are admitted, since it is held to be correct only over the range of observation from which it was deduced, including simply temperatures below 120 deg. fahr.
24Professor Ferrel’s formula as given in the tables of the United States Weather Bureau is
where
- = partial pressure of the moisture in the air, which also = vapor pressure corresponding to the dew point
- = the vapor pressure corresponding to saturation at wet bulb temperature
- = the barometric pressure
- = dry-bulb temperature in deg. fahr.
- = wet-bulb temperature in deg. fahr.
25The temperature of the dew point is found by selecting the temperature corresponding to the pressure , from the temperature pressure diagram or table. The per cent of relative humidity is , where , is the vapor pressure corresponding to the dry-bulb temperature , as previously demonstrated. The absolute humidity expressed in grains of moisture per cubic foot is then determined by multiplying the grains of moisture per cubic foot corresponding to saturation at dry-bulb temperature by the per cent of relative humid ity thus determined.
26The writer would substitute for such an empirical formula a rational one, having a thermodynamic basis, that is, a formula depending upon the transformation of sensible heat into latent heat in the adiabatic saturation of dry air.
27Historically, it is of interest to note in this connection, that James Apjohn[2] propounded in 1836 this same theory of wet-bulb temperature. However, he was unable to establish the correctness of his assumptions, partly because the data then extant regarding the specific heat of air and the latent heat of water vapor were inaccurate, but more particularly because he assumed the temperature indicated by the stationary wet-bulb thermometer which he used, to be the true temperature of evaporation, while as a matter of fact, it is considerably higher, owing, as we have shown, to the effect of radiation upon the stationary wet bulb.
28The author first observed that the wet-bulb temperature given in the psychrometric tables of the United States Weather Bureau agreed substantially with the computed temperature at which air of a known temperature and moisture content would become saturated adiabatically, i.e., without the addition or subtraction of heat. These calculations were made by the writer in 1903, in determining the moisture-absorbing capacity of air in connection with the fan systems of drying. Subsequently, this relationship was still further investigated and thoroughly established in connection with the system of air conditioning introduced by the writer.
29Tests upon progressive fan-system dry kilns in 1904 disclosed the fact that the wet-bulb temperature was substantially the same in all parts of the kiln regardless of the drop in temperature due to moisture absorption, a phenomenon which logically results from the identity of the wet-bulb temperature and the temperature of adiabatic saturation.
PSYCHROMETRIC PRINCIPLES
30The following principles underlie the entire theory of the evaporative method of moisture determination, as well as of air conditioning:
| (A) | When dry air is saturated adiabatically the temperature is reduced as the absolute humidity is increased, and the decrease of sensible heat is exactly equal to the simultaneous increase in latent heat due to evaporation. |
| (B) | As the moisture content of air is increased adiabatically the temperature is reduced simultaneously until the vapor pressure corresponds to the temperature, when no further heat metamorphosis is possible. This ultimate temperature may be termed the temperature of adiabatic saturation. |
| (C) | When an insulated body of water is permitted to evaporate freely in the air, it assumes the temperature of adiabatic saturation of that air and is unaffected by convection; i.e., the true wet-bulb temperature of air is identical with its temperature of adiabatic saturation. |
| (D) | The true wet-bulb temperature of the air depends entirely on the total of the sensible and the latent heat in the air and is independent of their relative proportions. In other words, the wet-bulb temperature of the air is constant, providing the total heat of the air is constant. |
32A statement of the experimental demonstration of these four principles is given in Appendix No. 2.
APPLICATION OF THE EVAPORATION CALORIMETER TO THE DETERMINATION OF THE SPECIFIC HEAT OF AIR
33In consequence of the psychrometric principles A, B and C, the moisture content of air from accurate psychrometric readings may be easily computed, provided the required temperature is known, as well as the density relations in a mixture of pure air and saturated water vapor, and also the exact latent heat of water vapor, and the specific heat of air and of water vapor at any temperature.
34No novelty is claimed for this method since the writer found, while preparing this paper, that this very means had been proposed by James Apjohn[3]. However, it does not seem to have been taken very seriously by contemporary scientists since it was never properly developed. Moreover, the details of his method were such as to make it worthless.
35Recent research into the properties of water vapor has fully established its properties to a great degree of exactness, with the possible exception of the specific heat, which is of minor importance in psychrometric calculations. The author, however, was surprised to find upon investigation that the usual value assigned to the specific heat of air was unquestionably incorrect, since it had been definitely proved to be variable, and not a constant as assumed by Regnault. Moreover, recent investigators conducting their experiments with modern apparatus, supposedly with extreme accuracy, differed from each other by more than 3 per cent, and from the generally accepted value of Regnault, by more than 2 per cent. Therefore, in order to use a rational formula in the construction of accurate psychrometric charts and tables, it becomes necessary to determine the specific heat of air to a much greater degree of accuracy than is known at present.
36At the time of this writing, the author is not prepared to give any definite data with regard to such determinations, but will present a method employing the evaporation calorimeter which apparently affords great accuracy and upon which greater reliance can be placed than upon previous methods, in all of which the air or other gas must be measured with precision. This measurement, when dealing with air quantities sufficient to give accurate determinations, seems to present the chief difficulty.
37In the present method, on the contrary, no air measurement, other than the determination of its density through temperature and barometric pressure, is required. It is, indeed, in this respect, closely allied to the throttling calorimeter method of determining the specific heat of steam. In other respects, however, it has a great advantage over that method in that it requires no subtractive calculations sensitive to error, but equates the known latent heat of water vapor, directly to the unknown specific heat of air, the weight of the water vapor having a known ratio to that of the air.
38This method consists, first, in bringing a continuous supply of air close to saturation, where its moisture content can be determined with great accuracy by means of a wet and dry-bulb thermometer and applying the rational psychrometric formula [3] assuming an approximate value for the specific heat; second, in heating this current of air of known moisture content to any desired amount andtaking the wet and dry-bulb readings as in experiment No. 2, Appendix No. 2. By applying the rational psychrometic formula derived in Pars. 58-67, we have
[3]
where
- = mean specific heat of air of constant pressure between temperatures and
- = mean specific heat of water vapor between temperatures and
- = temperature of the dry bulb
- = temperature of the wet bulb
- = latent heat of water vapor corresponding to
- = weight of water vapor actually contained in 1 lb. of dry air; i.e., it is the ratio of the weight of water vapor to the weight of air in the mixture
Fig. 5.—Plan of Apparatus for Determining Specific Heat.
- = weight of water vapor contained in 1 lb. of dry air at saturation at temperature
[4]
where
- = specific weight of water vapor
- = barometric pressure
- = vapor pressure at
39The apparatus for this determination is shown in Figs. 5 and 6. Two fans are required. Fan No. 1 draws the air through moist sponge A. The air in passing through the fan rises in temperature so that it is desirable to saturate it further by passing it through a moist sponge filter B. The wet and dry-bulb temperatures of the air are then taken with thermometers 1 and 2. These readings should be practically identical so that error in calculating the true dew point is negligible. The air is then heated by passing it through an electric heater provided with a rheostat for regulating the temperature. Thence it is blown, still under slight pressure, into fan No. 2, where it is thoroughly mixed and the pressure slightly increased. After the air passes through the second fan, the wet and dry temperatures are taken in the manner previously described, except that the greatest precaution is exercised in the construction of the air passage to avoid radiation from the thermometer bulbs. A differential gage is connected between chambers 2 and 3. Care is taken in regulating the pressures of the fans and in the damping of the discharge to keep the differential gage at zero, so that there will be the same pressure of air on both thermometers. This pressure is measured by a second draft gage D2, and a third draft gage D3, is connected to the second fan inlet where it is essential that the pressure be maintained above atmospheric so that any leakage occurring in the apparatus will be outward. Pitot tube and differential gages are used to determine the velocities on the thermometers.
40The accuracy of this method is apparently limited only by the accuracy of the thermometers. Wet-bulb depressions between 20 and 50 deg. may be used to advantage, and the determinations should be accurate to at least 110 of 1 per cent.
DERIVATION OF A RATIONAL PSYCHROMETRIC FORMULA
41As already pointed out, it is possible to derive a rational psychrometric formula based on the fundamental principles, A, B and C.
42In considering the interchanges of heat occurring in psychrometric phenomena, it is essential to consider primarily the relative weights of dry air and of water vapor rather than the usual density temperature relationship; that is, it is necessary to express moisture content as weight of water vapor per pound of pure air, rather than as weight of water vapor per cubic foot of space. Moreover, this relationship is much more adaptable to all of the usual calculations in air conditioning and in meteorology. The author, accordingly, has constructed all his formulae and psychrometric charts upon this basis. In the deduction of the formulae and in the construction of the accompanying charts, the following fundamental data were employed:
| a | Standard barometric pressure = 29.92 in. mercury = 14.6963 lb. per sq. in. = 2116.3 lb. per sq. ft. |
| b | Absolute temperature = + 459.62 deg. fahr. |
| c | B.t.u. = heat required to raise 1 lb. of water from 32° to 212°180° |
| d | Mechanical equivalent of heat = 777.52 ft-lb. |
| e | Specific volume of air = weight of 1 cu. ft. of pure air at 32 deg. fahr. and 29.92 in. barometric pressure = 0.080728 lb. per cu. ft. Therefore |
| f | Instantaneous specific heat of air[4] deg. fahr. |
| g | Vapor pressure, Holborn and Henning’s modification of the Theisen formula , as calculated in tables of Marks and Davis (1909) |
| h | Specific volume of steam as calculated in steam tables of Marks and Davis[5] (1909) |
| i | Latent heat of water vapor[6] ( = deg. fahr.) |
| j | Instantaneous specific heat of water vapor (approximately)
|
| k | Specific weight of water vapor at saturation for any pressure and temperature
|
43With respect to the reliability of these data, those on the latent heat of steam may be accepted as absolute within 0.1 per cent,
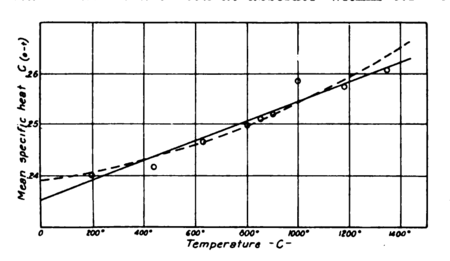
since the agreement of recent investigators seems to have established the present values beyond question. Strange to say, however, the specific heat of air, as already pointed out, has not been established with accuracy within 2 per cent. Regnault gives it as a constant, , and this value has generally been accepted. However, Holborn and Henning, whose valuable determinations in steam are well known, have demonstrated it to be a variable. For nitrogen they give a value ( in deg. cent.), a straight-line relationship, although for superheated vapors they find equations of a higher degree. The plot of their values for for nitrogen, as shown in Fig. 7, lacks considerable uniformity. So far as the points given are concerned they do not seem to warrant assuming a straight-line relationship. Their points would seem to indicate rather a curve with considerably greater values at lower temperatures than given by their line. If their values were accepted at atmospheric temperatures we would have a specific heat for air considerably lower than that given by Regnault, while psychrometric evidence seems to indicate that it should be considerably higher at such temperatures. The most reliable of recent determinations would seem to be that of W. F. G. Swann.[7] In his paper he points out a defect in the method of Regnault which would account for the latter’s value being too low. The values given by Swann have therefore been adopted in this paper; although they appear still to require confirmation, since there would seem to be considerable opportunity for error in the method of air measurement used in his experiments.
44The equation given for the specific heat of steam at low temperatures seems to agree fairly well with modern experimental data. Extreme accuracy is not pretended, nor is this essential at lower temperatures, since under 150 deg. the total heat value of the air is affected only 2 per cent at most by the specific heat of the water vapor. The values given by this equation, however, are undoubtedly more nearly correct at lower temperatures than the usual value, .
45The psychrometric charts, Figs. 1 and 2, are constructed accurately from the foregoing data. Fig. 2 exhibits all psychrometric relationships, between the temperatures of 20 deg. and 350 deg. and saturation temperatures up to 143 deg. Fig. 1 gives the same values between temperatures 20 deg. and 110 deg. and saturation temperatures to 95 deg. These charts are here shown to a greatly reduced scale. In its original form, Fig. 1 permits the reading of both the wet and dry-bulb temperatures to an accuracy of 0.1 deg. and of the moisture weight per pound of air to 0.2 grains. All calculations have been made with accuracy to five significant figures by means of a Thatcher slide rule.
SATURATION CURVE
46 The saturation curve, Fig. 2, expressed in grains of moisture per pound of air, was computed from the formula
[5]
where
- = grains of moisture per lb. of pure air at saturation
- = temperature of saturation in deg. fahr.
- = absolute temperature
- = density in lb. per cu. ft. of saturated water vapor at temperature
- = reciprocal of specific volume of steam
- = 29.92 = assumed standard of barometric pressure in in. of mercury
- = vapor pressure of saturated water vapor
- = constant of the equation
The derivation of equation [5] is given in Appendix No. 3.
TABLE 1 SPECIFIC WEIGHT OF STEAM
Corrected |
Corrected |
Grains Moisture per cu. ft | |||||||||||
| 40 | 0 | .2477 | 0 | .000410 | 0 | .6345 | 0 | .6228 | 0 | .0004089 | 2 | .8623 | |
| 50 | 0 | .3625 | 0 | .000587 | 0 | .6230 | 0 | .6231 | 0 | .0005871 | 4 | .1697 | |
| 60 | 0 | .5220 | 0 | .000828 | 0 | .6221 | 0 | .6223 | 0 | .0006296 | 4 | .4072 | |
| 70 | 0 | .7390 | 0 | .001148 | 0 | .6212 | 0 | .6236 | 0 | .0011524 | 8 | .0668 | |
| 80 | 1 | .0290 | 0 | .001570 | 0 | .6217 | 0 | .6239 | 0 | .0015755 | 11 | .0285 | |
| 90 | 1 | .1470 | 0 | .002130 | 0 | .6237 | 0 | .6242 | 0 | .0021820 | 14 | .9240 | |
| 100 | 1 | .9260 | 0 | .002851 | 0 | .63525 | 0 | .6246 | 0 | .0028482 | 19 | .9874 | |
| 110 | 2 | .5890 | 0 | .003766 | 0 | .6255 | 0 | .6250 | 0 | .0037630 | 28 | .3410 | |
| 120 | 3 | .4380 | 0 | .004924 | 0 | .62665 | 0 | .6254 | 0 | .0049140 | 34 | .3980 | |
| 130 | 4 | .5200 | 0 | .006370 | 0 | .6273 | 0 | .6260 | 0 | .0063570 | 44 | .4990 | |
| 140 | 5 | .8800 | 0 | .008140 | 0 | .6266 | 0 | .6266 | 0 | .0081400 | 55 | .9800 | |
| 150 | 7 | .5700 | 0 | .070320 | 0 | .6280 | 0 | .6273 | 0 | .0103100 | 72 | .1700 | |
| 160 | 9 | .6500 | 0 | .012960 | 0 | .6282 | 0 | .6280 | 0 | .012955 | 90 | .5920 | |
| 170 | 12 | .200 | 0 | .016140 | 0 | .6288 | 0 | .6288 | 0 | .016140 | 112 | .9800 | |
| 180 | 15 | .290 | 0 | .019940 | 0 | .6296 | 0 | .6298 | 0 | .019940 | 139 | .5800 | |
| 190 | 19 | .020 | 0 | .024440 | 0 | .6301 | 0 | .6307 | 0 | .024463 | 171 | .2550 | |
| 200 | 23 | .47 | 0 | .029760 | 0 | .6313 | 0 | .6316 | 0 | .029780 | 208 | .4600 | |
47The specific weight of saturated water vapor is not constant, but varies with the temperature of saturation and may be calculated from equation [1]. The theoretical value, computed from its molecular weight, assuming it to be a perfect gas, is 0.6221. This is the assumption made in the computation of the psychrometric tables published by the United States Weather Bureau, which are inaccurate, therefore, in proportion to the variation of from this theoretical value. The actual values for the specific weight of water vapor at various saturation temperatures, computed from equation [35] are given in Table 1.
48The specific weight of water vapor may also be given independent of the density as
Hence
At atmospheric temperature the term is negligible. Hence
CONSTRUCTIONS OF ADIABATIC SATURATION LINES
49As shown in Par. 30 any adiabatic change involving moisture content and temperature of air may be expressed by equating the change in total specific heat to the corresponding change in latent heat. It may also be expressed by equating the total heat contained in the air in the state resulting from adiabatic change. By either of these two methods, given in Appendix No. 4, the relations of formula [6] are established.
6
in which
- = the true wet-bulb depression
- = the moisture absorbed per lb. of pure air when it is adiabatically saturated from an initial dry-bulb temperature and an initial moisture content
- = mean specific heat of air at constant pressure between temperature and
- = specific heat of steam at constant pressure between and
- = latent heat of evaporation at wet-bulb temperature
Knowing any two of the three important values of , or , we may solve for the third or for any other required relation.
50Determination of Weight of Moisture in 1 Lb. of Pure Air, having a Dry-Bulb Temperature and Wet-Bulb Temperature . To determine the equation of the adiabatic line corresponding to a given saturation, or true wet-bulb temperature , and dry-bulb temperature , we have from equation [6]
[7]
[8]
51The diagonal adiabatic lines in the charts, Figs. 1 and 2, representing saturation or wet-bulb temperatures, are calculated from, this formula. It should be observed that they would be perfectly straight if it were not for the element , which produces a slight curvature, becoming more pronounced at higher saturation temperatures. The dew point corresponds to on the saturation curve. The slope of these lines, neglecting is . This will always give the intercept for .
52Wet-Bulb Depression and Cooling Effect. The wet-bulb depression or cooling effect obtained by having and known is
[9]
and
10
53Having and known, cannot be calculated except by relating to by an empirical equation. By referring to the psychrometric charts, Figs. 1 and 2, constructed chiefly for that purpose, is conveniently determined. The cooling effect , to be obtained by saturating air of known temperature and moisture content, is likewise obtained from the chart.
54Motsture-Absorbing Capacity of Air. For determining the moisture-absorbing capacity, or moisture deficit of air, having a known temperature and moisture content, we have per pound of pure air
[11]
55Per Cent Adiabatic Saturation. The per cent of adiabatic saturation is
[12]
or if we neglect
[13]
56Specific Heat of Air. The equation for the experimental determination of the specific heat of air by the evaporative method is
[14]
57For engineering purposes however, it is preferable to determine any unknown value directly from the psychrometric charts, which afford to a great degree of accuracy a simple graphic solution of any problem of psychrometry.
DERIVATION OF THE RATIONAL PSYCHROMETRIC FORMULA FOR VAPOR PRESSURE
58The present empirical psychrometric formula in use by the United States Weather Bureau was first deduced by Professor Ferrel,[8] while the constants of the formula were deduced from a series of experiments by Professor Marvin and Prof. H. A. Hazen. The error in Broch's and Regnault's values for vapor pressures which they adopted alone would require its revision. Moreover, the opportunity for error in their methods has already been pointed out. However, considering the difficulties of their experimental method and the correction necessary for radiation in the wet-bulb reading, the results obtained are remarkable for consistency and accuracy. There are errors in the form of the equation, however, as well as in the constants employed, which make its inaccuracy more pronounced at lower humidities and at the higher temperature. At very high temperatures used in mechanical drying it is entirely inoperative.
59The need of an accurate rational psychrometric formula for vapor pressures using modern data is therefore apparent. The required values could be obtained indirectly from the formula already given, but computation is facilitated by another derivation giving directly the vapor pressure .
60In equation [8]
let be the dew point corresponding to , and the vapor pressure corresponding to in in. of mercury. Referring to equation [5]
by substitution
[15]
Solving for
[16]
Assuming , this simplifies to
[17]
at 100 deg.
[18]
Therefore the value is ordinarily negligible. Hence we have
[18]
61By comparison it will be found that the difference between and is negligible. Hence it may be assumed [20]
For may be substituted the approximate value and for the value (approximately). Hence
[21]
[22]
TABLE 2 COMPARISON OF NEWLY DETERMINED PSYCHROMETRIC VALUES WITH OLD UNITED STATES WEATHER BUREAU VALUES
| Water Vapor Containd in 1 Lb. of Pure Air for Wet Bulb of 60 Deg. Fahr. and Dry Bulb of from U. S. Weather Bureau Fomulæ |
Water Vapor Actually Contained in 1 Lb. of Pure Air for Wet Bulb of 60 Deg. Fahr. | ||||||||||||||||||||
| Grain per Lb. Air |
Per Cent Error |
Grain per Lb. Air | |||||||||||||||||||
| 70 | 10 | 0 | .4053 | 29 | .515 | 59 | .8 | 0 | .0205 | 70 | 10 | 0 | .4540 | 0 | .24170 | 61 | .06 | ||||
| 75 | 15 | 0 | .3495 | 29 | .570 | 51 | .5 | 0 | .0280 | 75 | 15 | 0 | .4544 | 0 | .24172 | 52 | .98 | ||||
| 80 | 20 | 0 | .2936 | 29 | .625 | 43 | .1 | 0 | .0388 | 80 | 20 | 0 | .4549 | 0 | .24175 | 44 | .84 | ||||
| 85 | 25 | 0 | .2380 | 29 | .682 | 34 | .9 | 0 | .0548 | 85 | 25 | 0 | .4553 | 0 | .24177 | 38 | .915 | ||||
| 90 | 30 | 0 | .1820 | 29 | .738 | 26 | .6 | 0 | .0808 | 90 | 30 | 0 | .4558 | 0 | .24179 | 28 | .934 | ||||
| 95 | 35 | 0 | .1260 | 29 | .794 | 18 | .4 | 0 | .1238 | 95 | 35 | 0 | .4662 | 0 | .24181 | 20 | .995 | ||||
| 100 | 40 | 0 | .0700 | 29 | .850 | 10 | .2 | 0 | .2200 | 100 | 40 | 0 | .4667 | 0 | .24184 | 13 | .082 | ||||
| 105 | 45 | 0 | .0145 | 29 | .905 | 2 | .11 | 0 | .5960 | 105 | 45 | 0 | .4571 | 0 | .24187 | 5 | .220 | ||||
and if Swann’s value of is accepted for the value of as in the charts,
[23]
This equation has been carefully tested by comparing with values of the psychrometric coefficient as determined by means of the charts as shown in Table 2 and Fig. 9. This shows that it is permissible as the coefficient instead of , giving
[24]
This formula will give values of e for all wet and dry-bulb temperatures and all barometric pressures with an error of less than 0.5 per cent, assuming the chosen value of to be correct.
62This equation should be used where the true wet-bulb tempera ture is obtained as in the aspiration psychrometer. With the sling psychrometer a correction must be made for the error in depression due to radiation and stem correction. By referring to Fig. 10 showing the per cent of radiation error, it is seen that this is inversely proportional to the velocity. It is also, of course, greatly affected by the conditions of exposure, i.e., whether it is surrounded on all four sides by bodies at the temperature of the dry bulb, or only partly by bodies of that or a different temperature. The effect of radiation out side of an enclosure may be assumed to be approximately one-half of that within an enclosure.
64A sling psychrometer 15 in. in length is ordinarily revolved between 150 and 225 r.p.m. giving a velocity between 1200 and 1800 ft. per min. This will give, according to Fig. 10, a radiation error of 2.6 to 1.75 per cent within an enclosure, and 1.3 to 0.9 per cent with out an enclosure. Hence an average radiation error of 1.6 per cent of the wet-bulb depression may be arbitrarily assumed. The wet bulb depression given by the sling psychrometer may be corrected by this amount to give the true depression, which may be used in the foregoing psychrometric formula, or the formula itself may be modified to allow for this error.
65If this formula is corrected for 1.6 per cent radiation error
[25]
for the sling psychrometer.
66Using the true wet-bulb depression in formula [24], letting be the vapor pressure corresponding to saturation at the dry-bulb temperature
[26]
for the per cent of relative humidity.
67Let be the grains of moisture per cu. ft. at any vapor pressure , and , grains per cu. ft. at ; then
[27]
also
[28]
where , is the grains of moisture per cu. ft., corresponding to the dew point at vapor pressure .
EFFECT OF CHANGE IN BAROMETRIC PRESSURE
68Suppose that air in which the vapor pressure is is compressed from a barometric pressure to a barometric pressure , then the partial pressure of both the air and the vapor are increased proportionally and . The temperature corresponding to saturation at is the temperature of the dew point at pressure .
69The per cent of isothermal saturation becomes
[29]
where is the saturated vapor pressure corresponding to the dry bulb temperature .
TOTAL HEAT CURVE
70This curve shows the sensible heat in the air above a base temperature of 0 deg. fahr., plus the latent heat contained in the water vapor at saturation, but not including the heat of the liquid. Since the wet-bulb temperature, or adiabatic lines contain all points having the same total heat (neglecting heat of liquid), the curve serves to determine the total heat in the air under any and all conditions represented by the chart. This is of great convenience in calculating refrigeration required to cool and de-humidify air. For example, suppose it is required to find the refrigeration necessary to cool 1 lb. of air containing 98 grains of moisture and having a dry bulb temperature of 95 deg., to a final temperature of 40 deg. saturated. We find from the chart that the wet-bulb temperature is 75 deg. The total heat corresponding to a saturation temperature of 75 deg. is 37.8 B.t.u., while the total heat at 40 deg. is 15.3 B.t.u. The difference, 22.5 B.t.u. is the refrigeration required per pound of air.
The author wishes to acknowledge his indebtedness to his assistants, Mr. Theodore A. Weager and Mr. Frank L. Busey, for the actual work of computation and the construction of the diagrams.
- ↑ Phil. Trans. Royal Soc., 1851, p. 141.
- ↑ Irish Academy Trans., vol. 17, pp. 275-282, 1837.
- ↑ Irish Academy Trans., vol. 18, pp. 1-17, 1838.
- ↑ Harvey N. Davis, Trans.Am.Soc.M.E., vol. 30, p. 750, 1908.
- ↑ W. F. G. Swann, Phil. Trans. Royal Soc., series A, vol. 210, pp. 199-238, 1909.
- ↑ C. H. Peabody, Trans.Am.Soc.M.E., vol. 31. p. 334, 1909.
- ↑ Phil.Trans.Royal.Soc., series A, vol. 210, pp. 199-238, 1909.
- ↑ Annual Report, Ch. Signal Officer, 1886, Appendix 24, pp. 233 259.





































![{\displaystyle (t+495.6)\log {}{\frac {p}{14.70}}=5.409(t-212)-3.71x10^{-10}[(689-t)^{4}-(477)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3dcd76a027d8d7df3afec0b657629f5e5a20722)
























![{\displaystyle [r'+C_{ps}(t-t')]W=r'W'-C_{pa}(t-t')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/492ec2ba75b04862c4fb8741dd32b1a3c526c242)















![{\displaystyle e=P\left[{\frac {\left[{\frac {S'e'r'-(P-e')C_{pa}(t-t')}{(P-e')[r'+C_{ps}(t-t')]}}\right]}{\left\{{\frac {S_{1}(P-e')[r'+C_{ps}(t-t')]+[S'e'r'-(P-e')C_{pa}(t-t')]}{(P-e')[r'+C_{p}s(t-t')]}}\right\}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19bcff2eeba37e574d19fa87a5571c0dbcc0608)

![{\displaystyle e=P\left[{\frac {S'e'r'-(P-e')C_{pa}(t-t')}{S_{1}Pr'+(S_{1}C_{ps}-C_{pa})(P-e')(t-t')}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d94b519a3b953514f466cb7ffaa88850b963bc45)
![{\displaystyle S_{1}C_{ps}-C_{pa}=[(0.623\times 0.46)-0.242]=0.033}](https://wikimedia.org/api/rest_v1/media/math/render/svg/488c9ee6b2bd03a15954f2351fc0b905cb13d632)











































![{\displaystyle W=(RW_{2})={\frac {W_{2}}{e_{2}}}\left[e'-{\frac {(P-e')(t-t')}{2800-1.3t'}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab538786434e9e30e15a0c84e4b396d19570cba5)




