The Mathematical Principles of Natural Philosophy (1729)/Book 1/Section 6

Section VI.
How the motions are to be found in given orbits.
Proposition XXX. Problem XXII.
To find at any assigned time the place of a body moving in a given parabolic trajectory.

Let S (Pl. 14. Fig. 1.) be the focus, and A the principal vertex of the parabola; and suppose 4ASxM equal to the parabolic area to be cut off APS, which either was described by the radius SP, since the bodies departure from the vertex, or is to be described thereby before its arrival there. Now the quantity of that area to be cut of is known from the time which is proportional to it. Bisect AS in G, and erect the perpendicular GH equal to 3M, and a circle described about the centre H with the interval HS, will cut the parabola in the place P required. For letting fall PO perpendicular on the axis; and drawing PH, there will be Whence . For write ; Then dividing all the term by 3PO and multiplying them by 2AS, we shall have to the area of to the area APS but GH was 3M and therefore is Wherefore the area cut of APS is area that was, to he cut of 4ASxM. Q. E. D.
Cor 1. Hence GH is to AS, as the time in which the body described the arc AP to the time in which the body described the arc between the vertex A and the perpendicular erected from the focus S upon the axis.
Cor 2. And suppose a circle ASP perpetually to pass through the moving body P, the velocity of the point H, is to the velocity which the body had in the vertex A. as 3 to 8; and therefore in the same ratio is the line GH to the right line which the body, in the time of its moving from A to P, would describe with that velocity which it had in the vertex A.
Cor. 3. Hence also, on the other hand, the time
may be found, in which the body has described
any assigned arc AP. Join AP on its
middle point erect a perpendicular meeting the right
line GH in H.
Lemma XXVIII.
There is no oval figure whose area, cut off by right lines at pleasure, can be universally found by means of equations of any number of finite terms and dimensions.
Suppose that within the oval any point is given, about which as a pole a right line is perpetually revolving, with an uniform motion, while in that right line a moveable point going out from the pole, moves always forward with a velocity proportional to the square of that right line within the oval. By this motion that point will describe a spiral with infinite circumgyrations. Now if a portion of the area of the oval cut off by that right line could be found by a finite equation, the distance of the point from the pole, which is proportional to this area, might be found by the same equation, and therefore all the points of the spiral might be found by a finite equation also; and therefore the intersection of a right line given in position with the spiral might also be found by a finite equation. But every right line infinitely produced cuts a spiral in an infinite number of points; and the equation by which any one intersection of two lines is found, at the same time exhibits all their intersections by as many roots, and therefore rises to as many dimensions as there are interactions. Because two circles mutually cut one another in two points, one of those intersections is not to be found but by an equation of two dimensions, by which the other intersections may also found. Because there may be four intersections of two conic sections, any one of them is not to be found universally but by an equation of four dimensions, by which they may be all found together. For if those intersection severally sought, because the law and condition of all is the same. the calculus will be the same in every case, and therefore the conclusion always the same, which must therefore comprehend intersections at once within itself, and exhibit them all indifferently. Hence it is that the intersections of the conic sections with the curves of the third order, because they may amount to nine, come out together by equations of six dimensions and the intersections of two curves of third order, because they may amount to nine, come out together by equations of nine dimensions this did not necessarily happen, we might reduce all solid to plane problems and those higher than solid to solid problems. But here I speak of curves irreducible in power. For if the equations by which the curve is defined may be reduced to a lower power, the curve will not be only single curve, but composed of two or more, whose intersections may be severally found by different calculusses. After the same manner the two intersections of right lines with the conic sections come out always by equations of two dimensions; the three interactions of right lines with the irreducible curves of the third order by equations of dimensions; the four intersections of right lines with the irreducible curves of the fourth order, by equations of four dimensions, and so on in infinitum. Wherefore the innumerable intersections of a right line with a spiral, since this is but one simple curve. and not reducible to more curves, require equations infinite in number of dimensions and roots, by which they may be all exhibited together. For the law and calculus of all is the same. For if a perpendicular is let fall from the pole upon that intersecting right line, and that perpendicular together with the intersecting line revolves about the pole, the intersections of the spiral will mutually pass the one into the other; and that which was first or nearest, after one revolution, will be the second, after two, the third, and so on; nor will the equation in the mean time be changed, but as the magnitudes of those quantities are changed, by which the position of the intersecting line is determined. Wherefore since those quantities after every revolution return to their first magnitudes, the equation will return to its first form, and consequently one and the same equation will exhibit all the intersections, and will therefore have an infinite number of roots, by which they may be all exhibited. And therefore the intersection of a right line with a spiral cannot be universally found by any finite equation; and of consequence there is no oval figure whose area, cut off by right lines at pleasure, can be universally exhibited by any such equation.
By the same argument, if the interval of the pole and point by which the spiral is described, is taken proportional to that part of the perimeter of the oval which is cut off; it may be proved that the length of the perimeter cannot be universally exhibited by any finite equation. But here I speak of ovals that are not touched by conjugate figures running out in infinitum.
Cor. Hence the area of an ellipsis, described by a radius drawn from the focus to the moving body, is not to be found from the time given, by a finite equation; and therefore cannot be determined by the description of curves geometrically rational. Those curves I call geometrically rational, all the points whereof may be determined by lengths that are defineable by equations, that is, by the complicated ratio's of lengths. Other curves (such as spirals, quadratrixes, and cycloids) I call geometrically irrational. For the lengths which are or are not as number to number (according to the tenth book of elements) are arithmetically rational or irrational. And therefore I cut off an area of an ellipsis proportional to the time in which it is described by a curve geometrically irrational, in the following manner.
Proposition XXXI. Theorem XXIII.
To find the place of a body moving in a given elliptic trajectory at any assigned time.

Suppose A (Pl. 14. Fig. 2.) to be the principal vertex, S the focus, and O the centre of the ellipsis APB; and let P be the place of the body to be found. Produce OA to G, so as OG may be to OA as OA to OS. Erect the perpendicular GH; and about the centre O, with the interval OG, describe the circle GEF; and on the ruler GH as a base, suppose the wheel GEF to move forward, revolving about its axis, and in the mean time by its point A describing the cycloid ALI. which done, take GK to tEe perimeter GEFG of the wheel, in the ratio of the time in which the body, proceeding from A, desribed the arc AP, to the time of a whole revolution in the ellipsis. Erect the perpendicular KL meeting the cycloid in L, then LP drawn parallel to KG will meet this ellipsis in P the required place of the body.
For about the centre O with the interval OA describe the semi-circle AQB, and let LP, produced, if need be, meet the arc AQ in Q, and join SQ, OQ. Let OQ meet the arc EFG in F upon OQ let fall the perpendicular SR. The area APS is as the area AQS, that is, as the difference between the sector OQA and the triangle OQS, or as the difference of the rectangle , and , that is, because is given, as the difference between the arc AQ and the right line SR; and therefore (because the equality of the given ratios SR to the sine of the arc AQ, OS to OA, OA to OG, to GF, and by division. AQ - SR to GF - sine of the arc AQ) as GK the difference between the arc GF and the sine of the arc AQ. Q. E. D.
Scholium.

But since the description of this curve is difficult, a solution by approximation will be preferable. First let there be found a certain angle B which may be to an angle of 57,29578 degrees, which an arc equal to the radius subtends, as SH (Pl. 14. Fig. 3.) the distance of the foci, to AB the diameter of the ellipsis. Secondly, a certain length L, which may be to the radius in the same ratio inversely. And these being found, the problem may be solved by the following analysis. By any construction (or even by conjecture) suppose we know P the place of the body near its true place p. Then letting fall on the axis of the ellipsis the ordinate PR, from the proportion of the diameters of the ellipsis, the ordinate RQ of the circumscribed circle AQB will be given; which ordinate is the sine of the angle AOQ supposing AO to be the radius, and also cuts the ellipsis in P. It will be sufficient if that angle is found by a rude calculus in numbers near the truth. Suppose we also know the angle proportional to the time, that is, which is to four right angles, as the time in which the body described the arc Ap, to the time of one revolution in the ellipsis. Let this angle be N, Then take an angle D, which may be to the angle B as the sine of the angle AOQ to the radius; and an angle E which may be to the angle N - AOQ + D, as the length L to the same length L diminished by the co-sine of the angle AOQ, when that angle is less than a right angle, or increased thereby when greater. In the next place take an angle F that may be to the angle B, as the sine of the angle AOQ + E to the radius, and an angle G, that may be to the angle N - AOQ - E + F, as the length L to the same length L diminished by the co-sine of the angle AOQ + E, when that angle is less than a right angle, or increased thereby when greater. For the third time take an angle H, that may be to the angle B as the sine of the angle AOQ + E + G to the radius; and an angle I to the angle N - AQQ E - G + H, as the length L is to the same length L diminished by the co-sine of the angle AQQ + E - G when that angle is less than a right angle, or increased there by when greater. And so we may proceed in infinitum. Lastly, take the angle AOq equal to the angle AOQ + E + G + I + &c. and from its co-sine Or and the ordinate pr, which is to its line sine as the lesser axis of the ellipsis to the greater, we shall have p the correct place of the body. When the angle N - AOQ + D happens to be negative, the sign + of the angle E must be every where changed into -, and the sign - into +. And the same thing is to be understood of the signs of the angles G and I, when the angles N - AOQ - E + F, and N - AOQ - E - G + H come out negative. But the infinite series AOQ + B + G + I &c. converges so very fast, that it will be scarcely ever needful to proceed beyond the second term E. And the calculus is founded upon this theorem, that the area APS is as the difference between the arc AQ and the right line let fall from the focus S perpendicularly upon the radius OQ
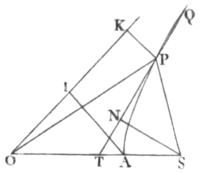
And by a calculus not unlike, the problem is solved in the hyperbola. Let its centre be O, (Pl. 14. Fig. 4.) its vertex A, its focus S, and asymptote OK. And suppose the quantity of the area to be cut off is known, as being proportional to the time. Let that be A, and by conjecture suppose we know the position of a right line SP, that cuts off an area APS near the truth. Join OP, and from A and P to the asymptote draw AI, PK parallel to the other asymptote and by the table of logarithms the area AIKP will be given, and equal thereto the area OPA, which subducted from the triangle OPS will leave the area cut off APS. And by applying 2APS - 2A, or 2A - 2APS, the double difference of the area A that was to be cut off, and the area APS that is cut off to the line SN that is let fall from the focus S. perpendicular upon the tangent TI, we shall have the length of the chord PQ. Which chord PQ is to be inscribed between A and P. if the area APS that is cut off be greater than the area A that was to be cut off, but towards the contrary side of the point P, if otherwise: and the point Q will be the place of the body more accurately. And by repeating the computation the place may be found perpetually to greater and greater accuracy.

And by such computations we have a general analytical revolution of the problem. But the particular calculus that follows, is better fitted for astronomical purposes. Supposing AO, OB, OD, (Pl. 14. Fig. 5.) to be the semi-axes of the ellipsis, and L its latus rectum, and D the difference betwixt the lesser semi-axis OD, and L, the half of the latus rectum: let an angle Y be found, whose line may be to the radius, as the rectangle under that difference D and AO + OD the half sum of the axes, to the figure of the greater axis AB. Find also an angle Z, whose sine may be to the radius, as the double rectangle under the distance of the foci SH and that difference D to triple the square of half the greater semi-axis AO. Those angles being once found, the place of the body may be thus determined. Take the angle T proportional to the time in which the arc BP was described, or equal to what is called the mean motion; and an angle V, the first equation of the mean motion to the angle Y, the greatest first eqation, as the line of double the angle T is to the radius; and an angle X, the second equation, to the angle Z, the second greatest equation, as the cube of the sine of the angle T is to the cube of the radius. Then take the angle BHP the mean motion equated equal to T + X + V the sum of the angles T, V, X, if the angle T is less than a right angle; or equal to T + X - V the difference of the same, if that angle T is greater than one and less than two right angles; and if HP meets the ellipsis in P, draw SP, and it will cut off the area BSP nearly proportional to the time.
This practice seems to be expeditious enough, because the angles V and X, taken in second minutes if you please, being very small, it will be sufficient to find two or three of their first figures. But it is likewise sufficiently accurate to answer to the theory of the planets motions. For even in the orbit of Mars, where the greatest equation of the centre amounts to ten degrees, the error will scarcely exceed one second. But when the angle of the mean motion equated BHP is found, the angle of the true motion BSP, and the distance SP are readily had by the known methods.
And so far concerning the motion of bodies in curve lines. But it may ascend come to pass that a moving body shall ascend or descend in a right line; and I shall now go on to explain what belongs to such kind of motions.


















