The Mathematical Principles of Natural Philosophy (1729)/Book 1/Section 7

by Isaac Newton

Section VII.

Concerning the rectilinear ascent and descent of bodies.

---

Proposition XXXII. Problem XXIV.

Supposing that the centripetal force is reciprocally proportional to the square of the distance of the places from the centre; it is required to define the spaces which a body, falling directly, describes in given times.

Plate 15, Figure 1

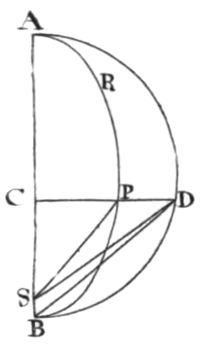
Case 1. If the body does not fall perpendicularly it will (by cor. 1. prop. 13.) describe some conic section whose focus is placed in the centre of force. Suppose that conic section to be ARPB (Pl. 15. Fig. 1.) and its focus S. And first, if the figure be an ellipsis; upon the greater axe thereof AB describe the semi-circle ADB, and let the right line DPC pass through the falling body, making right angles with the axis; and drawing DS, PS, the area ASD will be proportional to the area ASP, and therefore also to the time. The axis AB still remaining the same, let the breadth of the ellipsis be perpetually diminished, and the area ASD will always remain proportional the time. Suppose that breadth to be diminished in infinitum; and the orbit APB in that case coinciding with the axis AB, and the focus S with the extreme point of the axis B, the body will descend in the right line AC, and the area ABD will become proportional to the time. Wherefore the space AC will be given which the body describes in a given time by its perpendicular fall from the place A, if the area ABD is taken proportional to the time, and from the point D, the right line DC is let fall perpendicularly on the right line AB. Q. E. I.

Plate 15, Figure 2

Case 2. If the figure RPB is an hyperbola, (Fig. 2.) on the same principal diameter AB describe the rectangular hyperbola BED; and because the areas CSP, CBfP, SPfB, are severally to the several areas CSD, CBED, SDEB in the given ratio of the heights CP, CD; and the area SPfB is proportional to the time in which the body P will move through the arc PfB, the area SDEB will be also proportional to that time. Let the latus rectum of the hyperbola RPB be diminished in infinitum, the latus transversum remaining the seme; and the arc PB will come to coincide with the right line CB, and the focus S with the vertex B, and the right line SD with the right line BD. And there fire the area BDEB will be proportional to the time in which the body C, by its perpendicular descent, describes the line CB. Q. E. I.

Case 3. And by the like argument if the figure RPB is a parabola, (Fig. 3.) and to the same principal vertex B another parabola BED is described, that may always remain given while the former parabola in whose perimeter the body P moves, by having its latus rectum diminished and reduced to nothing, comes to coincide with the line CB; the segment BDEB will be proportional to the time in which that body P or C will descend to the centre S or B. Q. E. I.

Proposition XXXIII. Theorem IX.

The things above found being supposed, I say, that the velocity of a body in any place C is to the veolocity of a body, describing a circle about the centre B at the distance BC, in the subduplicate ratio of AC , the distance of the body from the remoter vertex A of the circle or rectangular hyperbola, to $\scriptstyle {\frac {1}{2}}AB$, the principal semi-diameter of the figure. Pl. 15. Fig. 4.

Plate 15, Figure 4 A

Plate 15, Figure 4 B

Let AB the common diameter of both figures RPB, DEB be bisected in O; and draw the right line PT that may touch the figure RPB in P, and likewise cut that common diameter AB (produced, if need be) in T; and let SY be perpendicular to this line. and BQ to this diameter, and suppose the latus rectum of the figure RPB to be L. From cor. 9. prop. 16. it is manifest that the velocity of a body, moving in the line RPB about the centre S, in any place P, is to the velocity of a body describing a circle about the same centre, at the distance SP, in the subduplicate ratio of the rectangle $\scriptstyle {\frac {1}{2}}\times SP$ to $\scriptstyle SY^{2}$.. For by the properties of the conic sections ACB is to $\scriptstyle CP^{2}$ as 2AO to L and therefore $\textstyle {\frac {2CP^{2}\times AO}{AP}}$ is equal to L. Therefore those velocities are to each other in the subduplicate $\textstyle {\frac {CP^{2}\times AO\times SP}{ACB}}$ to $\scriptstyle SY^{2}$. Moreover by the properties of the conic sections, CO is to BO as BO to TO, and (by composition or division) as CB to BT. Whence (by division or composition) as CB to BT. Whence (by division or composition) BO - or + CO will be to BO as CT to BT, that is AC will be to AO as CP to BQ; and therefore $\textstyle {\frac {CP^{2}\times AO\times SP}{ACB}}$ is equal to $\textstyle {\frac {BQ^{2}\times AC\times SP}{AO\times BC}}$. Now suppose CP, the breadth of the figure RPB, to be diminished in infinitum, so as the point P may come to coincide with the point C, and the point S with the point B, and the line SP with the line BC, and the line ST with the line BQ; and the velocity of the body now descending perpendicularly in the line CB will be to the velocity of a body describing a circle about the centre B at the distance BC, in the subduplicate ratio of $\textstyle {\frac {BQ^{2}\times AC\times SP}{AO\times BC}}$ to $\scriptstyle SY^{2}$, that is (neglecting the ratio's of equality of SP to BC, and $\scriptstyle BQ^{2}$ to $\scriptstyle SY^{2}$) in the subduplicate ratio of AC to AO or $\scriptstyle {\frac {1}{2}}AB$. Q. E. D.

Cor. 1. When the points B and S come to coincide, TC will become to TS, as AC to AO.

Cor. 2. A body revolving in any circle at a given distance from the centre, by its motion converted upwards will ascend to double its distance from the centre.

Proposition XXXUV. Theorem X.

Plate 15, Figure 5

If the figure BED is a parabola, I say that the velocity of a falling body in any place C is equal to the velocity by which a body may uniformly describe a circle about the centre B at half the interval BC. Pl. 15. fig. 5.

For (by cor. 7. prop. 16.) the velocity of a body describing a parabola RPB about the centre S, in any place P, is equal to the velocity of a body uniformly describing a circle about the same centre S at half the interval SP. Let the breadth CP of the parabola be diminished in infinitum, so as the parabolic arc PfB may come to coincide with the right line CB, the centre S with the vertex B, and the interval SP with the interval BC, and the proposition will be manifest. Q. E. D.

Proposition XXXV. Theorem XI.

The same things supposed, I say that the area of the figure DES, described by the indefinite radius SD, is equal to the area which a body with a radius equal to half the latus rectum of the figure DES, by uniformly revolving about the centre S, may be described in the same time.. Pl. 16. Fig. 1.

Plate 16, Figure 1

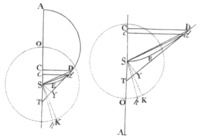
For suppose a body C in the smallest moment of time describes in falling the infinitely little line Cc, while another body K uniformly revolving about the centre S in the circle OKk, describes the arc Kk. Erect the perpendiculars CD, cd, meeting the figure DES in D. Join SD, Sd, SK, Sk, and draw Dd meeting the axis AS in T, and thereon let fall the perpendicular SY.

Case 1. If the figure DES is a circle or a rectangular hyperbola, bisect its transverse diameter AS in O, and SO will be half the latus rectum. And because TC is to TD as Cc to Dd, and TD to TS as CD to ST; ex æquo TC will be to TS, as CD x Cc to ST x Dd. But (by cor. 1. prop. 33) TC is to TS as AC to AO, to wit, if in the coalescence of the points D, d, the ultimate ratio's of the lines are taken. Wherefore AC is to AO or SK as CD x Cc to ST x Dd. Farther, the velocity of the descending body in C is to the velocity of a body describing a circle about the centre S, at the interval SC, in the subduplicate ratio of AC to AO or SK (by prop. 33.) and this velocity is to the velocity of a body describing the circle OKk in the subduplicate ratio of SK to SC (by cor. 6. prop. 4.) and ex æquo, the first velocity to the last, that is the little line Cc to the arc Kk, in the subduplicate ratio of AC to SC, that is in the ratio of AC to CD. Wherefore CD x Cc is equal to AC x Kk, and consequently AC to SK as AC x Kk to ST x Dd, and thence SK x KL equal to ST x Dd. and $\scriptstyle {\frac {1}{2}}SK\times Kk$ equal to $\scriptstyle {\frac {1}{2}}SY\times Dd$, that is, the area KSk equal to the area SDd. Therefore in every moment of time two equal particles, KSk and SDd, of areas are generated which, if their magnitude is diminished and their number increased in infinitum, obtain the ratio of equality, and consenquently (by cor. lem. 4.) the whole areas together generated are always equal. Q. E. D.

Plate 16, Figure 2

Case 2. But if the figure DES (Fig. 2.) is a parabola, we shall find as above CD x Cc to ST x Dd as TC to TS, that is, as 2 to 1; and that therefore $\scriptstyle {\frac {1}{4}}CD\times Cc$ is equal to $\scriptstyle {\frac {1}{2}}ST\times Dd$. But the velocity of the falling body in C is equal to the velocity with which a circle may be uniformly described at the interval $\scriptstyle {\frac {1}{2}}SC$, (by prop. 34.) And this velocity to the velocity with which a circle may be described with the radius SK, that is, the little line Cc to the arc Kk is (by cor. 5. prop. 4.) in the subduplicate ratio of SK to $\scriptstyle {\frac {1}{2}}CD$; that is, in the ratio of SK to $\scriptstyle {\frac {1}{2}}CD$. Wherefore $\scriptstyle {\frac {1}{2}}SK\times Kk$ is equal to $\scriptstyle {\frac {1}{4}}CD\times Cc$, and therefore equal to $\scriptstyle {\frac {1}{2}}SY\times Dd$; that is, the area KSk is equal to the area SDd as above. Q. E. D.

Proposition XXXVI. Problem XXV.

To determine the times of the descent of a body falling from a given place A. Pl. 16. Fig. 3.

Plate 16, Figure 3

Upon the diameter AS, the distance of the body from the centre at the beginning. describe the semi-circle ADS, as likewise the semi-circle OKH equal thereto, about the centre S. From any place C of the body, erect the ordinate CD, join SD, and make the sector OSI equal to the area ASD. It is evident by prop. 35. that the body in falling will describe the space AC in the same time in which another body, uniformly revolving about the centre S, may describe the arc OK. Q. E. F.

Proposition XXXVII. Problem XXVI.

To describe the times of the ascent or descent of a body projected upwards or downwards from a given place. Pl. 16. Fig. 4.

Plate 16, Figure 4

Suppose the body to go off from the given place G, in the direction of the line GS, with any velocity. In the duplicate ratio of this velocity to the uniform velocity in a circle, with which the body may revolve about the centre centre S at the given interval SG, take GA to $\scriptstyle {{\frac {1}{2}}AS}$. If that ratio is the same as of the number 2 to 1 the point A is infinitely remote; in which case a parabola is to be described with any latus rectum to the vertex S, and axis SG; as appears by prop. 34. But if that ratio is less or greater than ratio of 2 to 1, in the former case a circle, in the latter a rectangular hyperbola, is to be described on the diameter SA; as appears by prop. 33. Then about the centre S. with an interval equal to half the latus rectum, describe the circle HkK, and at the place G of the ascending or descending body, and at any other place C, erect the perpendiculars GI, CD; meeting the conic section or circle in I and D. Then joining SI, SD, let the sectors HSK, HSk be made equal to the segments SEIS, SEDS, and by prop. 35. the body G will describe the space GC in the same time in which the body K may describe the arc Kk. Q. E. F.

Proposition XXXVIII. Theorem XII.

Supposing that the centripetal force is proportional to the altitude or distance of places from the centre, I say, that the times and velocities of falling bodies, and the spaces which they describe, are respectively proportional to the arcs, and the right and versed sines of the arcs. Pl. 17. Fig. 1.

Suppose the body to fall from any place A in the right line AS; and about the centre of force S with the interval AS, describe the quadrant of a circle AE; and let CD be the right line of any arc AD; and the body A will in the time AD in falling describe the space AC, and in the place C will acquire the velocity CD.

This is demonstrated the same way from prop. 10. as prop. 32. was demonstrated from prop. 11.

cor. 1. Hence the times are equal in which one body falling from the place A arrives at the centre S, and another body revolving describes the quadrantal arc ADE.

cor. 2. Wherefore all the times are equal in which bodies falling from whatsoever places arrive at the centre. For all the periodic times of revolving bodies are equal, by cor. 3. prop. 4.

Proposition XXXIX. Problem XXVII.

Supossing a centripetal force of any kind, and granting the quadratures of curvilinear figures; it it required to find the velocity of a body, ascending or descending in a right line, in the several places through which it passes; as also the time in which it will arrive at any place; And vice versa.

Plate 17, Figure 1

Suppose the body E (Pl. 17. Fig. 1.) to fall from any place A in the right line ADEC; and from its place E imagine a perpendicular EG always erected, proportional to the centripetal force in that place tending to the centre C; and let BFG be a curve line, the locus of the point G. And in the beginning of the motion suppose EG to coincide with the perpendicular AB; and the velocity of the body in any place E will be as a right line whose power is the curvilinear area $\scriptstyle {\frac {1}{2}}ABGE$. Q. E. I.

In EG take EM reciprocally proportional to a right line whose power is the area $\scriptstyle {\frac {1}{2}}ABGE$, and let VLM be a curve line wherein the point M is always placed, and to which the right line AB produced is an asymptote, and the time in which the body is falling describes the line AE, will be as the curvilinear area ABTVME. Q. E. I.

For in the right line AE let there be taken the very small line DE of a given length, and let DLF be the place of the line EMG, when the body was in D; and if the centripetal force be such, that a right line whose power is the area $\scriptstyle {\frac {1}{2}}ABGE$, is as the velocity of the descending body, the area it self will be as the square of that velocity; that is, if for the velocities in D and E we write V and V + I, the area ABFD will be as VV, and the area $\scriptstyle {\frac {1}{2}}ABGE$ as VV + 2VI + II; and by division the area DFGE as 2VI + II and therefore $\textstyle {\frac {DFGE}{DE}}$ will be as $\textstyle {\frac {2VI+II}{DE}}$, that is, if we take the first ratio's of those quantities when just nascent, the length DF is as the quantity $\textstyle {\frac {2VI}{DE}}$ and therefore also as half that quantity $\textstyle {\frac {I\times V}{DE}}$. But the time, in which the body in falling describes the ver small line DE is as that line directly and the velocity V inversely, and the force will be as the increment I of the velocity directly and the time inversely, and therefore if we take the first ratio's when those quantities are just nascent as $\textstyle {\frac {I\times V}{DE}}$, that is as the length DF. Therefore a force proportional to DF or EG will cause the body to descend with a velocity that is as the right line whose power is the area ABGE. Q. E. D.

Moreover since the time, in which a very small line DE of a given length may be described, is as the velocity inversely, and therefore also inversely as a right line whose square is equal to the area ABFD; and since the line DL, and by consequence the nascent area DLME, will be as the same right line inversely: the time will be as the area DLME, and the sum of all the times will be as the sum of all the area's; that is (by cor. lem. 4.) the whole time in which the line AE is described will be as the whole area ATVME. Q. E. D,

Cor. 1. Let P be the place from whence a body ought to fall, so as that when urged by any known uniform centripetal force (such as gravity is vulgarly supposed to be) it may acquire in the place D a velocity, equal to the velocity which another body, falling by any force whatever, hath acquired in that place D. In the perpendicular DF let there be taken DR, which may be to DF as that uniform force to the other force in the place D. Compleat the rectangle PDRQ, and cut off the area ABFD equal to that rectangle. Then A will be the place from whence the other body fell. For compleating the rectangle DRSE, since the area AbFD is to the area DFGE as VV to 2VI, and therefore as $\scriptstyle {\frac {1}{2}}VI$, that is, as half the whose velocity to the increment of the velocity of the body falling by the unequable force; and in like manner the area PQRD to the area DRSE, as half the whole velocity to the increment of the velocity of the body falling by the uniform force; and since those increments (by reason of the equality of the nascent times) are as the generating forces, that is, as the ordinates DF, DR, and consequently as the nascent area's DFGE, DRSE; therefore ex æquo the whole areas ABFD, PQRD will be to one another as the halves of the whole velocities, and therefore, because the velocities are equal, they become equal also.

Cor. 2. Whence if any body be projected either upwards or downwards with a given velocity from any place D, and there be given the law of centripetal force acting on it, its velocity will be found in any other place as e, by erecting the ordinate eg, and taking that velocity to the velocity in the place D, as a right line whose power is the rectangle PQRD, either increased by the curvilinear area Dfge, if the place e is below the place D, or diminished by the same area DFge if it be higher, is to the right line whole power is the rectangle PQRD alone.

Cor. 3. The time is also known by erecting the ordinate em reciprocally proportional to the square root of PQRD + or - DFge, and taking the time in which the body has described the line De, to the time in which another body has fallen with an uniform force from P, and in falling arrived at D, in the proportion of the curvilinear area DLme to the rectangle 2PD x DL. For the time in which a body falling with an uniform force hath described the line PD, is to the time in which the same body has described the line PE, in the subduplicate ratio of PD to PE; that is (the very small line DE being just nascent) in the ratio of PD to $\scriptstyle PD+{\frac {1}{2}}DE$ to 2PD + DE, and by division to the time in which the body hath described the small line DE, as 2PD to DE, and therefore as the rectangle 2PD + DL to the area DLME; and the time in which both the bodies described the very small line DE is to the time in which the body moving unequably hath described the line De, as thearea DLME to the area DLme; and ex æquo the first mentioned of these times is to the last as the rectangle 2PD x DL to the area DLme.

Book 3, Section 7 - End decoration