Translation:On the Proof of the Reality of the Luminiferous Aether
On the proof of the reality of the luminiferous aether by the experiment with a rotating interferometer
Note by G. Sagnac, presented by E. Bouty.
In Comptes rendus of October 27 (p. 708 of this Volume), I showed that an interferometer whose optical circuit encloses a specific area, and which rotates in the plane of this circuit, detects its overall motion with respect to the vacuum aether.
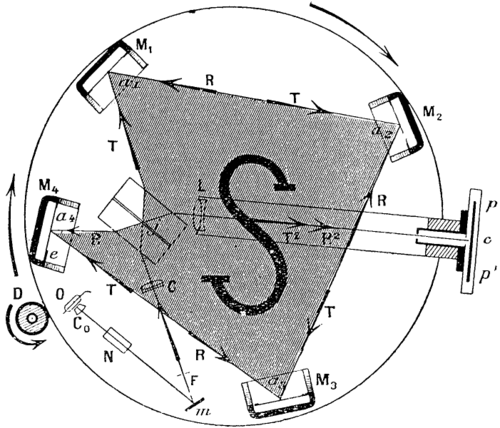
1. The interferometer, already described briefly, is schematically illustrated in the figure: a horizontally rotating plate (50cm in diameter) carries, firmly screwed on it (the adjustable screws being secured by lock screws), all the optical parts as well as the source of light O, a small lamp with a horizontal metal filament. A microscope objective projects the image of this filament through the Nicol prism N onto the horizontal slit F in the focal plane of the collimating objective C; m is a reflecting mirror. The vertically polarized (per Fresnel's convention) parallel beam is divided by an air gap beam splitter ,[1] as in the usual interferometer of my research (Comptes rendus, t. 150, 1910, p. 1676), which I applied to the optical study of the motion of the Earth (Congrès de Bruxelles, sept. 1910, t. I, p. 207; Comptes rendus, t. 152, 1911, p. 310; Le Radium, 1911, p. I): the ray T transmitted through the air gap is reflected successively on four mirrors M and traverses the closed circuit of area S. The beam R which is reflected by the same air gap traverses the same circuit in the opposite direction. Returning to , the beam T, again transmitted, and the beam R, again reflected, are superimposed in the same direction along T² and R², and form interference fringes at the principal focus of the lens L on the fine-grained photographic plate .
2. Mode of operation. I point out that perfect superposition of the two opposite beams T and R is characterized by general extinction of the telescope field for the radiation employed, which is here close to the indigo portion of the mercury arc spectrum. Starting from there, a small rotation ε of the beam splitter around a vertical axis, in the clockwise direction (swing-direction D[2]), or counter-clockwise (swing-direction S[3]), narrows the dark field into a central vertical fringe bordered by parallel side fringes.
With the fringes appropriately adjusted and the photographic plate mounted in its frame and uncovered in red light,[4] I gradually start up an electrical motor whose vertical axis carries a horizontal disc D that is encircled by a leather belt and which rolls this belt on the thick rim of the plate. When the desired rotational frequency N is reached, I make a photographic exposure by establishing electric current to the small lamp O, using a sliding contact on the axis of the revolving plate.
3. Direction and magnitude of the optical vortex effect. - In Fresnel's aether hypothesis, the light waves T and R are propagated in the aether of vacuum with a velocity V0 that is independent of the overall motion of the interferometer; the phase of the waves T in the clockwise direction of propagation (see the figure) is altered along the closed circuit, as if the luminiferous aether were driven by a counter-clockwise vortex when the circuit rotates in the D direction. The magnitude 4πNS of this vortex, that is, the relative circulation C of the aether in the optical circuit, gives, according to the expression , the phase delay x of the wave T and the equal advance of wave R propagating in the opposite direction; the displacement y of the fringes equals 2x. The absolute direction of this fringe displacement must be from p to p′, that is, the d direction, in the same sense as the rotation of the interferometer (the effect is in the positive direction) when the swing-direction adjustment of the beam-splitter is D. The
total fringe displacement z, equal to 2y or 4x, measured by comparing an s exposure with a d exposure,[5] then must be of direction d. If the swing-direction of the beam-splitter adjustment is S, displacements y and z will change sign.
During many tests, I constantly observed the predicted fringe displacements. The fact that effect z reverses when I turn the beam-splitter by only a fraction of degree to reverse the swing-direction of its adjustment, characterizes the effect as a phase difference related to the motion of the interferometer, and makes it possible to distinguish it from the effect of deformation of the optical components.[6]
Here are the examples of measurements of z compared with the computed values using the expression ; I determined the wavelength λ corresponding to the distance between the interference rings obtained by the small lamp O, by comparing this distance with the distance between the slightly different diameter interference rings obtained using the 436mμ line from a mercury arc. Measurements are made by one of the two methods indicated in my note of October 27. The central fringe c which is clear on the negative that we studied, and the dark lateral fringes f, are bordered by only relatively narrow penumbras, which was conducive to precision measurement of the fringe peaks which I performed under low magnification, while framing the fringe peak between two parallel threads of an ocular micrometer.
| Swing-direction. | N. | z from c | z from f. | z calc. | |
| Method 1 (S=863cm²).... | S | 0,86 | -0,026 | » | -0,029 |
| D | 1,88 | +0,070 | » | +0,065 | |
| Method 2 (S=866cm²).... | S | 2,2 | -0,072 | -0,078 | -0,075 |
| S | 2,35 | -0,077 | -0,080 | -0,079 |
The interferometer produces and measures, by the expression z, the first order vortex-effect of its overall motion, without using any external reference.
The result of these measurements shows that, in ambient space, light propagates with a velocity , independent of the collective motion of the source of light O and the optical system. This property of space experimentally characterizes the luminiferous aether. The interferometer measures, according to the expression , the relative circulation of the luminiferous aether in the closed circuit .
Translator's Notes
[edit]- ↑ The s-polarized light selected by the Nicol prism was strongly reflected by the uncoated surfaces of the air gap beam splitter. Fine adjustments to the air gap allowed control, through interference effects, of the percent transmission/reflection.
- ↑ D and d, used variously in the text, are abbreviations for the Latin dexter, right-handed
- ↑ S and s, used variously in the text, are abbreviations for the Latin sinister, left-handed
- ↑ Photographic plates of this period were almost totally insensitive to red light, so the experimenter could work with a red safelight turned on.
- ↑ s and d exposures were adjacent to each other on the same piece of film. This was done by positioning a razor edge to block off the upper or lower portion of the fringe pattern prior to starting up the turntable in a counter-clockwise (s) or clockwise (d) direction.
- ↑ At rotation rates of up to 2.35 revolutions per second, centrifugal effects at the edge of the turntable reached up to 5.5 times the force of gravity. Nevertheless, fringe shifts due to deformation of the optical components were minimal. This is due to the common-path design of the optical circuit: clockwise and counterclockwise beams traveled along the same path, so any change in path length to one beam would be exactly matched by the other.
![]()
![]() This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
This work is a translation and has a separate copyright status to the applicable copyright protections of the original content.
| Original: |
This work is in the public domain in the United States because it was published before January 1, 1929. The longest-living author of this work died in 1926, so this work is in the public domain in countries and areas where the copyright term is the author's life plus 97 years or less. This work may be in the public domain in countries and areas with longer native copyright terms that apply the rule of the shorter term to foreign works.
Public domainPublic domainfalsefalse |
|---|---|
| Translation: |
This work is released under the Creative Commons Attribution-ShareAlike 3.0 Unported license, which allows free use, distribution, and creation of derivatives, so long as the license is unchanged and clearly noted, and the original author is attributed.
Public domainPublic domainfalsefalse |









