1911 Encyclopædia Britannica/Abacus
ABACUS (Gr. ἄβαξ, a slab; Fr. abaque, tailloir), in architecture, the upper member of the capital of a column. Its chief function is to provide a larger supporting surface for the architrave or arch it has to carry. In the Greek Doric order the abacus is a plain square slab. In the Roman and Renaissance Doric orders it is crowned by a moulding. In the Archaic-Greek Ionic order, owing to the greater width of the capital, the abacus is rectangular in plan, and consists of a carved ovolo moulding. In later examples the abacus is square, except where there are angle volutes, when it is slightly curved over the same. In the Roman and Renaissance Ionic capital, the abacus is square with a fillet on the top of an ogee moulding, but curved over angle volutes. In the Greek Corinthian order the abacus is moulded, its sides are concave and its angles canted (except in one or two exceptional Greek capitals,
Fig. 1.—Roman Abacus. where it is brought to a sharp angle); and the same shape is adopted in the Roman and Renaissance Corinthian and Composite capitals, in some cases with the ovolo moulding carved.In Romanesque architecture the abacus is square with the lower edge splayed off and moulded or carved, and the same was retained in France during the medieval period; but in England, in Early English work, a circular deeply moulded abacus was introduced, which in the 14th and 15th centuries was transformed into an octagonal one. The diminutive of Abacus, Abaciscus, is applied in architecture to the chequers or squares of a tessellated pavement. “Abacus” is also the name of an instrument employed by the ancients for arithmetical calculations; pebbles, bits of bone or coins being used as counters. Fig. 1 shows a Roman abacus taken from an ancient monument. It contains seven long and seven shorter rods or bars, the former having four perforated beads running on them and the latter one. The bar marked I indicates units, X tens, and so on up to millions. The beads on the shorter bars denote fives,—five units, five tens, &c. The rod Θ and corresponding short rod are for marking ounces; and the short quarter rods for fractions of an ounce.
The Swan-Pan of the Chinese (fig. 2) closely resembles the Roman abacus in its construction and use. Computations are made with it by means of balls of bone or ivory running on slender bamboo rods, similar to the simpler board, fitted up with beads strung on wires, which is employed in teaching the rudiments of arithmetic in English schools.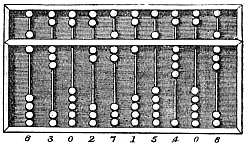
Fig. 2.—Chinese Swan-Pan.
The name of “abacus” is also given, in logic, to an instrument, often called the “logical machine,” analogous to the mathematical abacus. It is constructed to show all the possible combinations of a set of logical terms with their negatives, and, further, the way in which these combinations are affected by the addition of attributes or other limiting words, i.e. to simplify mechanically the solution of logical problems. These instruments are all more or less elaborate developments of the “logical slate,” on which were written in vertical columns all the combinations of symbols or letters which could be made logically out of a definite number of terms. These were compared with any given premises, and those which were incompatible were crossed off. In the abacus the combinations are inscribed each on a single slip of wood or similar substance, which is moved by a key; incompatible combinations can thus be mechanically removed at will, in accordance with any given series of premises. The principal examples of such machines are those of W. S. Jevons (Element. Lessons in Logic, c. xxiii.), John Venn (see his Symbolic Logic, 2nd ed., 1894, p. 135), and Allan Marquand (see American Academy of Arts and Sciences, 1885, pp. 303–7, and Johns Hopkins University Studies in Logic, 1883).