1911 Encyclopædia Britannica/Calorimetry
CALORIMETRY, the scientific name for the measurement of quantities of heat (Lat. calor), to be distinguished from thermometry, which signifies the measurement of temperature. A calorimeter is any piece of apparatus in which heat is measured. This distinction of meaning is purely a matter of convention, but it is very rigidly observed. Quantities of heat may be measured indirectly in a variety of ways in terms of the different effects of heat on material substances. The most important of these effects are (a) rise of temperature, (b) change of state, (c) transformation of energy.
§ 1. The rise of temperature of a body, when heat is imparted to it, is found to be in general nearly proportional to the quantity of heat added. The thermal capacity of a body is measured by the quantity of heat required to raise its temperature one degree, and is necessarily proportional to the mass of the body for bodies of the same substance under similar conditions. The specific heat of a substance is sometimes defined as the thermal capacity of unit mass, but more often as the ratio of the thermal capacity of unit mass of the substance to that of unit mass of water at some standard temperature. The two definitions are identical, provided that the thermal capacity of unit mass of water, at a standard temperature, is taken as the unit of heat. But the specific heat of water is often stated in terms of other units. In any case it is necessary to specify the temperature, and sometimes also the pressure, since the specific heat of a substance generally depends to some extent on the external conditions. The methods of measurement, founded on rise of temperature, may be classed as thermometric methods, since they depend on the observation of change of temperature with a thermometer. The most familiar of these are the method of mixture and the method of cooling.
§ 2. The Method of Mixture consists in imparting the quantity of heat to be measured to a known mass of water, or some other standard substance, contained in a vessel or calorimeter of known thermal capacity, and in observing the rise of temperature produced, from which data the quantity of heat may be found as explained in all elementary text-books. This method is the most generally convenient and most readily applicable of calorimetric methods, but it is not always the most accurate, for various reasons. Some heat is generally lost in transferring the heated body to the calorimeter; this loss may be minimized by performing the transference rapidly, but it cannot be accurately calculated or eliminated. Some heat is lost when the calorimeter is raised above the temperature of its enclosure, and before the final temperature is reached. This can be roughly estimated by observing the rate of change of temperature before and after the experiment, and assuming that the loss of heat is directly proportional to the duration of the experiment and to the average excess of temperature. It can be minimized by making the mixing as rapid as possible, and by using a large calorimeter, so that the excess of temperature is always small. The latter method was generally adopted by J. P. Joule, but the rise of temperature is then difficult to measure with accuracy, since it is necessarily reduced in nearly the same proportion as the correction. There is, however, the advantage that the correction is rendered much less uncertain by this procedure, since the assumption that the loss of heat is proportional to the temperature-excess is only true for small differences of temperature. Rumford proposed to eliminate this correction by starting with the initial temperature of the calorimeter as much below that of its enclosure as the final temperature was expected to be above the same limit. This method has been very generally recommended, but it is really bad, because, although it diminishes the absolute magnitude of the correction, it greatly increases the uncertainty of it and therefore the probable error of the result. The coefficient of heating of a calorimeter when it is below the temperature of its surroundings is seldom, if ever, the same as the coefficient of cooling at the higher temperature, since the convection currents, which do most of the heating or cooling, are rarely symmetrical in the two cases, and moreover, the duration of the two stages is seldom the same. In any case, it is desirable to diminish the loss of heat as much as possible by polishing the exterior of the calorimeter to diminish radiation, and by suspending it by non-conducting supports, inside a polished case, to protect it from draughts. It is also very important to keep the surrounding conditions as constant as possible throughout the experiment. This may be secured by using a large water-bath to surround the apparatus, but in experiments of long duration it is necessary to use an accurate temperature regulator. The method of lagging the calorimeter with cotton-wool or other non-conductors, which is often recommended, diminishes the loss of heat considerably, but renders it very uncertain and variable, and should never be used in work of precision. The bad conductors take so long to reach a steady state that the rate of loss of heat at any moment depends on the past history more than on the temperature of the calorimeter at the moment. A more serious objection to the use of lagging of this kind is the danger of its absorbing moisture. The least trace of damp in the lagging, or of moisture condensed on the surface of the calorimeter, may produce serious loss of heat by evaporation. This is another objection to Rumford’s method of cooling the calorimeter below the surrounding temperature before starting. Among minor difficulties of the method may be mentioned the uncertainty of the thermal capacity of the calorimeter and stirrer, and of the immersed portion of the thermometer. This is generally calculated by assuming values for the specific heats of the materials obtained by experiment between 100° C. and 20° C. Since the specific heats of most metals increase rapidly with rise of temperature, the values so obtained are generally too high. It is best to make this correction as small as possible by using a large calorimeter, so that the mass of water is large in proportion to that of metal. Analogous difficulties arise in the application of other calorimetric methods. The accuracy of the work in each case depends principally on the skill and ingenuity of the experimentalist in devising methods of eliminating the various sources of error. The form of apparatus usually adopted for the method of mixtures is that of Regnault with slight modifications, and figures and descriptions are given in all the text-books. Among special methods which have been subsequently developed there are two which deserve mention as differing in principle from the common type. These are (1) the constant temperature method, (2) the continuous flow method.
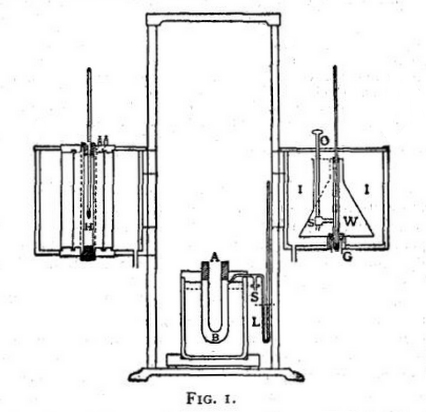
The constant temperature method of mixtures was proposed by N. Hesehus (Jour. Phys., 1888, vii. p. 489). Cold water at a known temperature is added to the calorimeter, immediately after dropping in the heated substance, at such a rate as to keep the temperature of the calorimeter constant, thus eliminating the corrections for the water equivalent of the calorimeter and the external loss of heat. The calorimeter is surrounded by an air-jacket connected to a petroleum gauge which indicates any small change of temperature in the calorimeter, and enables the manipulator to adjust the supply of cold water to compensate it. The apparatus as arranged by F. A. Waterman is shown in fig. 1 (Physical Review, 1896, iv. p. 161).
 |
A is the calorimetric tube, B the air-jacket and L the gauge. H is an electric heater for raising the body to a suitable temperature, which can swing into place directly over the calorimeter. W is a conical can containing water cooled by ice I nearly to 0°, which is swung over the calorimeter as soon as the hot body has been introduced and the heater removed. The cold water flow is regulated by a tap S with a long handle O, and its temperature is taken by a delicate thermometer with its bulb at G. The method is interesting, but the manipulations and observations involved are more troublesome than with the ordinary type of calorimeter, and it may be doubted whether any advantage is gained in accuracy.
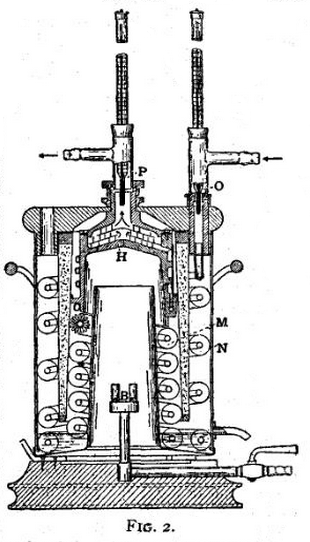
The continuous flow method is specially applicable to the important case of calorific value of gaseous fuel, where a large quantity of heat is continuously generated at a nearly uniform rate by combustion. Fig. 2 illustrates a recent type of gas calorimeter devised by C. V. Boys (Proc. R.S., 1906, A. 77, p. 122). The heated products of combustion from the burner B impinge on a metal box H, through which water is circulating, and then pass downwards and outwards through a spiral cooler which reduces them practically to the atmospheric temperature. A steady stream of water enters the apparatus by the inflow thermometer O, flows through the spiral coolers N and M, and finally through the box H, where it is well mixed before passing the outflow thermometer P. As soon as a steady state is reached, the difference of temperature between the outflow and inflow thermometers, multiplied by the current of water in grammes per minute gives the heat per minute supplied by combustion. The gas current is simultaneously observed by a suitable meter, which, with subsidiary corrections for pressure, temperature, &c., gives the necessary data for deducing calorific value.
A continuous flow calorimeter has been used by the writer for measuring quantities of heat conveyed by conduction (see Conduction of Heat), and also for determining the variation of the specific heat of water. In the latter case two steady currents of water at different temperatures, say 0° and 100° are passed through an equalizer, and the resulting temperature measured without mixing the currents, which are then separately determined by weighing. This is a very good method of comparing the mean specific heats over two ranges of temperature such as 0-50, and 50-100, or 0-20 and 20-40, but it is not so suitable as the electric method described below for obtaining the actual specific heat at any point of the range.
§ 3. Method of Cooling.—A common example of this method is the determination of the specific heat of a liquid by filling a small calorimeter with the liquid, raising it to a convenient temperature, and then setting it to cool in an enclosure at a steady temperature, and observing the time taken to fall through a given range when the conditions have become fairly steady. The same calorimeter is afterwards filled with a known liquid, such as water, and the time of cooling is observed through the same range of temperature, in the same enclosure, under the same conditions. The ratio of the times of cooling is equal to the ratio of the thermal capacities of the calorimeter and its contents in the two cases. The advantage of the method is that there is no transference or mixture; the defect is that the whole measurement depends on the assumption that the rate of loss of heat is the same in the two cases, and that any variation in the conditions, or uncertainty in the rate of loss, produces its full effect in the result, whereas in the previous case it would only affect a small correction. Other sources of uncertainty are, that the rate of loss of heat generally depends to some extent on the rate of fall of temperature, and that it is difficult to take accurate observations on a rapidly falling thermometer. As the method is usually practised, the calorimeter is made very small, and the surface is highly polished to diminish radiation. It is better to use a fairly large calorimeter to diminish the rate of cooling and the uncertainty of the correction for the water equivalent. The surface of the calorimeter and the enclosure should be permanently blackened so as to increase the loss of heat by radiation as much as possible, as compared with the losses by convection and conduction, which are less regular. For accurate work it is essential that the liquid in the calorimeter should be continuously stirred, and also in the enclosure, the lid of which must be water-jacketed, and kept at the same steady temperature as the sides. When all these precautions are taken, the method loses most of the simplicity which is its chief advantage. It cannot be satisfactorily applied to the case of solids or powders, and is much less generally useful than the method of mixture.
§ 4. Method of Fusion.—The methods depending on change of state are theoretically the simplest, since they do not necessarily involve any reference to thermometry, and the corrections for external loss of heat and for the thermal capacity of the containing vessels can be completely eliminated. They nevertheless present peculiar difficulties and limitations, which render their practical application more troublesome and more uncertain than is usually supposed. They depend on the experimental fact that the quantity of heat required to produce a given change of state (e.g. to convert one gramme of ice at 0° C. into water at 0° C., or one gramme of water at 100° C. into steam at 100° C.) is always the same, and that there need be no change of temperature during the process. The difficulties arise in connexion with the determination of the quantities of ice melted or steam condensed, and in measuring the latent heat of fusion or vaporization in terms of other units for the comparison of observations. The earlier forms of ice-calorimeter, those of Black, and of Laplace and Lavoisier, were useless for work of precision, on account of the impossibility of accurately estimating the quantity of water left adhering to the ice in each case. This difficulty was overcome by the invention of the Bunsen calorimeter, in which the quantity of ice melted is measured by observing the diminution of volume, but the successful employment of this instrument requires considerable skill in manipulation. The sheath of ice surrounding the bulb must be sufficiently continuous to prevent escape of heat, but it must not be so solid as to produce risk of strain. The ideal condition is difficult to secure. In the practical use of the instrument it is not necessary to know both the latent heat of fusion of ice and the change of volume which occurs on melting; it is sufficient to determine the change of volume per calorie, or the quantity of mercury which is drawn into the bulb of the apparatus per unit of heat added. This can be determined by a direct calibration, by inserting a known quantity of water at a known temperature and observing the contraction, or weighing the mercury drawn into the apparatus. In order to be independent of the accuracy of the thermometer employed for observing the initial temperature of the water introduced, it has been usual to employ water at 100° C., adopting as unit of heat the “mean calorie,” which is one-hundredth part of the heat given up by one gramme of water in cooling from 100° to 0° C. The weight of mercury corresponding to the mean calorie has been determined with considerable care by a number of observers well skilled in the use of the instrument. The following are some of their results:—Bunsen, 15.41 mgm.; Velten, 15.47 mgm.; Zakrevski, 15.57 mgm.; Staub, 15.26 mgm. The explanation of these discrepancies in the fundamental constant is not at all clear, but they may be taken as an illustration of the difficulties of manipulation attending the use of this instrument, to which reference has already been made. It is not possible to deduce a more satisfactory value from the latent heat and the change of density, because these constants are very difficult to determine. The following are some of the values deduced by well-known experimentalists for the latent heat of fusion:—Regnault, 79.06 to 79.24 calories, corrected by Person to 79.43; Person, 79.99 calories; Hess, 80.34 calories; Bunsen, 80.025 calories. Regnault, Person and Hess employed the method of mixture which is probably the most accurate for the purpose. Person and Hess avoided the error of water sticking to the ice by using dry ice at various temperatures below 0° C., and determining the specific heat of ice as well as the latent heat of fusion. These discrepancies might, no doubt, be partly explained by differences in the units employed, which are somewhat uncertain, as the specific heat of water changes rapidly in the neighbourhood of 0° C; but making all due allowance for this, it remains evident that the method of ice-calorimetry, in spite of its theoretical simplicity, presents grave difficulties in its practical application.
 |
| Fig. 3. |
One of the chief difficulties in the practical use of the Bunsen calorimeter is the continued and often irregular movement of the mercury column due to slight differences of temperature, or pressure between the ice in the calorimeter and the ice bath in which it is immersed. C. V. Boys (Phil. Mag., 1887, vol. 24, p. 214) showed that these effects could be very greatly reduced by surrounding the calorimeter with an outer tube, so that the ice inside was separated from the ice outside by an air space which greatly reduces the free passage of heat. The present writer has found that very good results may be obtained by enclosing the calorimeter in a vacuum jacket (as illustrated in fig. 3), which practically eliminates conduction and convection. If the vacuum jacket is silvered inside, radiation also is reduced to such an extent that, if the vacuum is really good, the external ice bath may be dispensed with for the majority of purposes. If the inner bulb is filled with mercury instead of water and ice, the same arrangement answers admirably as a Favre and Silbermann calorimeter, for measuring small quantities of heat by the expansion of the mercury.
The question has been raised by E. L. Nichols (Phys. Rev. vol. 8, January 1899) whether there may not be different modifications of ice with different densities, and different values of the latent heat of fusion. He found for natural pond-ice a density 0.9179 and for artificial ice 0.9161. J. Vincent (Phil. Trans. A. 198, p. 463) also found a density .9160 for artificial ice, which is probably very nearly correct. If such variations of density exist, they may introduce some uncertainty in the absolute values of results obtained with the ice calorimeter, and may account for some of the discrepancies above enumerated.
§ 5. The Method of Condensation was first successfully applied by J. Joly in the construction of his steam calorimeter, a full description of which will be found in text-books. The body to be tested is placed in a special scale-pan, suspended by a fine wire from the arm of a balance inside an enclosure which can be filled with steam at atmospheric pressure. The temperature of the enclosure is carefully observed before admitting steam. The weight of steam condensed on the body gives a means of calculating the quantity of heat required to raise it from the atmospheric temperature up to 100° C. in terms of the latent heat of vaporization of steam at 100° C. There can be no appreciable gain or loss of heat by radiation, if the admission of the steam is sufficiently rapid, since the walls of the enclosure are maintained at 100° C., very nearly. The thermal capacity of the scale-pan, &c., can be determined by a separate experiment, or, still better, eliminated by the differential method of counterpoising with an exactly similar arrangement on the other arm of the balance. The method requires very delicate weighing, as one calorie corresponds to less than two milligrammes of steam condensed; but the successful application of the method to the very difficult problem of measuring the specific heat of a gas at constant volume, shows that these and other difficulties have been very skilfully overcome. The application of the method appears to be practically limited to the measurements of specific heat between the atmospheric temperature and 100° C. The results depend on the value assumed for the latent heat of steam, which Joly takes as 536.7 calories, following Regnault. Joly has himself determined the mean specific heat of water between 12° and 100° C. by this method, in terms of the latent heat of steam as above given, and finds the result .9952. Assuming that the mean specific heat of water between 12° and 100° is really 1.0011 in terms of the calorie at 20° C. (see table, p. 66), the value of the latent heat of steam at 100° C., as determined by Joly, would be 540.2 in terms of the same unit. The calorie employed by Regnault is to some extent uncertain, but the difference is hardly beyond the probable errors of experiment, since it appears from the results of recent experiments that Regnault made an error of the same order in his determination of the specific heat of water at 100° C.
§ 6. Energy Methods.—The third general method of calorimetry, that based on the transformation of some other kind of energy into the form of heat, rests on the general principle of the conservation of energy, and on the experimental fact that all other forms of energy are readily and completely convertible into the form of heat. It is therefore often possible to measure quantities of heat indirectly, by measuring the energy in some other form and then converting it into heat. In addition to its great theoretical interest, this method possesses the advantage of being frequently the most accurate in practical application, since energy can be more accurately measured in other forms than in that of heat. The two most important varieties of the method are (a) mechanical, and (b) electrical. These methods have reached their highest development in connexion with the determination of the mechanical equivalent of heat, but they may be applied with great advantage in connexion with other problems, such as the measurement of the variation of specific heat, or of latent heats of fusion or vaporization.
§ 7. Mechanical Equivalent of Heat.—The phrase “mechanical equivalent of heat” is somewhat vague, but has been sanctioned by long usage. It is generally employed to denote the number of units of mechanical work or energy which, when completely converted into heat without loss, would be required to produce one heat unit. The numerical value of the mechanical equivalent necessarily depends on the particular units of heat and work employed in the comparison. The British engineer prefers to state results in terms of foot-pounds of work in any convenient latitude per pound-degree-Fahrenheit of heat. The continental engineer prefers kilogrammetres per kilogramme-degree-centigrade. For scientific use the C.G.S. system of expression in ergs per gramme-degree-centigrade, or “calorie,” is the most appropriate, as being independent of the value of gravity. A more convenient unit of work or energy, in practice, on account of the smallness of the erg, is the joule, which is equal to 10.7 ergs, or one watt-second of electrical energy. On account of its practical convenience, and its close relation to the international electrical units, the joule has been recommended by the British Association for adoption as the absolute unit of heat. Other convenient practical units of the same kind would be the watt-hour, 3600 joules, which is of the same order of magnitude as the kilo-calorie, and the kilowatt-hour, which is the ordinary commercial unit of electrical energy.
 |
| Fig. 4. |
§ 8. Joule.—The earlier work of Joule is now chiefly of historical interest, but his later measurements in 1878, which were undertaken on a larger scale, adopting G. A. Hirn’s method of measuring the work expended in terms of the torque and the number of revolutions, still possess value as experimental evidence. In these experiments (see fig. 4) the paddles were revolved by hand at such a speed as to produce a constant torque on the calorimeter h, which was supported on a float w in a vessel of water v, but was kept at rest by the couple due to a pair of equal weights k suspended from fine strings passing round the circumference of a horizontal wheel attached to the calorimeter. Each experiment lasted about forty minutes, and the rise of temperature produced was nearly 3° C. The calorimeter contained about 5 kilogrammes of water, so that the rate of heat-supply was about 6 calories per second. Joule’s final result was 772.55 foot-pounds at Manchester per pound-degree-Fahrenheit at a temperature of 62° F., but individual experiments differed by as much as 1%. This result in C.G.S. measure is equivalent to 4.177 joules per calorie at 16.5° C., on the scale of Joule’s mercury thermometer. His thermometers were subsequently corrected to the Paris scale by A. Schuster in 1895, which had the effect of reducing the above figure to 4.173.
§ 9. Rowland.—About the same time H. A. Rowland (Proc. Amer. Acad. xv. p. 75, 1880) repeated the experiment, employing the same method, but using a larger calorimeter (about 8400 grammes) and a petroleum motor, so as to obtain a greater rate of heating (about 84 calories per second), and to reduce the importance of the uncertain correction for external loss of heat. Rowland’s apparatus is shown in fig. 5. The calorimeter was suspended by a steel wire, the torsion of which made the equilibrium stable. The torque was measured by weights O and P suspended by silk ribbons passing over the pulleys n and round the disk kl. The power was transmitted to the paddles by bevel wheels, f, g, rotating a spindle passing through a stuffing box in the bottom of the calorimeter. The number of revolutions and the rise of temperature were recorded on a chronograph drum. He paid greater attention to the important question of thermometry, and extended his researches over a much wider range of temperature, namely 5° to 35° C. His experiments revealed for the first time a diminution in the specific heat of water with rise of temperature between 0° and 30° C., amounting to four parts in 10.000 per 1° C. His thermometers were compared with a mercury thermometer standardized in Paris, and with a platinum thermometer standardized by Griffiths. The result was to reduce the coefficient of diminution of specific heat at 15° C. by nearly one half, but the absolute value at 20° C. is practically unchanged. Thus corrected his values are as follows:—
| Temperature | 10° | 15° | 20° | 25° | 30° | 35° |
| Joules per cal. | 4.197 | 4.188 | 4.181 | 4.176 | 4.175 | 4.177 |
These are expressed in terms of the hydrogen scale, but the difference from the nitrogen scale is so small as to be within the limits of experimental error in this particular case. Rowland himself considered his results to be probably correct to one part in 500, and supposed that the greatest uncertainty lay in the comparison of the scale of his mercury thermometer with the air thermometer. The subsequent correction, though not carried out strictly under the conditions of the experiment, showed that the order of accuracy of his work about the middle of the range from 15° to 25° was at least 1 in 1000, and probably 1 in 2000. At 30° he considered that, owing to the increasing magnitude and uncertainty of the radiation correction, there “might be a small error in the direction of making the equivalent too great, and that the specific heat might go on decreasing to even 40° C.” The results considered with reference to the variation of the specific heat of water are shown in the curve marked Rowland in Fig. 6.
 |
| Fig. 5. |
§ 10. Osborne Reynolds and W. H. Moorby (Phil. Trans., 1897, p. 381) determined the mechanical equivalent of the mean thermal unit between 0° and 100° C., on a very large scale, with a Froude-Reynolds hydraulic brake and a steam-engine of 100 h.p. This brake is practically a Joule calorimeter, ingeniously designed to churn the water in such a manner as to develop the greatest possible resistance. The admission of water at 0° C. to the brake was controlled by hand in such a manner as to keep the outflow nearly at the boiling-point, the quantity of water in the brake required to produce a constant torque being regulated automatically, as the speed varied, by a valve worked by the lifting of the weighted lever attached to the brake.
 |
| Fig. 6. |
The accompanying illustration (fig. 7) shows the brake lagged with cotton-wool, and the 4-ft. lever to which the weights are suspended. The power of the brake may be estimated by comparison with the size of the rope pulley seen behind it on the same shaft. With 300 pounds on a 4-ft. lever at 300 revolutions per minute, the rate of generation of heat was about 12 kilo-calories per second. In spite of the large range of temperature, the correction for external loss of heat amounted to only 5%, with the brake uncovered, and was reduced to less than 2% by lagging. This is the special advantage of working on so large a scale with so rapid a generation of heat. But, for the same reason, the method necessarily presents peculiar difficulties, which were not overcome without great pains and ingenuity. The principal troubles arose from damp in the lagging which necessitated the rejection of several trials, and from dissolved air in the water, causing loss of heat by the formation of steam. Next to the radiation loss, the most uncertain correction was that for conduction of heat along the 4-in. shaft. These losses were as far as possible eliminated by combining the trials in pairs, with different loads on the brake, assuming that the heat-loss would be the same in the heavy and light trials, provided that the external temperature and the gradient in the shaft, as estimated from the temperature of the bearings, were the same. The values deduced in this manner for the equivalent agreed as closely as could be expected considering the impossibility of regulating the external condition of temperature and moisture with any certainty in an engine-room. The extreme variation of results in any one series was only from 776.63 to 779.46 ft.-pounds, or less than 12%. This variation may have been due to the state of the lagging, which Moorby distrusted in spite of the great reduction of the heat-loss, or it may have been partly due to the difficulty of regulating the speed of the engine and the water-supply to the brake in such a manner as to maintain a constant temperature in the outflow, and avoid variations in the heat capacity of the brake. Since hand regulation is necessarily discontinuous, the speed and the temperature were constantly varying, so that it was useless to take readings nearer than the tenth of a degree. The largest variation recorded in the two trials of which full details are given, was 4–9° F. in two minutes in the outflow temperature, and four or five revolutions per minute on the speed. These variations, so far as they were of a purely accidental nature, would be approximately eliminated on the mean of a large number of trials, so that the accuracy of the final result would be of a higher order than might be inferred from a comparison of separate pairs of trials. Great pains were taken to discuss and eliminate all the sources of constant error which could be foreseen. The results of the light trials with 400 ft.-pounds on the brake differ slightly from those with 600 ft.-pounds. This might be merely accidental, or it might indicate some constant difference in the conditions requiring further investigation. It would have been desirable, if possible, to have tried the effect of a larger range of variation in the experimental conditions of load and speed, with a view to detect the existence of constant errors; but owing to the limitations imposed by the use of a steam-engine, and the difficulty of securing steady conditions of running, this proved to be impossible. There can be no doubt, however, that the final result is the most accurate direct determination of the value of the mean calorie between 0° and 100° C. in mechanical units. Expressed in joules per calorie the result is 4.1832, which agrees very closely with the value found by Rowland as the mean over the range 15° to 20° C. The value 4.183 is independently confirmed in a remarkable manner by the results of the electrical method described below, which give 4.185 joules for the mean calorie, if Rowland’s value is assumed as the starting-point, and taken to be 4.180 joules at 20° C.
 |
| Fig. 7. |
§ 11. Electrical Methods.—The value of the international electrical units has by this time been so accurately determined in absolute measure that they afford a very good, though indirect, method of determining the mechanical equivalent of heat. But, quite apart from this, electrical methods possess the greatest value for calorimetry, on account of the facility and accuracy of regulating and measuring the quantity of heat supplied by an electric current. The frictional generation of heat in a metallic wire conveying a current can be measured in various ways, which correspond to slightly different methods. By Ohm’s law, and by the definition of difference of electric pressure or potential, we obtain the following alternative expressions for the quantity of heat H in joules generated in a time T seconds by a current of C amperes flowing in a wire of resistance R ohms, the difference of potential between the ends of the wire being E = CR volts:—
| H = ECT = C2RT = E2T/R | (1.) |
The method corresponding to the expression C2RT was adopted by Joule and by most of the early experimentalists. The defects of the earlier work from an electrical point of view lay chiefly in the difficulty of measuring the current with sufficient accuracy owing to the imperfect development of the science of electrical measurement. These difficulties have been removed by the great advances since 1880, and in particular by the introduction of accurate standard cells for measurements of electrical pressure.
§ 12. Griffiths.—The method adopted by E. H. Griffiths (Phil. Trans., 1893, p. 361), whose work threw a great deal of light on the failure of previous observers to secure consistent results, corresponded to the last expression E2T/R, and consisted in regulating the current by a special rheostat, so as to keep the potential difference E on the terminals of the resistance R balanced against a given number of standard Clark cells of the Board of Trade pattern. The resistance R could be deduced from a knowledge of the temperature of the calorimeter and the coefficient of the wire. But in order to obtain trustworthy results by this method he found it necessary to employ very rapid stirring (2000 revolutions per minute), and to insulate the wire very carefully from the liquid to prevent leakage of the current. He also made a special experiment to find how much the temperature of the wire exceeded that of the liquid under the conditions of the experiment. This correction had been neglected by previous observers employing similar methods. The resistance R was about 9 ohms, and the potential difference E was varied from three to six Clark cells, giving a rate of heat-supply about 2 to 6 watts. The water equivalent of the calorimeter was about 85 grammes, and was determined by varying the quantity of water from 140 to 260 or 280 grammes, so that the final results depended on a difference in the weight of water of 120 to 140 grammes. The range of temperature in each experiment was 14° to 26° C. The rate of rise was observed with a mercury thermometer standardized by comparison with a platinum thermometer under the conditions of the experiment. The time of passing each division was recorded on an electric chronograph. The duration of an experiment varied from about 30 to 70 minutes. Special observations were made to determine the corrections for the heat supplied by stirring, and that lost by radiation, each of which amounted to about 10% of the heat-supply. The calorimeter C, fig. 8, was gilded, and completely surrounded by a nickel-plated steel enclosure B, forming the bulb of a mercury thermo-regulator, immersed in a large water-bath maintained at a constant temperature. In spite of the large corrections the results were extremely consistent, and the value of the temperature-coefficient of the diminution of the specific heat of water, deduced from the observed variation in the rate of rise at different points of the range 15° to 25°, agreed with the value subsequently deduced from Rowland’s experiments over the same range, when his thermometers were reduced to the same scale. Griffiths’ final result for the average value of the calorie over this range was 4.192 joules, taking the E.M.F. of the Clark cell at 15° C. to be 1.4342 volts. The difference from Rowland’s value, 4.181, could be explained by supposing the E.M.F. of the Clark cells to have in reality been 1.4323 volts, or about 2 millivolts less than the value assumed. Griffiths subsequently applied the same method to the measurement of the specific heat of aniline, and the latent heat of vaporization of benzene and water.
 |
| Fig. 8. |
§ 13. Schuster and Gannon.—The method employed by A. Schuster and W. Gannon for the determination of the specific heat of water in terms of the international electric units (Phil. Trans. A, 1895, p. 415) corresponded to the expression ECT, and differed in many essential details from that of Griffiths. The current through a platinoid resistance of about 31 ohms in a calorimeter containing 1500 grammes of water was regulated so that the potential difference on its terminals was equal to that of twenty Board of Trade Clark cells in series. The duration of an experiment was about ten minutes, and the product of the mean current and the time, namely CT, was measured by the weight of silver deposited in a voltameter, which amounted to about 0.56 gramme. The uncertainty due to the correction for the water equivalent was minimized by making it small (about 27 grammes) in comparison with the water weight. The correction for external loss was reduced by employing a small rise of temperature (only 2.22°), and making the rate of heat-supply relatively rapid, nearly 24 watts. The platinoid coil was insulated from the water by shellac varnish. The wire had a length of 760 cms., and the potential difference on its terminals was nearly 30 volts. The rate of stirring adopted was so slow that the heat generated by it could be neglected. The result found was 4.191 joules per calorie at 19° C. This agrees very well with Griffiths considering the difficulty of measuring so small a rise of temperature at 2° with a mercury thermometer. Admitting that the electro-chemical equivalent of silver increases with the age of the solution, a fact subsequently discovered, and that the E.M.F. of the Clark cell is probably less than 1.4340 volts (the value assumed by Schuster and Gannon), there is no difficulty in reconciling the result with that of Rowland.
§ 14. H. L. Callendar and H. T. Barnes (Brit. Assoc. Reports, 1897 and 1899) adopted an entirely different method of calorimetry, as well as a different method of electrical measurement. A steady current of liquid, Q grammes per second, of specific heat, Js joules per degree, flowing through a fine tube, A B, fig. 9, is heated by a steady electric current during its passage through the tube, and the difference of temperature dθ between the inflowing and the outflowing liquid is measured by a single reading with a delicate pair of differential platinum thermometers at A and B. The difference of potential E between the ends of the tube, and the electric current C through it, are measured on an accurately calibrated potentiometer, in terms of a Clark cell and a standard resistance. If hdθ is the radiation loss in watts we have the equation,
| EC = JsQdθ + hdθ | (2). |
 |
| Fig. 9. |
The advantage of this method is that all the conditions are steady, so that the observations can be pushed to the limit of accuracy and sensitiveness of the apparatus. The water equivalent of the calorimeter is immaterial, since there is no appreciable change of temperature. The heat-loss can be reduced to a minimum by enclosing the flow-tube in a hermetically sealed glass vacuum jacket. Stirring is effected by causing the water to circulate spirally round the bulbs of the thermometers and the heating conductor as indicated in the figure. The conditions can be very easily varied through a wide range. The heat-loss hdθ is determined and eliminated by varying the flow of liquid and the electric current simultaneously, in such a manner as to secure approximately the same rise of temperature for two or more widely different values of the flow of liquid. An example taken from the Electrician, September 1897, of one of the earliest experiments by this method on the specific heat of mercury will make the method clearer. The flow-tube was about 1 metre long and 1 millim. in diameter, coiled in a short spiral inside the vacuum jacket. The outside of the vacuum jacket was immersed in a water jacket at a steady temperature equal to that of the inflowing mercury.
Specific Heat of Mercury by Continuous Electric Method
| Flow of Hg. | Rise of Temp. | Watts. | Heat-loss. | Specific Heat. |
| gm./sec. | dθ | EC | hdθ | Per gm. deg. |
| 8.753 | 11.764 | 14.862 | 0.655 | } .13780 joules |
| 4.594 | 12.301 | 7.912 | 0.865 | } .03297 cals. |
It is assumed as a first approximation that the heat-loss is proportional to the rise of temperature dθ, provided that dθ is nearly the same in both cases, and that the distribution of temperature in the apparatus is the same for the same rise of temperature whatever the flow of liquid. The result calculated on these assumptions is given in the last column in joules, and also in calories of 20° C. The heat-loss in this example is large, nearly 4.5% of the total supply, owing to the small flow and the large rise of temperature, but this correction was greatly reduced in subsequent observations on the specific heat of water by the same method. In the case of mercury the liquid itself can be utilized to conduct the electric current. In the case of water or other liquids it is necessary to employ a platinum wire stretched along the tube as heating conductor. This introduces additional difficulties of construction, but does not otherwise affect the method. The absolute value of the specific heat deduced necessarily depends on the absolute values of the electrical standards employed in the investigation. But for the determination of relative values of specific heats in terms of a standard liquid, or of the variations of specific heat of a liquid, the method depends only on the constancy of the standards, which can be readily and accurately tested. The absolute value of the E.M.F. of the Clark cells employed was determined with a special form of electrodynamometer (Callendar, Phil. Trans. A. 313, p. 81), and found to be 1·4334 volts, assuming the ohm to be correct. Assuming this value, the result found by this method for the specific heat of water at 20° C. agrees with that of Rowland within the probable limits of error.
§ 15. Variation of Specific Heat of Water.—The question of the variation of the specific heat of water has a peculiar interest and importance in connexion with the choice of a thermal unit. Many of the uncertainties in the reduction of older experiments, such as those of Regnault, arise from uncertainty in regard to the unit in terms of which they are expressed, which again depends on the scale of the particular thermometer employed in the investigation. The first experiments of any value were those of Regnault in 1847 on the specific heat of water between 110° C. and 192° C. They were conducted on a very large scale by the method of mixture, but showed discrepancies of the order of 0·5%, and the calculated results in many cases do not agree with the data. This may be due merely to deficient explanation of details of tabulation. We may probably take the tabulated values as showing correctly the rate of variation between 110° and 190° C., but the values in terms of any particular thermal unit must remain uncertain to at least 0·5% owing to the uncertainties of the thermometry. Regnault himself adopted the formula,
| s=1 + 0·00004t + 0·0000009t2 (Regnault), | (3) |
for the specific heat s at any temperature t C. in terms of the specific heat at 0° C. taken as the standard. This formula has since been very generally applied over the whole range 0° to 200° C., but the experiments could not in reality give any information with regard to the specific heat at temperatures below 100° C. The linear formula proposed by J. Bosscha from an independent reduction of Regnault’s experiments is probably within the limits of accuracy between 100° and 200° C., so far as the mean rate of variation is concerned, but the absolute values require reduction. It may be written—
| s=s100 + ·00023(t −100) (Bosscha-Regnault) | (4). |
The work of L. Pfaundler and H. Platter, of G. A. Hirn, of J. C. Jamin and Amaury, and of many other experimentalists who succeeded Regnault, appeared to indicate much larger rates of increase than he had found, but there can be little doubt that the discrepancies of their results, which often exceeded 5%, were due to lack of appreciation of the difficulties of calorimetric measurements. The work of Rowland by the mechanical method was the first in which due attention was paid to the thermometry and to the reduction of the results to the absolute scale of temperature. The agreement of his corrected results with those of Griffiths by a very different method, left very little doubt with regard to the rate of diminution of the specific heat of water at 20° C. The work of A. Bartoli and E. Stracciati by the method of mixture between 0° and 30° C., though their curve is otherwise similar to Rowland’s, had appeared to indicate a minimum at 20° C., followed by a rapid rise. This lowering of the minimum was probably due to some constant errors inherent in their method of experiment. The more recent work of Lüdin, 1895, under the direction of Prof. J. Pernet, extended from 0° to 100° C., and appears to have attained as high a degree of excellence as it is possible to reach by the employment of mercury thermometers in conjunction with the method of mixture. His results, exhibited in fig. 6, show a minimum at 25° C., and a maximum at 87° C., the values being ·9935 and 1·0075 respectively in terms of the mean specific heat between 0° and 100° C. He paid great attention to the thermometry, and the discrepancies of individual measurements at any one point nowhere exceed 0·3%, but he did not vary the conditions of the experiments materially, and it does not appear that the well-known constant errors of the method could have been completely eliminated by the devices which he adopted. The rapid rise from 25° to 75° may be due to radiation error from the hot water supply, and the subsequent fall of the curve to the inevitable loss of heat by evaporation of the boiling water on its way to the calorimeter. It must be observed, however, that there is another grave difficulty in the accurate determination of the specific heat of water near 100° C. by this method, namely, that the quantity actually observed is not the specific heat at the higher temperature t, but the mean specific heat over the range 18° to t. The specific heat itself can be deduced only by differentiating the curve of observation, which greatly increases the uncertainty. The peculiar advantage of the electric method of Callendar and Barnes, already referred to, is that the specific heat itself is determined over a range of 8° to 10° at each point, by adding accurately measured quantities of heat to the water at the desired temperature in an isothermal enclosure, under perfectly steady conditions, without any possibility of evaporation or loss of heat in transference. These experiments, which have been extended by Barnes over the whole range 0° to 100°, agree very well with Rowland and Griffiths in the rate of variation at 20° C., but show a rather flat minimum of specific heat in the neighbourhood of 38° to 40° C. At higher points the rate of variation is very similar to that of Regnault’s curve, but taking the specific heat at 20° as the standard of reference, the actual values are nearly 0·56% less than Regnault’s. It appears probable that his values for higher temperatures may be adopted with this reduction, which is further confirmed by the results of Reynolds and Moorby, and by those of Lüdin. According to the electric method, the whole range of variation of the specific heat between 10° and 80° is only 0·5%. Comparatively simple formulae, therefore, suffice for its expression to 1 in 10,000, which is beyond the limits of accuracy of the observations. It is more convenient in practice to use a few simple formulae, than to attempt to represent the whole range by a single complicated expression:—
Below 20° C. s=0·9982 + 0·0000045(t−40)2−0·0000005(t−20)3.
From 20° to 60°, s=0·9982 + 0·0000045(t−40)2 (5).
| Above 60° to 200° | s=0·9944 + ·00004t + 0·0000009t 2 (Regnault corrd.) |
| s=1·000 + 0·00022(t−60) (Bosscha corrd.) |
The addition of the cubic term below 20° is intended to represent the somewhat more rapid change near the freezing-point. This effect is probably due, as suggested by Rowland, to the presence of a certain proportion of ice molecules in the liquid, which is also no doubt the cause of the anomalous expansion. Above 60° C. Regnault’s formula is adopted, the absolute values being simply diminished by a constant quantity 0·0056 to allow for the probable errors of his thermometry. Above 100° C., and for approximate work generally, the simpler formula of Bosscha, similarly corrected, is probably adequate.
The following table of values, calculated from these formulae, is taken from the Brit. Assoc. Report, 1899, with a slight modification to allow for the increase in the specific heat below 20° C. This was estimated in 1899 as being equivalent to the addition of the constant quantity 0·20 to the values of the total heat h of the liquid as reckoned by the parabolic formula (5). This quantity is now, as the result of further experiments, added to the values of h, and also represented in the formula for the specific heat itself by the cubic term.
Specific Heat of Water in Terms of Unit at 20° C. 4·180 Joules
| t° C. | Joules. | s. | h | Rowland. |
| 0° | 4·208 | 1·0094 | 0 | 0 |
| 5° | 4·202 | 1·0054 | 5·037 | 5·037 |
| 10° | 4·191 | 1·0027 | 10·056 | 10·058 |
| 15° | 4·184 | 1·0011 | 15·065 | 15·068 |
| 20° | 4·180 | 1·0000 | 20·068 | 20·071 |
| 25° | 4·177 | 0·9992 | 25·065 | 25·067 |
| 30° | 4·175 | 0·9987 | 30·060 | 30·057 |
| 35° | 4·173 | 0·9983 | 35·052 | 35·053 |
| 40° | 4·173 | 0·9982 | 40·044 | |
| 50° | 4·175 | 0·9987 | 50·028 | |
| 60° | 4·180 | 1·0000 | 60·020 | |
| 70° | 4·187 | 1·0016 | 70·028 | |
| 80° | 4·194 | 1·0033 | 80·052 | |
| 90° | 4·202 | 1·0053 | 90·095 | Shaw |
| 100° | 4·211 | 1·0074 | 100·158 | Regnault |
| 120° | 4·231 | 1·0121 | 120·35 | 120·73 |
| 140° | 4·254 | 1·0176 | 140·65 | 140·88 |
| 160° | 4·280 | 1·0238 | 161·07 | 161·20 |
| 180° | 4·309 | 1·0308 | 181·62 | 182·14 |
| 200° | 4·341 | 1·0384 | 202·33 | |
| 220° | 4·376 | 1·0467 | 223·20 |
The unit of comparison in the following table is taken as the specific heat of water at 20° C. for the reasons given below. This unit is taken as being 4·180 joules per gramme-degree-centigrade on the scale of the platinum thermometer, corrected to the absolute scale as explained in the article Thermometry, which has been shown to be practically equivalent to the hydrogen scale. The value 4·180 joules at 20° C. is the mean between Rowland’s corrected result 4·181 and the value 4·179, deduced from the experiments of Reynolds and Moorby on the assumption that the ratio of the mean specific heat 0° to 100° to that at 20° is 1·0016, as given by the formulae representing the results of Callendar and Barnes. This would indicate that Rowland’s corrected values should, if anything, be lowered. In any case the value of the mechanical equivalent is uncertain to at least 1 in 2000.
The mean specific heat, over any range of temperature, may be obtained by integrating the formulae between the limits required, or by taking the difference of the corresponding values of the total heat h, and dividing by the range of temperature. The quantity actually observed by Rowland was the total heat. It may be remarked that starting from the same value at 5°, for the sake of comparison, Rowland’s values of the total heat agree to 1 in 5000 with those calculated from the formulae. The values of the total heat observed by Regnault, as reduced by Shaw, also show a very fair agreement, considering the uncertainty of the units. It must be admitted that it is desirable to redetermine the variation of the specific heat above 100° C. This is very difficult on account of the steam-pressure, and could not easily be accomplished by the electrical method. Callendar has, however, devised a continuous method of mixture, which appears to be peculiarly adapted to the purpose, and promises to give more certain results. In any case it may be remarked that formulae such as those of Jamin, Henrichsen, Baumgartner, Winkelmann or Dieterici, which give far more rapid rates of increase than that of Regnault, cannot possibly be reconciled with his observations, or with those of Reynolds and Moorby, or Callendar and Barnes, and are certainly inapplicable above 100° C.
§ 16. On the Choice of the Thermal Unit.—So much uncertainty still prevails on this fundamental point that it cannot be passed over without reference. There are three possible kinds of unit, depending on the three fundamental methods already given: (1) the thermometric unit, or the thermal capacity of unit mass of a standard substance under given conditions of temperature and pressure on the scale of a standard thermometer. (2) The latent-heat unit, or the quantity of heat required to melt or vaporize unit mass of a standard substance under given conditions. This unit has the advantage of being independent of thermometry, but the applicability of these methods is limited to special cases, and the relation of the units to other units is difficult to determine. (3) The absolute or mechanical unit, the quantity of heat equivalent to a given quantity of mechanical or electrical energy. This can be very accurately realized, but is not so convenient as (1) for ordinary purposes.
In any case it is necessary to define a thermometric unit of class (1). The standard substance must be a liquid. Water is always selected, although some less volatile liquid, such as aniline or mercury, would possess many advantages. With regard to the scale of temperature, there is very general agreement that the absolute scale as realized by the hydrogen or helium thermometer should be adopted as the ultimate standard of reference. But as the hydrogen thermometer is not directly available for the majority of experiments, it is necessary to use a secondary standard for the practical definition of the unit. The electrical resistance thermometer of platinum presents very great advantages for this purpose over the mercury thermometer in point of reproducibility, accuracy and adaptability to the practical conditions of experiment. The conditions of use of a mercury thermometer in a calorimetric experiment are necessarily different from those under which its corrections are determined, and this difference must inevitably give rise to constant errors in practical work. The primary consideration in the definition of a unit is to select that method which permits the highest order of accuracy in comparison and verification. For this reason the definition of the thermal unit will in the end probably be referred to a scale of temperature defined in terms of a standard platinum thermometer.
There is more diversity of opinion with regard to the question of the standard temperature. Many authors, adopting Regnault’s formula, have selected 0° C. as the standard temperature, but this cannot be practically realized in the case of water, and his formula is certainly erroneous at low temperatures. A favourite temperature to select is 4° C., the temperature of maximum density, since at this point the specific heat at constant volume is the same as that at constant pressure But this is really of no consequence, since the specific heat at constant volume cannot be practically realized. The specific heat at 4° could be accurately determined at the mean over the range 0° to 8° keeping the jacket at 0° C. But the change appears to be rather rapid near 0°, the temperature is inconveniently low for ordinary calorimetric work, and the unit at 4° would be so much larger than the specific heat at ordinary temperatures that nearly all experiments would require reduction. The natural point to select would be that of minimum specific heat, but if this occurs at 40° C. it would be inconveniently high for practical realization except by the continuous electrical method. It was proposed by a committee of the British Association to select the temperature at which the specific heat was 4·200 joules, leaving the exact temperature to be subsequently determined. It was supposed at the time, from the original reduction of Rowland’s experiments, that this would be nearly at 10° C., but it now appears that it may be as low is 5° C., which would be inconvenient. This is really only an absolute unit in disguise, and evades the essential point, which is the selection of a standard temperature for the water thermometric unit. A similar objection applies to selecting the temperature at which the specific heat is equal to its mean value between 0° and 100°. The mean calorie cannot be accurately realized in practice in any simple manner, and is therefore unsuitable as a standard of comparison. Its relation to the calorie at any given temperature, such as 15° or 20°, cannot be determined with the same degree of accuracy as the ratio of the specific heat at 15° to that at 20°, if the scale of temperature is given. The most practical unit is the calorie at 15° or 20° or some temperature in the range of ordinary practice. The temperature most generally favoured is 15°, but 20° would be more suitable for accurate work. These units differ only by 11 parts in 10,000 according to Callendar and Barnes, or by 13 in 10,000 according to Rowland and Griffiths, so that the difference between them is of no great importance for ordinary purposes. But for purposes of definition it would be necessary to take the mean value of the specific heat over a given range of temperature, preferably at least 10°, rather than the specific heat at a point which necessitates reference to some formula of reduction for the rate of variation. The specific heat at 15° would be determined with reference to the mean over the range 10° to 20°, and that at 20° from the range 15° to 25°. There can be no doubt that the range 10° to 20° is too low for the accurate thermal regulation of the conditions of the experiment. The range 15° to 25° would be much more convenient from this point of view, and a mean temperature of 20° is probably nearest the average of accurate calorimetric work. For instance 20° is the mean of the range of the experiments of Griffiths and of Rowland, and is close to that of Schuster and Gannon. It is readily attainable at any time in a modern laboratory with adequate heating arrangements, and is probably on the whole the most suitable temperature to select.
§ 17. Specific Heat of Gases.—In the case of solids and liquids under ordinary conditions of pressure, the external work of expansion is so small that it may generally be neglected; but with gases or vapours, or with liquids near the critical point, the external work becomes so large that it is essential to specify the conditions under which the specific heat is measured. The most important cases are, the specific heats (1) at constant volume; (2) at constant pressure; (3) at saturation pressure in the case of a liquid or vapour. In consequence of the small thermal capacity of gases and vapours per unit volume at ordinary pressures, the difficulties of direct measurement are almost insuperable except in case (2). Thus the direct experimental evidence is somewhat meagre and conflicting, but the question of the relation of the specific heats of gases is one of great interest in connexion with the kinetic theory and the constitution of the molecule. The well-known experiments of Regnault and Wiedemann on the specific heat of gases at constant pressure agree in showing that the molecular specific heat, or the thermal capacity of the molecular weight in grammes, is approximately independent of the temperature and pressure in case of the more stable diatomic gases, such as H2, O2, N2, CO, &c., and has nearly the same value for each gas. They also indicate that it is much larger, and increases considerably with rise of temperature, in the case of more condensible vapours, such as Cl2, Br2, or more complicated molecules, such as CO2, N2O, NH3, C2H4. The direct determination of the specific heat at constant volume is extremely difficult, but has been successfully attempted by Joly with his steam calorimeter, in the case of air and CO2. Employing pressures between 7 and 27 atmospheres, he found that the specific heat of air between 10° and 100° C. increased very slightly with increase of density, but that of CO2 increased nearly 3% between 7 and 21 atmospheres. The following formulae represent his results for the specific heat s at constant volume in terms of the density d in gms. per c.c.:—
Air, s=0·1715 + 0·028d,
CO2, s=0·165 + 0·213d + 0·34d 2.
§ 18. Ratio of Specific Heats.—According to the elementary kinetic theory of an ideal gas, the molecules of which are so small and so far apart that their mutual actions may be neglected, the kinetic energy of translation of the molecules is proportional to the absolute temperature, and is equal to 3/2 of pv, the product of the pressure and the volume, per unit mass. The expansion per degree at constant pressure is v/θ=R/p. The external work of expansion per degree is equal to R, being the product of the pressure and the expansion, and represents the difference of the specific heats S—s, at constant pressure and volume, assuming as above that the internal work of expansion is negligible. If the molecules are supposed to be like smooth, hard, elastic spheres, incapable of receiving any other kind of energy except that of translation, the specific heat at constant volume would be the increase per degree of the kinetic energy namely 3pv/2θ − 3R/2, that at constant pressure would be 5R/2, and the ratio of the specific heats would be 5/3 or 1·666. This appears to be actually the case for monatomic gases such as mercury vapour (Kundt and Warburg, 1876), argon and helium (Ramsay, 1896). For diatomic or compound gases Clerk Maxwell supposed that the molecule would also possess energy of rotation, and endeavoured to prove that in this case the energy would be equally divided between the six degrees of freedom, three of translation and three of rotation, if the molecule were regarded as a rigid body incapable of vibration-energy. In this case we should have s=3R, S=4R, S/s=4/3=1·333. In 1879 Maxwell considered it one of the greatest difficulties which the kinetic theory had yet encountered, that in spite of the many other degrees of freedom of vibration revealed by the spectroscope, the experimental value of the ratio S/s was 1·40 for so many gases, instead of being less than 4/3. Somewhat later L. Boltzmann suggested that a diatomic molecule regarded as a rigid dumb-bell or figure of rotation, might have only five effective degrees of freedom, since the energy of rotation about the axis of symmetry could not be altered by collisions between the molecules. The theoretical value of the ratio S/s in this case would be the required 7/5. For a rigid molecule on this theory the smallest value possible would be 4/3. Since much smaller values are found for more complex molecules, we may suppose that, in these cases, the energy of rotation of a polyatomic molecule may be greater than its energy of translation, or else that heat is expended in splitting up molecular aggregates, and increasing energy of vibration. A hypothesis doubtfully attributed to Maxwell is that each additional atom in the molecule is equivalent to two extra degrees of freedom. From an m-atomic molecule we should then have S/s = 1 + 2/(2m + 1). This gives a series of ratios 5/3, 7/5, 9/7, 11/9, &c., for 1, 2, 3, 4, &c., atoms in the molecule, values which fall within the limits of experimental error in many cases. It is not at all clear, however, that energy of vibration should bear a constant ratio to that of translation, although this would probably be the case for rotation. For the simpler gases, which are highly diathermanous and radiate badly even at high temperature, the energy of vibration is probably very small, except under the special conditions which produce luminosity in flames and electric discharges. For such gases, assuming a constant ratio of rotation to translation, the specific heat at low pressures would be very nearly constant. For more complex molecules the radiative and absorptive powers are known to be much greater. The energy of vibration may be appreciable at ordinary temperatures, and would probably increase more rapidly than that of translation with rise of temperature, especially near a point of dissociation. This would account for an increase of S, and a diminution of the ratio S/s, with rise of temperature which apparently occurs in many vapours. The experimental evidence, however, is somewhat conflicting, and further investigations are very desirable on the variation of specific heat with temperature. Given the specific heat as a function of the temperature, its variation with pressure may be determined from the characteristic equation of the gas. The direct methods of measuring the ratio S/s, by the velocity of sound and by adiabatic expansion, are sufficiently described in many text-books.
§ 19. Atomic and Molecular Heats.—The ideal atomic heat is the thermal capacity of a gramme-atom in the ideal state of monatomic gas at constant volume. This would be nearly three calories. For a diatomic gas, the molecular heat would be nearly five calories, or the atomic heat of a gas in the diatomic state would be 2·5. Estimated at constant pressure the atomic heat would be 3·5. Some authors adopt 2·5 and some 3·5 for the ideal atomic heat. The atomic heat of a metal in the solid state is in most cases larger than six calories at ordinary temperatures. Considering the wide variations in the physical condition and melting points, the comparatively close agreement of the atomic heats of the metals at ordinary temperatures, known as Dulong and Petit’s Law, is very remarkable. The specific heats as a rule increase with rise of temperature, in some cases, e.g. iron and nickel, very rapidly. According to W. A. Tilden (Phil. Trans., 1900), the atomic heats of pure nickel and cobalt, as determined from experiments at the boiling-points of O2, and CO2, diminish so rapidly at temperatures below 0° C. as to suggest that they would reach the value 2·42 at the absolute zero. This is the value of the minimum of atomic heat calculated by Perry from diatomic hydrogen, but the observations themselves might be equally well represented by taking the imaginary limit 3, since the quantity actually observed is the mean specific heat between 0° and −182·5° C. Subsequent experiments on other metals at low temperatures did not indicate a similar diminution of specific heat, so that it may be doubted whether the atomic heats really approach the ideal value at the absolute zero. No doubt there must be approximate relations between the atomic and molecular heats of similar elements and compounds, but considering the great variations of specific heat with temperature and physical state, in alloys, mixtures or solutions, and in allotropic or other modifications, it would be idle to expect that the specific heat of a compound could be accurately deduced by any simple additive process from that of its constituents.
Authorities.—Joule’s Scientific Papers (London, 1890); Ames and Griffiths, Reports to the International Congress (Paris, 1900), “On the Mechanical Equivalent of Heat,” and “On the Specific Heat of Water”; Griffiths, Thermal Measurement of Energy (Cambridge, 1901); Callendar and Barnes, Phil. Trans. A, 1901, “On the Variation of the Specific Heat of Water”; for combustion methods, see article Thermochemistry, and treatises by Thomsen, Pattison-Muir and Berthelot; see also articles Thermodynamics and Vaporization. (H. L. C.)