A Dictionary of Music and Musicians/Counterpoint
COUNTERPOINT is 'the art of combining melodies.' Its name arose from the ancient system of notation by points or 'pricks.' When one set of points was added to another, to signify the simultaneous performance of various melodies agreeing in harmony, it was called 'point against point'—i.e. contrapunctum, or counterpoint. Counterpoint is usually divided into two kinds—plain and double—and each of these is subdivided into various orders or species. There are very stringent rules about the use of different intervals in plain counterpoint, which are more or less relaxed in modern music; when, however, they are fully observed, the piece is said to be written in 'strict counterpoint.' It is usual to take some fragment of an old chant or chorale as the 'canto fermo' or plain-chant, to which other parts or melodies are added as accompaniments according to the rules above referred to. This is called 'adding a counterpoint to a given subject.'
The difference between the ancient strictness and modern laxity in plain counterpoint chiefly relates to the admission of consecutive octaves and fifths by contrary motion, even between extreme parts, and the doctrine of false relations, especially that of the tritone. Plain counterpoint, however, is most useful as a study, whereby facility may be acquired in conquering difficulties arising from the various motions of the different parts in a piece of music. It is obvious, therefore, that the more stringent rules should be observed by students with a view to this particular object, and that therefore they are enforced in the best text-books.
Plain counterpoint is generally divided into five species. The first is called 'note against note.'

The second species is called 'two notes to one.'
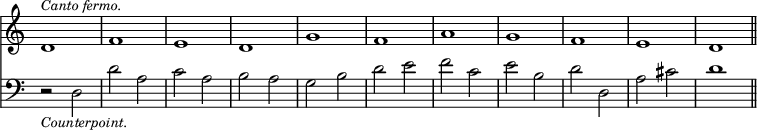
The third species is called 'four notes to one.'

The fourth is called 'syncopated counterpoint.'

The 'fifth species is called 'florid counterpoint,' and is a combination or rather alternation of the last three, with certain ornamental variations peculiar to itself.

Plain counterpoint may be in any number of parts, and the canto fermo may be assigned to the upper, middle, or lowest parts, according to circumstances.
Double counterpoint is when two or more melodies are so constructed that either of them may form a correct bass to the others; and when the various melodies may, by transposition, be placed in any relative order of acuteness, without infringing the laws of harmony. These transpositions may be such as to produce counterpoints at the octave, tenth, twelfth, or any other interval, but the most usual is double counterpoint at the octave.
Examples of various double counterpoints—
Mozart.


The above is a specimen of double counterpoint at the octave.
The next species is at the tenth, on a Canto fermo.
Fux.
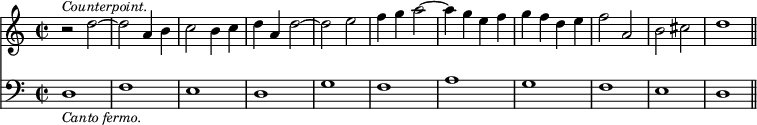
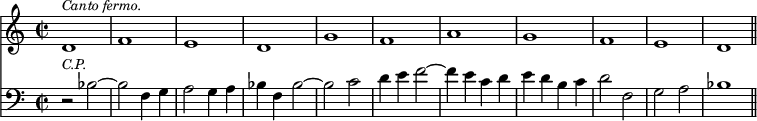
The above is double counterpoint at the tenth below.
Triple or quadruple counterpoints consist of three or four melodies so adopted that any of them may be a bass to the other. This can only be done with counterpoint at the octave.
Counterpoints may also be constructed by contrary motion, or by augmentation, or diminution, or retrogression. In compositions in more than two parts, the counterpoint is often confined to two parts, while the others are free accompaniments in order to fill up and complete the harmony.
In a fugue the subject and countersubject are necessarily constructed in double counterpoint. [See article Fugue.]
For a good example of counterpoint at the twelfth and in diminution, see the fine chorus 'Let all the Angels of God,' in Handel's 'Messiah.'
For an example of five subjects in double counterpoint at the octave, see the finale of Mozart's 'Jupiter' Symphony.[ F. A. G. O. ]