A Dictionary of Music and Musicians/Day, Alfred
DAY, Alfred, M.D., the author of an important theory of [1]harmony, was born in London in January 1810. In accordance with the wishes of his father he studied in London and Paris for the medical profession, and, after taking a degree at Heidelberg, practised in London as a homoeopathist. His father's want of sympathy for his musical inclinations in his earlier years having prevented him from attaining a sufficient degree of practical skill in the art, he turned his attention to the study of its principles, and formed the idea of making a consistent and complete theory of harmony, to replace the chaos of isolated rules and exceptions, founded chiefly on irregular observation of the practice of great composers, which till comparatively lately was all that in reality supplied the place of system. He took some years in maturing his theory, and published it finally in 1845, three years only before his death, Feb. 11, 1849.
In this work there was hardly any department in which he did not propose reforms. For instance, in view of the fact that the figures used in thorough bass did not distinguish the nature of the chord they indicated—since the same figures stood for entirely different chords, and the same chords in different positions would be indicated by different figures—he proposed that the same chord should always be indicated by the same figures, and that its inversions should be indicated by capital letters A, B, C, etc., placed under the bass, so that the chord of the seventh in its various positions would be indicated as follows:—


as under the old system. And whenever a chord had also a secondary root, as the chord of the augmented sixth, it would be indicated by a capital letter with a line drawn through it, and lines also drawn through the figures which indicated the intervals derived from that secondary root.
With respect to the differences of opinion about the minor scale, he insisted with determined consistency that the principles of its construction precluded the possibility of its containing a major sixth or a minor seventh, and that the only true minor scale is that with a minor sixth and major seventh, the same ascending and descending; and his concluding remarks are worth quoting as characteristic:—'This scale may not be so easy to some instruments and to voices as the old minor scale, therefore let all those who like it practise that form of passage, but let them not call it the minor scale. Even as a point of practice I deny the old minor scale to be the better; as practice is for the purpose of overcoming difficulties, and not of evading them.' The principle which throughout characterises his system is to get behind the mere shallow statement of rules and exceptions to the underlying basis from which the exceptions and rules will alike follow. Thus, in dealing with the theory of false relations, he points out that the objectionable nature of contradictory accidentals, such as C♮ and C♯ occurring in the same chord, or in succeeding chords or alternate chords, arises from the obscurity of tonality which thereby results, and which must always result when accidentals imply change of key: but since accidentals under particular circumstances do not imply change of key, contradictory accidentals are not necessarily a false relation; and he gives as an extreme instance, among others, the succession of the chords of the subdominant and supertonic in the key of C, in which F and F♯ follow one another in different parts in successive chords.
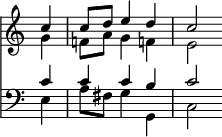
Proceeding after the same manner in his discussion of forbidden progressions of parts, he points out that as the objectionable effect of consecutive fifths is caused by the two parts seeming to move simultaneously in two different keys, there are cases in which the progression of the bass on which they are founded would prevent that effect and render them admissible; as, for instance, when the bass moves from Tonic to dominant, as in the Pastoral Symphony of Beethoven,

The most important part of his theory, and that which most distinguishes it, is its division of styles into Strict or Diatonic, and Free or Chromatic, and the discussion of the fundamental discords which can be used without preparation. His explanation of the 'Chromatic system' was quite new, and his prefatory remarks so well explain his principles that they may be fitly quoted. After pointing out that the laws of diatonic harmony had been so stretched to apply them to modern styles that they seemed 'utterly opposed to practice,' he proceeds—'Diatonic discords require preparation because they are unnatural; chromatic do not because they may be said to be already prepared by nature'—since the harmonics of a root note give the notes which form with it the combinations he calls fundamental discords. 'The harmonics from any given note are a major third, perfect fifth, minor seventh, minor or major ninth, eleventh, and minor or major thirteenth.' And this series gives the complete category of the fundamental chords of Day's chromatic system. Moreover, with the view of simplifying the tonal development of music, and giving a larger scope to the basis of a single key—and thereby avoiding the consideration of innumerable short transitions—he gives a number of chromatic chords as belonging essentially to every key, though their signatures may not be sufficient to supply them, and with the same object builds his fundamental discords on the basis of the supertonic and tonic as well as on the dominant. In respect of this he says—'The reason why the tonic, dominant, and supertonic are chosen for roots, is because the harmonics in nature rise in the same manner; first the harmonics of any given note, then those of its fifth or dominant, then those of the fifth of that dominant, being the second or supertonic of the original note. The reason why the harmonics of the next fifth are not used, is because that note itself is not a note of the diatonic scale, being a little too sharp, as the fifth of the supertonic, and can only be used as part of a chromatic chord.' The advantages of this system of taking a number of chromatic chords under the head of one key will be obvious to any one who wishes for a complete theory to analyse the progressions of keys in modern music as well as their harmonic structure. For instance, even in the early 'Sonata Pathetique' of Beethoven, under a less comprehensive system, it would be held that in the first bar there was a transition from the original key of C minor to G; whereas under this system the first modulation would be held to take place in the 4th bar, to E♭, which is far more logical and systematic.
The detailed examination of the series of chords which have been summarised above is very elaborate. In most cases his views of the resolutions, even of well-known chords, are more varied and comprehensive than is usual with works on harmony, and point to the great patience and care bestowed on the elaboration of the theory. The most salient points of this part of the work are the reduction of well-known chords and their recognised and possible resolutions under the author's system of fundamental discords. The chord of the diminished seventh (a) he points out to be the first inversion of that of the minor ninth (b);

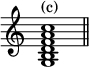

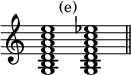
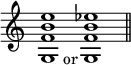


The chord of the augmented sixth he derives from the primary harmonics arising from a primary root, and the secondary harmonics arising from a secondary root. Thus in the following chord in the key of C, the lower note A♭ he
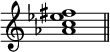
[ C. H. H. P. ]
- ↑ Treatise on Harmony, by Alfred Day. Royal 8vo. Novello & Co. [App. p.609 "Harrison & Co., Pall Mall."]