A Dictionary of Music and Musicians/Inversion
INVERSION. (Germ. Umkehrung.)
The word Inversion bears, in musical terminology, five different significations.
I. In Counterpoint it is used to signify the repetition of a phrase or passage with reversed intervals, or, as it is sometimes called, by contrary motion, e. g.—
Subject, or theme.
[ F. A. G. O. ]
II. Double Counterpoint is said to be inverted, when the upper part is placed beneath the lower, or vice versa: thus (from Cherubini)—
(a) Double Counterpoint for 2 Voices.

(b) Inversion.

We have, here, an example of what is called Double Counterpoint in the Octave, in which the Inversion is produced by simply transposing the upper part an octave lower, or the lower part an octave higher. But, the Inversion may take place in any other Interval; thus giving rise to fourteen different species of Double Counterpoint—those, namely, invertible in the Second, Third, Fourth, Fifth, Sixth, Seventh, Eighth, Ninth, Tenth, Eleventh, Twelfth, Thirteenth, Fourteenth, and Fifteenth, either above, or below. In order to ascertain what Intervals are to be avoided, in these several methods of Inversion, Contrapuntists use a table, constructed of two rows of figures, one placed over the other; the upper row beginning with the unit, and the lower one, (in which the numbers are reckoned backwards,) with the figure representing the particular kind of Counterpoint contemplated. Thus, for Inversion in the Ninth, the upper row will begin with one, and the lower, with nine; as in the following example—
1 2 3 4 5 6 7 8 9
9 8 7 6 5 4 3 2 1
By this table, we learn, that, when the relative position of two parts is reversed, the Unison will be represented by a Ninth; the Second, by an Eighth; the Third, by a Seventh; and so on, to the end: and we are thus enabled to see, at a glance, how every particular Interval must be treated, in order that it may conform strictly to rule, both in its normal and its inverted condition. In this particular case, the Fifth being the only Consonance which is answered by a Consonance, is, of course, the most important Interval in the series, and the only one with which it is possible to begin, or end: as in the following example from Marpurg—
(a) Double Counterpoint in the Ninth.

(b) Inversion—the upper part transposed a Ninth lower.

Each of the different kinds of Inversion we have mentioned is beset by its own peculiar difficulty. For each, a separate [1]table must be constructed; and, after carefully studying this, the Student will be able to distinguish, for himself, between the Intervals upon which he must depend for help, and those most likely to lead him into danger. Without the table, he will be unable to move a step: with its aid, the process is reduced to a certainty.
A detailed account of every possible kind of Inversion will be found in the works of Fux, Marpurg, Azzopardi, Cherubini, and other great writers on Counterpoint, to whom we must refer the reader for further information on the subject.
III. Intervals are said to be inverted, when their lowest notes are raised an octave higher, and thus placed above the highest ones, or vice versa; thus—

In order to ascertain the Inversion of a given Interval, add to it as many units as are necessary to make up the number nine. The sum of these units will represent the Inverted Interval. Thus, since six and three make nine, the inversion of a Sixth will be a Third: as eight and one make nine, the Inversion of an Octave will be an Unison. The following Table shews the Inversions of all Intervals lying within the compass of the Octave—
8 7 6 5 4 3 2 1
9 9 9 9 9 9 9 9
The process of Inversion not only changes the name of an Interval, but, in certain cases, and to a certain extent, influences its nature. Major Intervals, for instance, become Minor, by Inversion; and Minor Intervals, Major. Augmented Intervals become Diminished, and Diminished ones, Augmented. But, the essential character of the Interval survives the operation, unchanged, and asserts itself, with equal force, in the Inversion. In whatever positionthey may be taken, Consonant Intervals remain always [2]consonant; Dissonant Intervals, dissonant; and Perfect Intervals, perfect. [See Interval.]
IV. A Chord is said to be Inverted, when ary note, other than its Root, is taken in the lowest part.
Thus, if the Root of a Common Chord be transposed from the lowest part, to one of the upper parts, and the Third placed in the Bass, the change will produce the Chord of the 6-3. If the Fifth be similarly treated, the result of the transference will be the Chord of the 6-4. Hence, the Chord of the 6-3 is called the First Inversion of the Common Chord; and the Chord of the 6-4, the Second.

If the same process be applied to the Chord of the Seventh, we shall, by successively taking the Third, Fifth, and Seventh, in the Bass, obtain its three Inversions, the 6-5-3, the 6-4-3, and the 6-4-2.

Chords, in their normal form, with the Root in the Bass, are called Fundamental Harmonies: those in which any other note occupies this position are called Derivative, or Inverted Chords. [See Harmony.]
V. A Pedal Point (Point d'orgue) is described as Inverted, when the sustained note, instead of being placed in the Bass, is transferred to an upper part, as in Mozart's Pianoforte Fantasia in C minor (op. 11 ):—
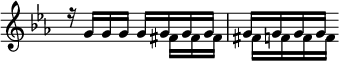
—or, to a middle one, as in the following passage from Deh vieni, non tardar, (Nozze di Figaro,) where the Inverted Pedal is sustained by the Second Violins:—

[ W. S. R. ]
- ↑ One and the same table will, however, serve for Inversion in the Ninth, and the Second; the Tenth and the Third; the Eleventh, and the Fourth, etc., etc.
- ↑ Although the Perfect Fourth—the Inversion of the Perfect Fifth—is classed, by Contrapuntists, among Discords, it only forms an apparent exception the general rule; since it is admitted to be a Consonance, when it appears between the upper parts of a Chord.