A Treatise on Electricity and Magnetism/Part III/Chapter VII
CHAPTER VII.
MAGNETIC MEASUREMENTS.
449.] The principal magnetic measurements are the determination of the magnetic axis and magnetic moment of a magnet, and that of the direction and intensity of the magnetic force at a given place.
Since these measurements are made near the surface of the earth, the magnets are always acted on by gravity as well as by terrestrial magnetism, and since the magnets are made of steel their magnetism is partly permanent and partly induced. The permanent magnetism is altered by changes of temperature, by strong induction, and by violent blows; the induced magnetism varies with every variation of the external magnetic force.
The most convenient way of observing the force acting on a magnet is by making the magnet free to turn about a vertical axis. In ordinary compasses this is done by balancing the magnet on a vertical pivot. The finer the point of the pivot the smaller is the moment of the friction which interferes with the action of the magnetic force. For more refined observations the magnet is suspended by a thread composed of a silk fibre without twist, either single, or doubled on itself a sufficient number of times, and so formed into a thread of parallel fibres, each of which supports as nearly as possible an equal part of the weight. The force of torsion of such a thread is much less than that of a metal wire of equal strength, and it may be calculated in terms of the observed azimuth of the magnet, which is not the case with the force arising from the friction of a pivot.
The suspension fibre can be raised or lowered by turning a horizontal screw which works in a fixed nut. The fibre is wound round the thread of the screw, so that when the screw is turned the suspension fibre always hangs in the same vertical line.
The suspension fibre carries a small horizontal divided circle called the Torsion-circle, and a stirrup with an index, which can be placed so that the index coincides with any given division of the torsion circle. The stirrup is so shaped that the magnet bar can be fitted into it with its axis horizontal, and with any one of its four sides uppermost.
To ascertain the zero of torsion a non-magnetic body of the same weight as the magnet is placed in the stirrup, and the position of the torsion circle when in equilibrium ascertained.
The magnet itself is a piece of hard-tempered steel. According to Gauss and Weber its length ought to be at least eight times its greatest transverse dimension. This is necessary when permanence of the direction of the magnetic axis within the magnet is the most important consideration. Where promptness of motion is required the magnet should be shorter, and it may even be advisable in observing sudden alterations in magnetic force to use a bar magnetized transversely and suspended with its longest dimension vertical[1].
450.] The magnet is provided with an arrangement for ascertaining its angular position. For ordinary purposes its ends are pointed, and a divided circle is placed below the ends, by which their positions are read off by an eye placed in a plane through the suspension thread and the point of the needle.
For more accurate observations a plane mirror is fixed to the magnet, so that the normal to the mirror coincides as nearly as possible with the axis of magnetization. This is the method adopted by Gauss and Weber.
Another method is to attach to one end of the magnet a lens and to the other end a scale engraved on glass, the distance of the lens from the scale being equal to the principal focal length of the lens. The straight line joining the zero of the scale with the optical centre of the lens ought to coincide as nearly as possible with the magnetic axis.
As these optical methods of ascertaining the angular position of suspended apparatus are of great importance in many physical researches, we shall here consider once for all their mathematical theory.
Theory of the Mirror Method.
We shall suppose that the apparatus whose angular position is to be determined is capable of revolving about a vertical axis. This axis is in general a fibre or wire by which it is suspended. The mirror should be truly plane, so that a scale of millimetres may be seen distinctly by reflexion at a distance of several metres from the mirror.
The normal through the middle of the mirror should pass through the axis of suspension, and should be accurately horizontal. We shall refer to this normal as the line of collimation of the apparatus.
Having roughly ascertained the mean direction of the line of collimation during the experiments which are to be made, a telescope is erected at a convenient distance in front of the mirror, and a little above the level of the mirror.
The telescope is capable of motion in a vertical plane, it is directed towards the suspension fibre just above the mirror, and a fixed mark is erected in the line of vision, at a horizontal distance from the object glass equal to twice the distance of the mirror from the object glass. The apparatus should, if possible, be so arranged that this mark is on a wall or other fixed object. In order to see the mark and the suspension fibre at the same time through the telescope, a cap may be placed over the object glass having a slit along a vertical diameter. This should be removed for the other observations. The telescope is then adjusted so that the mark is seen distinctly to coincide with the vertical wire at the focus of the telescope. A plumb-line is then adjusted so as to pass close in front of the optical centre of the object glass and to hang below the telescope. Below the telescope and just behind the plumb-line a scale of equal parts is placed so as to be bisected at right angles by the plane through the mark, the suspension-fibre, and the plumb-line. The sum of the heights of the scale and the object glass should be equal to twice the height of the mirror from the floor. The telescope being now directed towards the mirror will see in it the reflexion of the scale. If the part of the scale where the plumb-line crosses it appears to coincide with the vertical wire of the telescope, then the line of colliraation of the mirror coincides with the plane through the mark and the optical centre of the object glass. If the vertical wire coincides with any other division of the scale, the angular position of the line of collimation is to be found as follows:—
Let the plane of the paper be horizontal, and let the various points be projected on this plane. Let be the centre of the object glass of the telescope, P the fixed mark, P and the vertical wire of the telescope are conjugate foci with respect to the object glass. Let M be the point where OP cuts the plane of the mirror. Let MN be the normal to the mirror; then OMN = θ is the angle which the line of collimation makes with the fixed plane. Let MS be a line in the plane of OM and MN, such that NMS = OMN, then S will be the part of the scale which will be seen by reflexion to coincide with the vertical wire of the telescope. Now, since
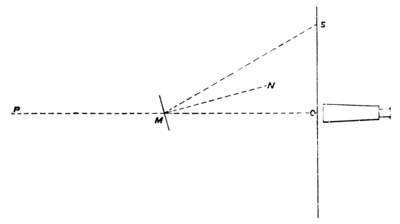
Fig. 14.
MN is horizontal, the projected angles OMN and NMS in the figure are equal, and OMS =2θ. Hence OS = 0M tan 2θ.
We have therefore to measure OM in terms of the divisions of the scale; then, if s0 is the division of the scale which coincides with the plumb-line, and s the observed division,
whence θ may be found. In measuring OM we must remember that if the mirror is of glass, silvered at the back, the virtual image of the reflecting surface is at a distance behind the front surface of the glass = t / μ, where t is the thickness of the glass, and μ is the index of refraction.
We must also remember that if the line of suspension does not pass through the point of reflexion, the position of M will alter with θ. Hence, when it is possible, it is advisable to make the centre of the mirror coincide with the line of suspension.
It is also advisable, especially when large angular motions have to be observed, to make the scale in the form of a concave cylindric surface, whose axis is the line of suspension. The angles are then observed at once in circular measure without reference to a table of tangents. The scale should be carefully adjusted, so that the axis of the cylinder coincides with the suspension fibre. The numbers on the scale should always run from the one end to the other in the same direction so as to avoid negative readings. Fig. 15

Fig. 15.
represents the middle portion of a scale to be used with a mirror and an inverting telescope.
This method of observation is the best when the motions are slow. The observer sits at the telescope and sees the image of the scale moving to right or to left past the vertical wire of the telescope. With a clock beside him he can note the instant at which a given division of the scale passes the wire, or the division of the scale which is passing at a given tick of the clock, and he can also record the extreme limits of each oscillation.
When the motion is more rapid it becomes impossible to read the divisions of the scale except at the instants of rest at the extremities of an oscillation. A conspicuous mark may be placed at a known division of the scale, and the instant of transit of this mark may be noted.
When the apparatus is very light, and the forces variable, the motion is so prompt and swift that observation through a telescope would be useless. In this case the observer looks at the scale directly, and observes the motions of the image of the vertical wire thrown on the scale by a lamp.
It is manifest that since the image of the scale reflected by the mirror and refracted by the object glass coincides with the vertical wire, the image of the vertical wire, if sufficiently illuminated, will coincide with the scale. To observe this the room is darkened, and the concentrated rays of a lamp are thrown on the vertical wire towards the object glass. A bright patch of light crossed by the shadow of the wire is seen on the scale. Its motions can be followed by the eye, and the division of the scale at which it comes to rest can be fixed on by the eye and read oif at leisure. If it be desired to note the instant of the passage of the bright spot past a given point on the scale, a pin or a bright metal wire may be placed there so as to flash out at the time of passage.
By substituting a small hole in a diaphragm for the cross wire the image becomes a small illuminated dot moving to right or left on the scale, and by substituting for the scale a cylinder revolving by clock work about a horizontal axis and covered with photographic paper, the spot of light traces out a curve which can be afterwards rendered visible. Each abscissa of this curve corresponds to a particular time, and the ordinate indicates the angular position of the mirror at that time. In this way an automatic system of continuous registration of all the elements of terrestrial magnetism has been established at Kew and other observatories.
In some cases the telescope is dispensed with, a vertical wire is illuminated by a lamp placed behind it, and the mirror is a concave one, which forms the image of the wire on the scale as a dark line across a patch of light.
451.] In the Kew portable apparatus, the magnet is made in the form of a tube, having at one end a lens, and at the other a glass scale, so adjusted as to be at the principal focus of the lens. Light is admitted from behind the scale, and after passing through the lens it is viewed by means of a telescope.
Since the scale is at the principal focus of the lens, rays from any division of the scale emerge from the lens parallel, and if the telescope is adjusted for celestial objects, it will shew the scale in optical coincidence with the cross wires of the telescope. If a given division of the scale coincides with the intersection of the cross wires, then the line joining that division with the optical centre of the lens must be parallel to the line of collimation of the telescope. By fixing the magnet and moving the telescope, we may ascertain the angular value of the divisions of the scale, and then, when the magnet is suspended and the position of the telescope known, we may determine the position of the magnet at any instant by reading off the division of the scale which coincides with the cross wires.
The telescope is supported on an arm which is centred in the line of the suspension fibre, and the position of the telescope is read off by verniers on the azimuth circle of the instrument.
This arrangement is suitable for a small portable magnetometer in which the whole apparatus is supported on one tripod, and in which the oscillations due to accidental disturbances rapidly subside.
Determination of the Direction of the Axis of the Magnet, and of the Direction of Terrestrial Magnetism.
452.] Let a system of axes be drawn in the magnet, of which the axis of z is in the direction of the length of the bar, and x and y perpendicular to the sides of the bar supposed a parallelepiped.
Let l, m, n and λ, μ, ν be the angles which the magnetic axis and the line of collimation make with these axes respectively.
Let M be the magnetic moment of the magnet, let Π be the horizontal component of terrestrial magnetism, let Z be the vertical component, and let δ be the azimuth in which H acts, reckoned from the north towards the west.
Let ζ be the observed azimuth of the line of collimation, let α be the azimuth of the stirrup, and β the reading of the index of the torsion circle, then α - β is the azimuth of the lower end of the suspension fibre.
Let γ be the value of α - β when there is no torsion, then the moment of the force of torsion tending to dimmish a will be
where τ is a coefficient of torsion depending on the nature of the fibre.
To determine λ, fix the stirrup so that y is vertical and up wards, z to the north and x to the west, and observe the azimuth ζ of the line of collimation. Then remove the magnet, turn it through an angle π about the axis of z and replace it in this inverted position, and observe the azimuth ζ' of the line of collimation when y is downwards and x to the east, | (1) |
| (2) |
| Hence | (3) |
Next, hang the stirrup to the suspension fibre, and place the magnet in it, adjusting it carefully so that y may be vertical and upwards, then the moment of the force tending to increase α is
| (4) |
But if ζ is the observed azimuth of the line of collimation
| (5) |
so that the force may be written
| (6) |
When the apparatus is in equilibrium this quantity is zero for a particular value of ζ.
When the apparatus never comes to rest, but must be observed in a state of vibration, the value of ζ corresponding to the position of equilibrium may be calculated by a method which will be described in Art. 735.
When the force of torsion is small compared with the moment of the magnetic force, we may put δ - ζ + l - λ for the sine of that angle.
If we give to β, the reading of the torsion circle, two different values, β1 and β2, and if ζ1 and ζ2 are the corresponding values of ζ,
| (7) |
or, if we put
| (8) |
and equation (7) becomes, dividing by M H sin m,
| (9) |
If we now reverse the magnet so that y is downwards, and adjust the apparatus till y is exactly vertical, and if ζ' is the new value of the azimuth, and δ' the corresponding declination,
| (10) |
whence
| (11) |
The reading of the torsion circle should now be adjusted, so that the coefficient of may be as nearly as possible zero. For this purpose we must determine , the value of when there is no torsion. This may be done by placing a non-magnetic bar of the same weight as the magnet in the stirrup, and determining when there is equilibrium. Since is small, great accuracy is required. Another method is to use a torsion bar of the same weight as the magnet, containing within it a very small magnet whose magnetic moment is of that of the principal magnet. Since remains the same, will become , and if and are the values of as found by the torsion bar,
| (12) |
| (13) |
the torsion circle, should he altered till
| (14) |
Then, since is a very small numerical quantity, and since its coefficient is very small, the value of the second term in the expression for will not vary much for small errors in the values of and , which are the quantities whose values are least accurately known.
The value of , the magnetic declination, may be found in this way with considerable accuracy, provided it remains constant during the experiments, so that we may assume .
When great accuracy is required it is necessary to take account ot the variations of during the experiment. For this purpose observations of another suspended magnet should be made at the some instants that the different values of are observed, and if are the observed azimuths of the second magnet corresponding to and , and if and are the corresponding values of , then
| (15) |
| (15) |
| (16) |
To find the direction of the magnetic axis within the magnet subtract (10) from (9) and add (15),
| (17) |
By repeating the experiments with the bar on its two edges, so that the axis of x is vertically upwards and downwards, we can find the value of m. If the axis of collimation is capable of adjustment it ought to be made to coincide with the magnetic axis as nearly as possible, so that the error arising from the magnet not being exactly inverted may be as small as possible [2].
On the Measurement of Magnetic Forces.
453.] The most important measurements of magnetic force are those which determine M, the magnetic moment of a magnet, and H, the intensity of the horizontal component of terrestrial magnetism. This is generally done by combining the results of two experiments, one of which determines the ratio and the other the product of these two quantities.
The intensity of the magnetic force due to an infinitely small magnet whose magnetic moment is M, at a point distant r from the centre of the magnet in the positive direction of the axis of the magnet, is
| (1) |
and is in the direction of r. If the magnet is of finite size but spherical, and magnetized uniformly in the direction of its axis, this value of the force will still be exact. If the magnet is a solenoidal bar magnet of length 2L,
| (2) |
If the magnet be of any kind, provided its dimensions are all small compared with r,
| (3) |
where A1,A2,&c. are coefficients depending on the distribution of the magnetization of the bar.
Let H be the intensity of the horizontal part of terrestrial magnetism at any place. H is directed towards magnetic north. Let r be measured towards magnetic west, then the magnetic force at the extremity of r will be H towards the north and R towards the west. The resultant force will make an angle 6 with the magnetic meridian, measured towards the west, and such that
| (4) |
Hence, to determine we proceed as follows :—
The direction of the magnetic north having been ascertained, a magnet, whose dimensions should not be too great, is suspended as in the former experiments, and the deflecting magnet is placed so that its centre is at a distance from that of the suspended magnet, in the same horizontal plane, and due magnetic east.
The axis of is carefully adjusted so as to be horizontal and in the direction of .
The suspended magnet is observed before is brought near and also after it is placed in position. If is the observed deflexion, we have, if we use the approximate formula (1),
| (5) |
or, if we use the formula (3),
| (6) |
Here we must bear in mind that though the deflexion can be observed with great accuracy, the distance between the centres of the magnets is a quantity which cannot be precisely deter mined, unless both magnets are fixed and their centres defined by marks.
This difficulty is overcome thus :
The magnet is placed on a divided scale which extends east and west on both sides of the suspended magnet. The middle point between the ends of is reckoned the centre of the magnet. This point may be marked on the magnet and its position observed on the scale, or the positions of the ends may be observed and the arithmetic mean taken. Call this , and let the line of the suspension fibre of the suspended magnet when produced cut the scale at , then where is known accurately and approximately. Let be the deflexion observed in this position of .
Now reverse , that is, place it on the scale with its ends reversed, then will be the same, but and ,, will have their signs changed, so that if is the deflexion,
| (7) |
| (8) |
Now remove to the west side of the suspended magnet, and place it with its centre at the point marked on the scale. Let the deflexion when the axis is in the first position be , and when it is in the second , then, as before,
| (9) |
Let us suppose that the true position of the centre of the suspended magnet is not but , then
| , | (10) |
and
| (11) |
and since may be neglected if the measurements are carefully made, we are sure that we may take the arithmetical mean of and for .
Hence, taking the arithmetical mean of (8) and (9),
| (12) |
or, making
| (13) |
454.] We may now regard and as capable of exact determination.
The quantity can in no case exceed , where is half the length of the magnet, so that when is considerable compared with we may neglect the term in and determine the ratio of to at once. We cannot, however, assume that is equal to , for it may be less, and may even be negative for a magnet whose largest dimensions are transverse to the axis. The term in , and all higher terms, may safely be neglected.
To eliminate , repeat the experiment, using distances &c., and let the values of be , &c., then
| &c. | &c. |
If we suppose that the probable errors of these equations are equal, as they will be if they depend on the determination of only, and if there is no uncertainty about , then, by multiplying each equation by and adding the results, we obtain one equation, and by multiplying each equation by and adding we obtain another, according to the general rule in the theory of the combination of fallible measures when the probable error of each equation is supposed the same.
Let us write
for &c.,
and use similar expressions for the sums of other groups of symbols, then the two resultant equations may be written
,
,
whence
,
The value of derived from these equations ought to be less
than half the square of the length of the magnet . If it is not
we may suspect some error in the observations. This method of
observation and reduction was given by Gauss in the 'First Report
of the Magnetic Association.'
When the observer can make only two series of experiments at distances and , the value of derived from these experiments is
, \quad .
If and are the actual errors of the observed deflexions and , the actual error of the calculated result will be
.
If we suppose the errors and to be independent, and that the probable value of either is , then the probable value of the error in the calculated value of will be , where
.
given, the value of the greater distance may be determined so as to make a minimum. This condition leads to an equation of the fifth degree in , which has only one real root greater than . From this the best value of is found to be [3].
If one observation only is taken the best distance is when
,
where is the probable error of a measurement of deflexion, and is the probable error of a measurement of distance.
Method of Sines.
455.] The method which we have just described may be called the Method of Tangents, because the tangent of the deflexion is a measure of the magnetic force.
If the line instead of being measured east or west, is adjusted till it is at right angles with the axis of the deflected magnet, then is the same as before, but in order that the suspended magnet may remain perpendicular to , the resolved part of the force in the direction of must be equal and opposite to . Hence, if is the deflexion, .
This method is called the Method of Sines. It can be applied only when is less than .
In the Kew portable apparatus this method is employed. The suspended magnet hangs from a part of the apparatus which revolves along with the telescope and the arm for the deflecting magnet, and the rotation of the whole is measured on the azimuth circle.
The apparatus is first adjusted so that the axis of the telescope coincides with the mean position of the line of collimation of the magnet in its undisturbed state. If the magnet is vibrating, the true azimuth of magnetic north is found by observing the extremities of the oscillation of the transparent scale and making the proper correction of the reading of the azimuth circle.
The deflecting magnet is then placed upon a straight rod which passes through the axis of the revolving apparatus at right angles to the axis of the telescope, and is adjusted so that the axis of the deflecting magnet is in a line passing through the centre of the suspended magnet.
The whole of the revolving apparatus is then moved till the line of collimation of the suspended magnet again coincides with the axis of the telescope, and the new azimuth reading is corrected, if necessary, by the mean of the scale readings at the extremities of an oscillation.
The difference of the corrected azimuths gives the deflexion, after which we proceed as in the method of tangents, except that in the expression for we put instead of .
In this method there is no correction for the torsion of the suspending fibre, since the relative position of the fibre, telescope, and magnet is the same at every observation.
The axes of the two magnets remain always at right angles in this method, so that the correction for length can be more accurately made.
456.] Having thus measured the ratio of the moment of the deflecting magnet to the horizontal component of terrestrial magnetism, we have next to find the product of these quantities, by determining the moment of the couple with which terrestrial magnetism tends to turn the same magnet when its axis is deflected from the magnetic meridian.
There are two methods of making this measurement, the dynamical, in which the time of vibration of the magnet under the action of terrestrial magnetism is observed, and the statical, in which the magnet is kept in equilibrium between a measurable statical couple and the magnetic force.
The dynamical method requires simpler apparatus and is more accurate for absolute measurements, but takes up a considerable time, the statical method admits of almost instantaneous measurement, and is therefore useful in tracing the changes of the intensity of the magnetic force, but it requires more delicate apparatus, and is not so accurate for absolute measurement.
Method of Vibrations.
The magnet is suspended with its magnetic axis horizontal, and is set in vibration in small arcs. The vibrations are observed by means of any of the methods already described.
A point on the scale is chosen corresponding to the middle of the arc of vibration. The instant of passage through this point of the scale in the positive direction is observed. If there is sufficient time before the return of the magnet to the same point, the instant of passage through the point in the negative direction is also observed, and the process is continued till positive and negative passages have been observed. If the vibrations are too rapid to allow of every consecutive passage being observed, every third or every fifth passage is observed, care being taken that the observed passages are alternately positive and negative.
Let the observed times of passage be , then if we put
;
then is the mean time of the positive passages, and ought to agree with , the mean time of the negative passages, if the point has been properly chosen. The mean of these results is to be taken as the mean time of the middle passage.
After a large number of vibrations have taken place, but before the vibrations have ceased to be distinct and regular, the observer makes another series of observations, from which he deduces the mean time of the middle passage of the second series.
By calculating the period of vibration either from the first series of observations or from the second, he ought to be able to be certain of the number of whole vibrations which have taken place in the interval between the time of middle passage in the two series. Dividing the interval between the mean times of middle passage in the two series by this number of vibrations, the mean time of vibration is obtained.
The observed time of vibration is then to be reduced to the time of vibration in infinitely small arcs by a formula of the same kind as that used in pendulum observations, and if the vibrations are found to diminish rapidly in amplitude, there is another correction for resistance, see Art. 740. These corrections, however, are very small when the magnet hangs by a fibre, and when the arc of vibration is only a few degrees.
The equation of motion of the magnet is
where is the angle between the magnetic axis and the direction of the force , is the moment of inertia of the magnet and suspended apparatus, is the magnetic moment of the magnet, H the intensity of the horizontal magnetic force, and the coefficient of torsion: is determined as in Art. 452, and is a very small quantity. The value of for equilibrium is
,a very small angle,
where is the periodic time, and the amplitude, and
;
whence we find the value of ,
.
Here is the time of a complete vibration determined from observation. , the moment of inertia, is found once for all for the magnet, either by weighing and measuring it if it is of a regular figure, or by a dynamical process of comparison with a body whose moment of inertia is known.
Combining this value of with that of formerly obtained, we get
,
and
.
457.] We have supposed that H and M continue constant during the two series of experiments. The fluctuations of // may be ascertained by simultaneous observations of the bifilar magnetometer to be presently described, and if the magnet has been in use for some time, and is not exposed during the experiments to changes of temperature or to concussion, the part of which depends on permanent magnetism may be assumed to be constant. All steel magnets, however, are capable of induced magnetism depending on the action of external magnetic force.
Now the magnet when employed in the deflexion experiments is placed with its axis east and west, so that the action of terrestrial magnetism is transverse to the magnet, and does not tend to increase or diminish . When the magnet is made to vibrate, its axis is north and south, so that the action of terrestrial magnetism tends to magnetize it in the direction of the axis, and therefore to increase its magnetic moment by a quantity , where is a coefficient to be found by experiments on the magnet.
There are two ways in which this source of error may be avoided without calculating , the experiments being arranged so that the magnet shall be in the same condition when employed in deflecting another magnet and when itself swinging. We may place the deflecting magnet with its axis pointing north, at a distance from the centre of the suspended magnet, the line making an angle whose cosine is with the magnetic meridian. The action of the deflecting magnet on the suspended one is then at right angles to its own direction, and is equal to
Here is the magnetic moment when the axis points north, as in the experiment of vibration, so that no correction has to be made for induction.
This method, however, is extremely difficult, owing to the large errors which would be introduced by a slight displacement of the deflecting magnet, and as the correction by reversing the deflecting magnet is not applicable here, this method is not to be followed except when the object is to determine the coefficient of induction.
The following method, in which the magnet while vibrating is freed from the inductive action of terrestrial magnetism, is due to Dr. J. P. Joule.[4]
Two magnets are prepared whose magnetic moments are as nearly equal as possible. In the deflexion experiments these magnets are used separately, or they may be placed simultaneously on opposite sides of the suspended magnet to produce a greater deflexion. In these experiments the inductive force of terrestrial magnetism is transverse to the axis.
Let one of these magnets be suspended, and let the other be placed parallel to it with its centre exactly below that of the suspended magnet, and with its axis in the same direction. The force which the fixed magnet exerts on the suspended one is in the opposite direction from that of terrestrial magnetism. If the fixed magnet be gradually brought nearer to the suspended one the time of vibration will increase, till at a certain point the equilibrium will cease to be stable, and beyond this point the suspended magnet will make oscillations in the reverse position. By experimenting in this way a position of the fixed magnet is found at which it exactly neutralizes the effect of terrestrial magnetism on the suspended one. The two magnets are fastened together so as to be parallel, with their axes turned the same way, and at the distance just found by experiment. They are then suspended in the usual way and made to vibrate together through small arcs.
The lower magnet exactly neutralizes the effect of terrestrial magnetism on the upper one, and since the magnets are of equal moment, the upper one neutralizes the inductive action of the earth on the lower one.
The value of is therefore the same in the experiment of vibration as in the experiment of deflexion, and no correction for induction is required.
458.] The most accurate method of ascertaining the intensity of the horizontal magnetic force is that which we have just described. The whole series of experiments, however, cannot be performed with sufficient accuracy in much less than an hour, so that any changes in the intensity which take place in periods of a few minutes would escape observation. Hence a different method is required for observing the intensity of the magnetic force at any instant.
The statical method consists in deflecting the magnet by means of a statical couple acting in a horizontal plane. If be the moment of this couple, the magnetic moment of the magnet, the horizontal component of terrestrial magnetism, and the deflexion,
.
Hence, if is known in terms of , can be found.
The couple may be generated in two ways, by the torsional elasticity of a wire, as in the ordinary torsion balance, or by the weight of the suspended apparatus, as in the bifilar suspension.
In the torsion balance the magnet is fastened to the end of a vertical wire, the upper end of which can be turned round, arid its rotation measured by means of a torsion circle.
We have then
.
Here is the value of the reading of the torsion circle when the axis of the magnet coincides with the magnetic meridian, and a is the actual reading. If the torsion circle is turned so as to bring the magnet nearly perpendicular to the magnetic meridian, so that
, then , or .
By observing , the deflexion of the magnet when in equilibrium, we can calculate provided we know .
If we only wish to know the relative value of at different times it is not necessary to know either or .
We may easily determine in absolute measure by suspending a non-magnetic body from the same wire and observing its time of oscillation, then if is the moment of inertia of this body, and the time of a complete vibration,
.
The chief objection to the use of the torsion balance is that the zero-reading is liable to change. Under the constant twisting force, arising from the tendency of the magnet to turn to the north, the wire gradually acquires a permanent twist, so that it becomes necessary to determine the zero-reading of the torsion circle afresh at short intervals of time.
Bifilar Suspension.
459.] The method of suspending the magnet by two wires or fibres was introduced by Gauss and Weber. As the bifilar suspension is used in many electrical instruments, we shall investigate it more in detail. The general appearance of the suspension is shewn in Fig. 16, and Fig. 17 represents the projection of the wires on a horizontal plane.
and are the projections of the two wires.
and are the lines joining the upper and the lower ends of the wires.
and are the lengths of these lines.
and their azimuths.
and the vertical components of the tensions of the wires.
and their horizontal components.
the vertical distance between and .
The forces which act on the magnet are its weight, the couple arising from terrestrial magnetism, the torsion of the wires (if any) and their tensions. Of these the effects of magnetism and of torsion are of the nature of couples. Hence the resultant of the tensions must consist of a vertical force, equal to the weight of the magnet, together with a couple. The resultant of the vertical components of the tensions is therefore along the line whose projection is , the intersection of and , and either of these lines is divided in in the ratio of to .
The horizontal components of the tensions form a couple, and are therefore equal in magnitude and parallel in direction. Calling either of them , the moment of the couple which they form is
where is the distance between the parallel lines and . To find the value of we have the equations of moments
and the geometrical equation
whence we obtain,
 |

|
| Fig. 18 | Fig. 17. |
If is the mass of the suspended apparatus, and the intensity of gravity,
If we also write
we find
The value of is therefore a maximum with respect to when is zero, that is, when the weight of the suspended mass is equally borne by the two wires.
We may adjust the tensions of the wires to equality by observing the time of vibration, and making it a minimum, or we may obtain a self-acting adjustment by attaching the ends of the wires, as in Fig. 16, to a pulley, which turns on its axis till the tensions are equal.
The distance of the upper ends of the suspension wires is regulated by means of two other pullies. The distance between the lower ends of the wires is also capable of adjustment.
By this adjustment of the tension, the couple arising from the tensions of the wires becomes
.
The moment of the couple arising from the torsion of the wires is of the form
,
where is the sum of the coefficients of torsion of the wires.
The wires ought to be without torsion when , we may then make .
The moment of the couple arising from the horizontal magnetic force is of the form
,
where is the magnetic declination, and is the azimuth of the axis of the magnet. We shall avoid the introduction of unnecessary symbols without sacrificing generality if we assume that the axis of the magnet is parallel to BB', or that .
The equation of motion then becomes
There are three principal positions of this apparatus.
(1) When is nearly equal to . If is the time of a complete oscillation in this position, then
(2) When is nearly equal to . If is the time of a complete oscillation in this position, the north end of the magnet being now turned towards the south,
The quantity on the right-hand of this equation may be made as small as we please by diminishing or , but it must not be made negative, or the equilibrium of the magnet will become unstable. The magnet in this position forms an instrument by which small variations in the direction of the magnetic force may be rendered sensible.
For when is nearly equal to , is nearly equal to , and we find
By diminishing the denominator of the fraction in the last term we may make the variation of very large compared with that of . We should notice that the coefficient of in this expression is negative, so that when the direction of the magnetic force turns in one direction the magnet turns in the opposite direction.
(3) In the third position the upper part of the suspension-apparatus is turned round till the axis of the magnet is nearly perpendicular to the magnetic meridian.
If we make
and if is the value of the horizontal force corresponding to a small angle ,
-
In order that the magnet may be in stable equilibrium it is necessary that the numerator of the fraction in the second member should be positive, but the more nearly it approaches zero, the more sensitive will be the instrument in indicating changes in the value of the intensity of the horizontal component of terrestrial magnetism.
The statical method of estimating the intensity of the force depends upon the action of an instrument which of itself assumes different positions of equilibrium for different values of the force. Hence, by means of a mirror attached to the magnet and throwing a spot of light upon a photographic surface moved by clockwork, a curve may be traced, from which the intensity of the force at any instant may be determined according to a scale, which we may for the present consider an arbitrary one.
460.] In an observatory, where a continuous system of registration of declination and intensity is kept up either by eye observation or by the automatic photographic method, the absolute values of the declination and of the intensity, as well as the position and moment of the magnetic axis of a magnet, may be determined to a greater degree of accuracy.
For the declinometer gives the declination at every instant affected by a constant error, and the bifilar magnetometer gives the intensity at every instant multiplied by a constant coefficient. In the ex periments we substitute for , where is the reading of the declinometer at the given instant, and is the unknown but constant error, so that is the true declination at that instant.
In like manner for , we substitute where is the reading of the magnetometer on its arbitrary scale, and is an unknown but constant multiplier which converts these readings into absolute measure, so that is the horizontal force at a given instant.
The experiments to determine the absolute values of the quantities must be conducted at a sufficient distance from the declinometer and magnetometer, so that the different magnets may not sensibly disturb each other. The time of every observation must be noted and the corresponding values of and inserted. The equations are then to be treated so as to find , the constant error of the declinometer, and the coefficient to be applied to the readings of the magnetometer. When these are found the readings of both instruments may be expressed in absolute measure. The absolute measurements, however, must be frequently repeated in order to take account of changes which may occur in the magnetic axis and magnetic moment of the magnets.
461.] The methods of determining the vertical component of the terrestrial magnetic force have not been brought to the same degree of precision. The vertical force must act on a magnet which turns about a horizontal axis. Now a body which turns about a horizontal axis cannot be made so sensitive to the action of small forces as a body which is suspended by a fibre and turns about a vertical axis. Besides this, the weight of a magnet is so large compared with the magnetic force exerted upon it that a small displacement of the centre of inertia by unequal dilatation, &c. produces a greater effect on the position of the magnet than a considerable change of the magnetic force.
Hence the measurement of the vertical force, or the comparison of the vertical and the horizontal forces, is the least perfect part of the system of magnetic measurements.
The vertical part of the magnetic force is generally deduced from the horizontal force by determining the direction of the total force.
If be the angle which the total force makes with its horizontal component, is called the magnetic Dip or Inclination, and if is the horizontal force already found, then the vertical force is , and the total force is .
The magnetic dip is found by means of the Dip Needle.
The theoretical dip-needle is a magnet with an axis which passes through its centre of inertia perpendicular to the magnetic axis of the needle. The ends of this axis are made in the form of cylinders of small radius, the axes of which are coincident with the line passing through the centre of inertia. These cylindrical ends rest on two horizontal planes and are free to roll on them.
When the axis is placed magnetic east and west, the needle is free to rotate in the plane of the magnetic meridian, and if the instrument is in perfect adjustment, the magnetic axis will set itself in the direction of the total magnetic force.
It is, however, practically impossible to adjust a dip-needle so that its weight does not influence its position of equilibrium, because its centre of inertia, even if originally in the line joining the centres of the rolling sections of the cylindrical ends, will cease to be in this line when the needle is imperceptibly bent or unequally expanded. Besides, the determination of the true centre of inertia of a magnet is a very difficult operation, owing to the interference of the magnetic force with that of gravity.
Let us suppose one end of the needle and one end of the pivot to be marked. Let a line, real or imaginary, be drawn on the needle, which we shall call the Line of Collimation. The position of this line is read off on a vertical circle. Let be the angle which this line makes with the radius to zero, which we shall suppose to be horizontal. Let be the angle which the magnetic axis makes with the line of collimation, so that when the needle is in this position the line of collimation is inclined to the horizontal.
Let be the perpendicular from the centre of inertia on the plane on which the axis rolls, then will be a function of , whatever be the shape of the rolling surfaces. If both the rolling sections of the ends of the axis are circular,
where is the distance of the centre of inertia from the line joining the centres of the rolling sections, and is the angle which this line makes with the line of collimation.
If is the magnetic moment, the mass of the magnet, and the force of gravity, the total magnetic force, and the dip, then, by the conservation of energy, when there is stable equilibrium,
must be a maximum with respect to , or
|
(3) |
if the ends of the axis are cylindrical.
Also, if be the time of vibration about the position of equilibrium,
where is the moment of inertia of the needle about its axis of rotation.
In determining the dip a reading is taken with the dip circle in the magnetic meridian and with the graduation towards the west.
Let be this reading, then we have
The instrument is now turned about a vertical axis through 180°, so that the graduation is to the east, and if is the new reading,
Taking (6) from (5), and remembering that is nearly equal to and nearly equal to , and that is a small angle, such that may be neglected in comparison with ,
Now take the magnet from its bearings and place it in the deflexion apparatus, Art. 453, so as to indicate its own magnetic moment by the deflexion of a suspended magnet, then
where is the tangent of the deflexion.
Next, reverse the magnetism of the needle and determine its new magnetic moment , by observing a new deflexion, the tangent of which is ,
Then place it on its bearings and take two readings, and , in which is nearly , and nearly ,
whence, as before,
adding (8),
whence we find the dip
where and are the tangents of the deflexions produced by the needle in its first and second magnetizations respectively.
In taking observations with the dip circle the vertical axis is carefully adjusted so that the plane bearings upon which the axis of the magnet rests are horizontal in every azimuth. The magnet being magnetized so that the end dips,, is placed with its axis on the plane bearings, and observations are taken with the plane of the circle in the magnetic meridian, and with the graduated side of the circle east. Each end of the magnet is observed by means of reading microscopes carried on an arm which moves concentric with the dip circle. The cross wires of the microscope are made to coincide with the image of a mark on the magnet, and the position of the arm is then read off on the dip circle by means of a vernier.
We thus obtain an observation of the end and another of the end when the graduations are east. It is necessary to observe both ends in order to eliminate any error arising from the axle of the magnet not being concentric with the dip circle.
The graduated side is then turned west, and two more observations are made.
The magnet is then turned round so that the ends of the axle are reversed, and four more observations are made looking at the other side of the magnet.
The magnetization of the magnet is then reversed so that the end dips, the magnetic moment is ascertained, and eight observations are taken in this state, and the sixteen observations combined to determine the true dip.
462.] It is found that in spite of the utmost care the dip, as thus deduced from observations made with one dip circle, differs perceptibly from that deduced from observations with another dip circle at the same place. Mr. Broun has pointed out the effect due to ellipticity of the bearings of the axle, and how to correct it by taking observations with the magnet magnetized to different strengths.
The principle of this method may be stated thus. We shall suppose that the error of any one observation is a small quantity not exceeding a degree. We shall also suppose that some unknown but regular force acts upon the magnet, disturbing it from its true position.
If is the moment of this force, the true dip, and the observed dip, then
since is small.
It is evident that the greater becomes the nearer does the needle approach its proper position. Now let the operation of taking the dip be performed twice, first with the magnetization equal to , the greatest that the needle is capable of, and next with the magnetization equal to , a much smaller value but sufficient to make the readings distinct and the error still moderate. Let and be the dips deduced from these two sets of observations, and let be the mean value of the unknown disturbing force for the eight positions of each determination, which we shall suppose the same for both determinations. Then
If we find that several experiments give nearly equal values for , then we may consider that must be very nearly the true value of the dip.
463.] Dr. Joule has recently constructed a new dip-circle, in which the axis of the needle, instead of rolling on horizontal agate planes, is slung on two filaments of silk or spider s thread, the ends of the filaments being attached to the arms of a delicate balance. The axis of the needle thus rolls on two loops of silk fibre, and Dr. Joule finds that its freedom of motion is much greater than when it rolls on agate planes.

Fig. 18.
In Fig. 18, is the needle, is its axis, consisting of a straight cylindrical wire, and , are the filaments on which the axis rolls. is the balance, consisting of a double bent lever supported by a wire, , stretched horizontally between the prongs of a forked piece, and having a counterpoise which can be screwed up or down, so that the balance is in neutral equilibrium about .
In order that the needle may be in neutral equilibrium as the needle rolls on the filaments the centre of gravity must neither rise nor fall. Hence the distance must remain constant as the needle rolls. This condition will be fulfilled if the arms of the balance and are equal, and if the filaments are at right angles to the arms.
Dr. Joule finds that the needle should not be more than five inches long. When it is eight inches long, the bending of the needle tends to diminish the apparent dip by a fraction of a minute. The axis of the needle was originally of steel wire, straightened by being brought to a red heat while stretched by a weight, but Dr. Joule found that with the new suspension it is not necessary to use steel wire, for platinum and even standard gold are hard enough.
The balance is attached to a wire about a foot long stretched horizontally between the prongs of a fork. This fork is turned round in azimuth by means of a circle at the top of a tripod which supports the whole. Six complete observations of the dip can be obtained in one hour, and the average error of a single observation is a fraction of a minute of arc.
It is proposed that the dip needle in the Cambridge Physical Laboratory shall be observed by means of a double image instrument, consisting of two totally reflecting prisms placed as in Fig. 19 and mounted on a vertical graduated circle, so that the plane of reflexion may be turned round a horizontal axis nearly coinciding with the prolongation of the axis of the suspended dip-needle. The needle is viewed by means of a telescope placed behind the prisms, and the two ends of the needle are seen together as in Fig. 20. By turning the prisms about the axis of the vertical circle, the images of two lines drawn on the needle may be made to coincide. The inclination of the needle is thus determined from the reading of the vertical circle.
 |
 |
The total intensity of the magnetic force in the line of dip may be deduced as follows from the times of vibration , , in the four positions already described,
The values of and must be found by the method of deflexion and vibration formerly described, and is the moment of inertia of the magnet about its axle.
The observations with a magnet suspended by a fibre are so much more accurate that it is usual to deduce the total force from the horizontal force from the equation
where is the total force, the horizontal force, and the dip.
464.] The process of determining the dip being a tedious one, is not suitable for determining the continuous variation of the magnetic force. The most convenient instrument for continuous observations is the vertical force magneto meter, which is simply a magnet balanced on knife edges so as to be in stable equilibrium with its magnetic axis nearly horizontal.
If is the vertical component of the magnetic force, the magnetic moment, and the small angle which the magnetic axis makes with the horizon
where is the mass of the magnet, the force of gravity, the distance of the centre of gravity from the axis of suspension, and the angle which the plane through the axis and the centre of gravity makes with the magnetic axis.
Hence, for the small variation of vertical force , there will be a variation of the angular position of the magnet such that
In practice this instrument is not used to determine the absolute value of the vertical force, but only to register its small variations.
For this purpose it is sufficient to know the absolute value of when , and the value of .
The value of , when the horizontal force and the dip are known, is found from the equation , where is the dip and the horizontal force.
To find the deflexion due to a given variation of , take a magnet and place it with its axis east and west, and with its centre at a known distance east or west from the declinometer, as in experiments on deflexion, and let the tangent of deflexion be .
Then place it with its axis vertical and with its centre at a distance above or below the centre of the vertical force magnetometer, and let the tangent of the deflexion produced in the magnetometer be . Then, if the moment of the deflecting magnet is ,
The actual value of the vertical force at any instant is
where is the value of when .
For continuous observations of the variations of magnetic force at a fixed observatory the Unifilar Declinometer, the Bifilar Horizontal Force Magnetometer, and the Balance Vertical Force Magnetometer are the most convenient instruments.
At several observatories photographic traces are now produced on prepared paper moved by clock work, so that a continuous record of the indications of the three instruments at every instant is formed. These traces indicate the variation of the three rectangular components of the force from their standard values. The declinometer gives the force towards mean magnetic west, the bifilar magnetometer gives the variation of the force towards magnetic north, and the balance magnetometer gives the variation of the vertical force. The standard values of these forces, or their values when these instruments indicate their several zeros, are deduced by frequent observations of the absolute declination, horizontal force, and dip.























































































![{\displaystyle {\frac {2M}{H}}{\big \{}\sum (r^{-6})\sum (r^{-10})-{[\sum (r^{-8})]}^{2}{\big \}}=\sum (Dr^{-3})\sum (r^{-10})-\sum (Dr^{-5})\sum (r^{-8})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/114c35e84090584ce727b227827668ea0312b95e)














































































































































































