A Voyage in Space/Lecture VI
LECTURE VI
THE STARS
We have now to make our longest journey of all—to the stars. Even as fast as the telescope will carry us it will take us some years to get there. It is difficult, perhaps, to realize that light seems to go quickly, yet really is taking time to travel; that really it takes time for light to travel, let us say, from me to you—not very long perhaps; but still you do not see me as I really am, but as I was a small fraction of a second ago. It is easier to realize the interval in the case of sound; and several times in his lecture I shall have to remind you of the likeness between light and sound, because it is so much easier to understand in the case of sound things which seem very difficult in the case of light. For instance, we all know that sound takes time to travel, because we have heard echoes. We shout, and presently we hear our shout coming back from some distant point. The time in between is the time taken by the sound to travel. When you look in your mirror in the morning, you really have to wait a little time before the light from your face goes to the mirror and comes back again, so that you get the echo or reflection from the mirror. I shall have something more to say about these light echoes towards the end of the lecture. Light, then, takes time to travel, but the time taken is very, very small. I wonder how small a fraction of a second you think it takes to travel from me to you? Well, you know how long a year is; and how long a second is. Have you any idea how many seconds there are in a year? About 30 millions. Now suppose you pretend that a second is itself like a year; divide it into its seconds, that is into 30 million parts; one of these tiny parts will be about the time that what we may call a "wireless" wave of electricity takes to vibrate. I do not mean the time that the spark takes, but the time a single wave takes to be transmitted its whole length. And then suppose you take one of these "wireless" wave times, and divide that up into 30 million parts, you get about the time that a light wave takes to vibrate. And the time that it takes you to see me is about one wireless vibration, a very small fraction of a second, but still containing 30 million light vibrations.
We might make a new set of tables for you to learn—
30 million light vibrations make one wireless vibration.
30 million wireless vibrations make one second.
30 million seconds make one year.
And 30 million years—what do they make? Well, I shall have something more to say about that towards the end of the lecture.
For the present we will start with a year or two. It takes a year or two to get to the very nearest star, and many years to get, for instance, to most of the bright stars of the zodiac. "The Ram, the Bull, the Heavenly Twins"—have you yet learnt their names and order?
These stars of the zodiac are comparatively bright and near. But there are many stars in the heavens which are fainter, that we cannot even see with the eye,Fig. 81.—Region near the Southern Cross.
(The Cross is on the right, two big stars and two much smaller.)
In Fig. 81 you see a very large number of stars, some of them big. Two of them are so bright that their light has made a kind of halo by reflection from the back of the photographic plate. That circle of light does not belong to the star; it is merely a photographic fault, showing how bright the star really is. But in the picture there are also many fainter stars, and even dark patches where there seem to be no stars at all. Now, do you think it is possible that there are no stars at all in those places? The photograph rather deceives us by being a flat thing; as though the stars were scattered over a flat surface; but that is not really the case. When Mr. Daily Mirror came and photographed us all the other day, his picture was also on a flat plate; but that does not deceive us into thinking that this room full of people is flat. We know that there are some in the front row who come out big in the picture and some in the back rows who come out smaller. And so in the case of the stars; big bright ones are probably in the front row near the Earth: the very faint ones in the back row. I say probably because we cannot be quite sure. Even in this room there are some very small people in the front row; and they come out small in the picture; while their grown-up parents may look large in the picture, in spite of the fact that they are in a row behind. In this case we can generally tell from the dress, or the character in the face, that the difference of size is due to age and not to the position in the room; but the stars do not help us in this way by their appearance, so that we are liable to mistakes if we assign their distances from us simply by the brightness.
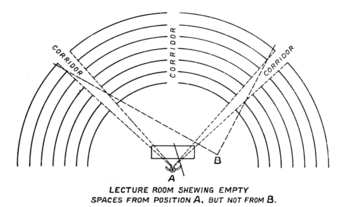
But now what are we to think of the places on the photograph where there seem to be no stars? There are some directions in which I can see no people in this room, namely, when I look along the corridors: but I have to be careful to stand in one special place (A) to see this emptiness. If I move to the right, as to B, then I lose the appearance of vacancy in all three corridors (Fig. 82).
You can try a similar thing for yourselves with an empty tube. If you point it straight to your eye you can see the vacant space at the far end; but if you incline the tube, the far end disappears behind one of the sides. If the tube is short, you may have to incline it a good deal before the end disappears; but if it is very long, the slightest tilt will make you lose the end.
Now, if these patches showing no stars are really vacant spaces, they must be like very long corridors or tubes pointed very straight at us: that they are very long, we know, because we have evidence that the stars extend to immense distances. The people in this audience are confined within a definite room—quite a nice, large room, it is true, but still a room bounded by solid walls. There are no walls confining the stars: behind the front rows there are others, and behind them others still, and again others, and we never come to walls, so far as we know at present; so that the corridors through the audience of stars must be enormously long. Therefore, if we really see blank spaces at the end of them, they must be pointed dead straight at us, because the very slightest tilt would cause the end to disappear when the corridor or tube is so very, very long.Now, can we think it likely that so many tubes or corridors or lanes through the stars should be pointed actually dead straight at our poor little Earth, or even at our tiny solar system? Here in this room the corridors all point at the lecturer, because he is a very important person. If there were no lecturer, I suppose you would all go away, wouldn't you? No lecturer, no audience! But we cannot think that our Earth, or our Sun, is of any particular importance to the audience of the stars—millions and thousands of millions of them, mostly far bigger and brighter than our Sun. In times gone by our ancestors thought that the Earth dominated the Universe; but we have gradually learnt modesty: nowadays we cannot think that the Earth and Sun are of any particular importance.
No! we must seek some other explanation of the blank patches; and it is not very difficult to find one. I can easily make a patch with no children visible by holding a screen in front of my eye. If the screen is near enough, quite a small one will do. A threepenny bit shuts out quite a lot of you. And similarly some kind of a screen, of dark nebulous matter, say, will easily explain any of these dark patches.
Hence we come to the conclusion that not only are there stars of the last degree of faintness, but there are in the heavens bodies of some kind not shining at all—"dogs in the manger," which not only do not shine themselves, but stop the light of other stars from reaching us. I don't know whether the argument seems to you convincing, but perhaps one or two other pictures may help it. Fig. 83 is a picture of a strip of nebula which seems curiously split down the middle. Here, again, we must remember that the nebula is not a flat object like a piece of paper, but a bulky object like a cushion. If here is a split, it must be a slice right through the cushion, and, besides this, the slice must be straight in the direction of the Earth. Both these difficult suppositions are unnecessary if we suppose there is a dark streak in front of the nebula; we may go further and presume that the streak is part of a flat ring surrounding the nebula, stopping the light where it passes in front. Fig. 84 is a picture of a nebula of a different kind. You see a gauzy mass running down the picture with a bright edge: and you will see that the stars are much more numerous on one side of the edge than on the other. It may be that they really are more numerous; but, if so, there must be a dividing wall pointed straight at the Earth, separating the region of many stars from that of few. It is much easier to believe that there is some obscuring stuff between us and the side which shows fewer stars; so that the light of many of the faint stars is blotted out. If we count the number of stars within a given area on one side of the edge, and also the number in an equal area on the other side, we shall get a notion how many are lost by the stoppage of light.This suggests that it may be of interest to count the stars generally; and it is not only a matter of interest but of great importance. Let me take an instance from this room. You know how the front row is a little bit shorter than the next row and won't seat so many people; the row behind will seat a few more, and so on till we get to the back row, which will seat a good many. If we knew the distance between the rows we could count how many people there ought to be in each succeeding row. And it is very much the same in the case of the stars. If we count the bright stars, we know how many there ought to be of the next order of magnitude; and how many there should be next after that. Suppose we count them, and there are not so many—suppose we counted the outside row and found there were not so many people as it would hold, we would say, "Why this audience is beginning to thin off at the back!" So with the stars, we are inclined to think from the counts we make that they begin to thin off in the distance; and perhaps if we go far enough we should not find any more stars. Look, for instance, at this table[1] of the numbers of stars of successive magnitudes. Up to and including the second magnitude (let us say, the front two rows), there are 38 stars, and we can calculate (though I will not bother you with the details) that when we add the third row, or magnitude, we ought to have 151, very nearly four times as many; but we only find in. Adding the next row, or magnitude, if 38 is right, we ought to get 603, but only find 300, and so on.
| Magnitude. | Observed | Calculated from, 38. | Calculated from 32,360. |
| 2.0 | 38 | (38) | 8 |
| 3.0 | 111 | 151 | 32 |
| 4.0 | 300 | 603 | 129 |
| 5.0 | 95 | 2,399 | 513 |
| 6.0 | 3,150 | 9,550 | 2,042 |
| 7.0 | 9,810 | 38,020 | 8,128 |
| 8.0 | 32,360 | 151,400 | (32,300) |
| 9.0 | 97,400 | — | 128,800 |
| 10.0 | 271,800 | — | 512,900 |
| 11.0 | 698,000 | — | 2,042,000 |
| 12.0 | 1,659,000 | — | 8,128,000 |
| 13.0 | 3,682,000 | — | 32,360,000 |
| 14.0 | 7,646,000 | — | 128,800,000 |
| 15.0 | 15,470,000 | — | 512,900,000 |
| 16.0 | 29,510,000 | — | 2,042,00,000 |
| 17.0 | 54,900,000 | — | 8,128,000,000 |
By the time we get to the eighth magnitude the numbers are so far behind the calculations that it seems useless to go further. But we can make a fresh start; let us assume that there is something peculiar about the first few rows—perhaps they are too closely packed, and let us start fair again with the eighth magnitude and the number 32,360 as shown in the last column. We can calculate both downwards and upwards, and we see that for the bright stars the calculations give fewer than there are, and for the faint stars many more.
We see then that the back rows are not properly full; and we get the idea that probably the stars do not go on for ever; they may not actually come to a sudden stop, as this audience does, owing to the walls of the room; because we cannot think there can be containing walls for the stars; but they seem to thin out and ultimately fail, as a small audience might in a very big hall—front rows full, middle rows rather scattered, back rows quite empty. It does not need a great stretch of our imagination to think of a cluster of stars of this kind, for we have many instances in the sky; Fig. 85 is a picture of one for you to look at. Looking at them from outside we can very easily see the way in which they thin out. When we ourselves are inside such a cluster, it is not so easy; but by careful counting of the different classes of stars, and reasoning upon the counts, we may be able to do it still.But we must be careful, and there is especially one mistake of which we must be careful; a possibility of mistake at which I have already hinted. There may be grown-ups in the back rows and small people in front: in other words, there may be very bright stars at a distance, and faint ones near to us; and if we do not remember this, our inferences from the counts will be wrong.
Let me give you an illustration. Fig. 86 is a picture of three men. You say unhesitatingly that the big man is near us, the tiny man far away, and the middle man in between. You say this because men are all nearly of the same height, and when they appear so very different in size as in the picture, the difference must be due to distance. So we think. But now I have deceived you in this picture by omitting certain details; these are not men, but puppets hung on a Christmas tree, as you see in Fig. 87. They are really all at the same distance; and their difference in size is real, because dolls and puppets can be as different in size as we like. What led us wrong was the quiet assumption that the figures were those of men all much the same in size. We must be careful not to assume that about the stars. They may vary as much as dolls or puppets in actual size; indeed we have found by experience that they do, and here is one of the pieces of experience. Sir David Gill, now, I grieve to say, lying very ill with pneumonia,[2] picked out a number of stars of about the same brightness and actually measured their distance away by the method of "squint," or parallax, which we dealt with in the second lecture. He found the distances very different indeed; so that the actual sizes of the stars must be also very different.
| Name of Star. | Brightness compared with an exactly first magnitude star. |
Parallax or "Squint." |
Distance in "Light Years." |
Diameter of star compared with α2 Centauri. | |
| Sirius | 13½ | 0.37 | 9 | 6 | |
| Canopus | 6½ | 0.00 | ? | > | 140 |
| Rigel | 2½ | 0.00 | ? | > | 75 |
| α2 Centauri | 2½ | 0.75 | 4 | 1 | |
| α Eridani | 1½ | 0.04 | 80 | 18 | |
| β Centauri | 1½ | 0.03 | 100 | 20 | |
| α Crucis | 1½ | 0.05 | 64 | 11 | |
| Spica | 1½ | 0.00 | ? | > | 55 |
In the first column is the name of the star: Sirius, or the Dog Star, I expect you have heard of, even if you don't know the others. In the next column you see that Sirius is not exactly a first magnitude star, it sends us actually thirteen times as much light as the standard which has been adopted as first magnitude, and others in the table are brighter than first magnitude. In the next column you see the amount of parallax or "squint"; but I expect you prefer to look at the column after that which shows that Sirius is nine "light years" away, meaning that light, travelling as we know at 186,000 miles per second, actually takes nine years to come to us from Sirius! Can you now tell how many miles away Sirius is? Remember that there are 30 million seconds in a year, and you will find that Sirius is more than 40 billion miles away using billion in our English way for a million million. (In France a billion means much less: they use it to mean only a thousand million.)
Now this is far enough in all conscience; but what are we to say of Canopus and Rigel and Spica? They are so far away that Sir David Gill could not find any "squint" or parallax at all, and had to write zero in the third column. If the "squint" had been as large as that for β Centauri, or even half as large, he could have measured it. These stars must be at least twice as far off as β Centauri, which is 100 "light years," or, say, 440 billion miles from us.
In the last column of the table I have calculated the actual sizes of the stars compared with α2 Centauri, assuming that their surfaces are all just as bright as that of α2 Centauri; which again is not a justifiable assumption, but we may venture to make it for the sake of illustration, and in order to bring out the next point. You will see that some are very big and some very small; they vary in size at least as much as dolls, I think. I never saw a doll more than four or five feet high say fifty inches; and I never saw one less than about half-an-inch; so that the biggest would be about 100 times the smallest. We may fairly say that Canopus must be at least 100 times the size of α2 Centauri.
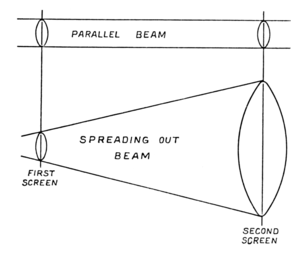
Before we go further, let us think for a moment how astonishing it is that light should reach us from those vast distances at all. If the stars sent out light in only one direction as a searchlight does, we could understand it better; the rays of a searchlight are nearly parallel and in consequence they can go a long distance without failing in brightness. Let us make the lantern send us a parallel beam of light like that of a searchlight: you can see that it does not alter much in cross-section from the lens right away to the wall; and if the rays were strictly parallel, it could go across a million or a billion miles without being diminished in brightness. But the light of a star does not behave like this: it spreads out in all directions continually, like the light from this other beam (see Fig. 88), getting, therefore, all the time fainter. On leaving the lantern it spreads out continually as wide as we like, if only we go far enough. That is how the light of a star behaves, and accordingly it gets fainter and fainter the farther it goes. You can see this very easily: we let both the beams fall on the same screen, and when we put the screen near the two lanterns we can make the two patches of about equal brightness. Now. they are about of equal brightness. But now if we move the screen away, the patch from the parallel beam remains about the same, while the other gets fainter and fainter. Let us stop here a moment; and now we will put a dark glass in front of the parallel beam lantern, so that its patch is made as faint as the other once more. Again move the screen further off, and the spreading beam again gets fainter. If we bring the screen back towards the lanterns, the spreading beam recovers its brightness, and finally it ends by being brighter than the other. So in spreading out in that way the light of a star is always losing itself; and it is wonderful that it should get to us across those vast distances without being so faint that we cannot really see it at all. The light even of some of the brightest stars must travel hundreds of years before we can see it. And we have seen that there may be other things which might diminish its light on the way, dark nebulae which may screen or stop its light. So that it seems wonderful that we should see stars at all. Nevertheless, we do; we get light from even faint stars across long distances; and that shows there cannot be very much in the way between us and them. There may be a little very fine "fog," as we might call it; according to our best information to-day there probably is a little very fine "fog" between us and the most distant stars; but there cannot be much; otherwise we should not get light and even some heat from the stars. The heat that we get is far harder to detect than the light: it has taxed the utmost resources of physicists at the present day to measure it. Apparatus so delicate that it could detect the warmth of a young lady's cheek some miles away, failed to record any heat from the stars.Perhaps you think the heat may get used up on the way because it has to pass through such frightfully cold space. There is no doubt that if we actually took our "Voyage in Space" instead of only pretending, we should be chilled to the marrow very soon indeed. It is terribly cold in space—far colder than we can possibly imagine. You remember the liquid air? Well, cold as that is, it is hot compared with the cold of space. And yet the heat does not get lost in passing through this cold any more than light in passing through simple darkness. If there is anything to stop the light—anything material, such as a dark nebula, however flimsy that is another story; then light would be lost. But if there is nothing of that kind in the way the light can go on for hundreds and thousands of years, and so also can heat. Let me show you rather a pretty experiment. Here is a flask of liquid air—very cold, as you know already. We can pass a beam of light and heat from the lantern through it so that the liquid air will not only transmit the heat, but will focus it like a "burning glass," so that we can set a piece of paper alight. There, you see, the paper is on fire! That is because the liquid air, cold as it is, and the flask containing it, are transparent to heat; and similarly space, cold as it is, is transparent to heat, so that we get the heat of the stars across these immense distances, and though the early experiments to detect it failed, others were more successful. The heat of some stars has been definitely measured.
Now let us turn to quite a different thing concerning the stars; to an announcement made two centuries ago by Halley, that great Englishman who first told us a comet would come back, and was so proud that an Englishman should have been the first to predict it. He also made an even greater announcement, namely, that the stars were moving. From the beginnings of intelligence in man up till then it had been believed that the stars were fixed; they were called "fixed stars," and the name still survives. Yet Halley pointed out that when old observations were compared with those made in his day, one could not but conclude that some stars had actually moved. He chose especially Sirius, Aldebaran and Arcturus, which had moved since the time of Ptolemy more than the Moon's diameter in one direction, while Betelgeuse, the brightest star in Orion, had moved nearly twice that distance in the opposite direction.
"What shall we say, then?" he wrote. "It is scarce credible that the Antients could be deceived in so plain a matter, three observers confirming each other. Again, these stars being the most conspicuous in Heaven, are in all probability the nearest to the Earth, and if they have any particular motion of their own it is most likely to be perceived in them."
He seems almost apologetic: for he knew how slow people are to accept a new idea, however plain the evidence may be. After so many centuries of believing the stars to be fixed, it was very hard to unhitch the ideas. "Again, these stars being the most conspicuous in Heaven, are in all probability nearest to the Earth." We have already seen that this is not quite true, but it is nearly true, and the failure from truth is only a detail. The great thing was to realize this wonderful fact for the first time—that the "fixed stars" were moving: and I think Halley might have been even more proud than in the case of his comet that the discovery was made by an Englishman.
It might have been a Rooshian,
Or a French, or Turk, or Prooshian.
Mr. W. S. Gilbert has chaffed us about our pride in being Englishmen; but there are some things in which we may justly feel a national pride, and surely one of them is that an Englishman (and I am glad to add an Oxford man, writing from Oxford) first set the "fixed" stars in motion. A great many important consequences have followed from this discovery of Halley's. In the first place we find that the movements of the stars afford us a much better test than their brightness for judging whether they are near us or far away. If they are very far away their movements will appear very slow: it is because even the nearest star is so far away that no one noticed any movement in them until Halley discovered it. They are really moving very quickly, but owing to the distance they seem to creep ever so slowly. Do you know Tennyson's beautiful verses about the Eagle?—
He clasps the crag with crooked hands,
Close to the Sun in lonely lands,
Ringed with the azure world, he stands.
The wrinkled sea beneath him crawls,
He watches from his mountain walls,
And like a thunderbolt he falls.
In the fourth line Tennyson uses both the effects of distance which we have been considering: it reduces the apparent size of objects so that big sea waves look like mere "wrinkles" and it reduces the apparent movement until the rolling of the billows looks like mere "crawling." So the huge globes of the stars dwindle at their vast distances into mere specks of light; and their terribly rapid movements—perhaps a hundred miles a second—look like mere "crawling," so slow that it wanted the eagle-eye of a Halley to detect them.
Astronomers have followed up the clue thus found; by watching the stars very carefully for a century and more they have measured the rates at which a good many of them are "crawling." Some seem to go very slowly indeed; others more quickly; and Sir David Gill has found that those which seem to move quickly are, generally speaking, near to us. Here is a table of his results—
| Star's Name. | Brightness compared with a first magnitude star. |
Annual Motion. |
Parallax or "Squint." |
Distance in "Light Years." |
Diameter of star compared with α2 Centauri. |
| " | " | ||||
| ZC.Vh243 | 1/1000 | 8.7 | 0.31 | 11 | 1/17 |
| Lacaille 9352 | 1/250 | 7.0 | 0.28 | 12 | 1/8 |
| ε Indi | 1/33 | 4.7 | 0.27 | 12 | 1/3 |
| ο2 Eridani | 1/25 | 4.1 | 0.17 | 19 | 2/3 |
| e Eridani | 1/21 | 3.1 | 0.15 | 22 | 1 |
| β Hydri | 1/6 | 2.2 | 0.13 | 25 | 2 |
| ζ Tucanae | 1/21 | 2.0 | 0.14 | 24 | 1 |
| τ Ceti | 1/11 | 2.0 | 0.31 | 11 | 2 |
| Lacaille 2957 | 1/100 | 1.7 | 0.06 | 55 | 1 |
The names in the first column need not concern you further than to notice that they are mostly of a weird kind; clearly these are not familiar stars, but small fry; and the brightness in the second column shows this even more clearly. They are stars which are chiefly of interest to astronomers because of their rapid movements shown in the third column: and you see that they all have measurable "squint" and are within 100 light years of us. The last column shows that they are probably much smaller than the former stars.
The table therefore shows that if a star seems to be moving quickly it is probably nearer us than other stars: if very slowly it is probably far away. But again we must not be too sure in either case, because appearances are often deceptive. Have you ever noticed a train coming nearly straight at you from a long way off? When you are waiting at a station sometimes the lines curl round a corner, so that you do not see the train till it is pretty close; but sometimes they run straight for a long distance and then you can see your train coming from a long way off. It looks no bigger than a toy train, and moreover it seems to be quite still. You know that it is coming towards the station (at least you hope so if it is the train you want to join), but you cannot see it move because it is coming at you end-on. It might even be going the opposite way for all you can tell by looking at it. Similarly, if a star seems to us to remain nearly still, we must not be too hasty in thinking that it has very little movement of any kind, and therefore it is very far away, for it may be coming directly at us, or going directly away from us; by merely watching it we cannot tell. Fortunately, a beautiful method has been discovered by which we can determine whether this is so—whether the star is coming towards us, and how fast it is approaching. Halley showed us how to watch the stars moving across our line of sight, and another great Englishman, Sir William Huggins, showed us how to find out with the spectroscope whether they are coming end-on to us, or moving away from us: and I want now to say something of how he did it.
Let us return to the train for a moment and suppose it whistles as it approaches the station. It will whistle a high note; let us say high D on the piano. Now if the train is coming at us the note will not sound like D, but like a note higher in the scale, say D sharp; if on the contrary it is running away from us, the whistle will sound lower in the scale, say D flat. Sometimes a train rushes right through a station whistling all the time, and then you can notice the change from D sharp to D flat quite easily. Many people have thought that the train changed its whistle as it went through, but that is not the case, it keeps on whistling the same note all the time; but while it is still approaching you hear a higher note; immediately it has passed you and begins to run away you hear the lower note.
You can hear much the same kind of thing with a passing motor-car if it happens to sound its horn. Or without the horn at all, if you listen to the hum of the machinery you will hear it change its note as it passes. If the motor-car is going slow, the change will not be much; but if it is going very fast, the change will be great. It would be quite If this does not seem clear, never mind: you will perhaps find a better explanation some day. But now I want you to think of light instead of sound, because the stars do not whistle to us, but they do send us light. You remember that we were to compare light and sound several times in this lecture? And I want you to realize that just as there are scales in sound, which you have to practise on the piano, so there are scales in light—nothing more nor less than those beautiful colours which a prism makes for us. We will throw one of those rainbow-coloured strips on the screen; and to fix the likeness of colours to scales in your minds I will put this harmonium underneath the strip and play a scale. The low notes in the bass correspond to the red colour, and as we go up the scale we pass through orange, yellow, etc. all the colours of the rainbow up to violet. You might sing the names to a scale so as to remember this fact.

Perhaps you don't know that last colour; it is mainly put in to fill up the scale, which would otherwise stop awkwardly short; it does not mean ultra-marine, but ultra-violet. I don't mean that the colours correspond to these notes in detail, but that in passing from red to violet the pitch rises.
If a star is whistling a green note, that is to say sending us green light, then if it is also coming directly at us the green note will rise in the scale towards the blue; if the star is running away the green note will fall in the scale towards the yellow. How much it rises or falls depends on the rate of movement, and I may say at once that the rise or fall is very slight indeed, because however quick the movement of the star may seem to us, it is very, very slow compared with the enormous velocity of light. But the rise or fall is noticeable and measurable; by noticing it and measuring it astronomers have found out which stars are coming at us and which are running away, and how fast they are coming or going.
Some of the best illustrations of this way of measuring velocities, whether by sound or by light, are afforded by bodies which are whirling or turning round, because sometimes they approach, sometimes they recede. Here is an instrument called a "bull-roarer" which some of you may have made for yourselves a shaped piece of wood with a string tied to it. If I whirl it round it makes a humming noise. Now I can whirl it round so that it remains always at the same distance from you, and then the hum is steady; but if I turn end-on to you, sometimes it approaches and sometimes it recedes, and you can hear the note change up and down.
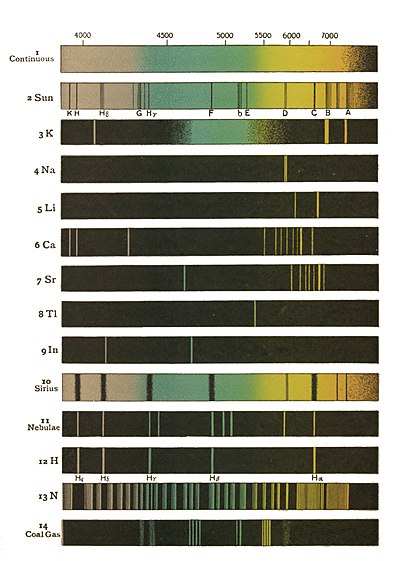
Similarly, if one star is whirling round another, it may do so in such a way as to remain nearly at the same distance from us, when its light remains of uniform colour; but the orbit may also be end-on to us, when we see the colours go up and down. I am using the word colour in a special sense: when we spread out the light of a star into colours by a spectroscope, we see the band crossed by a number of dark lines which mean special colours: and it is these lines which are displaced towards the violet or towards the red (see Plate facing p. 273). And now we will look at a very beautiful instance of this displacement in the case of the planet Saturn and its ring.
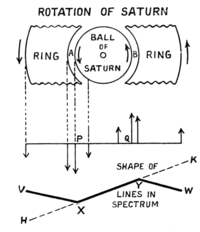
Let us first consider the planet himself or the "ball," as it is usually called to distinguish it from the "ring." Suppose we have cut a slice right through the centre O; the slice will be turning round O (Fig. 89). The left side A is coming at us and the right side B is running away; so that if we pass the light of this slice through a spectroscope, one end of the colour-line will be displaced one way and the other the other, in consequence of which we get a sloped line XY instead of a horizontal one PQ. Next, if the ring were solid and attached to the ball, the same state of things would continue in the ring; the line XY would be merely extended to HK. But the ring is not solid, as we have seen: it is made up of little satellites, the outer ones moving, not faster than the inner ones, as they would if the ring were solid, but slower than the inner ones. Hence the ends of the line, instead of being more displaced, are less displaced, and we get an elongated Z shape VXYW. This was predicted from knowledge of the movements, and when the spectroscope was actually turned on to Saturn the prediction was beautifully verified! So that we may feel all confidence in the power of the spectroscope to tell us about these movements of approach and recession.We have, then, two different ways of measuring the movements of the stars; it is a piece of great good luck for us that we have two, for we can often test what one method has told us by using the other. And now I want to tell you some of the things we have found out by watching the movements of the stars in these two ways.
First of all let us pay a few visits to the double stars—cases where two stars are seen close together, and where careful watching has shown that they are revolving round each other. Sometimes one is so much the larger that we may almost say that the smaller is revolving round it, like our Earth round the Sun; but there are other cases when the stars are so nearly equal in size that we cannot give one the preference in this way; and in all cases it is more correct to regard both stars as revolving round some point in between them than to regard one as fixed and the other as revolving round it.
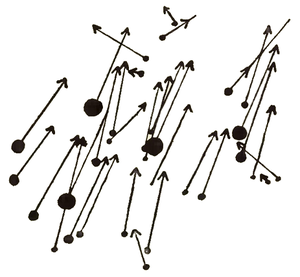
These double stars are often beautifully coloured; one of them being of a different colour from the other. But our chief concern to-day is not with the colours, but with the movements of the two partners. They are waltzing round one another just like a pair of dancers in a ballroom: the idea of waltzing will help us very much, because the dancers not only turn round one another but move down the room at the same time. At the corners of the room they have to turn, and it is possible that our waltzing double stars may have to turn at some corner or other in the future: at present we cannot say because we have not been watching them waltz long enough; we have only had about a century to watch them since they were discovered, and even a century is but a short time in the life of a double star. Some of them take as long as that to make a single waltz-turn, and others take much longer—so much longer that in the century since they have been watched they have scarcely turned at all. You may ask how we know that they are partners in that case. Well, sometimes you see a pair of partners in a ballroom not waltzing round at all, but going down the room without turning. We know that they are partners because they keep together as they move down the room; and so it is with these double stars which do not seem to be turning they are nevertheless moving together among the other stars hand-in-hand so to speak; so that we may safely regard them as partners. Thus a ballroom helps us in several ways to think of the movements of the stars, but now I come to a point where it ceases to help us. Partners in a ballroom are always in pairs; I have seen three people waltzing together for fun, but you would not see it often; and I doubt whether you would ever see four or five together, let alone twenty or thirty. But with the stars it is different. The general rule is for a pair of stars to waltz together, but we often have three or four, and lately we have been finding groups of thirty or forty together, or even more. We detect the partnership because they move together in the ballroom: when there are only three or four, we can sometimes see them also turning round one another, but the movements are apt to be complicated when there are more than two, because it is difficult to know which of the several partners you are to pay attention to at any one time. All the partners in the group are pulling at one another, and though we know the exact law of the pulls (which is simply that great Law of Gravitation which Newton found out for us), it is quite impossible for mathematicians, with all their present skill, to trace out the consequences of the law. Perhaps they may have better success in the future, but meantime we need not trouble so much about the treatment of one partner or another because what I want you to notice chiefly is that the whole group moves together. Look (Fig. 90) at the picture of the group called the Pleiades, in which arrows are drawn to represent the movements of the separate stars in a given time: you will see that many of these arrows are about in the same direction and about of the same length. The stars are shown as round black dots (as they would be on a photographic negative) in their present positions, and the arrow-heads show where they will get to after thousands of years.
Since the arrows are not quite equal in length, and quite the same in direction, the arrow-heads form a figure rather different from the arrow-tails: that is to say, after this lapse of time the partners will have taken up rather different positions. They have felt the pulls of gravitation and responded to them—at any rate this is a reasonable explanation. They are waltzing to a certain extent, but not enough to prevent them all keeping together and moving down the room as a group of partners.
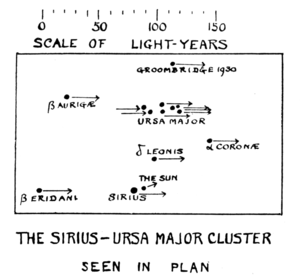
This noticeable fact about the Pleiades is not very new. The late Mr. R. A. Proctor called attention to it forty or fifty years ago. But another group of stars in the constellation of the Bull was only noticed quite lately, by Mr. Lewis Boss, a great American astronomer. The movements of these stars are so slow—such a snail's "crawl"—that it required very great care and skill to measure them. The main point about the arrows in Fig. 91 (which again represent the movements in a given time about 50,000 years) is that they are not parallel to each other, but would meet in a point if carried far enough. It looks as though the stars would collide with one another at some time in the future, but that need not be the case. If you stand on the railway, where the lines run straight they will seem to meet in the distance, whereas we know that they always remain the same distance apart. The apparent meeting is an effect of "perspective." Some of you have no doubt learnt perspective drawing and you know that parallel lines have to be drawn to meet in a "vanishing point." So Mr. Boss's group of stars may be moving along parallel lines, without closing up: and indeed we can find out that this is the fact, by using the second method of watching their movements which we noticed, with the spectroscope. The "vanishing point" represents the direction in the far distance to which they are migrating, like a flock of birds such as we see in Fig. 92.There is one more group which I should like you to know of, part of which was also identified long ago by Mr, Proctor. He pointed out that if we omit the first and last stars in the Great Bear or Dipper, the five remaining in the middle form a group flying along together. But it has recently been discovered that several other stars belong to this group, notably Sirius the Dog-star. Now I hope you know where to look for Sirius away in the south. We in Europe never see him very far
away from the south: and, as you know, the Great Bear is in the north. Does it not seem strange that Sirius in the south should belong to the same group of stars as the five Great Bear stars in the north? The group is like a flock of birds flying just over our heads, some of which have passed us while others have not yet come up. There seems to be no doubt about the association of these stars, for their movements have been tested in both the ways we described; and besides that, the distances of some of them (especially Sirius) have been measured; and all the facts fit in well together, so that we can actually make a model of this system of stars. Miss Bellamy has kindly made one for us by sticking hatpins into this cork mat: and please notice how very flat it is. The pinheads are nearly all at the same height from the mat—not quite the same, but nearly enough to be
noteworthy. We may almost compare this group of stars to a fleet of ships sailing on the flat ocean: but the fleet is of a stupendous size—its length is about 150 light years; that is to say that if the admiral on the leading ship signalled to his fleet, it would be 150 years before the last ship would even see the signal! How long it would take us to go round and pay a visit to each ship in turn you can perhaps imagine for yourselves.
We have now noticed three groups of stars and found that, though they may be altering their places a little in the group, each group is nevertheless steadily moving in a particular direction—making a sort of migration. Whence did they come and whither are they going? Will they go on for ever or will they come back after a time as migrating birds do? These are questions which suggest themselves at once, though they are not so easily answered. I think, however, that an answer can be given: an answer which suggests itself if we go back to that notion of our belonging to a large cluster of stars to which we were led earlier in the lecture. You remember that our "audience" of stars, as we called it, thins off in the back rows, giving us the notion that we form part of a definite cluster such as we see in the picture (Fig. 85). Now let us think out the consequences of this arrangement, remembering that by the great Law of Gravitation each star is pulling every other star. We have already said that even with three or four stars it is so difficult to tell what will happen in detail that the best mathematicians have not yet been able to work it out: so you may think that with millions and millions of stars it would be quite hopeless. But curiously enough it makes the problem in some ways simpler to have a very large number, and I do not think we shall find it very hard to think out some of the consequences. For instance, it is easy to see that a star right in the middle of the bunch will be pulled in all directions at once—to right as well as to left, up as much—as down so that it will not know which way to move; and if it had already no movement it would not acquire any. But it would be very different for a star on the boundary: all the pulls would be on one side, namely, more or less towards the centre of the bunch. Some stars would pull it rather to one side of the centre, others rather to the other side: but there would be no stars at all to pull it away from the centre, "and hence it would know very definitely in which direction to move, namely towards the centre. Let us go with it in its journey and see what happens. After a little time it would be no longer quite on the boundary, but would have penetrated a little way into the bunch. There would now be a few stars pulling it away from the centre, but only very few compared with those urging it on; it would still be urged centrewards and would quicken its pace: and without troubling about the details you will see that this sort of thing would go on until the star arrived at the centre, when there would be no force on it either way, as we said before. But that does not mean that it would stop, for it has got "way on." Let us look for a moment at this pendulum. When I let it hang vertically it is like a star at rest in the middle of the bunch; there is nothing to make it move. But if I pull it to one side it is like our star on the outside of the bunch—it is being pulled towards the centre, and if I let it go it swings thither. But on arriving at the centre it does not stop, because, although there is no force moving it forwards, it has got "way on" and so passes through. Directly it has passed through, the force begins to call it back, but it cannot stop it all at once—the pendulum swings out to the other side before returning. So with our star which we started from the outside of the bunch or cluster: it will arrive at the centre, pass through it, and swing out to the other side. Then it would come back again as the pendulum does; and that is what I think the stars are doing in our great cluster, some of them moving alone, some in pairs (the double stars) and others in groups; but all swinging to and fro through the centre of the whole bunch.
But now how is it that they keep clear of one another? If I take, instead of a single pendulum as before, a whole lot of pendulums all swinging through the same centre, they will be liable to strike one another. Let us try the experiment. Here we have several billiard balls hung by long strings to the theatre roof, and we will see how much they hit. Indeed, we will try to make them hit. If several of my young friends will each hold one ball in different directions, and then all let go at exactly the same moment I think we shall get a good crash at the centre when they meet: but if they do not let go at exactly the same moment, then they will miss.[3] Now are you all ready to let go when I say "three"? Don't fling the balls at all, just open your fingers and let them drop. One, two, three!
Some of them hit, you see, but one or two missed: and now you see that after a few turns they seem to avoid one another very cleverly partly because some of them have been knocked a little sideways and do not pass accurately through the centre, and partly because some arrive there at one time and some at another: so that though they are all still oscillating through the centre in a general kind of way, collisions are comparatively rare.
I think the stars in our cluster are moving somewhat in this way—oscillating to and fro through the centre—and I have tried to represent the movements very crudely by means of the kinematograph.
[Exhibition here of the results with kinemato-graph. The opportunity was taken to show also some features of a total solar eclipse; such as fowls going in to roost during the darkness and coming out afterwards.]
I think there are occasional collisions, which perhaps make what we call "new stars": and in times gone by these collisions may have been more serious and more frequent. But I do not want to trouble you about the collisions so much as the general movements to and fro. That very phrase "to and fro" reminds us of one most important feature of the movements, namely that they are sometimes "to" the centre and sometimes "fro" or from it. At any given moment, therefore, we can divide the stars into two lots, one lot going to the centre and the other lot coming from it. Let us think of the first lot alone. If we watch their movements and represent them by arrows, then all these arrows will point to the centre: they will converge towards a point just like the arrows in the picture of Mr. Boss's cluster (Fig. 91). Now, in the case of this cluster, we said that the stars were not really moving towards a point, but in parallel lines: we knew that because we had the second method of watching the velocities to help the first. But if we had not had that second method to help us, we could not really have told whether the movement was in parallel lines or to a point: the perspective appearance would be just the same. And we might easily make a mistake in concluding, when we see arrows representing star movements directed to a point, that the movements are really parallel. They may really be to a point. Lots of boys christened Henry are called Harry "for short," but you might easily make a mistake if you concluded that every Harry had been really christened Henry, for some of them are christened Harry direct. And I think that astronomers are liable to make just this very mistake about the star movements. They see one lot going to the centre of the system and another lot coming away: and they have argued that since the first lot seem to be converging to a point their movements are really parallel. They might be parallel just as Harry's real name might be Henry; but they also may be actually moving towards a point as they seem to be, just as Harry's name may be really Harry outright. And when there is a very good reason why they should be moving to a point, because all the stars belonging to the system are all being pulled towards the centre, as we know, then it seems better to take that as the explanation rather than go out of our way to treat the movements as parallel. The same may be said of the outgoing stream: their arrows seem to diverge from a point, and they might be merely a perspective appearance of movements that were really parallel; but it might also be true that the stars are moving outwards from the centre (like the pendulum that passes through the centre because it has got way on), and when there is a good reason for the latter alternative it seems sensible to adopt it.
In mentioning this great fact, that we can divide the stars into two lots, one going one way and one going the other, I have omitted several very important things so as to keep the argument simple. One important thing is who first found it out. It was first announced by Professor Kapteyn of Groningen in 1904, not yet ten years ago: and it reflects the very greatest credit upon him that he made the discovery. Many other people have confirmed it since, and the evidence is so clear that now it seems wonderful that it should have been overlooked so long. That is often the case in science: once the way is shown, it is easy enough to follow it; but it may require a genius to show the way in the first instance. Have you ever hunted for seabirds' eggs on the shore? They are so nearly the colour of the stones that it takes a very sharp eye to find them, though when once they are pointed out they are easily seen.
Another thing is that the arrows of the star movements do not converge accurately to a point: indeed many of them are wildly wrong. That is what made the great discovery so difficult. It is only by taking careful averages of hundreds of stars that the general tendencies were discovered. This means that, although there is on the whole a tendency to the centre of our cluster, many of the stars have had knocks which carry them to one side or the other, just as our billiard balls had after the first few swings. There is no difficulty in this, however; indeed, it removes a difficulty that might have otherwise existed, for it shows how too-frequent collisions are avoided by the stars passing to one side or other of the centre. Some of them, indeed, may never go near the centre at all; they may whirl round and round it just as I can make this pendulum-bob whirl round and round instead of oscillating to and fro. To make it describe a circle I need only give it enough sideways motion, and now you see it never goes near the centre. But if all the stars moved like this, there would be none near the centre, except some almost stationary, as the pendulum is now. There must be a certain number, at any rate, which swing backwards and forwards through the centre, and though these are mixed with others which swing wide, there is still enough oscillation to enable Professor Kapteyn to make his great discovery. I must not, however, mislead you into thinking that he agrees with my interpretation of it, for he does not. He prefers to regard the movements as parallel.
There is another point to be noticed about the stars which circle round the centre of the cluster instead of passing to and fro through it or near it. They remain at a distance from the centre, possibly at a great distance; if so they may form a separate ring round the central cluster. This might explain the Milky Way, that beautiful soft track of light which you can see crossing the sky when there is not too much moonlight. It makes a complete ring round us, though we cannot realize that without going into the southern hemisphere as well as the northern: and when we look at it through a powerful telescope, or take photographs of it, we find that it is dotted over with thousands and thousands of stars. Perhaps it is a ring of the stars which always keep far away from the centre, but as yet we cannot tell, because we have not sufficient knowledge of the movements of these stars. To measure the movement of a star we must record its position carefully at some selected time, then wait a number of years and note how far it has changed. If the star is far away, the change will be very slow and we must wait proportionately longer in order to detect it. For the stars near us a few years may suffice: there are one or two stars moving so rapidly that we can see their change of position in a week—almost in a day; but such cases are quite exceptional, and we may go much further and say that it is quite exceptional to find a star which has moved appreciably even after ten years. We have spent a great deal of time at Oxford lately in looking for such changes, by comparing photographs of the same region in the sky taken at intervals of at least ten years, and out of the hundreds of stars on the plates we only find one or two which have moved appreciably in ten years. Moreover, we find about the same number on a plate whether the region represented be in the Milky Way or far from it. In the former case there may be one thousand stars shown on the plate: in the latter case only one hundred: and yet we are just as likely to find two stars which have moved appreciably in the latter case as in the former. The inference seems to be that the extra 900 stars are all too far away to show the slightest motion in ten years: we must wait fifty or one .hundred years to see them move. If any one had photographed them fifty or one hundred years ago, we might to-day have known something of their movements; but unfortunately astronomers had not learnt how to photograph faint stars at that time; they began only twenty or thirty years ago.
It is time that we said a word as to the position of our own Earth in all this organized movement. Our Earth and all the other planets and satellites must be regarded as being carried along with the Sun. Compared with the distances of the stars our distance from the Sun is really very small, You remember how we said in the last lecture that it takes us only eight minutes to get to the Sun on the wings of light, whereas it takes years to get to the nearest star. Another way to think of it is this: suppose our path round the Sun were represented by a wedding-ring, then on the same scale the nearest star would be some miles away. Hence we can regard all the planets and satellites as a tiny little bunch travelling with the Sun, and we can talk of the Sun alone as travelling, carrying us with him in his pocket so to speak. Now how is our Sun behaving in this matter of migrations? Is he one of the stars that pass to and fro through the centre, or does he remain at a distance from it? The answer seems to be, from the best evidence we can get at the moment, that he travels to and fro, and at the present moment he has just been through or near the centre—only about a million years ago. Perhaps you think that is so long ago that we must by this time have come very far away; but a million years is probably only a small fraction of the time for a whole swing, which may be estimated roughly at about 200 million years. And that brings us back to that little table which we made at the beginning of the lecture; we had to leave it incomplete, but now we can complete it.
30 million light vibrations make one wireless vibration.
30 million wireless vibrations make one second.
30 million seconds make one year.
30 million years make one "migration."
I have now put 30 million years for a migration instead of 200, firstly to make the table simpler by having all the figures the same, and secondly to remind us that when I said 200 millions just now it was little more than a guess. It was the best guess I could make, but it may be wildly wrong; perhaps 30 million will do just as well, and it has the advantage of making our table simple.
We on our Earth, then, are accompanying the Sun in these migrations—we are all making this great Voyage in Space, not metaphorically by telescope, but actually and in reality. We are doing it in a leisurely manner, perhaps you will think, seeing that it takes so many million years to make even one "migration": we cannot, even the youngest of us, hope to see the end of a turn, or even to see the scenery change much: it takes us all our time and attention to detect that we are moving at all. Have you read how Mark Twain once boarded a glacier to travel downhill? He had learnt that a glacier was really a moving river of ice, and solemnly pretended to use it for a journey, and to "be astonished and bitterly disappointed when he learnt that it would take years to go a few yards. I hope you will not form any similar expectations about our journey. We are certainly making it, but as regards change of scenery in our short lives it is slower even than a glacier.
And I have used the word "migration" to denote the time taken by the Sun to swing from one end of its tether to the other. It seems possible that all of the stars in our cluster take about the same time to make their "migrations," just as the billiard balls did when hung by strings of the same ength. It is not at all likely that the "migrations" are accurately in the same time: all I mean is that they may not differ so much as the periods of our planets, for instance, the innermost of which (Mercury) takes only eighty-eight days to go round the Sun, while the outermost (Neptune) takes 160 years. It would take too long to explain the reason for and against the "migrations" being all nearly equal in point of time: perhaps you will allow me to state it without further explanation. And now let me add that this does not mean that the swings are of the same length as regards distance. We can pull a pendulum far out from its position of rest, and then when we let it go it makes a big swing: or we can pull it out only a little way and then its swing will be small; but the time of swing will remain the same. This was Galileo's great discovery about the pendulum. In the same way I fancy there are stars with big swings and stars which take only little swings and so never get far from the centre. On the whole the big bright stars will swing out farthest, and the little faint ones will swing quietly; but all much in the same time.
The question arises whether there is likely to be a collision occasionally between the stars migrating in opposite directions. This would doubtless make a considerable "flare-up," and it is tempting to suppose that the "new stars" which we see suddenly appear in the sky represent a collision of this kind. The chief difficulty is that stars are so small compared with the enormous distances between them that a collision between two must be extremely rare. What seems to me much more likely is that a star may collide with a dark nebula such as we concluded must exist in order to account for the patches empty of stars. To take an illustration from a well-known game, it is extremely unlikely that two golf balls will hit one another in mid-air, though on links like those of St. Andrews they may be struck off in opposite directions. I believe such a collision has happened, but thousands and thousands of balls must have passed more or less near one another without hitting. On the other hand it is pretty easy for a golf ball to hit a furze bush, as all golfers know. Now I think these dark nebulae are like the furze bushes and bunkers on a golf course, which almost seem sometimes to attract the ball out of perversity. Up till a few years ago such an idea would have been mere speculation: but in 1901 we had a splendid "new star" which gave us direct evidence of such an occurrence. Nova Persei, the "new star of the new century," blazed up suddenly, and died down slowly like all "new" stars: but after it had become faint again, a photograph of it showed a nebula surrounding it: and by comparing photographs the nebula was seen to be changing its shape (Fig. 96). At first it was thought that there had been an explosion of some kind and the nebula represented the scattering fragments; but it was presently realized that the rate of scattering was far too great for this explanation; and ultimately the startling truth was realized that we were witnessing some of those light "echoes" to which I referred at the beginning of the lecture. Let us think of actual echoes first. Suppose I repeat Tennyson's lines from the "Charge of the Light Brigade" in an even voice thus—
Came through the jaws of Death,
Back from the mouth of Hell,
All that was left of them.
We might take that to represent the light of a star shining steadily, because I said the words in
September 20, 1901.November 13, 1901.
Fig. 96.—The expansion of the nebulous appearance about Nova Persei.
an even monotonous way. But now let me say them to represent the way a new star blazes up suddenly—
Came through the
Back from the mouth of Hell,
All that was left of them,
Left of six hundred.
You see I began faint and steady, because there seems to be generally a faint steady star which blazes out into a new one: then suddenly I mounted up to the word "Back," which represents the fiercest outblaze, and then gradually down again to faintness.
Now suppose when my voice had become faint again we were to hear the word "Back," "Back," "Back," repeated several times: we should say at once that those were the echoes of my biggest shout from some distant hills or buildings. And that is what probably happened with light echoes in the case of Nova Persei. A fair explanation seems to be that a faint star in its travels came across a dark nebula, one of the "bunkers" of space; and thereupon blazed up. The blaze lit up the previously dark nebula or bunker for us to see; but as light takes time to travel, it was not until some months after the flare-up that we got the light echoes from the nebula. We identify the illumination as an echo much as we could identify the sound echo: the word "Back" was repeated, not "mouth" or "hell," and this is reasonable because "Back" was the loudest word. Similarly the light of the echo, when analysed with the spectroscope, was found to correspond with the light of the greatest flare-up: the chain of evidence is complete. There is just one alternative supposition in detail which I will mention, but cannot dwell upon. It is possible that the big "flare-up" was caused, not by the entry of a wandering star into the nebula, but by the contraction of a part of the nebula under its own gravitation. The rest of the explanation would then follow as before.
But now I have tried your patience quite enough. Our visits to the stars have been rather more arduous than those which have gone before; just as visits to very distant acquaintances are apt to be more tedious than family parties. You have, however, listened very patiently, and I offer you my best thanks and best wishes for a Happy New Year.